滞后校正

串联滞后校正使用条件串联滞后校正是一种常用于系统控制中的校正方法，可以有效地提高系统的稳定性和控制性能。

它是通过将系统的控制信号与系统的输出信号进行比较，并根据比较结果对控制信号进行调整，从而实现对系统的校正。

在实际应用中，串联滞后校正通常需要满足以下几个条件：1.系统可测量：为了进行串联滞后校正，系统的输出信号必须是可测量的。

只有能够测量到系统的输出信号，才能与控制信号进行比较，从而进行校正。

通常情况下，系统的输出信号可以通过传感器、仪器等测量设备来获取。

2.系统动态性：串联滞后校正主要用于调节系统的动态性能，因此被校正的系统必须具备一定的动态特性。

一般来说，系统的动态特性可以通过其阶数、传递函数或差分方程等数学模型来描述。

只有具备一定的动态特性的系统才能够通过串联滞后校正来提高其动态性能。

3.可调参数：串联滞后校正需要根据比较结果对控制信号进行调整，因此被校正的系统必须具备可调参数。

这些可调参数可以通过调节系统中的一些物理或数学参数来实现，比如增益、时间常数等。

只有具备可调参数的系统才能通过串联滞后校正来对其进行调整和优化。

4.可修改控制信号：串联滞后校正需要将系统的控制信号与系统的输出信号进行比较，并根据比较结果对控制信号进行调整。

因此，被校正的系统必须具备可修改控制信号的能力。

对于数字控制系统而言，该要求通常通过软件编程来实现。

而对于模拟控制系统而言，可能需要使用一些电子元器件来实现对控制信号的调节。

5.系统稳定性：串联滞后校正可以提高系统的稳定性，但仅适用于稳定的系统。

如果被校正的系统本身就不稳定，那么串联滞后校正可能会进一步破坏系统的稳定性。

因此，在进行串联滞后校正之前，需要确保被校正的系统是稳定的。

6.输入信号满足要求：在进行串联滞后校正时，输入信号需要满足一定的要求。

一般来说，输入信号需要具备一定的特性（如平稳性、随机性等），以确保校正的有效性和准确性。

根据具体的应用和系统要求，可能需要对输入信号进行预处理，例如滤波、去噪等操作。

超前校正和滞后校正的使用条件超前校正和滞后校正，这听起来像是那些高深莫测的数学概念，其实不然，今天我们就来聊聊这两位“调皮的小朋友”，看看它们在生活中怎么为我们服务的。

超前校正就像那种总是提前到达的朋友，永远想着“我得早点儿准备好”，而滞后校正呢，就像那种总是慢半拍的家伙，总是说“等一下，我再想想”。

这两者在实际应用中，真的是各有千秋，缺一不可。

说到超前校正，想象一下你正在开车，前方的红灯闪烁着，哦，这时候你得赶紧减速，不能等到快到才急急忙忙踩刹车。

超前校正的意思就是让你提前预判，防止意外的发生。

比如，在生产线上，如果你能提前发现产品的缺陷，咱们就可以及时调整，避免大规模的返工，这不就是为后续省下了不少麻烦嘛！在生活中，我们常常需要这种能力，想想考试前的复习，提前准备，才能在考试时游刃有余，不至于手忙脚乱。

咱们得提提滞后校正，它可不是“慢半拍”的代名词，虽然有时候让人觉得有点儿拖拉。

它其实是一种反应机制，更多的是在事后总结经验教训。

比如说，你刚刚做完一个项目，结果发现有些地方做得不够好，这个时候你得坐下来，分析一下问题出在哪儿，然后再来个大改进。

就像在玩游戏的时候，死了再重来，慢慢积累经验，下次就能把关卡打得漂亮多了。

滞后校正让我们在失误中成长，反思之后再出发，确实是种智慧。

现在，咱们再聊聊这两个“小家伙”在实际应用中的使用条件。

超前校正需要的是清晰的信息和准确的数据。

你得知道前方会发生什么，这样才能提前做出反应。

这就像是天气预报一样，知道今天要下雨，那就提前带把伞。

反之，如果你没有准确的数据，盲目预判，那就容易犯错误，搞得自己手忙脚乱。

试想一下，开车的时候，如果前面有个大坑，你不知道，结果“咣当”一声，别提有多尴尬了。

至于滞后校正，它最适合用在那些可以慢慢调整的地方，比如说生产流程、项目管理之类的。

你得留出时间来反思，不然就是在白忙活，像个无头苍蝇，乱撞不知所措。

特别是在团队合作中，每个人都有自己的意见，慢慢来，听听大家的反馈，咱们才能一起进步。

串联超前校正和滞后校正的不同之处在控制系统中，超前校正和滞后校正是两种常见的校正方法。

它们都是为了提高系统的稳定性和性能而采取的措施。

然而，它们的实现方式和效果却有很大的不同。

本文将从理论和实践两个方面，分别探讨串联超前校正和滞后校正的不同之处。

一、理论分析1. 超前校正超前校正是指在控制系统中，通过提前控制信号的相位，使得系统的相位裕度增加，从而提高系统的稳定性和响应速度。

具体来说，超前校正是通过在控制信号中加入一个比例项和一个积分项，来提高系统的相位裕度。

这样，系统就能更快地响应外部干扰和变化，从而提高系统的性能。

2. 滞后校正滞后校正是指在控制系统中，通过延迟控制信号的相位，使得系统的相位裕度减小，从而提高系统的稳定性和抗干扰能力。

具体来说，滞后校正是通过在控制信号中加入一个比例项和一个微分项，来减小系统的相位裕度。

这样，系统就能更好地抵抗外部干扰和变化，从而提高系统的性能。

二、实践应用1. 超前校正超前校正在实践中的应用非常广泛。

例如，在电力系统中，超前校正可以用来提高电力系统的稳定性和响应速度。

在机械控制系统中，超前校正可以用来提高机械系统的精度和响应速度。

在化工生产中，超前校正可以用来提高化工生产的稳定性和生产效率。

2. 滞后校正滞后校正在实践中的应用也非常广泛。

例如，在飞行控制系统中，滞后校正可以用来提高飞行器的稳定性和抗干扰能力。

在汽车控制系统中，滞后校正可以用来提高汽车的稳定性和安全性。

在医疗设备中，滞后校正可以用来提高医疗设备的精度和稳定性。

总之，串联超前校正和滞后校正是两种常见的校正方法，它们都是为了提高系统的稳定性和性能而采取的措施。

然而，它们的实现方式和效果却有很大的不同。

在实践中，我们需要根据具体的应用场景和需求，选择合适的校正方法，以达到最佳的控制效果。

相位超前和滞后在控制系统中的作用如下：
1. 超前校正：目的是改善系统的动态性能，在系统静态性能不受损的前提下，提高系统的动态性能。

通过加入超前校正环节，利用其相位超前特性来增大系统的相位裕度，改变系统的开环频率特性。

一般使校正环节的最大相位超前角出现在系统新的穿越频率点。

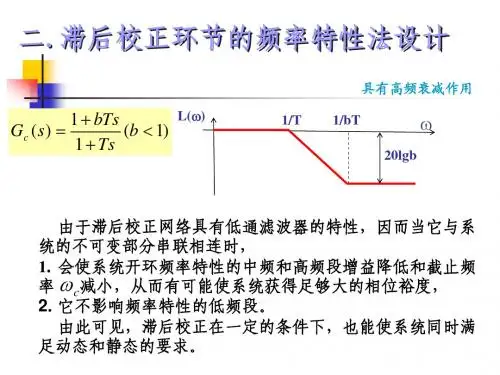
2. 滞后校正：通过加入滞后校正环节，使系统的开环增益有较大幅度增加，同时又使校正后的系统动态指标保持原系统的良好状态。

它利用滞后校正环节的低通滤波特性，在不影响校正后系统低频特性的情况下，使校正后系统中高频段增益降低，从而使其穿越频率前移，达到增加系统相位裕度的目的。

3. 滞后-超前校正：是滞后校正与超前校正的组合。

它具有超前校正的提高系统相对稳定性和响应快速性；同时又具有滞后校正的不影响原有动态性能的前提下，提高系统的开环增益，改善系统的稳定性能。

它具有低频端和高频端频率衰减的特性，故又称带通滤波器。

这种校正方式适用于对校正后系统的动态和静态性能有更多更高要求的场合。

相位超前校正和滞后校正的区别相位超前校正和滞后校正是电路中常用的两种方法，用于调整信号的相位。

它们在电子领域中具有重要的应用，尤其在通信系统和控制系统中起着至关重要的作用。

本文将详细介绍相位超前校正和滞后校正的区别。

一、相位超前校正相位超前校正是一种使信号相位提前的技术。

在电路中，我们常常遇到信号相位滞后或者信号延迟的情况，这是由于电路元件的特性或者传输介质的影响所致。

为了解决这个问题，我们可以采用相位超前校正的方法。

相位超前校正的原理是在信号路径中引入一个或多个滤波器，并通过合理设计滤波器的参数，使得滤波器对频率较低的信号具有较大的增益，从而使得信号的相位提前。

相位超前校正常用于控制系统中，以提高系统的稳定性和响应速度。

例如，在飞机的自动驾驶系统中，采用相位超前校正可以使飞机更加稳定地飞行。

二、滞后校正滞后校正则是一种使信号相位延迟的技术。

在某些情况下，我们需要延迟信号的相位，以满足特定的要求。

比如，在音频处理中，我们可能需要将不同的音频信号进行时间对齐，以达到更好的音效效果。

此时，我们可以采用滞后校正的方法来实现。

滞后校正的原理是通过引入一个或多个滤波器，在信号路径中对频率较高的信号进行衰减，从而使得信号的相位发生延迟。

滞后校正常用于音频处理、图像处理等领域，以实现信号的同步和对齐。

例如，在音频混音中，我们可以采用滞后校正的方法，将不同音轨的信号进行时间对齐，以获得更好的混音效果。

三、相位超前校正与滞后校正的区别相位超前校正和滞后校正的区别主要体现在以下几个方面：1. 目的不同：相位超前校正的目的是使信号的相位提前，以提高系统的稳定性和响应速度；滞后校正的目的是使信号的相位延迟，以实现信号的同步和对齐。

2. 原理不同：相位超前校正通过引入滤波器来增益低频信号，从而使得信号的相位提前；滞后校正通过引入滤波器来衰减高频信号，从而使得信号的相位延迟。

3. 应用领域不同：相位超前校正主要应用于控制系统中，以提高系统的稳定性和响应速度；滞后校正主要应用于音频处理、图像处理等领域，以实现信号的同步和对齐。

滞后校正的原理
滞后校正是一种用于修正系统响应滞后的方法，常用于控制系统中。

其原理基于对系统的输出信号进行滞后处理，在时间上对信号进行一定的延迟，以使系统的响应更加准确、稳定。

滞后校正的原理是通过引入一个滞后补偿器来改变控制系统的传递函数。

滞后补偿器由一个或多个衰减器和一个延迟器组成。

衰减器可以减小信号的振幅，而延迟器可以延迟信号的相位。

具体来说，当系统的响应滞后时，可以通过增加延迟器的时间常数来减小滞后。

延迟器会导致系统的相位响应滞后，并减弱系统的频率响应。

通过在系统的传递函数中引入延迟器，可以使系统的相位响应向后移动，从而达到校正滞后的效果。

实际上，滞后校正可以看作是一种频率域设计方法，通过调整系统的频率响应曲线，使其更加接近期望的频率响应。

在控制系统中应用滞后校正可以提高系统的稳定性和响应速度。

总之，滞后校正通过引入延迟器来改变系统的传递函数，从而校正系统响应中的滞后现象。

这种方法可用于改善控制系统的稳定性和响应特性，使系统的性能更加优良。

超前滞后校正的原理
超前滞后校正是一种用于系统控制的方法，目的是根据系统特性来补偿系统的超前或滞后相位，以提高系统的稳定性和性能。

超前滞后校正的原理基于系统的频率响应特性，即系统的幅频响应曲线。

在频率响应曲线上，超前滞后校正通过调整系统的相位和幅度来补偿系统的相位超前或滞后，使系统的频率响应曲线更接近预期的目标曲线。

具体来说，超前滞后校正一般包括以下几个步骤：
1. 频率分析：首先对系统进行频率响应分析，获取系统的幅频响应曲线和相频响应曲线。

2. 设计目标曲线：根据系统的要求，设计一个理想的幅频响应曲线和相频响应曲线。

3. 相位补偿：根据实际系统的相频响应曲线和目标曲线的相位差异，设计合适的相位补偿网络，使系统的相位更接近目标曲线。

4. 幅度补偿：根据实际系统的幅频响应曲线和目标曲线的幅度差异，设计合适的幅度补偿网络，使系统的幅度更接近目标曲线。

5. 调整参数：根据实际系统的频率响应，对相位补偿和幅度补偿网络的参数进行调整，使得系统的频率响应更接近目标曲线，
同时保持系统的稳定性。

通过超前滞后校正，可以有效地补偿系统的相位超前或滞后，提高系统的稳定性和性能。

超前滞后校正原理你看啊，在控制系统里就像在管理一个小世界一样。

有时候这个系统它表现得不太好，就像一个调皮的小孩，老是达不到我们想要的效果。

这时候呢，超前校正和滞后校正就像是两位神奇的小助手跑出来帮忙啦。

先说说超前校正吧。

超前校正就像是一个充满活力的小机灵鬼。

想象一下，系统就像一辆汽车在行驶，但是它的转向有点慢，不能很快地按照我们想要的方向改变。

超前校正就像是给这辆汽车装了一个超级灵敏的转向助力器。

它的原理呢，就是在系统的某个地方加进去一些东西，让系统能够提前做出反应。

比如说，在信号还没完全变大或者变小之前，就提前调整系统的状态。

这就好比你知道前面的路要拐弯了，你提前就开始转动方向盘，而不是等到到了拐弯的地方才开始转。

超前校正它主要是改变了系统的相角裕度，让系统变得更加稳定而且快速响应。

就像那个提前做好准备的人，不管遇到什么情况都能快速应对，不会手忙脚乱的。

再来说说滞后校正。

滞后校正就像是一个沉稳的老大哥。

它的作用方式有点不一样哦。

如果说超前校正像是快刀斩乱麻，那滞后校正就是慢条斯理地调整。

比如说系统里有些高频的噪声或者干扰，就像一群小苍蝇在捣乱。

滞后校正就像是一个大扇子，慢慢地把这些苍蝇给赶走。

它主要是通过降低系统的高频增益来达到这个目的的。

就像是在一个热闹的派对上，那些吵闹的高音部分被慢慢地降低了音量，让整个系统变得更加平稳。

滞后校正不会像超前校正那样让系统快速反应，但是它能让系统在长期的运行中更加稳定可靠。

它就像是给系统打了一针镇定剂，让那些过度兴奋或者不稳定的因素慢慢平静下来。

这超前校正和滞后校正啊，它们的存在都是为了让系统变得更好。

有时候我们的系统可能既需要快速反应的能力，又需要长期稳定的状态。

这时候呢，我们可能就要把超前校正和滞后校正结合起来用啦。

就像一个超级英雄组合，一个负责冲锋陷阵，快速应对危机，一个负责稳住后方，保证长期的稳定和平静。

你可别小看这两个校正原理哦。

在很多实际的工程应用里，它们可是发挥着巨大的作用呢。

滞后校正的最大滞后角滞后校正的最大滞后角，这听起来像是从科幻电影里走出来的词汇，对吧？但这东西就在我们的生活中，想象一下，咱们家里的小车子，每次打方向的时候，总得等几秒钟才能转过来。

那种感觉就像是大海中的巨轮，想要调头，得等好久才能看到效果。

滞后校正嘛，就是给这个过程加点调味料，让它更顺畅。

你瞧，咱们在开车时，想要迅速应对突发情况，最好就得懂点这些原理。

说到滞后，脑海中浮现的就是那种一两秒的延迟。

就像咱们玩游戏时，敌人早已动手，结果你还在原地呆着，手忙脚乱。

这就说明了，反应得跟上去才行，要不然就是“慢半拍”。

在技术上，这个最大滞后角其实是用来衡量系统反应速度的，就像那小孩等着要吃糖果，眼巴巴地盯着，结果却得等个不停，真是让人着急。

想象一下，开车时，前方出现了个小猫，咱们得快速反应，可是车子却像是喝醉了一样，慢悠悠地才开始转向。

这时候，滞后校正就显得尤为重要了。

它就像是给车子喝了提神饮料，让它能迅速应对各种突发情况。

生活中不止开车需要这种东西，任何时候的反应都得灵活，比如我们在工作中，遇到突发状况得及时处理，那就需要这种“滞后校正”的思维了。

说到这里，我就忍不住想起我那可爱的老爸，每次看电视时，总喜欢调高音量，结果每次人家说完了，他才反应过来。

这种情况就像在做滞后校正，反应慢半拍，关键时刻总是掉链子。

生活中的各种小细节，都在告诉我们，反应要快，才不至于错失良机。

在技术上，滞后校正最大滞后角就像是一种魔法，让系统的反应更加灵活。

就像咱们做饭时，油温上升得太慢，想炸个鸡腿，等了老半天，结果鸡腿已经凉了。

这时候，就得控制好油温的调节速度，确保它能迅速到位。

就算是一点小小的变化，也能影响最终的结果，真是让人感慨科技的神奇。

有些朋友可能会问，滞后校正的最大滞后角到底有什么用呢？这玩意儿不仅仅在机械设备中用得到，日常生活中也能找到它的身影。

比如说，在运动中，身体的反应速度就是一个滞后校正的过程。

咱们在打篮球时，得迅速判断球的方向，如果等得太久，那可就成了“慢半拍”的典型，球飞过头顶，真是让人哭笑不得。

滞后校正原理
滞后校正原理是一种控制系统的校正方法，主要用于改善系统的稳态性能。

其基本原理是利用滞后网络的高频幅值衰减特性，使系统的截止频率下降，从而使系统获得足够的相位裕度。

具体来说，滞后校正通过降低高频增益，使系统的总增益增大，从而改善了稳态精度（降低了稳态误差）。

同时，系统中包含的高频噪音也可以得到衰减，增强了系统的抗干扰能力。

此外，滞后校正还可以保持暂态性能不变的基础上，提高开环增益。

或者等价地说，滞后校正可以补偿因开环增益提高而发生的暂态性能的变化。

总的来说，滞后校正是一种有效的控制系统校正方法，能够改善系统的稳态性能和抗干扰能力。