六年级计算综合

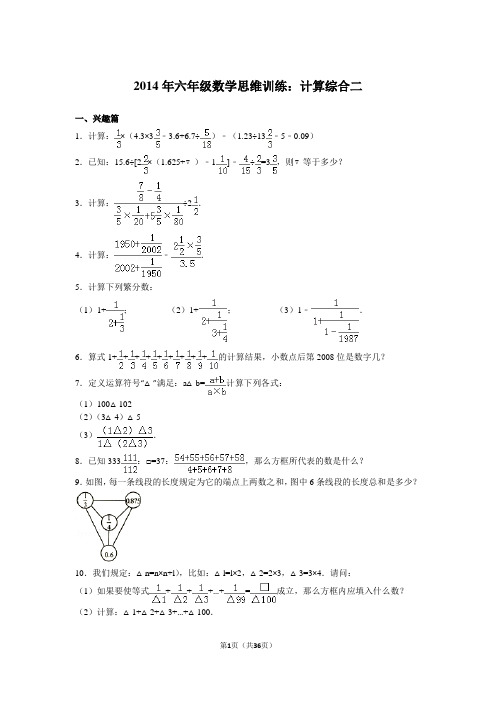
2014年六年级数学思维训练：计算综合二一、兴趣篇1．计算：×（4.3×3﹣3.6+6.7÷）﹣（1.23÷13﹣5﹣0.09）2．已知：15.6÷[2×（1.625+▽）﹣1]﹣÷=3，则▽等于多少？3．计算：÷2．4．计算：﹣．5．计算下列繁分数：（1）1+；（2）1+；（3）1﹣．6．算式1+++++++++的计算结果，小数点后第2008位是数字几？7．定义运算符号“△”满足：a△b=计算下列各式：（1）100△102（2）（3△4）△5（3）．8．已知333：□=37：，那么方框所代表的数是什么？9．如图，每一条线段的长度规定为它的端点上两数之和，图中6条线段的长度总和是多少？10．我们规定：△n=n×n+l），比如：△l=l×2，△2=2×3，△3=3×4．请问：（1）如果要使等式+++…+=成立，那么方框内应填入什么数？（2）计算：△1+△2+△3+…+△100．二、解答题（共12小题，满分0分）11．计算：（3.85÷+12.3×1）÷3．12．计算：÷2．13．．14．我们规定，符号“○”表示选择两数中较大数的运算，例如：3.5○2.9=2.9○3.5=3.5．符号“△”表示选择两数中较小数的运算，例如：3.5△2.9=2.9△3.5=2.9．请计算：．15．计算：（++）×（++）﹣（+++）×（+）16．算式（+++++++++++）×2004计算结果的小数点后第2004位数字是多少？17．古埃及人计算圆形面积的方法是：将直径减去直径的，然后再平方．由此看来，古埃及人认为圆周率л等于多少？（结果精确到小数点后两位数字）18．（1）将下面这个繁分数化为最简真分数；．（2）若下面的等式成立，x应该等于多少？=．19．已知符号“*”表示一种运算，它的含义是：a*b=+，已知2*3=，那么：（1）A等于多少？（2）计算（1*2）+（3*4）+（5*6）+A+（99*100）20．已知A=+++A+，B=+++A比较A和B的大小．21．根据图中5个图形的变化规律，求第99个图形中所有圆圈（实心圆圈与空心圆圈）的个数．22．定义：a n=．（1）求出a1，a2，a100，a200的大小；（2）计算：++++…+．三、解答题（共6小题，满分0分）23．1×（2﹣）﹣×+．24．真分数化为小数后，如果小数点后连续2004个数字之和是8684，那么a可能等于多少？25．定义运算“Ω”满足：①aΩ1=1，②aΩn=[aΩ（n﹣1）]+a已知mΩ4=30．问：（1）m等于多少？（2）mΩ 8等于多少？26．已知：A=×××…×，B=×××…××，C=．请比较A、B、C三个数的大小．27．求下列两个算式结果的整数部分：（1）×100；（2）．28．定义运算：a⊕b=a+b﹣请问（1）定义的运算是否满足交换律？（2）请根据定义计算下面两个算式：①2009⊕（2009×2008）；②⊕2008⊕．2014年六年级数学思维训练：计算综合二参考答案与试题解析一、兴趣篇1．计算：×（4.3×3﹣3.6+6.7÷）﹣（1.23÷13﹣5﹣0.09）【分析】第一个小括号根据乘法分配律进行计算，第二个小括号先算除法，再根据减法的性质进行计算．【解答】解：×（4.3×3﹣3.6+6.7÷）﹣（1.23÷13﹣5﹣0.09）=×（4.3×3.6﹣3.6+6.7×3.6）﹣（0.09﹣5﹣0.09）=×（4.3﹣1+6.7）×3.6+5+（0.09﹣0.09）=×（10×3.6）+5+0=×36+5=12+5=17．2．已知：15.6÷[2×（1.625+▽）﹣1]﹣÷=3，则▽等于多少？【分析】等式15.6÷[2×（1.625+▽）﹣1]﹣÷=3，把▽看作未知数x，式子转化为：15.6÷[2×（1.625+x）﹣1]﹣÷=3，求出方程的解即可．【解答】解：15.6÷[2×（1.625+x）﹣1]﹣÷=315.6÷[×+x﹣1]﹣=315.6÷[+x﹣1]=415.6÷[+x]=4+x=15.6÷4+x=3.9+x=3.9﹣x=x=；答：则▽等于．3．计算：÷2．【分析】分子分母同时化简，分母中先算乘法，再算加法，化简完繁分数后，再算除法．【解答】解：÷2=÷=÷=÷=×=4．计算：﹣．【分析】分子分母同时化简，最后算减法，注意把小数化为分数．【解答】解：﹣=﹣=﹣=﹣=5．计算下列繁分数：（1）1+；（2）1+；（3）1﹣．【分析】这三道题都属于阶梯式的繁分数化简，应从下往上依次计算，最终得出结果．【解答】解：（1）1+=1+=1+=1（2）1+=1+=1+=1+=1+=（3）1﹣=1﹣=1﹣=1﹣=1﹣=6．算式1+++++++++的计算结果，小数点后第2008位是数字几？【分析】=0.5，=0.25，=0.2，=0.125，=0.1，连同1，都是有限小数，不用考虑；只要求出=0.、=0.1和=4285和=0.的和，其中0.+0.1+0.=0.6，只要在的循环节上都加1，找出循环节的规律，然后求第2008位的数字，即可得解．【解答】解：=0.=0.1=0.4285=0.所以算式1+++++++++=1+0.5+0.25+0.2+0.125+0.1+0.+0.1+0.4285+0.=2.175+0.333333+0.1666666+0.1428574285+0.111111=2.9289685396从第7位后是2、5、3、9、6、8共6个数字一个循环的循环小数，（2008﹣6）÷6=333 (4)余数是4，所以小数点后第2008位是数字是第334个周期的第四个数9．答：小数点后第2008位是数字9．7．定义运算符号“△”满足：a△b=计算下列各式：（1）100△102（2）（3△4）△5（3）．【分析】（1）直接将数字代入a△b=计算即可；（2）先算小括号里面的3△4，再算括号外面的；（3）先分别计算分子和分母小括号里面的定义运算，再算括号外面的，进一步即可求解．【解答】解：（1）100△102==；（2）（3△4）△5=△5=△5==；（3）=====．8．已知333：□=37：，那么方框所代表的数是什么？【分析】根据比例的基本性质，把原式改写成37×□=333×，再根据等式的性质，两边同时除以37求解．【解答】解：333：□=37：37×□=333×37×□÷37=333×÷37□=答：方框所代表的数是．9．如图，每一条线段的长度规定为它的端点上两数之和，图中6条线段的长度总和是多少？【分析】根据题意，每一条线段的长度规定为它的端点上两数之和，6条线段的长度分别是+0.875、+0.6、+、0.875+、0.875+0.6、+0.6，然后把这6条线段相加即可．【解答】解：（+0.875）+（+0.6）+（+）+（0.875+）+（0.875+0.6）+（+0.6）=×3+0.875×3+×3+0.6×3=1+2.625+2.25+1.8=3.625+2.25+1.8=5.875+1.8=7.675．答：图中6条线段的长度总和是7.675．10．我们规定：△n=n×n+l），比如：△l=l×2，△2=2×3，△3=3×4．请问：（1）如果要使等式+++…+=成立，那么方框内应填入什么数？（2）计算：△1+△2+△3+…+△100．【分析】（1）将式子+++…+变形为+++…+，再拆项抵消即可求解；（2）将△1+△2+△3+…+△100变形为l×2+2×3+3×4+…+100×101，再根据1×2+2×3+3×4+…+n （n+1）=n（n+1）（n+2）进行计算即可求解．【解答】解：（1）+++…+=+++…+=1﹣+﹣+﹣+…+﹣=1﹣=．答：方框内应填入99．（2）△1+△2+△3+…+△100=l×2+2×3+3×4+…+100×101=×100×101×102=343400．二、解答题（共12小题，满分0分）11．计算：（3.85÷+12.3×1）÷3．【分析】小括号里面根据乘法分配律进行简算，最后算除法．【解答】解：（3.85÷+12.3×1）÷3=（3.85×3.6+6.15×2×1）÷3=（3.85×3.6+6.15×3.6）÷3=（3.85+6.15）×3.6÷3=10×3.6÷3=36÷3=．12．计算：÷2．【分析】分子分母同时化简，最后算除法，求得结果．【解答】解：÷2，=÷2，=÷2，=÷2，=××，=．13．．【分析】此繁分式中的分子与分母，数字有一定特点，抓住此特点，把原式变为÷，运用运算技巧和运算定律简算．【解答】解：，=÷，=1÷，=1÷，=．14．我们规定，符号“○”表示选择两数中较大数的运算，例如：3.5○2.9=2.9○3.5=3.5．符号“△”表示选择两数中较小数的运算，例如：3.5△2.9=2.9△3.5=2.9．请计算：．【分析】根据符号○表示选择两数中较大数的运算，符号△表示选择两数中较小数的运算，得出新的运算方法，用新的运算方法，计算所给出的式子，即可得出答案．【解答】解：，=（0.65×0.4）÷（0.3+2.25），=0.26÷2.55，=．15．计算：（++）×（++）﹣（+++）×（+）【分析】本题分数较大，可设++=a，+=b，运用换元法代入计算求解．【解答】解：设++=a，+=b，则原式=a×（b+）﹣（a+）×b=ab+a﹣ab﹣ b=（a﹣b）=×=1．16．算式（+++++++++++）×2004计算结果的小数点后第2004位数字是多少？【分析】2004能被2，3，4，6，12整除，所以可以不考虑，，，，2004除以5，8，10是有限小数，所以也可以不考虑，，只要分析、、、的第2004位，2005位数字，把这四个两位数字加起来，十位数字就是计算结果的小数点后第2004位数字．【解答】解：2004能被2，3，4，6，12整除，所以可以不考虑，，，，2004除以5，8，10是有限小数，所以也可以不考虑，，=286.285714285714…，是一个6位的循环，小数点后第2004位，2005位是42=222.66…是一个1位的循环，小数点后第2004位，2005位是66=182，1818…是一个2位的循环，小数点后第2004位，2005位是81=154.153846153846…是一个6位的循环，小数点后第2004位，2005位是6142+66+81+61=250，5就是计算结果的小数点后第2004位数字．答：计算结果的小数点后第2004位数字是5．17．古埃及人计算圆形面积的方法是：将直径减去直径的，然后再平方．由此看来，古埃及人认为圆周率л等于多少？（结果精确到小数点后两位数字）【分析】根据圆周率的含义：圆的周长和它直径的比值，叫做圆周率；圆周率是无限不循环小数，用“π”表示，π≈3.14，由此解答即可．【解答】解：根据圆周率的含义可知：π≈3.14．18．（1）将下面这个繁分数化为最简真分数；．（2）若下面的等式成立，x应该等于多少？=．【分析】（1）对于阶梯式的繁分数化简，从下而上逐步进行，直至结果为整数、小数或最简分数为止．（2）先化简等是左边的繁分数，然后根据解比例的方法求出未知数即可．【解答】解：（1）======（2）=======96x+56=88x+668x=10x=19．已知符号“*”表示一种运算，它的含义是：a*b=+，已知2*3=，那么：（1）A等于多少？（2）计算（1*2）+（3*4）+（5*6）+A+（99*100）【分析】（1）根据定义新运算：a*b=+，和已知2*3=，得到关于A 的方程，解方程即可求解；（2）将式子变形为++++++1++，再拆项抵消进行计算．【解答】解：（1）因为2*3=所以+=+=2（3+A）+4=3（3+A）3+A=4A=1．答：A等于1．（2）（1*2）+（3*4）+（5*6）+A+（99*100）=++++++1++=1﹣+﹣+﹣+﹣+﹣+﹣+1+﹣+﹣=2﹣+﹣=1．20．已知A=+++A+，B=+++A比较A和B的大小．【分析】先把A拆项，然后减去B，看看计算结果与0的关系，即可解决问题．【解答】解：A=+++…+=1﹣+﹣+﹣+…+﹣因此，A﹣B=（1﹣+﹣+﹣+…+﹣）﹣（+++…+）=[（1+++…+）﹣（+++…+）]﹣（+++…+）=（1+++…+﹣﹣﹣﹣﹣﹣…﹣﹣）＜0因此A＜B．21．根据图中5个图形的变化规律，求第99个图形中所有圆圈（实心圆圈与空心圆圈）的个数．【分析】首先根据已知的5个图形，分析出每个图形有几层圆圈，每层圆圈的个数分别是多少；然后总结出第n层圆圈个数的公式，代入求出第99个图形中所有圆圈（实心圆圈与空心圆圈）的个数即可．【解答】解：设第1个图形的所有圆圈的个数是S1，第2个图形的所有圆圈的个数是S2，…第n个图形的所有圆圈的个数是S n，S1=1S2=1+（1+2）S3=1+（1+2）+（1+2+3）S4=1+（1+2）+（1+2+3）+（1+2+3+4）S5=1+（1+2）+（1+2+3）+（1+2+3+4）+（1+2+3+4+5）…S n=1+（1+2）+（1+2+3）+（1+2+3+4）+（1+2+3+4+5）+…+（1+2+3+…+n）因为（1+2+3+…+n）=n（n+1）÷2，所以第n个图形所有圆圈的个数为：S n=（∑n2+∑n）÷2=[n（n+1）（2n+1）÷6+n（n+1）÷2]÷2=n（n+1）（n+2）÷6，则第99个图形中所有圆圈的个数为：S99=99×（99+1）×（99+2）÷6=166650．答：第99个图形中所有圆圈（实心圆圈与空心圆圈）的个数是166650．22．定义：a n=．（1）求出a1，a2，a100，a200的大小；（2）计算：++++…+．【分析】（1）将1，2，100，200分别代入a n=计算即可求解；（2）通过观察，把原式变为1×（1+1）+2×（2+1）+3×（3+1）+…+99×（99+1）+100×（100+1），然后把各项展开，得到12+1+22+2+32+3+…+992+99+1002+100，再把平方数余平方数相加，其余数相加，然后运用公式12+22+32+…+n2=n（n+1）（2n+1）÷6，解决问题．【解答】解：（1）a1==a2===a100===a200===；（2）++++…+=1×2+2×3+3×4+4×5+…+100×101=（12+1）+（22+2）+（32+3）+…+（1002+100）=（12+22+32+...+1002）+（1+2+3+ (100)=+=338350+5050=343400．三、解答题（共6小题，满分0分）23．1×（2﹣）﹣×+．【分析】此题是一道分数四则运算的繁分数化简题，数据较多，所以计算时要细心观察，避免出错．先算括号内的以及繁分数的分子分母中的计算，然后根据分数四则混合运算的顺序进行．注意在计算过程中能约分要约分．【解答】解：1×（2﹣）﹣×+=×﹣×+=×﹣×+×=×﹣×+×=×﹣×+×=×（+）﹣=×14﹣=﹣=24．真分数化为小数后，如果小数点后连续2004个数字之和是8684，那么a可能等于多少？【分析】把a=1、2、3、4，…26，的值一一列出，规律是循环节为3位的循环小数．2004÷3=668，8684÷668=13，所以循环节3位数字和等于13，即可得解．【解答】解：=0.3，=0.7，==0.，=0.4，=0.8，==0.，=5，=0.9，==0.，=0.7，=0.0，==0.，=0.8，=1，==0.，=0.9，=0.2，==0.，=0.0，=0.4，==0.，=0.1，=0.5，==0.，=0.2，=0.6，2004÷3=668，8684÷668=13，所以循环节3位数字和等于13，通过观察以上循环节，a=4、13和22时，循环节的和是1+4+8=13，所以a=4，13，22；答：a可能等于4、13和22．25．定义运算“Ω”满足：①aΩ1=1，②aΩn=[aΩ（n﹣1）]+a已知mΩ4=30．问：（1）m等于多少？（2）mΩ 8等于多少？【分析】（1）根据定义运算“Ω”得到关于m的方程，解方程即可求解；（2）将mΩ8变形为只含有mΩ1的式子进行计算即可求解．【解答】解：（1）mΩ4=30mΩ3+m=30mΩ2+m+m=30mΩ1+m+m+m=301+m+m+m=303m=29m=9．答：m等于9；（2）mΩ8=9Ω8=1+9×7=68．答：mΩ8等于68．26．已知：A=×××…×，B=×××…××，C=．请比较A、B、C三个数的大小．【分析】先比较A和B中每项的大小，进而得出A和B的大小，进一步比较得出A和B都小于，问题即可得解．【解答】解：因为A=×××…×，B=×××…××，且，…，所以A＜B；又：A×B=故：A×A＜所以，A＜B＜．27．求下列两个算式结果的整数部分：（1）×100；（2）．【分析】（1）把分子和分母中的每一个加数分别拆写，如11×66=（13﹣2）×（68﹣2）=13×68﹣2×13﹣2×68+4…；11×65=（13﹣2）×（67﹣2）…，再把分子分母合并，约分可得问题答案．（2）分子不变，把分母扩大或缩小，计算出结果在什么范围内，即可得解．【解答】解：（1）因为分子：11×66=（13﹣2）×（68﹣2）=13×68﹣2×13﹣2×68+412×67=（13﹣1）×（68﹣1）=13×68﹣13﹣68+113×68=13×6814×69=（13+1）×（68+1）=13×68+13+68+115×70=（13+2）×（68+2）=13×68+2×13+2×68+4∴11×66+12×67+13×68+14×69+15×70=13×68×5+10，又因为分母：11×65=（13﹣2）×（67﹣2），12×66=（13﹣1）×（67﹣1），13×67=13×67，14×68=（13+1）×（67+1），15×69=（13+2）×（67+2），∴11×65+12×66+13×67+14×68+15×69=13×67×5+10，所以×100=×100所以整数部分是101．（2）++…＜×20++…＞×20所以＜++…＜2所以＜原式＜=1.45所以原式的整数部分是1．28．定义运算：a⊕b=a+b﹣请问（1）定义的运算是否满足交换律？（2）请根据定义计算下面两个算式：①2009⊕（2009×2008）；②⊕2008⊕．【分析】（1）根据加法交换律和乘法交换律即可求解；（2）①将数字代入定义运算计算即可求解；②根据交换律变形为2009⊕（2009×2008）（2009个）⊕2008，依此计算即可求解．【解答】解：（1）因为a⊕b=a+b﹣，b⊕a=b+a﹣，a+b﹣=b+a﹣，所以a⊕b=b⊕a，所以定义的运算满足交换律；（2）①2009⊕（2009×2008）=2009+2009×2008﹣=2009+2009×2008﹣2009×2009=0；②⊕2008⊕=2009⊕（2009×2008）（2009个）⊕2008 =0⊕2008=0+2008﹣=2008．参与本试卷答题和审题的老师有：zlx；张召伟；齐敬孝；duaizh；WX321；zhuyum；忘忧草；奋斗；rdhx（排名不分先后）菁优网2016年5月22日考点卡片1．分数大小的比较【知识点归纳】分数比较大小的方法：（1）真、假分数或整数部分相同的带分数；分母相同，分子大则分数大；分子相同，则分母小的分数大；分子和分母都不相同，通分后化成同分母或者同分子的分数再进行比较大小．（2）整数部分不同的带分数，整数部分大的带分数就比较大．【命题方向】常考题型：例1：小于而大于的分数只有一个分数．×（判断对错）分析：依据分数的基本性质，将两个分数的分子和分母同时扩大若干倍，介于它们中间的真分数就会有无数个，据此即可进行判断．解：分别将和的分子和分母扩大若干个相同的倍数，在和间会出现无数个真分数，所以，大于而小于的真分数只有一个是错误的．故答案为：×．点评：解答此题的关键是依据分数的基本性质将两个的分子和分母扩大若干倍，即可找到无数个介于它们中间的真分数，从而能推翻题干的说法．2．整数、分数、小数、百分数四则混合运算【知识点归纳】1、加法运算：①加法交换律：两个加数交换位置，和不变．如a+b=b+a②加法结合律：先把前两个数相加，或先把后两个数相加，和不变．如：a+b+c=a+（b+c）2、乘法运算：①乘法交换律：两个因数交换位置，积不变．如a×b=b×a．②乘法结合律：先乘前两个数，或先乘后两个数，积不变．如a×b×c=a×（b×c）③乘法分配律：两个数的和，乘以一个数，可以拆开来算，积不变．如a×（b+c）=ac+bc④乘法分配律的逆运算：一个数乘另一个数的积加它本身乘另一个数的积，可以把另外两个数加起来再乘这个数．如ac+bc=a×（b+c）3、除法运算：①除法性质：一个数连续除以两个数，可以先把后两个数相乘，再相除．如a÷b÷c=a÷（b×c）②商不变规律：被除数和除数同时乘上或除以相同的数（0除外）它们的商不变．如a÷b=（an）÷（bn）=（a÷n）÷（b÷n）（n≠0 b≠0）4、减法运算：减法性质：一个数连续减去两个数，可以用这个数减去两个数的和．如a﹣b﹣c=a﹣（b+c）运算顺序：同级运算，从左往右依次运算，两级运算，先算乘除，后算加减；有括号的，先算小括号里面的，再算中括号里面的，然后算大括号里面的，最后算括号外面的．【命题方向】常考题型：例：计算（1）3.41÷2×5.875﹣（21﹣19.18）（2）[（13.75﹣7）×2]÷[（1+12.5%）÷（2÷9）]．分析：本题根据四则混合运算的运算顺序计算即可：先算乘除，再算加减，有括号的要先算括号里面的．（1）的计算过程中可利用一个数减两个数的差，等于用这个数减去两个数中的被减数，加上减数的减法性质计算．（2）可根据一个数除以两个数的商等于除以这两个数中的被除数乘以除数的除法性质计算．解：（1）3.41÷2×5.875﹣（21﹣19.18）=××﹣（21﹣19），=6+19﹣21，=26﹣21，=4；（2）[（13.75﹣7）×2]÷[（1+12.5%）÷（2÷9）]=[（13﹣7）×]÷[（1+）÷（×）]，=[×]÷[÷]，=×××，=3．点评：本题中数据较为复杂，完成时要细心，注意小数、分数之间的互化及通分约分．3．方程的解和解方程【知识点归纳】使方程左右两边相等的未知数的值，叫做方程的解．求方程的解的过程，叫做解方程．【命题方向】常考题型：例1：使方程左右两边相等的未知数的值，叫做（）A、方程B、解方程C、方程的解D、方程的得数分析：根据方程的解的意义进行选择即可．解：使方程左右两边相等的未知数的值，叫做方程的解．故选：C．点评：此题主要考查方程的解的意义．例2：x=4是方程（）的解．A、8x÷2=16B、20x﹣4=16C、5x﹣0.05×40=0D、5x﹣2x=18 分析：使方程的左右两边相等的未知数的值，是这个方程的解，把x=4代入下列方程中，看左右两边是否相等即可选择．解：A、把x=4代入方程：左边=8×4÷2=16，右边=16；左边=右边，所以x=4是这个方程的解；B、把x=4代入方程：左边=20×4﹣4=76，右边=16；左边≠右边，所以x=4不是这个方程的解；C、把x=4代入方程：左边=5×4﹣0.05×40=20﹣2=18，右边=0；左边≠右边，所以x=4不是这个方程的解；D、把x=4代入方程：左边=5×4﹣2×4=12，右边=18；左边≠右边，所以x=4不是这个方程的解；故选：A．点评：将x的值代入方程中进行检验，使方程左右两边相等的未知数的值就是方程的解．4．解比例【知识点归纳】根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项．求比例中的未知项，叫做解比例．一般来说，求比例的未知项有以下两种情况：（1）求未知外项=（2）求未知内项=【命题方向】常考题型：例1：在比例中，两个外项的积是，其中的一个内项是4，另一个内项是．分析：分析“两个外项的积是，其中的一个内项是4”这两个条件，根据比例的基本性质“两外项之积等于两内项之积”，用两个外项的积除以其中的一个内项，算出另一个内项是多少．解：÷4=×=故答案为：．点评：这道题重点考查学生对于比例的基本性质的应用．例2：如果比例的两个外项互为倒数，那么比例的两个内项（）A、成反比例B、成正比例C、不成比例分析：根据互为倒数的定义和比例的两内项之积等于两外项之积，可得比例的两个内项之积等于1，再根据成反比例的定义即可求解．解：因为比例的两个外项互为倒数，那么比例的两个内项之积=1（为恒指），则比例的两个内项成反比例．故选：A．点评：本题考查了倒数的定义和成反比例的条件，两种相关联的量，一种量变化，另一种量也随着变化，这两种量中相对应的两个数的积一定．这两种量叫做成反比例的量．它们的关系叫做反比例关系．5．算术中的规律【知识点归纳】在数学算式中探索规律，应认真观察算式的特点，再观察结果的特点，进而，根据规律填出这一类算式的结果．例如：1×1=1；11×11=121；111×111=12321；1111×1111=1234321；通过观察发现：每个算式中，两个因数各个数位上的数字都是1，且个数相同．积里的数字呈对称形式，且前半部分是从1开始，写至某个数字（此数即因数的位数），积的后半部分再顺次写出．①一个数乘11，101的规律一个数乘11的规律：可采用“两头一拉，中间相加”的方法计算．如：123×11=1353一个数乘101的规律：可采用“两两一位，隔位一加”的方法计算．如：58734×101=5932134②一个数乘5，15，25，125的规律一个数乘5，转化为一个数乘10，然后，再除以2．如：28×5=28×10÷2=280÷2=140这种情况可以概括为“添0求半”．根据同级运算可交换位置的性质，也可以先除以2，再乘10．如：28×5=28÷2×10=14×10=140．即“求半添0”的方法．一个数乘15，可分解为先用这个数乘10，再加上这个数乘5，乘5的方法同上．如：264×15=264×10+264×5=2640+264×10÷2=2640+2640÷2=2640+1320=3960．这种情况可以概括为“添0补半”一个数乘125，因为125×8=1000，所以，可将一个数乘125转化为先乘1000，再除以8，或先除以8，再乘1000．如：864×125=864×1000÷8=864000÷8=108000．【命题方向】常考题型：例1：4÷11的商用循环小数表示，则小数点后面第20位数字是（）A、0B、3C、7D、6分析：把4÷11的商用循环小数表示出来，看看循环节有几位小数，然后用20除以循环节的位数即可判断．解：4÷11=0.，循环节是36两个数字；20÷2=10，所以20位上的数是6；故选：C．点评：此题考查学生循环节的概念，以及分析判断能力．例2：按规律计算．3+6+12=12×2﹣3=213+6+12+24=24×2﹣3=453+6+12+24+48=48×2﹣3=933+6+12+24+…+192=192×2﹣3=381a+2a+4a+8a+16a+…+1024a=2047a．分析：由3+6+12=12×2﹣3=21，3+6+12+24=24×2﹣3=45，3+6+12+24+48=48×2﹣3=93可知：结果都是算式中的最后一个数乘以2再减去第一个数所得，由此得出结论．解：（1）3+6+12+24+…+192=192×2﹣3=381；（2）a+2a+4a+8a+16a+…+1024a=1024a×2﹣a=2048a﹣a=2047a．故答案为：381，2047a．点评：此题在于考查学生总结规律的能力．6．数与形结合的规律【知识点归纳】在探索数与形结合的规律时，一方面要考虑图形的对称（上下对称和左右对称），另一方面要考虑数的排列规律，通过数形结合、对应等方法，来解决问题．【命题方向】常考题型：例：用小棒照下面的规律搭正方形，搭一个用4根，搭2个用7根…，搭10个要用31根小棒，搭n个要用3n+1根小棒．．分析：能够根据图形发现规律：多一个正方形，则多用3根火柴．解：观察图形发现：第一个图形需要4根火柴，多一个正方形，多用3根火柴，则第n个图形中，需要火柴4+3（n﹣1）=3n+1．当n=10，3n+1=31，答：搭10个要用3根小棒，搭n个要用3n+1根小棒．故答案为：31，3n+1．点评：本题考查了图形的变化类问题，主要培养学生的观察能力和总结能力．7．圆的认识与圆周率【知识点归纳】1．圆的认识：圆是一种几何图形．当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆．2．圆周率：圆周率符号一般以π来表示，是一个在数学及物理学普遍存在的数学常数．它定义为圆形之周长与直径之比．它也等于圆形之面积与半径平方之比．【命题方向】常考题型：例1：圆周率π是一个（）A、有限小数B、循环小数C、无限不循环小数分析：根据圆周率的含义：圆的周长和它直径的比值，叫做圆周率，用字母“π”表示，它是一个无限不循环小数；进而解答即可．解：根据圆周率的含义可知：圆周率π是一个无限不循环小数；故选：C．点评：此题考查了圆周率的含义．例2：把一个圆分成若干等份，然后把它剪拼成一个近似的长方形，已知长方形的长是6.28cm，这个长方形的宽是2cm，这个圆的面积是12.56cm2．分析：长方形的两个长的和即为圆的周长，利用圆的周长公式即可求出圆的半径，也就是长方形的宽；从而可求出圆的面积．解：C=2πr，r=C÷2π，=6.28×2÷6.28，=2cm；长方形的宽=2cm；圆的面积：3.14×22，=12.56cm2．故答案为：2，12.56．点评：此题主要考查圆的周长及面积公式，关键是明白圆的半径等于长方形的宽．8．分数的巧算【知识点归纳】分数运算符合的定律．（1）乘法交换律a×b=b×a（2）乘法结合律a×（b×c）=（a×b）×c（3）乘法分配律a×（b+c）=a×b+a×c；a×（b﹣c）=a×b﹣a×c（4）逆用乘法分配律a×b+a×c=a×（b+c）；a×b﹣a×c=a×（b﹣c）（5）互为倒数的两个数乘积为1．除法的几个重要法则（1）商不变性质被除数和除数乘以（或除以）同一个非零的数，商不变，即a÷b=（a×n）÷（b×n）（n≠0）a÷b=（a÷m）÷（b÷m）（m≠0）（2）当n个数都除以同一个数后再加减时，可以将它们先加减之后再除以这个数；反之也成立（也可称为除法分配律）．如：（a±b）÷c=a÷c±b÷c；a÷c±b÷c=（a±b）÷c．【命题方向】常考题型：例1：（1+）×（1﹣）×（1+）×（1﹣）×…×（1+）×（1﹣）等于．分析：此题如果按部就班地进行计算，计算量可想而知，所以要寻求巧算的方法，此题可利用乘法结合律进行简算．解：（1+）×（1﹣）×（1+）×（1﹣）×…×（1+）×（1﹣），=[（1+）×（1+）×…×（1+）]×[（1﹣）×（1﹣）×…×（1﹣）]，=[××…×]×[××…×]，=×，=．故答案为：．点评：此题考查了学生乘法结合律的知识，以及巧算的能力．例2：的值是多少．（）A、B、C、D、分析：通过观察，每个分数的分母中的两个因数相差3，分子都是3，于是可把每个分数都可以拆成两个分数相减的形式，然后通过加减相抵消的方法，求得结果．解：，=（﹣）+（﹣）+（﹣）+（﹣）+（﹣）+（﹣），=﹣，=；故选：B．点评：解答此题，应注意观察分数的特点，根据特点，对分数进行拆分，达到简算的目的．【题方法点拨】分数巧算就是熟能生巧的过程，综合运用乘法分配律，分数化小数，小数化分数以及带分数化假分数、带分数拆分等方法达到巧算的目的．1、把同分母的分数凑成整数．a．先去括号；b．利用交换律把同分母分数凑在一起；c．利用减法性质把同分母分数凑在一起．2、分数乘法中，利用乘法交换律，交换数的位置，以达到约分的目的；利用乘法结合律，以达到约分的目的，从而简算．3、分数混合运算中有除法，先将除法转化为乘法，然后再利用乘法的分配律的方法来计算以达到凑整的目的．4、懂得拆分．9．繁分数的化简【知识点归纳】繁分数的定义：如分数形式，分子或分母含有分数，或分子与分母都含有分数的数，叫繁分数．把繁分数化为最简分数或整数的过程，叫做繁分数的化简．【命题方向】常考题型：例1：=．分析：根据繁分数的化简方法先化简=，再化简=，再化简=，从而得解．解：===．故答案为：．点评：考查了繁分数的化简．繁分数的化简方法：1、可利用分数与除法的关系把繁分数写成分子除以分母的形式；2、利用分数的基本性质，去掉分子、分母上分数后化为最简分数．一般情况下，分子、分母所乘上的适当非零整数为分子、分母部分的两个分数分母的最小公倍数．易错题型：例2：计算的结果为（）A、B、1 C、1D、2分析：分别化简分数的分子与分母，求出繁分式的结果后，就比较好计算了．解：=÷=×=×=××=．故选：A．点评：对于这类分数，分子与分母同时计算，一步步进行．【解题方法点拨】繁分数化简的基本方法：1、可利用分数与除法的关系把繁分数写成分子除以分母的形式．2、利用分数的基本性质，去掉分子、分母上分数后化为最简分数．一般情况下，分子、分母所乘上的适当非零整数为分子、分母部分的两个分数分母的最小公倍数．繁分数化简一般采用以下两种方法：（1）先找出中主分线，确定出分母部分和分子部分，然后这两部分分别进行计算，每部分的计算结果，能约分的要约分，最后写成“分子部分÷分母部分”的形式，再求出最后结果．（2）繁分数化简的另一种方法是：根据分数的基本性质，经繁分数的分子部分、分母部分同时扩大相同的倍数（这个倍数必须是分子部分与分母部分所有分母的最小公倍数），从而去掉分子部分和分母部分的分母，然后通过计算化为最简分数或整数．化复杂为简单：繁分数的分子或分母部分若含有加减运算，则先加减运算再按繁分数化简方法进行化简．繁分数的分子、分母都是连乘运算可以分子、分母直接约分化简．10．比较大小【知识点归纳】【命题方向】常考题型：例1：甲数的与乙数的相等，甲数的25%与丙数的20%相等．比较甲、乙、丙三个数的大小，下列结果正确的是哪一个？（）A、甲＞乙＞丙B、丙＞乙＞甲C、甲＞丙＞乙D、丙＞甲＞乙分析：由题意可得：甲数×=乙数×，甲数×25%=丙数×20%，则可以求出三个数的比，继而确定出三个数的大小关系．解：因为甲数×=乙数×，甲数×25%=丙数×20%，甲数：乙数=：=5：4；甲数：丙数=20%：25%=4：5；乙数=甲数，丙数=甲数，所以丙数＞甲数＞乙数；故选：D．点评：此题主要考查比例的基本性质的灵活应用．经典题型：例2：在a×b=c中，a，b，c都不等于0，如果要使c＜a，那么b必须（）A、大于1B、等于1C、小于1分析：由已知条件a×b=c，可得b=；再根据c＜a，推得＜1，进而得出结果．解：因为a×b=c，所以b=；因为c＜a，所以＜1，即b=＜1．故选：C．点评：先根据两个因数（a和b）以及它们的积（c），表示出另一个因数b=，然后根据c ＜a，推出＜1，进而解决问题．【解题方法点拨】1、整数的大小比较：位数越多的整数越大，如果位数相同，则从最高位起依次比较各位数字大小，相同位上数字越大的整数越大．2、小数的大小比较：小数由整数部分和小数部分组成．整数部分的比较规则与整数的比较规则相同，整数部分越大的小数越大．如果整数部分相同，则从十分位起依次比较各位数字，相同位上数字越大的那个小数越大．3、分数的大小比较：分母相同，分子越小的分数越小；分子相同，分母越小的分数越大．4、循环小数的大小比较：将所有循环小数补足到足够的相同的位数，即可按照小数的比较法则进行比较．5、循环小数和分数的大小比较：①对于较简单的情形，将分数化为小数，再按照小数比较大小的规则比较即可．②对于分数形式较复杂的情形，将循环小数化为分数与分数比较大小．6、特殊方法：①放缩法：根据分子不变分母改变或者分母不变分子改变，对分数进行一定的处理，得到形式简单的、大小介于两者之间的数，参与比较，简化比较过程．②倒数法：倒数越大，数越小．某些分子分母之间的关系相差不大的分数作比较时，如果分数结构复杂不适合通分解决，取它们的倒数是比较有效的方法，但必须对分数有特定要求．③等值放缩比较法：两个分数比较，分母或者分子相差一定的倍数时，使用通分法将分母或者分子放缩为相近的数，然后比较得到的结果．④归一法：如果相比较的两个分数结构复杂，但是分子分母相差很小，即分数值与1很接近，则将问题转化为比较两个分数与1的差的大小．11．定义新运算【知识点归纳】定义新运算是指用一个符号和已知运算表达式表示一种新的运算．注意：（1）解决此类问题，关键是要正确理解新定义的算式含义，严格按照新定义的计算顺序，将数值代入算式中，再把它转化为一般的四则运算，然后进行计算．（2）我们还要知道，这是一种人为的运算形式．它是使用特殊的运算符号，如：*、▲、★、◎、△、◆、■等来表示的一种运算．（3）新定义的算式中，有括号的，要先算括号里面的．【命题方向】常考题型：例1：规定：a△b=3a﹣2b．已知x△（4△1）=7，那么x△5=（）A、7B、17C、9D、19分析：根据所给出是等式，知道a△b等于3与a的积减去2与b的积，由此用此方法计算4△1的值，再求出x的值，进而求出x△5的值．解：4△1=3×4﹣2×1，=10，x△（4△1）=7，x△10=7，3x﹣2×10=7，3x﹣20=7，3x=20+7，3x=27，。

六年级数学上册计算题专项综合练习1. 直接写出得数。

0.24÷0.6=2. 计算。

3. 直接写得数。

0.25+0.75=4505÷5= 24.3-8.87-0.13=4. 直接写得数175％+ =650×20=5. 直接写出得数。

1－6. 直接写出得数。

7. 直接写出得数。

1-0.92= 3.5+4.28= 30÷100=1÷0.1-1×0.1= 1+0.94+0.06= 0.056×8. 口算7+13＝ 12－6＝19－8＝ 13－7＝12+5＝14－6＝ 11+0＝ 16－5＝11－3＝ 10+5＝15－9＝ 11－5＝14－7＝ 16－6＝7+8＝12+4－9＝ 10－5+8＝ 9+7－2＝11－5+3＝9. 直接写出得数。

6÷==10. 口算下面各题。

37+54= 46+34= 90+20= 32÷4= 960-900=55+35= 90-43= 110-70= 64÷8= 350+200=11. 口算0+76= 84×0= 0÷18= 36-0=8×125= 25×4= 50×20= 404÷4=56-22-18= 56-(22-18)= 56-22+18=12. 如果小明向南走80米，记作+80米，那么小华从同一地点向北走50米，记作______米，这时他们两人相距______米．13. 列竖式计算。

(除不尽的保留两位小数)①347.6-29.8=②0.048×1.5=③174÷0.03=④0.013×423=⑤1.9÷0.03≈⑥0.28÷4.6≈14. 计算下列各题，要写出主要计算过程，能用简便方法的要用简便方法计算。

①875+450÷18×25②36÷0.8÷1.25③④⑤⑥15. 列式计算。

第7讲几何综合一兴趣篇1. 图中八条边的长度正好分别是1、2、3、4、5、6、7、8厘米。

已知a=2厘米，b=4厘米，c=5厘米，求图形的面积。

【分析】2S=⨯+⨯+⨯=++=2716531461535(cm)2. 如图所示，∠+∠+∠+∠+∠+∠123456等于多少度？【分析】将这六个角用中心六边形的六个内角代换，利用六边形内角和为720，列方程得(1801)(1802)(1803)(1804)(1805)(1806)720-∠+-∠+-∠+-∠+-∠+-∠=，所以12345)6360∠+∠+∠+∠+∠+∠=3. 如图，平行四边形ABCD 的周长为75厘米。

以BC 为底时高是14厘米，以CD 为底时高是16厘米。

求平行四边形ABCD 的面积。

【分析】 75237.5BC CD +=÷=,根据面积相等，底的比与高的比成反比例，所以:16:148:7BC CD ==,因此37.5(87)820BC =÷+⨯=,平行四边形ABCD 的面积是2014280⨯=平方厘米4. 如图所示，一个边长为1米的正方形被分成4个小长方形，它们的面积分别是310平方米、25平方米、15平方米和110平方米。

已知图中的阴影部分是正方形，那么它的面积是多少平方米？【分析】 1251110CH HD ==,因此23CH =,13HD =,3310245AE EB ==,所以37AE =,47EB =,因此2353721FG =-=,那么它的面积是252521441⎛⎫= ⎪⎝⎭平方米5. 如图，红、黄、绿三块大小一样的正方形纸片，放在一个正方体盒内，它们之间相互重叠。

已知露在外面的部分中，红色的面积是20，黄色的面积是14，绿色的面积是10。

那么，正方体盒子的底面积是多少？绿黄红【分析】 将黄色纸片推到左边，则每块纸片露出的形状如右上图.黄、绿两色的面积之和保持14+10=24不变，则在右图中这两块面积相等，均为24212÷=.根据公式可知，空白处面积=黄⨯绿÷红=1212207.2⨯÷=，则正方形盒底面积是7.212122051.2+++=.6. 如图，在三角形ABC 中，IF 和BC 平行，GD 和AB 平行，HE 和AC 平行。

六年级综合计算题
一、四则混合运算
1. 计算：公式
解析：
这道题可以运用乘法分配律进行简便计算。

乘法分配律的公式为公式。

在式子公式中，公式，公式，公式。

先计算公式，然后再乘以公式，得到公式。

2. 计算：公式
解析：
同样运用乘法分配律，将公式分别与括号里的公式和公式相乘，再把积相加。

即公式。

公式，公式，最后公式。

3. 计算：公式
解析：
先算小括号里的式子：公式。

再算中括号里的式子：公式。

最后算括号外面的除法：公式。

二、分数与小数混合运算
1. 计算：公式
解析：
先把公式转化为分数公式。

则式子变为公式。

先算公式，再算公式。

2. 计算：公式
解析：
运用乘法分配律，公式。

先算括号里公式，再乘以公式，结果是公式。

三、解方程（可看作是综合计算的一种）
1. 解方程：公式
解析：
首先方程两边同时减去公式，得到公式。

公式，则公式。

然后方程两边同时除以公式，公式。

2. 解方程：公式
解析：
先计算方程左边公式，将公式转化为公式，则公式。

所以公式，方程两边同时乘以公式，得到公式。

整数混合运算及答案【例 1】 计算：315325335345÷+÷+÷+÷．【解析】 原式313233345=+++÷（）130526=÷= 【答案】26【巩固】 计算：⑴ 36196419⨯+⨯⑵ 361964144⨯+⨯【解析】 ⑴原式3664191900=+⨯=（）⑵原式36196419125=⨯+⨯+（）36641964125190088125190080009900=+⨯+⨯=+⨯⨯=+=（） 【答案】⑴1900 ⑵9900【例 2】 计算：234432483305+-⨯+÷= 。

（4级）【解析】 234+432-32+66=666-32+66=634+66=700【答案】700【例 3】 9000－9＝ ×9【解析】 （9000-9）÷9＝1000-1＝999【巩固】 900000－9＝________×99999。

【解析】 原式9(1000001)999999=⨯-=⨯【答案】9【例 4】 123(45)6+⨯÷+⨯=【解析】 原式＝1+2×2＝5【答案】5【例 5】 23422640⨯+⨯=（ ）。

【解析】 简单计算为2006【答案】2006【例 6】 20082006200720052007200620082005⨯+⨯-⨯-⨯【解析】 原式2006(20082007)2005(20082007)=⨯--⨯-20061200511=⨯-⨯=【答案】1【巩固】 计算2000 × 1999－1999 × 1998 ＋ 1998 × 1997－1997 × 1996＋1996 × 1995－1995 × 1994【解析】 题目是六项乘积的和差运算 , 其中 , 每两项中都有公因数 , 于是 , 我们先分组简算 . 原式 =1999 × (2000-1998)+1997 × (1998-1996)+1995 × (1996-1994)=1999 × 2+1997 × 2+1995 × 2=2 × (1999+1997+1995)=2 × (2000+2000+2000-9)=2 × (6000-9)=2 × 6000-2 × 9=12000-18=11982【答案】11982【巩固】计算：⨯-⨯+⨯-⨯++⨯-⨯________。

六年级上册综合计算题
六年级上册的综合计算题通常会涵盖之前学过的各种数学概念和技能，包括整数、小数、百分数、分数、四则运算、几何初步等。

以下是一些综合计算题的例子：
1.四则混合运算
计算：(36÷6+2)×5−8
2.分数与小数的转换与计算
计算：43+0.75−21
3.百分数的计算
计算：120的25%是多少？
4.几何初步：面积与周长
一个长方形的长是12厘米，宽是8厘米。

求这个长方形的周长和面积。

5.应用题
小明买了5本练习本和3支铅笔，每本练习本1.5元，每支铅笔0.5元。

小明一共花了多少钱？
6.文字题
一个数的3倍加上5，再减去10，结果是20。

求这个数。

7.综合题
妈妈买了一套衣服，上衣的价格是80元，裤子的价格是上衣的75%。

这套衣服一共多少钱？。

以下是提供给你的答案：
综合计算：
2.1853-796=1057
4.892÷4=223
5.1245+506×2=2257
6.3091-(687+432)=1972
8.6789÷89=76
9.4321+5678-9876=123简便计算：
1.230×20=4600
2.456÷8=57
3.536+120=656
4.980-250=730
5.478×5=2390
6.766÷7=109
7.409+79=488
8.690-180=510
9.956×6=5736
10.832÷4=208
解决问题的策略应用题：
1.小明有12个苹果，他分给3个朋友，每人分了几个苹果？
答案：每人分到4个苹果。

2.一条绳子的长度是9米，如果要分成3段长度相等的绳子，每段的
长度是多少？
答案：每段的长度是3米。

3.小红花了18元买了3盒饼干，每盒饼干的价格相同，每盒饼干多
少钱？
答案：每盒饼干6元。

4.小华买了一本书，原价是45元，打了9折，小华实际支付多少钱？
答案：小华实际支付40.5元。

5.一个长方形的长是6米，宽是4米，它的面积是多少平方米？
答案：面积是24平方米。

六年级数学下册综合算式练习题应用题之平均速度计算平均速度是物体在一段时间内所经过的路程与所用时间的比值。

在六年级数学下册综合算式练习题中，应用题经常涉及到平均速度的计算。

通过解决这些问题，学生能够加深对平均速度概念的理解，并应用所学知识解决实际问题。

本文将介绍几个常见的平均速度计算题目，并提供解题思路和步骤。

1. 题目一：小明骑自行车去市场，花费了30分钟，全程5公里。

请计算小明骑自行车的平均速度。

解题思路：首先，我们需要了解平均速度的计算公式：平均速度=总路程÷总时间。

根据题目，小明骑行的总路程为5公里，总时间为30分钟。

但我们知道速度通常以时速进行计算，因此，我们需要将分钟转换为小时。

1小时=60分钟，所以，小明骑行的总时间为30÷60=0.5小时。

将总路程5公里和总时间0.5小时代入平均速度的计算公式，我们可以得出小明的平均速度：5÷0.5=10公里/小时。

2. 题目二：小红乘坐公交车从家到学校，全程8公里，花费了40分钟。

小红中途下车玩了10分钟，然后又乘坐公交车抵达学校。

请计算小红的平均速度。

解题思路：根据题目，小红中途下车玩了10分钟，那么实际上她在公交车上花费的时间为40分钟-10分钟=30分钟。

同样地，我们将这30分钟转换为小时，得到0.5小时。

根据题目，小红的总路程为8公里，总时间为0.5小时。

代入平均速度的计算公式，我们可以得出小红的平均速度：8÷0.5=16公里/小时。

3. 题目三：李华乘坐高铁从A城到B城，全程320公里，乘车时间为2小时。

然后，他转乘出租车从B城到C城，全程40公里，乘车时间为30分钟。

请计算李华的整个行程的平均速度。

解题思路：对于整个行程的平均速度计算，我们可以将两段行程合并计算。

首先，我们将出租车的乘车时间转换为小时，30分钟=0.5小时。

然后，计算整个行程的总路程和总时间。

总路程=320公里+40公里=360公里；总时间=2小时+0.5小时=2.5小时。

六年级思维训练5 计算综合1.如下图所示,用一条直线上的点来表示数,那么0.12所在的位置应该是下列选项中的。

A.S的右边B.R和S之间C.Q和R之间D.P和Q之间E.P的左边2. 在下面四个算式中,得数最大的是 .A.（117−119)÷20 B.（115−121)÷60C.（113−123)÷100 D.（111−125)÷1403. 分数ba在印刷版中记为a/b,符号 /”是19世纪英国数学家德・摩根在1845年提出的, 德・摩根是一个个生性乐观、热爱生活、嗜好猜谜的人,每当有人问他年龄或出生时，他常风趣地答道:“我在X2年是X岁!”由此判断,他出生在年。

4.1×(11×12×13×14×15×16×17×18×19×110)+3×(12×13×14×15×16×17×18×19×110)+5×(13×14×15×16×17×18×19×110)+7×(14×15×16×17×18×19×110)+9×(15×16×17×18×19×1 10)+11×(16×17×18×19×110)+13×(17×18×19×110)+15×(18×19×110)+17×(19×110)+19×110=。

5.2009×(1+12+13+⋯+12008)−〔1+(1+12)+(1+12+13)+⋯+(1+12+13+⋯+12008)〕= .6. 如果A◆B=1A×B,那么1◆2-2◆3-3◆4—…-2002◆2003—2003◆2004= .7.11+1311×12×13+12+1412×13×14+13+1513×14×15+⋯+119+121119×120×121= 。

六年级数学上册小数的综合运算练习题（本文为虚构内容，仅供参考）在六年级数学上册中，小数的综合运算是一个重要且基础的知识点。

通过练习题的形式，可以巩固和提升学生们对小数的运算能力。

以下是一些六年级数学上册小数的综合运算练习题，希望能帮助同学们更好地掌握这一知识点。

1. 小数的加减法运算（1）0.32 + 0.97 = ?（2）2.15 - 0.76 = ?（3）4.6 + 1.23 = ?2. 小数的乘法运算（1）1.2 × 0.5 = ?（2）0.6 × 3.4 = ?（3）0.25 × 0.4 = ?3. 小数的除法运算（1）2.28 ÷ 0.6 = ?（2）3.45 ÷ 1.5 = ?（3）0.96 ÷ 0.8 = ?4. 小数间的综合运算（1）2.1 + 0.3 - 1.67 = ?（2）4.5 × 1.2 - 0.6 = ?（3）6.72 ÷ 0.6 + 3.12 = ?通过以上练习题，同学们可以运用小数的加减乘除法进行计算。

为了顺利解答练习题，有一些注意事项需要大家注意：首先，在进行小数的加减乘除法时，需要保持数位对齐，即小数点要相应对齐。

这样可以使计算更加准确，避免出现错误的答案。

其次，当遇到小数相加减或乘除时，可以将其转化为分数进行计算。

这样更有利于理解和解决问题。

此外，同学们还应注意计算机两边的数值大小，合理选择运算顺序，以避免产生计算错误。

以上练习题仅为数学上册小数的综合运算的一部分，希望同学们能够通过多做练习，掌握小数的运算技巧。

总之，小数的综合运算在数学学习中是非常重要的。

通过不断练习和巩固，同学们可以逐渐掌握这一知识点，并且在实际问题中灵活运用。

希望同学们能够认真对待每一个练习题，积极参与课堂讨论，提高自己的数学能力。

加油！。