单筋,矩形,正截面受弯,承载力计算

单筋矩形截面正截面承载力计算方法
在计算单筋矩形截面的承载力时，我们需要考虑两种主要的受力情况：剪力和弯矩。

以下是单筋矩形截面承载力计算的详细方法。

1.剪力承载力计算：
首先，计算纵向筋的贡献：
Vr = φ × As × fy /γs
其中，Vr为纵向筋的承载力，φ为抗剪强度折减系数，一般取0.75，As为纵向筋的截面面积，fy为纵向筋的抗拉强度设计值，γs为安全系数，一般取1.15
然后，计算混凝土的贡献：
Vc = φ × b × x × fcd /γc
其中，Vc为混凝土的承载力，b为矩形截面的宽度，x为截面混凝土
受剪应力点至受拉纵筋的距离，fcd为混凝土的抗压强度设计值，γc为
混凝土安全系数，一般取1.5
最终，剪力承载力为：
V=Vr+Vc
2.弯矩承载力计算：
首先，计算纵向筋的承载力：
Mr = φ × (As × fy) × (d - a/2) / γs
其中，Mr为纵向筋的弯矩承载力，d为矩形截面的有效高度，a为纵向筋至受压边缘的距离，As为纵向筋的截面面积，fy为纵向筋的抗拉强度设计值，γs为安全系数。

3.组合效应计算：
在实际情况中，剪力和弯矩通常是同时作用于单筋矩形截面的。

根据极限状态设计原则，剪力和弯矩的组合效应需要考虑。

计算组合效应时，可以根据相应的超信度进行组合，采用相应的抗风定额规定即可。

综上所述，单筋矩形截面的承载力计算主要包括剪力承载力和弯矩承载力的计算，并根据实际受力情况考虑组合效应。

详细的计算公式和参数需要根据具体情况进行设计和选择，以确保梁的安全可靠性。

单筋矩形截面受弯构件正截面承载力计算单筋矩形截面受弯构件是指具有一个纵向钢筋（单筋）和一个矩形截面的构件。

在受弯时，矩形截面受到压力，而钢筋受到拉力，通过计算正截面承载力可以确定该构件的安全性能。

下面将介绍单筋矩形截面受弯构件正截面承载力的计算方法。

首先，计算正截面的受压区高度h和内力矩M。

假设构件受弯时的截面高度为h，宽度为b，截面厚度为d。

根据等截面原则，构件的正截面宽度和截面高度相等，即b=h。

构件的弯矩M由下式计算得出：M=Rd·Z，其中Rd为设计弯矩，Z为正截面抵抗矩。

然后，计算正截面抵抗矩Z。

在单筋矩形截面中，正截面抵抗矩由钢筋和混凝土组成。

钢筋的抵抗矩可由以下公式计算得出：Zs=As·fy·(h-d/2)，其中As为钢筋截面面积，fy为钢筋的抗拉强度。

混凝土的抵抗矩可由以下公式计算得出：Zc=0.85·fck·(b·h-(As+Asc)·(h/2-d/2))，其中fck为混凝土的抗压强度，Asc为纵向钢筋表面积。

正截面的抵抗矩由钢筋的抵抗矩和混凝土的抵抗矩之和得出：Z=Zs+Zc。

接下来，计算正截面的承载力。

正截面受弯构件的承载力由以下条件中的最不利情况决定：1.混凝土达到极限压应力或者钢筋达到屈服应力；2. 混凝土达到达到破坏应变时，即混凝土压应力达到0.45fck或者钢筋达到屈服应变。

计算混凝土达到极限压应力的情况下的承载力，可以得到下式：Nc=0.85·fcd0·A+(Rd-Zs)/Rd·fctd0·A，其中fcd0为混凝土的设计强度，fctd0为混凝土的设计抗拉强度，A为截面面积。

计算钢筋达到屈服应力的情况下的承载力，可以得到下式：Ns=(Zs/0.9zτs)·fsd，其中z为混凝土的截面中和高度，τs为混凝土的应力分布系数，fsd为钢筋的设计抗拉强度。

综合两种情况，正截面受弯构件的正截面承载力Fc为较小值：Fc=min{Nc,Ns}。

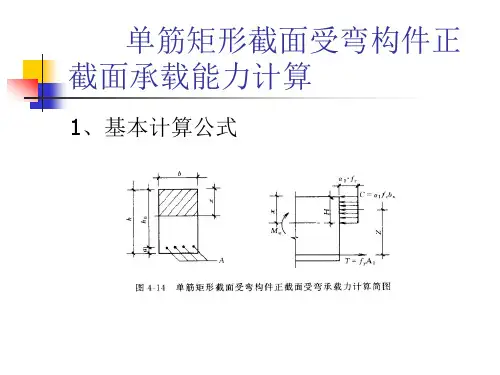
单筋矩形正截面受弯承载力计算公式根据图1和截面内力平衡条件，并满足承载能力极限状态计算表达式的要求，可得出如下基本计算公式：图1 单筋矩形截面梁板正截面受弯承载力计算简图∑x=0 f c bx=f y A s（1）∑M=0 KM≤f c bx（h0−）（2）式中M——弯矩设计值（N·mm）；f c——混凝土轴心抗压强度设计值（N/mm2），按附表1–2取用；b——矩形截面宽度（mm）；x——混凝土受压区计算高度（mm）；h0——截面有效高度（mm）；f y——受拉钢筋的强度设计值（N/mm2），按附表1–5取用；A s——受拉钢筋的截面面积（mm2）；K——承载力安全系数, 按表1–7取用。

利用基本公式进行截面计算时，必须求解方程组，比较麻烦。

为简化计算，将式（1）、(2）改写如下：将ξ=x/h0代入公式（1）、(2)，并引入截面抵抗矩系数αs，令αs =ξ（1–ξ）（3）则基本公式改写为：f c bξh0=f y A s（4）KM≤αs f c bh02（5）由式（4）可得：ρ= ξf c/f y基本公式是根据适筋破坏的情况推导出来的。

因此，它的适用条件为：（1）ρ≤ρmax或x ≤ξb h0或ξ≤ξb，以防止发生超筋破坏，ρmax=ξb f c/f y；基本公式是依据适筋构件破坏时的应力图形情况推导的，当受拉钢筋屈服的同时，受压区混凝土也达到极限压应变εcu，梁发生的临界破坏状态，就是适筋梁与超筋梁的界限。

但为了结构的安全，更有效地防止发生超筋破坏,，应用基本公式和由它派生出来的公式计算时，必须符合此条件。

（2）ρ≥ρmin，以防止发生少筋破坏钢筋混凝土梁板构件破坏时承担的弯矩等于同截面素混凝土梁板构件所能承担的弯矩时的受力状态，为适筋破坏与少筋破坏的分界。

这时梁板的配筋率应是适筋梁板的最小配筋率。

《规范》不仅考虑了这种“等承载力”原则，而且还考虑了混凝土的性质和工程经验等。

因此，基本公式应符合此条件。

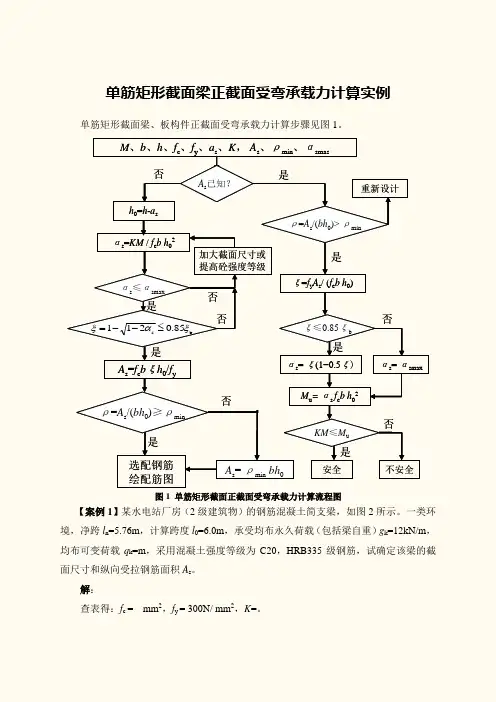
单筋矩形截面梁正截面受弯承载力计算实例单筋矩形截面梁、板构件正截面受弯承载力计算步骤见图1。

选配钢筋加大截面尺寸或是M 、b 、h 、f c 、f y 、a s 、K ，A s 、ρmin 、αsmasαs =KM / f c b h 02A s =f c b ξh 0/f ybs 85.0211ξαξ≤--=h 0=h -a s否A s = ρmin bh 0绘配筋图是是A s 已知？αs ≤αsmax提高砼强度等级ρ=A s /(bh 0)≥ρmin是ξ=f y A s / (f c b h 0)ξ≤0.85ξbαs = ξ(1−0.5ξ)M u = αs f c b h 02KM ≤M u是是安全αs = αsmax否否不安全否否否ρ=A s /(bh 0)> ρmin是重新设计图1 单筋矩形截面正截面受弯承载力计算流程图【案例1】某水电站厂房（2级建筑物）的钢筋混凝土简支梁，如图2所示。

一类环境，净跨l n =5.76m ，计算跨度l 0=6.0m ，承受均布永久荷载（包括梁自重）g k =12kN/m ，均布可变荷载q k =m ，采用混凝土强度等级为C20，HRB335级钢筋，试确定该梁的截面尺寸和纵向受拉钢筋面积A s 。

解：查表得：f c = mm 2，f y = 300N/ mm 2，K =。

（1）确定截面尺寸 由构造要求取：h =（1/8～1/12）l 0 =（1/8～1/12）×6000=750～500，取h =500mm b =（1/2～1/3）h =（1/2～1/3）×500=250～167，取b =250mm （2）内力计算M =（+ ）l 02/8=（×12+×）×62 /8 = ·m （3）配筋计算取a s =40mm ，则h 0=h –a s =500–40=460mm==2c s bh f KMα248.04602506.91076.10420.126=⨯⨯⨯⨯ 290.0248.0211211s =⨯--=--=αξ＜ξb =×=A s =f c bξh 0/f y =×250××460/300=1067mm 2 ρ= 1067/（250×460）=﹪＞ρmin =﹪（4）选配钢筋，绘制配筋图选受拉纵筋为322（A s =1140 mm 2），需要最小梁宽b min =2c +3d +2e =2×30+ 3×22+2×25=176（mm ）＜250mm ，符合构造要求。

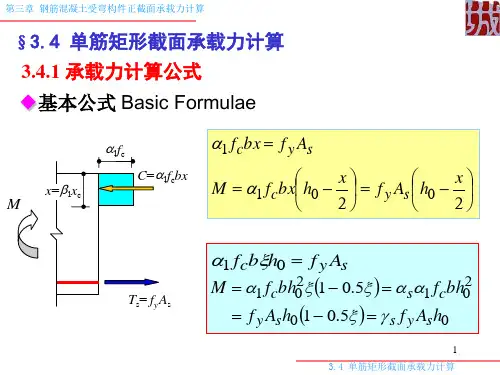
基本构件计算：单筋矩形梁正截面承载力计算一、计算简图二、基本公式1．公式法的三个基本公式：单筋矩形梁正截面受弯承载力计算的三个基本公式：s y c A f bx f =1α⎪⎭⎫ ⎝⎛-=≤201x h bx f M M c u α⎪⎭⎫ ⎝⎛-=≤20x h A f M M s y u式中 M —— 弯矩设计值；M u —— 受弯承载力设计值，即破坏弯矩设计值；c f 1α—— 混凝土等效矩形应力图的应力值； y f —— 钢筋抗拉强度设计值； s A —— 受拉钢筋截面面积； b —— 梁截面宽度； x —— 混凝土受压区高度；h 0 —— 截面有效高度，即截面受压边缘到受拉钢筋合力点的距离，h 0=h-a ； a —— 受拉钢筋合力点到梁受拉边缘的距离，当受拉钢筋为一排时，a =c+d/2； c —— 混凝土保护层厚度； d —— 受拉钢筋直径。

2．系数法的基本公式（1）系数的公式).(s ξ-ξ=α501(4-21)s αξ211--= (4-25)ξ-=α-+=γ5012211.ss (4-26)（2）基本公式 21201)5.01(bh f bh f M c s c ααξξα=-=0h A f M s s y γ=三、基本公式的适用条件1）防止超筋破坏b ξξ≤ 或 b ρρ≤ 或 0h x b ξ≤2）防止少筋破坏bh A A s s min min ,ρ=≥四、计算方法1．截面选择（设计题）按已知的荷载设计值作用下的弯矩M 设计截面时，常遇到下列两种情形： 情形1 ： 已知：M 、混凝土强度等级及钢筋等级；构件截面尺寸b 及h 。

求：所需的受拉钢筋截面面积A s 。

[解]（1）确定基本数据c f ；y f ；a h h -=0（2）计算有关系数21bh f Mc s αα=s αξ211--=ξ-=α-+=γ5012211.ss（3）计算受拉钢筋 0h f MA s y s γ=或 01bh f f A ycs αξ=（4）根据求得的受拉钢筋A s ，按照有关构造要求从附表20中选用钢筋直径和根数 （5）验算适用条件1）适用条件：b ξ≤ξ；2）若b ξ>ξ：需加大截面，或提高混凝土强度等级，或改用双筋矩形截面 3）验算bh A A m in m in ,s s ρ=≥。

单筋矩形梁正截面承载力计算基本公式的适
用条件是
单筋矩形梁是结构工程中常见的一种梁型，其正截面承载力计算
基本公式的适用条件是指在满足以下条件的情况下，可以通过该公式
计算单筋矩形梁的正截面承载力。

首先，单筋矩形梁的截面形状必须为矩形或近似矩形，梁的纵向
应力分布应为线性分布，且配筋符合规定。

在满足这些基本条件的情
况下，我们可以使用以下的正截面承载力计算公式：
Mrd = As * fy * (d - a/2)
其中，Mrd为弯矩承载力，As为钢筋截面积，fy为钢筋的抗拉强度，d为截面的有效高度，a为受压破坏区的高度。

这个公式的使用需要涉及一些常识和要点，下面我们就来详细了
解一下：
首先，对于单筋梁的受压区混凝土强度的计算，我们需要考虑许
多因素，如混凝土的强度等级、钢筋的截面积和布置方式、截面的形
状和尺寸等。

在确定好这些参数后，我们可以采用双曲线拟合式或者
折线近似式来计算混凝土的受压强度。

另外，对于弯矩承载力的计算，我们需要注意钢筋的屈服点位置，根据不同的材料强度和计算方法，屈服点位置的计算方式也不同。

在
实际工程中，根据结构的具体情况和设计要求，可以采用不同的计算方法进行弯矩承载力的计算。

除此之外，我们还需要考虑一些其他因素，如混凝土的徐变效应和干缩效应、钢筋的锚固长度等。

在进行正截面承载力计算时，需要全面了解这些因素，并根据实际情况进行适当修正。

综上所述，单筋矩形梁正截面承载力计算基本公式的适用条件是在满足一定前提条件并考虑到一些细节和特殊情况的基础上使用的，工程设计师在进行计算时需要注意这些因素，以确保计算的准确性和可靠性。