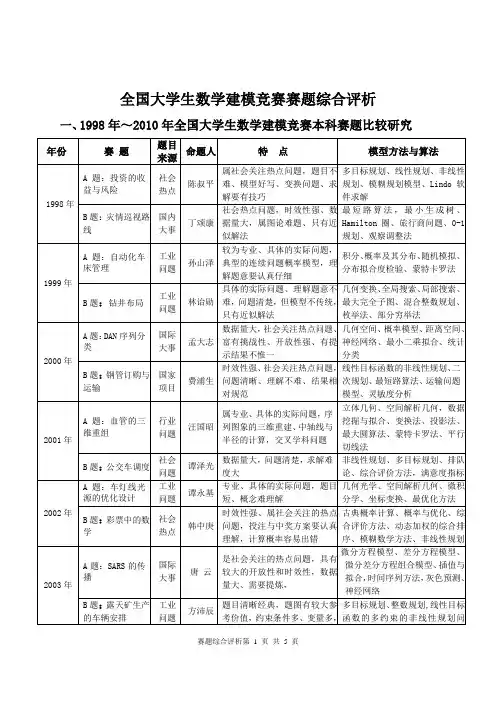
全国大学生数学建模竞赛2009年D题_会议筹备问题
- 格式:ppt
- 大小:288.00 KB
- 文档页数:30
2010年湖北省数模会议交流报告2009全国赛D题“会议筹备”简要解答及阅卷情况介绍海军工程大学李卫军2010.06 湖北咸宁各位专家、教练大家好!一、2009全国赛D题题目:已知:10家宾馆的有关信息(附表1)本届会议的代表回执中有关住房要求的信息(附表2)以往几届会议代表回执和与会情况(附表3)会议期间有一天的上下午各安排6个分组会议,筹备组需要在代表下榻的某几个宾馆租借会议室。
由于事先无法知道哪些代表准备参加哪个分组会,筹备组还要向汽车租赁公司租用客车接送代表。
现有45座、36座和33座三种类型的客车,租金分别是半天800元、700元和600元。
请你们通过数学建模方法,从经济、方便、代表满意等方面,为会议筹备组制定一个预订宾馆客房、租借会议室、租用客车的合理方案。
二、问题的分析据题目要求,需要解决的问题是:会务组需要在那几家宾馆预订哪些规格的客房与会议室各多少间,以及租借何种规格的车辆各多少辆,使得租车费用与“空房”损失费最少,同时使得代表相对满意,管理方便等等。
解决问题的前提:需要预测与会代表的人数。
进一步:需要预测各类与会代表的人数(按住房要求,可分为5类)。
再下一步,在预测的各类与会代表的人数基础上,确定在那几家宾馆预订哪些规格的客房与会议室各多少间,以及租借何种规格的车辆各多少辆,目标是总费用最少,同时还要考虑尽量减少代表因达不到住房要求的不满以及管理方便。
以上是一个比较复杂的规划问题,求解有一定的困难。
可以将该问题近似地分成两步进行:先确定在那几家宾馆预订哪些规格的客房各多少间,然后确定在那几家宾馆预订哪些规格的会议室各多少间,以及租借何种规格的车辆各多少辆。
也就是先订客房,后订会议室与车辆。
于是所述问题分解为下面三个问题:1)预测本届会议与会代表的数量,并且确定需要预订的各类客房的总量;2)确定在哪些宾馆预订客房及预订各类客房的数量;3)确定在哪些宾馆预订哪些类型的会议室以及租车的规格和数量。


会议筹备模型摘要本文以经济、方便、代表满意等方面的要求为约束,建立预订客房、租借会议室和租用客车的优化模型。
首先,通过以往几届会议代表回执和与会的情况,利用线性最小二乘拟合法预测本届发来回执但未与会的代表人数;并建立)1,1(GM灰色预测模型,预测未发回执但到会的代表人数,再对附表1进行统计分析,排除明显不符合要求的宾馆。
然后,在充分满足代表住房要求的前提下,通过制定合理的分配原则,使出现空客房的几率最低,并以各客房到各个宾馆的总距离之和最小为目标,建立预订宾馆客房的线性整数优化模型一。
利用lingo软件编程求得每个宾馆的预订客房详情如下表:花费之和最小为目标的0-1整数规划模型。
利用lingo软件编程求得租车最优级方案为:租用33化,通过合理的假设建立适当的优化模型,运用数学软件求解,得到了比较符合实际的结果。
关键词:线性最小二乘拟合灰色预测统计分析0-1整数规划一、问题重述某市的一家会议服务公司负责承办某专业领域的一届全国性会议,会议筹备组要为与会代表预订宾馆客房,租借会议室,并租用客车接送代表。
由于预计会议规模庞大,而适于接待这次会议的几家宾馆的客房和会议室数量均有限,所以只能让与会代表分散到若干家宾馆住宿。
为了便于管理,除了尽量满足代表在价位等方面的需求之外,所选择的宾馆数量应该尽可能少,并且距离上比较靠近。
筹备组经过实地考察,筛选出10家宾馆作为备选,它们的名称用代号①至⑩表示相对位置,且给出客房及会议室的规格、间数、价格等数据。
根据这届会议代表回执整理出来的有关住房的信息(见附录1)。
从以往几届会议情况看,有一些发来回执的代表不来开会,同时也有一些与会的代表事先不提交回执,相关数据见附录2。
需要说明的是,虽然客房房费由与会代表自付,但是如果预订客房数量大于实际用房数量,筹备组需要支付一天的空房费,而若出现预订客房不足,则将造成非常被动的局面,引起代表的不满。
会议期间有一天的上下午各安排6个分组会议,筹备组需要在代表下榻的某几个宾馆租借会议室。

2009年数学建模考题A题制动器试验台的控制方法分析(缺附录)汽车的行车制动器(以下简称制动器)联接在车轮上,它的作用是在行驶时使车辆减速或者停止。
制动器的设计是车辆设计中最重要的环节之一,直接影响着人身和车辆的安全。
为了检验设计的优劣,必须进行相应的测试。
在道路上测试实际车辆制动器的过程称为路试,其方法为:车辆在指定路面上加速到指定的速度;断开发动机的输出,让车辆依惯性继续运动;以恒定的力踏下制动踏板,使车辆完全停止下来或车速降到某数值以下;在这一过程中,检测制动减速度等指标。
假设路试时轮胎与地面的摩擦力为无穷大,因此轮胎与地面无滑动。
为了检测制动器的综合性能,需要在各种不同情况下进行大量路试。
但是,车辆设计阶段无法路试,只能在专门的制动器试验台上对所设计的路试进行模拟试验。
模拟试验的原则是试验台上制动器的制动过程与路试车辆上制动器的制动过程尽可能一致。
通常试验台仅安装、试验单轮制动器,而不是同时试验全车所有车轮的制动器。
制动器试验台一般由安装了飞轮组的主轴、驱动主轴旋转的电动机、底座、施加制动的辅助装置以及测量和控制系统等组成。
被试验的制动器安装在主轴的一端,当制动器工作时会使主轴减速。
试验台工作时,电动机拖动主轴和飞轮旋转,达到与设定的车速相当的转速(模拟实验中,可认为主轴的角速度与车轮的角速度始终一致)后电动机断电同时施加制动,当满足设定的结束条件时就称为完成一次制动。
路试车辆的指定车轮在制动时承受载荷。
将这个载荷在车辆平动时具有的能量(忽略车轮自身转动具有的能量)等效地转化为试验台上飞轮和主轴等机构转动时具有的能量,与此能量相应的转动惯量(以下转动惯量简称为惯量)在本题中称为等效的转动惯量。
试验台上的主轴等不可拆卸机构的惯量称为基础惯量。
飞轮组由若干个飞轮组成,使用时根据需要选择几个飞轮固定到主轴上,这些飞轮的惯量之和再加上基础惯量称为机械惯量。
例如,假设有4个飞轮,其单个惯量分别是:10、20、40、80 kg·m2,基础惯量为10 kg·m2,则可以组成10,20,30,…,160 kg·m2的16种数值的机械惯量。

会议筹备问题的多目标最优化模型林斌【摘要】利用2009年全国大学生数学建模竞赛D题的会议筹备问题,通过预测与会代表总人数和合理的住宿安排方案,建立预订宾馆客房的多目标最优化模型;在租借会议室和租用客车上采用等可能假设,并给出费用的最优化模型.最后利用LING09.0得出会议筹备总费用的全局最优解.【期刊名称】《温州职业技术学院学报》【年(卷),期】2010(010)001【总页数】4页(P44-46,50)【关键词】会议筹备;多目标最优化;等可能假设;全局最优解【作者】林斌【作者单位】温州职业技术学院,公共教学部,浙江,温州,325035【正文语种】中文【中图分类】O221.6会议筹备问题是2009年全国大学生数学建模竞赛D题,要求参赛队伍为会议筹备组制定一个预订宾馆客房、租借会议室、租用客车的合理方案。
同时,竞赛D题给出了两类数据:一是前几届会议代表回执和与会情况及本届会议代表回执中有关住房要求的信息,包含独住、合住、对房间的价位要求。
二是会议筹备组经过实地考察,筛选出10家备选宾馆的相对位置以及各宾馆客房和会议室的规格、间数、价格等数据。
通过初步分析可以发现,会议筹备问题的解题思路是多目标最优化分析[1],即预定宾馆客房在满足与会代表住房要求的前提下不仅要使空房费用最低,而且宾馆数量应该尽可能少、距离上比较靠近;会议室的安排上必须先给出各宾馆间与会代表流动的合理假设。
最后利用LINGO9.0简化编程并高效求解。
对竞赛D题给出的前几届会议代表回执和与会情况数据进行统计发现,发来回执但未与会的代表比例稳定,为30%,未发回执而与会的代表比例约为17.6%。
与会代表比例、均值和方差见表1。
可以认为,发来回执未与会的代表比例和未发回执而与会的代表比例服从正态分布,并取置信度为95%,则应取置信区间下分位点作为发来回执未与会的代表预测数量,取置信区间上分位点作为未发回执而与会的代表预测数量。
其计算公式[2]为:将数据代入上式计算得到与会代表总数为685.25人,向上取整数为686人,其中发来回执且与会的代表539人,未发回执而与会的代表147人。


承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): D我们的参赛报名号为(如果赛区设置报名号的话):20093701所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):会议筹备方案的优化设计模型摘要:本文研究对会议筹备方案的设计,本文的整体方案在满足实际参会代表要求的前提下使会议开支成本更经济。
对于预订宾馆客房数,首先根据附表二和附表三预估实际参会代表人数和参会代表的住宿要求,在此基础上使用0-1规划和矩阵性质求出实际需要宾馆的最少数目、为了便于集中管理采用层次分析将宾馆的具体安排地点加以确定。
租借会议室以经济方便为原则,使用弗洛伊德(Floyd)算法求出作为会议地点最合适的宾馆,便于推广。
租赁客车按照经济、方便的原则,提出三种方案加以比较最终的出最有的租赁方案。
在总结中我们为主办方会议服务公司为这次大会提出整体筹划方案。
帮助解决了在筹备会议中的成本运算和地点安排中的难题。
并在模型推广中提出合理的建设性意见。
关键字:层次分析 0-1规划运筹路线约束目标优化1问题的提出:大会会议筹备组为了更好的组织好会议,需要筹备的事务主要有以下几部分:为大会会议代表预订宾馆客房,租借会议室,并租用客车从宾馆开会地点接送代表。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): D我们的参赛报名号为(如果赛区设置报名号的话):2926所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:20089 年9 月14 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):会议筹备的合理方案摘要:本文从经济、方便、代表满意等方面来深入分析问题,为会议筹备组制定一个预订宾馆客房、租借会议室、租用客车的合理方案。
1、根据以往几届会议代表回执和与会的数据,用matlab软件进行线性拟合,得到一元一次线性回归方程y=8.9x1-230和y=3.3x2+3.5及其图形(见模型一、二),根据附表2所给的数据,得出本届发来回执的代表人数y为755人。
结合一元一次线性回归方程,可以算出本届可能与会的代表数量U为638人。
2、用会议厅的价格除以其规模,得到的比例系数r越小,会议厅的价格相对就越便宜。
按比例系数r的大小升序排列,取出一组靠前的数据(见表2),再以筹备组租用会议室总费用最小为目标函数,用lingo计算出较优的6个会议厅,结果显示这6个会议厅都是在代号7的宾馆内。
所有的与会代表只需到代号7的宾馆开会。

2009高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)D题会议筹备某市的一家会议服务公司负责承办某专业领域的一届全国性会议,会议筹备组要为与会代表预订宾馆客房,租借会议室,并租用客车接送代表。
由于预计会议规模庞大,而适于接待这次会议的几家宾馆的客房和会议室数量均有限,所以只能让与会代表分散到若干家宾馆住宿。
为了便于管理,除了尽量满足代表在价位等方面的需求之外,所选择的宾馆数量应该尽可能少,并且距离上比较靠近。
筹备组经过实地考察,筛选出10家宾馆作为备选,它们的名称用代号①至⑩表示,相对位置见附图,有关客房及会议室的规格、间数、价格等数据见附表1。
根据这届会议代表回执整理出来的有关住房的信息见附表2。
从以往几届会议情况看,有一些发来回执的代表不来开会,同时也有一些与会的代表事先不提交回执,相关数据见附表3。
附表2,3都可以作为预订宾馆客房的参考。
需要说明的是,虽然客房房费由与会代表自付,但是如果预订客房的数量大于实际用房数量,筹备组需要支付一天的空房费,而若出现预订客房数量不足,则将造成非常被动的局面,引起代表的不满。
会议期间有一天的上下午各安排6个分组会议,筹备组需要在代表下榻的某几个宾馆租借会议室。
由于事先无法知道哪些代表准备参加哪个分组会,筹备组还要向汽车租赁公司租用客车接送代表。
现有45座、36座和33座三种类型的客车,租金分别是半天800元、700元和600元。
请你们通过数学建模方法,从经济、方便、代表满意等方面,为会议筹备组制定一个预订宾馆客房、租借会议室、租用客车的合理方案。
附表1 10家备选宾馆的有关数据说明:表头第一行中的数字1、2、3分别指每天每间120~160元、161~200元、201~300元三种不同价格的房间。
合住是指要求两人合住一间。
独住是指可安排单人间,或一人单独住一个双人间。
附图(其中500等数字是两宾馆间距,单位为米)。

2009高教社杯全国大学生数学建模竞赛题目A题制动器试验台的控制方法分析汽车的行车制动器(以下简称制动器)联接在车轮上,它的作用是在行驶时使车辆减速或者停止。
制动器的设计是车辆设计中最重要的环节之一,直接影响着人身和车辆的安全。
为了检验设计的优劣,必须进行相应的测试。
在道路上测试实际车辆制动器的过程称为路试,其方法为:车辆在指定路面上加速到指定的速度;断开发动机的输出,让车辆依惯性继续运动;以恒定的力踏下制动踏板,使车辆完全停止下来或车速降到某数值以下;在这一过程中,检测制动减速度等指标。
假设路试时轮胎与地面的摩擦力为无穷大,因此轮胎与地面无滑动。
为了检测制动器的综合性能,需要在各种不同情况下进行大量路试。
但是,车辆设计阶段无法路试,只能在专门的制动器试验台上对所设计的路试进行模拟试验。
模拟试验的原则是试验台上制动器的制动过程与路试车辆上制动器的制动过程尽可能一致。
通常试验台仅安装、试验单轮制动器,而不是同时试验全车所有车轮的制动器。
制动器试验台一般由安装了飞轮组的主轴、驱动主轴旋转的电动机、底座、施加制动的辅助装置以及测量和控制系统等组成。
被试验的制动器安装在主轴的一端,当制动器工作时会使主轴减速。
试验台工作时,电动机拖动主轴和飞轮旋转,达到与设定的车速相当的转速(模拟实验中,可认为主轴的角速度与车轮的角速度始终一致)后电动机断电同时施加制动,当满足设定的结束条件时就称为完成一次制动。
路试车辆的指定车轮在制动时承受载荷。
将这个载荷在车辆平动时具有的能量(忽略车轮自身转动具有的能量)等效地转化为试验台上飞轮和主轴等机构转动时具有的能量,与此能量相应的转动惯量(以下转动惯量简称为惯量)在本题中称为等效的转动惯量。
试验台上的主轴等不可拆卸机构的惯量称为基础惯量。
飞轮组由若干个飞轮组成,使用时根据需要选择几个飞轮固定到主轴上,这些飞轮的惯量之和再加上基础惯量称为机械惯量。
例如,假设有4个飞轮,其单个惯量分别是:10、20、40、80 kg·m2,基础惯量为10 kg·m2,则可以组成10,20,30,…,160 kg·m2的16种数值的机械惯量。
内涵。
“仁政”是孟子学说的一个重要组成部分,“以民为本”是仁政学说的核心,以身行道、宽猛相济、与民同乐、选贤举能、礼治德教等不仅是仁政说的思想内涵,也是实施仁政理想的具体措施。
但是,孟子从历史的教训中强调统治阶级要施行“仁政”,这在当时具有一定的积极意义和进步性,但也不能掩盖其保守落后的一面,孟子的仁政实质上是美化了贵族统治,毫无限制地夸大了仁政的作用。
虽然孟子的“仁政”学说有一定的历史局限性,但对于今天我们构建社会主义和谐社会仍然具有重要的借鉴价值。
三、构建和谐社会必须“强国富民”孟子认为,国家强大,人民富裕,社会才能稳定和谐。
要使国家强大必须施“仁政”,经济上要使百姓更加富裕,百姓越富裕则社会文明水平越高,社会越稳定,二者相辅相成。
他提出富民的最高理想是“至足”使家家“有菽粟如水火”,若能“食之以时,用之以礼,则财不可胜用也”。
如果做到这样的话,“民焉有不仁者乎”。
[9]第一,孟子富民思想的基础是“制民恒产”。
他说:“五亩之宅,树之从桑,五十者可以衣帛矣。
鸡豚狗彘之畜,无失其时,七十者可以食肉矣。
百亩之田,勿夺其时,八口之家,可以无饥矣。
”[10]“民之为道也,有恒产者有恒心,无恒产者无恒心,苟无恒心,放辟邪侈,无不为已。
”[11]孟子的意思是说,要使每个人都有一定的稳固产业,他才有一定的道德观念和行为准则;没有一定的稳固产业的人,便不会有一定的道德观念和行为准则。
有恒产,人心就思稳,人心就思定,人心就思进。
按照孟子的描述,以八口之家为单位占有一定数量的土地,使他们成为自给自足的小农,他们的生产就有了积极性。
孟子强调以统治阶级的道德意识向人民灌输稳定社会秩序外,也注意到保障人民的物质生活,是使人民心服的重要条件。
“明君制民之产,必使仰足以事父母,俯足以畜妻子,乐岁终身饱,凶年免于死亡,然后驱而之善,故民之从之也轻。
”[11]所以统治者应考虑到人民的疾苦,不能独行其乐。
只有这样,才能得到天下。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞赛规则的行为,我们将受到严肃处理.我们参赛选择的题号是(从A/B/C/D中选择一项填写): D我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):XXXXXX参赛队员(打印并签名) :1 . XXXXX2 . XXXXX3 .指导教师或指导教师组负责人(打印并签名):XXXXXX日期:2009年 9 月 14日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):会议筹备最优化一.摘要在激烈的市场竞争中,随着市场经济在中国大陆的不断发展,各种新兴行业也在悄然而起 .会议服务公司通过对宾馆客房、租借会议室、租用客车接送代表等几块服务,让顾客觉得经济、方便同时使满意度达到最高,会议服务公司需要从公司的经济利益和社会声誉等诸多因素来考虑,在此,我们运用线性规划和概率统计的知识,来解决对宾馆客房分配问题 .会议的经济安排从预定房间的量和安排的合理性来决定;在安排客车接送会议代表运用运筹学分成几条路线;服务公司的社会声誉在市场竞争中是非常重要的,在此我们用会议代表对总体的满意度来衡量.我们应用概率统计的知识,得出参加会议人员大约为661人 .根据与会人员对住房的要求,我们设计了第一个模型,且有3个方案,第一个方案利用Lingo软件计算得其无解,同样利用Lingo软件计算得最优解.通过调整第一类单人间住房的人数建立模型二,得出所有与会代表住房安排,此时得出住房费的最少价格为80630元 .对模型二进一步优化,通过对宾馆调整,把与会代表集中按排在①、②、⑤、⑥、⑦、⑧、⑨宾馆 .利用“中心极限”定理,计算得出可能出现空床费赔偿的概率大约是12%.同样应用“中心地址”的算法确定开会会议宾馆定为⑦、⑧宾馆 .用运筹学的知识确定出接送与会代表路线,并安排出了接送的车辆类型和数量关键词:线性规划概率统计 Lingo 中心地址运筹学二.问题重述某市的一家会议服务公司负责承办某专业领域的一届全国性会议,会议筹备组要为与会代表预订宾馆客房,租借会议室,并租用客车接送代表 .由于预计会议规模庞大,而适于接待这次会议的几家宾馆的客房和会议室数量均有限,所以只能让与会代表分散到若干家宾馆住宿 .为了便于管理,除了尽量满足代表在价位等方面的需求之外,所选择的宾馆数量应该尽可能少,并且距离上比较靠近 .筹备组经过实地考察,筛选出10家宾馆作为备选,它们的名称用代号①至⑩表示,相对位置见附图,有关客房及会议室的规格、间数、价格等数据见附表1 .根据这届会议代表回执整理出来的有关住房的信息见附表2 .从以往几届会议情况看,有一些发来回执的代表不来开会,同时也有一些与会的代表事先不提交回执,相关数据见附表3 .附表2,3都可以作为预订宾馆客房的参考 .需要说明的是,虽然客房房费由与会代表自付,但是如果预订客房的数量大于实际用房数量,筹备组需要支付一天的空房费,而若出现预订客房数量不足,则将造成非常被动的局面,引起代表的不满 .会议期间有一天的上下午各安排6个分组会议,筹备组需要在代表下榻的某几个宾馆租借会议室 .由于事先无法知道哪些代表准备参加哪个分组会,筹备组还要向汽车租赁公司租用客车接送代表 .现有45座、36座和33座三种类型的客车,租金分别是半天800元、700元和600元 .我们通过数学建模方法,从经济、方便、代表满意等方面,为会议筹备组制定一个预订宾馆客房、租借会议室、租用客车的合理方案 .元三种不同价格的房间 .合住是指要求两人合住一间 .独住是指可安排单人间,或一人单独住一个双人间 .附图(其中500等数字是两宾馆的距离)三. 模型假设1. 假设模型一中满足所有与会代表的回执要求;2. 假设与会代表参加每组会议是随机的;3. 假设本届与会代表参加会议人数服从往届参加会议人数规律;4. 假设每个与会代表每半天只开一次会议,且会议地点相同;5. 假设每半天所开会议的主题都一致;7.假设每条路线车辆只搭载同一条路线的与会代表 .四. 符号说明ij x 为第i 个宾馆所住的与会代表的第j 种类型住房人数;p 为参加会议人数的总频率;)(i a p 为回执且与会代表的频率(i 取1,2,3,4); )(i b p 为未回执且与会代表的比例(i 取1,2,3,4);M 为找宾馆中心地址问题的矩阵;abc x 表示a 宾馆到b 宾馆c 会议室的与会人数 .五.建立与分析模型一:通过观察附表2可以得到本届回执人数总共为755人,由往届会议代表的回执和与会情况可得知本届与会人数的概率p .因此我们假定模型如下: 设p 为与会的总频率)(i a p 为回执且与会的频率(i 取1,2,3,4) )(i b p 为未回执且与会的比例(i 取1,2,3,4)与会人数的频率:()()b p a p p += 有回执且与会人数的频率)(i a p()7175.03158911=-=a p 677.03561151)(2=-=a p 7034.04081211)(3=-=a p 7004.07112131)(4=-=a p未回执且与会人数的比例()i b p ()1810.0315571==b p ()1938.0356692==b p()1838.0408753==b p ()1463.07111044==b p()()1762.06996.0==b p a p8758.01762.06996.0=+=p通过以往一、二、三、四会议代表回执和与会情况,利用统计分析法,可计算出以往几届参加会议人数的的平均概率,通过平均概率推算本届与会代表的总人数 . 本届与会人数:661755=⨯=p S为了使预定的房间数达到最优,使得空房数量最小,支付空房会达到最小优化 .我们以661人来进行预定房间,我们假设有三种方案 .方案一:我们为了满足各代表的要求,且达到经济,结合表一:利用表一我们建立模型并求解102101949392918382817372716463626153525142413332312423222114131211min 14013028014026013018080903001607511018085160100807010070150907510090807022018011090x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x z +++++++++++++++++++++++++++++++=约束条件:单人间:5384145949214836313726133=++=++=++x x x x x x x x x两人间:431332031021019391736412816253423224231182715251412221=++++++=+++++++=++++++x x x x x x x x x x x x x x x x x x x x x x S.t.9011030603060458080304010060308040407070901002748100706070100203060100102101949392918382817372716463626153525142413332312423222114131211≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x运用计算机计算出结果,并对解进行数据分析发现方案一无解 .因为第一种价格范围的单间数和与会人员的回执信息矛盾 .例如61x 在约束条件下则不能满足与会人员的要求 .宾馆61x 的单间数在代表要求的房间数数量上不能满足,则我们在考虑到经济和尽量使与会代表满意的情况下,建议代表住双人间,即方案二:将61x 的118人在满足了40人之后,考虑到与会人员对宾馆的品质要求 .把剩下的78名分到91x 和93x ,这样在品质要求方面让与会人员达到最大的满意,建立模型:102101949392918382817372716463626153525142413332312423222114131211min 14013028014026013018080903001607511018085160100807010070150907510090807022018011090x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x z +++++++++++++++++++++++++++++++=约束条件:单人间:5384145949214836313726133=++=++=++x x x x x x x x x两人间:431332031021019391736412816253423224231182715251412221=++++++=+++++++=++++++x x x x x x x x x x x x x x x x x x x x x x s.t.90110306030604580803040100308040707090100274810070607010020306010010210194939291838281737271636253525142413332312423222114131211≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤≤x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x运用计算机软件计算,计算结果见附录表一,并对解进行数据分析。
全国大学生数学建模竞赛的历年赛题(1992年—2011年)1992年:(A)作物生长的施肥效果问题(北理工:叶其孝)(B)化学试验室的实验数据分解问题(复旦:谭永基)1993年:(A)通讯中非线性交调的频率设计问题(北大:谢衷洁)(B)足球甲级联赛排名问题(清华:蔡大用)1994年:(A)山区修建公路的设计造价问题(西电大:何大可)(B)锁具的制造、销售和装箱问题(复旦:谭永基等)1995年:(A)飞机的安全飞行管理调度问题(复旦:谭永基等)(B)天车与冶炼炉的作业调度问题(浙大:刘祥官等)1996年:(A)最优捕鱼策略问题(北师大:刘来福)(B)节水洗衣机的程序设计问题(重大:付鹂)1997年:(A)零件参数优化设计问题(清华:姜启源)(B)金刚石截断切割问题(复旦:谭永基等)1998年:(A)投资的收益和风险问题(浙大:陈淑平)(B)灾情的巡视路线问题(上海海运学院:丁颂康)1999年:(A)自动化机床控制管理问题(北大:孙山泽)(B)地质堪探钻井布局问题(郑州大学:林诒勋)(C)煤矸石堆积问题(太原理工大学:贾晓峰)(D)钻井布局问题2000年:(A)DNA序列的分类问题(北工大:孟大志)(B)钢管的订购和运输问题(武大:费甫生)(C)飞越北极问题(复旦:谭永基)(D)空洞探测问题(东北电力学院:关信)2001年:(A)三维血管的重建问题(浙大:汪国昭)(B)公交车的优化调度问题(清华:谭泽光)(C)基金使用计划问题(东南大学:陈恩水)(D)公交车调度问题2002年:(A)汽车车灯的优化设计问题(复旦:谭永基等)(B)彩票中的数学问题(信息工程大学:韩中庚)(C)车灯线光源的计算问题(D)球队的赛程安排问题(清华:姜启源)2003年:(A)SARS的传播问题(集体)(B)露天矿生产的车辆安排问题(吉林大:方沛辰)(C)SARS的传播问题(D)抢渡长江问题(华中农大:殷建肃)2004年:(A)奥运会临时超市网点设计问题(北工大:孟大志)(B)电力市场的输电阻塞管理问题(浙大:刘康生)(C)酒后开车问题(清华:姜启源)(D)公务员的招聘问题(信息工程大学:韩中庚)2005年:(A)长江水质的评价与预测问题(信息工大:韩中庚)(B)DVD在线租赁问题(清华:谢金星等)(C)雨量预报方法的评价问题(复旦:谭永基)(D)DVD在线租赁问题2006年:(A)出版社的资源管理问题(北工大:孟大志)(B)艾滋病疗法的评价及预测问题(天大:边馥萍)(C)易拉罐形状和尺寸的设计问题(北理工:叶其孝)(D)煤矿瓦斯和煤尘的监测与控制问题(信息工程大学:韩中庚)2007年: (A)中国人口增长预测问题(B) 乘公交,看奥运问题(C) 手机“套餐”优惠几何问题(D) 体能测试时间安排问题2008年:(A) 数码相机定位问题(B) 高等教育学费标准探讨问题(C) 地面搜索问题(D) NBA赛程的分析与评价问题2009年:(A) 制动器试验台的控制方法分析问题(B) 眼科病床的合理安排问题(C) 卫星和飞船的跟踪测控问题(D) 会议筹备问题2010年:(A) 储油罐的变位识别与罐容表标定问题(B) 2010年上海世博会影响力的定量评估问题(C) 输油管的布置问题(D) 对学生宿舍设计方案的评价问题2011年:(A) 城市表层土壤重金属污染分析问题(B) 交巡警服务平台的设置与调度问题(C) 企业退休职工养老金制度的改革问题(D) 天然肠衣搭配问题问题。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):湖南交通职业技术学院参赛队员(打印并签名) :1. 聂隆喜2. 任畅3. 吕芳刚指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):会议筹备优化方案【摘要】针对会议筹备中的人数估计、房间预订、会议室租借、车辆租借等关键问题,综合考虑与会代表满意度、会议成本、组织的方便程度等多方面因素,对所给会议筹备问题进行了全面的优化设计。
建立了三个模型,模型一确定了最少宾馆数目,给出了保证与会代表完全满意条件下的宾馆选择方案;模型二综合考虑了成本、方便性、用户满意度等因素,对模型一的结果进行优化,确定宾馆选择和订房方案;模型三对租车方案进行了优化。
文章首先利用附表中数据,对历届发回回执且参加会议的代表比例进行了统计,认为在大数定律作用下,该类代表数量近似服从高斯分布,在90%的置信概率下该类代表不超过544人;对未发回回执而参加会议的代表进行了统计,经过分析后得出该类代表数约为110人。
最终得出与会代表数不超过654人。
利用概率模型对会议室的大小进行了估计,认为在95%置信概率下参加任意分组会议的代表人数不超过124人,选择130人以上的会议室是恰当的。