实训一 方格网法计算场地平整土方量

简述正方形网格法计算场地平整土方量的计算步骤
正方形网格法是一种利用坐标系的方法来计算场地平整土方量的一种特
定法则。

一般情况下，它包括划分网格、计算实际面积和土方量等步骤。

下
面介绍正方形网格法的计算步骤：
第一步，首先选取一个坐标系，在飞线大地测量中选用经纬度表示即可，即可在网格系上计算。

第二步，根据实际情况，划分正方形网格，每个网格的边长一般为20或50米，当地建筑物的位置也可以把网格划在有建筑物的位置上；
第三步，根据天气、视觉断面和流向分布情况，从事地形测量，并计算
出每个网格的实际面积。

第四步，然后计算每个网格中植被量和土方量，不同网格植被量和土方
量也不一样，它们大小由视觉断面决定。

第五步，最后计算每个网格的土方量并累加计算得出场地所需起伏土方
量总值。

正方形网格法可以有效解决测量场地起伏土方量的问题，并且也可以帮
助我们比较准确地统计出每个网格的土方量。

因为其精确的可比性，已经成
为建筑行业中测量起伏土方量的一种重要方法。

总之，正方形网格法在计算
场地平整土方量中的应用令人印象深刻，将会更深入地使建筑行业从测量上
得到更多帮助。

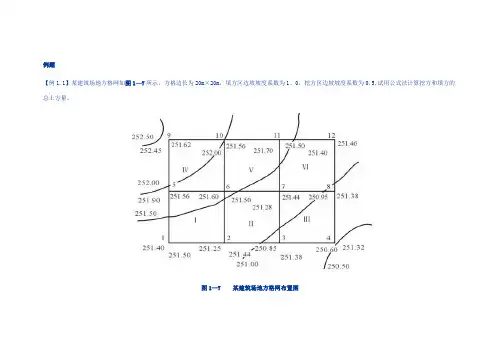
例题【例1.1】某建筑场地方格网如图1—7所示，方格边长为20m×20m，填方区边坡坡度系数为1。

0，挖方区边坡坡度系数为0.5,试用公式法计算挖方和填方的总土方量。

图1—7 某建筑场地方格网布置图【解】（1)根据所给方格网各角点的地面设计标高和自然标高，计算结果列于图1—8中。

由公式1。

9得：h1=251.50-251.40=0.10m h2=251。

44—251。

25=0.19mh3=251。

38-250.85=0。

53m h4=251.32-250.60=0。

72mh5=251.56-251。

90=—0.34m h6=251。

50—251.60=—0。

10mh7=251。

44-251.28=0.16m h8=251.38—250.95=0.43mh9=251。

62-252.45=-0。

83m h10=251。

56-252.00=—0.44mh11=251。

50—251.70=—0.20m h12=251.46—251.40=0.06m图1-8 施工高度及零线位置（2)计算零点位置.从图1-8中可知，1-5、2—6、6-7、7—11、11-12五条方格边两端的施工高度符号不同,说明此方格边上有零点存在. 由公式1.10求得：1-5线x1=4.55（m）2—6线x1=13。

10（m)6—7线x1=7。

69(m）7—11线x1=8。

89(m）11-12线x1=15。

38（m）将各零点标于图上，并将相邻的零点连接起来,即得零线位置，如图1—8.(3)计算方格土方量.方格Ⅲ、Ⅳ底面为正方形，土方量为：VⅢ（+)=202/4×（0。

53+0.72+0.16+0。

43）=184(m3）VⅣ(—）=202/4×(0.34+0.10+0.83+0。

44)=171（m3)方格Ⅰ底面为两个梯形,土方量为：VⅠ（+）=20/8×(4。

55+13.10）×(0。

10+0。

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时，常需要进行土方工程量的计算。

计算方法有方格网法和横断面法两种。

（1)方格网法用于地形较平缓或台阶宽度较大的地段。

计算方法较为复杂，但精度较高，其计算步骤和方法如下：1)划分方格网根据已有地形图（一般用1：500的地形图）将欲计算场地划分成若干个方格网，尽量与测量的纵、横坐标网对应，方格一般采用20m×20m或40m×40m，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。

将自然地面标高与设计地面标高的差值，即各角点的施工高度（挖或填），填在方格网的左上角，挖方为（－），填方为（＋）。

2）计算零点位置在一个方格网内同时有填方或挖方时，应先算出方格网边上的零点的位置，并标注于方格网上，连接零点即得填方区与挖方区的分界线（即零线）。

零点的位置按下式计算（图6-3）：（6-8）式中x1、x2——角点至零点的距离（m）；h1、h2——相邻两角点的施工高度（m），均用绝对值；a——方格网的边长（m）。

图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算，亦可采用图解法直接求出零点位置，如图6-4所示，方法是用尺在各角上标出相应比例，用尺相接，与方格相交点即为零点位置。

这种方法可避免计算（或查表）出现的错误。

3)计算土方工程量按方格网底面积图形和表6-31所列体积计算公式计算每个方格内的挖方或填方量，或用查表法计算，有关计算用表见表6-31。

常用方格网点计算公式表6-31注：1.a——方格网的边长（m）；b、c——零点到一角的边长（m）；h1、h2、h3、h4——方格网四角点的施工高程（m），用绝对值代入；Σh——填方或挖方施工高程的总和（m），用绝对值代入；V——挖方或填方体积（m3）。

2.本表公式是按各计算图形底面积乘以平均施工高程而得出的。

4）计算土方总量将挖方区（或填方区）所有方格计算土方量汇总，即得该场地挖方和填方的总土方量。

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时，常需要进行土方工程量的计算。

计算方法有方格网法和横断面法两种。

（1)方格网法用于地形较平缓或台阶宽度较大的地段。

计算方法较为复杂，但精度较高，其计算步骤和方法如下：1)划分方格网根据已有地形图（一般用1：500的地形图）将欲计算场地划分成若干个方格网，尽量与测量的纵、横坐标网对应，方格一般采用20m ×20m 或40m ×40m ，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。

将自然地面标高与设计地面标高的差值，即各角点的施工高度（挖或填），填在方格网的左上角，挖方为（－），填方为（＋）。

2）计算零点位置在一个方格网内同时有填方或挖方时，应先算出方格网边上的零点的位置，并标注于方格网上，连接零点即得填方区与挖方区的分界线（即零线）。

零点的位置按下式计算（图6-3）：a h h h x ⨯+=2111 a h h h x ⨯+=2122 （6-8） 式中 x 1、x 2——角点至零点的距离（m ）；h 1、h 2——相邻两角点的施工高度（m ），均用绝对值；a ——方格网的边长（m ）。

图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算，亦可采用图解法直接求出零点位置，如图6-4所示，方法是用尺在各角上标出相应比例，用尺相接，与方格相交点即为零点位置。

这种方法可避免计算（或查表）出现的错误。

3)计算土方工程量按方格网底面积图形和表6-31所列体积计算公式计算每个方格内的挖方或填方量，或用查表法计算，有关计算用表见表6-31。

常用方格网点计算公式表6-31注：1.a——方格网的边长（m）；b、c——零点到一角的边长（m）；h1、h2、h3、h4——方格网四角点的施工高程（m），用绝对值代入；Σh——填方或挖方施工高程的总和（m），用绝对值代入；V——挖方或填方体积（m3）。

方格网计算土方量
在土建工程中，计算土方量是非常重要的一个环节。

而计算土方量的方法也有很多，其中一种方法就是通过方格网来计算。

方格网计算法通常适用于分块比较规则的场地。

下面将详细介绍如何使用方格网来计算土方量。

步骤一：绘制方格网
首先，需要绘制方格网，即把场地按照一定的比例划分成小块。

具体的比例应该根据场地大小和地形情况来确定。

划分好方块之后，可以用绳子或者直尺来把方块连接起来，形成方格网。

步骤二：测量地形高度
接着，需要在方格网的交点处，即每个小块的四个角落处进行地形高度测量。

可以使用测高仪等工具来进行测量。

在测量时，需要保证精度，以确保计算的土方量准确无误。

步骤三：计算每个小块的体积
有了每个小块的高度数据之后，就可以计算每个小块的体积。

计算公式如下：体积 = 面积 × 平均高度
其中，面积可以通过方格网的尺寸来直接计算，平均高度则是该小块四个角高度的平均值。

步骤四：计算总体积
所有小块体积计算完毕之后，需要把它们加起来，得到场地的总体积。

为了便于计算，可以把各个小块的体积逐个列出来，然后进行累加，最终得到总体积。

步骤五：检查计算结果
计算出总体积之后，需要对结果进行检查。

可以再次对各个小块的高度进行测量，以确保计算结果的准确性。

另外，也需要检查方格网的划分是否准确，以及每个小块的面积是否计算正确。

方格网计算法是一种简单易行的土方量计算方法，适用于场地比较规则且地形比较平缓的情况。

在进行方格网计算时，需要注意测量高度的精度，以及对结果进行检查。

一、设计题目——方格网法计算场地平整土方量二、设计目的本课程设计利用方格网法计算出场地平整时的土方量，其属于设计地面的一项重要工作，设计地面是将自然地形加以适当整平，使其成为满足使用要求和建筑布置的平整地面。

对于平整场地，合理设定土方工程量的大小具有决定性的意义。

是《总图设计》课程的主要教学环节之一。

通过该设计的教学，进一步掌握利用方格网法计算场地平整时的土方量的工程。

三、设计内容与要求1.方格网法的基本原理方格网法是将基地化分为若干个方格，根据自然地面与设计地面的高差，计算挖方和填方的体积，分别汇总即为土方量。

该方法一般适用于平坦场地。

设计时要求填方和挖方基本相等，即要求土方就地平衡，平整前后这块土体的体积是相等的。

对于一块表面上崎岖不平的土体，经整平后使其表面成为平面。

设平整前的土方体积为V：V=)(4)432(441243212∑∑∑∑∑∑=+++ijjjjjhPiahhhha式中：V——土体自水准面起算自然地面下土体的体积；a ——方格边长（m ）；——方格网交点的权值，i=1表示角点，i=2表示边点，i=3表示凹点，i=4表示中间点，其权值分别为1，2，3，4。

h 1j h 2j h 3j h 4j ——各角点，边点，凹点，中间点的自然地面的标高（m 3）。

h ij ——各角点（或边点，凹点，中间点）的自然地面的标高（m 3）。

设方格坐标原点的设计标高为x ，则整平后土体的体积为：∑∑=412'))((4x f P a V i式中：——土体自水准面起算平整后土体的体积（m 3）；x ——方格网坐标原点的设计标高（m ）；a ——方格边长（m ）；m ，i ——X 轴方向的放个数与设计坡度（%），从原点起，上坡为证，下坡为负；n ，j ——Y 轴方向的放个数与设计坡度（%），从原点起，上坡为证，下坡为负； 当土方平衡时，平整前后这块土体的体积是相等的，即'V V =∑∑41ijh Pi =∑∑41))((x f P i由于式中只有x 为未知数，所以可以求出来，从而求出方格网各个交叉点的设计标高。

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时，常需要进行土方工程量的计算。

计算方法有方格网法和横断面法两种。

（1）方格网法用于地形较平缓或台阶宽度较大的地段。

计算方法较为复杂，但精度较高，其计算步骤和方法如下：1）划分方格网根据已有地形图(一般用1：500的地形图）将欲计算场地划分成若干个方格网，尽量与测量的纵、横坐标网对应，方格一般采用20m ×20m 或40m ×40m ，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角.将自然地面标高与设计地面标高的差值，即各角点的施工高度（挖或填），填在方格网的左上角，挖方为（－)，填方为（＋）。

2）计算零点位置在一个方格网内同时有填方或挖方时，应先算出方格网边上的零点的位置，并标注于方格网上，连接零点即得填方区与挖方区的分界线（即零线）。

零点的位置按下式计算(图6-3):a h h h x ⨯+=2111 a h h h x ⨯+=2122 （6—8） 式中 x 1、x 2—-角点至零点的距离（m ）；h 1、h 2——相邻两角点的施工高度(m ），均用绝对值；a ——方格网的边长（m ）。

图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算，亦可采用图解法直接求出零点位置，如图6—4所示，方法是用尺在各角上标出相应比例，用尺相接，与方格相交点即为零点位置。

这种方法可避免计算（或查表）出现的错误.3）计算土方工程量按方格网底面积图形和表6—31所列体积计算公式计算每个方格内的挖方或填方量，或用查表法计算，有关计算用表见表6—31.常用方格网点计算公式表6-31注:1。

a——方格网的边长(m)；b、c——零点到一角的边长(m)；h1、h2、h3、h4——方格网四角点的施工高程（m)，用绝对值代入;Σh—-填方或挖方施工高程的总和（m）,用绝对值代入；V——挖方或填方体积（m3）.2.本表公式是按各计算图形底面积乘以平均施工高程而得出的。

方格网法：方格网法是把平整场地的设计工作与土方量计算工作结合在一起进行的。

方格网法的具体工作程序为：在附有等高线的施工现场地形图上作方格网控制施工场地，依据设计意图，如地面形状、坡向、坡度值等。

确定各角点的设断面法：是以一组等距（或不等距）的相互平行的截面将拟计算的地块、地形单体（如山、溪涧、池、岛等）和土方工程（如堤、沟渠、路堑、路槽等）分截成"段"，分别计算这些"段"的体积，再将各段体积累加，以求得该计算对象的总土方量。

交叉口的立面设计有三种方法：方格网法、设计等高线法和方格网设计等高线法三种。

方格网法是在交叉口的设计范围内，以相交道路的中心线为坐标基线打方格网，方格网线一般用5×5米或10×10米平行于路中线，斜交道路应选便于施工放线的测量的方向，测出方格网上的地面高程并求出其设计标高，从而算出施工高度。

设计等高线法是在交叉口的设计范围内，选定路脊线和划分标高计算网，算出路脊线和标高计算线上的各点的设计标高，最后勾画出设计等高线。

并算出各点的施工高度。

设计等高线法的主要优点是比方格网法能更加清晰地反映出交叉口的设计地形，其缺点是设计等高线上的各点不易放样。

通常是两种方法结合使用，取长补短1．方格网法方格网计算步骤及方法2. 常用方格网计算公式当注：1）a——方格网的边长,m；b、c——零点到一角的边长,m；h1,h2,h3,h4——方格网四角点的施工高程,m，用绝对值代入；Σh——填方或挖方施工高程的总和 ,m，用绝对值代入；——挖方或填方体积,m。

2）本表公式是按各计算图形底面积乘以平均施工高程而得出的。

3. 横截面计算步骤及方法常用横截面计算公式土方量汇总表边坡土方计算步骤及方法边坡土方计算K D、K V值表。

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进展土方的平衡调配以及检查验收土方工程时，常需要进展土方工程量的计算。

计算方法有方格网法和横断面法两种。

〔1)方格网法用于地形较平缓或台阶宽度较大的地段。

计算方法较为复杂，但精度较高，其计算步骤和方法如下：1)划分方格网根据已有地形图〔一般用1：500的地形图〕将欲计算场地划分成假设干个方格网，尽量与测量的纵、横坐标网对应，方格一般采用20m ×20m 或40m ×40m ，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。

将自然地面标高与设计地面标高的差值，即各角点的施工高度〔挖或填〕，填在方格网的左上角，挖方为〔－〕，填方为〔＋〕。

2〕计算零点位置在一个方格网内同时有填方或挖方时，应先算出方格网边上的零点的位置，并标注于方格网上，连接零点即得填方区与挖方区的分界限〔即零线〕。

零点的位置按下式计算〔图6-3〕：a h h h x ⨯+=2111 a h h h x ⨯+=2122 〔6-8〕 式中 x 1、x 2——角点至零点的距离〔m 〕；h 1、h 2——相邻两角点的施工高度〔m 〕，均用绝对值；a ——方格网的边长〔m 〕。

图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算，亦可采用图解法直接求出零点位置，如图6-4所示，方法是用尺在各角上标出相应比例，用尺相接，与方格相交点即为零点位置。

这种方法可防止计算〔或查表〕出现的错误。

3)计算土方工程量按方格网底面积图形和表6-31所列体积计算公式计算每个方格内的挖方或填方量，或用查表法计算，有关计算用表见表6-31。

常用方格网点计算公式表6-31注：1.a——方格网的边长〔m〕；b、c——零点到一角的边长〔m〕；h1、h2、h3、h4——方格网四角点的施工高程〔m〕，用绝对值代入；Σh——填方或挖方施工高程的总和〔m〕，用绝对值代入；V——挖方或填方体积〔m3〕。

土方施工技术场地平整理论知识：一、平整场地土方量计算公式与步骤1. 读识方格网图 方格网图由设计单位(一般在1：500的地形图上)将场地划分为边长a=10～40m的若干方格,与测量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高(H)和设计标高(Hn),如图所示.　2.确定场地设计标高　1）场地初步标高：H0=S(H11+H12+H21+H22)/4MH11、H12、H21、H22 ——一个方格各角点的自然地面标高；M ——方格个数.或： H0=(∑H1+2∑H2+3∑H3+4∑H4)/4MH1－－一个方格所仅有角点的标高；H2、H3、H4－－分别为两个、三个、四个方格共用角点的标高.　2)场地设计标高的调整　按泄水坡度调整各角点设计标高：　①单向排水时，各方格角点设计标高为: Hn = H0 ± Li　②双向排水时，各方格角点设计标高为：Hn = H0 ± Lx ix ± L yi y　3.计算场地各个角点的施工高度　施工高度为角点设计地面标高与自然地面标高之差，是以角点设计标高为基准的挖方或填方的施工高度.各方格角点的施工高度按下式计算：式中 hn------角点施工高度即填挖高度(以“+”为填，“-”为挖)，m； n------方格的角点编号(自然数列1，2，3，…，n). Hn------角点设计高程， H------角点原地面高程.　4.计算“零点”位置，确定零线 方格边线一端施工高程为“+”,若另一端为“-”,则沿其边线必然有一不挖不填的点，即“零点”(如图1-4所示). 图1-4 零点位置　零点位置按下式计算：式中 x1、x2 ——角点至零点的距离,m； h1、h2 ——相邻两角点的施工高度(均用绝对值),m； a —方格网的边长，m.　确定零点的办法也可以用图解法，如图1-5所示.　方法是用尺在各角点上标出挖填施工高度相应比例，用尺相连，与方格相交点即为零点位置。

例题【例1.1】某建筑场地方格网如图1-7所示，方格边长为20m×20m,填方区边坡坡度系数为1.0,挖方区边坡坡度系数为0.5,试用公式法计算挖方和填方的总土方量.图1-7 某建筑场地方格网布置图【解】(1)根据所给方格网各角点的地面设计标高和自然标高，计算结果列于图1-8中. 由公式1.9得：h1=251.50-251.40=0.10m h2=251.44-251.25=0.19mh3=251.38-250.85=0.53m h4=251.32-250.60=0.72mh5=251.56-251.90=-0.34m h6=251.50-251.60=-0.10mh7=251.44-251.28=0.16m h8=251.38-250.95=0.43mh9=251.62-252.45=-0.83m h10=251.56-252.00=-0.44mh11=251.50-251.70=-0.20m h12=251.46-251.40=0.06m图1-8 施工高度及零线位置(2)计算零点位置.从图1-8中可知,1—5、2—6、6—7、7—11、11—12五条方格边两端的施工高度符号不同,说明此方格边上有零点存在. 由公式1.10求得：1—5线x1=4.55(m)2—6线x1=13.10(m)6—7线x1=7.69(m)7—11线x1=8.89(m)11—12线x1=15.38(m)将各零点标于图上,并将相邻的零点连接起来,即得零线位置，如图1-8.(3)计算方格土方量.方格Ⅲ、Ⅳ底面为正方形,土方量为：VⅢ(+)=202/4×(0.53+0.72+0.16+0.43)=184(m3)VⅣ(-)=202/4×(0.34+0.10+0.83+0.44)=171(m3)方格Ⅰ底面为两个梯形,土方量为：VⅠ(+)=20/8×(4.55+13.10)×(0.10+0.19)=12.80(m3)VⅠ(-)=20/8×(15.45+6.90)×(0.34+0.10)=24.59(m3)方格Ⅱ、Ⅴ、Ⅵ底面为三边形和五边形,土方量为：VⅡ(+)=65.73 (m3)VⅡ(-)=0.88 (m3)VⅤ(+)=2.92(m3)VⅤ(-)=51.10 (m3)VⅥ(+)=40.89(m3)VⅥ(-)=5.70 (m3)方格网总填方量：∑V(+)=184+12.80+65.73+2.92+40.89=306.34(m3)方格网总挖方量：∑V(-)=171+24.59+0.88+51.10+5.70=253.26 (m3)(4)边坡土方量计算.如图1.9,④、⑦按三角棱柱体计算外,其余均按三角棱锥体计算, 可得：V①(+)=0.003(m3)V②(+)=V③(+)=0.0001(m3)V④(+)=5.22(m3)V⑤(+)=V⑥(+)=0.06(m3)V⑦(+)=7.93(m3)图1-9 场地边坡平面图V⑧(+)=V⑨(+)=0.01(m3)V⑩=0.01(m3)V11=2.03 (m3)V12=V13=0.02 (m3)V14=3.18 (m3)边坡总填方量：∑V(+)=0.003+0.0001+5.22+2×0.06+7.93+2×0.01+0.01=13.29(m3) 边坡总挖方量：∑V(-)=2.03+2×0.02+3.18=5.25 (m3)。

场地平整土方工程量的计算在编制场地平整土方工程施工组织设计或施工方案、进行土方的平衡调配以及检查验收土方工程时，常需要进行土方工程量的计算。

计算方法有方格网法和横断面法两种.（1）方格网法用于地形较平缓或台阶宽度较大的地段.计算方法较为复杂，但精度较高,其计算步骤和方法如下：1）划分方格网根据已有地形图（一般用1：500的地形图）将欲计算场地划分成若干个方格网，尽量与测量的纵、横坐标网对应,方格一般采用20m×20m或40m×40m，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。

将自然地面标高与设计地面标高的差值，即各角点的施工高度(挖或填），填在方格网的左上角，挖方为（－),填方为（＋).2）计算零点位置在一个方格网内同时有填方或挖方时,应先算出方格网边上的零点的位置，并标注于方格网上，连接零点即得填方区与挖方区的分界线（即零线）。

零点的位置按下式计算(图6-3）:(6-8）式中x1、x2——角点至零点的距离（m)；h1、h2—-相邻两角点的施工高度（m)，均用绝对值；a-—方格网的边长（m）。

图6-3 零点位置计算示意图图6-4 零点位置图解法为省略计算，亦可采用图解法直接求出零点位置,如图6-4所示，方法是用尺在各角上标出相应比例，用尺相接，与方格相交点即为零点位置.这种方法可避免计算(或查表)出现的错误。

3）计算土方工程量按方格网底面积图形和表6-31所列体积计算公式计算每个方格内的挖方或填方量，或用查表法计算，有关计算用表见表6-31.常用方格网点计算公式表6—31注：1.a—-方格网的边长（m)；b、c-—零点到一角的边长（m）;h1、h2、h3、h4——方格网四角点的施工高程（m），用绝对值代入；Σh-—填方或挖方施工高程的总和（m），用绝对值代入；V—-挖方或填方体积(m3）.2。

本表公式是按各计算图形底面积乘以平均施工高程而得出的.4）计算土方总量将挖方区(或填方区）所有方格计算土方量汇总，即得该场地挖方和填方的总土方量.［例6—1］厂房场地平整，部分方格网如图6-5所示,方格边长为20m×20m，试计算挖填总土方工程量。