The Calderon Projection New Definition and Applications
- 格式:pdf
- 大小:710.28 KB
- 文档页数:58

启蒙运动(英⽂版)The EnlightenmentThe Enlightenment is mankind‘s final coming of age, the emancipation of the human consciousness from an immature state of ignorance and error.-Immanuel KantThe Enlightenment usually refers to a period between the early 18th century and the French Revolution in1789, in which new thougts were emerging . The Age of Enlightenment (or Age of Reason) was an elite cultural movement of intellectuals in 18th century Europe that sought to use the power of reason in order to reform society and advance knowledge. It promoted intellectual interchange and opposed intolerance and abuses in Church and state.EvolutionThe enlightenment originated in England in 17th century,it was sparked by philosophers such as John Locke (1632-1704), mathematician Newton (1643-1727) and others. The Enlightenment flourished in late 18th century. The enlightenment met its climax in France. After that, it extended to Germany, the Netherland and North America.1. Feudalism suppressed the bourgeois political rights, so they carry out anti-feudal and antichurch propaganda ideologically, to prepare for the struggle for power.2.With the Capitalist economic development, the bourgeoisie‘s economic s trength surges ,so they required their own interests ideologically.3. ①The Renaissance and religious reform promoted the people's ideological emancipation;②With the development of modern science, rationalism, as an asset Anti-feudal class provides the ideological and theoretical weapon.Representative figuresDenis DiderotHe was a French philosopher, art critic, and writer. He was a prominent person during the Enlightenment and is best known for serving as co-founder and chief editor of the Encyclopedie.EncyclopedieThe first Encyclopedia is considered to be the pinnacle of the Enlightenment period. It was compiled by Denis Diderot in 1751-1772.VoltaireHe was famous for his wit and for his advocacy of civil liberties , including freedom of religion, free trade, and separation of church and state. Voltaire was a prolific writer, producing works in almost every literary form, including plays, poetry, novels, essays, and historical and scientific works. He wrote more than 20,000 letters and more than 2,000 books and pamphlets. He was an outspoken supporter of social reform, despite strict censorship laws and harsh penalties for those who broke them. As a satirical polemicist , he frequently made use of his works to criticize intolerance, religious dogma and the French institutions of his day. His most famous work is Candide.RousseauJean-Jacques Rousseau was a philosopher, writer, and composer. His political philosophy heavily influenced the Fench Revolution,as well as the overall development of modern political,sociological,and educational thought.The Industrial Revolution in Great BritainThe ground was prepared by the voyages of discovery from Western Europe in the 15th and 16th cent., which led to a vast influx of precious metals from the New World, raising prices, stimulating industry, and fostering a money economy. Expansion of trade an d the money economy stimulated the development of new institutions of finance and credi t (see commercial revolution). In the 17th cent. the Dutch were in the forefront financially, but with the establishment (1694) of theBank of England, their supremacy was effectivel y challenged. Capitalism appeared on a large scale, and a new type of commercial entrepr eneur developed from the old class of merchant adventurers. Many machines were already known, and there were sizable factories using them, but these were the exceptions rather than the rule. Wood was the only fuel, water and wind the power of these early factorie s. As the 18th cent. began, an expanding and wealthier population demanded more and be tter goods. In the productive process, coal came to replace wood. Early-model steam engin es were introduced to drain water and raise coal from the mines. The crucial development of the Industrial Revolution was the use of steam for power, and the greatly improved e ngine (1769) of James Watt marked the high point in this development. Cotton textiles w as the key industry early in the Industrial Revolution. John Kay's fly shuttle (1733), Jame s Hargreaves's spinning jenny (patented 1770), Richard Arkwright's water frame (1769), Sa muel Crompton's mule (1779), which combined the features of the jenny and the frame, a nd Edmund Cartwright's power loom (patented 1783) facilitated a tremendous increase in output. The presence of large quantities of coal and iron in close proximity in Britain was a decisive factor in its rapid industrial growth. The use of coke in iron production had f ar-reaching effects. The coal mines from the early 1700s had become paramount in import ance, and the Black Country appeared in England at the same time that Lancashire and Y orkshire were being transformed into the greatest textile centers of the world. Factories an d industrial towns sprang up. Canals and roads were built, and the advent of the railroad and the steamship widened the market for manufactured goods. The Bessemer process mad e a gigantic contribution, for it was largely responsible for the extension of the use of ste am and steel that were the two chief features of industry in the middle of the 19th cent. Chemical innovations and, most important of all, perhaps, machines for making machinesplayed an important part in the vast changes. The Industrial Revolution did not in fact en d in Britain in the mid-1800s. New periods came in with electricity and the gasoline engi ne. By 1850, however, the transformation wrought by the revolution was accomplished, in that industry had become a dominant factor in the nation's life.。

北美博士的物理启蒙课中英文双版北美博士的物理启蒙课North American Doctoral Physics Enlightenment Course物理是一门关于自然界基本规律的科学,为了帮助初学者建立起对物理学的基本认知,我们特别设计了这门北美博士的物理启蒙课。
这门课程将向学生介绍物理学的基本概念和原则,并引导他们了解物理学在现实世界中的应用。
Physics is a science that deals with the fundamental laws of nature. In order to help beginners establish a basic understanding of physics, we have specially designed this North American Doctoral Physics Enlightenment Course. This course will introduce students to the fundamental concepts and principles of physics, and guide them to understand the applications of physics in the real world.课程大纲Course Outline第一部分:基本概念Part 1: Fundamental Concepts我们将首先介绍物理学的基本概念,包括质量、力、能量和运动。
通过解析力学和运动学的基本原理,学生将了解物体运动和力的关系,并学会运用牛顿的三大运动定律来解决各种问题。
We will first introduce the fundamental concepts of physics, including mass, force, energy, and motion. By analyzing the basic principles of mechanics and kinematics, students will understand the relationship between object motion and forces, and learn to apply Newton's three laws of motion to solve various problems.第二部分:热力学Part 2: Thermodynamics在第二部分,我们将介绍热力学的基本原理和规律。

《寂静的革命》重点词汇解析《寂静的革命》是法国哲学家让-博德里亚(Jean Baudrillard)的一本著作,于1977年首次出版。
该书是他对21世纪社会及其文化状况的深刻分析和批判。
以下将对《寂静的革命》中的重点词汇进行解析。
一、“消费社会”(Société de consommation)消费社会是指以消费为中心的社会形态。
博德里亚认为,在现代社会,消费不再是满足个人和群体需求的手段,而成为了统治和定义社会关系的方式。
消费社会中,商品的价值不再根据其实用性而是其象征价值和符号价值来决定。
消费不再仅仅是生产的附属品,而是一个独立的社会系统。
二、“符号交换”(échange symbolique)符号交换是指在社会中进行的非物质性的交换。
博德里亚认为,在现代社会中,人们的交往和交换不再是物质上的直接交换,而是通过符号系统来实现。
符号交换建立在符号的价值和符号的等价性之上,追求符号的差异性和符号的升值。
三、“模拟”(simulation)与“真实”(réel)模拟和真实是博德里亚对现代社会与现实世界的关系进行的重要分析。
他认为,在现代社会,模拟已经取代了真实,模拟所代表的是一种虚假的表象,而真实则已经丧失。
模拟是通过符号和象征来建立的,它不再有与真实世界的对应关系,而是自成一体,与真实脱离关系。
真实已经被模拟所淹没,人们很难辨别模拟和真实的区别。
四、“反权力”(contre-pouvoir)反权力是指对权力的反抗和对抗。
博德里亚认为,在现代社会中,权力不再是一种集中的、可自觉的存在,而是一种弥散的、隐蔽的力量。
他主张通过反权力来抵抗权力的压迫和统治,以及揭示权力的本质。
五、“好战的秩序”(ordre agonique)好战的秩序是指在现代社会中,人们通过争斗和竞争来获取自己的地位和权力。
博德里亚认为,在消费社会中,人们不再通过合作和和平来建立社会秩序,而是通过竞争和战斗来争夺资源和地位。

理想国的名词解释英语The Noun Definition of "Utopia" in EnglishIntroduction:Utopia is a concept that has intrigued and inspired people for centuries. Coined by Sir Thomas More in his 1516 book of the same name, this term describes an ideal society or community that is perfect, harmonious, and free from the flaws and problems of the real world. In English, the word "Utopia" has come to signify an idyllic and aspirational place. This article aims to explore the noun definition of "Utopia" in English, highlighting its historical origins, characteristics, and the impact it has had on society's imagination.Origins and Etymology:The word "Utopia" comes from the Greek words "ou" and "topos," meaning "no" and "place" respectively. It was initially introduced by Sir Thomas More as the fictional name of an ideal island society in his book. The term was intentionally ambiguous, signifying both "no place" and "good place," setting the stage for the ongoing philosophical debates and interpretations surrounding the concept of utopia.Characteristics of Utopia:1. Perfection and Harmony:Utopian societies envision a world where all aspects of life are perfect and harmonious. In such societies, individuals live in peace, sharing resources equitably, and cooperating for the greater good. Conflict, inequality, and injustice are absent, creating a sense of unity and contentment for all members of the community.2. Social Equality:Another crucial characteristic of utopia is the absence of social divisions based on wealth, power, or social status. Utopian societies prioritize equality, ensuring that allcitizens have access to the same opportunities, rights, and resources. This creates a fair and just society, where everyone is valued and treated equitably.3. Innovative and Progressive:Utopias often emphasize the pursuit of knowledge, the advancement of technology, and the development of human potential. These societies encourage creativity, innovation, and intellectual pursuits, fostering an environment that promotes personal growth and collective progress.4. Sustainable and Balanced:Utopias strive to maintain a sustainable balance between human needs and the natural environment. They prioritize ecological harmony, adopting practices that ensure the longevity of resources and protect the planet. Utopian societies recognize the interdependence of humans and nature, nurturing a symbiotic relationship for the benefit of both.Influence on Society's Imagination:The concept of utopia has had a profound impact on society's imagination throughout history. It has served as a powerful tool for reflection, questioning the flaws and limitations of existing social structures. Utopian visions have inspired movements seeking to create a better world, such as the socialists, anarchists, and environmentalists. These ideologies have attempted to implement elements of utopia in their visions of a more just and sustainable society.Additionally, literature and art have often used utopian themes to explore societal ideals and aspirations. From Thomas More's original work to Aldous Huxley's "Brave New World" and other dystopian novels, utopia's counterpart, the concept of an ideal society has provided rich material for literary exploration, encouraging readers to contemplate the possibilities and pitfalls of a perfect world.Conclusion:In conclusion, the noun definition of "utopia" in English encapsulates an idealistic vision of a perfect society. The term's origins lie in Sir Thomas More's 16th-century book, which introduced this concept to the world. Utopia embodies characteristics such as perfection, harmony, social equality, innovation, and sustainability. While utopia remains an unattainable ideal, its influence has been far-reaching, stimulating social and political movements and inspiring artistic expression. The concept of utopia continues to provoke contemplation on how to create a better world, challenging societies to strive for a more just and harmonious future.。
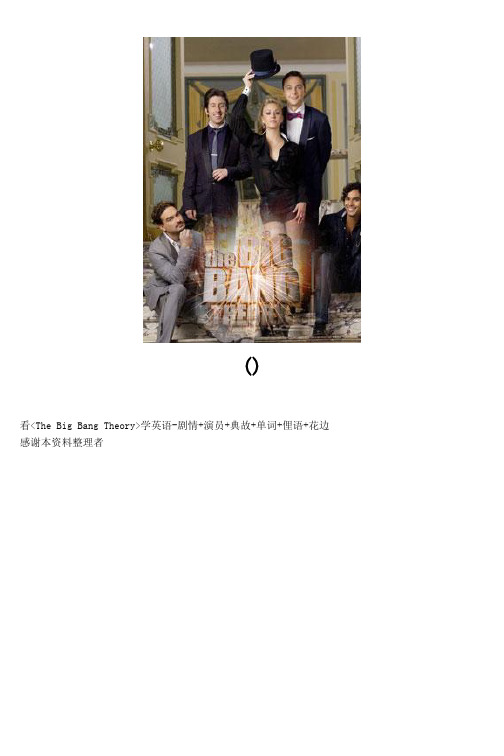
()看<The Big Bang Theory>学英语-剧情+演员+典故+单词+俚语+花边感谢本资料整理者3011.普通级词汇sass:vt. 对…出言不逊,说无礼的话effusive:adj. 流出的,感情奔放的luau:n. (常伴有文娱节目的)夏威夷式宴会toga:n. (古罗马)宽外袍,罗马主题plummeting:adj. 骤然下降,像铅球那样急速垂直下降般obnoxious:adj. 可憎的,不愉快的dictator:n. 独裁者Dickensian:adj. 如同狄更斯笔下的人物那样自私、消沉repentance:n. 悔改Mush:int. 走!,前进!trouper:n. 演员,老练演员buoy:n. 救生圈 vt. 使浮起;鼓舞,激励trajectory:n. 轨道detour:n. 绕路,迂回blunder:n. 大错scathing:adj. 严厉的,尖刻的doozy:n. 非常好或非常糟糕的东西heathen:n. 异教徒turtleneck:n. 高领tumbleweeds:n. 风滚草red-eye:n. 通宵航班demon:n. 魔鬼2.爆炸级词汇post hoc ergo propter hoc:[拉丁语]发生于其后者必然是其结果(指一种普通的逻辑上的谬误,即后此谬误)Vulcan:瓦肯人(from the Star Trek),相信大家都不陌生了,Spock那群人,耳朵尖尖,听力好,有如葫芦娃里二娃的顺风耳(字幕组真是油菜)cosmological constant:宇宙常数,含宇宙常数项的场方程是R_uv-1/2*R*g_uv+L*g_uv=κ*T_uv,其中L代表宇宙常数,其物理意义是宇宙真空场。
L*g_uv为宇宙常数项。
R_uv为里契张量,代表空间的弯曲状况。
T_uv为能量-动量张量,代表物质分布和运动状况。
g_uv为度规,κ为系数,可由低速的牛顿理论来确定。

Universities in Evolutionary Systems of InnovationMarianne van der Steen and Jurgen EndersThis paper criticizes the current narrow view on the role of universities in knowledge-based economies.We propose to extend the current policy framework of universities in national innovation systems(NIS)to a more dynamic one,based on evolutionary economic principles. The main reason is that this dynamic viewfits better with the practice of innovation processes. We contribute on ontological and methodological levels to the literature and policy discussions on the effectiveness of university-industry knowledge transfer and the third mission of uni-versities.We conclude with a discussion of the policy implications for the main stakeholders.1.IntroductionU niversities have always played a major role in the economic and cultural devel-opment of countries.However,their role and expected contribution has changed sub-stantially over the years.Whereas,since1945, universities in Europe were expected to con-tribute to‘basic’research,which could be freely used by society,in recent decades they are expected to contribute more substantially and directly to the competitiveness offirms and societies(Jaffe,2008).Examples are the Bayh–Dole Act(1982)in the United States and in Europe the Lisbon Agenda(2000–2010) which marked an era of a changing and more substantial role for universities.However,it seems that this‘new’role of universities is a sort of universal given one(ex post),instead of an ex ante changing one in a dynamic institutional environment.Many uni-versities are expected nowadays to stimulate a limited number of knowledge transfer activi-ties such as university spin-offs and university patenting and licensing to demonstrate that they are actively engaged in knowledge trans-fer.It is questioned in the literature if this one-size-fits-all approach improves the usefulness and the applicability of university knowledge in industry and society as a whole(e.g.,Litan et al.,2007).Moreover,the various national or regional economic systems have idiosyncratic charac-teristics that in principle pose different(chang-ing)demands towards universities.Instead of assuming that there is only one‘optimal’gov-ernance mode for universities,there may bemultiple ways of organizing the role of univer-sities in innovation processes.In addition,we assume that this can change over time.Recently,more attention in the literature hasfocused on diversity across technologies(e.g.,King,2004;Malerba,2005;Dosi et al.,2006;V an der Steen et al.,2008)and diversity offormal and informal knowledge interactionsbetween universities and industry(e.g.,Cohenet al.,1998).So far,there has been less atten-tion paid to the dynamics of the changing roleof universities in economic systems:how dothe roles of universities vary over time andwhy?Therefore,this article focuses on the onto-logical premises of the functioning of univer-sities in innovation systems from a dynamic,evolutionary perspective.In order to do so,we analyse the role of universities from theperspective of an evolutionary system ofinnovation to understand the embeddednessof universities in a dynamic(national)systemof science and innovation.The article is structured as follows.InSection2we describe the changing role ofuniversities from the static perspective of anational innovation system(NIS),whereasSection3analyses the dynamic perspective ofuniversities based on evolutionary principles.Based on this evolutionary perspective,Section4introduces the characteristics of a LearningUniversity in a dynamic innovation system,summarizing an alternative perception to thestatic view of universities in dynamic economicsystems in Section5.Finally,the concludingVolume17Number42008doi:10.1111/j.1467-8691.2008.00496.x©2008The AuthorsJournal compilation©2008Blackwell Publishingsection discusses policy recommendations for more effective policy instruments from our dynamic perspective.2.Static View of Universities in NIS 2.1The Emergence of the Role of Universities in NISFirst we start with a discussion of the literature and policy reports on national innovation system(NIS).The literature on national inno-vation systems(NIS)is a relatively new and rapidly growingfield of research and widely used by policy-makers worldwide(Fagerberg, 2003;Balzat&Hanusch,2004;Sharif,2006). The NIS approach was initiated in the late 1980s by Freeman(1987),Dosi et al.(1988)and Lundvall(1992)and followed by Nelson (1993),Edquist(1997),and many others.Balzat and Hanusch(2004,p.196)describe a NIS as‘a historically grown subsystem of the national economy in which various organizations and institutions interact with and influence one another in the carrying out of innovative activity’.It is about a systemic approach to innovation,in which the interaction between technology,institutions and organizations is central.With the introduction of the notion of a national innovation system,universities were formally on the agenda of many innovation policymakers worldwide.Clearly,the NIS demonstrated that universities and their interactions with industry matter for innova-tion processes in economic systems.Indeed, since a decade most governments acknowl-edge that interactions between university and industry add to better utilization of scienti-fic knowledge and herewith increase the innovation performance of nations.One of the central notions of the innovation system approach is that universities play an impor-tant role in the development of commercial useful knowledge(Edquist,1997;Sharif, 2006).This contrasts with the linear model innovation that dominated the thinking of science and industry policy makers during the last century.The linear innovation model perceives innovation as an industry activity that‘only’utilizes fundamental scientific knowledge of universities as an input factor for their innovative activities.The emergence of the non-linear approach led to a renewed vision on the role–and expectations–of universities in society. Some authors have referred to a new social contract between science and society(e.g., Neave,2000).The Triple Helix(e.g.,Etzkowitz &Leydesdorff,1997)and the innovation system approach(e.g.,Lundvall,1988)and more recently,the model of Open Innovation (Chesbrough,2003)demonstrated that innova-tion in a knowledge-based economy is an inter-active process involving many different innovation actors that interact in a system of overlapping organizationalfields(science, technology,government)with many interfaces.2.2Static Policy View of Universities in NIS Since the late1990s,the new role of universi-ties in NIS thinking emerged in a growing number of policy studies(e.g.,OECD,1999, 2002;European Commission,2000).The con-tributions of the NIS literature had a large impact on policy makers’perception of the role of universities in the national innovation performance(e.g.,European Commission, 2006).The NIS approach gradually replaced linear thinking about innovation by a more holistic system perspective on innovations, focusing on the interdependencies among the various agents,organizations and institutions. NIS thinking led to a structurally different view of how governments can stimulate the innovation performance of a country.The OECD report of the national innovation system (OECD,1999)clearly incorporated these new economic principles of innovation system theory.This report emphasized this new role and interfaces of universities in knowledge-based economies.This created a new policy rationale and new awareness for technology transfer policy in many countries.The NIS report(1999)was followed by more attention for the diversity of technology transfer mecha-nisms employed in university-industry rela-tions(OECD,2002)and the(need for new) emerging governance structures for the‘third mission’of universities in society,i.e.,patent-ing,licensing and spin-offs,of public research organizations(OECD,2003).The various policy studies have in common that they try to describe and compare the most important institutions,organizations, activities and interactions of public and private actors that take part in or influence the innovation performance of a country.Figure1 provides an illustration.Thefigure demon-strates the major building blocks of a NIS in a practical policy setting.It includesfirms,uni-versities and other public research organiza-tions(PROs)involved in(higher)education and training,science and technology.These organizations embody the science and tech-nology capabilities and knowledge fund of a country.The interaction is represented by the arrows which refer to interactive learn-ing and diffusion of knowledge(Lundvall,Volume17Number42008©2008The AuthorsJournal compilation©2008Blackwell Publishing1992).1The building block ‘Demand’refers to the level and quality of demand that can be a pull factor for firms to innovate.Finally,insti-tutions are represented in the building blocks ‘Framework conditions’and ‘Infrastructure’,including various laws,policies and regula-tions related to science,technology and entre-preneurship.It includes a very broad array of policy issues from intellectual property rights laws to fiscal instruments that stimulate labour mobility between universities and firms.The figure demonstrates that,in order to improve the innovation performance of a country,the NIS as a whole should be conducive for innovative activities in acountry.Since the late 1990s,the conceptual framework as represented in Figure 1serves as a dominant design for many comparative studies of national innovation systems (Polt et al.,2001;OECD,2002).The typical policy benchmark exercise is to compare a number of innovation indicators related to the role of university-industry interactions.Effective performance of universities in the NIS is judged on a number of standardized indica-tors such as the number of spin-offs,patents and licensing.Policy has especially focused on ‘getting the incentives right’to create a generic,good innovative enhancing context for firms.Moreover,policy has also influ-enced the use of specific ‘formal’transfer mechanisms,such as university patents and university spin-offs,to facilitate this collabo-ration.In this way best practice policies are identified and policy recommendations are derived:the so-called one-size-fits-all-approach.The focus is on determining the ingredients of an efficient benchmark NIS,downplaying institutional diversity and1These organizations that interact with each other sometimes co-operate and sometimes compete with each other.For instance,firms sometimes co-operate in certain pre-competitive research projects but can be competitors as well.This is often the case as well withuniversities.Figure 1.The Benchmark NIS Model Source :Bemer et al.(2001).Volume 17Number 42008©2008The AuthorsJournal compilation ©2008Blackwell Publishingvariety in the roles of universities in enhanc-ing innovation performance.The theoretical contributions to the NIS lit-erature have outlined the importance of insti-tutions and institutional change.However,a further theoretical development of the ele-ments of NIS is necessary in order to be useful for policy makers;they need better systemic NIS benchmarks,taking systematically into account the variety of‘national idiosyncrasies’. Edquist(1997)argues that most NIS contribu-tions are more focused onfirms and technol-ogy,sometimes reducing the analysis of the (national)institutions to a left-over category (Geels,2005).Following Hodgson(2000), Nelson(2002),Malerba(2005)and Groenewe-gen and V an der Steen(2006),more attention should be paid to the institutional idiosyncra-sies of the various systems and their evolution over time.This creates variety and evolving demands towards universities over time where the functioning of universities and their interactions with the other part of the NIS do evolve as well.We suggest to conceptualize the dynamics of innovation systems from an evolutionary perspective in order to develop a more subtle and dynamic vision on the role of universities in innovation systems.We emphasize our focus on‘evolutionary systems’instead of national innovation systems because for many universities,in particular some science-based disciplinaryfields such as biotechnology and nanotechnology,the national institutional environment is less relevant than the institu-tional and technical characteristics of the technological regimes,which is in fact a‘sub-system’of the national innovation system.3.Evolutionary Systems of Innovation as an Alternative Concept3.1Evolutionary Theory on Economic Change and InnovationCharles Darwin’s The Origin of Species(1859)is the foundation of modern thinking about change and evolution(Luria et al.,1981,pp. 584–7;Gould,1987).Darwin’s theory of natural selection has had the most important consequences for our perception of change. His view of evolution refers to a continuous and gradual adaptation of species to changes in the environment.The idea of‘survival of thefittest’means that the most adaptive organisms in a population will survive.This occurs through a process of‘natural selection’in which the most adaptive‘species’(organ-isms)will survive.This is a gradual process taking place in a relatively stable environment, working slowly over long periods of time necessary for the distinctive characteristics of species to show their superiority in the‘sur-vival contest’.Based on Darwin,evolutionary biology identifies three levels of aggregation.These three levels are the unit of variation,unit of selection and unit of evolution.The unit of varia-tion concerns the entity which contains the genetic information and which mutates fol-lowing specific rules,namely the genes.Genes contain the hereditary information which is preserved in the DNA.This does not alter sig-nificantly throughout the reproductive life-time of an organism.Genes are passed on from an organism to its successors.The gene pool,i.e.,the total stock of genetic structures of a species,only changes in the reproduction process as individuals die and are born.Par-ticular genes contribute to distinctive charac-teristics and behaviour of species which are more or less conducive to survival.The gene pool constitutes the mechanism to transmit the characteristics of surviving organisms from one generation to the next.The unit of selection is the expression of those genes in the entities which live and die as individual specimens,namely(individual) organisms.These organisms,in their turn,are subjected to a process of natural selection in the environment.‘Fit’organisms endowed with a relatively‘successful’gene pool,are more likely to pass them on to their progeny.As genes contain information to form and program the organisms,it can be expected that in a stable environment genes aiding survival will tend to become more prominent in succeeding genera-tions.‘Natural selection’,thus,is a gradual process selecting the‘fittest’organisms. Finally,there is the unit of evolution,or that which changes over time as the gene pool changes,namely populations.Natural selec-tion produces changes at the level of the population by‘trimming’the set of genetic structures in a population.We would like to point out two central principles of Darwinian evolution.First,its profound indeterminacy since the process of development,for instance the development of DNA,is dominated by time at which highly improbable events happen (Boulding,1991,p.12).Secondly,the process of natural selection eliminates poorly adapted variants in a compulsory manner,since indi-viduals who are‘unfit’are supposed to have no way of escaping the consequences of selection.22We acknowledge that within evolutionary think-ing,the theory of Jean Baptiste Lamarck,which acknowledges in essence that acquired characteris-tics can be transmitted(instead of hereditaryVolume17Number42008©2008The AuthorsJournal compilation©2008Blackwell PublishingThese three levels of aggregation express the differences between ‘what is changing’(genes),‘what is being selected’(organisms),and ‘what changes over time’(populations)in an evolutionary process (Luria et al.,1981,p.625).According to Nelson (see for instance Nelson,1995):‘Technical change is clearly an evolutionary process;the innovation generator keeps on producing entities superior to those earlier in existence,and adjustment forces work slowly’.Technological change and innovation processes are thus ‘evolutionary’because of its characteristics of non-optimality and of an open-ended and path-dependent process.Nelson and Winter (1982)introduced the idea of technical change as an evolutionary process in capitalist economies.Routines in firms function as the relatively durable ‘genes’.Economic competition leads to the selection of certain ‘successful’routines and these can be transferred to other firms by imitation,through buy-outs,training,labour mobility,and so on.Innovation processes involving interactions between universities and industry are central in the NIS approach.Therefore,it seems logical that evolutionary theory would be useful to grasp the role of universities in innovation pro-cesses within the NIS framework.3.2Evolutionary Underpinnings of Innovation SystemsBased on the central evolutionary notions as discussed above,we discuss in this section how the existing NIS approaches have already incor-porated notions in their NIS frameworks.Moreover,we investigate to what extent these notions can be better incorporated in an evolu-tionary innovation system to improve our understanding of universities in dynamic inno-vation processes.We focus on non-optimality,novelty,the anti-reductionist methodology,gradualism and the evolutionary metaphor.Non-optimality (and Bounded Rationality)Based on institutional diversity,the notion of optimality is absent in most NIS approaches.We cannot define an optimal system of innovation because evolutionary learning pro-cesses are important in such systems and thus are subject to continuous change.The system never achieves an equilibrium since the evolu-tionary processes are open-ended and path dependent.In Nelson’s work (e.g.,1993,1995)he has emphasized the presence of contingent out-comes of innovation processes and thus of NIS:‘At any time,there are feasible entities not present in the prevailing system that have a chance of being introduced’.This continuing existence of feasible alternative developments means that the system never reaches a state of equilibrium or finality.The process always remains dynamic and never reaches an optimum.Nelson argues further that diversity exists because technical change is an open-ended multi-path process where no best solu-tion to a technical problem can be identified ex post .As a consequence technical change can be seen as a very wasteful process in capitalist economies with many duplications and dead-ends.Institutional variety is closely linked to non-optimality.In other words,we cannot define the optimal innovation system because the evolutionary learning processes that take place in a particular system make it subject to continuous change.Therefore,comparisons between an existing system and an ideal system are not possible.Hence,in the absence of any notion of optimality,a method of comparing existing systems is necessary.According to Edquist (1997),comparisons between systems were more explicit and systematic than they had been using the NIS approaches.Novelty:Innovations CentralNovelty is already a central notion in the current NIS approaches.Learning is inter-preted in a broad way.Technological innova-tions are defined as combining existing knowledge in new ways or producing new knowledge (generation),and transforming this into economically significant products and processes (absorption).Learning is the most important process behind technological inno-vations.Learning can be formal in the form of education and searching through research and development.However,in many cases,innovations are the consequence of several kinds of learning processes involving many different kinds of economic agents.According to Lundvall (1992,p.9):‘those activities involve learning-by-doing,increasing the efficiency of production operations,learning-characteristics as in the theory of Darwin),is acknowledged to fit better with socio-economic processes of technical change and innovation (e.g.,Nelson &Winter,1982;Hodgson,2000).Therefore,our theory is based on Lamarckian evolutionary theory.However,for the purpose of this article,we will not discuss the differences between these theo-ries at greater length and limit our analysis to the fundamental evolutionary building blocks that are present in both theories.Volume 17Number 42008©2008The AuthorsJournal compilation ©2008Blackwell Publishingby-using,increasing the efficiency of the use of complex systems,and learning-by-interacting, involving users and producers in an interac-tion resulting in product innovations’.In this sense,learning is part of daily routines and activities in an economy.In his Learning Economy concept,Lundvall makes learning more explicit,emphasizing further that ‘knowledge is assumed as the most funda-mental resource and learning the most impor-tant process’(1992,p.10).Anti-reductionist Approach:Systems and Subsystems of InnovationSo far,NIS approaches are not yet clear and systematic in their analysis of the dynamics and change in innovation systems.Lundvall’s (1992)distinction between subsystem and system level based on the work of Boulding implicitly incorporates both the actor(who can undertake innovative activities)as well as the structure(institutional selection environment) in innovation processes of a nation.Moreover, most NIS approaches acknowledge that within the national system,there are different institu-tional subsystems(e.g.,sectors,regions)that all influence each other again in processes of change.However,an explicit analysis of the structured environment is still missing (Edquist,1997).In accordance with the basic principles of evolutionary theory as discussed in Section 3.1,institutional evolutionary theory has developed a very explicit systemic methodol-ogy to investigate the continuous interaction of actors and institutional structures in the evolution of economic systems.The so-called ‘methodological interactionism’can be per-ceived as a methodology that combines a structural perspective and an actor approach to understand processes of economic evolu-tion.Whereas the structural perspective emphasizes the existence of independent institutional layers and processes which deter-mine individual actions,the actor approach emphasizes the free will of individuals.The latter has been referred to as methodological individualism,as we have seen in neo-classical approaches.Methodological indi-vidualism will explain phenomena in terms of the rational individual(showingfixed prefer-ences and having one rational response to any fully specified decision problem(Hodgson, 2000)).The interactionist approach recognizes a level of analysis above the individual orfirm level.NIS approaches recognize that national differences exist in terms of national institu-tions,socio-economic factors,industries and networks,and so on.So,an explicit methodological interactionist approach,explicitly recognizing various insti-tutional layers in the system and subsystem in interaction with the learning agents,can improve our understanding of the evolution of innovation.Gradualism:Learning Processes andPath-DependencyPath-dependency in biology can be translated in an economic context in the form of(some-times very large)time lags between a technical invention,its transformation into an economic innovation,and the widespread diffusion. Clearly,in many of the empirical case studies of NIS,the historical dimension has been stressed.For instance,in the study of Denmark and Sweden,it has been shown that the natural resource base(for Denmark fertile land,and for Sweden minerals)and economic history,from the period of the Industrial Revolution onwards,has strongly influenced present specialization patterns(Edquist& Lundvall,1993,pp.269–82).Hence,history matters in processes of inno-vation as the innovation processes are influ-enced by many institutions and economic agents.In addition,they are often path-dependent as small events are reinforced and become crucially important through processes of positive feedback,in line with evolutionary processes as discussed in Section3.1.Evolutionary MetaphorFinally,most NIS approaches do not explicitly use the biological metaphor.Nevertheless, many of the approaches are based on innova-tion theories in which they do use an explicit evolutionary metaphor(e.g.,the work of Nelson).To summarize,the current(policy)NIS approaches have already implicitly incorpo-rated some evolutionary notions such as non-optimality,novelty and gradualism.However, what is missing is a more explicit analysis of the different institutional levels of the economic system and innovation subsystems (their inertia and evolution)and how they change over time in interaction with the various learning activities of economic agents. These economic agents reside at established firms,start-upfirms,universities,govern-ments,undertaking learning and innovation activities or strategic actions.The explicit use of the biological metaphor and an explicit use of the methodological interactionst approach may increase our understanding of the evolu-tion of innovation systems.Volume17Number42008©2008The AuthorsJournal compilation©2008Blackwell Publishing4.Towards a Dynamic View of Universities4.1The Logic of an Endogenous‘Learning’UniversityIf we translate the methodological interaction-ist approach to the changing role of universities in an evolutionary innovation system,it follows that universities not only respond to changes of the institutional environment(government policies,business demands or changes in scientific paradigms)but universities also influence the institutions of the selection envi-ronment by their strategic,scientific and entre-preneurial actions.Moreover,these actions influence–and are influenced by–the actions of other economic agents as well.So,instead of a one-way rational response by universities to changes(as in reductionist approach),they are intertwined in those processes of change.So, universities actually function as an endogenous source of change in the evolution of the inno-vation system.This is(on an ontological level) a fundamental different view on the role of universities in innovation systems from the existing policy NIS frameworks.In earlier empirical research,we observed that universities already effectively function endogenously in evolutionary innovation system frameworks;universities as actors (already)develop new knowledge,innovate and have their own internal capacity to change,adapt and influence the institutional development of the economic system(e.g., V an der Steen et al.,2009).Moreover,univer-sities consist of a network of various actors, i.e.,the scientists,administrators at technology transfer offices(TTO)as well as the university boards,interacting in various ways with indus-try and governments and embedded in various ways in the regional,national or inter-national environment.So,universities behave in an at least partly endogenous manner because they depend in complex and often unpredictable ways on the decision making of a substantial number of non-collusive agents.Agents at universities react in continuous interaction with the learn-ing activities offirms and governments and other universities.Furthermore,the endogenous processes of technical and institutional learning of univer-sities are entangled in the co-evolution of institutional and technical change of the evo-lutionary innovation system at large.We propose to treat the learning of universities as an inseparable endogenous variable in the inno-vation processes of the economic system.In order to structure the endogenization in the system of innovation analysis,the concept of the Learning University is introduced.In thenext subsection we discuss the main character-istics of the Learning University and Section5discusses the learning university in a dynamic,evolutionary innovation system.An evolution-ary metaphor may be helpful to make theuniversity factor more transparent in theco-evolution of technical and institutionalchange,as we try to understand how variouseconomic agents interact in learning processes.4.2Characteristics of the LearningUniversityThe evolution of the involvement of universi-ties in innovation processes is a learningprocess,because(we assume that)universitypublic agents have their‘own agenda’.V ariousincentives in the environment of universitiessuch as government regulations and technol-ogy transfer policies as well as the innovativebehaviour of economic agents,compel policymakers at universities to constantly respondby adapting and improving their strategiesand policies,whereas the university scientistsare partly steered by these strategies and partlyinfluenced by their own scientific peers andpartly by their historically grown interactionswith industry.During this process,universityboards try to be forward-looking and tobehave strategically in the knowledge thattheir actions‘influence the world’(alsoreferred to earlier as‘intentional variety’;see,for instance,Dosi et al.,1988).‘Intentional variety’presupposes that tech-nical and institutional development of univer-sities is a learning process.University agentsundertake purposeful action for change,theylearn from experience and anticipate futurestates of the selective environment.Further-more,university agents take initiatives to im-prove and develop learning paths.An exampleof these learning agents is provided in Box1.We consider technological and institutionaldevelopment of universities as a process thatinvolves many knowledge-seeking activitieswhere public and private agents’perceptionsand actions are translated into practice.3Theinstitutional changes are the result of inter-actions among economic agents defined byLundvall(1992)as interactive learning.Theseinteractions result in an evolutionary pattern3Using a theory developed in one scientific disci-pline as a metaphor in a different discipline mayresult,in a worst-case scenario,in misleading analo-gies.In the best case,however,it can be a source ofcreativity.As Hodgson(2000)pointed out,the evo-lutionary metaphor is useful for understandingprocesses of technical and institutional change,thatcan help to identify new events,characteristics andphenomena.Volume17Number42008©2008The AuthorsJournal compilation©2008Blackwell Publishing。
康德的哥白尼革命英文介绍"Copernican Revolution" is a term coined by Immanuel Kant to describe the revolutionary shift in the way people perceive the universe, brought about by Nicolaus Copernicus's theory that the Earth and other planets revolve around the Sun. Kant used this term to describe the Copernican Revolution as a "Copernican Turnabout" that reversed the traditional understanding of the universe, which had assumed that the Earth was the center of the universe.Nicolaus Copernicus (1473-1543) was a Polish astronomer who proposed that the Sun was at the center of the universe and that the Earth and other planets orbited around it. This was a departure from the previously accepted view that the Earth was the center of the universe. Copernicus's theory, which he proposed in his book "De revolutionibus orbium coelestium" ("On the Revolutions of the Heavenly Spheres"), was based on mathematical calculations and observations made by astronomers over many years.Kant believed that Copernicus's theory had a profound impact on people's understanding of the universe and their place in it. He believed that this impact was so significant that it could be likened to a Copernican Revolution, a term he used to describe a fundamental shift in thinking about the universe. Kant's use of the term "Copernican Revolution" has since become a widely used metaphor to describe any significant shift in perspective or worldview.。
TPO30 R-2 原文翻译The Pace of Evolutionary Change最近的一个关于进化的研究引发了激烈的争论。
达尔文的原始论点和进化渐进主义者支持的观点是物种会持续地改变,但非常缓慢,增量也很小。
这种改变到处都是,但是短时间的近代观察是不能察觉的,并且,这个观点声称,它们通常被掩盖于不完美的化石记录的不可计数的缺口中。
渐进主义,与其慢速的变化压力,处于一种令人欣慰的位置,在世代的教科书中重复出现。
在20世纪早前之前,令大部分的生物学家满意的是,大部分关于进化比率问题的答案都支持了渐进论有时,已经有了结论的问题必须由基于已有证据的曝光而出现的新的证据和新的论点使其重新展开讨论。
在1972年,古生物学者Stephen Jay Gould和Niles Eldredge用相反的论点挑战了世俗认知,即断点平衡说,它假设了物种演变为新的物种是通过相对突然的爆发,并非通过长时间的过渡时期。
这种迅速的进化的发生是被相对长时间的静态贯穿的,而在静态时期,物种是几乎完全不变的。
断点平衡论试着去解释化石记录的一个古怪的特点,它已经为古生物学者所熟悉超过一个世纪,但一直被忽视。
许多物种似乎在上百万年的化石记录中一直没有改变,这个情况对于不断变化的达尔文模型来说是不符合的。
渐进学者预测,这之间的化石形成是不完整的。
在大部分蛤和珊瑚的聚集地,其化石在很厚的岩石中都表现出了本质上的一致性,只是突然被另一新的或者不同的物种而取代。
北美马的进化曾经被用作经典的教科书案例来证明渐变进化论,现在却为点断平衡学提供了同样有说服力的证据。
一个有说服力的5千万年的马祖先的进化模型,每一代都稍稍大一点,有更复杂的牙齿,更长的连,和更中间突出的脚趾,这一切都看似强有力的支持了达尔文的论点,物种是逐步地进化的。
但是,对这些化石更严谨的验证现在揭示了一个不太一样的故事。
马是在不连续的步骤中进化的,其中每个进化步骤中间都间隔了上百万年的不变时间,在最后被一个不同的更新的模型取代。
The Calder´o n Projection:New Definition and ApplicationsBernhelm Booss-Bavnbek,Matthias Lesch,and Chaofeng ZhuAbstract.We consider an arbitrary linear elliptic first–order differential op-erator A with smooth coefficients acting on sections of a complex vector bundleE over a compact smooth manifold M with smooth boundary Σ.We describethe analytic and topological properties of A in a collar neighborhood U of Σand analyze various ways of writing A U in product form;we discuss the sec-torial projections of the corresponding tangential operator;construct variousinvertible doubles of A by suitable local boundary conditions;obtain Poissontype operators with different mapping properties;and provide a canonical con-struction of the Calder´o n projection.We apply our construction to generalizethe Cobordism Theorem and to determine sufficient conditions for continuousvariation of the Calder´o n projection and of well–posed self-adjoint Fredholmextensions under continuous variation of the data.ContentsList of Figures 21.Introduction 21.1.Dirac operator folklore 21.2.In search of generalization 31.3.Our present approach 42.Elliptic differential operators of first order on manifolds with boundary 62.1.Product form and metric structures near the boundary 62.2.The general set–up 92.3.Regular boundary conditions 103.Sectorial projections of an elliptic operator 123.1.Parameter dependent ellipticity 123.2.Sectorial operators:abstract Hilbert space framework 143.3.Sectorial operators:parametric elliptic differential operators 184.The invertible double 202000Mathematics Subject Classification.Primary 58J32;Secondary 35J67,58J50,57Q20.Key words and phrases.Calder´o n projection,Cauchy data spaces,cobordism theorem,con-tinuous variation of operators and boundary conditions,elliptic differential operator,ellipticity with parameter,Lagrangian subspaces,regular boundary value problem,sectorial projection,self-adjoint Fredholm extension,Sobolev spaces,symplectic functional analysis.This work was supported by the network “Mathematical Physics and Partial Differential Equations”of the Danish Agency for Science,Technology and Innovation.The second named author was partially supported by Sonderforschungsbereich/Transregio “Symmetries and Univer-sality in Mesoscopic Systems”(Bochum–Duisburg/Essen–K¨o ln–Warszawa)and the HausdorffCenter for Mathematics (Bonn).The third named author was partially supported by FANEDD 200215,973Program of MOST,Fok Ying Tung Edu.Funds 91002,LPMC of MOE of China,and Nankai University.1a r X i v :0803.4160v 1 [m a t h .D G ] 28 M a r 20082BERNHELM BOOSS-BA VNBEK,MATTHIAS LESCH,AND CHAOFENG ZHU4.1.The construction of˜A P(T)204.2.The local ellipticity of P(T)for˜A214.3.The solution space ker˜A P(T)224.4.The main result235.Calder´o n projector from the invertible double235.1.Sobolev scale235.2.Induced Poisson type operators and inverses245.3.The Calder´o n projection286.The Cobordism Theorem,revisited306.1.The General Cobordism Theorem316.2.Elements of symplectic functional analysis326.3.Proof of Theorem6.1376.4.Alternative routes to the General Cobordism Theorem417.Parameter dependence427.1.Some estimates447.2.Continuous dependence ofϕR T(B0)467.3.Continuous dependence of the invertible double467.4.Continuous dependence of S(A,T)487.5.Continuous dependence of P±on input data487.6.Continuity of families of well–posed self–adjoint Fredholm extensions50Appendix A.Smooth symmetric elliptic continuations with constantcoefficients in normal direction52 References56List of Figures1Construction of a closed coneΛsuch that B0−λId is elliptic with parameterλ∈Λ13 2The contoursΓ±in the plane defining the sectorial projections Q±15 3A two-component contourΓ,separating an inner sector around the real axis where all eigenvalues of B0show up,from two outer sectors whichtotally belong to the resolvent set of B017 4Three contours encircling all eigenvalues in the right half plane,on the imaginary axis,and all eigenvalues in the left half plane,respectively.391.IntroductionThis paper is about basic analytical properties of elliptic operators on compact manifolds with smooth boundary.Our main achievements are(i)to develop the basic elliptic analysis in full generality,and not only for the generic case of opera-tors of Dirac type in product metrics(i.e.,we assume neither constant coefficients in normal direction nor symmetry of the tangential operator);(ii)to establish the cobordism invariance of the index in greatest generality;and(iii)to prove the con-tinuity of the Calder´o n projection and of related families of global elliptic boundary value problems under parameter variation.We take our point of departure in the following observations.1.1.Dirac operator folklore.Most analysis of geometrical and physical problems involving a Dirac operator A on a compact manifold M with smooth boundaryΣacting on sections of a(complex)bundle E seems to rely on quite a few basic facts which are part of the shared folklore of people working in thisTHE Calder´o n PROJECTION3field of global analysis(e.g.,see Booßand Wojciechowski[BBW93]for properties (WiUCP),(InvDoub)and(Cob),and Nicolaescu[Nic97,Appendix]and Booß, Lesch and Phillips[BBLP05]for property(Param)):WiUCP:the weak inner unique continuation property(also called weak UCP to the boundary),i.e.,there are no nontrivial elements in the nullspace ker A vanishing at the boundaryΣof M;InvDoub:the existence of a suitable elliptic invertible continuation A of A, acting on sections of a vector bundle over the closed double or anothersuitable closed manifold M which contains M as submanifold;this yieldsa Poisson type operator K+which maps sections over the boundary intosections over M;and a precise Calder´o n projector C+,i.e.,an idempotentmapping of sections over the boundary onto the Cauchy data space whichconsists of the traces at the boundary of elements in the nullspace of A(possibly in a scale of Sobolev spaces);Cob:the existence of a self–adjoint regular Fredholm extension of any total (formally self–adjoint)Dirac operator A in the underlying L2-space withdomain given by a pseudodifferential boundary condition;that implies thevanishing of the signature of the associated quadratic form,induced bythe principal symbol in normal direction at the boundary;moreover,thatactually is equivalent to the Cobordism Theorem asserting a canonicalsplitting of the tangential operator B=B+⊕B−with ind B+=0;Param:the continuous dependence of a family of operators,their associated Calder´o n projections,and of any family of well-posed(elliptic)boundaryvalue problems on continuous or smooth variation of the coefficients.1.2.In search of generalization.With the renewed interest in geometri-cally defined elliptic operators offirst order of general type,arising,e.g.,from perturbations of Dirac operators,we ask to what extent the preceding list can be generalized to arbitrary linear elliptic differential operators with smooth coeffi-cients.It is hoped that the results of this paper can serve as guidelines for similar constructions and results for hypo-and sub-elliptic operators where the symbolic calculus is not fully available.There are immediate limits for generalization of some of the mentioned features by counter examples:UCP,even weak inner UCP may not hold for arbitrary elliptic systems offirst order,see indications in that direction in Pli´s[Pli61,Corollary1, p.610]and thefirst-order Alinhac type counterexample to strong UCP[B¨a r99, Example,p.184].Moreover,from just looking at the deficiency indices,we seethat the formally self-adjoint operator i ddx on the positive line does not admit aself-adjoint extension.This example is instructive because,quite opposite to the half-infinite domain,on a bounded one-dimensional interval any system offirst-order differential equations satisfies property(Cob)by a deformation argument.We go through the list.Property(WiUCP):It seems that the precise domain of validity is unknown. The local stability of weak inner UCP has been obtained by Booßand Zhu in [BBZ05,Lemma3.2].In spite of the local definition of UCP,the property(WiUCP) has a threefold global geometric meaning:(i)there are no ghost solutions,i.e., each section u∈C∞(M,E)belonging to the null space ker A over the manifold M has a non-trivial trace u Σat the boundary;(ii)equivalently,the maximal extension A max=(A t min)∗is surjective in L2(M,E)for densely defined closed minimal A min:D(A min)=H10(M,E)→L2(M,E);and(iii),as noted by Booßand Furutani in[BBF98,Section3.3]and in various follow-ups,it seems that assuming weak inner UCP of A and A t is mandatory for obtaining the continuity4BERNHELM BOOSS-BA VNBEK,MATTHIAS LESCH,AND CHAOFENG ZHUof Cauchy data spaces and the continuous change of the Calder´o n projection under variation of the coefficients,i.e.,property (Param).Property (InvDoub ):Different approaches are available:one approach ([BBW93,Chapter 9])has been the gluing of A and its formal adjoint A t to an invertibleelliptic operator Aover the closed double M .This construction is explicit,if the metric structures underlying the Dirac operator’s definition are product near the boundary.In the self-adjoint case,it yields at once the Lagrangian property of the Cauchy data space in the symplectic Hilbert space L 2(Σ,E Σ)of square integrable sections in E Σ:=E Σ.Then (Cob)follows.Property (InvDoub)generalizes to the non-product case for operators of Dirac type and,as a matter of fact,for any elliptic operator satisfying weak inner UCP un-der the somewhat restrictive condition that the tangential operator has self-adjoint principal symbol.Here the trick is that this condition permits the prolongation of the given operator to a slightly larger manifold M with boundary reaching con-stant coefficients in normal direction close to the new boundary and maintaining UCP under the prolongation (as well as formal self-adjointness of the coefficients,if present at the old boundary).This is explained in the Appendix.But what can be done for general elliptic operators?A very general and elegant construction of the Calder´o n projection was given by H¨o rmander in [H¨o r85,Theo-rem 20.1.3]on the symbol level.Unfortunately,he obtains only an almost projection (up to smoothing operators)which limits its applicability in our context.In this paper,we shall exploit another general definition of the Calder´o n pro-jection which is due to Seeley [See69,Theorem 1and Appendix,Lemma].Seeley’s construction provides a precise projection,not only an approximate one,and does not require UCP.First he replaces A by an invertible operator A 1by adding the projection onto the finite–dimensional space of inner solutions.Then he extends the operator D := 0A t 1A 10to the closed double M of a slightly extended man-ifold M with boundary.In general,such a prolongation may,however,destroy weak inner UCP even when UCP was established on the original manifold.Seeley constructs on the symbol level (and by adding a suitable correction term)an el-liptic extension D of D over the whole of the closed manifold M which is always invertible.He shows that Dprovides the wanted Poisson operator and a truly pseudodifferential Calder´o n projection P +along the original boundary Σ.In the formally self-adjoint case,P +has self-adjoint principal symbol and can be replaced by the orthogonal projection which is also pseudodifferential and has the same sym-bol (and may be denoted by the same letter P +).In this way,the choices in the construction of the invertible double are removed totally,as the operation of the resulting P +is concerned.This makes P +a good candidate for property (Cob).However,Seeley’s general construction,in difference to the simple gluing in the case of Dirac type operators of [BBW93,Chapter 9],does not lead immedi-ately to the Lagrangian property of im P +.Moreover and more seriously,when working with curves of elliptic problems Seeley’s construction does not give a hint under what conditions the Calder´o n projections vary continuously when varying a parameter.There are too many choices involved in Seeley’s construction.1.3.Our present approach.This motivates our present approach (inspired by Himpel,Kirk and Lesch [HKL04]),namely the construction of the invertible double as a canonically given local boundary problem for the double D exactly on the original manifold M ,without any choices,prolongations etc.This leaves us with full control of the UCP situation;leads directly to the wanted Fredholm LagrangianTHE Calder´o n PROJECTION5 property(Cob);and,moreover and here most decisively,provides explicit formulas for treating the parameter dependence in property(Param).This program is opened in Section2by explaining our basic choice of product structures near the boundary for the sake of comprehensible analysis,even if the original geometric structures are non-product;moreover,for the convenience of the reader and forfixing our notation we summarize a few basic facts about regular boundary conditions.To begin with,we do not assume self–adjoint principal symbol of the tangential operator B0nor constant coefficients B x=B0along an inward coordinate x.Most of our estimates depend on the single fact that B0−λis parameter dependent elliptic forλin a conic neighborhood of i R in the sense of Shubin[Shu80,Sec-tion II.9].More precisely,we depend on the related concept of sectorial spectral projections introduced in1970by Burak[Bur70]and recently further developed in Ponge[Pon06,Section3]as part of the current upsurge of interest in spectral properties of non-selfadjoint elliptic operators.Because of our interest in the con-tinuous dependence of this kind of generalized positive spectral projections on the input data we found it necessary to develop the concept of sectorial projections once again from scratch.This is done in Section3where we develop an abstract Hilbert space framework for the concept of sectorial projections and apply it to tangential operators perceived as parametric elliptic operators.In Section4we provide the construction and the relevant properties of the invertible double yielded by a local elliptic boundary value problem.In Section5we establish suitable Sobolev regularity of the inverse operator which leads to the definition and basic properties of Poisson operator and Calder´o n projection.Property(Cob):In Section6,we give afirst application of our construction of the Calder´o n projection:we give our reading of Ralston[Ral70]and infer that the arguments of this1970paper establish the followingfindings for any formally self-adjoint differential operator A over a compact manifold M with smooth boundary Σ:•the existence of a self-adjoint Fredholm extension A P given by a pseudo-differential boundary condition P;•the vanishing of the signature of iωon the space V(B0)of all purely imag-inary eigensections of the tangential operator B0of A over the boundary(or on ker B0in the case that B0is formally self-adjoint);here iωdenotesthe form induced by the Green form of A on the symplectic von Neumannspaceβ(A):=D(A max)/D(A min),i.e.,the principal symbol of A over theboundaryΣin normal direction;•and,equivalently,but seemingly never recognized by people working inglobal analysis,the General Cobordism Theorem,stating that the indexof any elliptic differential operator B+over a closed manifoldΣmustvanish,if B+can be written as the left lower corner of a formally self-adjoint tangential operator overΣinduced by an elliptic formally self–adjoint A on a smooth compact manifold M with∂M=Σ.Property(Param):In Section7,as a second application of our construction of the Calder´o n projection,we establish that property in great generality.Roughly speaking,we let an operator family(A z)and the family(A t z)of formally adjoint operators vary continuously in the operator norm from L21(M)to L2(M)and as-sume that the principal symbol(J0(A z))of(A z)over the boundaryΣin normal direction also varies continuously in the L2(Σ)operator norm with z running in1/2a parameter space Z.We assume for all A z and A t z property(WiUCP)or,almost equivalently,that the dimensions of the spaces of“ghost solutions”without trace at6BERNHELM BOOSS-BA VNBEK,MATTHIAS LESCH,AND CHAOFENG ZHUthe boundary remain constant under the variation.Then in Theorems 7.9and 7.2a we show that the inverse of the “invertible double”and,under slightly sharpened continuity,the Poisson operator in respective operator norms vary continuously;and so does the resolvent of a family (A z P z )of well-posed Fredholm extensions of now formally self–adjoint (A z )with orthogonal pseudodifferential projections (P z )varying in L 21/2(Σ)operator norm.Unfortunately,in the same generality we can neither prove nor disprove the continuous variation of the Calder´o n projection.However,if the principal symbol of the tangential operator is self-adjoint,we can prove the continuous variation of the sectorial projection (Proposition 7.15)and so (Theorem 7.4)of the Calder´o n projections by our correction formula (5.30)and Theorem 7.2b.Our Proposition7.13shows that the difficulties for proving continuous variation of the sectorial projection disappears also for non-selfadjoint principal symbol,if the variation is of order <1.In Appendix A we discuss various special cases with emphasis on constant coefficients in normal direction in a collar around the boundary.2.Elliptic differential operators of first order on manifolds withboundary2.1.Product form and metric structures near the boundary.We shall begin with a basic observation:Dirac operators emerge from a Riemannian struc-ture on the manifold and a Hermitian metric on the vector bundle (together with Clifford multiplication and a connection).Talking about a general differential op-erator it is in our view very misleading to pretend that the operator will depend on metrics and such.All we need is the operator and an L 2–structure on the sections.The latter basically only requires a density (take dvol in the Riemannian case)on the manifold and a metric on the bundle.In this paper,we prefer to choose metrics and such as simple as possible and push all complications into the operator.The message is this:we can always work in the product case and do have to worry only about the operator.In detail:Let M be a compact manifold (with or without boundary)and π:E →M a vector bundle.Given a Hermitian metric h on E and a Riemannian metric g on M we can form the Hilbert space L 2(M,E ;g,h )which is the completion of C ∞0(M \∂M,E )with regard to the scalar product(2.1) u,v g,h := Mh (u (x ),v (x ))dvol g (x ).Given another Riemannian metric g 1and another Hermitian metric h 1on E there is a smooth positive function ∈C ∞(M )such that(2.2)dvol g 1= dvol g ,and there is a smooth section θ∈C ∞(M,End E )such that for x ∈M,ξ,η∈E x we have(2.3)h 1,x (ξ,η)=h x (θ(x )ξ,η).Furthermore,with regard to h the operator θ(x )is self–adjoint and positive definite,thus we may form √θwhich is again a smooth self–adjoint and positive definite section of End E .It is clear that (2.3)determines θ(x )uniquely and the claimed smoothness of x →θ(x )can be checked easily in local coordinates.In sum,we findTHE Calder´o n PROJECTION7 for u,v∈C∞(M,E)u,v g1,h1=Mh1(u(x),v(x))dvol g1(x)=Mh(θ(x)u(x),v(x)) (x)dvol g(x) =θu,θv g,h.(2.4)Thus we arrive atLemma2.1.The mapΨ:C∞(M,E)−→C∞(M,E),u→θuextends to an isometry from L2(M,E;g1,h1)onto L2(M,E;g,h).Now assume that we are given a differential operator A in L2(M,E;g1,h1)of first order.It may be a Dirac operator which is constructed from the metrics g1and h1.g1and h1may be wildly non–product near the boundary.Suppose there are metrics g,h which we like more,e.g.,product near the boundary.Then consider the differential operatorΨAΨ−1in L2(M,E;g,h).ΨAΨ−1is still a differential operator and sinceΨis unitary all spectral properties are preserved.Let us be even more specific and choose a neighborhood U of∂M=:Σand a diffeomorphismφ:U→[0,ε)×Σwithφ Σ=idΣ.Furthermore,we choose a metric g on M such thatφ∗g=dx2⊕gΣ,gΣ:=g1 Σ,(2.5)is a product metric which induces the same metric on the boundary as g1.Here x denotes the normal inward coordinate near the boundary in the metric g.φis covered by a bundle isomorphism F:E U→[0,ε)×EΣ,EΣ:=E Σ,i.e., we have the commutative diagram(2.6)E U Fπ[0,ε)×EΣid×πUφ[0,ε)×Σ.Likewise,we may now choose a metric h on E such that h(x):=F∗h {x}×Σ=h Σ=h1 Σ=:hΣis independent of x∈[0,ε).The mappings F andφinduce a map(2.7)Ψ1:C∞(U,E)→C∞([0,ε),C∞(EΣ))f→x→p→F(f(φ−1(x,p)))which extends to a unitary isomorphism L2(U,E;g,h)→L2([0,ε],L2(Σ,EΣ)).On Σand EΣwe have thefixed metrics gΣrespectively hΣand we suppress the reference to them in the notation.Together with the unitary isomorphismΨof Lemma2.1we obtain the claimed isometry(2.8)Φ:=Ψ1◦Ψ:L2(U,E;g1,h1)→L2([0,ε],L2(EΣ)).NowΦAΦ−1is afirst order differential operator in the product Hilbert space L2([0,ε))⊗L2(Σ,EΣ;gΣ,h)and hence it takes the form(2.9)D:=ΦAΦ−1=:J ddx+Bwith a bundle endomorphism J∈C∞([0,ε),C∞(Σ,End EΣ))and a smooth family offirst order differential operators B∈C∞([0,ε),Diff1(Σ,EΣ)).For the moment8BERNHELM BOOSS-BA VNBEK,MATTHIAS LESCH,AND CHAOFENG ZHUwe consider here only the smooth case,but so far one can replace’smooth’by ’continuous’or’Lipschitz’or whatever.Let us repeat:now all metric structures are product near the boundary and we do not have to worry about them.If we start with a Dirac operator on a Riemannian manifold with non–product metric the’non–product situation’is reflected in the varying coefficients of D.From now on we have to worry only about those varying coefficients and nothing else.We assume that product metrics g,h arefixed and therefore we will suppress them in the notation.For further reference we record Green’s formula for A:Lemma2.2.Letν∈C∞(Σ,T M Σ)be the outward normal vectorfield.Then we have for f,g∈C∞(M,E)Af,g L2(M,E;g1,h1)− f,A t g L2(M,E;g1,h1)=1iΣσ1A(νb)f Σ,g Σ dvol=− J(0)f Σ,g Σ L2(Σ,EΣ;gΣ,h1),(2.10)where i:=√−1,νb denotes the cotangent vectorfield corresponding toνin themetric g1,andσ1Adenotes the leading symbol of A.Note thatφ∗ν=−ddx .Note also that by construction all transformations aretrivial on the boundary,that is,φ Σ=id;F EΣ=id,(Ψ1f) Σ=f Σ;(Ψf) Σ=f Σ;(Φf) Σ=f Σ.(2.11)For a differential operator A we denote by A t its formal adjoint.If A is viewed as an unbounded operator in some Hilbert space,we denote by A∗its functional an-alytic adjoint.For0th order operators and for elliptic operators on closed manifolds the difference between formal adjoint and(true)adjoint does not really matter;so in this case we use both notations interchangeably.NearΣwe haveA=J x ddx+B xand(2.12)−A t=J t xddx−B t x J t x+(J x)t(2.13)=J t x ddx−(J t x)−1B t x J t x+(J x)t.If A is formally self–adjoint,we have the relations(2.14)J t=−J,JB=J −B t J( denotes differentiation by x).The ellipticity of A implies that J(x)is invertible and that B(x)is elliptic for all x.Alternatively,we may choose the following normal form in a collar of the bound-ary:A=J(x) ddx+B(x)+12J (x),=:J x ddx+B x+12J x.(2.15)To avoid an inflation of parentheses we will most often use the notation B x,J x instead of B(x),J(x)etc.Only to avoid double subscripts we will write B(x),J(x) in subscripts.A=A t implies the relations(2.16)J t=−J,JB=−B t J.THE Calder´o n PROJECTION9 The normal form(2.15)determines J and B uniquely.2.2.The general set–up.We are going tofix some notation which will be used throughout the paper.Assume that the following data are given:•a compact smooth Riemannian manifold(M,g)with smooth boundaryΣ:=∂M,•Hermitian vector bundles(E,h E),(F,h F),•afirst order elliptic differential operator(2.17)A:C∞(M,E)→C∞(M,F).We consider A as an unbounded operator between the Sobolev(and Hilbert) spaces(2.18)L2s(M,E;g,h E),L2s(M,F;g,h F),s≥0.1The closure of A C∞0(M\Σ,E)in L2is denoted by A min and we put(2.19)D(A max):=f∈L2Af∈L2.As explained in Section2.1there exists a collar U≈[0,ε)×Σand linear isomor-phisms(2.20)ΦG:C∞(U,G)→C∞([0,ε),C∞(GΣ)),G=E,F,which extend to isometries(2.21)L2(U,G;g,h G)→L2([0,ε],L2(Σ,GΣ;gΣ,h GΣ),G=E,F, where gΣ=g Σ,GΣ:=G Σand h GΣ=h G GΣ.Now we consider(2.22)D:=ΦF A(ΦE)−1:C∞([0,ε),C∞(EΣ))→C∞([0,ε),C∞(FΣ)). Since A is afirst order elliptic differential operator wefind(2.23)D=J x ddx+B x,where J x∈Hom(EΣ,FΣ),0≤x≤ε,is a smooth family of bundle homomorphisms and(B x)0≤x≤εis a smooth family offirst order elliptic differential operators between sections of EΣ.The ellipticity of D imposes another restriction on B ly,ellipticity ofD means that forλ∈R,ξ∈T∗pΣ,(λ,ξ)=(0,0)the operator(2.24)iλ+σ1B(x)(p,ξ)is invertible for all(x,p)∈[0,ε)×Σ.Here,σ1B(x)denotes the leading symbol ofB x.In other words,forξ∈T∗pΣ\{0}the endomorphismσ1B(x)(p,ξ)∈End(E p)has no eigenvalues on the imaginary axis i R.Furthermore we note that in view of(2.10)J0equals iσ1A (νb),whereν=−ddxis the outward normal vectorfield.1For simplicity we content ourselves to Sobolev spaces of nonnegative order.On a manifold with boundary Sobolev spaces of negative order are a nuisance,although with some care they could be dealt with here.Cf.[LM72]10BERNHELM BOOSS-BA VNBEK,MATTHIAS LESCH,AND CHAOFENG ZHU2.3.Regular boundary conditions.For the convenience of the reader and to fix some notation we briefly summarize a few basic facts about boundary condi-tions for A .Standard references are [BBW93,H¨o r85,LM72,See69].We will adopt the point of view of the elementary functional analytic presentation [BL01].However,we try to be as self-contained as possible.It is well-known that the trace map(2.25):C ∞0(M,E )→C ∞(Σ,E ),f →f Σextends by continuity to a bounded linear map between Sobolev spaces (2.26)L 2s (M,E )→L 2s −1/2(Σ,E Σ),s >1/2.For the domain of A max this can be pushed a bit ly,for s ≥0the trace map extends by continuity to a bounded linear map(2.27)D (A max ,s )→L 2s −1/2(Σ,E Σ),s ≥0,that is,there is a constant C s ,such that for f ∈L 2s (M,E )with Af ∈L 2s (M,E )(2.28) f s −1/2≤C s ( f s + Af s )Here f s denotes the Sobolev norm of order s.Furthermore,norms of operatorsfrom L 2s to L 2s will be denoted by · s,s ,and · ∞denotes the sup-norm of afunction.The proof (2.27),(2.28)in [BBW93,Theorem 13.8and Corollary 13.9]simpli-fies [LM72]for operators of Dirac type but remains valid for any elliptic differential operator of first order.cf.also [BL01,Lemma 6.1].Definition 2.3.(a)Let CL 0(Σ;E Σ,G )denote the space of classical pseudo-differential operators of order 0,acting from sections of E Σto sections of another smooth Hermitian bundle G over Σ.(b)Let P ∈CL 0(Σ;E Σ,G ).We denote by A P the operator A acting on the domain (2.29)D (A P ):= f ∈L 21(M,E ) P ( f )=0 ,and by A max ,P the operator A acting on the domain (2.30)D (A max ,P ):= f ∈L 2(M,E ) Af ∈L 2(M,F ),P ( f )=0 .(c)The boundary condition P for A is called regular if A max ,P =A P ,i.e.,if f,Af ∈L 2,P ( f )=0already implies that f ∈L 21(M,E ).(d)The boundary condition P is called strongly regular if f ∈L 2,Af ∈L 2k ,P ( f )=0already implies f ∈L 2k +1(M,E ),k ≥0.(2.28)shows that D (A P )is in any case a closed subspace of L 21(M,E ).Proposition 2.4.Let P be regular for A .Then A P is a closed semi-Fredholm operator with finite–dimensional kernel.Proof.Let (f n )⊂D (A P )be a sequence with f n →f and Af n →g ∈L 2(M,F ).Then Af =g weakly and hence in view of (2.27),(2.28)we have P ( f )=0and the regularity of P implies f ∈L 21(M,E ),thus f ∈D (A P ).Hence A P is closed and thus D (A P )is complete in the graph norm.The pre-vious argument shows in view of the Closed Graph Theorem that the inclusion ι:D (A P ) →L 21(M,E )is bounded.ιis thus an injective bounded linear map from the Hilbert space D (A P )(equipped with the graph norm)onto a closed subspace of L 21(M,E );the closedness is also a consequence of the argument at the begin-ning of this proof.Consequently,on D (A P )the graph norm and the L 21-norm are equivalent.I.e.,for f ∈D (A P )we have(2.31)1C f 1≤ f 0+ Af 0≤C f 1.。