下载文档原格式
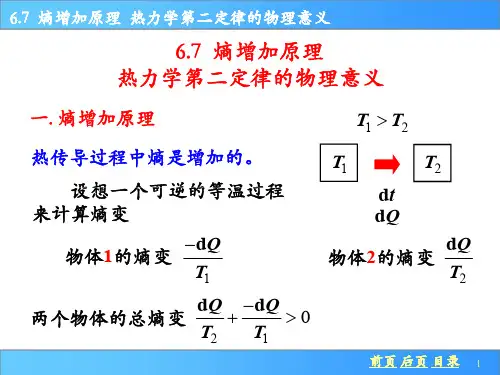
热力学中的熵与热力学第二定律熵是热力学中一个非常重要的概念，它与热力学第二定律密切相关。
本文将介绍熵的概念以及它在热力学中的应用，同时探讨熵与热力学第二定律的关系。
一、熵的概念熵是热力学中描述系统无序程度的物理量。
熵的增加代表了系统的无序程度增加。
根据能量守恒定律，一个孤立系统的能量是守恒的，那么系统的状态必然朝着熵增的方向演化。
热力学第二定律正是描述了这一演化趋势，即在孤立系统中，熵总是不减的。
二、熵的公式熵的计算公式为：S = k ln Ω其中，S表示熵，k为玻尔兹曼常数，Ω为系统的微观状态数。
这个公式告诉我们，熵与系统的微观状态数成正比。
微观状态数越多，系统的熵越大，也就代表了系统的无序程度越高。
三、熵的应用熵在热力学中具有广泛的应用。
例如在化学反应中，可以通过计算反应前后的熵变来判断反应的进行方向。
若反应前的熵较大，反应后的熵较小，那么反应是自发进行的。
另外，在热力学研究中，熵也经常用于描述物质的相变过程以及平衡态的性质。
四、熵与热力学第二定律熵与热力学第二定律密不可分。
热力学第二定律规定了自然界中的过程必须遵循的规律，即孤立系统的熵不减。
热力学第二定律的一个重要表述是熵增原理，即孤立系统的熵趋向于最大值。
这意味着熵对自发过程的方向性起着决定性的作用。
通过熵的概念和热力学第二定律，我们可以更好地理解自然界中广泛存在的一些现象。
例如，为什么热量总是从高温物体传递到低温物体？这是因为热传导过程中，系统的熵增加，使得整个系统达到更高的无序状态。
总之，熵是热力学中一个重要的概念，它描述了系统的无序程度。
熵与热力学第二定律密切相关，它帮助我们理解自然界中的各种现象。
更深入地理解熵的概念和研究其应用，对于热力学及相关领域的科学研究具有重要意义。
熵与热力学第二定律热力学是一门研究能量转化和传递的学科，而熵则是热力学的一个重要概念。
熵是描述系统无序度的物理量，也可以理解为系统的混乱程度。
热力学第二定律则给出了一个有关熵变化的基本规律，对于理解自然界中各种现象都具有重要意义。
首先，我们来了解一下熵的概念。
熵最初由德国物理学家鲁道夫·克劳修斯在19世纪提出，用以描述能量在转化和传递过程中的无序度。
熵的单位是焦耳/开尔文（J/K）。
在热力学中，我们通常用S表示熵。
对于一个封闭系统来说，其熵的变化可以通过以下公式表示：ΔS = Q/T其中，ΔS表示熵变化，ΔQ表示系统所吸收或释放的热量，T表示温度。
从这个公式可以看出，熵的变化与温度和能量的传递有着密切的关系。
进而，熵的变化与热力学第二定律密切相关。
热力学第二定律是热力学中的一条基本定律，它通过熵的变化来描述了自然界中一种普遍存在的变化趋势：任何一个孤立系统总是朝着熵增的方向进行变化。
热力学第二定律可以用以下两种表述方式进行阐述：1. 克劳修斯表述：不可能自发地将热量从低温物体传递到高温物体，而不做额外的功。
这个表述是从能量守恒的角度上来看待熵增的原理。
2. 开尔文表述：不可能从单一热源吸热，使之完全转化为有效功而不产生其他变化。
这个表述则是从热力学循环的角度上来看待熵增的原理。
无论是克劳修斯表述还是开尔文表述，都体现了一个重要的观点：自然界的变化总是朝着更高的熵方向发展，即朝着能量的分散和无序性的增加。
这进一步表明了熵在物理系统中的重要性。
熵的概念不仅在热力学领域有着广泛的应用，还可以引申到其他领域。
在信息论中，熵被用来度量信息的不确定性，即信息的无序度。
熵在信息论中与热力学中的熵有着数学上的相似性，都是描述系统无序度的物理量。
这种类比为信息论提供了一个重要的工具，使之能够研究信息的流动和传递。
总结起来，熵是热力学中一个重要的概念，用于描述系统的无序度。
熵的变化与热力学第二定律密切相关，从而给出了自然界中的一种普遍存在的变化趋势。
熵与热力学第二定律
热力学第二定律是热力学的基本定律之一，也被称为热力学不可逆
性定律。
它规定了一个系统在孤立过程中，熵的增加是不可逆过程的
一个必然结果。
熵（Entropy）是一个描述系统无序程度的物理量。
熵越大，系统的无序程度越高。
熵的概念最早由热力学第二定律引入，后来被推广应
用于信息论和统计力学领域。
热力学第二定律可以用不同的形式表达，其中最常用的形式是开尔
文表述和克劳修斯表述。
开尔文表述指出，任何一个孤立系统不可避免地趋向于热力学平衡态，而这个平衡态是具有最大熵的状态。
这意味着在孤立系统中，熵
始终增加，直到系统达到平衡态为止。
克劳修斯表述则通过热机的工作循环来表达热力学第二定律。
克劳
修斯表述指出，不存在一种热机可以从单一热源吸热，将全部吸收的
热量完全转化为对外做的功，而不产生其他效果。
在实际应用中，熵的增加可以被看作是能量向无用能量转化的过程。
热能在能量转化中是不能完全转化为有用功的，总是会有一部分能量
被转化为无用的热量，从而增加系统的熵。
总而言之，熵与热力学第二定律密切相关。
熵的增加是热力学不可
逆性的表现，热力学第二定律规定了熵的增加是一个孤立系统无法避
免的过程。
这一定律为热力学提供了一个基本原则，对于能量转化和自然过程有重要的理论和应用价值。
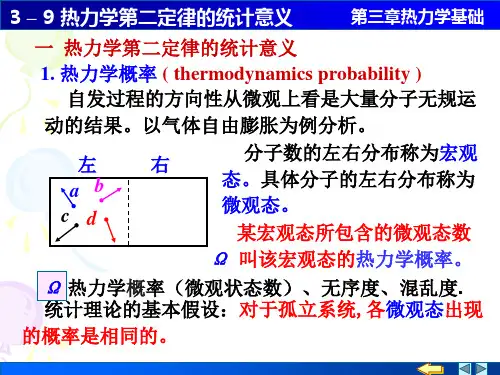
熵与热力学第二定律物理名词,用热量除温度所得的商,标志热量转化为功的程度 [entropy]熵：在《博弈圣经》中是生物亲序，是行为携灵现象物理意义：物质微观热运动时，混乱程度的标志。
热力学中表征物质状态的参量之一，通常用符号S表示。
在经典热力学中，可用增量定义为dS＝(dQ/T)，式中T为物质的热力学温度；dQ为熵增过程中加入物质的热量。
下标“可逆”表示加热过程所引起的变化过程是可逆的。
若过程是不可逆的，则dS＞(dQ/T)不可逆。
单位质量物质的熵称为比熵，记为s。
熵最初是根据热力学第二定律引出的一个反映自发过程不可逆性的物质状态参量。
热力学第二定律是根据大量观察结果总结出来的规律，有下述表述方式：①热量总是从高温物体传到低温物体，不可能作相反的传递而不引起其他的变化；②功可以全部转化为热，但任何热机不能全部地、连续不断地把所接受的热量转变为功（即无法制造第二类永动机）；③在孤立系统中，实际发生的过程总使整个系统的熵值增大，此即熵增原理。
摩擦使一部分机械能不可逆地转变为热，使熵增加。
热量dQ由高温(T1)物体传至低温(T2)物体，高温物体的熵减少dS1=dQ/T1，低温物体的熵增加dS2=dQ/T2，把两个物体合起来当成一个系统来看，熵的变化是dS＝dS2－dS1＞0，即熵是增加的。
◎ 物理学上指热能除以温度所得的商，标志热量转化为功的程度。
◎ 科学技术上泛指某些物质系统状态的一种量（liàng）度，某些物质系统状态可能出现的程度。
亦被社会科学用以借喻人类社会某些状态的程度。
◎ 在信息论中，熵表示的是不确定性的量度。
只有当你所使用的那个特定系统中的能量密度参差不齐的时候，能量才能够转化为功，这时，能量倾向于从密度较高的地方流向密度较低的地方，直到一切都达到均匀为止。
正是依靠能量的这种流动，你才能从能量得到功。
江河发源地的水位比较高，那里的水的势能也比河口的水的势能来得大。
由于这个原因，水就沿着江河向下流入海洋。
熵增和热力学第二定律热力学是研究热与其他形式能量转化以及热能转化与不可逆性关系的学科。
熵增和热力学第二定律是热力学中重要的概念和定律。
熵增是指系统总熵的增加，而热力学第二定律则是描述了熵增的方向性，即自发过程中系统总熵必然增加的趋势。
熵增是热力学中的一个基本概念，它是描述系统混乱程度或无序程度的物理量。
根据热力学第二定律，对于封闭系统，自发过程总是会使系统的总熵增加。
熵增可以被看作是系统状态朝着更多的微观状态的方向发展，因为更多的微观状态对应着更大的无序性。
熵增的思想可以从统计学的角度理解，即系统具有更多的微观状态的概率更高。
熵增是描述不可逆过程的一个重要指标。
不可逆过程是指不能完全逆转的过程，一旦发生就无法回到原来的状态。
不可逆过程中，能量不可完全转化为有效的形式，而是转化为无用的热能，增加了系统的总熵。
而可逆过程是指可以完全逆转的过程，能量可以完全转化为有效的形式而没有熵增。
热力学第二定律告诉我们，自然界中所有的过程都是不可逆的，总的熵不会减小。
热力学第二定律是描述自然界不可逆性的定律。
它有多种表述方式，其中最常见的是克劳修斯表述和开尔文表述。
克劳修斯表述指出，不可能将热量从低温物体传输到高温物体而不产生其他效果。
这也意味着热量不会自发地从冷物体传输到热物体。
开尔文表述则指出，不可能通过一个循环过程从单一热源吸收热量，完全转化为功而不产生其他效果。
换言之，不可能实现完全的热能到功的转化，总会有一部分能量转化为无用的热能。
熵增和热力学第二定律在许多实际应用中起到了重要的作用。
例如，热机的效率就受到热力学第二定律的限制。
根据卡诺热机的原理，热机的最大效率只取决于工作物体的高温和低温温度，与工作物体的性质无关。
这是因为根据热力学第二定律，无法通过一个循环过程将热量完全转化为功，总会有一部分热量流失为无用的热能，导致热机的效率不可能达到100%。
此外，熵增和热力学第二定律在生态学和环境科学中也有重要的应用。
热力学是研究能量转化和传递的一门学科，它探讨能量的守恒以及能量转换的规律。
熵和热力学第二定律是热力学中的两个重要概念，它们有着密切的关系。
首先，我们来介绍一下熵的概念。
熵是一个用来描述系统无序度的物理量。
一个有序的系统具有较低的熵值，而一个无序的系统则有较高的熵值。
熵的增加表示系统的无序度增加，而熵的减少则表示系统的有序度增加。
例如，一个整齐摆放的房间的熵较低，而一个散乱不堪的房间的熵较高。
在热力学中，熵是一个基本的概念，它可以用来描述一个系统所处的状态。
其次，我们来讨论熵与热力学第二定律之间的关系。
热力学第二定律是一个描述自然界过程方向性的定律。
它指出，自发过程在孤立系统中只能是增加系统熵的方向。
换句话说，孤立系统总是趋向于有序度较低的状态。
这个定律揭示了自然界中一种普遍的趋势，即无序度增加的趋势。
熵作为一种衡量系统无序度的物理量，与热力学第二定律密切相关。
进一步来说，熵的增加可以通过热力学第二定律中的一些过程来实现。
例如，热传导过程中热量从高温物体流向低温物体，使得系统的能量分布更加均匀，从而增加了熵。
再如，热力学第二定律中的等压过程和等温过程都是自发过程，它们使得系统的有序度减少，系统的熵增加。
因此，熵与热力学第二定律共同描述了自然界的无序化趋势。
最后，我们来探讨一下熵和热力学第二定律在实际应用中的意义。
熵的概念在许多领域都有着广泛的应用，特别是在工程领域和环境科学中。
熵可以用来描述一个系统的纯度、混乱程度以及不可逆性。
例如，在能源转化工程中，熵增原理可以用来解释能量转化的效率限制。
在环境科学中，熵被广泛用于地球系统中物质和能量的传递和转化的研究中。
总的来说，熵和热力学第二定律是热力学中的两个重要概念。
熵描述了系统的无序度，而热力学第二定律揭示了自然界的趋势，即无序度增加的趋势。
这两个概念可以互相解释和补充，共同描述了自然界中能量转化和传递的规律。
它们的应用也给人们在能源转化和环境保护等方面提供了指导和启示。
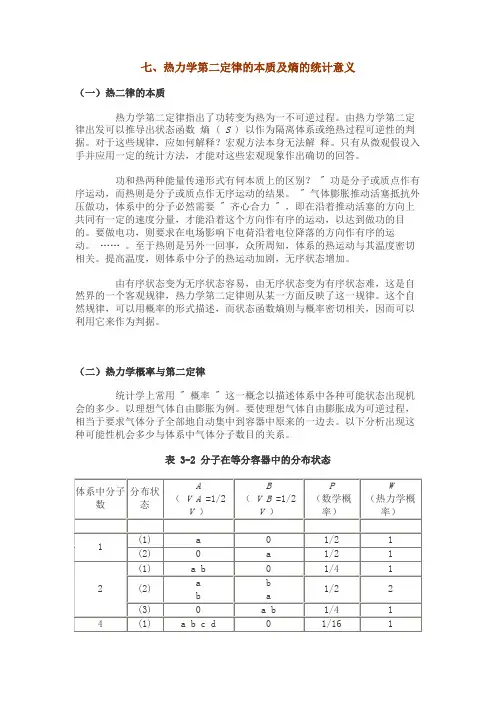
七、热力学第二定律的本质及熵的统计意义（一）热二律的本质热力学第二定律指出了功转变为热为一不可逆过程。
由热力学第二定律出发可以推导出状态函数熵 ( S ) 以作为隔离体系或绝热过程可逆性的判据。
对于这些规律，应如何解释？宏观方法本身无法解释。
只有从微观假设入手并应用一定的统计方法，才能对这些宏观现象作出确切的回答。
功和热两种能量传递形式有何本质上的区别？ " 功是分子或质点作有序运动，而热则是分子或质点作无序运动的结果。
" 气体膨胀推动活塞抵抗外压做功，体系中的分子必然需要 " 齐心合力 " ，即在沿着推动活塞的方向上共同有一定的速度分量，才能沿着这个方向作有序的运动，以达到做功的目的。
要做电功，则要求在电场影响下电荷沿着电位降落的方向作有序的运动。
……。
至于热则是另外一回事，众所周知，体系的热运动与其温度密切相关。
提高温度，则体系中分子的热运动加剧，无序状态增加。
由有序状态变为无序状态容易，由无序状态变为有序状态难，这是自然界的一个客观规律，热力学第二定律则从某一方面反映了这一规律。
这个自然规律，可以用概率的形式描述，而状态函数熵则与概率密切相关，因而可以利用它来作为判据。
（二）热力学概率与第二定律统计学上常用 " 概率 " 这一概念以描述体系中各种可能状态出现机会的多少。
以理想气体自由膨胀为例。
要使理想气体自由膨胀成为可逆过程，相当于要求气体分子全部地自动集中到容器中原来的一边去。
以下分析出现这种可能性机会多少与体系中气体分子数目的关系。
表 3-2 分子在等分容器中的分布状态如表 3-2 所示，设容积为 V 的容器等分为 A 和 B 两边( ) 。
1、若容器中只有一个分子 " a " 。
则 a 处于 A 边或 B 边的机会均等，实现自由膨胀成为可逆（a 处于 A 的一边）的数学概率： 。
2、若容器中有两个分子 " a " 和 " b " 。
