当前位置：文档之家 › 第二章 线性规划解析

第二章 线性规划解析

  • 格式：ppt
  • 大小：9.43 MB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

第二章 线性规划课件

第二章 线性规划课件
否
be max bi bi 0
是没
所有a i k 0
有
否
最 优
计算
min
bi a ik
a ik
0
be aek
解
没是
有
所有 a e j 0
最 优
否
解
计算
min
i aej
aej
<0
k aek
以为中心元素进行迭代
以为中心元素进行迭代
例6 用单纯形表求解例1。（见书P25） 解 已知该问题的标准型为:
§1 对线性规划的回顾
非标准形式化为标准形式总结
线性规划模型
变量 Xj≥0
Xj≤0
Xj无约束
约 右端 bi≥0
束项 条
bi<0
件 形式 ai1x1+…+ainxn =bi
ai1x1+…+ainxn ≤bi
ai1x1+…+ainxn ≥ bi 目标函数 max z= c1x1+…+cnxn
min z= c1x1+…+cnxn
Y*分别是问题 P和D 的最优解。
【性质4】 (强对偶性) 原规划与对偶规划同有最优解，且两者最优值相等。
【性质5】互补松弛定理：设X、Y各为原规划与对偶规划的一个可行解，则X、Y为最
优解的充分必要条件为 Y XS = YS X = 0。 【性质6】 (基解对应性) 原规划单纯形表中检验数行对应对偶规划的一个基解。
推论⑴.若X和Y分别是问题（P）和（D）的可行解，则 CX是（D）的目标函数最小 值的一个下界；Yb是（P）的目标函数最大值的一个上界。
推论⑵.在一对对偶问题（P）和（D）中，若其中一个问题可行但目标函数无界，则 另一个问题不可行；反之不成立。这也是对偶问题的无界性。

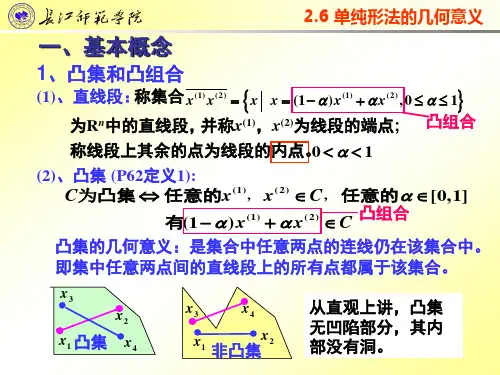
9《线性规划》092第二章2.6几何意 义 2.5初始基=第九次课解析

9《线性规划》092第二章2.6几何意 义 2.5初始基=第九次课解析

2.6 单纯形法的几何意义
一、基本概念
H { x ax , x R n } H { x ax , x R n } H { x ax , x R n }
4、多面凸集和凸多面体
例如，在空间R3中，设超平面如下：
H 1 {( x , y , z ) (1, 0, 0)( x , y , z )T 0 }
有(1 ) x
(1)
C为凸集 任意的x (1)，x ( 2) C，任意的 [0,1] x
( 2)
C
凸组合
凸集的几何意义：是集合中任意两点的连线仍在该集合中。 即集中任意两点间的直线段上的所有点都属于该集合。
x3
x2
x1 凸集 x4
x3
x4
x1
非凸集
x2
从直观上讲，凸集 无凹陷部分，其内 部没有洞。
如果线段 x(1) x(2) 上的任意一点都不可能是K中其他任何线段 的内点，则称x(1)与x(2)是K的相邻极点。 只能是其他线段的端点 换言之，多面凸集K的两个极点是x(1) , x(2)是相邻极点 x(1)≠x(2)且任取 x(0) x(1) x(2) ，若存在x(3)，x(4) ∈K，使得 x(0)＝(1-)x(3)+x(4) , 0<<1，则必有 x(3) , x(4) x(1) x(2) 。
2.6 单纯形法的几何意义
一、基本概念
√ √
一些关于凸集的结论：
结论1：超平面是闭凸集。
结论2：任意多个凸集的交还是凸集。(P69第3题)
结论3：凸集C中任意有限个点的凸组合仍属于C。(P69第5题)
结论4：闭半空间是闭凸集(P69第2题)。 结论5：闭半空间的交集是闭凸集。

运筹学第二章线性规划

运筹学第二章线性规划

第二章线性规划教学目的和要求：目的：使学生具备线性规划的基本知识以及应用线性规划的基本能力。

要求：理解线性规划概念，标准型，解的概念，基本定理；掌握单纯形法，人工变量法，了解图解法。

重点：线性规划标准型，解的概念，单纯形法，人工变量法。

难点：线性规划基本定理，单纯形法。

教学方法：讲授法，习题法。

学时分配：12学时 作业安排：见教材P 38.线性规划是运筹学的一个重要分支。

1939年苏联科学家康托罗维奇提出了生产组织和计划中的线性规划模型。

1947年美国学者丹捷格(George B.Dantzig)提出了求解一般线性规划问题的方法。

此后，线性规划理论日趋成熟，应用也日益广泛和深入。

第一节线性规划问题一、问题的提出在企业的生产经营活动中经常会面临这样两类问题：一是如何合理地利用有限的人力、物力、财力等资源，取得最佳的经济效果；二是在取得一定的经济效果的前提下，如何合理安排使用人力、物力、财力等资源，使花费的成本最低。

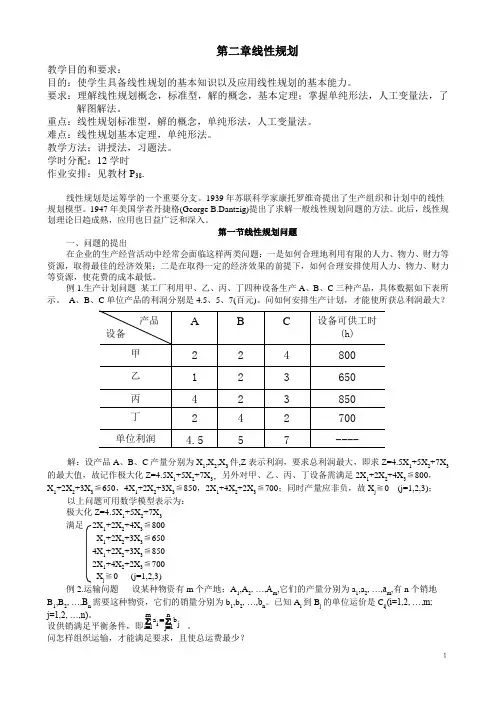
例1.生产计划问题 某工厂利用甲、乙、丙、丁四种设备生产A 、B 、C 三种产品，具体数据如下表所示。

A 、B 、C 单位产品的利润分别是4.5、5、7(百元)。

问如何安排生产计划，才能使所获总利润最大？解：设产品A 、B 、C 产量分别为X 1,X 2,X 3件,Z 表示利润，要求总利润最大，即求Z=4.5X 1+5X 2+7X 3的最大值，故记作极大化Z=4.5X 1+5X 2+7X 3，另外对甲、乙、丙、丁设备需满足2X 1+2X 2+4X 3≦800，X 1+2X 2+3X 3≦650，4X 1+2X 2+3X 3≦850，2X 1+4X 2+2X 3≦700；同时产量应非负，故X j ≧0 (j=1,2,3)；以上问题可用数学模型表示为： 极大化Z=4.5X 1+5X 2+7X 3 满足 2X 1+2X 2+4X 3≦800 X 1+2X 2+3X 3≦6504X 1+2X 2+3X 3≦850 2X 1+4X 2+2X 3≦700X j ≧0 (j=1,2,3)例2.运输问题 设某种物资有m 个产地；A 1,A 2, …,A m ,它们的产量分别为a 1,a 2, …,a m ,有n 个销地B 1,B 2, …,B n 需要这种物资，它们的销量分别为b 1,b 2, …,b n 。

管理运筹学第二章线性规划的图解法

管理运筹学第二章线性规划的图解法

02
图解法的基本原理
图解法的概念
图解法是一种通过图形来直观展示线性规划问题解的方法。它通过在坐标系中绘 制可行域和目标函数，帮助我们理解问题的结构和最优解的位置。
图解法适用于线性规划问题中变量和约束条件较少的情况，能够直观地展示出最 优解的几何意义。
图解法的步骤
确定决策变量和目标函数
明确问题的决策变量和目标函数，以便在图 形中表示。
目标函数是要求最小化或最大化的函数，通常表示为 $f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
04
约束条件是限制决策变量取值的条件，通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
LINDO是一款开源的线性规划求解器，用 户可以免费使用。
软件工具的使用方法
Excel
用户需要先在Excel中设置好线性规划模型，然后使 用“数据”菜单中的“规划求解”功能进行求解。
Gurobi/CPLEX/LINDO
这些软件通常需要用户先在软件界面中输入线性规划 模型，然后通过点击“求解”按钮进行求解。
实例三：分配问题
总结词
分配问题是指如何根据一定的分配原则 或目标，将有限的资源分配给不同的需 求方，以最大化整体效益。
VS
详细描述
分配问题在实际生活中广泛存在，如物资 分配、任务分配等。通过图解法，可以将 分配问题转化为线性规划模型，并利用图 形直观地展示最优解的资源分配方案。在 分配问题中，通常需要考虑不同需求方的 重要性和优先级，以及资源的有限性等因 素，以实现整体效益的最大化。

2 线性规划

2 线性规划

第一节 线性规划问题及其数学模型
可加性假定：每个决策变量对目标函数和约
束方程的影响是独立于其他变量的，目标函 数值是每个决策变量对目标函数贡献的总和 连续性假定：线性规划问题中的决策变量应 取连续值。 确定性假定：线性规划问题中的所有参数都 是确定的参数。线性规划问题不包含随机因 素。
约 束 方 程
约束条件
变量约束
第一节 线性规划问题及其数学模型
线性规划问题隐含的假定： 比例性假定 可加性假定 连续性假定 确定性假定
比例性假定：决策变量变化引起的目标函数
的改变量和决策变量的改变量成比例，同样， 每个决策变量的变化引起约束方程左端值的 改变量和该变量的改变量成比例
≥0
=
≥0
第一节 线性规划问题及其数学模型
标准型的简缩形式
max Z
c x
j j 1
n
j
s .t
n aij x j bi , i 1,2 , , m j 1 x j 0 , i 1,2 , , m

第一节 线性规划问题及其数学模型
或
松弛变量
a i 1 x 1 a i 2 x 2 a in x n bi
a i 1 x1 a i 2 x 2 a in x n x p bi , x p 0
剩余变量
练习
例:将下列线性规划问题划为标准形式： min Z = x1+3x2
s.t.
6x1+7x28 -x1+3x2-6 x1-x2=3 x10
可行域无界
x1+2x2 10 x2 0 x1
可行域无界
x2
x1 0

第2章 线性规划原理与解法

第2章 线性规划原理与解法
2、最优性检验与解的判别 （以下判定定理针对标准型而言 ）
（1）最优解的判定定理： 对于一个基可行解，如果其所有非基变量的检验数 j 0 ， 则该解称为最优解。 （2）唯一最优解：所有非基变量的检验数都 < 0 （3）无穷多最优解： 已经是最优解，有某个非基变量的检验数 = 0
（4）无界解判定定理： 对于一个基可行解，其非基变量中有某个 m k 0 ， 同时它对应的系数列向量所有的 ai ,mk 0 ， 则该线性规划问题具有无界解。
x1
二、一般线性规划问题的求解基础
max z 2 x1 3 x2 0 x3 0 x4 0 x5 x1 2 x2 x3 8 （2）换出变量的确定 4 x1 x4 16 4 x2 x5 12 为了确保所有的变量均为非负，需确定换入变量的值为：
3、基变换
bi' ' bl' xk min ( ' aik 0) ' i aik alk
得: z 2 x1 9 3 4 x5 0 9 2 x1 3 4 x5
将式（2-5）代入目标函数
0 16 4 x1 0 x5
一、举例说明
步骤4 重复步骤2、3，直到目标函数中非基变量的系数均为负，无改进可能， 即找到最优解 本例依次向下迭代得到的基可行解分别为：
1确定初始可行解2解的最优性的判断3基变换换入和换出变量的确定1检验数单纯形表的矩阵表述3218141314161221812123人工变量及其处理二两阶段法三线性规划问题的各种情况讨论当约束条件出现或时不能直接找到单位矩阵如下例例22
第二章 线性规划原理与解法
§2-1 线性规划求解原理 §2-2 单纯形方法 §2-3 人工变量及其处理

管理运筹学课件第2章线性规划

管理运筹学课件第2章线性规划

2019/7/14
课件
4
2.1.1 线性规划问题的提出
承导入案例
产品甲 产品乙 生产能力
设备A
2
1
10
设备B
1
1
8
单位利润 3
2
决策变量 （decision variable）
设两种产品产量为x1,x2,则有: 总利润表三达要式素
最大化 max z 3x1 2x2
目标函数 （objective function） 约束条件
最优值：z=18
10 2x1+x2=10
8
6
(2,6) z=3×2+2×6=18
【例2.3】用图解法求LP最优解
max z 3x1 2x2
s.t.
2xx11

x2 x2
≤10 ≤8
x1, x2 ≥ 0
可行域
o
45
令3x1+2x2=12
x1+x2=8
8
x1
2019/7/14
课件
课件
6
2.1.2 线性规划的数学模型
线性规划的一般形式：
max(min)z c1x1 c2x2 cn xn
a11x1 a12 x2 s.t.a21x1 a22 x2
am1x1 am2 x2
a1n xn ≤ (或≥， ）b1 a2n xn ≤ (或≥， ）b2
11
2.2.3 线性规划几何解的讨论
线性规划几何解存在四种情况：唯一最优解、无穷 多最优解、无界解、无可行解。 可行域为封闭有界区域时，可能存在唯一最优解， 无穷多最优解两种情况； 可行域为非封闭无界区域时，可能存在唯一最优解， 无穷多最优解，无界解三种情况； 可行域为空集时，没有可行解，原问题没有最优解。

线性规划原理与解法

线性规划原理与解法

c1 b1 a1,m 1 xm 1 a1,m 2 xm 2 ... a1n xn
z c1b1 c2b ... cmbm
cm1 ci ai,m1
i 1
m
cm 1 c1a1, m 1 c2 a2, m 1 ... cm am , m 1 xm 1 c c a i i ,m 2 m 2

i 1

对增广矩阵 作初等行变换 将基变为单位阵
1 0 0
x2 0 ... 0 a1, m 1 ... a1n b : 1 1 ... 0 a2, m 1 ... a2 n b xm 2 ...... x : m 1 bm 0 ... 1 am, m 1 ... amn : x n
第一节 线性规划求解原理
5）若约束条件为“≥”，“≤”和“=”的混合性， 则综合应用以上方法，确定初始基。
max z 3 x1 4 x2 例： x1 2 x2 ≤8 4 x ≤16 1 s.t. 4 x2 ≤12 x1 , x2≥0 max z 3x1 4 x2 0 x3 0 x4 0 x5 =8 x1 2 x2 x3 4 x x4 =16 1 s.t. x5 12 4 x2 x1 , x2 , x3 , x4 , x5≥0
xi bi
j m 1
a x (i 1, 2,..., m)
ij j
n
x1 b1 a1,m1 xm1 a1,m2 xm2 ... a1n xn x2 b2 a2,m1 xm1 a2,m2 xm2 ... a2 n xn ...... xm bm am,m1 xm1 am,m 2 xm 2 ... amn xn

运筹学第二章习题和答案

运筹学第二章习题和答案

运筹学第二章习题和答案运筹学是一门研究如何通过数学模型和方法来优化决策和资源分配的学科。

在运筹学的学习过程中，习题是非常重要的一部分。

通过做习题，我们可以巩固理论知识，提高解决问题的能力。

本文将针对运筹学第二章的习题进行讨论和答案解析。

第二章主要介绍了线性规划的基本概念和方法。

线性规划是一种常见的优化问题，其数学模型可以表示为最大化或最小化一个线性目标函数的同时满足一组线性约束条件。

在解决线性规划问题时，我们常常使用单纯形法或者内点法等方法。

习题2.1：一个公司生产两种产品A和B，每个单位A产品的利润为3万元，每个单位B产品的利润为4万元。

公司的生产能力为每天生产A产品100个单位，B产品80个单位。

产品A和B分别需要2个和3个单位的原材料X和Y。

而公司每天可用的原材料X和Y分别为180个单位和210个单位。

问该公司应如何安排生产，才能使利润最大化？解析：首先，我们需要定义决策变量。

假设公司每天生产A产品x个单位，B 产品y个单位。

则我们的目标是最大化利润，即最大化目标函数Z=3x+4y。

同时，我们需要满足生产能力和原材料约束条件。

生产能力约束条件为x≤100，y≤80。

原材料约束条件为2x+3y≤180，2x+3y≤210。

通过绘制约束条件的图形，我们可以得到可行解的区域。

在该区域内，我们需要找到目标函数Z=3x+4y的最大值点。

通过计算，我们可以得到最大利润为320万元，此时生产100个单位的A产品和60个单位的B产品。

习题2.2：某工厂生产两种产品，产品A和产品B。

产品A的生产需要1个单位的原材料X和2个单位的原材料Y，产品B的生产需要2个单位的原材料X 和1个单位的原材料Y。

每个单位的产品A的利润为3万元，每个单位的产品B的利润为4万元。

工厂每天可用的原材料X和Y分别为10个单位和12个单位。

问该工厂应如何安排生产，才能使利润最大化？解析：同样地，我们首先定义决策变量。

假设工厂每天生产A产品x个单位，B产品y个单位。

第二章线性规划知识课件

第二章线性规划知识课件

方案 x1 x2 x3 x4 x5
2.9米 1 2 0 1 0
2.1米 0 0 2 2 1
1.5米 3 1 2 0 3
合计 7.4 7.3 7.2 7.1 6.6
余料 0 0.1 0.2 0.3 0.8
OBJ: MinZ 0x1 0.1x2 0.2x3 0.3x4 0.8x5
x1 2x2 x4 100 s.t. 3x12x3x2 2x24x3 x53x5101000
4) 移动等值线到可行域边界得到最优点
11
1.用图解法求解极大化问题
例1 OBJ : max Z 2 x1 3 x 2
x1 2x2 8
s
.
t
.
4
x
1
16 4 x 2 12
x1 , x 2 0
x x12x2 2
2x13x24
做目标函数2x1+3x2的等值线，与 3 阴影部分的边界相交于Q(4,2)点， 这表明最优解是:x1= 4,x2 =2
0
4x1=16 x1+2x2=8
Q(4,2) 4x2=12
4 Z=2x1+3x2
8 x1
12
例2
max Z 6 x 1 4 x 2
2 x 1 x 2 10
s
.t
.
x1 x2 8 x2 7
x 1 , x 2 0
最优解 : x1 2 x2 6 Z 36
x2
10 F
9
8E
7 ABG 3
A
533
1.5
B
221
0.7
每人每月最低需求量（单位） 60 40 35
例3 现要做100套钢架，每套需2.9米、2.1米和1.5米的圆钢各一

《管理运筹学》第2章_线性规划

《管理运筹学》第2章_线性规划

我们通过画图可以知道该线性规划问题的可行解所在 的范围是无界的,目标函数值可以增大到无穷大,称这种 情况为无界解或无最优解,如下图所示: x2
Z
0
x优解呢?那也不一定,如在(1.3)中,将目 标函数由 Max Z = x1 + x2 改为 Min Z = x1 + x2 , 则可行解所在的范围虽然无界,但有最优解 x1 = x2 = 0 ,即 (0,0)点. 当求解结果出现(2)、(3)两种 情况时,一般均说明线性规划问题的数学模型存在错误 ,前者缺乏必要的约束条件,后者是存在矛盾的约束条 件,在建立数学模型时，应当注意。
可行域D非空有界：（1）有唯一解、（2）有无 穷多最优解 可行域D非空无界：求max（1）无界解。求min （1）有唯一解、 （2）有无穷多组最优解 可行域D空：无可行解
幻灯片 18
从图解法中可直观地看到:
※ 当线性规划问题的可行域非空时, 它是有界或无界凸多面体(形).
※若线性规划问题存在有界最优解,则
无可行解(Infeasibility Solution)
无可行解是指不存在满足全部约束条件 的解。在图形中，无可行解是指可行域不 存在。也就是说，没有任何一个点能够同 时满足所有约束条件。
举例说明这一情况。在2.1中如果我们增加约束条 件，生产Ⅰ、Ⅱ两种产品至少分别需要3千克。
现有的资源无法生产满足需要（3，3）的产品， 此外，我们可以准确地告诉管理者要生产(3,3) 换需要多少资源
1 A B C 价 格 3 1 0.5 2
2 2 0.5 1 7
3 1 0.2 0.2 4
4 6 2 2 9
5 18 0.5 0.8 5
需 求 700 30 200
解：设 x j

第二章线性规划(运筹学讲义)

第二章线性规划(运筹学讲义)

产品Ⅰ 产品Ⅱ
设备使用成本和单价
资源限制
设备
1
1
10元 / 时
300台时
原料A
2
1
12元 / kg
400kg
原料B
0
1
18元 / kg
250kg
销售单价(元)
84
140
单位产品利润(元)
50
100
问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多？
设工厂生产产品Ⅰ、Ⅱ分别为x1，x2单位， 则线性规划模型：
确定需求的约束，它们表示了一定数量的确定的需求，提供的数量等于要 求的数量。网络配送问题的共性就是它们的主要函数约束为一种特定形式 的确定需求的约束。
混合问题（mixed Problem）除以上三类以外的问题
建模过程
1.理解要解决的问题，了解解题的目标和条件；
2.定义决策变量（ x1 ，x2 ，… ，xn ），每一组值表示一个方案；
因此,凸集用数学表示为:对任何X1 ∈C, X2 ∈C, 有α X1 ＋(1- α) X2 ∈C (其中0<α<1),则称道C为凸集。 规定：单点集 {X} 为凸集，空集为凸集。
A B
E
C
D
顶点:设C是凸集, X∈C;若X不能用不同的两点X1∈C和 X2∈C的线性组合表示为X= αX1＋(1－α) X2 (其中 0<α<1),则称X为C的一个顶点
x2 49
z=10000=50x1+100x2
AB
250
C
z=27500=50x1+100x2 z=20000=50x1+100x2
z =0=50x1+100x2

OR第二章(线性规划的图解法)

OR第二章(线性规划的图解法)

此目标函数值称为最优目标函数值，简
称最优值。
17
生产安排问题的解决方案
最优解 就对应最佳的生产方案。
最优值 对应最佳生产方案产生的最大利润。
18
这里的生产安排问题需要作出产品I和产
品II的产量安排，即作出两个不同的决
策，这是一种所谓的多重决策问题。 这种问题可以采取顺序决策
方法或同步决策方法解决。
总利润 = 产品I提供的利润 + 产品II提供的利润
max
z 50 x1 100 x2
11
约束条件
生产所使用的设备台时≤拥有的设备台时
x1 x2 300
12
约束条件
生产所使用的原料A的数量≤原料A的拥有量
2 x1 x2 400
13
约束条件
生产所使用的原料B的数量≤原料B的拥有量
27
约束条件： a11 x1 a12 x2 a1n xn (, )b1,
线性规划问题的假设 Proportionality(比例性)

决策变量变化引起的目标函数的改变量和决策变 量的改变量成比例。

每个决策变量的变化引起约束方程左端值的改变 量和该变量的改变量成比例。

比例性假设意味着每种经营活动对目标函数的贡 献是一个常数，对资源的消耗也是一个常数。
3. 4.
5.
26
线性规划模型的一般形式
目 标： max(min) z c1 x1 c2 x2 cn xn . a21 x1 a22 x2 a 2n xn (, )b2 , am1 x1 am 2 x2 amn xn (, )bm , x1 , x2 , , xn 0.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章 线性规划 LINEAR PROGRAMMING
本章的主要内容
• 一般线性规划问题的数学模型 • 图解法 • 单纯形法原理 • 单纯形法的计算步骤 • 单纯形法的进一步讨论 • 数据包络分析
School of Management Harbin Institute of Technology 2
线性规划问题的数学模型
School of Management Harbin Institute of Technology 12
线性规划数学模型假设
（1）比例性 （2）可叠加性
（3）可分性
（4）确定性
School of Management Harbin Institute of Technology 13
线性规划问题的数学模型
• 标准形式的转换
–目标函数的转换 –无约束决策变量的转换 –约束方程的转换
• 松弛变量 • 剩余变量
–非正决策变量的转换
School of Management Harbin Institute of Technology 10
线性规划问题的数学模型
School of Management Harbin Institute of Technology 11
构建线性规划数学模型
例2：设有下面四个投资机会： 甲：在三年内，投资人应在每年年初投资，每年每元投 资可获利0.2元，每年取息后可重新将本息用于投资。 乙：在三年内，投资人应在第一年年初投资，每两年每 元投资可获利0.5元，两年后取息，取息后可重新将本息用 于投资。这种投资最多不得超过20,000元。 丙：在三年内，投资人应在第二年年初投资，两年后每 元投资可获利0.6元。这种投资最多不得超过15,000元。 丁：在三年内，投资人应在第三年年初投资，一年后每 元投资可获利0.4元。这种投资最多不得超过10,000元。 假定在这三年为一期的投资中，每期的开始有30,000元 资金可供使用，问：采取怎样的投资计划，才能在第三年 年底获得最大收益？
School of Management Harbin Institute of Technology 3
线性规划问题的数学模型
School of Management Harbin Institute of Technology 4
线性规划问题的数学模型
• 例子1.2 某企业计划生产甲，乙两种产品。这两 种产品需要在A，B，C三种不同的设备上进行 加工。按工艺需求，加工各种产品所需每种设 备的单位工时如下表所示，问如何安排生产计 划，使企业的总利润最大？
A 甲 乙 2 2 12 B 4 0 16 C 0 5 15 2 3
School of Management Harbin Institute of Technology 5
线性规划问题的数学模型
School of Management Harbin Institute of Technology 6
构建线性规划数学模型
例1：某工厂在生产过程中需要使用浓度为80% 的硫酸100 吨，而市面上只有浓度为30%，45% ，73%，85%，92%的硫酸出售， 每吨的价格
分别为400、700、1400、1900和2500元。 问：
采用怎样的购买方案，才能使所需总费用最小？
School of Management Harbin Institute of Technology 15
2
Ⅲ
Ⅳ
1Ⅴຫໍສະໝຸດ 22 7.1 0.3
1
1.5米
合 计 (米 ) 料 头 (米 )
3 7.4
0
1 7.3
0.1
2 7.2
0.2
3 6.6
0.8
School of Management Harbin Institute of Technology 17
构建线性规划数学模型
思考题：
目标函数是否可以选取为 min z'=x1+x2+x3+x4+x5 ，为什么？
School of Management Harbin Institute of Technology 16
构建线性规划数学模型
例3：合理下料问题：
要制作100套钢筋架子，每套含2.9米、2.1米、1.5米的 钢筋各一根。已知原料长7.4米，问：如何下料，使用料最 省？
长度
2.9米 2.1米
Ⅰ
1
Ⅱ
构建线性规划数学模型
（1）分析问题：确定决策内容、要实 现的目标以及所受到的限制条件。 （2）具体构造模型：选择合适的决策 变量、确定目标函数的表达式、约 束条件的表达式，分析各变量取值 的符号限制。
School of Management Harbin Institute of Technology 14
线性规划问题的数学模型
• 线性规划的数学模型由以下三个要素
–决策变量 decision variable –目标函数 objective function –约束条件 constrains
• 线性规划问题的辨别
–目标函数是多个决策变量的线性函数，取最 大值或最小值 –约束条件是一组多个决策变量的线性不等式 或等式
School of Management Harbin Institute of Technology 7
线性规划问题的数学模型
School of Management Harbin Institute of Technology 8
线性规划问题的数学模型
School of Management Harbin Institute of Technology 9
School of Management Harbin Institute of Technology 18
构建线性规划数学模型
例4：有A、B两种产品，都需要经过前、后两到化学反应过程。每种产品需 要的反应时间及其可供使用的总时间如表示。
每生产一个单位产品B的同时，会产生2个单位的副产品C，且不需 外加任何费用。副产品C的一部分可以出售盈利，其余的只能加以销毁。
线性规划问题的数学模型
• 规划问题
–生产和经营管理中经常提出如何合理安排， 使人力、物力等资源得到充分利用，获得最大 的效益，这就是规划问题
• 线性规划通常解决以下两类问题
–当任务和目标确定后，如何统筹兼顾，合理 安排，用最少的资源去完成确定的任务和目标 –在一定的资源限制下，如何组织安排生产获 得最好的经济效益