圆与抛物线综合试题

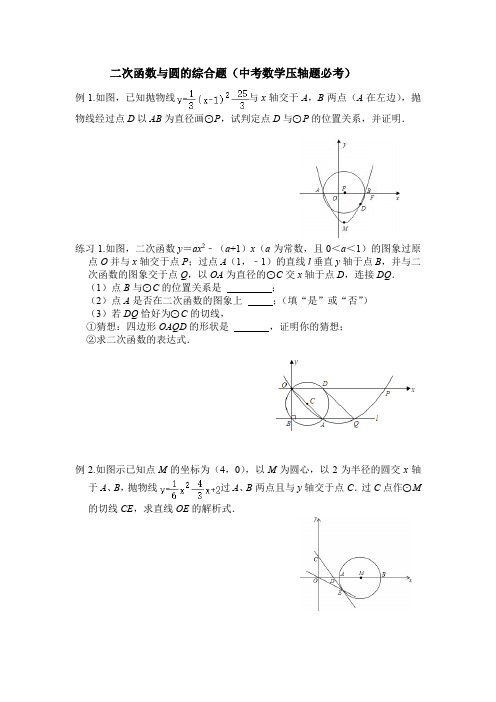
二次函数与圆的综合题（中考数学压轴题必考）例1.如图，已知抛物线与x轴交于A，B两点（A在左边），抛物线经过点D以AB为直径画⊙P，试判定点D与⊙P的位置关系，并证明．练习1.如图，二次函数y＝ax2﹣（a+1）x（a为常数，且0＜a＜1）的图象过原点O并与x轴交于点P；过点A（1，﹣1）的直线l垂直y轴于点B，并与二次函数的图象交于点Q，以OA为直径的⊙C交x轴于点D，连接DQ．（1）点B与⊙C的位置关系是；（2）点A是否在二次函数的图象上；（填“是”或“否”）（3）若DQ恰好为⊙C的切线，①猜想：四边形OAQD的形状是，证明你的猜想；②求二次函数的表达式．例2.如图示已知点M的坐标为（4，0），以M为圆心，以2为半径的圆交x轴于A、B，抛物线过A、B两点且与y轴交于点C．过C点作⊙M 的切线CE，求直线OE的解析式．练习2.平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴，设平行于x轴的直线交抛物线y＝﹣x2﹣x+2于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．练习3.如图，抛物线y＝﹣x2﹣x+2与x轴交于A（﹣4，0），B（2，0），与y 轴交于点C（0，2）．以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．练习4.如图，抛物线y＝﹣x2+x+2．经过A、B、C三点，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C，M为抛物线的顶点，试说明直线MC与⊙P的位置关系，并证明你的结论．练习5.如图，抛物线与x轴交于A、B两点，与y轴交于C点．以AB为直径作⊙M．（1）求出M的坐标并证明点C在⊙M上；（2）若P为抛物线上一动点，求出当CP与⊙M相切时P的坐标；练习6.在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．（1）求点C的坐标和过A，B，C三点的抛物线的析式；（2）求点D的坐标：（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．练习7.如图，在平面直角坐标系中，已知OA＝n，OC＝m，⊙M与y轴相切于点C，与x轴交于A，B两点，∠ACD＝90°，抛物线y＝ax2+bx+c经过A，B，C三点．（1）求证：∠OCA＝∠OBC；（2）若A（x1，0），B（x2，0），且x1，x2满足x1+x2＝5，x1•x2＝4，求点C 的坐标和抛物线的解析式；（3）若△ACD≌△ABD，在四边形ABDC内有一点P，且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小，求此时距离之和的最小值及P点的坐标（用含n的式子表示）．练习8.已知二次函数y＝mx2+（m﹣3）x﹣3（m＞0）（1）求证：它的图象与x轴必有两个交点；（2）这条抛物线与x轴交于两点A、B（A在B左），与y轴交于点C，顶点为D，sin∠ABD＝，⊙M过A、B、C三点，求⊙M的面积；（3）在（2）的条件下，抛物线上是否存在点P，使P A是⊙M的切线？若存在，求出P点的坐标，若不存在，说明理由．例3.如图，抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．（1）求a，b，c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN 为等腰三角形时，求圆心P的纵坐标．练习9.已知：如图，抛物线y＝ax2+bx+1的图象关于y轴对称，且抛物线过点（2，2），点P为抛物线上的动点，以点P为圆心的⊙P与x轴相切，当点P运动对，⊙P始终经过y轴上的一个定点E．（1）求抛物线的解析式；（2）当⊙P的半径为时，⊙P与y轴交于M、N两点，求MN的长；（3）求定点E到直线y＝kx﹣8k的距离的最大值．练习10.已知：直线y＝﹣x﹣4分别交x、y轴于A、C两点，抛物线y＝ax2+bx （a＞0）经过A、O两点，且顶点B的纵坐标为﹣2（1）判断点B是否在直线AC上，并求该抛物线的函数关系式；（2）以点B关于x轴的对称点D为圆心，以OD为半径作⊙D，试判断直线AC与⊙D的位置关系，并说明理由；（3）若E为⊙D的优弧AO上一动点（不与A、O重合），连接AE、OE，问在抛物线上是否存在点P，使∠POA：∠AEO＝2：3？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．练习11.已知A是x轴正半轴上一个动点，以线段OA为直径作⊙B，圆心为点B，直径OA＝m，线段EF是⊙B的一条弦，EF∥x轴，点C为劣弧EF的中点，过点E作DE垂直于EF，交抛物线C1：y＝ax2+bx（a＞0）于点G，抛物线经过点O和点A．（1）求证：DG＝m；（2）拖动点A，如果抛物线C1与⊙B除点O和点A外有且只有一个交点，求b的值；（3）拖动点A，抛物线C1交⊙B于点O、E、F、A，①求证：DE＝m﹣；②直接写出FC2的值（用a，m的代数式表示）练习13.如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A．B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．（1）求∠ACB的大小；（2）写出A，B两点的坐标；（3）由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3），求出抛物线的解析式；（4）在该抛物线上是否存在一点D点，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．例4.如图1，抛物线y＝ax2+3ax（a为常数，a＜0）与x轴交于O，A两点，点B 为抛物线的顶点，点D是线段OA上的一个动点，连接BD并延长与过O，A，B三点的⊙P相交于点C，过点C作⊙P的切线交x轴于点E．（1）①求点A的坐标；②求证：CE＝DE；（2）如图2，连接AB，AC，BE，BO，当，∠CAE＝∠OBE时，①求证：AB2＝AC•BE；②求的值．练习14.如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E 四点，B为OD中点．（1）求过A，B，C三点的抛物线解析式；（2）如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；（3）如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．练习15.如图，二次函数与x轴的一个交点A的坐标为（﹣3，0），以点A为圆心作圆A，与该二次函数的图象相交于点B，C，点B，C的横坐标分别为﹣2，﹣5，连接AB，AC，并且满足AB⊥AC．过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N．（1）求该二次函数的关系式；（2）经过点B作直线BD，在A点右侧与x轴交于点D，与二次函数的图象交于点E，使得∠ADB＝∠ABM，连接AE，求证：AE＝AD；（3）若直线y＝kx+1与圆A相切，请求出k的值．例5.已知抛物线y＝ax2+bx+5（a≠0）经过A（5，0），B（6，1）两点，且与y 轴交于点C．（1）求抛物线y＝ax2+bx+5（a≠0）的函数关系式；（2）如图1，连接AC，E为线段AC上一点且横坐标为1，⊙P是△OAE外接圆，求圆心P点的坐标；（3）如图2，连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F；①点E在运动过程中四边形OEAF的面积是否为定值？如果是，请求出这个定值；如果不是，请说明理由；②求出当△AEF的面积取得最大值时，点E的坐标．练习16.如图1，已知抛物线y＝﹣x2+bx+c经过点A（1，0），B（﹣5，0）两点，且与y轴交于点C．（1）求b，c的值．（2）在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值．若不存在，请说明理由．（3）如图2，点E为线段BC上一个动点（不与B，C重合），经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．练习17.如图1，抛物线y＝+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，顶点为D．（1）求抛物线的解析式；（2）如图2，以AB为直径在x轴上方画半圆交y轴于点E，圆心为G，P为半圆上一动点，连接DP，点Q为PD的中点．①判断点C、D与⊙G的位置关系，并说明原因；②当点P沿半圆从点B运动到点A时，求线段AQ的最小值．练习18.如图1，二次函数y＝ax2﹣3ax+b（a、b为参数，其中a＜0）的图象与x 轴交于A、B两点，与y轴交于点C，顶点为D．（1）若b＝﹣10a，求tan∠CBA的值（结果用含a的式子表示）；（2）若△ABC是等腰三角形，直线AD与y轴交于点P，且AP：DP＝2：3．求抛物线的解析式；（3）如图2，已知b＝﹣4a，E、F分别是CA和CB上的动点，且EF＝AB，若以EF为直径的圆经过点C，并交x轴于M、N两点，求MN的最大值．课后练习1.抛物线y＝ax2+bx﹣4交x轴于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是介于B、C之间的抛物线上的动点（包括B、C两点），点E是△ABP 的外接圆圆心．（1）求抛物线的解析式；（2）如图1，当P为抛物线的顶点时，求圆心E的坐标；（3）如图2，作PH⊥x轴于点H，延长PH交⊙E于点Q，当P从C点出发，沿该抛物线运动到B点，求点Q在这个运动过程中的路径长．2.如图，在正方形OABC中，AB＝4，点E是线段OA（不含端点）边上一动点，作△ABE的外接圆交AC于点D．抛物线y＝ax2﹣x+c过点O，E．（1）求证：∠BDE＝90°；（2）如图1，若抛物线恰好经过点B，求此时点D的坐标；（3）如图2，AC与BE交于点F．①请问点E在运动的过程中，CF•AD是定值吗？如果是，请求出这个值，如果不是，请说明理由；②若，求点E坐标及a的值．。

高二数学抛物线试题1.抛物线上的点到直线的距离最小值为A．B．C．D．3【答案】A【解析】在抛物线上任设一点，则该点到直线的距离为，所以最小值为.【考点】点到直线的距离.2.斜率为2的直线L经过抛物线的焦点F，且交抛物线与A、B两点，若AB的中点到抛物线准线的距离1，则P的值为（）.A.1B.C.D.【答案】B【解析】设斜率为2且经过抛物线的焦点F的直线L的方程为，联立，得，即；设，中点；则；因为AB的中点到抛物线准线的距离为1，所以，.【考点】直线与抛物线的位置关系.3.已知圆C：的圆心为抛物线的焦点，直线3x＋4y＋2＝0与圆C相切，则该圆的方程为（）.A．B．C．D．【答案】C.【解析】因为抛物线的焦点为，即为圆C的圆心，又直线3x＋4y＋2＝0与圆C相切，所以圆心到直线的距离即为半径，则有，故选C.【考点】点到直线的距离公式，圆的切线的性质，抛物线的焦点坐标公式，圆的标准方程.4.已知抛物线关于轴对称，它的顶点在坐标原点，并且经过点，若点到该抛物线焦点的距离为3，则=（）A．B．C．4D．【答案】B.【解析】由题意可设抛物线方程为，因为点到该抛物线焦点的距离为3，所以，即，即抛物线方程为，又因为点在抛物线上，所以，所以，故选B．【考点】抛物线的简单性质．5.已知点M是抛物线上的一点，F为抛物线的焦点，A在圆C:上，则的最小值为__________．【答案】4【解析】抛物线的准线方程为：x=-1过点M作MN⊥准线，垂足为N∵点M是抛物线y2=4x的一点，F为抛物线的焦点∵A在圆C：，圆心C（4，1），半径r=1∴当N，M，C三点共线时，|MA|+|MF|最小∴=4．【考点】圆与圆锥曲线的综合；考查抛物线的简单性质；考查距离和的最小．6.抛物线的焦点坐标是( )A．B．C．D．【答案】B【解析】根据题意可知条件中表示的是焦点在y轴上抛物线，2p=4，p=2，而焦点坐标为，故选B.【考点】抛物线的焦点坐标.7.已知过曲线上任意一点作直线的垂线，垂足为,且.⑴求曲线的方程；⑵设、是曲线上两个不同点，直线和的倾斜角分别为和，当变化且为定值时，证明直线恒过定点，并求出该定点的坐标.【答案】⑴⑵当时，直线恒过定点，当时直线恒过定点.【解析】⑴要求曲线方程,但是不知道是哪种曲线,所以只能设点.根据,转化为求曲线方程即可;⑵要证明直线恒过定点,必须得有直线方程,所以首先设出直线方程.又因为两个角是直线和的倾斜角,所以点也得设出来.利用韦达定理,然后讨论的范围变化,证明并得出定点坐标. 试题解析：⑴设，则，由得，;即;所以轨迹方程为;⑵设，由题意得（否则）且,所以直线的斜率存在，设其方程为，因为在抛物线上,所以，将与联立消去，得;由韦达定理知①;(1)当时，即时，,所以，,所以.由①知：,所以因此直线的方程可表示为，即.所以直线恒过定点(2)当时，由，得==将①式代入上式整理化简可得：，所以，此时，直线的方程可表示为,即,所以直线恒过定点;所以由(1)(2)知，当时，直线恒过定点，当时直线恒过定点. 12分【考点】相关点法求曲线方程;分类讨论.8.已知为抛物线上的两点，且的横坐标分别为，过分别作抛物线的切线，两切线交于点，则的纵坐标为( )A．B．C．D．【答案】C【解析】因为为由抛物线上的两点，且的横坐标分别为，所以两点的坐标分别为.由抛物线得，求导可得.所以过点的切线的斜率为4，故过点的切线方程为.同理写出过点的切线方程.所以它们交点的纵坐标是-4.故选C.【考点】1.曲线上的点.2.曲线的切线.3.直线的交点.9.设斜率为2的直线过抛物线的焦点F,且和轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为A．B．C．D．【答案】B【解析】抛物线的焦点F坐标为(，0)，则直线l的方程为y=2(x-)，它与y轴的交点为A(0，-)，所以△OAF的面积为，解得a=±8．所以抛物线方程为y2=±8x，故选B．【考点】本题主要考查抛物线的标准方程及其几何性质，直线方程的点斜式。

抛物线与圆专题讲解抛物线与圆综合探究题，综合性强，难度较大，通常都作为“压轴题”，解此类题通常需要熟练掌握抛物线与圆相关的基本知识和基本技能（切线的性质与判定、切线长定理、圆与点、线、圆的位置关系等），求解时注意运用有关性质，进行综合、分析、探究解题思路。

在解答中常渗透6大数学思想：数形结合思想、分类思想、化归与转化思想、函数与方程思想、整体思想、建模思想。

你想快速进步请注意：独立思考，与他人合作，题后析题总结。

1．如图，在平面直角坐标系中，二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点，与y 轴交于C 点，与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），OB ＝OC ，tan∠ACO＝31．（1）求这个二次函数的表达式．（2）若平行于x 轴的直线与该抛物线交于M 、N 两点，且以MN 为直径的圆与x 轴相切，求该圆半径的长度．2、已知：如图，抛物线m x x y +-=332312与x 轴交于A 、B 两点，与y 轴交于C 点，∠ACB ＝90°， ⑴求m 的值及抛物线顶点坐标； ⑵过A 、B 、C 的三点的⊙M 交y 轴于另一点D ，连结DM 并延长交⊙M 于点E ，过E 点的⊙M 的切线分别交x 轴、y 轴于点F 、G ，求直线FG 的解析式； ⑶在条件⑵下，设P 为上的动点（P 不与C 、D 重合），连结PA 交y 轴于点H ，问是否存在一个常数k ，始终满足AH ·AP ＝k ，如果存在，请写出求解过程；如果不存在，请说明理由.3、如图3已知抛物线2y ax bx c=++，经过点A(0，5)和点B（3 ，2）(1)求抛物线的解析式：(2)现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标：若不存在，请说明理由；(3)若⊙Q的半径为r，点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值课后巩固：1、已知：如图，抛物线233y x x =--+x 轴分别交于A B ，两点，与y轴交于C 点，经过原点O 及点A C ，，点D 是劣弧⋂OA 上一动点（D 点与A O ，不重合）．（1）求抛物线的顶点E 的坐标； （2）求的面积；（3）连CD 交AO 于点F ，延长CD 至G ，使2FG =，试探究当点D 运动到何处时，直线GA 与⊙M 相切，并请说明理由．2、如图，在平面直角坐标系中，已知点(B -，(0)A m，(0)m <<，以AB 为边在x 轴下方作正方形ABCD ，点E 是线段OD 与正方形ABCD 的外接圆除点D 以外的另一个交点，连结BE 与AD 相交于点F ． （1）求证：BF DO =；（2）设直线l 是BDO △的边BO 的垂直平分线，且与BE 相交于点G ．若G 是BDO △的外心，试求经过BF O ，，三点的抛物线的解析表达式；3、如图1，直线y ＝43x －1与抛物线y ＝－41x 2交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ．（1）求线段AB 的长；（2）若以AB 为直径的圆与直线x ＝m 有公共点，求m 的取值范围；（3）如图2，把抛物线向右平移2个单位，再向上平移n 个单位（n ＞0），抛物线与x 轴交于P ，Q 两点，过C ，P ，Q 三点的圆的面积是否存在最小值的情况？若存在，请求出这个最小值和此时n 的值，若不存在，请说明理由．图2图1。

抛物线与圆综合题徐州王黎之1．（2016赤峰）在平面直角坐标系中，已知点A（﹣2，0），B（2，0），C（3，5）．（1）求过点 A，C 的直线解析式和过点 A，B，C 的抛物线的解析式；（2）求过点 A，B 及抛物线的顶点 D 的⊙P的圆心 P 的坐标；（3）在抛物线上是否存在点 Q，使 AQ 与⊙P相切，若存在请求出 Q 点坐标．2.（2015 • 陕西）如图，在直角坐标系中，⊙ C 过原点 O，交 x 轴于点 A（2，0），交y 轴于点 B（0，2 √3）．（1）求圆心的坐标；（2）抛物线 y=ax 2 +bx+c 过 O、A 两点，且顶点在正3．（2016 宿迁）如图，在平面直角坐标系 xOy 中，将二次函数 y=x2﹣1 的图象 M 沿 x 轴翻折，把所得到的图象向右平移 2 个单位长度后再向上平移 8 个单位长度，得到二次函数图象N．（1）求 N 的函数表达式；（2）设点 P（m，n）是以点 C（1，4）为圆心、1 为半径的圆上一动点，二次函数的图象 M 与x 轴相交于两点 A、B，求PA2+PB2 的最大值；（3）若一个点的横坐标与纵坐标均为整数，则该点称为整点．求 M 与N 所围成封闭图形内（包括边界）整点的个数．比例函数y=- x 的图象上，求抛物线的解析式；3（3）过圆心 C 作平行于 x 轴的直线 DE ，交⊙C 于 D、E 两点，试判断 D、E 两点是否在（2）中的抛物线上；（4）若（2）中的抛物线上存在点 P（x0 ，y），满足∠ APB 为钝角，求 x0 的取值范围．34、已知抛物线 y ＝ ax２＋bx ＋３ ( a ≠０ )经过 A ( ３ , ０ ), B ( ４ , １ )两点,且与 y 轴交于点 C ．(１ )求抛物线 y ＝ ax２＋bx ＋３( a ≠０ )的函数关系式及点 C 的坐标;(２ )如图１ ,连接 AB ,在题( １ )中的抛物线上是否存在点 P ,使△ PAB 是以 AB 为直角边的直角三角形? 若存在,求出点 P 的坐标;若不存在,请说明理由;(３ )如图２ ,连接 AC , E 为线段 AC 上任意一点(不与A , C 重合),经过 A , E , O 三点的圆交直线 AB 于点 F , 当△ OEF的面积取得最小值时,求点 E 的坐标．5.抛物线 y=ax2+bx+c 交x 轴于A、B 两点，交 y 轴于点 C，已知抛物线的对称轴为 x=1，B（3，0），C（0，-3），（1）求二次函数 y=ax2+bx+c 的解析式；（2）在抛物线对称轴上是否存在一点 P，使点 P 到 B、C 两点距离之差最大？若存在，求出 P 点坐标；若不存在，请说明理由；（3）平行于 x 轴的一条直线交抛物线于 M、N 两点，若以 M N 为直径的圆恰好与 x 轴相切，求此圆的半径。

2017届高三数学跨越一本线精品问题三：椭圆、双曲线、抛物线与圆相结合问题通过近几年各地高考试题能够发觉,对圆的考查在慢慢加深,并与圆锥曲线相结合在一路命题,成为一个新的动向.与圆相关几何性质、最值问题、轨迹问题等都能与椭圆、双曲线和抛物线想结合能够呈现别具一格的新颖试题,为此,为了深切明确命题动向,本文总结如下. 一、圆与椭圆的结合点 圆的几何性质与椭圆相联系【例1】【2017届湖南师大附中高三上学期月考四】已知椭圆C 的中心在原点,离心率为22,其右核心是圆E ：22(1)1x y -+=的圆心．（1）求椭圆C 的标准方程；（2）如图,过椭圆C 上且位于y 轴左侧的一点P 作圆E 的两条切线,别离交y 轴于点M 、N ．试推断是不是存在点P ,使14||MN =,求出点P 的坐标；假设不存在,请说明理由．【分析】(1)由已知条件别离求出,a c 的值,而222b ac =-,代入求出椭圆的方程；(2)假设存在点P 知足题意,设点00(,)P x y （00x <）,(0,)M m ,(0,)N n ,利用条件求出直线PM 方程,依照圆心(1,0)E 到直线PM 的距离为,求出m 与点P 坐标之间的关系,同理求出与点P 坐标之间的关系,利用韦达定理求出,m n mn +的表达式,算出MN ,求出P 点坐标.【解析】（1）设椭圆方程22221(0)x y a b a b+=>>,半焦距为,因为椭圆的右核心是圆E 的圆心,那么1c =,因为椭圆的离心率为22,那么22c a =,即22a c ==,从而2221b a c =-=,故椭圆C 的方程为2212x y +=．由此可知,m ,为方程2000(2)20x x y x x -+-=的两个实根,因此0022y m n x +=--,002x mn x =--, 2||||()4MN m n m n mn =-=+-20020044(2)2y x x x =+--220002044(2)x y x x +-=-．因为点00(,)P x y 在椭圆C 上,那么220012x y +=,即220012x y =-, 则2200022002842(2)4||(2)(2)x x x MN x x -+--==--2042(2)x =--, 204142(2)x -=-则20(2)9x -=,因为00x <,那么01x =-,220012x y =-12=,即022y =±, 故存在点2(1,)2P -±知足题设条件． 【点评】(1)处置直线与圆的弦长问题时多用几何法,即弦长的一半、弦心距、半径组成直角三角形．(2)圆的切线问题的处置要抓住圆心到直线的距离等于半径,从而成立关系解决问题．【小试牛刀】【2017届江西吉安一中高三上学期段考二】已知椭圆()2222:10x y W a b a b+=>>的离心率为32,其左极点A 在圆22:16O x y +=上. （Ⅰ）求椭圆W 的方程；（Ⅱ）假设点P 为椭圆W 上不同于点A 的点,直线AP 与圆O 的另一个交点为Q ,是不是存在点P ,使得3PQ AP=？假设存在,求出点P 的坐标；假设不存在,说明理由.【答案】（I ）221164x y +=；（II ）不存在,理由观点析. （II ）设点()11,P x y ,()22,Q x y ,设直线AP 的方程为()4y k x =+,与椭圆方程联立得()2241164y k x x y =+⎧⎪⎨+=⎪⎩,化简取得()2222143264160k x k x k +++-=,因为-4为方程的一个根,因此()21232414k x k -+-=+,因此21241614k x k-=+ 因此228114k AP k+=+ 因为圆心到直线AP 的距离为2414kd k=+, 因此222168216211AQ d k k=-==++. 因为1PQ AQ AP AQ APAPAP-==-,代入取得222222228143311*********PQ k k k AP k k kk k ++=-=-==-+++++, 显然23331k -≠+,因此不存在直线AP ,使得3PQ AP=.利用椭圆的性质判定直线与圆的位置关系 【例2】已知椭圆C ：2224x y +=.（1）求椭圆C 的离心率；（2）设O 为原点,假设点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,试判定直线AB 与圆222x y +=的位置关系,并证明你的结论.【分析】（1）把椭圆C ：2224x y +=化为标准方程,确信2a ,2b ,利用ace =求得离心率；（2）设点),(00y x A ,)2,(t B ,其中00≠x ,由OB OA ⊥,即0=•OB OA ,用0x 、0y 表示,当t x =0或t x ≠0别离依照点到直线的距离公式求出圆心到直线的距离,与圆的半径比较,从而判定直线AB 与圆222x y +=的位置关系.【解析】（1）由题意椭圆C 的标准方程为12422=+y x ,因此42=a ,22=b ,从而224222=-=-=b a c ,因此22==a c e . （2）直线AB 与圆222=+y x 相切,证明如下：设点),(00y x A ,)2,(t B ,其中00≠x ,因为OB OA ⊥,因此0=•OB OA ,即0200=+y tx ,解得02x y t -=, 当t x =0时,220t y -=,代入椭圆C 的方程得2±=t ,现在直线AB 与圆222=+y x 相切.当t x ≠0时,直线AB 的方程为)(2200t x tx y y ---=-,即02)()2(0000=-+---ty x y t x x y , 圆心到直线AB 的距离为202000)()2(|2|t x y ty x d -+--=,又422020=+y x ,02x y t -=, 故22168|4|4|22|20204002020202020020=+++=++-=x x x x x x y y x x y x d .故此直线AB 与圆222=+y x 相切.【小试牛刀】【2021福建高考理18】已知椭圆()2222:10x y E a b a b+=>>过点()0,2,且离心率22e =．(1)求椭圆E 的方程；(2)设直线():1l x my m =-∈R 交椭圆E 于A ,B 两点,判定点94G ⎛⎫- ⎪⎝⎭,0与以线段AB 为直径的圆的位置关系,并说明理由．【解析】解法一：（1）由已知得222222b caa b c ⎧=⎪⎪=⎨⎪⎪=+⎩,解得222a b c =⎧⎪=⎨⎪=⎩因此椭圆E 的方程为22142x y +=．故()22201252514216AB GH my m y y -=+++=()()()22222231525172021622162m m m m m m ++-+=>+++,因此2AB GH >． 故点9,04G ⎛⎫-⎪⎝⎭在以AB 为直径的圆外． 解法二：（1）同解法一．（2）设点()11,A x y ,()22,B x y ,那么119,4GA x y ⎛⎫=+⎪⎝⎭,229,4GB x y ⎛⎫=+ ⎪⎝⎭．由221142x my x y =-⎧⎪⎨+=⎪⎩,得()222230m y my +--=,因此12222m y y m +=+,12232y y m =-+,从而12129944GA GB x x y y ⎛⎫⎛⎫=+++= ⎪⎪⎝⎭⎝⎭12125544my my y y ⎛⎫⎛⎫+++= ⎪⎪⎝⎭⎝⎭()()212125251416m y y m y y ++++=()22225312522216m m m m -+++=++()221720162m m +>+,因此cos ,0GA GB >．又GA ,GB 不共线,因此AGB ∠为锐角．故点9,04G ⎛⎫-⎪⎝⎭在以AB 为直径的圆外． 二、圆与双曲线的结合点利用圆的性质解决双曲线的相关问题由于双曲线具有渐近线,故渐近线与圆的位置关系便成为命题的常考点.圆本身所具有的几何性质在探讨等量关系也常常考查,进而求解双曲线的几何性质,如离心率的求解.【例3】已知点(,0)(0)F c c ->是双曲线22221x y a b-=的左核心,离心率为e ,过F 且平行于双曲线渐近线的直线与圆222x y c +=交于点P ,且点P 在抛物线24y cx =上,那么e 2 =（ ）A ．352+ B ．5 C ．512- D ．152+ 【答案】D【点评】此题将双曲线的渐近线与圆的位置关系联系到一路,从而确信点P 的坐标,进而成立等量关系求解双曲线的离心率.【小试牛刀】【2017届河北武邑中学高三上学期调研四】已知双曲线()2222:10,0x y C a b a b==>>的右极点为A ,O 为坐标原点,以A 为圆心的圆与双曲线C 的某渐近线交于两点P ,Q ．假设60PAQ ∠=︒,且3OQ OP =,那么双曲线C 的离心率为＿＿＿＿．【解析】因为60PAQ ∠=︒且3OQ OP =,因此QAP 为等边三角形,设2AQ R =,那么OP R =,渐近线方程为by xa =,0A a （，）,取PQ 的中点M ,那么AM =由勾股定理可得2222R R -=（）,因此22223ab R a b =+（）（）①,在OQA中,()()2223212322R R a R R+-=⋅⋅,因此227R a =②,①②结合222c a b =+,可得c e a =＝．故答案. 圆的切线与双曲线相联系【例4】已知双曲线12222=-by a x 的左右核心别离为12F F 、,O 为双曲线的中心,P 是双曲线右支上的点,21F PF ∆的内切圆的圆心为,且圆与轴相切于点A ,过2F 作直线PI 的垂线,垂足为B ,假设为双曲线的离心率,那么( )A. ||||OA e OB =B. ||||OB e OA =C. ||||OA OB =D. ||OA 与||OB 关系不确信 【答案】C【解析】设内切圆在1PF 上的切点为N ,2PF 上的切点为M ,12F F 上的切点为A ,A 的坐标为(m,0),∴12112(DM MF)AF m (c m)2a PF PF PN NF AF c -=+-+=-=+--=,即OA a =,延长2BF 交1PF 于S ,∵PB 是角平分线和垂线,∴B 是2SF 的中点,O 是12F F 的中点,BO 是中位线,11211(PF PF )a 22BO F S ==-=,∴OA OB a ==,∴||||OA OB =. 【小试牛刀】已知点1F 、2F 为双曲线C ：()01222>=-b by x 的左、右核心,过2F 作垂直于轴的直线,在轴上方交双曲线C 于点M ,且︒=∠3021F MF ．圆O 的方程是222b y x =+． （1）求双曲线C 的方程；（2）过双曲线C 上任意一点P 作该双曲线两条渐近线的垂线,垂足别离为1P 、2P ,求21PP PP ⋅的值；（3）过圆O 上任意一点()00y ,x Q 作圆O 的切线交双曲线C 于A 、B 两点,AB 中点为M ,求证：2AB OM =．（2）由条件可知：两条渐近线别离为1220;20l x y l x y -=+= 设双曲线C 上的点00(,)Q x y ,设两渐近线的夹角为θ,那么那么点Q 到两条渐近线的距离别离为00001222|||33x y x y PP PP -+==因为00(,)Q x y 在双曲线C ：2212y x -=上,因此220022x y -= 又1cos 3θ=,因此220000002221233933x y x y x y θ-+-==⋅=（3）由题意,即证：OA OB ⊥.设1122(,),(,)A x y B x y ,切线的方程为：002x x y y += ①当00y ≠时,切线的方程代入双曲线C 中,化简得：22220000(2)4(24)0y x x x x y -+-+=因此：2001212222200004(24),(2)(2)x y x x x x y x y x ++=-=--- 又22010201201201222200000(2)(2)82142()2x x x x x y y x x x x x x y y y y x ---⎡⎤=⋅=-++=⎣⎦- 因此②当00y =时,易知上述结论也成立． 因此综上,OA OB ⊥,三、圆与抛物线的结合点 3. 1圆的性质与抛物线相结合【例5】一个酒杯的轴截面是开口向上的抛物线的一段弧,它的口宽是的410杯深20,在杯内放一玻璃球,当玻璃球的半径r 最大取 时,才能使玻璃球触及杯底． 【答案】1【解析】成立如下图的直角坐标系,酒杯所在抛物线的方程设为22(0)x py p =>,因为过点(210,20),因此2(210)220,1p p =⨯=,即22(020)x y y =≤≤.玻璃球触及杯底,确实是小球的截面圆222()x y r r +-=与抛物线22x y =有且仅有一个交点,即原点.由222()x y r r +-=与22x y =消去得：0y =或2 2.y r =-因为有且仅有一个交点,即原点,因此220,1,r r -≤≤即半径r最大取1.【小试牛刀】【2017吉林长春五县上学期期末】已知点A 是抛物线()2:20C x px p =>上一点,O 为坐标原点,假设,A B 是以点()0,10M 为圆心,OA 的长为半径的圆与抛物线C 的两个公共点,且ABO ∆为等边三角形,那么p 的值是 ．【答案】56抛物线的性质与圆的相联系【例6】【2017届重庆市第一中学高三12月月考】已知椭圆()2212210x y C a b a b+=>>：离心率6焦距为22抛物线()22:20C x py p =>的核心F 是椭圆1C 的极点. （Ⅰ）求1C 与2C 的标准方程；（Ⅱ）设过点F 的直线交2C 于,P Q 两点,假设1C 的右极点A 在以PQ 为直径的圆内,求直线的斜率的取值范围.【分析】（Ⅰ）椭圆1C 的焦距为222=c ,36=a c ,得椭圆的标准方程,取得抛物线核心,可得抛物线方程；（Ⅱ）联立直线与抛物线的方程结合韦达定理得k x x 421=+,421-=⋅x x ,A 在以PQ 为直径的圆内⇔0<⋅AQ AP ,得结果.（Ⅱ）由题意可设直线的方程为：1y kx =+,设点()11,P x y ,()22,Q x y ,联立214y kx x y=+⎧⎨=⎩得2440x kx --=,由韦达定理得124x x k +=,124x x =-.A 在以PQ 为直径的圆内)1212120330AP AQ x x x x y y ⇔<⇔+++<)2212121216163480x x x x x x ⇔-+++<641634481600k k --++<⇒>.【小试牛刀】已知抛物线C ：22(0)y px p =>的核心为F ,直线4y =与y 轴的交点为P ,与C 的交点为Q ,且5||||4QF PQ =. （I ）求C 的方程；（II ）过F 的直线与C 相交于A ,B 两点,假设AB 的垂直平分线与C 相较于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求的方程. 【解析】（I ）设0,4Q x ,代入22y px ,得0888,,.22p p x PQQF x pp p．由题设得85824p pp,解得2p （舍去）或2p ,∴C 的方程为24y x ；（II ）由题设知与坐标轴不垂直,故可设的方程为10x my m,代入24y x 得2440y my．设1122,,,,A x y B x y 则124,y y m124y y ．故AB 的中点为2221221,2,141D m m AB m y y m ．又的斜率为,m l 的方程为2123xy m m．将上式代入24y x ,并整理得2244230y y m m．设3344,,,,M x y B x y 则234344,423y y y y m m．故MN 的中点为22234222412122123,,1m m E mMN y y mmm m ．由于MN 垂直平分线AB ,故,,,A M B N 四点在同一圆上等价于12AEBEMN ,从而22211,44AB DEMN 即2222222244121224122m m m mmm m,化简得210m ,解得1m 或1m ．所求直线的方程为10x y 或10xy ．【迁移运用】1．【2017河北定州市上学期期中】过双曲线22115y x -=的右支上一点P ,别离向圆1C ：22(+4)+4x y =和圆2C ：22(4)1x y -+=作切线,切点别离为M ,N ,那么22||||PM PN -的最小值为（ ）A ．10B ．13C ．16D ．19 【答案】B【解析】由题可知,)1|(|)4|(|||||222122---=-PC PC PN PM ,因此=--=-3||||||||222122PC PC PN PM 121212(||||)2(||||)32||3PC PC PC PC C C -=+-≥-13=.应选B ．2．【2017届四川双流中学高三上学期必得分训练】已知P 为抛物线x y 42=上一个动点,Q 为圆1)4(22=-+y x 上一个动点,当点P 到点Q 的距离与点P 到抛物线的准线的距离之和最小时,点P 的横坐标为（ ）A ．8179- B ．89C ．817D ．17【答案】A【解析】设P 到抛物线准线的距离为d ,抛物线的核心为F ,圆心为C ,则()()min min 1PQ d PQ PF CF r +=+=-=,应选A.3．【2017届湖南长沙一中高三月考五】已知双曲线22221(a 0,b 0)x y a b-=>>的左、右核心别离为1F 、2F ,过1F 作圆222x y a +=的切线别离交双曲线的左、右两支于点B 、C ,假设2|BC ||CF |=,那么双曲线的渐近线方程为（ ）A.3y x =±B.22y x =±C.(31)y x =±+D.(31)y x =±- 【答案】C4．【2016届河南省郑州市一中高三上学期联考】如图,已知椭圆111:221=+y x C ,双曲线)0,0(1:22222>>=-b a by a x C ,假设以1C 的长轴为直径的圆与2C 的一条渐近线交于A 、B 两点,且1C 与该渐近线的两交点将线段AB 三等分,那么2C 的离心率为（ ）A ．5B ．5C ．17D ．7142【答案】A【解析】设椭圆与双曲线的渐近线相交于1122(,),(,)M x y N x y 两点（设M 在轴上方）和33(,)A x y ,那么由题意知,3OA OM =,即313x x =．于是联立方程组2211x y b y xa ⎧+=⎪⎨=⎪⎩可得,2232211a x a b =+；联立方程组22111x y b y x a ⎧+=⎪⎪⎨⎪=⎪⎩可得,221221111a x a b =+；即2222119()a b a b +=+,因此224b a =,即225c a =,因此5e =．故应选A ．5．【2016届河南省郑州市一中高三上学期联考】已知抛物线28y x =,点Q 是圆22:28130C x y x y ++-+=上任意一点,记抛物线上任意一点到直线2x =-的距离为d ,那么PQ d +的最小值为（ ）A ．5B ．4C ．3D ．2 【答案】C6.过双曲线22221(0,0)y x a b a b-=>>的左核心F 作圆222x y a +=的两条切线,切点别离为A 、B ,双曲线左极点为M ,假设0120AMB ∠=,那么该双曲线的离心率为 （ ） A 2 B ． 3 C ． D ．【答案】D【解析】OA 即为双曲线的渐近线,OAM ∆为等边三角形,直线OA 的倾斜角为60,因此3ba=2222342b a c a e =⇒=⇒=.选D.7．【2017届湖南师大附中高三上学期月考三】如图,抛物线21:8C y x =与双曲线()22222:10,0x y C a b a b-=>>有公共核心2F ,点A 是曲线12,C C 在第一象限的交点,且25AF =.（Ⅰ）求双曲线2C 的方程；（Ⅱ）以1F 为圆心的圆M 与双曲线的一条渐近线相切,圆()22:21N x y -+=.已知点(3P ,过点P 作相互垂直且别离与圆M 、圆N 相交的直线和,设被圆M 截得的弦长为,被圆N 截得的弦长为.试探讨ts是不是为定值？请说明理由.【答案】（Ⅰ）2213y x -=；（Ⅱ）s t 3【解析】（Ⅰ）抛物线21:8C y x =的核心为()22,0F ,∴双曲线2C 的核心为()()122,02,0F F -、. 设()00,A x y 在抛物线21:8C y x =上,且25AF =.由抛物线的概念得,025x +=,∴03x =.∴2083y =⨯,∴026y =±()()22132267AF =++±=又∵点A 在双曲线上,由双曲线概念得,2752a =-=,∴1a =.∴双曲线的方程为：2213y x -=. （Ⅱ）s t为定值.下面给出说明：设圆M 的方程为：()2222x y r ++=,双曲线的渐近线方程为：y =.∵圆M与渐近线y =相切,∴圆M的半径为r ==故圆()22:23M x y ++=.依题意12l l 、的斜率存在且均不为零,因此设的方程为()1y k x =-,即0kx y k -=,设的方程为()11y x k=--,即10x ky +-=, ∴点M到直线的距离为1d =,点N到直线的距离为2d =,∴直线被圆M截得的弦长s ==直线被圆N截得的弦长t ==∴s t===故st7．【2017学年吉林长春五县高二上学期期末】已知()222210x y a b a b+=>>的左、右核心别离为12F F 、,12F F =点P 在椭圆上,21tan 2PF F ∠=,且12PF F ∆的面积为4. （1）求椭圆的方程；（2）点M 是椭圆上任意一点,12A A 、别离是椭圆的左、右极点,直线12MA MA ，与直线x =,E F 两点,试证：以EF 为直径的圆交轴于定点,并求该定点的坐标. 【答案】（1）22194x y +=；（2）证明观点析,1,0⎫+⎪⎪⎝⎭或1,0⎫-⎪⎪⎝⎭. 【解析】（1）因为21tan 2PF F ∠=,因此21sin 5PF F∠=,21cos 5PF F ∠=.由题意得((22221221255425225PF PF PF PF ⎧⨯⨯=⎪⎪⎨⎪=+-⨯⨯⎪⎩,解得1242PF PF ⎧=⎪⎨=⎪⎩.从而1224263a PF PF a =+=+=⇒=,结合2c =得24b =,故椭圆的方程为22194x y +=. （2）由（1）得()13,0A-,()23,0A ,设()00,M x y,那么直线1MA 的方程为()0033y y x x =++, 它与直线x =003232y E x⎛⎫⎛⎫+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭,直线2MA 的方程为()0033y y x x =--,它与直线2x =的交点的坐标为0033y F x ⎫⎫-⎪⎪⎪⎪-⎝⎭⎝⎭,再设以EF 为直径的圆交轴于点(),0Q m ,那么QE QF ⊥,从而1QE QF k k =-,即033y x ⎫+⎪+0 0331 35y x⎫-⎪-⎝=--,即222949ymx⎫=⎪⎪-⎝⎭,解得1m=.故以EF为直径的圆交轴于定点,该定点的坐标为1,0⎫+⎪⎪⎝⎭或1,0⎫⎪⎪⎝⎭.8．【2017届广西陆川县中学高三上学期二模】已知椭圆D：()222101yx bb+=<<的左核心为F,其左、右极点为A、C ,椭圆与y轴正半轴的交点为B,FBC的外接圆的圆心(),P m n在直线x y+=上.（I）求椭圆D的方程；（II ）已知直线：x=N是椭圆D上的动点,NM l⊥,垂足为M,是不是存在点N,使得FMN为等腰三角形？假设存在,求出点N的坐标,假设不存在,请说明理由.【答案】(I)2221x y+=；(II)N36⎛-±⎝⎭或0,2⎛⎫±⎪⎪⎝⎭.【解析】（I）由题意知,圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,设F的坐标为()(),00c c->,则FC的垂直平分线方程为12cx-=…①因为BC的中点坐标为1,22b⎛⎫⎪⎝⎭,BC的斜率为b-因此BC的垂直平分线的方程为1122by xb⎛⎫-=-⎪⎝⎭…②联立①②解得:12cx-=,22b cyb-=即12cm-=,22b cnb-=因为(),P m n 在直线0x y +=上,因此21022c b cb--+=………（4分） 即()()10b b c +-= 因为()10b +>,因此b c =再由221b c =-求得2212b c ==因此椭圆D 的方程为2221x y +=………（7分）9．【2017届湖南长沙雅礼中学高三月考四】已知椭圆)0(12222>>=+b a by a x 的右核心为)0,1(2F ,点)3102,2(H 在椭圆上. （1）求椭圆的方程；（2）点M 在圆222b y x =+上,且M 在第一象限,过M 作222b y x =+的切线交椭圆于Q P ,两点,问：Q PF 2∆的周长是不是为定值？假设是,求出定值；假设不是,说明理由.【答案】（1）18922=+y x ；（2）．【解析】（1）由题意得⎪⎩⎪⎨⎧=+==-19404122222b ac b a ,∴⎪⎩⎪⎨⎧==9922b a ,∴椭圆的方程为18922=+y x . （2）由题意,设PQ 的方程为)0,0(><+=m k m kx y ,∵PQ 与圆822=+y x 相切,∴221||2=+k m ,即2122k m +=,⎪⎩⎪⎨⎧=++=18922y x mkx y 得072918)98(222=-+++m kmx x k , 设),(),,(2211y x Q y x P ,那么222122198729,9818k m x x k km x x +-=+-=+,∴222222212212212986987294)9818(14)(1||1||k km k m k km kx x x x kx x k PQ +-=+--+-+=-++=-+=又212121212122)9(91)91(8)1()1(||-=-+-=+-=x x x y x PF ,∴112313)9(31||x x PF -=-=,同理222313)9(31||x x QF -=-=,∴22129866)(316||||k kmx x QF PF ++=+-=+, ∴69869866||||||222=+-++=++k kmk km PQ QF PF （定值）.10．【2017山东菏泽一中宏志部月考三】已知椭圆)0(1:2222>>=+b a by a x C 的焦距为2,左、右极点别离为B A ,,P 是椭圆上一点,记直线PB PA ,的斜率为21,k k ,且有2121-=k k . （1）求椭圆C 的方程；（2）假设直线)0(:≠+=k m kx y l 与椭圆C 交于N M ,两点,以N M ,为直径的圆通过原点,且线段MN 的垂直平分线在y 轴上的截距为21-,求直线的方程. 【答案】（1）2212x y +=；（2）1y x =+．（2）设()()1122,,M x y N x y 、,MN 的中点为()00,Q x y ,联立2212y kx mx y =+⎧⎪⎨+=⎪⎩取得()222124220k x kmx m +++-=,()22221621021k m m k ∆=-+>⇒<+ ①122412km x x k +=-+,21222212m x x k-=+,12022212x x km x k +==-+,00212my kx m k =+=+ ② 因为以MN 为直径的圆通过原点,因此0OM ON =,12120x x y y +=,()()12120x x kx m kx m +++=,()()22121210k x xkm x x m++++=,()()2222222122401212k m k m m k k+--+=++, 化简得22322m k =+ ③将②式代入取得223121m k -=+代入①式取得212m >, 由于线段MN 的垂直平分线通过点1(0,)2-,00112y x k+∴=-,将②代入取得2122k m += ④联立③④得13m =-或1,因为212m >,因此1m =,22k =±. 因此直线的方程为212y x =±+. 11．【2016-2017学年河北枣强中学高二12月月考】设椭圆22221(0)x y a b a b+=>>,过(2,2)M 、(6,1)N 两点,O 为坐标原点．（1）求椭圆E 的方程；（2）假设直线4(0)y kx k =+>与圆2283x y +=相切,而且与椭圆E 相交于两点A 、B ,求证：OA OB ⊥．【答案】（1）22184x y +=；（2）证明观点析．（2）设11(,)A x y ,22(,)B x y ,由题意得2261d k ==+, 因此5k =联立直线与椭圆方程得211240x ++=,有12x x +=122411x x =,因此121212126)160x x y y x x x x +=+++=,因此OA OB ⊥．12．【2017届甘肃肃南裕固族自治县一中高三12月月考】已知椭圆()2222:10x y E a b a b+=>>的离心率2e =,过椭圆的左核心F 且倾斜角为30°的直线与圆222x y b +=相交所得弦的长度为1.（Ⅰ）求椭圆E 的方程；（Ⅱ）假设动直线交椭圆E 于不同两点()()2211,,,y x N y x M ,设()()1122,,,OP bx ay OQ bx ay ==,O 为坐标原点.当以线段PQ 为直径的圆恰好于点O 时,求证：MON ∆的面积为定值,并求出该定值.【答案】(I)2214x y +=；(II)证明观点析,. 【解析】（Ⅰ）由题意知23=e 得23=a c ,即c a 23=. ① 因为直线过左核心()0,c F -且倾斜角为30°可得直线方程为()c x y +=33又因为直线()c x y +=33与圆222b y x =+相交弦长为1, 因此圆心到直线距离2323933c c c d ==+=, 再由勾股定理得：41422=-c b ②由①②联立222222144cc b a b c=⎪-=⎨⎪⎪=+⎩可知222413a b c ⎧=⎪=⎨⎪=⎩即椭圆方程为2214x y += （Ⅱ）（ⅰ）当直线MN 的斜率不存在时,2121,y y x x -==,因为以线段PQ 为直径的圆过原点,因此OP OQ ⊥,即0OP OQ ⋅=,因此22121212120,40b x x a y y x x y y +=+=, 即221140x y -=,③又因为点()11,M x y 在椭圆上,因此221114x y +=,④把③代入④得：2112,x y ==,因此11211122OMN S x y y ∆=-==. （ⅱ）当直线MN 的斜率存在时,设直线MN 的方程为y kx t =+,()2222214844014y kx tk x ktx t x y =+⎧⎪⇒+++-=⎨+=⎪⎩, 因为交于不同两点,因此0∆>,()()22226414440k t k t ∆=-4+->,即22410k t ∆=-+>,由韦达定理得：2121222844,1414kt t x x x x k k --+==++,由题意知0OP OQ ⋅=即121240x x y y +=,又1122,y kx t y kx t =+=+,因此()2212121240x x k x x kt x x t ⎡⎤+⋅+++=⎣⎦,∴()()22121214440k x x kt x x t ++++=,代入整理得22214t k =+.⑤又()22121214MN kx x x x =++-22222844141414kt t k k k --⎛⎫=+-⋅ ⎪++⎝⎭2222414114k t k k+-=+⋅+ 点O 到直线y kx t =+的距离21kt d +=,因此2222211414122141MONt k t S d MN k kk ∆+-=⨯=⨯⨯+⋅++ 2221414214k t t k+-=⨯+,⑥ 将⑤代入⑥得241122MON t S t t∆=⨯=, 13.如下图,已知A 、B 、C 是长轴长为的椭圆E 上的三点,点A 是长轴的一个端点,BC 过椭圆中心O ,且0AC BC ⋅=,2BC AC =．（1）求椭圆E 的方程；（2）在椭圆E 上是不是存点Q ,使得222QB QA -=？假设存在,有几个（没必要求出Q 点的坐标）,假设不存在,请说明理由；（3）过椭圆E 上异于其极点的任一点P ,作圆224:3O x y +=的两条线,切点别离为M 、N ,假设直线MN 在轴、y 轴上的截距别离为m 、,证明：22113m n +为定值. 【解析】（1）依题意知：椭圆的长半轴长2a =,那么()2,0A ,设椭圆E 的方程为22214x y b+=,由椭圆的对称性知OC OB = 又0AC BC ⋅=,2BC AC =,AC BC ∴⊥,OC AC =,AOC ∴∆为等腰直角三角形,∴点C 的坐标为()1,1,点B 的坐标为()1,1--,将C 的坐标()1,1代入椭圆方程得243b =, ∴所求的椭圆E 的方程为223144x y +=. （2）解法一：设在椭圆E 上存在点Q ,使得222QB QA -=,设()00,Q x y ,那么()()()2222220000001126222QB QA x y x y x y -=+++---=+-=,即点Q 在直线320x y +-=上,∴点Q 即直线320x y +-=与椭圆E 的交点,直线320x y +-=过点2,03⎛⎫⎪⎝⎭,而点椭圆2,03⎛⎫⎪⎝⎭在椭圆E 的内部, ∴知足条件的点Q 存在,且有两个；解法二：设在椭圆E 上存在点Q ,使得222QB QA -=,设()00,Q x y ,那么()()()2222220000001126222QB QA x y x y x y -=+++---=+-=,即00320x y +-=,①又点Q 在椭圆E 上,2200340x y ∴+-=,②由①式得0023y x =-代入②式并整理得：2007920x x -+=,③方程③的根判别式8156250∆=-=>,∴方程③有两个不相等的实数根,即知足条件的点Q 存在,且有两个；（3）解法一：设点()11,P x y ,由M 、N 是圆O 的切点知,OM MP ⊥,ON NP ⊥,O ∴、M 、P 、N 四点在同一圆上,且圆的直径为OP ,那么圆心为11,22x y ⎛⎫⎪⎝⎭, 其方程为22221111224x y x y x y +⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭, 即22110x y x x y y +--=,④即点M 、N 知足方程④,又点M 、N 都在圆O 上,M ∴、N 坐标也知足圆O 的方程2243x y +=,⑤ ⑤④得直线MN 的方程为1143x x y y +=, 令0y =,得143m x =,令0x =得143n y =, 143x m ∴=,143y n =,又点P 在椭圆E 上,22443433m n ⎛⎫⎛⎫∴+= ⎪ ⎪⎝⎭⎝⎭,即2211334m n +=（定值）；14 【2021山东高考理20】平面直角坐标系xOy 中,已知椭圆()2222:10x y C a b a b+=>>的离心,左、右核心别离是12F F ，. 以1F 为圆心以为半径的圆与以2F 为圆心以为半径 的圆相交,且交点在椭圆C 上. （1）求椭圆C 的方程；（2） 设椭圆2222:144x y E a b+=,P 为椭圆C 上任意一点. 过点P 的直线y kx m =+交椭圆E于A B ，两点,射线PO 交椭圆E 于点Q .（i ）求OQ OP的值；（ii ）求△ABQ 面积的最大值.【解析】（1）由题意知24a =,那么2a =．又2c a =,222a c b -=,可得1b =, 因此椭圆C 的方程为2214x y +=． （2）由（1）知椭圆E 的方程为221164x y +=． （ⅰ）设()00,P x y ,OQOPλ=,由题意知()00,Q x y λλ--．因为2214x y +=,又()()22001164x y λλ--+=,即222144x y λ⎛⎫+= ⎪⎝⎭,因此2λ=,即2OQ OP =． （ⅱ）设()11,A x y ,()22,B x y ．将y kx m =+代入椭圆E 的方程,可得()2221484160k x kmx m +++-=,由0∆>,可得22416m k <+ ①那么有122814km x x k +=-+,212241614m x x k -=+,因此12x x -= 因为直线y kx m =+与y 轴的交点坐标为()0,m ,因此AOB △的面积1212S m x x =-===． 设2214m t k=+．将y kx m =+代入椭圆C 的方程, 可得()222148440k x kmx m +++-=, 由0∆,可得 2214m k + ②由①②可知01t <,因此S ==故23S ,当且仅当1t =,即2214m k=+时取得最大值由（ⅰ）知,ABQ △面积为3S ,因此ABQ △面积的最大值为。

中考专题： 圆与函数综合题1、如图，平面直角坐标系中，以点C （2，3）为圆心，以2为半径的圆与轴交于A 、B 两点． （1）求A 、B 两点的坐标； （2）若二次函数2y x bx c =++的图象经过点A 、B ，试确定此二次函数的解析式．￥（2、如图，半径为2的⊙C 与x 轴的正半轴交于点A ，与y 轴的正半轴交于点B ，点C 的坐标为（1，0）．若抛物线23y x bx c =-++过A 、B 两点． （1）求抛物线的解析式；（2）在抛物线上是否存在点P ，使得∠PBO=∠POB 若存在，求出点P 的坐标；若不存在说明理由；（3）若点M 是抛物线（在第一象限内的部分）上一点，△MAB 的面积为S ，求S 的最大（小）值．|~3、如图，抛物线2y ax bx c =++的对称轴为轴，且经过（0,0），（1a,16）两点，点P 在抛物线上运动，以P 为圆心的⊙P 经过定点A （0,2），(1)求a,b,c 的值；~(2)求证：点P 在运动过程中，⊙P 始终与轴相交；（3）设⊙P 与轴相交于M ()1x ,0，N ()()212x ,0x x 两点，当△AMN 为等腰三角形时，求圆心P 的纵坐标。

|4、如图，二次函数y =x 2+bx －3b +3的图象与x 轴交于A 、B 两点（点A 在点B 的左边），交y 轴于点C ，且经过点（b －2，2b 2－5b －1）.·（1）求这条抛物线的解析式；（2）⊙M 过A 、B 、C 三点，交y 轴于另一点D ，求点M 的坐标；（3）连接AM 、DM ，将∠AMD 绕点M 顺时针旋转，两边MA 、MD 与x 轴、y 轴分别交于点E 、F ，若△DMF 为等腰三角形，求点E 的坐标.{.5、类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到，如下是一个案例，请补充完整。

原题：如图1，在⊙O 中，MN 是直径，AB ⊥MN 于点B ，CD ⊥MN 于点D ，∠AOC =90°，AB =3，CD =4，则BD = 。

中考数学压轴题分类强化训练3-抛物线与圆CDEOAB重合，的等边△恰好与坐标系中的△1、如图①②，在平面直角坐标系中，边长为2CDEABGGDECDE180°到△点也是现将△绕边，按顺时针方向旋转的中点的中点()1的位置。

C点的坐标；求 (1)1OA、C求经过三点的抛物线的解析式；、 (2)1GABBGxFBF求切线是以的切线与为直径的圆，过，点作⊙(3)如图③，⊙轴相交于点的解析式；S:S?16:3MM的坐标；请求出点使得．(4)抛物线上是否存在一点若存在，，OAB??AMF若不存在，请说明理由。

3)(3，解(1)C1 2:*#z@zste~p.c^om]来源xyax[b＝ (2)∵抛物线过原点O(0，0)，设抛物线解析式为＋0?2b4a??323?3a＝－＝C`(3，， )带入，得解得b，把A(2，0)?333b?9a?3??3232xyx－∴抛物线解析式为＝33 :~zzste^p.c@*#om]∵∠ABF＝90°，∠BAF＝60°，∴∠AFB＝30°[来源(3)0)，(－2又AB＝2 ∴AF＝4 ∴OF＝2 ∴F xy*~@#%][k中国教育出版网＋b 设直线BF的解析式为＝?3323b?k??3，＝解得k，0)2F(－，＝带入，得b B(1把，)?330??bk?2??332xy＝BF∴直线的解析式为＋33．2332xxxx) M(， (4)①当M在－轴上方时，存在33332112xx)]：[×2×4]＝16：3[中国×4×#@*(教育出－S△AMF：S△OAB＝[%~版网] 33222xxxx＝－2 ＝48＝0得，解得－2，－21338322yx]%网中@~国教育出#&版×4当4＝时，－×4＝＝；[1333 383232yx＝2 当时，－2)－×(－2)＝－＝×(13333388，2) ∴M(4，，M(－)21333232xxxx，M在M(－轴下方时，不存在，设点) ②当33323112xx)]：[×2×4]＝ S△AMF：S△OAB＝[－×4×16(：－3332222xxa c＜0 无实解 0，b－得4－28＋＝3883，)． (4 综上所述，存在点的坐标为M，，M(－2)21333）为圆心的圆与y轴相切于（2 ，2．已知：如图，在平面直角坐标系xOy中，以点P点A，与x轴相交于B、C两点（点B在点C的左边）．（1）求经过A、B、C三点的抛物线的解析式；1．如果的面积是菱形ABCP面积的1）在（）中的抛物线上是否存在点M，使△MBP（22存在，请直接写出所有满足条件的M点的坐标；如果若不存在，请说明理由；（3）如果一个动点D自点P出发，先到达y轴上的某点，再到达x轴上某点，最后运动到（1）中抛物线的顶点Q处，求使点D运动的总路径最.短的路径的长．G．⊥P作PGBC于点，过点，1 解：（）联结PAPB，PC A，P∵⊙与y轴相切于点轴，A⊥yP∴3 2，，）（∵PZ*X*X*K]网*科*学来源[3 =PG=OA∴OG=AP=2，∴PB==2．PC =1．∴BG yBC=2．∴CG=1，OC=3．∴OB=1，PA3 1，0），C（3，0∴A（0），），B（GCOB x3)x?1)(x?y?a(根据题意设二次函数解析式为：，33(0?1)(0?3)a?，解得a∴．= 334323?xy??x∴二次函数的解析式为：333338，，0（，7），（3，0），（4，））的坐标为（（2）存在．点M334333222?)x?2x?x?x?3)3y??((x?43=，）∵（33333y3?，2∴抛物线的顶点Q （）．3PP'A3OBC-2，．）y作点P关于轴的对称点P'，则P'（x Q83 =P' Q'Q，则P Q是最短总路径，根据勾股定理，可得联结P'3P(2,3)PA?y轴yA Pxoy，以点3中，已知点作．如图，在直角坐标系交，过轴于点2?bx?cy?axxCB,PAP APBC三点．，轴于点经过，，抛物线为圆心为半径作⊙交，ABC的坐标；）求点，，（1（2）求出该抛物线的解析式；Q?BPQ ABCP面积的面积是（3）抛物线上是否存在点，使得四边形的2倍？若存在，请求出所有满足条件的点；若不存在，请说明理由．PD?BCBCDP,1解：（）过交作于PD?OA?32PBPA???PC :由题意得,1CDBD??, ∴1OB?∴)3A(0,)),0C(3B(1,0 ,∴,)3)(x?y?a(x?1，则有（2）设该抛物线解析式为：3?a)33?a0(?1)(0?解之得33)x?3y?(x?1)(故该抛物线的解析式为3 3）存在（2?BD?1,BP??BDP?90∵,1BD???DBPcos∴2BP?60DBP??∴??60BPA?∴BPC?ABP?∴与都是等边三角形S2?S2S?∴BCP??ABPABCP四边形)(23,P)0B1(,，∵3?3x?yPB,两点的直线解析式为：∴过?y?b3x BPA平行的直线解析式为：则可设经过点且与13x?y?3?03??bb3?3且有解之得即11?33yx??7x?x?0???或得解方程组???333y8?y??y3)(x?)1(x????3?b3x?y?CBP且与也可设经过点平行的直线解析式为：23x??3??3y3b0?33?b3解之得即且有22?33?3x?y4x??3x???或解方程组得???3y?0y?3y?)(x?3)?(x1???3?Q(0,3),(7,83),(3,0),(4,3)∴．x32CB，，(3A0)，4．如图，在直角坐标系中，轴相交于点为圆心，以点为半径的圆与以ED，y轴相交于点与．12D，C c?x??bxyB是否在）若抛物线经过两点，求抛物线的解析式，并判断点1（3该抛物线上．PBD△P2）在（1）中的抛物线的对称轴上求一点的周长最小．，使得（QM，使得为（1（3）设）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点BCQMM是平行四边形．若存在，求出点的坐标；若不存在，说明理由．四边形yECBO A x32?AC∵?OA?3AB0)，，0)C(3∴3B(?3）1，, 解：，（DAODRt△3OA??23AD又在中，，223?OA∴OD??AD，3)(0?D∴的坐标为,C，D又两点在抛物线上，3?2c????3b???∴解得31??20?c??(33)33b??3?c?3??32123???xxy∴抛物线的解析式为：333?x?，?3B0)(0y?∴点当时，, 在抛物线上3121223∵?xy??x4?3)?x?( 2）（33332123x???yx?3x∴抛物线的对称轴方程为33PBD△P，使的周长最小．在抛物线的对称轴上存在点PBD△PDPB∴∵BD?周长最小只需最小．的长为定值要使PBD△DCDC周长最小的点．连结，则与对称轴的交点即为使y?mx?nDC．的解析式为设直线?33?n??3?m??DC?yx?3∴的解析式为,直线由得??3333m?n?0???n??3??3??yx?33?x??2)，-(3P3的坐标为,故点由得??2??y???3?x?3?x3，(t)Q M在抛物线上要使四边形3（为抛物线对称轴上一点，）存在，设BCQMBC∥QMBC?QMM在对称轴的左侧．且为平行四边形，则，点L∥BC M(x，t)Q作直线于是，过点与抛物线交于点m t?123?3?x3?QM4QM?BC,由，得从而m M(?，312)BCQM故在抛物线上存在点，使得四边形为平行四边形．。

专题三 压轴解答题第四关 以解析几何中与圆相关的综合问题【名师综述】纵观近三年的高考题，解析几何题目是每年必考题型，主要体现在解析几何知识内的综合及与其它知识之间的综合，圆不会单独出大题，一般是结合椭圆、抛物线一起考查，预计在15年高考中解答题仍会重点考查圆与椭圆、抛物线相结合的综合问题，同时可能与平面向量、导数相交汇，每个题一般设置了两个问，第（1）问一般考查曲线方程的求法，主要利用定义法与待定系数法求解，而第（2）问主要涉及最值问题、定值问题、对称问题、轨迹问题、探索性问题、参数范围问题等.这类问题综合性大，解题时需根据具体问题，灵活运用解析几何、平面几何、函数、不等式、三角知识，正确构造不等式，体现了解析几何与其他数学知识的密切联系.这体现了考试中心提出的“应更多地从知识网络的交汇点上设计题目，从学科的整体意义、思想含义上考虑问题”的思想. 类型一 以圆的切线为背景的相关问题典例1（2019·山东省实验中学高考模拟（文））已知椭圆()2222:10x y O a b a b+=>>的左、右顶点分别为A ，B ，点P 在椭圆O 上运动，若△PAB 面积的最大值为23，椭圆O 的离心率为12． (1)求椭圆O 的标准方程；(2)过B 点作圆E ：()()2222,02x y r r +-=<<的两条切线，分别与椭圆O 交于两点C ，D(异于点B)，当r 变化时，直线CD 是否恒过某定点?若是，求出该定点坐标，若不是，请说明理由.【名师指点】圆的切线的应用，往往从两个方面进行考查，一是设切线方程，利用圆心到切线的距离等于半径列方程求解；二是结合切线长定理与勾股定理求解． 【举一反三】【浙江省台州市2019届高三上学期期末质量评估】设点为抛物线外一点，过点作抛物线的两条切线，，切点分别为，．（Ⅰ）若点为，求直线的方程； （Ⅱ）若点为圆上的点，记两切线，的斜率分别为，，求的取值范围．类型二 与圆有关的面积问题典例2 （2019·山东高考模拟（理））已知椭圆22122:1(0)x y C a b a b+=>>的左、右焦点分别为1F 、2F ，椭圆的离心率为12，过椭圆1C 的左焦点1F ，且斜率为1的直线l ，与以右焦点2F 为圆心，半径为2的圆2C 相切.（1）求椭圆1C 的标准方程；（2）线段MN 是椭圆1C 过右焦点2F 的弦，且22MF F N λ=，求1MF N ∆的面积的最大值以及取最大值时实数λ的值.【名师指点】对于平面图形的面积问题，可以直接表示或者可以利用割补的办法，以及弦长公式等，将面积科学有效表示，其中通过设直线和曲线的交点，利用韦达定理是解决该种问题的关键．【举一反三】设圆x 2＋y 2＋2x －15＝0的圆心为A ，直线l 过点B (1，0)且与x 轴不重合，l 交圆A 于C ，D 两点，过B 作AC 的平行线交AD 于点E .(1)证明|EA |＋|EB |为定值，并写出点E 的轨迹方程；(2)设点E 的轨迹为曲线C 1，直线l 交C 1于M ，N 两点，过B 且与l 垂直的直线与圆A 交于P ，Q 两点，求四边形MPNQ 面积的取值范围． 类型三 圆与其他圆锥曲线的结合问题典例3【山东省济南外国语学校2019届高三1月份阶段模拟】抛物线的焦点为F ，圆，点为抛物线上一动点.已知当的面积为.（I ）求抛物线方程； （II ）若，过P 做圆C 的两条切线分别交y 轴于M ，N 两点，求面积的最小值，并求出此时P点坐标.【名师指点】圆与圆锥曲线的交汇问题以公共点为基点,派生出弦长问题、中点问题、垂直问题、切线问题、恒过定点问题、定长问题等等,应对不同的题目,会采用不同的方式方法,但总体上仍以设而不求的处理策略为主.常规的策略是数形结合,将数反映的形画出来,结合图形解决问题．【举一反三】（2019·山东高三月考（文））已知椭圆C ：22221(0)x y a b a b+=>>的离心率为12，以原点为圆120+=相切． （1）求椭圆C 的方程；（2）设(4,0)A -，过点(3,0)R 作与x 轴不重合的直线l 交椭圆C 于P ，Q 两点，连接AP ，AQ 分别交直线163x =于M ，N 两点，若直线MR 、NR 的斜率分别为1k 、2k ，试问：12k k 是否为定值？若是，求出该定值，若不是，请说明理由． 【精选名校模拟】1．（2019·山东新泰市第一中学高三月考（文））已知抛物线C 的顶点在坐标原点，焦点为圆22:40M x y x +-=的圆心，直线l 与抛物线C 的准线和y 轴分别交于点P 、Q ，且P 、Q 的纵坐标分别为13t t-、()2,0t t R t ∈≠． （1）求抛物线C 的方程；（2）求证：直线l 恒与圆M 相切．2．（2020·山东高三期末）设中心在原点O ，焦点在x 轴上的椭圆C 过点12A ⎫⎪⎭，F 为C 的右焦点，⊙F的方程为221104x y +-+= （1）求C 的方程；（2）若直线:(l y k x =(0)k >与⊙O 相切，与⊙F 交于M 、N 两点，与C 交于P 、Q 两点，其中M 、P 在第一象限，记⊙O 的面积为()S k ，求(||||)()NQ MP S k -⋅取最大值时，直线l 的方程. 3．（2020·山东高三期末）在平面直角坐标系中，()()1 ,0,1,0A B -，设ABC 的内切圆分别与边,,AC BC AB 相切于点,,P Q R ，已知1CP =，记动点C 的轨迹为曲线E .(1)求曲线E 的方程;(2)过()2,0G 的直线与y 轴正半轴交于点S ，与曲线E 交于点,H HA x ⊥轴，过S 的另一直线与曲线E 交于M N 、两点，若6SMGSHNSS=，求直线MN 的方程.4．（2020·山东高三期末）已知椭圆E :()222210y x a b a b+=>>的一个焦点为()0,3,长轴与短轴的比为2:1.直线l y kx m =+：与椭圆E 交于P ､Q 两点,其中k 为直线l 的斜率. (1)求椭圆E 的方程;(2)若以线段PQ 为直径的圆过坐标原点O ,问:是否存在一个以坐标原点O 为圆心的定圆O ,不论直线l 的斜率k 取何值,定圆O 恒与直线l 相切?如果存在,求出圆O 的方程及实数m 的取值范围;如果不存在,请说明理由.5．（2012·山东高三月考（理））如图，椭圆G 的中心在坐标原点，其中一个焦点为圆F ：x 2+y 2﹣2x ＝0的圆心，右顶点是圆F 与x 轴的一个交点．已知椭圆G 与直线l ：x ﹣my ﹣1＝0相交于A 、B 两点． （I ）求椭圆的方程；（Ⅱ）求△AOB 面积的最大值．6．（2019·山东高三月考）已知椭圆L ：()222210x y a b a b +=>>32.（1）求椭圆L 的标准方程；（2）过点()0,2Q 的直线l 与椭圆L 交于A 、B 两点，若以AB 为直径的圆恰好过坐标原点，求直线l 的方程及AB 的大小.7．（2019·济南市历城第二中学高二月考）已知椭圆C ：()222210x y a b a b+=>>，圆Q （x ﹣2）2+（y 2）2=2的圆心Q 在椭圆C 上，点P （02）到椭圆C 6 ．（1）求椭圆C 的方程；（2）过点P 作互相垂直的两条直线l 1 .l 2 ， 且l 1交椭圆C 于A ，B 两点，直线l 2交圆Q 于C ，D 两点，且M 为CD 的中点，求△MAB 的面积的取值范围．8.【河北省邢台市2018届高三上学期期末考试】已知椭圆2222:1(0)y x W a b a b +=>>的焦距与椭圆22:14x y Ω+=的短轴长相等，且W 与Ω的长轴长相等，这两个椭圆在第一象限的交点为A ，与直线OA（O 为坐标原点）垂直的直线l 与W 交于,M N 两点，且l 与圆222:C x y R +=相切．（1）求W 的方程； （2）若2030MN =，求圆C 的方程． 9．【河南省郑州市2019届高中毕业年级第一次（1月)质量预测】已知抛物线的焦点为，过的直线与抛物线交于，两点，过，分别向抛物线的准线作垂线，设交点分别为，，为准线上一点. （1）若，求的值； （2）若点为线段的中点，设以线段为直径的圆为圆，判断点与圆的位置关系.10．在平面直角坐标系xOy 中,O 为坐标原点,以O 为圆心的圆与直线x-y-4=0相切.（1）求圆O 的方程;（2）直线l:y=kx+3与圆O 交于A,B 两点,在圆O 上是否存在一点M,使得四边形OAMB 为菱形,若存在,求出此时直线l 的斜率;若不存在,说明理由.11．已知抛物线2:2(0)C y px p =>的焦点为F ，过F 且倾斜角为45︒的直线与抛物线C 相交于,P Q 两点，且线段PQ 被直线2y =平分.（1）求p的值；，求以A为圆心且与PQ相切的圆的标准方程. （2）直线l是抛物线C的切线，A为切点，且l PQ12．【山东省新泰市第一中学2019届高三上学期第二次质量检测】已知抛物线的顶点在坐标原点，焦点为圆的圆心，直线与抛物线的准线和轴分别交于点、，且、的纵坐标分别为、．（1）求抛物线的方程；（2）求证：直线恒与圆相切．13. 【安徽省黄山市2019届高三第一次质量检测】设椭圆（）的左、右焦点分别为，以线段为直径的圆与直线相切，若直线与椭圆交于两点，坐标原点为. （Ⅰ）求椭圆的离心率；（Ⅱ）若，求椭圆的方程．14．【陕西省榆林市2019届高考模拟第一次测试】已知椭圆的离心率，左顶点到直线的距离，为坐标原点.（1）求椭圆的方程；（2）设直线与椭圆相交于两点，若以为直径的圆经过坐标原点，证明：到直线的距离为定值. 15．【黑龙江省哈尔滨市第三中学2019届高三上学期期末考试】在圆上取一点，过点作轴的垂线段，为垂足，当点在圆上运动时，设线段中点的轨迹为.（1）求的方程；（2）试问在上是否存在两点关于直线对称，且以为直径的圆恰好经过坐标原点？若存在，求出直线的方程；若不存在，请说明理由.。

综合与实践、圆、二次函数有关重难点题型题型一综合与实践1.综合与实践问题情境：综合与实践课上，老师让同学们以“等腰直角三角形”为主题开展数学活动，并提出如下问题：如题2-1图，将等腰Rt△ABC的直角边AC与等腰Rt△ADC的斜边AC 重合，∠BAC=∠ADC=90°,试判断线段BC 与CD之间的数量关系，并加以证明.(1)数学思考：请你解答老师提出的问题；(2)猜想证明：如题2-2图，点 E 是线段AD上的一个动点(不与A，D重合)，连接CE，过点 E作EF⊥CE,分别交AB,AC于F,G两点,连接FC,试判断△CEF的形状，并说明理由.2.综合与实践【阅读理解】如题1-1图，在△ABC中，AM是BC边上的高线，由勾股定理得AM²=AB²−BM²,AM²= AC²−CM²,故AB²−BM²=AC²−CM².【知识迁移】如题1-2 图,在矩形ABCD中,当点P在矩形ABCD内任意位置时,连接AP,BP,CP,DP.求证: AP²+ CP²=BP²+DP².【探索发现】如题1-3 图，若点 P在矩形ABCD 的外部时，上述结论是否仍然成立?请加以判断，并说明理由.【尝试应用】如题1-4图，在△ABC中, AB=3,AC=4,Q为平面内一点，且AQ=1,∠BQC=90°,求 BC 的最大值.3.如题1-1图,正方形ABCD的边AB上有一点E,连接DE.(1)若AD=3AE,则sin∠ADE= ;(2)如题1-2图，将边 CB绕点 C顺时针旋转，旋转角为α，使得点 B 的对应点 F 落在DE上(点F不与点D 重合),连接BF,求∠BFE的度数;(3)如题1-3图,在(2)的条件下,若E为AB的中点,DF=n,正方形ABCD的面积为S,求S关于n的函数关系式.4.小颖在学习了摩擦力的相关知识后，准备在水平面上探究滑动摩擦力与压力之间的关系，探究步骤如下：第一步：如题3-1图，在一水平放置的木板上放置一个质量为1kg的木块(压力大小=重力大小)，用弹簧测力计沿水平方向拉动木块，使木块做匀速直线运动(滑动摩擦力的大小可以由弹簧测力计读出)；第二步：在木块上增加质量不同的砝码，使木块做匀速直线运动；当在木块上增加质量不同的砝码后，设弹簧测力计所拉物体的质量为m(kg)，弹簧测力计的示数为F(N)，通过多次测量，得到如下数据：(1)把表中的图的坐标系中，描点，连线，画出弹簧测力计拉力F关于物体质量m的图象；(2)观察所画的图象，猜测F和m之间的函数关系，求出函数表达式；(3)小颖将水平拉动木块实验变成在斜面拉动木块实验，如题3-3图，用弹簧测力计拉着木块分别沿倾斜程度不同的斜面向上做匀速直线运动.经测算，在弹性范围内，沿斜面的拉力 F(N)是高度h(m)的一次函数.当斜面水平放置在地面上时，弹簧测力计的读数为2N，高度h每增加0.1m，弹簧测力计的读数增加0.8N，若弹簧测力计的最大量程是8N，求装置高度h的取值范围.5.综合与实践某数学实验小组在学习了电阻的知识后，计划通过实验探究铂电阻在0∼100°C范围内的温度特性，具体过程如下：【知识背景】电阻温度计是根据导体电阻随温度而变化的规律来测量温度的温度计，铂电阻温度计是最精确的温度计.【实验过程】如题2-1图，将电阻温度计接入电路，开始使导体温度升温，控制温度在( 0°C−100°C范围内，每升温20°C记录一次指示仪表输出的电阻值(单位：Ω)，实验完毕后，关闭所有电源.【收集数据】记录的数据如下表：(1)如题2-2图，建立平面直角坐标系，横轴表示温度( (°C),纵轴表示电阻值(Ω)，描出以上表中的数据为坐标的各点，并进行连线；(2)观察上述各点的分布规律，判断它们是否在同一条直线上，若在同一条直线上，请你建立适当的函数模型，并求出解析式，若不在同一条直线上，请说明理由；(3)当温度为50°C时，求铂电阻的电阻值.题型二圆的综合题1. 如题1图, △ABC内接于⊙O,AB是⊙O 的直径,分别过点 C 作⊙O 的切线，过点 O作AB的垂线，两线相交于点 D.(1)求证: ∠D=2∠A;(2)请用无刻度的直尺和圆规过点O 作AC 的垂线交AC 于点 E(保留作图痕迹，不写作法)；(3)在(2)的条件下,若AB=8,CD=3,求OE的长.2. 如题2图, △ABC内接于⊙O,延长BA至点D,连接DC,使DB=DC,过点A作AE⊥AB交DC于点E,连接B E,BE 与AC相交于点F，且满足∠ADE=2∠EAC.(1)求证:CA=CB;(2)若AD:AB=1:4,求tan∠ABC的值；的值.(3)在(2)的条件下,求AFFC3.如题1-1图, △ABC内接于⊙O,BC是⊙O的直径,CD是∠ACB的平分线,交⊙O 于点D,连接OD,交AB于点E.(1)求证:OD∥AC;,求直线AF与⊙O的位关系.(2)如题1-2图,延长OD至点 F,连接AF,使得AF=BC,且tanB=12在△ABC中,AB=AC,点O是AB边上一动点,以点O为圆心,OB长为半径作圆,交BC于点 D.过点 D作DE⊥AC,垂足为E.(1)如题2-1图,若点O为AB的中点,求证:BD=CD;(2)如题2-2图,当点O为AB 上任意一点时,求证:DE 与⊙O 相切;(3)如题2-3图,若⊙O与AC相切于点F,且⊙O的半径为3,CE=1,求AF的长.如题4图,四边形ABCE内接于⊙O, AB=AC,CE⊥BC,，过点A作BC的平行线交CE的延长线于点 D.(1)求证:AD是⊙O的切线;(2)若DE=2,AE平分∠CAD,求⊙O的半径；(3)新考法探究线段数量关系若( CE=m,DE=n,⊙O的直径为d，探究m，n与d的数量关系，并说明理由.题型三二次函数综合题1. 已知抛物线y₁=ax²−4ax+c经过点(3,−2),与x轴交于点A(x₁,0),B两点.(1)若抛物线过点(−1,2),求抛物线的解析式；(2)若−1<x₁<0,点P(5,n)(n⟩0))在该抛物线上，求a的取值范围；(3)若抛物线y₁向上平移两个单位长度后得到抛物线y₂，抛物y₁与直线y₁=kx+b(k≠0)交于点(x₁,0)(x₁<2),且函数y=y₁+y₁的图象与x轴仅有一个交点.求证：k=2a.2.如题2图，在平面直角坐标系中，抛物线y=−x²+bx+c交x轴于A,B(1,0)两点,交y轴于点C(0,3),连接AC,BC.(1)求抛物线的解析式；(2)N是线段AC上一点，过点N作NN′⊥x轴于点N′,若△ABC的面积被 NN'分为1∶2的两部分，求点N 的坐标；(3)将抛物线向左平移m(m⟩0))个单位长度，与原抛物线的交点为点 D,连接 AD,BD,AC 与 BD 相交于点 E,若△ADE与△BCE的面积差为1，求m的值.3.已知抛物线y=25x2+bx+c的顶点坐标为(−2,185),与x轴交于点A,B(点A在点 B左侧),与y轴交于点C.(1)求b,c的值;(2)点M(-4，2)，N是抛物线上两点，若点N到对称轴的距离等于点M到对称轴距离的2倍，求点 N的坐标；(3)若点 P是第二象限内抛物线上一点，连接PB交AC于点D,求PDBD的最大值.x−3与x轴，y轴交于A，B两点，抛物线y=x²+bx+c经过A，B两点，M是射线4.如题2图,直线y=34BA上一动点，过点 M作MN∥y轴交抛物线于点 N.(1)求抛物线的解析式；(2)当M在线段BA上时,连接AN,BN,若S∆ABN=S∆ABO,求此时点M的坐标；(3)新考法与点的运动结合点M从点 B 出发，沿射线BA方向以每秒5个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，MB=MN?请直接写出所有符合条件的t值.5.如题3图，在平面直角坐标系中，已知抛物线y=ax²+bx−2(a≠0)与x轴交于点A(−1,0),B(0)，与y 轴交于点 C，点P为直线BC下方抛物线上一动点.(1)求抛物线的解析式；(2)过点P作PE⊥x轴于点 E，连接OP，是否存在点 P 使得. ∠OPE=∠ABC?若存在，求出点的横坐标；若不存在，请说明理由；(3) 将抛物线沿着x轴翻折，点P 的对应点为P′,连接P'B,求△P′CB面积的最大值及此时点 P的坐标.。

二次函数压轴题（与圆综合问题）【典例分析】例1 如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C 三点的圆与y轴的另一个交点为D．（1）如图1，已知点A，B，C的坐标分别为（-2，0），（8，0），（0，-4）；①求此抛物线的函数解析式；②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；（2）如图2，若a=1，c=-4，求证：无论b取何值，点D的坐标均不改变．思路点拨（2）连接AD、BC，如图2．若a=1，c=-4，则抛物线的解析式为y=x2+bx-4，可得C（0，-4），OC=4．设点A（x1，0），B（x2，0），则OA=-x1，OB=x2，且x1、x2是方程x2+bx-4=0的两根，根据根与系数的关系可得OA•OB=4．由A、D、B、C四点共圆可得∠ADC=∠ABC，∠DAB=∠DCB，从而可得△ADO∽∽△CBO，根据相似三角形的性质可得OC•OD=OA•OB=4，从而可得OD=1，即可得到D（0，1），因而无论b 取何值，点D的坐标均不改变．满分解答（1）①∵抛物线y=ax2+bx+c过点A（-2，0），B（8，0），C（0，-4），∴42064804a b ca b cc-+=⎧⎪++=⎨⎪=-⎩，解得14324abc⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩．学#科网∴抛物线的解析式为y=14x2-32x-4；②过点M作ME∥y轴，交BD于点E，连接BC，如图1．∴D（0，4）．设直线BD的解析式为y=mx+n．∵B（8，0），D（0，4），∴804m nn+=⎧⎨=⎩，学&科网解得124mn⎧=-⎪⎨⎪=⎩，（2）连接AD、BC，如图2．若a=1，c=-4，则抛物线的解析式为y=x2+bx-4，则C（0，-4），OC=4．设点A（x1，0），B（x2，0），则OA=-x1，OB=x2，且x1、x2是方程x2+bx-4=0的两根，∴OA•OB=-x1•x2=-（-4）=4．考点：圆的综合题例2已知抛物线经过A(3，0), B(4，1)两点，且与y轴交于点C．（1）求抛物线的函数关系式及点C的坐标；（2）如图（1）,连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；（3）如图（2）,连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB 于点F，当△OEF的面积取得最小值时，求点E的坐标．思路点拨(1)用待定系数法求解;(2) 假设存在，分两种情况讨论(3)根据面积公式,列出二次函数,求函数的最值.满分解答（1）将A(3,0),B(4,1)代人得∴∴∴C(0,3) 学科@网②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P. ∵A(3,0),C(0,3)∴直线AC的函数关系式为将直线AC向上平移2个单位与直线BP重合.则直线BP的函数关系式为由,得又B(4,1),∴P2(-1,6).综上所述,存在两点P1(0,3), P2(-1,6).(3)∵∠OAE=∠OAF=45O,而∠OEF=∠OAF=45O, ∠OFE=∠OAE=45O,∴∠OEF=∠OFE=45O,∴OE=OF,∠EOF=90O∵点E在线段AC上,∴设E∴=∴===∴当时,取最小值,此时,∴例3如图，在平面直角坐标系中，圆D与y轴相切于点C(0，4)，与x轴相交于A、B两点，且AB＝6.(1)求D点的坐标和圆D的半径；(2)求sin∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式；(3)设抛物线的顶点为F，证明直线AF与圆D相切．思路点拨（1）连接CD，过点D作DE⊥AB，垂足为E，连接AD．依据垂径定理可知AE=3，然后依据切线的性质可知CD⊥y轴，然后可证明四边形OCDE为矩形，则DE=4，然后依据勾股定理可求得AD的长，故此可求得⊙D的半径和点D的坐标；学科.网（2）先求得A（2，0）、B（8，0）．设抛物线的解析式为y=a（x﹣2）（x﹣8），将点C的坐标代入可求得a 的值．根据三角形面积公式得：S△ABC=BC×AC sin∠ACB=AB×CO，代入计算即可；（3）求得抛物线的顶点F的坐标，然后求得DF和AF的长，依据勾股定理的逆定理可证明△DAF为直角三角形，则∠DAF=90°，故此AF是⊙D的切线．满分解答（2）如图1所示：∵D（5，4），∴E（5，0），∴A（2，0）、B（8，0）．设抛物线的解析式为y=a（x﹣2）（x﹣8），将点C的坐标代入得：16a=4，解得：a，∴抛物线的解析式为y x 2x +4．∵S △ABC =BC ×AC sin ∠ACB =AB ×CO ，∴sin ∠ACB ==．例4如图，已知二次函数()22y x m 4m =--（m ＞0）的图象与x 轴交于A 、B 两点．（1）写出A 、B 两点的坐标（坐标用m 表示）；（2）若二次函数图象的顶点P 在以AB 为直径的圆上，求二次函数的解析式； （3）设以AB 为直径的⊙M 与y 轴交于C 、D 两点，求CD 的长． 思路点拨（1）解关于x 的一元二次方程()22x m 4m 0--=，求出x 的值，即可得到A 、B 两点的坐标。

【压轴必刷】中考数学压轴大题之经典模型培优案专题17函数与圆综合问题【例1】如图，抛物线y＝ax2+bx+2经过A（﹣1，0），B（4，0）两点，与y轴交于点C．（1）求该抛物线的解析式；（2）在y轴上是否存在点P使得∠OBP+∠OBC＝45°，若存在，求出点P的坐标，若不存在，请说明理由；（3）点M是BC为直径的圆上的动点，将点M绕原点O顺时针旋转90°得点N，连接NA，求NA的取值范围．【例2】如图1：抛物线y＝﹣x2+bx+c过点A（﹣1，0），点B（3，0），与y轴交于点C．动点E（m，0）（0＜m＜3），过点E作直线l⊥x轴，交抛物线于点M．（1）求抛物线的解析式及C点坐标；（2）连接BM并延长交y轴于点N，连接AN，OM，若AN∥OM，求m的值．（3）如图2．当m＝1时，P是直线l上的点，以P为圆心，PE为半径的圆交直线l于另一点F（点F 在x轴上方），若线段AC上最多存在一个点Q使得∠FQE＝90°，求点P纵坐标的取值范围．【例3】如图，抛物线y＝ax2+bx+2与直线AB相交于A（﹣1，0），B（3，2），与x轴交于另一点C．（1）求抛物线的解析式；（2）在y上是否存在一点E，使四边形ABCE为矩形，若存在，请求出点E的坐标；若不存在，请说明理由；（3）以C为圆心，1为半径作⊙O，D为⊙O上一动点，求DA+DB的最小值【例4】如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+3的对称轴是直线x＝2，与x轴相交于A，B 两点（点A在点B的左侧），与y轴交于点C．（Ⅰ）求抛物线的解析式及顶点坐标；（Ⅱ）M为第一象限内抛物线上的一个点，过点M作MN⊥x轴于点N，交BC于点D，连接CM，当线段CM＝CD时，求点M的坐标；（Ⅲ）以原点O为圆心，AO长为半径作⊙O，点P为⊙O上的一点，连接BP，CP，求2PC+3PB的最小值．1．如图，在平面直角坐标系上，一条抛物线y＝ax2+bx+c（a≠0）经过A（1，0）、B（3，0）、C（0，3）三点，连接BC并延长．（1）求抛物线的解析式；（2）点M是直线BC在第一象限部分上的一个动点，过M作MN∥y轴交抛物线于点N．1°求线段MN的最大值；2°当MN取最大值时，在线段MN右侧的抛物线上有一个动点P，连接PM、PN，当△PMN的外接圆圆心Q在△PMN的边上时，求点P的坐标．2．如图1，已知抛物线y＝ax2﹣12ax+32a（a＞0）与x轴交于A，B两点（A在B的左侧），与y轴交于点C．（1）连接BC，若∠ABC＝30°，求a的值．（2）如图2，已知M为△ABC的外心，试判断弦AB的弦心距d是否有最小值，若有，求出此时a的值，若没有，请说明理由；（3）如图3，已知动点P（t，t）在第一象限，t为常数．问：是否存在一点P，使得∠APB达到最大，若存在，求出此时∠APB的正弦值，若不存在，也请说明理由．3．如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．（1）求抛物线的表达式；（2）判断△BCE的形状，并说明理由；（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP+EP的值最小，若存在，请求出最小值；若不存在，请说明理由．4．如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B（8，0）．（1）求二次函数的表达式；（2）求顶点A的坐标及直线AB的表达式；（3）判断△ABO的形状，试说明理由；（4）若点P为⊙O上的动点，且⊙O的半径为2，一动点E从点A出发，以每秒2个单位长度的速度沿线段AP匀速运动到点P，再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动，求点E的运动时间t的最小值．5．如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值：x…﹣10123…y…03430…（1）求出这条抛物线的解析式及顶点M的坐标；（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC的最小值；（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．6．如图，抛物线的顶点为A（0，2），且经过点B（2，0）．以坐标原点O为圆心的圆的半径r＝，OC ⊥AB于点C．（1）求抛物线的函数解析式．（2）求证：直线AB与⊙O相切．。

高二数学抛物线综合测试满分：150分 时间：100分钟一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项符合题目的要求，请将答案填写在题后的表格中．1．抛物线y 2＝ax (a ≠0)的焦点到其准线的距离是( )A.|a |4B.|a |2 C ．|a | D ．－a 22．[2010·陕西卷] 已知抛物线y 2＝2px (p >0)的准线与圆x 2＋y 2－6x －7＝0相切，则p 的值为( ) A.12B ．1C ．2D ．4 3．在y ＝2x 2上有一点P ，它到A (1,3)的距离与它到焦点的距离之和最小，则点P 的坐标是( )A ．(－2,1)B ．(1,2)C ．(2,1)D ．(－1,2) 4．已知动圆圆心在抛物线y 2＝4x 上，且动圆恒与直线x ＝－1相切，则此动圆必过定点( )A ．(2,0)B ．(1,0)C ．(0,1)D ．(0，－1)5．设斜率为2的直线l 过抛物线y 2＝ax (a ≠0)的焦点F ，且和y 轴交于点A ，若△OAF (O 为坐标原点)的面积为4，则抛物线的方程为( )A ．y 2＝±4xB ．y 2＝±8xC ．y 2＝4xD ．y 2＝8x6．(2011·北京)已知点A (0,2)，B (2,0)．若点C 在函数y ＝x 2的图像上，则使得△ABC 的面积为2的点C 的个数为( )A ．4B ．3C ．2D ．17．(2011·大纲全国理)已知抛物线C ：y 2＝4x 的焦点为F ，直线y ＝2x －4与C 交于A ，B 两点，则 cos ∠AFB ＝( )A.45B.35 C ．－35 D ．－458．(2010·辽宁)设抛物线y 2＝8x 的焦点为F ，准线为l ，P 为抛物线上一点，P A ⊥l ，A 为垂足．如果直线AF 的斜率为－3，那么|PF |＝( )A ．4 3B ．8C ．83D ．169．[2010·山东卷] 已知抛物线y 2＝2px (p >0)，过其焦点且斜率为1的直线交抛物线于A ，B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的准线方程为( )A ．x ＝1B ．x ＝－1C ．x ＝2D ．x ＝－210．抛物线y 2＝2px (p >0)的焦点为F ，准线为l ，经过F 的直线与抛物线交于A 、B 两点，交准线于C 点，点A 在x 轴上方，AK ⊥l ，垂足为K ，若|BC |＝2|BF |，且|AF |＝4，则△AKF 的面积是( )A ．4B ．3 3C ．4 3D ．8高二数学抛物线综合测试选择题答题卡题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题：本大题共5个小题，每小题5分，共25分．请将答案填写在横线上．11．过抛物线y 2＝4x 的焦点作直线l 交抛物线于A 、B 两点，若线段AB 中点的横坐标为3，则|AB |等 于 .12．如果直线l 过定点M (1,2)，且与抛物线y ＝2x 2有且仅有一个公共点，那么l 的方程为 . 13．抛物线y 2＝x 上的点到直线x －2y ＋4＝0的距离最小的点的坐标是________．14．[2010·浙江卷] 设抛物线y 2＝2px (p >0)的焦点为F ，点A (0,2)．若线段F A 的中点B 在抛物线上，则B 到该抛物线准线的距离为________． 15．[2010·全国卷Ⅱ] 已知抛物线C ：y 2＝2px (p ＞0)的准线为l ，过M (1,0)且斜率为3的直线与l 相交于点A ，与C 的一个交点为B .若AM →＝MB →，则p ＝________．三、解答题：本大题共5小题，每题14分，共70分．解答应写出文字说明，证明过程或演算步骤． 16．斜率为1的直线l 经过抛物线24y x 焦点F ，且与抛物线相交于A 、B 两点，求线段AB 的长。

沪科版九年级数学下册第24章圆综合测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、点P(－3，1)关于原点对称的点的坐标是（）A．(－3，1) B．(3，1) C．(3，－1) D．(－3，－1)2、如图，AB为O的直径，C为D外一点，过C作O的切线，切点为B，连接AC交O于D，38∠=︒，点E在AB右侧的半圆周上运动（不与A，B重合），则AEDC∠的大小是（）A．19°B．38°C．52°D．76°3、ABC的边BC经过圆心O，AC与圆相切于点A，若20∠=︒，则CB∠的大小等于（）A ．50︒B ．25︒C ．40︒D ．20︒4、随着2022年北京冬奥会日渐临近，我国冰雪运动发展进入快车道，取得了长足进步．在此之前，北京冬奥组委曾面向全球征集2022年冬奥会会徵和冬残奥会会徽设计方案，共收到设计方案4506件，以下是部分参选作品，其中既是轴对称图形又是中心对称图形的是（ ）A ．B ．C ．D ．5、如图，PA 是O 的切线，切点为A ，PO 的延长线交O 于点B ，若40P ∠=︒，则B 的度数为（ ）．A ．20°B ．25°C ．30°D ．40°6、下列叙述正确的有( )个.（1）y y =随着x 的增大而增大； （2）如果直角三角形斜边的长是斜边上的高的4倍，那么这个三角形两个锐角的度数分别是75和15；（3）斜边为BC 的直角三角形顶点A 的轨迹是以BC 中点为圆心，BC 长为直径的圆；（4）三角形三边的垂直平分线的交点到三角形三个顶点的距离相等；（5）以2211(1)22m m m m -+>、、为三边长度的三角形，不是直角三角形． A ．0 B ．1 C ．2 D ．37、如图，A ，B ，C ，D 都是O 上的点，OA BC ⊥，垂足为E ，若26OBC ∠=︒，则ADC ∠的度数为（ ）A ．26︒B ．32︒C ．52︒D ．64︒8、如图是一个含有3个正方形的相框，其中∠BCD ＝∠DEF ＝90°，AB ＝2，CD ＝3，EF ＝5，将它镶嵌在一个圆形的金属框上，使A ，G ， H 三点刚好在金属框上，则该金属框的半径是（ ）A B C ．D 9、如图，C 与AOB ∠的两边分别相切，其中OA 边与C 相切于点P ．若90AOB ∠=︒，4OP =，则OC 的长为（ ）A ．8B ．C ．D ．10、如图，四边形ABCD 内接于O ，如果它的一个外角64DCE ︒∠=，那么BOD ∠的度数为（ ）A ．20︒B ．64︒C ．116︒D ．128︒第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在Rt ABC △中，90ACB ∠=︒，D 是ABC 内的一个动点，满足222AC AD CD -=．若AB =4BC =，则BD 长的最小值为_______．2、如图，在平行四边形ABCD 中，7AB =，3AD =，120A ︒∠=，以点B 为圆心，BC 为半径的圆弧交AB 于点E ，连接DE ，则图中黑色阴影部分的面积为________．（结果保留π）3、如图，已知，在ABC 中，AB AC =，30BAC ∠=︒．将ABC 绕点A 逆时针旋转一个α角()0180α︒<<︒至ADE 位置，连接BD ，CE 交于点F ．（I ）求证：ABD ACE △△≌；（2）若四边形ABFE 为菱形，求α的值；（3）在（2）的条件下，若2AB =，直接写出CF 的值．4、如图，A 与x 轴交于()2,0B 、()4,0C 两点，3OA =，点P 是y 轴上的一个动点，PD 切O 于点D ，则△ABD 的面积的最大值是________；线段PD 的最小值是________．5、如图，将半径为10cm 的圆形纸片沿一条弦AB 折叠，折叠后弧AB 的中点C 与圆心O 重叠，则弦AB 的长度为________cm ．三、解答题（5小题，每小题10分，共计50分）1、如图，抛物线y ＝－212x ＋32x ＋2与x 轴负半轴交于点A ，与y 轴交于点B ． （1）求A ，B 两点的坐标；（2）如图1，点C 在y 轴右侧的抛物线上，且AC ＝BC ，求点C 的坐标；（3）如图2，将△ABO 绕平面内点P 顺时针旋转90°后，得到△DEF （点A ，B ，O 的对应点分别是点D ，E ，F ），D ，E 两点刚好在抛物线上．①求点F 的坐标；②直接写出点P 的坐标．2、已知，P 是直线AB 上一动点（不与A ，B 重合），以P 为直角顶点作等腰直角三角形PBD ，点E 是直线AD 与△PBD 的外接圆除点D 以外的另一个交点，直线BE 与直线PD 相交于点F ．（1）如图，当点P 在线段AB 上运动时，若∠DBE ＝30°，PB ＝2，求DE 的长；（2）当点P在射线AB上运动时，试探求线段AB，PB，PF之间的数量关系，并给出证明．⊥，并经过圆心O）．3、如图，已知弓形的长12AB=，弓高2CD=，（CD AB（1）请利用尺规作图的方法找到圆心O；（2）求弓形所在O的半径的长．4、下面是小明设计的“作圆的内接等腰直角三角形”的尺规作图过程.已知：⊙O.求作：⊙O的内接等腰直角三角形ABC.作法：如图，①作直径AB；②分别以点A, B为圆心，以大于12AB的长为半径作弧，两弧交于M点；③作直线MO交⊙O于点C，D；④连接AC，BC．所以△ABC就是所求的等腰直角三角形.根据小明设计的尺规作图过程，解决下面的问题：（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明.证明：连接MA，MB．∵MA=MB，OA=OB，∴MO是AB的垂直平分线．∴AC= ．∵AB是直径,∴∠ACB= ( ) (填写推理依据) ．∴△ABC是等腰直角三角形．5、解题与遐想．如图，Rt△ABC的内切圆与斜边AB相切于点D，AD＝4，BD＝5．求Rt△ABC的面积．王小明：这道题算出来面积刚好是20，太凑巧了吧．刚好是4×5＝20，有种白算的感觉…赵丽华：我把4和5换成m、n再算一遍，△ABC的面积总是m•n!确实非常神奇了…数学刘老师：大家想一想，既然结果如此简单到极致，不计算能不能得到呢？比如，拼图？霍佳：刘老师，我在想另一个东西，这个图能不能尺规画出来啊感觉图都定了．我怎么想不出来呢？计算验证（1）通过计算求出Rt△ABC的面积．拼图演绎（2）将Rt△ABC分割放入矩形中（左图），通过拼图能直接“看”出“20”请在图中画出拼图后的4个直角三角形甲、乙、丙、丁的位置，作必要标注并简要说明．尺规作图（3）尺规作图：如图，点D在线段AB上，以AB为斜边求作一个Rt△ABC，使它的内切圆与斜边AB 相切于点D．（保留作图的痕迹，写出必要的文字说明）-参考答案-一、单选题1、C【分析】据平面直角坐标系中任意一点P （x ，y ），关于原点的对称点是（-x ，-y ），然后直接作答即可．【详解】解：根据中心对称的性质，可知：点P （-3，1）关于原点O 中心对称的点的坐标为（3，-1）． 故选：C ．【点睛】本题考查关于原点对称的点坐标的关系，是需要熟记的基本问题，记忆方法可以结合平面直角坐标系的图形．2、B【分析】连接,BD 由AB 为O 的直径，求解903852,CBD ∠=︒-︒=︒ 结合CB 为O 的切线，求解905238,ABD ABC DBC ∠=∠-∠=︒-︒=︒ 再利用圆周角定理可得答案.【详解】解：连接,BD AB 为O 的直径，90,90,ADB BDC ∴∠=︒∠=︒38,C ∠=︒903852,CBD ∴∠=︒-︒=︒CB 为O 的切线，90,905238,ABC ABD ABC DBC ∴∠=︒∠=∠-∠=︒-︒=︒38,AED ABD ∴∠=∠=︒故选B【点睛】本题考查的是三角形的内角和定理，直径所对的圆周角是直角，圆周角定理，切线的性质定理，熟练运用以上知识逐一求解相关联的角的大小是解本题的关键.3、A【分析】连接OA ，根据圆周角定理求出AOC ∠，根据切线的性质得到90OAC ∠=︒，根据直角三角形的性质计算，得到答案．【详解】解：连接OA ，20B ︒∠=，240AOC B ∴∠=∠=︒， AC 与圆相切于点A ，90OAC ∴∠=︒，904050C ∴∠=︒-︒=︒，故选：A ．【点睛】本题考查的是切线的性质、圆周角定理，掌握圆的切线垂直于经过切点的半径是解题的关键．4、C【分析】根据轴对称图形与中心对称图形的概念求解．【详解】A．是轴对称图形，不是中心对称图形，故此选项不合题意；B．不是轴对称图形，是中心对称图形，故此选项不符合题意；C．是轴对称图形，也是中心对称图形，故此选项合题意；D．不是轴对称图形，也不是中心对称图形，故此选项不合题意．故选：C．【点睛】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．5、B【分析】连接OA，如图，根据切线的性质得∠PAO=90°，再利用互余计算出∠AOP=50°，然后根据等腰三角形的性质和三角形外角性质计算∠B的度数．【详解】解：连接OA，如图，∵PA是⊙O的切线，∴OA ⊥AP ，∴∠PAO =90°，∵∠P =40°，∴∠AOP =50°，∵OA =OB ，∴∠B =∠OAB ，∵∠AOP =∠B +∠OAB ，∴∠B =12∠AOP=12×50°=25°．故选：B ．【点睛】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．6、D【分析】根据反比例函数的性质，得当0x <或者0x >时，y 随着x 的增大而增大；根据直径所对圆周角为直角的性质，得斜边为BC 的直角三角形顶点A 的轨迹是以BC 中点为圆心，BC 长为直径的圆；根据垂直平分线的性质，得三角形三边的垂直平分线的交点到三角形三个顶点的距离相等；根据勾股定理逆定理、完全平方公式的性质计算，可判断直角三角形，即可完成求解．【详解】y =当0x <或者0x >时，y 随着x 的增大而增大，故（1）不正确； 如果直角三角形斜边的长是斜边上的高的4倍，那么这个三角形两个锐角的度数分别是75和15；，故（2）正确；∵圆的直径所对的圆周角为直角∴斜边为BC 的直角三角形顶点A 的轨迹是以BC 中点为圆心，BC 长为直径的圆，故（3）正确； 三角形三边的垂直平分线的交点到三角形三个顶点的距离相等，故（4）正确； ∵224212124m m m ⎛⎫--+= ⎪⎝⎭ ∴242422221211442m m m m m m ⎛⎫-+++++== ⎪⎝⎭∴以2211(1)22m m m m -+>、、为三边长度的三角形，是直角三角形，故（5）错误； 故选：D ．【点睛】本题考查了三角形、垂直平分线、反比例函数、圆、勾股定理逆定理的知识；解题的关键是熟练掌握反比例函数、垂直平分线、圆周角、勾股定理逆定理的性质，从而完成求解．7、B【分析】连接OC ．根据OA BC ⊥确定AC AB =，90OEB ∠=︒，进而计算出AOB ∠，根据圆心角的性质求出AOC ∠，最后根据圆周角的性质即可求出ADC ∠．【详解】解：如下图所示，连接OC ．∵OA BC ⊥，∴AC AB =，90OEB ∠=︒．∴AOC AOB ∠=∠．∵26OBC ∠=︒．∴64AOB ∠=︒．∴64AOC ∠=︒∵ADC ∠和AOC ∠分别是AC 所对的圆周角和圆心角， ∴3122A ADC OC ∠=︒∠=．故选：B ．【点睛】本题考查垂径定理，圆心角的性质，圆周角的性质，综合应用这些知识点是解题关键．8、A【分析】如图，记过A ，G ， H 三点的圆为,Q 则Q 是HG ，AG 的垂直平分线的交点，,QH QG QA 记,PM EF 的交点为,N ,HG PM 的交点为,M 延长AB 交QM 于,P PM 为HG 的垂直平分线，结合正方形的性质可得：,AP PM 再设,PQ x 利用勾股定理建立方程，再解方程即可得到答案.【详解】 解：如图，记过A ，G ， H 三点的圆为,Q 则Q 是HG ，AG 的垂直平分线的交点，,QH QG QA 记,PM EF 的交点为,N ,HG PM 的交点为,M 延长AB 交QM 于,P PM 为HG 的垂直平分线，结合正方形的性质可得：,AP PM四边形HGFE 为正方形，则,HG EF ∥,,QM HG QM EF设,PQ x 而AB ＝2，CD ＝3，EF ＝5，结合正方形的性质可得：5,NQ x而222,HM MQ HQ 115,5,5510,222HM HG EF MN EF MQ x x 222510,4HQ x 又222,AQ PQ AP 而51523,22AP 22215,2AQ x222522510,44x x 解得：5,2x 25225250510.4442AQ 故选A【点睛】本题考查的是正方形的性质，三角形外接圆圆心的确定，圆的基本性质，勾股定理的应用，二次根式的化简，确定过A，G，H三点的圆的圆心是解本题的关键.9、C【分析】如图所示，连接CP，由切线的性质和切线长定理得到∠CPO=90°，∠COP=45°，由此推出CP=OP=4，再根据勾股定理求解即可．【详解】解：如图所示，连接CP，∵OA，OB都是圆C的切线，∠AOB=90°，P为切点，∴∠CPO=90°，∠COP=45°，∴∠PCO=∠COP=45°，∴CP=OP=4，∴OC=，故选C．【点睛】本题主要考查了切线的性质，切线长定理，等腰直角三角形的性质与判定，勾股定理，熟知切线长定理是解题的关键．10、D【分析】由平角的性质得出∠BCD =116°，再由内接四边形对角互补得出∠A =64°，再由圆周角定理即可求得∠BOD =2∠A =128°．【详解】∵64DCE ∠=︒∴18064116BCD ∠=︒-︒=︒∵四边形ABCD 内接于O∴180********A BCD ∠=︒-∠=︒-︒=︒又∵2BOD A ∠=∠∴264128A ∠=⨯︒=︒．故选：D ．【点睛】本题考查了圆内接四边形的性质、圆周角定理，圆内接四边形的对角互补，并且任何一个外角都等于它的内对角；在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半．二、填空题1、2【分析】取AC 中点O ，由勾股定理的逆定理可知∠ADC =90°，则点D 在以O 为圆心，以AC 为直径的圆上，作△ADC 外接圆，连接BO ，交圆O 于1D ，则BD 长的最小值即为1BD ，由此求解即可．【详解】解：如图所示，取AC 中点O ，∵222AC AD CD -=，即222=AC AD CD +，∴∠ADC =90°，∴点D 在以O 为圆心，以AC 为直径的圆上，作△ADC 外接圆，连接BO ，交圆O 于1D ，则BD 长的最小值即为1BD ，∵AB =4BC =，∠ACB =90°，∴AC =， ∴1132OC OD AC ===，∴5OB =，∴112BD OB OD =-=，故答案为：2．【点睛】本题主要考查了一点到圆上一点的最短距离，勾股定理的逆定理，勾股定理，解题的关键在于确定点D 的运动轨迹．232π 【分析】过点C 作CH AB ⊥于点H ，根据正弦定义解得CH 的长，再由扇形面积公式、三角形的面积公式解题即可．【详解】解：过点C 作CH AB ⊥于点H ，在平行四边形ABCD 中，120A ∠=︒18012060B ∴∠=︒-︒=︒=sin sin 603CH BC B AD ∴⋅=⨯︒=平行四边形ABCD 的面积为：7AB CH ⨯= 图中黑色阴影部分的面积为：()2216016037323602360BC AE CH ππ⋅⨯⋅⋅-=⨯-=32π，32π． 【点睛】 本题考查平行四边形的性质、扇形面积等知识，是基础考点，掌握相关知识是解题关键．3、（1）见解析；（2）120°；（3）2【分析】（1）根据旋转的性质和全等三角形的判定解答即可；（2）根据等腰三角形的性质求得∠ABD =90°－12α，∠BAE =α+30°，根据菱形的邻角互补求解即可；（3）连接AF ，根据菱形的性质和全等三角形的性质可求得∠FAC =45°，∠FCA =30°，过F 作FG ⊥AC 于G ，设FG=x ，根据等腰直角三角形的性质和含30°角的直角三角形的性质求解即可．【详解】解：（1）由旋转得：AB=AD ，AC=AE ，∠BAD =∠CAE =α，∵AB=AC ，∴AB=AC =AD=AE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩， ∴△ABD ≌△ACE （SAS ）；（2）∵AB=AD ，∠BAD =α，∠BAC =30°，∴∠ABD =（180°－∠BAD ）÷2=（180°－α）÷2=90°－12α，∠BAE =α+30°，∵四边形ABFE 是菱形，∴∠BAE +∠ABD=180°，即α+30°+90°－12α=180°，解得：α=120°；(3)连接AF ，∵四边形ABFE 是菱形，∠BAE =α+30°=150°，∴∠BAF =12∠BAE =75°，又∠BAC =30°，∴∠FAC =75°－30°=45°，∵△ABD ≌△ACE ，∴∠FCA =∠ABD =90°－12α=30°， 过F 作FG ⊥AC 于G ，设FG=x ，在Rt△AGF 中，∠FAG =45°，∠AGF=90°，∴∠AFG =∠FAG =45°，∴△AGF 是等腰直角三角形，∴AG=FG=x ，在在Rt△AGF 中，∠FCG =30°，∠FGC =90°，∴CF =2FG =2x ，CG ==，∵AC=AB=2，又AG+CG=AC ，∴2x =，解得：1x =，∴CF =2x = 2．【点睛】本题考查全等三角形的判定与性质、旋转的性质、菱形的性质、等腰三角形的判定与性质、含30°角的直角三角形的性质、三角形的内角和定理、解一元一次方程等知识，熟练掌握相关知识的联系与运用是解答的关键．4、12 【分析】根据题中点的坐标可得2BC =圆的直径，半径为1，分析ABD 以AB 定长为底，点D 在圆上，高最大为圆的半径，即可得出三角形最大的面积；连接AP ，设点()0,P y ，根据切线的性质及勾股定理可得PD【详解】解：如图所示：当点P 到如图位置时，ABD 的面积最大，∵()2,0B 、()4,0C ，∴2BC =圆的直径，半径为1，∴ABD 以AB 定长为底，点D 在圆上，高最大为圆的半径，如图所示：此时ABD 面积的最大值为：111122⨯⨯=； 如图所示：连接AP ，∵PD 切A 于点D ，∴AD PD ⊥，∴90ADP ∠=︒，设点()0,P y ，在Rt AOP 中，3OA =，OP y =，∴22229AP OA OP y =+=+，在Rt APD 中，1AD =，∴22222918PD AP AD y y =-=+-=+，则PD当0y =时，PD 取得最小值，=故答案为：①12；②【点睛】题目主要考查切线的性质及勾股定理的应用，理解题意，作出相应图形求出解析式是解题关键．5、【分析】连接OC 交AB 于点D ，再连接OA ．根据轴对称的性质确定OC AB ⊥，OD =CD ；再根据垂径定理确定AD =BD ；再根据勾股定理求出AD 的长度，进而即可求出AB 的长度．【详解】解：如下图所示，连接OC 交AB 于点D ，再连接OA ．∵折叠后弧AB 的中点C 与圆心O 重叠，∴OC AB ⊥，OD =CD ．∴AD =BD ．∵圆形纸片的半径为10cm ，∴OA =OC =10cm ．∴OD =5cm ．∴AD =．∴BD =．∴AB AD BD =+=．故答案为：【点睛】本题考查轴对称的性质，垂径定理，勾股定理，综合应用这些知识点是解题关键．三、解答题1、（1）A （-1，0），B （0，2）；（2）点C ）；（3）①求点F 的坐标（1，2）；②点P 的坐标（32，12） 【分析】（1）令x =0，求得y 值，得点B 的坐标；令y =0，求得x 的值，取较小的一个即求A 点的坐标；（2）设C 的坐标为（x ，－212x ＋32x ＋2），根据AC ＝BC ，得到22AC BC =，令t =－212x ＋32x ，解方程即可；（3）①根据题意，得∠BPE =90°，PB =PE 即点P 在线段BE 的垂直平分线上，根据B ，E 都在抛物线上，则B ，E 是对称点，从而确定点P 在抛物线的对称轴上，点F 在BE 上，且BE ∥x 轴，点E （3，2），确定BE =3，根据旋转性质，得EF =BO =2，从而确定点F 的坐标；②根据BE =3，∠BPE =90°，PB =PE ，确定P 到BE 的距离，即可写出点P 的坐标．【详解】（1）令x =0，得y =2，∴点B 的坐标为B （0，2）；令y =0，得－212x ＋32x ＋2=0， 解得 121,4,x x =-=∵点A 在x 轴的负半轴；∴A 点的坐标（-1，0）；（2）设C 的坐标为（x ，－212x ＋32x ＋2）， ∵AC ＝BC ，A （-1，0），B （0，2），∴22AC BC =，∵A （-1，0），B （0，2）， ∴2222221313(1)(2)(22)2222x x x x x x ++-++=+-++-， 即2222221313(1)(2)()2222x x x x x x ++-++=+-+， 设t =－212x ＋32x ， ∴2222(1)(2)x t x t +++=+，∴22222144x x t t x t +++++=+，∴2450x t ++=，∴21324()5022x x x +-++=， 整理，得22850x x --=，解得12x x == ∵点C 在y 轴右侧的抛物线上，∴x =，此时y∴点C ）； （3）①如图，根据题意，得∠BPE =90°，PB =PE 即点P 在线段BE 的垂直平分线上，∵B ，E 都在抛物线上，∴B ，E 是对称点，∴点P 在抛物线的对称轴上，点F 在BE 上，且BE ∥x 轴，∵抛物线的对称轴为直线x =32，B （0，2）， ∴点E （3，2），BE =3，∵EF=BO=2，∴BF=1，∴点F的坐标为（1，2）；②如图，设抛物线的对称轴与BE交于点M，交x轴与点N，∵BE=3，∴BM=32，∵∠BPE=90°，PB=PE，∴PM=BM=32，∴PM=BM=32，∴PN=2-32=12，∴点P的坐标为（32，12）．【点睛】本题考查了抛物线与坐标轴的交点，旋转的性质，两点间的距离公式，一元二次方程的解法，换元法解方程，熟练掌握抛物线的对称性，灵活理解旋转的意义，熟练解一元二次方程是解题的关键．2、（1（2）PF=AB-PB或PF=AB+PB，理由见解析【分析】（1）根据△PBD等腰直角三角形，PB＝2，求出DB的长，由⊙O是△PBD的外接圆，∠DBE＝30°，可得答案；（2）根据同弧所对的圆周角，可得∠ADP=∠FBP，由△PBD等腰直角三角形，得∠DPB=∠APD=90°，DP=BP，可证△APD≌△FPB，可得答案．【详解】解：（1）由题意画以下图，连接EP ，∵△PBD 等腰直角三角形，⊙O 是△PBD 的外接圆， ∴∠DPB =∠DEB =90°，∵PB ＝2，∴DB ，∵∠DBE ＝30°，∴1122DE DB ==⨯=（2）①点P 在点A 、B 之间，由（1）的图根据同弧所对的圆周角相等，可得： ∠ADP =∠FBP ，又∵△PBD 等腰直角三角形，∴∠DPB =∠APD =90°，DP =BP ，在△APD 和△FPB 中ADP FBP DP BPDPB APD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△APD ≌△FPB∴AP =FP ，∵AP +PB =AB∴FP +PB =AB ，∴FP =AB -PB ，②点P 在点B 的右侧，如下图：∵△PBD 等腰直角三角形，∴∠DPB =∠APF =90°，DP =BP ，∵∠PBF+∠EBP =180°，∠PDA +∠EBP =180°，∴∠PBF =∠PDA ，在△APD 和△FPB 中DPB APF DP BPPBF PDA ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△APD ≌△FPB∴AP =FP ，∴AB +PB =AP ，∴AB +PB =PF ，∴PF = AB +PB ．综上所述，FP =AB -PB 或PF = AB +PB ．【点睛】本题考查了圆的性质，等腰直角三角形，三角形全等的判定，做题的关键是注意（2）的两种情况． 3、（1）见解析（2）10【分析】（1）作BC 的垂直平分线，与直线CD 的交点即为圆心；（2）连接OA ，根据勾股定理列出方程即可求解．（1）解：如图所示，点O 即是圆心；（2）解：连接OA ，∵CD AB ⊥，并经过圆心O ，12AB =， ∴162AD BD AB ===， ∵2CD =，∴2226(2)OA OA +-=解得，10OA =，答：半径为10．【点睛】本题考查了垂径定理和确定圆心，解题关键是熟练作图确定圆心，利用垂径定理和勾股定理求半径．4、（1）见解析；（2）BC，90°，直径所对的圆周角是直角【分析】（1）过点O任作直线交圆于AB两点，再作AB的垂直平分线OM，直线MO交⊙O于点C，D；连结AC、BC即可；（2）根据线段垂直平分线的判定与性质得出AC=BC，根据圆周角定理得出∠ACB=90°即可．【详解】（1）①作直径AB；②分别以点A, B为圆心，以大于12AB的长为半径作弧，两弧交于M点；③作直线MO交⊙O于点C，D；④连接AC，BC．所以△ABC就是所求的等腰直角三角形.（2）证明：连接MA，MB．∵MA=MB，OA=OB，∴MO是AB的垂直平分线．∴AC=BC．∵AB是直径，∴∠ACB=90°(直径所对的圆周角是直角) ．∴△ABC是等腰直角三角形．故答案为：BC，90°，直径所对的圆周角是直角．【点睛】本题考查尺规作圆内接等腰直角三角形，圆周角定理，线段垂直平分线判定与性质，掌握尺规作圆内接等腰直角三角形，圆周角定理，线段垂直平分线判定与性质是解题关键．5、（1）S△ABC＝20；（2）见解析；（3）见解析．【分析】（1）设⊙O的半径为r，由切线长定理得，AE＝AD＝4，BF＝BD＝5，CE＝CF＝r，由勾股定理得，（r+4）2+（r+5）2＝92，进而求得结果；（2）根据切线长定理可证明甲和乙两个三角形全等，丙丁两个三角形全等，故将甲乙图形放在OE为边的上方，将丙丁以OP为边放在右侧，围成矩形的边长是4和5；（3）可先计算∠AFB＝135°，根据“定弦对定角”作F点的轨迹，根据切线性质，过点F作AB的垂线，再根据直径所对的圆周角是90°，确定点C．【详解】解：（1）如图1，设⊙O的半径为r，连接OE，OF，∵⊙O内切于△ABC，∴OE⊥AC，OF⊥BC，AE＝AD＝4，BF＝BD＝5，∴∠OEC＝∠OFC＝∠C＝90°，∴四边形ECFO 是矩形，∴CF ＝OE ＝r ，CE ＝OF ＝r ，∴AC ＝4+r ，BC ＝5+r ，在Rt△ABC 中，由勾股定理得，（r +4）2+（r +5）2＝92，∴r 2+9r ＝20，∴S △ABC ＝12AC BC ⋅ ＝1(4)(5)2r r +⋅+ ＝21(920)2x r ++ ＝1(2020)2⨯+ ＝20；（2）如图2，（3）设△ABC 的内切圆记作⊙F ，∴AF 和BF 平分∠BAC 和∠ABC ，FD ⊥AB ，∴∠BAF＝12∠CAB，∠ABF＝12ABC∠，∴∠BAF+∠ABF＝12（∠BAC+∠ABC）＝1902⨯︒＝45°，∴∠AFB＝135°，可以按以下步骤作图（如图3）：①以BA为直径作圆，作AB的垂直平分线交圆于点E，②以E为圆心，AE为半径作圆，③过点D作AB的垂线，交圆于F，④连接EF并延长交圆于C，连接AC，BC，则△ABC就是求作的三角形．【点睛】本题考查三角形的内切圆性质、切线长定理、勾股定理、矩形的判定与性质、尺规作图-作垂线，熟练掌握相关知识的联系与运用是解答的关键．。

初中数学二次函数应用题型分类——抛物线形物体问题2（附答案）1．如图，池中心竖直水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（）A．2.1m B．2.2m C．2.3m D．2.25m2．烟花厂某种礼炮的升空高度h（m）与飞行时间t（s）的关系式是h＝﹣2t2+20t+1，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要的时间为（）A．3s B．4s C．5s D．10s3．某建筑物，从10m高的窗口A，用水管向外喷水，喷出的水呈抛物线状（抛物线所在的平面与墙面垂直），如图所示，如果抛物线的最高点M离墙1m，离地面403m，则水流落地点B离墙的距离OB是（）A．2m B．3m C．4m D．5m4．如图，公园中一正方形水池中有一喷泉，喷出的水流呈抛物线状，测得喷出口高出水面0.8m，水流在离喷出口的水平距离1.25m处达到最高，密集的水滴在水面上形成了一个半径为3m的圆，考虑到出水口过高影响美观，水滴落水形成的圆半径过大容易造成水滴外溅到池外，现决定通过降低出水口的高度，使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面（）A．0.55米B．1130米C．1330米D．0.4米5．如图，某幢建筑物从2.25米高的窗口A用水管向外喷水，喷的水流呈抛物线型(抛物线所在平面与墙面垂直)，如果抛物线的最高点M 离墙1米，离地面3米，则水流下落点B 离墙的距离OB 是( )A ．2.5米B ．3米C ．3.5米D ．4米6．广场上水池中的喷头微露水面，喷出的水线呈一条抛物线，水线上水珠的高度y （米）关于水珠和喷头的水平距离x （米）的函数解析式是()236042y x x x =-+≤≤，那么水珠的高度达到最大时，水珠与喷头的水平距离是（ ）A ．1米B ．2米C ．5米D ．6米 7．同学发现在宾馆房间的洗手盘台面上有一瓶洗手液（如图①）．于是好奇的小王同学进行了实地测量研究．当小王用一定的力按住顶部A 下压如图②位置时，洗手液从喷口B 流出，路线近似呈抛物线状，且a ＝﹣118．洗手液瓶子的截面图下部分是矩形CGHD ．小王同学测得：洗手液瓶子的底面直径GH ＝12cm ，喷嘴位置点B 距台面的距离为16cm ，且B 、D 、H 三点共线．小王在距离台面15.5cm 处接洗手液时，手心Q 到直线DH 的水平距离为3cm ，若学校组织学生去南京进行研学实践活动，若小王不去接，则洗手液落在台面的位置距DH 的水平距离是（ ）cm ．A ．3B ．2C ．3D ．2 8．某广场有一喷水池，水从地面喷出，如图，以水平地面为x 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y ＝－x 2＋4x(单位：米)的一部分，则水喷出的最大高度是( )A ．4米B ．3米C ．2米D ．1米9．某公园有一个圆形喷水池，喷出的水流的高度h (单位：m)与水流运动时间t (单位:s)之间的关系式为2305h t t =-，那么水流从喷出至回落到地面所需要的时间是( ) A ．6 s B ．4 s C ．3 s D ．2 s10．某公园一喷水池喷水时水流的路线呈抛物线（如图）．若喷水时水流的高度y （m ）与水平距离x （m ）之间的函数关系式是y=﹣x 2+2x+1.25，则水池在喷水过程中水流的最大高度为（ ）A ．1.25米B ．2.25米C ．2.5米D ．3米11．市政府大楼前广场有一喷水池，水从地面喷出，喷出水的路径是一条抛物线．如果以水平地面为x 轴，建立如图所示的平面直角坐标系，水在空中划出的曲线是抛物线y ＝－x 2＋4x(单位：米)的一部分．则水喷出的最大高度是____米．12．如图，在喷水池的中心A 处竖直安装一个水管AB ，水管的顶端安有一个喷水池，使喷出的抛物线形水柱在与池中心A 的水平距离为1m 处达到最高点C ，高度为3m ，水柱落地点D 离池中心A 处3m ，以水平方向为x 轴，建立平面直角坐标系，若选取A 点为坐标原点时的抛物线的表达式为()()2313034y x x =--+≤≤，则选取点D 为坐标原点时的抛物线表达式为______，水管AB 的长为______m ．13．某市民广场有一个直径16米的圆形喷水池，喷水池的周边有一圈喷水头(喷水头高度忽略不计)，各方向喷出的水柱恰好在喷水池中心的装饰物OA 的顶端A 处汇合，水柱离中心3米处达最高5米，如图所示建立直角坐标系．王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的他站立时必须在离水池中心O________米以内．14．某公园有一个圆形喷水池，喷出的水流呈抛物线，水流的高度h （单位：m ）与水流喷出时间t （单位：s ）之间的关系式为2305h t t =-，那么水流从喷出至回落到水池所需要的时间是__________s ．15．如图，是某公园一圆形喷水池，在池中心竖直安装一根水管OA ＝1.25m ，A 处是喷头，水流在各个方向沿形状相同的抛物线落下，水落地后形成一个圆，圆心为O ，直径为线段CB ．建立如图所示的平面直角坐标系，若水流路线达到最高处时，到x 轴的距离为2.25m ，到y 轴的距离为1m ，则水落地后形成的圆的直径CB ＝_____m ．16．如图，公园里喷水池中的水柱的形状可以看成是抛物线，小明想知道水柱的最大高度，于是画出示意图，并测出了一些数据：水柱上的点C,D 到地面的距离都是1.6米，即 1.6BC OD ==米，1AB =米，5AO =米，则水柱的最大高度是______米.17．消防员的水枪喷出的水流可以用抛物线212y x bx =-+来描述，已知水流的最大高度为20m ，则b 的值为________． 18．某体育公园的圆形喷水池的水柱如图①所示，如果曲线APB 表示落点B 离点O 最远的一条水流(如图②)，其上的水珠的高度y(米)关于水平距离x(米)的函数解析式为y ＝－x 2＋4x ＋94，那么圆形水池的半径至少为_______米时，才能使喷出的水流不落在水池外．19．某广场有一喷水池，水从地面喷出，如图，以水平地面为x 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线是抛物线y ＝﹣x 2+4x （单位：米）的一部分．则水喷出的最大高度是_____米．20．两幢大楼的部分截面及相关数据如图，小明在甲楼A 处透过窗户E 发现乙楼F 处出现火灾，此时A ,E ,F 在同一直线上.跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m 高的D 处喷出，水流正好经过E ,F . 若点B 和点E 、点C 和F 的离地高度分别相同，现消防员将水流抛物线向上平移0.4m ，再向左后退了____m ，恰好把水喷到F 处进行灭火．21．要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷头，使喷出的抛物线形水柱在与水池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离中心3m．（1）在给定的坐标系中画出示意图；（2）求出水管的长度．22．如图1，已知水龙头喷水的初始速度v0可以分解为横向初始速度v x和纵向初始速度v y，θ是水龙头的仰角，且v02=v x2+v y2．图2是一个建在斜坡上的花圃场地的截面示意图，水龙头的喷射点A在山坡的坡顶上（喷射点离地面高度忽略不计），坡顶的铅直高度OA为15米，山坡的坡比为13．离开水龙头后的水（看成点）获得初始速度v0米/秒后的运动路径可以看作是抛物线，点M是运动过程中的某一位置．忽略空气阻力，实验表明：M与A的高度之差d（米）与喷出时间t（秒）的关系为d=v y t-5t2；M与A 的水平距离为v x t米．已知该水流的初始速度v0为15米/秒，水龙头的仰角θ为53°．（1）求水流的横向初始速度v x和纵向初始速度v y；（2）用含t的代数式表示点M的横坐标x和纵坐标y，并求y与x的关系式（不写x 的取值范围）；（3）水流在山坡上的落点C离喷射点A的水平距离是多少米？若要使水流恰好喷射到坡脚B处的小树，在相同仰角下，则需要把喷射点A沿坡面AB方向移动多少米？（参考数据：sin53°≈45，cos53°≈35，tan53°≈43）23．如图，斜坡AB长10米，按图中的直角坐标系可用y=3+5表示，点A，B分别在x轴和y轴上．在坡上的A处有喷灌设备，喷出的水柱呈抛物线形落到B处，抛物线可用y =13-x 2+bx +c 表示．（1）求抛物线的函数关系式（不必写自变量取值范围）；（2）求水柱离坡面AB 的最大高度；（3）在斜坡上距离A 点2米的C 处有一颗3.5米高的树，水柱能否越过这棵树？ 24．游乐园新建的一种新型水上滑道如图，其中线段PA 表示距离水面（x 轴）高度为5m 的平台（点P 在y 轴上）.滑道AB 可以看作反比例函数图象的一部分，滑道BCD 可以看作是二次函数图象的一部分，两滑道的连接点B 为二次函数BCD 的顶点，且点B 到水面的距离2BE m =，点B 到y 轴的距离是5m.当小明从上而下滑到点C 时，与水面的距离3m 2CG =，与点B 的水平距离2m CF =.（1）求反比例函数的关系式及其自变量的取值范围；（2）求整条滑道ABCD 的水平距离；（3）若小明站在平台上相距y 轴1m 的点M 处，用水枪朝正前方向下“扫射”，水枪出水口N 距离平台3m 2，喷出的水流成抛物线形，设这条抛物线的二次项系数为p ，若水流最终落在滑道BCD 上（包括B 、D 两点），直接写出p 的取值范围.25．如图，在喷水池的中心A 处竖直安装一个水管AB ．水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A 的水平距离为1m 处达到最高点C ．高度为3m ．水柱落地点D 离池中心A 处3m ．建立适当的平面直角坐标系，解答下列问题．（1）求水柱所在抛物线的函数解析式；（2）求水管AB 的长．26．某小区有一半径为8m 的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线．在距水池中心3m 处达到最高，高度为5m ，且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合．以水平方向为x 轴，喷水池中心为原点建立如图所示的平面直角坐标系．（1）求水柱所在抛物线对应的函数关系式；（2）王师傅在喷水池维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8m 的王师傅站立时必须在离水池中心多少米以内？27．某地要建造一个圆形喷水池，在水池中央垂直于水面安装一个柱子OA ，点O 恰好在水面中心，安装在柱子顶端A 处的圆形喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA 的任意平面上，水流喷出的高度()y m 与水平距离()x m 之间的关系如图所示，建立平面直角坐标系，右边抛物线的关系式为2y x 2x 3=-++.请完成下列问题：（1）将2y x 2x 3=-++化为()2y a x h k =-+的形式，并写出喷出的水流距水平面的最大高度是多少米；（2）写出左边那条抛物线的表达式；（3）不计其他因素，若要使喷出的水流落在池内，水池的直径至少要多少米？ 28．现代城市绿化带在不断扩大，绿化用水的节约是一个非常重要的问题．如图1、图2所示，某喷灌设备由一根高度为0.64 m 的水管和一个旋转喷头组成，水管竖直安装在绿化带地面上，旋转喷头安装在水管顶部（水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计），旋转喷头可以向周围喷出多种抛物线形水柱，从而在绿化带上喷灌出一块圆形区域．现测得喷的最远的水柱在距离水管的水平距离3 m 处达到最高，高度为1 m ．（1）求喷灌出的圆形区域的半径；（2）在边长为16 m 的正方形绿化带上固定安装三个该设备，喷灌区域可以完全覆盖该绿化带吗？如果可以，请说明理由；如果不可以，假设水管可以上下调整高度，求水管高度为多少时，喷灌区域恰好可以完全覆盖该绿化带．（以上需要画出示意图，并有必要的计算、推理过程）29．某广场喷泉的喷嘴安装在平地上．有一喷嘴喷出的水流呈抛物线状，喷出的水流高度y （m ）与喷出水流喷嘴的水平距离x （m ）之间满足2122y x x =-+ （l ）喷嘴能喷出水流的最大高度是多少？（2）喷嘴喷出水流的最远距离为多少？30．图1是一个倾斜角为α的斜坡的横截面，1tan 2α=．斜坡顶端B 与地面的距离BC 为3米．为了对这个斜坡上的绿地进行喷灌，在斜坡底端安装了一个喷头A ，喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分．设喷出水珠的竖直高度为y （单位：米）（水珠的竖直高度是指水珠与地面的距离），水珠与喷头A 的水平距离为x （单位：米），y 与x 之间近似满足函数关系2y ax bx =+（a ，b 是常数，0a ≠），图2记录了x 与y 的相关数据．（1）求y关于x的函数关系式；（2）斜坡上有一棵高1.8米的树，它与喷头A的水平距离为2米，通过计算判断从A 喷出的水珠能否越过这棵树．参考答案1．D【解析】【分析】设抛物线的解析式为y= a(x-1)2+3(0≤x≤3)，将(3，0)代入求得a值，则x=0时得的y值即为水管的长．【详解】解：由于在距池中心的水平距离为1m时达到最高，高度为3m，则设抛物线的解析式为：y=a(x-1)2+3(0≤x≤3)，代入(3，0)得，0=a×(3-1)2+3，求得：a=34．将a值代入得到抛物线的解析式为：y=-34(x-1)2+3(0≤x≤3)，令x=0，则y=94=2.25．则水管长为2.25m，故选：D．【点睛】本题考查了二次函数在实际生活中的运用，重点是二次函数解析式的求法，利用顶点式求出解析式是解题关键．2．C【解析】【分析】将h关于t的函数关系式变形为顶点式，即可得出升到最高点的时间，从而得出结论．【详解】解：∵h＝﹣2t2+20t+1＝﹣2（t﹣5）2+51，∴当t＝5时，礼炮升到最高点．故选：C．【点睛】本题考查了二次函数的应用，解题的关键是将二次函数的关系式变形为顶点式．本题属于基础题，难度不大，解决该题型题目时，将函数的关系式进行变换找出顶点坐标即可．3．B【解析】【分析】以OB为x轴，OA为y轴建立平面直角坐标系，A点坐标为（0，10），M点的坐标为（1，403），设出抛物线的解析式，代入解答球的函数解析式，进一步求得问题的解．【详解】解：设抛物线的解析式为y＝a(x﹣1)2+403，把点A（0，10）代入a(x﹣1)2+403，得a(0﹣1)2+403＝10，解得a＝﹣103，因此抛物线解析式为y＝﹣103(x﹣1)2+403，当y＝0时，解得x1＝3，x2＝﹣1（不合题意，舍去）；即OB＝3米．故选B．【点睛】本题是一道二次函数的综合试题，考查了利用待定系数法求函数的解析式的运用，运用抛物线的解析式解决实际问题．解答本题是时设抛物线的顶点式求解析式是关键．4．B【解析】【分析】如图，以O为原点，建立平面直角坐标系，由题意得到对称轴为x＝1.25＝54，A（0，0.8），C（3，0），列方程组求得函数解析式，即可得到结论．【详解】解：如图，以O为原点，建立平面直角坐标系，由题意得，对称轴为x＝1.25＝54，A（0，0.8），C（3，0），设解析式为y＝ax2+bx+c，∴9305240.8a b cbac++=⎧⎪⎪-=⎨⎪=⎪⎩，解得：8154345abc⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩，所以解析式为：y＝815-x2+43x+45，当x＝2.75时，y＝13 30，∴使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面08﹣1330＝1130，故选：B．【点睛】本题考查了二次函数的实际应用，根据题意建立合适的坐标系，找到点的坐标，用待定系数法解出函数解析式是解题的关键5．B【解析】【分析】由题意可以知道M（1，3），A（0，2.25），用待定系数法就可以求出抛物线的解析式，当y=0时就可以求出x的值，这样就可以求出OB的值．【详解】解：设抛物线的解析式为y=a（x-1）2+3，把A（0，2.25）代入，得2.25=a+3，a=-0.75．∴抛物线的解析式为：y=-0.75（x-1）2+3．当y=0时，0=-0.75（x-1）2+3，解得：x1=-1（舍去），x2=3．OB=3米．故选：B．【点睛】本题是一道二次函数的综合试题，考查了利用待定系数法求函数的解析式的运用，运用抛物线的解析式解决实际问题，解答本题是求出抛物线的解析式．6．B【解析】【分析】先把函数关系式配方，即可求出函数取最大值时自变量的值．【详解】解：∵y=-32x2+6x=-32（x2-4x）=-32[（x-2）2-4]=-32（x-2）2+6，∴当x=2时，y有最大值，∴水珠的高度达到最大时，水珠与喷头的水平距离是2．故选B．【点睛】本题考查了二次函数的实际应用，关键是把二次函数变形，求出当函数取最大值时自变量的值，此题为数学建模题，借助二次函数解决实际问题．7．B【解析】【分析】根据题意得出各点坐标，利用待定系数法求抛物线解析式进而求解．【详解】解：如图：根据题意，得Q （9，15.5），B （6，16），OH ＝6，设抛物线解析式为y ＝﹣118x 2+bx +c ， 12×81915.5,,183114.×36616,18b c b c b c ⎧-++=⎧⎪=⎪⎪⎨⎨⎪⎪=-++=⎩⎪⎩解得， 所以抛物线解析式为y ＝﹣118x 2+23x +14． 当y ＝0时，即0＝﹣118x 2+23x +14， 解得：x ＝2（负值舍去），又OH=6， 所以洗手液落在台面的位置距DH 的水平距离是2cm ．故选：B ．【点睛】本题考查了二次函数的应用，解决本题的关键是明确待定系数法求二次函数的解析式及准确进行计算．8．A【解析】）∵y=－x 2＋4x=2x-24-+（），∴当x=2时，y 有最大值4，∴最大高度为4m9．A【解析】由于水流从抛出至回落到地面时高度h 为0，把h =0代入h =30t -5t 2即可求出t ，也就求出了水流从抛出至回落到地面所需要的时间．解：水流从抛出至回落到地面时高度h 为0，把h =0代入h =30t −5t 2得：5t 2−30t =0，解得：t 1=0(舍去),t 2=6.故水流从抛出至回落到地面所需要的时间6s.故选A.10．B【解析】试题分析：直接利用二次函数解析式得出水流离地面的最大高度．解：∵y=﹣x 2+2x+1.25=﹣（x ﹣1）2+2.25，∴水池在喷水过程中水流的最大高度为2.25米．故选B ．考点：二次函数的应用．11．4【解析】【分析】根据题意可以得到喷水的最大高度就是水在空中划出的抛物线24y x x =-+的顶点坐标的纵坐标，利用配方法或公式法求得其顶点坐标的纵坐标即为本题的答案.【详解】水在空中划出的曲线是抛物线24y x x =-+， ∴喷水的最大高度就是水在空中划出的抛物线24y x x =-+的顶点坐标的纵坐标， ∴()22424y x x x =-+=--+，∴顶点坐标为：()2,4， ∴喷水的最大高度为4米.故答案为：4.【点睛】本题考查了二次函数的应用，解决此类问题的关键是从实际问题中整理出函数模型，利用函数的知识解决实际问题.12．()()2323304y x x =-++-≤≤ 2.25． 【解析】【分析】直接利用二次函数的平移规律进而得出答案，再由题意可得，3x =-时得到的y 值即为水管的长．【详解】以喷水池中心A 为原点，竖直安装的水管为y 轴，与水管垂直的为x 轴建立直角坐标系． 抛物线的解析式为：()23134y x =--+， 当选取点D 为坐标原点时，相当于将原图象向左平移3个单位， 故平移后的抛物线表达式为：()()2323304y x x =-++-≤≤； 令3x =-，则33 2.254y =-+=． 故水管AB 的长为2.25m ． 故答案为：()()2323304y x x =-++-≤≤；2.25． 【点睛】本题考查了二次函数在实际生活中的运用，重点是二次函数解析式的求法，直接利用二次函数的平移性质是解题关键．13．7【解析】【分析】根据顶点坐标可设二次函数的顶点式，代入点（8，0），求出a 值，求出函数解析式，利用二次函数图象上点的坐标特征，求出当y=1.8时x 的值，由此即可得出结论；【详解】设水柱所在抛物线（第一象限部分）的函数表达式为y=a （x －3）2+5（a≠0），将（8，0）代入y=a （x －3）2+5，得：25a+5=0，解得：a=－15，∴水柱所在抛物线（第一象限部分）的函数表达式为y=－15（x－3）2+5（0＜x＜8）．当y=1.8时，有－15（x－3）2+5=1.8，解得：x1=－1（舍去），x2=7，∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心7米以内．故答案为：7【点睛】本题考查了待定系数法求二次函数解析式以及二次函数图象上点的坐标特征，解题的关键是：根据点的坐标，用利用待定系数法求出二次函数表达式并利用二次函数图象上点的坐标特征求出当y=1.8时x的值．14．6【解析】【分析】由于水流从抛出至回落到地面时高度h为0，把h=0代入h=30t-5t2即可求出t，也就求出了水流从抛出至回落到地面所需要的时间．【详解】水流从抛出至回落到地面时高度h为0，把h=0代入h=30t-5t2得：5t2-30t=0，解得：t1=0（舍去），t2=6．故水流从抛出至回落到地面所需要的时间6s．故答案为：6【点睛】本题考查的是二次函数在实际生活中的应用，关键是正确理解题意，利用函数解决问题，结合实际判断所得出的解．15．5【解析】【分析】设y轴右侧的抛物线解析式为：y＝a（x−1）2＋2.25，将A（0，1.25）代入，求得a，从而可得抛物线的解析式，再令函数值为0，解方程可得点B 坐标，从而可得CB 的长．【详解】解：设y 轴右侧的抛物线解析式为：y ＝a （x ﹣1）2+2.25∵点A （0，1.25）在抛物线上∴1.25＝a （0﹣1）2+2.25解得：a ＝﹣1∴抛物线的解析式为：y ＝﹣（x ﹣1）2+2.25令y ＝0得：0＝﹣（x ﹣1）2+2.25解得：x ＝2.5或x ＝﹣0.5（舍去）∴点B 坐标为（﹣2.5，0）∴OB ＝OC ＝2.5∴CB ＝5故答案为：5．【点睛】本题考查了二次函数在实际问题中的应用，明确二次函数的相关性质及正确的解方程，是解题的关键．16．7225【解析】【分析】设解析式为2y ax bx c =++，由题意可知点D 为（0，1.6），点C 为（4，1.6），点A 为（5，0），代入后得到三元一次方程组，解方程组即可求出抛物线解析式，再求顶点坐标即可．【详解】解：设解析式为2y ax bx c =++，由题意可知点D 为（0，1.6），点C 为（4，1.6），点A 为（5，0）， ∴ 1.6164 1.62550c a b c a b c =⎧⎪++=⎨⎪++=⎩，解得825322585a b c ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩， ∴解析式为：2832825255y x x =-++， ∴当3225282()25x =-=⨯-时，y 有最大值为7225. ∴水柱的最大高度是7225米. 【点睛】此题主要考查了二次函数的应用，用待定系数法求出二次函数的解析式是解题关键． 17．±【解析】【分析】利用二次函数的性质列出关于b 的方程，求出方程的解即可得到b 的值．【详解】解：抛物线y =12-x 2+bx ， 根据题意得： 2b a - =122b -⎛⎫⨯- ⎪⎝⎭=b ，当x =b 时，取得最大值为20，21202b b b -+=， 12b 2=20， b =±． 故答案为：b =±． 【点睛】本题主要考查了二次函数的应用，解决本题的关键是要熟练掌握二次函数的性质． 18．92【解析】【详解】当y=0时，即-x2+4x+94=0，解得x1=92，x2=-12（舍去）．答：水池的半径至少92米时，才能使喷出的水流不落在水池外．故答案是：92．19．4米【解析】【分析】根据题意可以得到喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标，利用配方法或公式法求得其顶点坐标的纵坐标即为本题的答案．【详解】解：∵水在空中划出的曲线是抛物线y=﹣x2+4x，∴喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标，∴y=﹣x2+4x=﹣（x﹣2）2+4，∴顶点坐标为：（2，4），∴喷水的最大高度为4米，故选A．【点睛】考点：二次函数的应用．理解二次函数性质是关键.2010【解析】设直线AE的解析式为:y=kx+21.2.把E（20,9.2）代入得，20k+21.2=9.2,∴k=-0.6,∴y =-0.6x +21.2. 把y =6.2代入得， -0.6x +21.2=6.2， ∴x =25, ∴F (25,6.2).设抛物线解析式为：y=ax 2+bx +1.2, 把E （20,9.2）, F (25,6.2)代入得，40020 1.29.262525 1.2 6.2a b a b ++=⎧⎨++=⎩解之得0.041.2a b =-⎧⎨=⎩ ， ∴y =-0.04x 2+1.2x +1.2，设向上平移0.4m ，向左后退了h m, 恰好把水喷到F 处进行灭火由题意得 y =-0.04(x +h )2+1.2(x+h )+1.2+0.4, 把F (25,6.2)代入得，6.2=-0.04×(25+h )2+1.2(25+h )+1.2+0.4， 整理得 h 2+20h -10=0, 解之得110x =-,210x =-（舍去）.∴向后退了10)m点睛：本题考查了二次函数和一次函数的实际应用，设直线AE 的解析式为:y =kx +21.2. 把E （20,9.2）代入求出直线解析式，从而求出点F 的坐标.把E （20,9.2）, F (25,6.2)代入y=ax 2+bx +1.2求出二次函数解析式.设向左平移了h m ，表示出平移后的解析式，把点F 的坐标代入可求出k 的值.21．（1）详见解析；（2）水管长为2.25m ． 【解析】 【分析】（1）以池中心为原点，竖直安装的水管为y 轴，与水管垂直的为x 轴建立直角坐标系； （2）设抛物线的解析式为y ＝a （x ﹣1）2+3（0≤x ≤3），将（3，0）代入求得a 值，则x ＝0时得的y 值即为水管的长． 【详解】解：（1）建立以池中心为原点，竖直安装的水管为y 轴，与水管垂直的为x 轴建立直角坐标系；（2）由于在距池中心的水平距离为1m 时达到最高，高度为3m ， 则设抛物线的解析式为： y ＝a （x ﹣1）2+3（0≤x ≤3）， 代入（3，0）求得：a ＝﹣34． 将a 值代入得到抛物线的解析式为： y ＝﹣34（x ﹣1）2+3（0≤x ≤3）， 令x ＝0，则y ＝94＝2.25． 故水管长为2.25m ．【点睛】此题主要考查二次函数的应用，解题的关键是根据图形建立合适的直角坐标系. 22．（1）水流的横向初始速度v x 是9米/秒，纵向初始速度v y 是12米/秒；（2）y=-2581x +43x+15；（3）水流在山坡上的落点C 离喷射点A 的水平距离是27米，需要把喷射点A 沿坡面AB 方向移动610 【解析】【分析】（1）根据题意利用θ的正弦和余弦定义可得结论；（2）由（1）的表示出v x 表示出x ，OA 已知，利用y=d+OA ，代入OA 的值和d 与t 的函数关系式，可以得解；（3）先求得点A 和点B 的坐标，进而写出其直线解析式，再将其与（2）中抛物线解析式联立，从而求得落点C 的坐标，再利用平移知识及勾股定理可以求解． 【详解】解：（1）∵v 0为15米/秒，水龙头的仰角θ为53°，∴cosθ=0xv v ，sinθ=0y v v ，∴v x =15cos53°=15×35=9，v y =15sin53°=15×45=12；答：水流的横向初始速度v x 是9米/秒，纵向初始速度v y 是12米/秒； （2）x=v x t=9t ， ∴t=9x ， 又M 与A 的高度之差d （米）与喷出时间t （秒）的关系为d=v y t-5t 2∴y=d+OA=12t-5t 2+15=-5×2()9x +12×9x +15=-2581x +43x+15；∴y 与x 的关系式为：y=-2581x +43x+15．（3）∵坡顶的铅直高度OA 为15米，山坡的坡比为13，∴OB=45米，点A （0，15）点B （45，0）∴直线AB 的解析式为：y=13x -+15，将其与抛物线解析式联立得：254158131153y x x y x ⎧=-++⎪⎪⎨⎪=-+⎪⎩， 解得015x y =⎧⎨=⎩（舍）或276x y =⎧⎨=⎩，∴水流在山坡上的落点C 坐标为（27，6），喷射点A 沿坡面AB 方向移动的距离等于BC 的距离，而答：水流在山坡上的落点C 离喷射点A 的水平距离是27米，需要把喷射点A 沿坡面AB 方向移动 【点睛】本题考查了二次函数的应用以及坡度问题和解直角三角形的应用等知识，正确构造出直角三角形是解题关键． 23．（1）y =-13x 2+3x +5；（2）当x=2时，水柱离坡面的距离最大，最大距离为254；（3）水柱能越过树，理由见解析 【解析】 【分析】（1）根据题意先求出A,B 的坐标，再把其代入解析式即可 （2）由（1）即可解答（3）过点C 作CD ⊥OA 于点D ，求出ODOD 代入解析式即可 【详解】（1）∵AB =10、∠OAB =30°， ∴OB =12AB =5、OA则A （0）、B （0，5），将A 、B 坐标代入y =-13x 2+bx +c，得：175035c c ⎧-⨯++=⎪⎨⎪=⎩，解得：5b c ⎧=⎪⎨⎪=⎩，∴抛物线解析式为y =-13x 2+5； （2）水柱离坡面的距离d =-13x 2+3x +5-（-3x +5）=-13x 2+533x =-13（x 2-53x ） =-13（x -532）2+254， ∴当x =532时，水柱离坡面的距离最大，最大距离为254； （3）如图，过点C 作CD ⊥OA 于点D ，∵AC =2、∠OAB =30°， ∴CD =1、AD 3 则OD 3， 当x 3时，y =-13×（32+33×3＞1+3.5， 所以水柱能越过树． 【点睛】此题考查二次函数的应用，解题关键在于求出A,B 的坐标 24．（1）10y x=，25x ≤≤；（2）7m ；（3）91332128p -≤≤-. 【解析】 【分析】（1）在题中，BE=2，B 到y 轴的距离是5，即反比例函数图象上一点的横坐标和纵坐标都已告知，则可求出比例系数k ；（2）根据B ，C 的坐标求出二次函数解析式，得到点D 坐标，即OD 长度再减去AP 长度，可得滑道ABCD 的水平距离；（3）由题意可知点N 为抛物线的顶点，设水流所成抛物线的表达式为213(1)2y p x =-+，通过计算水流分别落到点B 和点D 可以得出p 的取值范围.。

拔高专题抛物线与圆的综合二、拔高精讲精练探究点一：抛物线、圆和直线相切的问题例1: 如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x 轴相交于A，B两点．（1）则点A，B，C的坐标分别是A（2，0），B（8，0），C （0，4）；（2）设经过A，B两点的抛物线解析式为y=14（x-5）2+k，它的顶点为E，求证：直线EA与⊙M相切；（3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形？如果存在，请求出点P的坐标；如果不存在，请说明理由．（1）解：连接MC、MA，如图1所示：∵⊙M与y轴相切于点C，∴MC⊥y轴，∵M（5，4），∴MC=MA=5，OC=MD=4，∴C（0，4），∵MD⊥AB，∴DA=DB，∠MDA=90°，∴=3，∴BD=3，∴OA=5-3=2，OB=5+3=8，∴A（2，0），B（8，0）；（2）证明：把点A（2，0）代入抛物线y=14（x-5）2+k，得：k=-94，∴E（5，-94），∴DE=94，∴ME=MD+DE=4+94=254，EA2=32+（94）2=22516，∵MA2+EA2=52+22516=22516，ME2=225 16，∴MA2+EA2=ME2，∴∠MAE=90°，即EA⊥MA，∴EA与⊙M相切；（3）解：存在；点P坐标为（5，4），或（5，或（5，；理由如下：由勾股定理得：PB=PC时，点P 在BC的垂直平分线上，点P与M重合，∴P（5，4）；②当如图2所示：∵，∴P（5）；③当PC=BC=4时，连接MC，如图3所示：则∠PMC=90°，根据勾股定理得：∴P（5，；综上所述：存在点P，且点P在x轴的上方，使△PBC是等腰三角形，点P的坐标为（5，4），或（5），或（5，．【变式训练】如图，已知抛物线y=-12（x2-7x+6）的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．（1）用配方法将抛物线的解析式化为顶点式：y=a（x-h）2+k（a≠0），并指出顶点M的坐标；（2）在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；（3）以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N 的切线．（1）解：∵y=-12（x2-7x+6）=-12（x2-7x）-3=-12（x-72）2+258，∴抛物线的解析式化为顶点式为：y=-12（x-72）2+258，顶点M的坐标是（72，258）；（2）解：∵y=-12（x2-7x+6），∴当y=0时，-12（x2-7x+6）=0，解得x=1或6，∴A（1，0），B（6，0），∵x=0时，y=-3，∴C（0，-3）．连接BC，则BC与对称轴x=72的交点为R，连接AR，则CR+AR=CR+BR=BC，根据两点之间线段最短可知此时CR+AR的值最小，最小值为BC的解析式为y=kx+b，∵B（6，0），C（0，-3），∴603k bb⎨⎩+-⎧＝＝，解得231kb-⎧⎪⎨⎪⎩＝＝，∴直线BC的解析式为：y=12x-3，令x=72，得y=12×7 2-3=-54，∴R点坐标为（72，-54）；（3）证明：设点P坐标为（x，-12x2+72x-3）．∵A（1，0），B（6，0），∴N（72，0），∴以AB为直径的⊙N的半径为12AB=52，∴NP=52，即（x-72）2+（-12x2+72x-3）2=（52）2，化简整理得，x4-14x3+65x2-112x+60=0，（x-1）（x-2）（x-5）（x-6）=0，解得x1=1（与A 重合，舍去），x2=2，x3=5（在对称轴的右侧，舍去），x4=6（与B重合，舍去），∴点P坐标为（2，2）．∵M（72，258），N（72，0），∴PM2=（2-72）2+（2-258）2=22564，PN2=（2-72）2+22=254=40064，MN2=（258）2=62564，∴PM2+PN2=MN2，∴∠MPN=90°，∵点P在⊙N上，∴直线MP是⊙N的切线．。