高数第三章第三次泰勒公式
- 格式:ppt
- 大小:768.50 KB
- 文档页数:43


泰勒公式与三阶泰勒公式(TaylorFormula)是数学中一种使用级数计算函数值的方法,由英国数学家蒂姆泰勒于1715年发现。
泰勒公式的形式为由n项的级数展开构成的公式,它可用于计算函数在某一点的值,以及函数在某一点的极限。
泰勒公式有无限项,但实际应用中只需要计算有限多个项即可。
具体取几项,取决于计算的精度要求。
当取到第三项时,可以构成三阶(third order)的泰勒公式。
三阶泰勒公式的标准形式是:f(x)=f(x_0)+f(x_0)(x-x_0)+frac{1}{2!}f(x_0)(x-x_0)^2+frac{1 }{3!}f(x_0)(x-x_0)^3+…其中x_0是函数f(x)的一点,f(x_0)表示f(x)的导数在点x_0的值,f’(x_0)表示f(x)的二阶导数在点x_0的值,f’’’(x_0)表示f(x)的三阶导数在点x_0的值。
三阶泰勒公式在实际应用中可以用来计算复杂函数的极限和值。
它是数值分析中一种常用的有限差分(finite difference)方法,广泛应用于工程中。
在数学研究中,三阶泰勒公式用来计算函数的变化趋势,主要有两种用法:一是用来估计函数的局部极大值、极小值;二是用来估计函数的极限值。
首先,可以判断f(x_0)的正负,从而进一步确定函数在点x_0附近是极大值还是极小值。
首先,如果f(x_0)>0,则说明函数在x_0附近是增加的,即f(x)是极小值;反之,如果f(x_0)<0,则说明函数在x_0附近是减少的,即f(x)是极大值。
再以f(x_0)判断,如果f(x_0)>0,则f(x_0)>0;如果f(x_0)<0,则f(x_0)<0。
其次,可以用三阶泰勒公式估计函数的极限值。
如果函数f(x)在点x_0附近是可导的,并且f(x_0)和f(x_0)的绝对值越来越小,那么函数在点x_0附近的极限值就可以用三阶泰勒公式估计出来,因此可以用三阶泰勒公式估计函数在某一点的极限值。



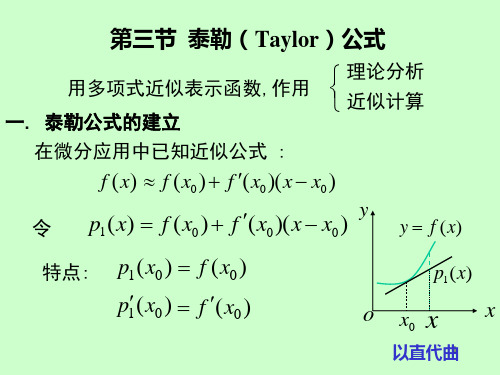
笫三节泰勒公式对于一些比较复杂的两数,为了便于研究,往往希望用一些简单的函数來近似表达.多项 式函数是最为简单的一类函数,它只要对自变量进行有限次的加、减、乘三种算术运算,就能 求出其函数值,因此,多项式经常被用于近似地表达函数,这种近似表达在数学上常称为逼近. 英国数学家泰勒(Taylor. Brook, 1685-1731)在这方面作出了不朽的贡献.其研究结果表明: 具有直到n + 1阶导数的函数在一个点的邻域内的值可以用函数在该点的函数值及各阶导数 值组成的n 次多项式近似表达.本节我们将介绍泰勒公式及其简单应用.分布图示★引言 ★多项式逼近 ★泰勒中值定理★例1★常用函数的麦克劳林公式★例5 ★内容小结 ★习题3・3 ★返回 内容要点问题:设函数/(X )在含有勺的开区间(Q,历内具有直到八+ 1阶导数,问是否存在一个77 次多项式函数/2/J (X )= 6f 0+a 1(X-X O ) + «2(X-X O )2 ++ (3.1)使得 且误差R n M = fM-PnM 是比勺)”高阶的无穷小,并给出误差估计的具体表达式.泰勒中值公式fM = /(勺)+ /©0)(兀一勺)+ / 即)(X-勺尸 + …+ —―(X-x ())" + R n (x) (3.3) 2! tv.拉格朗日型余项 心(兀)=广刊忆)(兀一兀()严 (3.4) (/? + 1)!皮亚诺形式余项R n (x) = o[(x -x ()r 1. (3.6) 带有皮亚诺型余项的麦克劳林公式/(X) = /(0) + /z (0)x + /+... + 2^21 疋 + 0(0) (3.9)2! iv. ★例2★例6★课堂练习 (3.2)例题选讲直接展开法例1写出函数/(x) = x 3lnx 在斗)=1处的四阶泰勒公式.解 /(x) = x 3lnx, /(I) = 0,0 = 1 + 1 + 丄+ ••• + 丄, 2! nl其误差从公式(3.11)或(3.⑵可得近似公式心"0) +门0)’+警宀…+畔疋 2!m 误差估计式(3.8)相应变成 I^WI< M S + 1)! I 兀I" (3.13)(3.⑷间.f\x)3x 2 lnx + ^2,/*(x)6xlnx + 5x,/"(x)61nx +11,/%)」,X/⑸(兀)=—2, 兀一 r (i )=u 厂⑴=5, r (i )=n, /⑷(1) = 6, 严)©=-于是小心(-1) +詁-1)2 +牛-1)3 +扣"-召(兀-1P,其中§在1与兀之 例2 (E01)求f(x) = e v 的n 阶麦克劳林公式.解•・• fXx)=f \x)=^=f (n \x)=e x ,••・ /(0)=/z (0)=r (0)=... =/°°(0) =1,注意到/(”"(%) =严代入泰勒公式,得 //+! =l + x + —+ ••• + —+ ——厂 (0<6><1), 2! nl (川+1)!由公式可知e v ~ 1 + X + — + • •・ + 2!其误差=x z,+1 < -------- X(n + 1)! (斤 + 1)!取兀=1,得 /?! 曲(0<6><1)例3 (E02)求/(x) = sinx的//阶麦克劳林公式.解f\x) = cosx,= -sinx, /^(x) = -cosx, /(4>(x) = sinx,P(n\z、• |n 兀'...... , f (x) = sin x + —,\ /丿由此得厂(0) = 1,厂(0) = 0, r(0) = -l,严(0) = 0,……,sinx的各阶导数依序循环地取四个数0,1,0,-1,令n = 2m,则+尺2加⑴,其中sin 6r + (2/72 + 1)—(兀)=― ----------- 兀加+】(ov&vi).取加= 1,2,3的近似函数与原函数图像比较.(2加 + 1)!常用初等函数的麦克劳林公式:e x =1 + 兀 + — + ・・・ + — + x2! nl (n + 1)!ln(l + x) = x ——+ -------- + (—1)〃——+。
§3.3 泰勒公式教学内容:一.泰勒中值定理1.定理:(泰勒中值定理) 如果()f x 在含有0x 的某(,)a b 内具有直到1n +阶导数,则对任意(,)x a b ∈,有()20000000()()()()()()()()()2!!n n n f x f x f x f x f x x x x x x x R x n '''=+-+-++-+,(1)10()()()(1)!n n n f R x x x n ξ++=-+,其中ξ介于0x 与x 之间.2. 泰勒多项式:n 次多项式()20000000()()()()()()()()2!!n n n f x f x p x f x f x x x x x x x n '''=+-+-++-称为函数()f x 在0x 处的n 阶泰勒多项式,其系数()0()(0,1,2,)!k k f x a k n n ==称为()f x 在0x 处泰勒系数.3.泰勒中值定理是拉格朗日中值定理的推广.4.称()200000000()()()()()()()()[()]2!!n n n f x f x f x f x f x x x x x x x o x x n '''=+-+-++-+-为n 阶带有佩亚诺型余项的泰勒公式.二.麦克劳林公式1.定理:如果函数()f x 在含有0=x 的某个开区间(,)a b 内具有直到1n +阶的导数,则对任意(,)x a b ∈,称()(1)21(0)(0)()()(0)(0)(01)2!!(1)!n n n n f f f x f x f f x x x x n n θθ++'''=+++++<<+为函数()f x 的n 阶带有拉格朗日型余项的麦克劳林公式 .2.带有佩亚诺型余项的n 阶麦克劳林公式为()2(0)(0)()(0)(0)()2!!n n n f f f x f f x x x o x n '''=+++++.三.几个重要初等函数的麦克劳林公式例1.求函数()e xf x =的n 阶麦克劳林公式.例2.求函数()sin f x x =的n 阶麦克劳林公式.另外几个常用函数的麦克劳林公式:(1)242121cos 1(1)()2!4!(2)!mm m x x x x R x m -+=-+-+-+,其中 []2212221cos (1)πcos ()(1)(01)(22)!(22)!m m m m x m x R x x x m m θθθ++++++==-<<++.(2)231ln(1)(1)()23nn n x x x x x R x n-+=-+-+-+,其中11(1)()(01)(1)(1)n n n n R x x n x θθ++-=<<++. (3)2(1)(1)(1)(1)1()2!!n n n x x x x R x n ααααααα---++=+++++,其中11(1)(1)()()(1)(01)(1)!n n n n n R x x x n αααααθθ--+--+-=+<<+;(4)2311(1)()1nnn x x x x R x x=-+-++-++,其中,1x ≠-,112(1)()(01)(1)n n n n R x x x θθ+++-=<<+.四.泰勒公式的应用1.泰勒公式间接展开法:利用已知函数的麦克劳林公式,可以间接的写出某些复杂函数的泰勒公式或麦克劳林公式.2.利用泰勒公式求极限:带有佩亚诺型余项的麦克劳林公式应用于求极限运算中,可以简化运算,它是求某些未定式极限的重要工具.3.求高阶导数值:若函数()f x 在点0x 处的泰勒公式可以使用间接展开法得到,则根据泰勒公式的唯一性,可以确定函数()f x 在点0x 处的各阶导数值.4.近似计算.五.例题讲解例3.求函数()e x f x x -=的带有佩亚诺型余项的n 阶麦克劳林公式.例4.求函数1()3f x x=+在1x =处的带有佩亚诺型余项的n 阶泰勒公式.例5.求极限240e 2cos 3lim →+-x x x x .例6.设2()sin =f x x x ,试求(99)(0)f.例7.求无理数e 的近似值,使误差不超过610-.。