第三章理想流动均相反应器设计题解

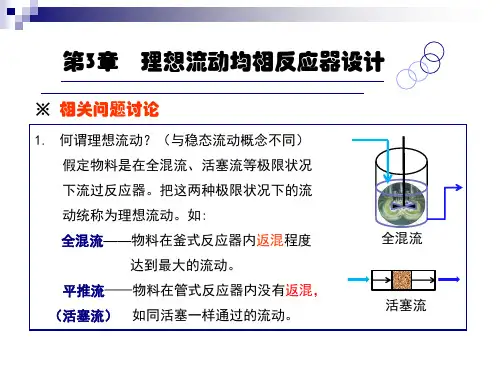
第三章非理想流动一、主要基本理论、基本概念1.停留时间：物料质点从进入反应器开始，到离开为止，在反应器中总共停留的时间。

2.平均停留时间：整个物料在反应器内平均停留的时间。

3.停留时间分布密度函数E(t)同时进入反应器的N 个流体质点中，停留时间介于t 与t+dt 之间的质点所占的分率dN/N 为E(t)dt 。

1)(0=⎰∞dt t E4.停留时间分布函数F(t)流过反应器的物料中停留时间小于t 的质点(或停留时间介于0～t 之间的质点)分率。

⎰=tdt t E t F 0)()(5.停留时间分布的数字特征 ① 数 学期 望 t =⎰⎰∞∞0)()(dtt E dt t tE② 方 差2t σ=⎰⎰∞∞-02)()()(dtt E dtt E t t③ 无因次方差22//t tt t θσσθ==6.停留时间分布的实验方法及对应曲线 ① 脉冲示踪 E(t) 曲线 ② 阶跃示踪 F(t) 曲线 ③ 无因次化 /()()()()t tE tE tF F t θθθ===7.理想流动模型的停留时间分布① 平推流 001()()1t t E t E t t θθθ≠≠⎧⎧==⎨⎨∞=∞=⎩⎩ 001()()111t t F t F t tθθθ〈〈⎧⎧==⎨⎨≥≥⎩⎩2210t t θτθσσ====② 全混流 ()1/exp(/)()E t t t t E e θθ-=-=()1exp(/)()1F t t t F e θθ-=--=-2/1t t tθτθσ===8.非理想流动模型的停留时间分布①扩散模型：是在平推流模型的基础上再迭加一个轴向扩散的校正，模型参数是轴向扩散系数Ｄl （或P e 数），停留时间分布可表示为Ｄl 的函数。

适用于返混不大的系统。

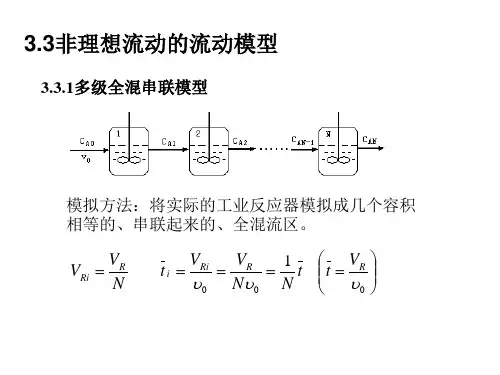
Pe >100时: θ=1 22/2/t t Pe θσσ==闭 式: θ=1222/2/(1)Pe Pe Pe e θσ-=--②多级串联全混流模型：是用m 个等体积的全混流模型串联来模拟实际反应器。

第三章理想均相反应器设计本章核心内容：从间歇釜反应器、稳态全混流反应器和平推流管式反应器这三种理想反应器的结构和流动特性出发，给出了它们数学模型的建立方法、不同反应过程中的反应体积设计公式和热量计算式以及具体的应用实例。

对这三种理想反应器性能进行了比较，特别是对稳态全混流反应器和平推流管式反应器及其组合内容进行了详细叙述。

针对不同反应过程讲述了优化设计方法。

化学反应工程学的主要目的是设计不同型式和大小的反应器，实现最佳的操作与控制，取得最佳的经济效益。

在用数学模型法来设计放大反应器的过程中，首先要了解进行化学反应的动力学特征、反应物的性质、产物的性质与分布，才能进行反应器的选型、操作方式的选择，进而进行反应器设计和计算。

由于生产中的化学反应器都很大，都或大或小存在着温度的差异和浓度的差异，都存在着动力消耗和反应器的各种结构的差异，对于实际生产中的化学反应过程一般很难做到反应物的温度、压力和流速完全均一，即非理想化。

这些差异给实际反应器的设计和放大带来了很大的困难。

实际反应过程的理想化是研究生产实践中千变万化的各种反应器的基础和前提，也是均相反应过程接近实际的反应器模型。

间歇釜式反应器（BSTR）、稳态全混流反应器(CSTR)和活塞流（平推流）管式反应器(PFR)，这三种理想反应器的设计原理具有普遍意义和广泛的应用性。

3-1 间歇釜式反应器3-2间歇釜示意图图3-1间歇釜式反应器如图3-1所示，间歇釜式反应器简称间歇釜，它的最大特点是分批装料和卸料。

因此，其操作条件较为灵活，可适用于不同品种和不同规格的液态产品生产，尤其适合于多品种而小批量的化学品生产，它在医药、助剂、添加剂、涂料、应用化学品等精细化工生产部门中经常得到应用，很少用于气相过程。

间歇釜的结构主要有釜体、搅拌装置、加热和冷却装置、进出料口和管件、温度和压力测量装置以及视孔、排污口和液位计等。

釜体上部釜盖用法兰与釜体连接，釜体上一般不开孔，都在釜盖上开孔用以安装管阀件，釜体上有四个吊耳用于固定反应釜，釜体外部是换热夹套。

第三章均相理想反应器反应器的开发主要有两个任务：1．优化设计—反应器选型、定尺寸、确定操作条件。

2．优化操作—根据实际操作情况，修正反应器的数学模型参数，优化操作条件。

最根本任务—最高的经济和社会效益。

3．1 反应器设计基础3．1．1反应器中流体的流动与混合理想反应器的分类对理想反应器（ideal reactor），主要讨论三种类型：1．间歇反应器(Batch Reactor—BR);2．平推流反应器(Plug /Piston Flow Reactor—PFR)；3．全混流反应器(Continuously Stirred Tank Reactor—CSTR)。

返混(back mixing)—不同停留时间的粒子之间的混合;混合(mixing)—不同空间位置的粒子之间的混合。

注意：返混≠混合！平推流—物料以均一流速向前推进。

特点是粒子在反应器中的停留时间相同，不存在返混。

T、P、C i随轴向位置变（齐头并进无返混，变化随轴不随径）。

全混流（理想混合）—物料进入反应器后能够达到瞬间的完全混合。

特点是反应器内各处的T、P、C i相同，物性不随反应器的位置变，返混达到最大。

3．1．2 反应器设计的基础方程反应器的工艺设计包括两方面的内容：1．由给定生产任务和原料条件设计反应器；2．对已有的反应器进行较核，看达到质量要求时，产量是否能保证，或达到产量时，质量能否保证。

反应器设计的基础方程主要是：1．动力学方程；2．物料衡算方程；3．热量衡算方程；4．动量衡算方程。

一、物料衡算方程对反应器内选取的一个微元，在单位时间内，对物质A有：进入量=排出量+反应消耗量+积累量(3.1-1)用符号表示：F in F out F r F b即：F in=F out+F r+F b(3.1-2) 1．对间操作，反应过程无进料和出料，即：F in=F out=0则：-F r=F b(3.1-4) 反应量等于负积累量。

2．对连续稳定操作，积累量为零，即：F b=0则F in=F out+F r（3.1-6）二、热量衡算方程对反应器内选定的微元，单位时间内的热量变化有：随物料流－随物料流＋与边界交＋反应热=积累热量入的热量出的热量换的热量符号：Q in Q out Q u Q r Q b入为正放热为正即：Q in－Q out＋Q u＋Q r=Q b(3.1-8) 1．对于稳定操作的反应器，热的积累为零，即：Q b=0Q in－Q out＋Q u＋Q r=0(3.1-9) 2．对稳态操作的绝热反应器，Q u=Q b=0，即：Q in－Q out＋Q r=0(3.1-10) 反应热全部用来升高或降低物料的温度。

第三章 理想流动反应器 1.10=A B C C 时：()[]⎰-=A fx A A AA x C k dx C t 02001积分得到：01110AfA A xx kC t -⋅=即：AfAf A x x kC t -⋅=11k=0.615L/(mol h), C A0=0.307mol/L ： x Af =0.5 ,t=5.30 h x Af =0.9 ,t=47.67 h x Af =0.99 ,t=524.35 h50=A B C C 时：()()⎰--=A fx AA A A A AA x C C x kC dx C t 0000051积分：⎪⎪⎭⎫ ⎝⎛---=5ln 15ln 41Af Af A x x kC t k=0.615L/(mol h), C A0=0.307mol/L ： x Af =0.5 ,t=0.78 h x Af =0.9 ,t=2.79 h x Af =0.99 ,t=5.81h 2.由于B A C C =，所以2A B A A kC C kC r ==；()[]⎰⎰-==A f A f x A A AA x A A A x C k dx C r dx C t 0200001积分：AfAf A x kC t -⋅=10k=5.6 L/(mol min), C A0=0.02 mol/L ，x Af =0.95,t=169.64 min 3．对于平推流(等温一级反应):⎰-=A f x A A AA R x kC dx C V V 0000)1(对于全混流(等温一级反应):)1(000Afc A Afc A R x kC x C V V -=由题设两类型的反应器体积相等,所以:⎰-=-A f x A A AA Afc A Afc A x kC dx C V x kC x C V 0000000)1()1(化简:()()⎰-=-A fx A AAfcAfcx dx x x 011 即:()AfAfcAfcx x x -=-11ln1代入9.0=Af x ,得:6972.0=Afc x4.对于平推流(等温一级反应):⎰-=A f x A A AA R x C k dx C V V 00100)1(对于全混流(等温一级反应):)1(0200Afc A Afc A R x C k V -=两反应器体积相等:)1()1(020000100Afc A Afc A x A A AA x C k x C V x C k dx C V A f -=-⎰由于流率，初始浓度均相同，所以可化简为：()Afc Afc Af x k x x k -=-111ln 121 6.0=Af x ，7.0=Afc x ，代入，得到： 3927.021=k k 由阿累尼乌斯方程：3927.0exp exp 2010=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-RTE A RTE A aa15.42315015.2731=+=T K ，83680=a E J/mol ，314.8=R J/(mol K)，代入，解得：46.4402=T K5．设每股料液流量为V 0，则总流量为2V 0，所以A 的初始浓度为3.0/2=1.5mol/L ，B 的初始浓度为2.0/2=1.0mol/L ；由公式：()()20000007.1))1(82Bf B Bf B A Bf B BfB R xC x C C x C x C V V ---=1.0=R V L ，%80=Bf x ，解得：002.00=V L/min6.（1）：因为是二级反应，逐釜计算：对于第一个全混流反应器（料液密度恒定，因此可按等容处理）：()2101001)1(Af A Af A R x C k x C V V -=代入已知数据，化简：()0135.421=--x x Af解得：%2.621=Af x70.21=A C mol/L对于第二个全混流反应器：()2212102)1(Af A Af A R x C k x C V V -=代入已知数据，化简得：()01645.122=--x x Af%71.462=Af x 44.12=A C mol/L所以总转化率为：%8.79020=-=A A A C C C X （2）对于第一个全混流反应器（料液密度恒定，因此可按等容处理）：()2101001)1(Af A Af A R x C k x C V V -=代入已知数据，化简：()0135.421=--x x Af解得：%2.621=Af x70.21=A C mol/L对于后接的平推流反应器：()⎰-=221102)1(A fx A A AA R x C k dx C V V化简：221021Af Af A R x x kC V V -⋅=代入已知数据，解得：%2.622=Af x 02.12=A C mol/L总转化率：%7.85020=-=A A A C C C X （3）对于第一个平推流反应器：()⎰-=120001)1(A f x A A AA R x C k dx C V V化简：110011Af Af A R x x kC V V -⋅=代入已知数据，解得：%3.811=Af x 33.11=A C mol/L对于后接的全混流反应器：()2212102)1(Af A Af A R x C k x C V V -=代入已知数据，化简得：()018130.022=--x x Af 解得：%68.342=Af x 872.02=A C mol/L总转化率：%8.87020=-=A A A C C C X (4)平推流反应器串联相当于一个大平推流反应器，5.021=+=R R R V V V m3由平推流反应器公式：()⎰-=A fx A A AA R x C k dx C V V 02000)1(化简得：AfAf A R x x kC V V -⋅=100代入已知数据，得：%7.89=Af x7.（1）对于单个平推流反应器：⎰-=A f x AA A A AA R x C x kC dx C V V 00000)1(化简得：()()01ln ln 0AfA A A R x x x kC V V --=由于ln （0）为无穷大，因此V R 为无穷大，单个平推流反应器无法完成题设任务。

第二章 均向反应动力学1.在473K 等温及常压下进行气相反应：（1）3→A R 1.5R A r C = （2）2→A S0.5S Ar C =（3）→A T 2.1TA r C= 式中C A 为反应物A 的浓度（kmol/l ），原料中A 和惰性气体各为一半（体积比），试求当A 的转化率达85%时，其转化速率是多少？解：先求出总摩尔变化数δA ，首先将产物的生成速率变为对应的反应物的转化速率：10.53AR R A r r C ==10.252AS S A r r C == 2.1AT T A r r C== 总反应速率为： 2.85A AR AS AT AR r r r C =++= 以一摩尔反应物A 为基准，总摩尔变化数为：0.50.25 2.13210.4392.85 2.85 2.85A δ=⨯+⨯+-=初始浓度为：200030.10130.5 1.28810/8.31410473A A P y C kmol l RT --⨯===⨯⨯⨯则有：2300(1) 1.288100.151.62810/110.50.4390.85A A A A A A C X C kmol ly X δ---⨯⨯===⨯++⨯⨯332.85 2.85 1.62810 4.64010/(.min)A A R C kmol l --==⨯⨯=⨯2.可逆一级液相反应PA −−←−→−，已知0,m kmol 5.0P030=⋅=-c c A ；当此反应在间歇反应器中进行，经过8min 后，A 的转化率为33.3%，而平衡转化率是66.7%，求此反应的动力学方程式。

解：()()x c k x c k txc t c x c c x c c c c k c k c k c k tc r A02A01A0A A0P A0A A A02A 1P 2A 1AA 1d d d d )1(d d --==-=-=--=-=-=-⎩⎨⎧=====+-+-=xx t t x t txk k k xx k k k tx,0,0d )(d )(d d 2112118333.022667.01667.01)1()(ln 121e e e 0A e 0A Ae Pe 21121121=====-=-=-====+-+-t x k k K x x x c x c c c k k K t k xk k k k k ()PA A A 1211212121212102888.005776.0d d min02888.0min 05776.02/08664.086931.05.0ln 18333.02111ln 1c c tcr k k k k k k k k k k k k -=-=-⎩⎨⎧==⎩⎨⎧==+=+=+-=⎪⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛+-+--- 3.液相自催化反应的动力学方程A+P-P+P 速率表达式00()/(.) c 0.95/ c 0.05/AA A P A P dc r kc c mol l h mol L mol L dt -=-===，1h 后测得速率最大值，求反应速率常数。

第三章 理想流动均相反应器设计题解1、[间歇反应器与全混釜恒容一级]有一等温操作的间歇反应器进行某一级液相反应，13分钟后,反应物转化了70%.今拟将此反应转至全混流反应器,按达到相同的转化率应保持多大的空速?解:㏑CA 0CA =kt, CA0CACA0- =0.7 ， C A =0.3C A0 间歇釜中∴㏑0.3=－13k ， k=0.0926 min-1在全混釜中τ=VR V0=CA0 XA k CA =0.70.30.0926⨯=25.2 min -1∴空速S=1τ=125.2=0.0397min -12、[平推流恒容一级]有一个活塞流管式反应器于555K,0.3MPa 压力下进行A →P 气相反应,已知进料中含30%A(mol)，其余70%为惰性物料.加料流量为6.3mol/s.该反应的动力学方程为r A =0.27C Amol/m 3·s,要求达到95%转化.试求⑴所需的空时? ⑵反应器容积?解: τP =VR V0=1k ㏑CA 0CA =1k ㏑PA0PA =1k ㏑A0Ay y =1k ㏑11Ax -=10.27㏑110.95-=11.1 S∴V R =τP ·v 0=τP 00A A FC而C A0=A P RT=30.30.082555⨯⨯=0.0198mol/L=19.8mol/m 3V R =11.1s ×36.3/19.8/mol s mol m =3.53m 33、[平推流变容过程一级]有一纯丙烷裂解反应方程式为C 3H 8→C 2H 4+CH 4.该反应在772℃等温条件下进行,其动力学方程式为-dP A /dt=kP A ,忽略存在的副反应,并已知k=0.4h -1 反应过程保持恒压0.1MPa.772℃和0.1MPa 下的体积进料量为800L/h,求转化率为0.5时所需的平推流反应器的体积.解: ∵εA =212-=0.5∵k τP =－(1＋εA )㏑(1-ΧA )- εA ΧAf0.4τP =－(1+0.5)㏑(1-0.5)-0.5×0.5∴τP =1.5ln 20.250.4-=1.974hV R =τP v 0=1.974×800=1579L=1.579 m 34、[间歇釜变容一级]一级气相反应A →2R+S ,在等温等压间歇实验反应器中进行,原料中含75%A(mol),25%(mol)惰性气体,经8分钟后,其体积增加一倍.求此时达到了多大的转化率? 速率常数多大? 解: 膨胀因子 δA =3-11=2膨胀率 εA =y A0δA =0.75×2=1.5对应转化率X A 的反应体积 V=V 0(1＋εA ΧA ) 所以，ΧA =V V 0A1ε-=2-11.5=66.7%K=1t ㏑11Ax -=18㏑110.667-=0.0735 min -15、[全混流恒容二级反应]在全混流反应器中进行液相均相二级反应:A+B →C,在298K 下的动力学方程式为r A =0.6C A C B mol/(L.min),该反应的进料速率为ν0 =0.018m 3/min.A,B 的初始浓度相同,均为0.1mol/L,要求出口的转化率为90%,求需多大的全混釜? 解:R 0V v =A0Af AC x r =A0Af A BC x kC C =A02Af A C x kC =A0220(1)AfA Af C x kCx -=τmτm =20.90.60.1(10.9)⨯-=150 min∴V R =v 0τm =0.018 m 3/mi n ×150min=2.7 m 36、[多釜串联液相二级]某一液相反应A+B →R+S,其速率常数k=9.92m 3/(Kmol ·KS),初始浓度为0.08Kmol/m 3，在两个等体积的全混釜中进行反应,最终出口转化率0.875.进料体积流量为0.278m 3/KS .求全混釜的总体积? 解： τ1=10R V v =011A A C C r -=012201(1)A A A A C x kCx -τ2=20R V v =122A A A C C r -=021222()(1)A A A A A C xx kC x--∵ τ1=τ2 两釜相同所以， 121(1)A A x x -=2122(1)AA A xx x--, 而x A2 =0.875整理有 (1-0.875)2x A1=(0.875- x A1)(1- x A1)2试差解得 x A1=0.7251所以，V R1=0012201(1)A A A A v C xkC x ⨯-=20.2780.75219.920.08(10.7521)⨯⨯⨯-=4.16 m 3总反应器体积 V R =2V R1=2×4.16=8.33 m 37.【自催化反应优化】自催化反应 A+R →R+R ，速度方程为-r=kC A C R ，体系总浓度为C 0= C A +C R 。

第三章 理想流动均相反应器设计题解1、[间歇反应器与全混釜恒容一级]有一等温操作的间歇反应器进行某一级液相反应，13分钟后,反应物转化了70%.今拟将此反应转至全混流反应器,按达到相同的转化率应保持多大的空速?解:㏑CA 0CA =kt, CA0CACA0- =0.7 ， C A =0.3C A0 间歇釜中∴㏑0.3=－13k ， k=0.0926 min-1在全混釜中τ=VR V0=CA0 XA k CA =0.70.30.0926⨯=25.2 min -1∴空速S=1τ=125.2=0.0397min -12、[平推流恒容一级]有一个活塞流管式反应器于555K,0.3MPa 压力下进行A →P 气相反应,已知进料中含30%A(mol)，其余70%为惰性物料.加料流量为6.3mol/s.该反应的动力学方程为r A =0.27C Amol/m 3·s,要求达到95%转化.试求⑴所需的空时? ⑵反应器容积?解: τP =VR V0=1k ㏑CA 0CA =1k ㏑PA0PA =1k ㏑A0Ay y =1k ㏑11Ax -=10.27㏑110.95-=11.1 S∴V R =τP ·v 0=τP 00A A FC而C A0=A P RT=30.30.082555⨯⨯=0.0198mol/L=19.8mol/m 3V R =11.1s ×36.3/19.8/mol s mol m =3.53m 33、[平推流变容过程一级]有一纯丙烷裂解反应方程式为C 3H 8→C 2H 4+CH 4.该反应在772℃等温条件下进行,其动力学方程式为-dP A /dt=kP A ,忽略存在的副反应,并已知k=0.4h -1 反应过程保持恒压0.1MPa.772℃和0.1MPa 下的体积进料量为800L/h,求转化率为0.5时所需的平推流反应器的体积.解: ∵εA =212-=0.5∵k τP =－(1＋εA )㏑(1-ΧA )- εA ΧAf0.4τP =－(1+0.5)㏑(1-0.5)-0.5×0.5∴τP =1.5ln 20.250.4-=1.974hV R =τP v 0=1.974×800=1579L=1.579 m 34、[间歇釜变容一级]一级气相反应A →2R+S ,在等温等压间歇实验反应器中进行,原料中含75%A(mol),25%(mol)惰性气体,经8分钟后,其体积增加一倍.求此时达到了多大的转化率? 速率常数多大? 解: 膨胀因子 δA =3-11=2膨胀率 εA =y A0δA =0.75×2=1.5对应转化率X A 的反应体积 V=V 0(1＋εA ΧA ) 所以，ΧA =V V 0A1ε-=2-11.5=66.7%K=1t ㏑11Ax -=18㏑110.667-=0.0735 min -15、[全混流恒容二级反应]在全混流反应器中进行液相均相二级反应:A+B →C,在298K 下的动力学方程式为r A =0.6C A C B mol/(L.min),该反应的进料速率为ν0 =0.018m 3/min.A,B 的初始浓度相同,均为0.1mol/L,要求出口的转化率为90%,求需多大的全混釜? 解:R 0V v =A0Af AC x r =A0Af A BC x kC C =A02Af A C x kC =A0220(1)AfA Af C x kCx -=τmτm =20.90.60.1(10.9)⨯-=150 min∴V R =v 0τm =0.018 m 3/min ×150min=2.7 m 36、[多釜串联液相二级]某一液相反应A+B →R+S,其速率常数k=9.92m 3/(Kmol ·KS),初始浓度为0.08Kmol/m 3，在两个等体积的全混釜中进行反应,最终出口转化率0.875.进料体积流量为0.278m 3/KS .求全混釜的总体积? 解： τ1=10R V v =011A A C C r -=012201(1)A A A A C x kCx -τ2=20R V v =122A A A C C r -=021222()(1)A A A A A C xx kC x--∵ τ1=τ2 两釜相同所以， 121(1)A A x x -=2122(1)AA A xx x--, 而x A2 =0.875整理有 (1-0.875)2x A1=(0.875- x A1)(1- x A1)2试差解得 x A1=0.7251所以，V R1=0012201(1)A A A A v C xkC x ⨯-=20.2780.75219.920.08(10.7521)⨯⨯⨯-=4.16 m 3总反应器体积 V R =2V R1=2×4.16=8.33 m 37.【自催化反应优化】自催化反应 A+R →R+R ，速度方程为-r=kC A C R ，体系总浓度为C 0= C A +C R 。

1.理想反应器包括___平推流反应器、__全混流反应器_ 。

2.具有良好搅拌装置的釜式反应器按_全混流__反应器处理，而管径小，管子较长和流速较大的管式反应按_平推流_反应器处理。

3.全混流反应器的空时τ是_反应器的有效容积____与___进料流体的容积流速_之比。

4.全混流反应器的返混__∞__，平推流反应器的返混为_零__。

5.如果将平推流反应器出口的产物部分的返回到入口处与原始物料混合，这类反应器为_循环操作_的平推流反应器6.对于循环操作的平推流反应器，当循环比β→0时为___平推流__反应器，而当β→∞时则相当于_全混流___反应器。

7. 对于循环操作的平推流反应器，当循环比β→0时反应器内返混为_零_，而当β→∞时则反应器内返混为_∞_。

8.对于反应级数n＜0的反应，为降低反应器容积，应选用_全混流__反应器为宜。

9.对于反应级数n＞0的反应，为降低反应器容积，应选用_平推流__反应器为宜。

10.分批式操作的完全混合反应器非生产性时间不包括下列哪一项___B____。

A. 加料时间B. 反应时间C. 物料冷却时间D. 清洗釜所用时间11.在间歇反应器中进行等温二级反应A →B，，当时，求反应至所需时间t=__D_____秒。

A. 8500B. 8900C. 9000D. 990012.在间歇反应器中进行等温一级反应A →B，，当时，求反应至所需时间t=__B_____秒。

A. 400B. 460C. 500D. 56013.在全混流反应器中，反应器的有效容积与进料流体的容积流速之比为__A__。

A. 空时τB. 反应时间tC. 停留时间tD. 平均停留时间14.一级不可逆液相反应，，出口转化率，每批操作时间，装置的生产能力为50000 kg产物R/天，=60，则反应器的体积V为__C__。

A. 19.6B. 20.2C. 22.2D. 23.415.对于单一反应组分的平行反应，其瞬间收率随增大而单调增大，则最适合的反应器为___A____。

第三章均相理想反应器反应器的开发主要有两个任务：1．优化设计—反应器选型、定尺寸、确定操作条件。

2．优化操作—根据实际操作情况，修正反应器的数学模型参数，优化操作条件。

最根本任务—最高的经济和社会效益。

3．1 反应器设计基础3．1．1反应器中流体的流动与混合理想反应器的分类对理想反应器（ideal reactor），主要讨论三种类型：1．间歇反应器(Batch Reactor—BR);2．平推流反应器(Plug /Piston Flow Reactor—PFR)；3．全混流反应器(Continuously Stirred Tank Reactor—CSTR)。

返混(back mixing)—不同停留时间的粒子之间的混合;混合(mixing)—不同空间位置的粒子之间的混合。

注意：返混≠混合！平推流—物料以均一流速向前推进。

特点是粒子在反应器中的停留时间相同，不存在返混。

T、P、C i随轴向位置变（齐头并进无返混，变化随轴不随径）。

全混流（理想混合）—物料进入反应器后能够达到瞬间的完全混合。

特点是反应器内各处的T、P、C i相同，物性不随反应器的位置变，返混达到最大。

3．1．2 反应器设计的基础方程反应器的工艺设计包括两方面的内容：1．由给定生产任务和原料条件设计反应器；2．对已有的反应器进行较核，看达到质量要求时，产量是否能保证，或达到产量时，质量能否保证。

反应器设计的基础方程主要是：1．动力学方程；2．物料衡算方程；3．热量衡算方程；4．动量衡算方程。

一、物料衡算方程对反应器内选取的一个微元，在单位时间内，对物质A有：进入量=排出量+反应消耗量+积累量(3.1-1)用符号表示：F in F out F r F b即：F in=F out+F r+F b(3.1-2) 1．对间操作，反应过程无进料和出料，即：F in=F out=0则：-F r=F b(3.1-4) 反应量等于负积累量。

2．对连续稳定操作，积累量为零，即：F b=0则F in=F out+F r（3.1-6）二、热量衡算方程对反应器内选定的微元，单位时间内的热量变化有：随物料流－随物料流＋与边界交＋反应热=积累热量入的热量出的热量换的热量符号：Q in Q out Q u Q r Q b入为正放热为正即：Q in－Q out＋Q u＋Q r=Q b(3.1-8) 1．对于稳定操作的反应器，热的积累为零，即：Q b=0Q in－Q out＋Q u＋Q r=0(3.1-9) 2．对稳态操作的绝热反应器，Q u=Q b=0，即：Q in－Q out＋Q r=0(3.1-10) 反应热全部用来升高或降低物料的温度。