二次函数图像的平移、旋转、对称

二次函数中平移变换的规律和性质二次函数是高中数学中一个重要的概念，具有广泛的应用。

其中，平移是二次函数的基本变换之一，它可以使二次函数在坐标平面上发生横向或纵向的移动。

本文将探讨二次函数中平移变换的规律和性质。

一、平移变换的基本概念在二次函数y = ax^2 + bx + c中，平移变换通过改变a, b, c的值来实现函数图像在平面上的平移。

其中，a决定了二次函数的开口方向和是否对称于y轴，b和c则决定了函数图像在横纵方向的平移。

二、平移变换的规律1. 横向平移：当二次函数y = ax^2 + bx + c中的c值保持不变时，随着b值的变化，函数图像在横向上发生平移。

当b > 0时，函数图像向左平移；当b < 0时，函数图像向右平移。

2. 纵向平移：当二次函数y = ax^2 + bx + c中的b值保持不变时，随着c值的变化，函数图像在纵向上发生平移。

当c > 0时，函数图像向上平移；当c < 0时，函数图像向下平移。

3. 综合平移：当二次函数y = ax^2 + bx + c中的b和c同时变化时，函数图像即在横向又在纵向上发生平移。

平移的方向和大小由b和c的值决定。

三、平移变换的性质1. 平移不改变二次函数的开口方向：无论进行何种平移变换，二次函数的开口方向都保持不变。

例如，当二次函数的开口向上时，平移后它仍然向上开口。

2. 平移不改变二次函数的最值：无论进行何种平移变换，二次函数的最值不发生改变。

例如，对于开口向上的二次函数，平移只会改变它的顶点位置，但最大值或最小值不会发生改变。

3. 平移不改变二次函数的对称性：无论经过何种平移变换，二次函数的对称性仍然保持不变。

例如，对称于y轴的二次函数平移后仍然对称于y轴。

综上所述，平移是二次函数中常见的一种变换方式，能够改变函数图像在平面上的位置，并且不改变二次函数的开口方向、最值和对称性。

熟练掌握平移变换的规律和性质，有助于我们更好地理解和应用二次函数，解决与之相关的数学问题。

二次函数像的平移与伸缩规律二次函数的平移与伸缩规律二次函数是一种常见的数学函数形式，其图像呈现为抛物线的形状。

在数学中，我们可以通过改变二次函数的参数来实现对其图像的平移和伸缩操作。

本文将详细介绍二次函数的平移和伸缩规律，以帮助读者更好地理解和应用这些数学概念。

一、平移规律对于一般形式的二次函数 y = ax² + bx + c，我们可以通过改变参数b 和c 来实现平移操作。

1. 水平平移当二次函数的参数 c 不为零时，整个图像将沿x轴平移。

当 c > 0 时，图像将向左平移 |c| 个单位；当 c < 0 时，图像将向右平移 |c| 个单位。

2. 垂直平移当二次函数的参数 b 不为零时，整个图像将沿y轴平移。

当 b > 0 时，图像将向上平移 |b| 个单位；当 b < 0 时，图像将向下平移 |b| 个单位。

二、伸缩规律对于一般形式的二次函数 y = ax² + bx + c，我们可以通过改变参数 a 来实现伸缩操作。

1. 水平伸缩当 a > 1 时，图像将在 x 轴方向上进行水平压缩；当 0 < a < 1 时，图像将在 x 轴方向上进行水平拉伸。

这一规律可以通过观察二次函数的顶点来进行判断。

2. 垂直伸缩当 a > 1 时，图像将在 y 轴方向上进行垂直拉伸；当 0 < a < 1 时，图像将在 y 轴方向上进行垂直压缩。

这一规律可以通过观察二次函数的开口方向来进行判断。

综合平移和伸缩规律，我们可以得出以下结论：1. 若 a > 0，则二次函数的图像开口向上；若 a < 0，则二次函数的图像开口向下。

2. 若a ≠ 0，则二次函数的顶点为 (-b/2a, f(-b/2a))；若 a = 0，则二次函数为一次函数。

3. 给定二次函数 y = ax² + bx + c，当a ≠ 0 时，通过平移和伸缩操作，我们可以得到新的二次函数 y = a(x - h)² + k。

二次函数旋转90度后的解析式在数学中，二次函数是一种常见的函数类型，可以表示为y=ax^2+bx+c的形式，其中a、b和c都是实数常数。

二次函数在平面直角坐标系中呈现出一条抛物线的形状，通常具有一个顶点和一个对称轴。

然而，当我们将二次函数旋转90度后，它将呈现出不同的形态和特征。

当我们说二次函数旋转90度时，实际上是指将原始的二次函数图像逆时针旋转90度。

这意味着原来的x轴变为y轴，y轴变为-x轴。

为了表示旋转后的二次函数的解析式，我们需要对原始的二次函数进行一些变换。

我们可以考虑将原始的二次函数表示为标准形式，即将其写成完全平方的形式。

对于一般的二次函数y=ax^2+bx+c，我们可以将其变换为y=a(x-h)^2+k的形式，其中(h,k)是顶点的坐标。

这个变换可以通过平移和缩放来实现。

然后，我们可以将x轴和y轴进行交换，即将x变为y，y变为-x。

这个变换可以通过对原始的二次函数解析式进行代换来实现。

综合上述变换，我们可以得到二次函数旋转90度后的解析式为x=a(y-k)^2+h。

接下来，让我们更详细地讨论一下旋转后二次函数的特征。

旋转后的二次函数仍然具有一个顶点，只是顶点的坐标发生了变化。

原来的顶点坐标为(h,k)，旋转后的顶点坐标变为(k,-h)。

旋转后的二次函数的对称轴也发生了变化。

原来的对称轴是x=h，旋转后的对称轴变为y=k。

旋转后的二次函数的开口方向也发生了变化。

原来的二次函数开口向上或向下，旋转后的二次函数开口方向变为向左或向右。

旋转后的二次函数的图像形态也发生了改变。

原来的二次函数呈现出抛物线的形状，旋转后的二次函数则呈现出一种类似于倒立的抛物线的形状。

二次函数旋转90度后的解析式为x=a(y-k)^2+h。

旋转后的二次函数具有新的顶点坐标、对称轴、开口方向和图像形态。

通过理解和掌握旋转后二次函数的特征，我们能够更好地应用二次函数来解决实际问题，从而拓展数学的应用领域。

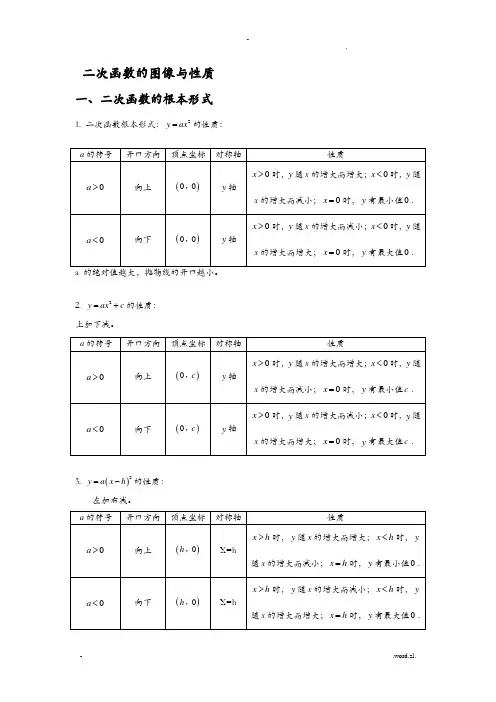
二次函数的图像与性质一、二次函数的根本形式1. 二次函数根本形式：2=的性质：y ax2. 2=+的性质：y ax c上加下减。

3. ()2=-的性质：y a x h左加右减。

4. ()2y a x h k =-+的性质：二、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的根底上“h 值正右移，负左移；k 值正上移，负下移〞． 概括成八个字“左加右减，上加下减〞． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上〔下〕平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2〔或m c bx ax y -++=2〕⑵c bx ax y ++=2沿轴平移：向左〔右〕平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2〔或c m x b m x a y +-+-=)()(2〕三、二次函数()2y a x h k =-+与2y ax bx c =++的比拟从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，． 四、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，〔假设与x 轴没有交点，那么取两组关于对称轴对称的点〕.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.五、二次函数2y ax bx c =++的性质1.当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a-．六、二次函数解析式的表示方法1. 一般式：2y ax bx c =++〔a ，b ，c 为常数，0a ≠〕；2. 顶点式：2()y a x h k =-+〔a ，h ，k 为常数，0a ≠〕；3. 两根式：12()()y a x x x x =--〔0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标〕. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1.二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba->，即抛物线对称轴在y 轴的右侧．⑵ 在0a <的前提下，结论刚好与上述相反，即 当0b >时，02ba->，即抛物线的对称轴在y 轴右侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边那么0>ab ，在y 轴的右侧那么0<ab ，概括的说就是“左同右异〞总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式确实定：根据条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 抛物线上三点的坐标，一般选用一般式；2. 抛物线顶点或对称轴或最大〔小〕值，一般选用顶点式；3. 抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 抛物线上纵坐标一样的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-；4. 关于顶点对称〔即：抛物线绕顶点旋转180°〕2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原那么，选择适宜的形式，习惯上是先确定原抛物线〔或表达式的抛物线〕的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．二次函数图像参考：十一、【例题精讲】一、一元二次函数的图象的画法【例1】求作函数64212++=x x y 的图象 【解】 )128(21642122++=++=x x x x y2-4)(214]-4)[(21 2222+=+=x x以4-=x 为中间值，取x 的一些值，列表如下：【例2】求作函数342+--=x x y 的图象。

二次函数的平移问题关于二次函数的平移变换问题二次函数的平移变换可以分为上下平移和左右平移两种情况。

1.上下平移对于原函数y=ax²+bx+c，若要进行上下平移，可以进行以下变换：向上平移m个单位，得到平移后的函数y=ax²+bx+c+m；向下平移m个单位，得到平移后的函数y=ax²+bx+c-m。

需要注意的是，m为正数，若m为负数，则对应的加（减）号需要改为减（加）号。

一般称这种变换为上加下减或上正下负。

2.左右平移对于原函数y=ax²+bx+c，若要进行左右平移，可以进行以下变换：先将函数化为顶点式y=a(x-h)²+k；向左平移n个单位，得到平移后的函数y=a(x-h+n)²+k；向右平移n个单位，得到平移后的函数y=a(x-h-n)²+k。

需要注意的是，n为正数，若n为负数，则对应的加（减）号需要改为减（加）号。

一般称这种变换为左加右减或左正右负。

例题：1.将抛物线y=-x²向左平移一个单位，再向上平移三个单位，平移后的表达式为（）A。

y=-(x-1)²+3B。

y=-(x+1)²+3C。

y=-(x-1)²-3D。

y=-(x+1)²-32.抛物线y=x²+bx+c向右平移两个单位，再向下平移三个单位，得到的抛物线表达式为y=x²-2x-3，则b、c的值分别为（）A。

b=2，c=2B。

b=2，c=0C。

b=-2，c=-1D。

b=-3，c=23.将函数y=x²+x的图像向右平移a（a>0）个单位，得到函数y=x²-3x+2的图像，则a的值为（）A。

1B。

2C。

3D。

44.已知二次函数y=x²-bx+1（-1≤b≤1），当b从-1逐渐变化到1的过程中，它所对应的抛物线位置也随之变动。

下列关于抛物线移动方向的描述中，正确的是（）A。

知识导航经典例题1在平面直角坐标系中，抛物线2已知二次函数的图象以3已知抛物线4在平面直角坐标系中，二次函数5若二次函数知识导航经典例题1如果将抛物线2如果将某一抛物线向右平移3将抛物线4已知抛物线知识导航经典例题1将二次函数2抛物线3将二次函数4先作二次函数1在平面直角坐标系中，抛物线2如图，已知抛物线帝通过数来统治宇宙。

这是毕达哥拉斯学派和其他教派的主要区别。

他们很重视数学，企图用数来解释一切。

宣称数是宇宙万物的本原，研究数学的目的并不在于使用而是为了探索自然的奥秘。

他们从五个苹果、五个手指等事物中抽象出了五这个数。

这在今天看来很平常的事，但在当时的哲学和实用数学界，这算是一个巨大的进步。

但是，他们同时任意地把非物质的、抽象的数夸大为宇宙的本原，认为'万物皆数'，'数是万物的本质'，是'存在由之构成的原则'，而整个宇宙是数及其关系的和谐的体系。

毕达哥拉斯将数神秘化，说数是众神之母，是普遍的始原，是自然界中对立性和否定性的原则。

毕达哥拉斯本人以发现勾股定理(西方称毕达哥拉斯定理)著称于世。

这定理早已为巴比伦人所知，不过最早的证明大概可归功于毕达哥拉斯。

他是用演绎法证明了直角三角形斜边平方等于两直角边平方之和，即毕达哥拉斯定理（勾股定理）。

任何一个学过代数或几何的人，都会听到毕达哥拉斯定理。

这一著名的定理，在许多数学分支、建筑以及测量等方面，有着广泛的应用．【毕达哥拉斯定理】毕达哥拉斯对数论作了许多研究，将自然数区分为奇数、偶数、素数、完全数、平方数、三角数和五角数等。

在几何学方面，毕达哥拉斯学派证明了'三角形内角之和等于两个直角'的论断；研究了黄金分割；发现了正五角形和相似多边形的作法；还证明了正多面体只有五种：正四面体、正六面体、正八面体、正十二面体和正二十面体。

【黄金分割】然而，最让毕达哥拉斯学派出名的却是他们中的一个'叛逆者'--希帕索斯，正是他发现了第一个无理数根号2的存在，从而在当时的数学界掀起了一场巨大风暴。

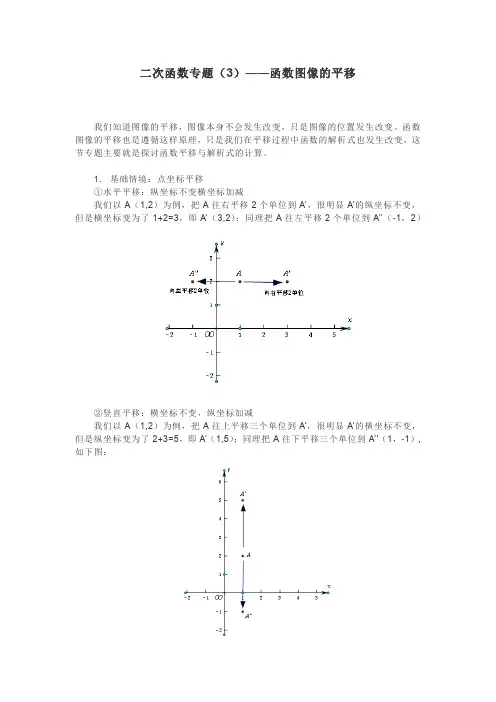
二次函数专题（3）——函数图像的平移我们知道图像的平移，图像本身不会发生改变，只是图像的位置发生改变。

函数图像的平移也是遵循这样原理，只是我们在平移过程中函数的解析式也发生改变，这节专题主要就是探讨函数平移与解析式的计算。

1. 基础情境：点坐标平移①水平平移：纵坐标不变横坐标加减我们以A（1,2）为例，把A往右平移2个单位到A’，很明显A’的纵坐标不变，但是横坐标变为了1+2=3，即A’（3,2）；同理把A往左平移2个单位到A’’（-1，2）②竖直平移：横坐标不变，纵坐标加减我们以A（1,2）为例，把A往上平移三个单位到A’，很明显A’的横坐标不变，但是纵坐标变为了2+3=5，即A’（1,5）；同理把A往下平移三个单位到A’’（1，-1）,如下图：2. 函数平移：一次函数图像平移①水平平移问题：我们以y=2x+2为例，把它向右平移2个单位，那么新的图像函数解析式为何？分析：由于平移过后仍然是条直线，两点决定一条直线，所以我们选取两个特殊点就可以算出新的函数表达式。

解答：选取原一次函数上两点（0,2）、（-1,0），经过平移后这两点坐标变为（2,2）和（1,0），计算得y=2x-2.观察：平移后，一次函数的系数k（2）不变，b减小了两倍（由2变为-2）推广：对于所有一次函数y=kx+b，向右平移2个单位的函数解析式怎么求？分析：可以按照上面的思路，取特殊点求取新的一次函数解析式解答：方法一：坐标法取两个特殊点（0，b）、（1，k+b），经过平移后这两点坐标变为（2,b）和（3,k+b），计算函数表达式得y=kx+b-2k。

这个式子我们还可以改写成这样y=（k-2）x+b。

反思：解析法特殊点法虽然可以帮助我们解决问题，但是需要计算，有没有更加快速的计算一次函数解析式方法？有！我们回到最初函数的定义，比如坐标系中有一个点A（x,y）,其中y=kx+b 代表是x与y之间的等量关系。

如果把A（x,y）向右平移2单位变成A’（m,y），此时m=x+2。

《二次函数的对称性与变换》《二次函数的对称性与变换》是一个关于研究二次函数形式，其中包括其对称性和变换性的课题。

人们常常会注意到，二次函数在图形上展示出来具有一定的对称性，这个对称性对于理解二次函数、构造变换和后续的数学研究有重要的意义。

首先，我们探讨一下二次函数的基本特点，它是指一元二次运算式f(x)=ax^2+bx+c（a≠0），用此式子来表示在直角坐标系中的一个曲线，当a>0时，这一曲线在x轴两侧向上凹陷，即函数图形具有拱形，即形如一个弓或蝴蝶结；a<0时，图形具有凸起，即形似一个盔甲或自环。

然后，我们再研究二次函数的对称性，它指的是曲线以某一垂直于x轴的线段或平行于x轴的线段作为中心的对称性。

二次函数的对称性主要有两种，一种是y轴对称，即以y轴作为对称轴的对称，如果以一个曲线围绕y轴的旋转180°不变的称为y轴对称；另外一种是原点对称，即以原点O（0,0）作为对称轴的对称，如果以一个形状围绕原点旋转180°不变的称为原点对称。

最后，我们来讨论二次函数的变换，其中包括平移、旋转、放大、缩小、上下颠倒、左右颠倒，同一种变换可重复多次。

平移指在原曲线上上下左右移动，旋转指以某一点为原点，曲线以该点为中心旋转，放大指曲线的变形过程中曲线的总长不变，但它的所有部分的长度均增大；上下颠倒指曲线的上半部分变成下半部分，下半部分变成上半部分；左右颠倒指曲线的左半部分变成右半部分，右半部分变成左半部分。

综上所述，《二次函数的对称性与变换》是一个关于研究二次函数形式，其中包括其对称性以及变换的课题。

从基本特点上来讲，当a>0时，函数图形具有拱形，即形如一个弓或蝴蝶结；而当a<0时，图形具有凸起，即形似一个盔甲或自环。

此外，二次函数的对称性主要有两种，一种是y轴对称，一种是原点对称。

最后，二次函数的变换包括平移、旋转、放大、缩小、上下颠倒、左右颠倒等，同一种变换可重复多次。

二次函数平移规律口诀二次函数平移规律口诀：加左减右，加上减下。

意思就是当二次函数写成下面这个样子时：y=a(x+b)²+c，只要将y=ax²的函数图像按以下规律平移：b>0时，图像向左平移b个单位(加左)；b<0时，图像向右平移b个单位(减右)；c>0时，图像向上平移c个单位(加上)；c<0时，图像向下平移c个单位(减下)。

二次函数平移规律口诀图像应该怎么画1二次函数平移规律口诀加左减右，加上减下。

意思就是当二次函数写成下面这个样子时：y=a(x+b)²+c，只要将y=ax²的函数图像按以下规律平移：(1)b>0时，图像向左平移b个单位(加左)；(2)b<0时，图像向右平移b个单位(减右)；(3)c>0时，图像向上平移c个单位(加上)；(4)c<0时，图像向下平移c个单位(减下)。

2二次函数图像怎么画二次函数图像画法：一般地，二次函数的图像用五点法画出。

当x=0时，y的值（一个点）。

这个点关于二次函数对称轴的对称点（一个点）。

当y=0时，x的值（两个点）。

二次函数的顶点[一b/2a，（4ac一b^2）/4a]。

二次函数的基本表示形式为y=ax²+bx+c（a≠0）。

二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

二次函数表达式为y=ax²+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。

3二次函数的性质（1）二次函数的图像是抛物线，抛物线是轴对称图形。

对称轴为直线x=-b/2a。

（2）二次项系数a决定抛物线的开口方向和大小。

（3）一次项系数b和二次项系数a共同决定对称轴的位置。

（4）常数项c决定抛物线与y轴交点。

抛物线与y轴交于(0，c）4二次函数的历史大约在公元前480年，古巴比伦人和中国人已经使用配方法求得了二次方程的正根，但是并没有提出通用的求解方法。

二次函数的性质总结二次函数是数学中重要的一类函数，其一般形式为y = ax^2 + bx + c，其中a、b和c为常数，并且a不等于零。

在本文中，我们将总结二次函数的几个主要性质。

1. 对称性：二次函数的图像关于一个对称轴对称。

该对称轴是一个垂直于x轴的直线，其方程可通过求解二次函数的顶点坐标得到。

具体而言，对于函数y = ax^2 + bx + c，对称轴的方程为x = -b/2a。

2. 开口方向：二次函数的开口方向由二次系数a的正负决定。

当a > 0时，二次函数的图像开口向上；当a < 0时，二次函数的图像开口向下。

3. 零点：二次函数的零点是函数图像与x轴的交点，即使得y = 0的x值。

二次函数的零点可以通过求解二次方程ax^2 + bx + c = 0获得。

若二次方程有实数解，则函数与x轴有两个交点；若二次方程有两个相等的实数解，则函数与x轴有一个切点；若二次方程无实数解，则函数与x轴没有交点。

4. 极值点：二次函数的极值点是函数图像的最高点或最低点，又称顶点。

二次函数的顶点的x坐标为 -b/2a，y坐标为二次函数在该点的函数值。

当二次函数的开口向上时，顶点为函数的最小值；当二次函数的开口向下时，顶点为函数的最大值。

5. 函数增减性：二次函数在开口的两侧具有不同的增减性。

当二次函数的开口向上时，函数在顶点左侧递减，在顶点右侧递增；当二次函数的开口向下时，函数在顶点左侧递增，在顶点右侧递减。

6. 对称轴划分：对称轴将二次函数的图像分为两个对称部分。

通过对称性质，我们可以根据其中一部分的特征来得到另一部分的性质。

7. 图像与平移：对于给定的二次函数y = ax^2 + bx + c，通过平移可以得到一族相关的二次函数。

平移的方式包括上下平移和左右平移，改变二次函数的顶点位置和图像的位置。

综上所述，二次函数具有对称性、开口方向、零点、极值点、函数增减性、对称轴划分和图像与平移等性质。

二次函数图像与性质详解二次函数是高中数学中的重要概念之一，它在许多领域都有广泛的应用。

本文将详细介绍二次函数图像的性质，包括图像类型、顶点坐标、对称轴、开口方向以及图像的平移等内容。

1. 二次函数的基本形式二次函数的一般形式为：y=ax2+bx+c其中，a、b、c是实数且a ≠ 0。

在这个公式中，x 是自变量，y 是因变量。

二次函数图像是一条曲线，其形状取决于系数 a、b 和 c 的值。

2. 二次函数图像的类型根据系数 a 的取值，二次函数的图像可以分为以下三种类型：2.1 开口向上的二次函数当a > 0 时，二次函数的图像开口向上，形状类似于一个U 字形。

这种情况下，函数的最小值在顶点处达到，曲线在顶点处取得最小值。

2.2 开口向下的二次函数当 a < 0 时，二次函数的图像开口向下，形状类似于一个倒过来的 U 字形。

这种情况下，函数的最大值在顶点处达到，曲线在顶点处取得最大值。

2.3 平行于 x 轴的二次函数当 a = 0 时，二次函数退化为一次函数 y = bx + c，图像为一条平行于 x 轴的直线。

3. 二次函数图像的顶点坐标对于一般形式的二次函数，可以通过求解顶点来确定其顶点坐标。

顶点坐标可以表示为(ℎ,k)，其中 h 和 k 分别是顶点在 x 轴和 y 轴上的坐标。

顶点的坐标可以使用以下公式进行计算：$$ h = \\frac{-b}{2a} $$k=aℎ2+bℎ+c通过计算可以得到顶点坐标(ℎ,k)，进而确定二次函数图像上的最值点。

4. 二次函数图像的对称轴对称轴是指二次函数图像的对称线。

对于一般形式的二次函数，对称轴的方程可以通过以下公式计算：$$ x = \\frac{-b}{2a} $$对称轴与 x 轴垂直，并通过顶点。

5. 二次函数图像的平移二次函数图像可以通过平移作出一些调整。

平移可以分为沿 x 轴平移和沿 y 轴平移两种。

5.1 沿 x 轴平移沿 x 轴平移时，顶点(ℎ,k)的横坐标 h 会发生变化。

二次函数向上下左右平移规律二次函数是形如f(x) = ax^2 + bx + c的函数，其中a、b、c是常数且a≠0。

二次函数的向上、下、左、右平移是指对函数图像进行上下、左右平移的操作。

下面将详细介绍二次函数的向上下左右平移规律。

一、向上平移：对于二次函数f(x) = ax^2 + bx + c来说，向上平移就是把整个图像沿y轴的负方向平移h个单位。

形式上可以表示为f(x) = a(x - x0)^2 + c，其中(x0, c)是平移后图像上任意一点的坐标。

二、向下平移：向下平移是指把整个图像沿y轴的正方向平移h个单位，可以使用f(x)=a(x+x0)^2+c进行表示，其中(x0,c)是平移后图像上任意一点的坐标。

三、向左平移：对于二次函数f(x) = ax^2 + bx + c，向左平移就是把整个图像沿x轴的正方向平移k个单位，可以使用f(x) = a(x +k)^2 + b(x + k) + c进行表示。

四、向右平移：向右平移是指把整个图像沿x轴的负方向平移k个单位，可以使用f(x)=a(x-k)^2+b(x-k)+c进行表示。

接下来，我们将详细分析每种平移的规律。

1.向上平移规律：在二次函数f(x) = ax^2 + bx + c中，向上平移可以通过改变c的值来实现。

当c的值增加时，整个图像沿y轴的负方向平移；当c的值减少时，整个图像沿y轴的正方向平移。

2.向下平移规律：向下平移可以通过改变c的值来实现。

当c的值增加时，整个图像沿y轴的正方向平移；当c的值减少时，整个图像沿y轴的负方向平移。

3.向左平移规律：向左平移可以通过改变b的值来实现。

当b的值增加时，整个图像沿x轴的正方向平移；当b的值减少时，整个图像沿x轴的负方向平移。

4.向右平移规律：向右平移可以通过改变b的值来实现。

当b的值增加时，整个图像沿x轴的负方向平移；当b的值减少时，整个图像沿x轴的正方向平移。

需要注意的是，向上、下、左、右平移所改变的是函数图像的位置，而不改变图像的形状。