第三章45刚体运动方程与转动惯量
- 格式:ppt
- 大小:428.00 KB
- 文档页数:33




第三章刚体定点转动§3.1定点转动运动学一、什么是定点转动?刚体转动时,如果刚体内只有一点始终保持不动,这种运动叫刚体的定点转动。
由于做定点转动时刚体上有一点固定不动,一般以定点为基点。
陀螺、回转罗盘(用于航空和航海方面)等,都是刚体绕定点转动的实例。
它们都只有一点不动。
如图3.1.1所示的常平架中的圆盘可绕对称轴z O ′转动,对称轴固结在内悬架上,内悬架可绕固结于外悬架的图3.1.1此,ON 轴转动而外悬架又可绕固定轴Oz 转动,此三轴的交点O 则是始终不动的,所以这种运动和定轴转动的情形不同。
二、定点转动和定轴转动的联系与区别1.联系:定点转动可以看成绕瞬时轴的定轴转动。
把某一瞬时角速度ω的取向,亦即在该瞬时的转动轴叫转动瞬轴。
跟转动瞬心相仿,转动瞬轴在空间和刚体内各描绘一个定点在O 的锥面,前者叫空间极面,后者则叫本体极面。
刚体绕固定点的转动,也可看作时本体极面在空间极面上作无滑动的滚动,如图3.1.2所示。
2.区别:(1)关于转轴:定点转动的轴恒通过一定点,但其在空间的取向随着时间的改变而改变,定轴转动的转轴在空间的取向不变。
(2)关于角速度:定点转动矢量的量值和方向都是时间的函数。
而定轴转动的角速度方向恒沿着固定的转动轴,量值可以是时间的函数。
ω三、定点转动时刚体上任一点的速度r dt r d v v vv ×==ωυ (3.1.1)P图3.1.3如图3.1.3所示,刚体上任一点P 的运动可以看成是绕瞬时轴的转动,所以其速度在圆周的切线方向,大小为R ωυ=.四、定点转动时刚体上任一点的加速度由加速度的定义知r r r dtd r r dt d r dt d dt d a vv v v v vv v v v v v v v v v v 2)()(ωωωωωωωυωωυ−⋅+×=××+×=×+×==而 R r r v v v v v 22)(ωωωω−=−⋅则R r dtd a v v v v 2ωω−×= (3.1.2)上式中的第一项r dtd vv×ω为转动加速度,第二项R v 2ω−为向轴加速度. 例:半径为a 的碾盘在水平面上做无滑滚动,长为b 的水平轴OA 绕竖直轴OE 以匀角速度1ω转动,如图3.1.4所示.求碾盘最高点P 的速度和加速度.x图3.1.4解: 碾盘绕定点O 运动,取如图所示的直角坐标系,OA=b,AB=OE=a,j a i b r P ˆˆ+−=v 要使碾盘在水平面上做无滑滚动,则瞬时角速度的方向为BO 方向,且iab j j i ˆˆˆˆ1121ωωωωω+=+=v.则 kb j a i b i ab j r P P ˆ2)ˆˆ()ˆˆ(111ωωωωυ=+−×+=×=vv v . 或用瞬轴法:P 点速度大小:b PD P 12ωωυ=⋅=. 方向:oz 轴方向.加速度: ja b i b r dt d dt d a P P Pˆˆ321221ωωυωωυ−=×+×==v v v v v v§3.2定点转动刚体对定点的动量矩一、刚体的动量矩图3.2.1刚体是一特殊的质点系,刚体作定点转动时对定点O 的动量矩(角动量)等于刚体上的各质点对定点O 的动量矩之和(矢量和)。

刚体转动知识点总结1. 刚体的定义在物理学中,刚体是一个理想化的概念,用来描述物体的力学性质。
刚体是一个不会发生形变的物体,它具有不变的形状和大小。
在刚体转动的过程中,可以忽略物体的形变,只需考虑刚体的质量分布和外力作用情况。
2. 转动定律在刚体转动的过程中,存在着转动定律,即牛顿第二定律在转动运动中的应用。
根据转动定律,刚体的角加速度与作用在刚体上的合外力成正比,与刚体的转动惯量成反比。
转动定律可以用数学公式表示为:\[ \tau = I \alpha \]其中,$\tau$ 表示合外力矩,$I$ 表示刚体的转动惯量,$\alpha$ 表示刚体的角加速度。
3. 角动量角动量是描述刚体转动运动的物理量,它是刚体的转动惯量和角速度的乘积。
角动量可以用数学公式表示为:\[ L = I \omega \]其中,$L$ 表示角动量,$I$ 表示刚体的转动惯量,$\omega$ 表示角速度。
4. 转动惯量转动惯量是描述刚体对转动运动的惯性大小的物理量,它反映了刚体的质量分布对其转动运动的影响程度。
转动惯量的计算需要考虑刚体的形状和质量分布,通常需要使用积分来进行计算。
5. 转动运动方程刚体转动运动的规律可以通过转动运动方程来描述,转动运动方程可以表示为:\[ \tau = \frac{dL}{dt} \]其中,$\tau$ 表示合外力矩,$L$ 表示角动量,$t$ 表示时间。
转动运动方程描述了刚体的转动运动受到外力矩作用时角动量的变化规律。
6. 刚体的转动运动在刚体的转动运动中,需要考虑刚体的转动惯量、角速度、角加速度等物理量。
刚体的转动运动可以在直角坐标系下进行描述,通过使用牛顿运动定律和转动运动方程来分析刚体的转动运动规律。
7. 平行轴定理和垂直轴定理在计算刚体的转动惯量时,可以利用平行轴定理和垂直轴定理来简化计算过程。
根据平行轴定理和垂直轴定理,刚体绕与其质心平行(或垂直)且距离为$d$的轴转动的转动惯量可以表示为:\[ I = I_{\text{CM}} + Md^2 \]其中,$I$ 表示绕过质心平行(或垂直)轴转动的转动惯量,$I_{\text{CM}}$ 表示绕质心转动的转动惯量,$M$ 表示刚体的质量,$d$ 表示轴与质心的距离。
§3-1 刚体运动的描述§3-2 转动定律§3-3 刚体定轴转动的的功和能§3-4 角动量定理角动量守恒定律一. 刚体内部任意两点的距离在运动过程中始终保持不变的物体,即运动过程中不发生形变的物体。
➢刚体是实际物体的一种理想的模型二. 刚体的运动刚体的任意运动都可视为某一点的平动和绕通过该点的轴线的转动1.平动:运动过程中刚体内任意一条直线在运动过程中始终保持方向不变。
特点:刚体内所有点具有相同的位移、速度和加速度。
--刚体上任一点的运动规律即代表刚体的平动规律。
2. 转动:刚体上所有质点都绕同一轴线作圆周运动。
若转轴固定不变,则称为定轴转动。
特点:刚体内所有点具有相同的角位移、角速度和角加速度。
--刚体上任一点作圆周运动的规律即代表了刚体定轴转动的规律。
zO三. 刚体定轴转动的描述角位置: 1. 定轴转动的角量描述θθ=()t 角位移:)()(0t t θθθ∆-=角速度:ωθ=d dt角加速度:22dt d dt d θωβ==➢角速度和角加速度均为矢量,定轴转动中其方向沿转轴的方向并满足右手螺旋定则。
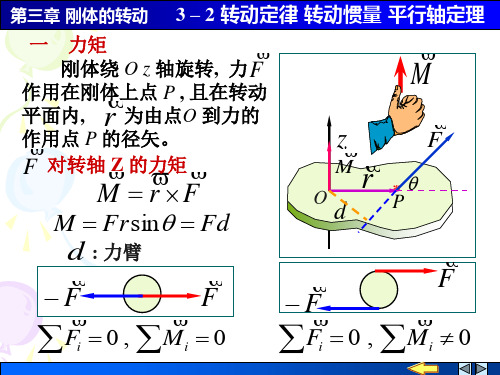
2. 角量和线量的关系ωr v =⎩⎨⎧==2ωβτr a r a n矢量表示:r r a r v 2ωβω-⨯=⨯=一. 力对转轴的力矩⊥⨯=F r M z||F r ⊥F ϕd FPO 大小:d F r F M ⊥⊥==ϕsin 方向: 沿⊥⨯F r 方向。
定轴转动中沿转动轴的方向。
二. 定轴转动定律O ϕi图26iriFifiθim∆Zωsin M r F i i i i =∑ϕ——合外力矩0)sin(=-∑i i i i r f θπ——内力的合力矩为零J r m ii =∑2∆——刚体的转动惯量 ()2⨯r i 并求和:)sin(sin 2β∆θπϕ∑∑∑=-+i i ii i i i i i i r m r f rF )('∑==+j ij i i i i i f f a m f F ∆⎪⎩⎪⎨⎧=-+-=-+ (2) )cos(cos )1( )sin(sin 2ω∆θπϕβ∆θπϕi i i i i i i i i i i i r m f F r m f FβJ M=--转动定律三. 转动惯量2i i r m J ∆∑=连续体:dmr J 2⎰=1. 转动惯量的物理意义:刚体转动惯性大小的量度。