刚体的转动惯量的计算表格

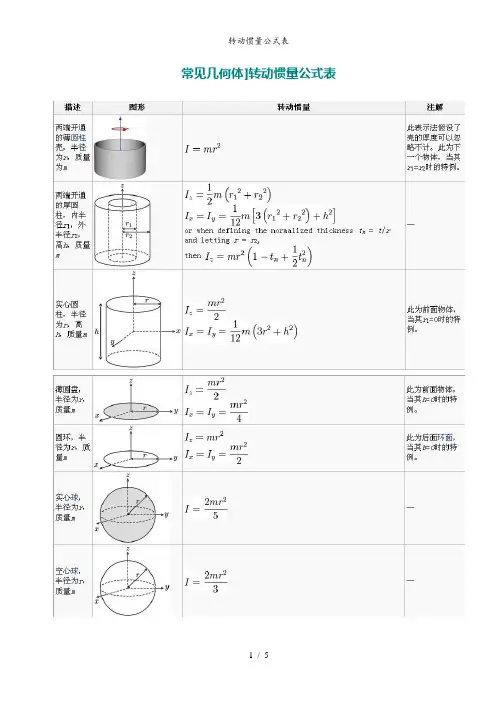
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。

当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。

对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。

对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。

对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。

对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。

只知道转动惯量的计算方式而不能使用是没有意义的。

下面给出一些（绕定轴转动时）的刚体动力学公式。

角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。

可以看出这个式子与牛顿第二定律是对应的。

角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。

只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v 只代表刚体的质心运动情况。

由这一公式，可以从能量的角度分析刚体动力学的问题。

转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。

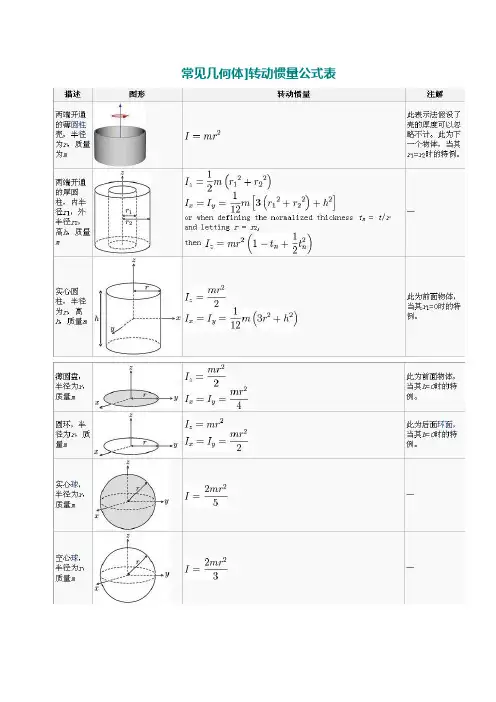
常见几何体]转动惯量公式表对于细杆当回转轴过杆得中点并垂直于杆时;J=m(L^2)/12 其中m就是杆得质量,L就是杆得长度。

当回转轴过杆得端点并垂直于杆时:J=m(L^2)/3 其中m就是杆得质量,L就是杆得长度。

对于圆柱体当回转轴就是圆柱体轴线时;J=m(r^2)/2其中m就是圆柱体得质量,r就是圆柱体得半径。

对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1与R2分别为其内外半径。

对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳得切线时,J=﹙5/3﹚mR^2;R为球壳半径。

对于实心球体当回转轴为球体得中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体得切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。

只知道转动惯量得计算方式而不能使用就是没有意义得。

下面给出一些(绕定轴转动时)得刚体动力学公式。

角加速度与合外力矩得关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。

可以瞧出这个式子与牛顿第二定律就是对应得。

角动量:角动量刚体得定轴转动动能:转动动能注意这只就是刚体绕定轴得转动动能,其总动能应该再加上质心动能。

只用E=(1/2)mv^2不好分析转动刚体得问题,就是因为其中不包含刚体得任何转动信息,里面得速度v只代表刚体得质心运动情况。

由这一公式,可以从能量得角度分析刚体动力学得问题。

转动惯量(Moment of Inertia)就是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止得特性)得量度,用字母I或J表示。

测量刚体的转动惯量实验实验目的：1. 了解刚体的转动惯量的概念；3. 通过实验测量出不同物体的转动惯量，并计算出实验数据的平均值和标准偏差。

实验原理1.定义在物理学中，转动惯量是刚体沿着某个轴线转动的惯性量度。

当物体绕某一轴线旋转时，与转动轴垂直距离为r的质点，其对轴线的力矩为Fr，力矩的大小与质点的距离r有关。

一个物体的转动惯量就是其质量分布规律和物体构形、轴线位置等因素所决定的惯性量度。

2.具体计算方法刚体绕轴转动时，转动惯量与转动轴有关。

设转动轴为z轴，物体某一质点的坐标为（x,y,z）,其质量为m，与z轴的距离为r，此质点对z轴的贡献是：Ir=m r2对于整个物体，所有质点对z轴的贡献叠加起来，就得到了整个物体相对于z轴的转动惯量，即通常情况下，应用叠加原理将整个物体内部相对于其它轴的转动惯量算出来，然后贝努利原理求得相对于某个轴的转动惯量。

3.实验方法本实验采用转动台平衡法，将受测物体弯挂在牵引线上，在规定的时间内给它以规定的角度的转动，然后测量转动惯量。

1) 弯挂物体，使它沿著摇晃轴（即z轴）平衡，确定物体与转动轴是平衡状态。

2) 水平移动弯挂物体的位置，使物体在水平方向上产生一个小的竖直角度。

松开物体后，它将在规定时间内平衡起来。

3)测量不同位移下回复振动的周期T，通过计算得到物体的转动惯量。

4. 实验仪器转动惯量测量装置、感应式编码器，数据采集器，计算机等。

5.实验步骤1)根据实验要求选择实验物体：小木棒、小圆盘、大木棒等。

（注：必须在实验前仔细测量物体的质量）3)将物体的初始位置水平移动一点，然后将其松开，记录振动的周期T1。

4)重复上述步骤，但每次增加一个小的角度，直到转动惯量达到了所需的最大值，记录全部数据。

5)把所有实验数据填入实验数据表中，并计算出相对误差、标准偏差，将结果汇总到汇总表中。

注意事项：1) 实验中所使用的支撑杆垂直于地面,固定牢靠，并要保持牵引线的水平状态使实测数据尽量准确。

常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。

当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。

对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。

对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。

对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。

对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。

只知道转动惯量的计算方式而不能使用是没有意义的。

下面给出一些（绕定轴转动时）的刚体动力学公式。

角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。

可以看出这个式子与牛顿第二定律是对应的。

角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。

只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v 只代表刚体的质心运动情况。

由这一公式，可以从能量的角度分析刚体动力学的问题。

转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。

转动惯量公式表 Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12其中m是杆的质量，L是杆的长度。

当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3其中m是杆的质量，L是杆的长度。

对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。

对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。

对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。

对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。

只知道转动惯量的计算方式而不能使用是没有意义的。

下面给出一些（绕定轴转动时）的刚体动力学公式。

角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外，β为。

可以看出这个式子与牛顿第二定律是对应的。

角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。

只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v只代表刚体的质心运动情况。

由这一公式，可以从能量的角度分析刚体动力学的问题。

说明：本文《转动惯量的计算》特地收集贡献出来供各位工程技术人员在参阅本人劣作《风机动平衡调试方法》时参考。

深圳华晶玻璃瓶有限公司工程部（动力车间）李宜斌编辑2010-10-21转动惯量的计算转动惯量应用于刚体各种运动的动力学计算中。

单个质点的转动惯量：I = m× r2.质点系的转动惯量：I = Σ m i×r i2.质量连续分布的刚体的转动惯量：I = ∫m r2dm。

以上各式中的r理解为质点到转轴的距离。

刚体绕轴转动惯性的度量。

其数值为J=∑ mi*ri^2，式中mi表示刚体的某个质点的质量，ri表示该质点到转轴的垂直距离。

求和号（或积分号）遍及整个刚体。

转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。

规则形状的均质刚体，其转动惯量可直接计得。

不规则刚体或非均质刚体的转动惯量，一般用实验法测定。

描述刚体绕互相平行诸转轴的转动惯量之间的关系，有如下的平行轴定理：刚体对一轴的转动惯量，等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。

由于和式的第二项恒大于零，因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。

垂直轴定理：一个平面刚体薄板对于垂直它的平面轴的转动惯量，等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。

表达式:Iz=Ix+Iy刚体对一轴的转动惯量，可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。

由此折算所得的质点到转轴的距离，称为刚体绕该轴的回转半径κ，转动惯量的量纲为L^2M，在SI单位制中，它的单位是kg·m^2。

刚体绕某一点转动的惯性由更普遍的惯量张量描述。

惯量张量是二阶对称张量，它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。

补充对转动惯量的详细解释及其物理意义：先说转动惯量的由来，先从动能说起大家都知道动能E=(1/2)mv^2，而且动能的实际物理意义是：物体相对某个系统（选定一个参考系）运动的实际能量，（P势能实际意义则是物体相对某个系统运动的可能转化为运动的实际能量的大小）。

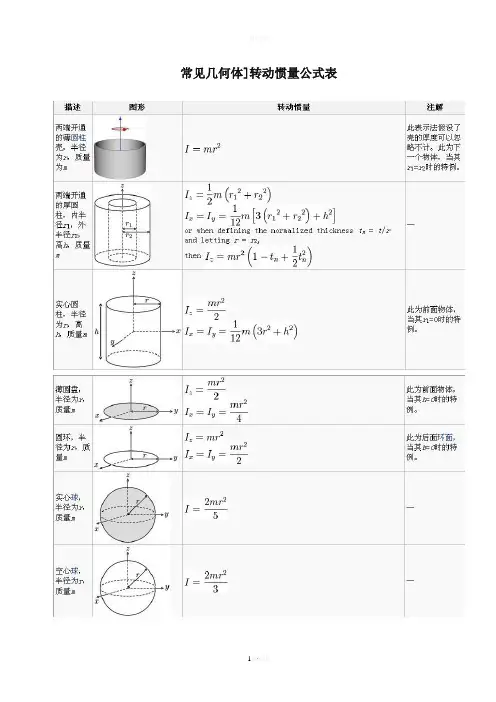
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时；J=m(L^2)/12 其中m是杆的质量，L是杆的长度。

当回转轴过杆的端点并垂直于杆时：J=m(L^2)/3 其中m是杆的质量，L是杆的长度。

对于圆柱体当回转轴是圆柱体轴线时；J=m(r^2)/2其中m是圆柱体的质量，r是圆柱体的半径。

对于细圆环当回转轴通过中心与环面垂直时，J=mR^2；当回转轴通过边缘与环面垂直时，J=2mR^2；R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时，J=﹙1/2﹚mR^2；当回转轴通过边缘与盘面垂直时，J=﹙3/2﹚mR^2；R为其半径对于空心圆柱当回转轴为对称轴时，J=﹙1/2﹚m[（R1）^2+（R2）^2]；R1和R2分别为其内外半径。

对于球壳当回转轴为中心轴时，J=﹙2/3﹚mR^2；当回转轴为球壳的切线时，J=﹙5/3﹚mR^2；R为球壳半径。

对于实心球体当回转轴为球体的中心轴时，J=﹙2/5﹚mR^2；当回转轴为球体的切线时，J=﹙7/5﹚mR^2；R为球体半径对于立方体当回转轴为其中心轴时，J=﹙1/6﹚mL^2；当回转轴为其棱边时，J=﹙2/3﹚mL^2；当回转轴为其体对角线时，J=（3/16）mL^2；L为立方体边长。

只知道转动惯量的计算方式而不能使用是没有意义的。

下面给出一些（绕定轴转动时）的刚体动力学公式。

角加速度与合外力矩的关系：角加速度与合外力矩式中M为合外力矩，β为角加速度。

可以看出这个式子与牛顿第二定律是对应的。

角动量：角动量刚体的定轴转动动能：转动动能注意这只是刚体绕定轴的转动动能，其总动能应该再加上质心动能。

只用E=（1/2）mv^2不好分析转动刚体的问题，是因为其中不包含刚体的任何转动信息，里面的速度v 只代表刚体的质心运动情况。

由这一公式，可以从能量的角度分析刚体动力学的问题。

转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。

实验四 刚体的转动惯量1、 测量环对中心轴的转动惯量实验中的有关参数： （砝码每片5.0g ，砝码钩：5.0g ） 铝环半径：外R =120.00（0.02）mm ，内R =105.00（0.02）mm 铝环质量：2m =砝码与钩质量：1m =25.0（0.5）g塔轮半径：r =25.00（0.02）mm 角位移πθ21= πθ82=（1） 有铝环时转动惯量的测量数据转动惯量)(u I（2） 无铝环时转动惯量的测量数据转动惯量)(0u I（3） 铝环的转动惯量实验值：0I I I x -= 0II I u u u x +==)(0u I理论值：2/)(2外2理2理R R m I +==）u （理I2、 测铝盘对中心的转动惯量（用最小二乘法处理数据）实验中有关参数：铝环半径：外R =120.00（0.02）mm 塔轮半径：r =25.00（0.02）mm 初角速度00=ω 角位移：πθ8=铝盘质量：=3m （1） 有铝盘时转动惯量的测量数据用最小二乘法拟合2/1～m t 曲线计算：直线方程：斜率： =k转动惯量： ==)2/(·θrad kgI （2） 无铝盘时转动惯量的测量数据测量数据：用最小二乘法拟合2/1～m t 曲线计算：直线方程： 斜率： =k转动惯量： ==)2/(·θrad kgI （3） 铝盘的转动惯量 实验值：=-=0I I I x理论值：==2/）u （23理R m I3、 验证平行轴定理实验中有关参数： 两个钢柱的质量 =02m质心相对轴平移的距离 mm d 25= 角位移πθ21= πθ82=（1） 钢柱在)2,2(位置时转动惯量的测量数据转动惯量1I（2） 钢柱在)3,1('或)3,1('位置时转动惯量的测量数据转动惯量1I计算：=-12I I=202d m思考题。

刚体转动惯量的测量转动惯量是刚体转动时惯性大小的量度，它与刚体的质量、质量对轴的分布以及转轴位置有关。

如果刚体形状规则，质量分布均匀，可以直接计算出它绕特定轴的转动惯量。

但对于几何形状不规则和质量分布不均匀的刚体，只能用实验的方法来测量。

测量转动惯量的方法有很多种，如三线摆法、单悬扭摆法、双悬扭摆法、螺旋弹簧式扭摆法等，本实验介绍了利用螺旋弹簧式扭摆法来测量刚体的转动惯量。

一、实验目的1．观察扭摆振动现象。

2．用扭摆法测量不同形状刚体的转动惯量。

二、实验原理螺旋弹簧式扭摆如图6.1所示，在垂直轴上装有螺旋弹簧，用以产生恢复力矩。

在轴的上方可以装上各种待测刚体。

将刚体在水平面内转过某一角度θ后，在弹簧的恢复力矩的作用下，刚体就开始绕垂直转轴作往返扭转运动。

根据胡克定律，弹簧产生的恢复力矩M 与所转过的角位移θ成正比：θK M −= （1）式中，K 为弹簧的扭转系数，负号表示恢复力矩M 的方向与角位移θ的方向相反。

又根据转动定律，则有22dt d JJ M θβ== （2）其中，J 为刚体的转动惯量，β为角加速度。

联立式(1)、(2)可得：022=+θθJ Kdtd 令ω2=K /J ，上式变为：0222=+θωθdtd （3） 方程(3)表明扭摆运动具有角简谐振动的特征：角加速度与角位移成正比，而方向相反。

其通解为：)cos(0ϕωθθ+=t 式中，θ0为谐振动的角振幅，ϕ为初相位，ω为角速度。

扭摆的振动周期为：KJ T πωπ22==或 K J T 224π=（4） 上式表明，扭摆周期T 的平方与转动惯量J 成正比。

若单独测出扭摆周期，因扭摆系数K 是未知量，所以还不能由式(4)计算出转动惯量，为此，一般采用比较法求出K 。

实验中用一个几何形状规则的圆柱体，它的转动惯量J 1可以根据其质量和几何尺寸用理论公式直接计算得到。

设金属载物圆盘的转动惯量为J 0，转动的周期为T 0，若将圆柱体置于金属载物盘上，测出它的摆动周期T 1，则KJ T 0224π= KJ J T 012214+=π （5） 由式(5)可以确定K ，J 0。

描述图形转动惯量注解
两端开
通的薄
圆柱壳，
半径为
r，质量
为m
此表示法假设
了壳的厚度可
以忽略不计。

此为下一个物
体，当其r1=r2
时的特例。

两端开
通的厚
圆柱，内
半径r1，
外半径
r2，高h，
质量m
or when defining the normalized thickness
t n = t/r and letting r = r2,
then
—
实心圆
柱，半径
为r，高
h，质量
m
此为前面物
体，当其r1=0
时的特例。

薄圆盘，
半径为
r，质量
m
此为前面物
体，当其h=0
时的特例。

圆环，半径为r，质量m 此为后面环面，当其b=0时的特例。

实心球，
半径为
r，质量
m
—
空心球，
半径为
r，质量
m
—
圆锥，半
径为r，
高h，质
量m
—
实心长方体，高h，宽w，长d，质量m 边长为s的立方体的转动惯量
.
细棒，长L，质量m 此表示法假设了棒的宽度和厚度可以忽略不计。

此为前面物体，当其w=L，h=d=0时的特例。

细棒，长L，质量m 此表示法假设了棒的宽度和厚度可以忽略不计。

环面，圆
管的半径a，截面的半径b，质量m。

关于直径：
关于纵轴：
—
薄多边形，顶点
，，
，……，
，质量m。