当前位置：文档之家 › 第五章 虚拟变量模型和滞后变量模型

第五章 虚拟变量模型和滞后变量模型

  • 格式：doc
  • 大小：546.00 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

虚拟变量模型滞后变量模型

虚拟变量模型滞后变量模型

• 可以通过传统的回归检验，对2的统计显著性 进行检验，以判断企业男女职工的平均薪金
水平是否有显著差异。
年薪 Y
男职工
女职工
2
0
工龄 X
又例：在横截面数据基础上，考虑个人保 健支出对个人收入和教育水平的回归。
教育水平考虑三个层次：高中以下， 高中， 大学及其以上。
这时需要引入两个虚拟变量：
1 D1 0
将n1与n2次观察值合并，并用以估计以下回归：
Yi 0 1 X i 3 Di 4 (Di X i ) i
Di为引入的虚拟变量：
1 Di 0
90年前 90年后
于是有： E(Yi | Di 0, X i ) 0 1 X i
E(Yi | Di 1, X i ) ( 0 3 ) (1 4 ) X i
一、滞后变量模型
在经济运行过程中，广泛存在时间滞后 效应。某些经济变量不仅受到同期各种因素 的影响，而且也受到过去某些时期的各种因 素甚至自身的过去值的影响。
通常把这种过去时期的，具有滞后作用的 变量叫做滞后变量（Lagged Variable），含有 滞后变量的模型称为滞后变量模型。
滞后变量模型考虑了时间因素的作用，使 静态分析的问题有可能成为动态分析。含有滞 后解释变量的模型，又称动态模型 （Dynamical Model）。
其矩阵形式为：
Y (X,D)α β μ
如果只取六个观测值，其中春季与夏季取了 两次，秋、冬各取到一次观测值，则式中的：
1 1 (X,D) 1 1 11
X 11 X 12 X 13 X 14 X 15 X 16
X k1 X k2 X k3 X k4 X k5 X k6
1 0 0 0 0 1
E(Yi | X i , Di 0) 0 1 X i 企业男职工的平均薪金为：

《滞后变量模型 》课件

《滞后变量模型 》课件
特点
滞后变量模型考虑了时间序列数据的 自相关性和时间依赖性，能够更好地 解释和预测时间序列数据的变化趋势 。
滞后变量模型的应用场景
经济预测
用于预测股票价格、消费、投资等经济指标的 变化趋势。
金融分析
用于分析股票、债券、期货等金融产品的价格 波动和趋势。
自然灾害研究
用于预测地震、洪水等自然灾害的发生和影响。
要点三
案例分析
例如，在分析气温变化时，可以引入 前一期的气温作为滞后变量。通过建 立滞后变量模型，可以对未来气候变 化趋势进行预测，为应对气候变化提 供科学依据。
06
总结与展望
滞后变量模型的优势与不足
01
优势
02
考虑了时间滞后效应，能够更好地描述经济现象的 动态变化。
03
在数据不足的情况下，可以利用已知信息进行预测 ，提高预测精度。
找最优解。
参数估计的步骤
模型设定
根据研究目的和数据特征，设 定合适的滞后变量模型。
模型检验
对估计的参数进行检验，确保 模型的拟合效果和预测能力。
数据收集
收集与滞后变量模型相关的数 据，确保数据的准确性和完整 性。
估计参数
根据设定的模型选择合适的参 数估计方法，对模型中的未知 参数进行估计。
结果解释
滞后变量模型与其他模型的比较
与线性回归模型相比
滞后变量模型考虑了自相关性，能够 更好地处理时间序列数据。
与ARIMA模型相比
滞后变季节性 和趋势的影响。
02
滞后变量模型的原理
滞后变量的产生原因
经济现象的惯性
经济现象的变化往往具有惯性， 一个变量的变化往往会影响其未 来的变化趋势，因此需要引入滞

计量经济学习题与解答5.

计量经济学习题与解答5.

第五章经典单方程计量经济学模型：专门问题一、内容提要本章主要讨论了经典单方程回归模型的几个专门题。

第一个专题是虚拟解释变量问题。

虚拟变量将经济现象中的一些定性因素引入到可以进行定量分析的回归模型，拓展了回归模型的功能。

本专题的重点是如何引入不同类型的虚拟变量来解决相关的定性因素影响的分析问题，主要介绍了引入虚拟变量的加法方式、乘法方式以及二者的组合方式。

在引入虚拟变量时有两点需要注意，一是明确虚拟变量的对比基准，二是避免出现“虚拟变量陷阱”。

第二个专题是滞后变量问题。

滞后变量包括滞后解释变量与滞后被解释变量，根据模型中所包含滞后变量的类别又可将模型划分为自回归分布滞后模型与分布滞后模型、自回归模型等三类。

本专题重点阐述了产生滞后效应的原因、分布滞后模型估计时遇到的主要困难、分布滞后模型的修正估计方法以及自回归模型的估计方法。

如对分布滞后模型可采用经验加权法、Ａlmon多项式法、Koyck方法来减少滞项的数目以使估计变得更为可行。

而对自回归模型，则根据作为解释变量的滞后被解释变量与模型随机扰动项的相关性的不同，采用工具变量法或OLS法进行估计。

由于滞后变量的引入，回归模型可将静态分析动态化，因此，可通过模型参数来分析解释变量对被解释变量影响的短期乘数和长期乘数。

第三个专题是模型设定偏误问题。

主要讨论当放宽“模型的设定是正确的”这一基本假定后所产生的问题及如何解决这些问题。

模型设定偏误的类型包括解释变量选取偏误与模型函数形式选取取偏误两种类型，前者又可分为漏选相关变量与多选无关变量两种情况。

在漏选相关变量的情况下，OLS估计量在小样本下有偏，在大样本下非一致；当多选了无关变量时，OLS估计量是无偏且一致的，但却是无效的；而当函数形式选取有问题时，OLS估计量的偏误是全方位的，不仅有偏、非一致、无效率，而且参数的经济含义也发生了改变。

在模型设定的检验方面，检验是否含有无关变量，可用传统的t检验与F检验进行；检验是否遗漏了相关变量或函数模型选取有错误，则通常用一般性设定偏误检验（RESET检验）进行。

5专门问题hf

5专门问题hf
女职工本科以上学历的平均薪金： E ( Y i | X i , D 1 0 , D 2 1 ) ( 0 3 ) 1 X i
男职工本科以上学历的平均薪金： E ( Y i | X i , D 1 1 , D 2 1 ) ( 0 2 3 ) 1 X i
பைடு நூலகம்
2、乘法方式
• 加法方式引入虚拟变量，考察：截距的不同。
• 其未违背任何基本假设，可直接用OLS法估计。 • 其可检验H0: B2= 0,大学教育对起薪没有益处。 • 在社会学、心理学、教育学及市场研究等领域
，ANOVA模型用广泛，经济学中用得很少。
2、虚拟变量模型
• 同时含有定量解释变量与虚拟变量的模型称为 协方差分析（analysis-of covariance, ANCOVA） 模型。
个D，一共引入的虚拟变量数为：
k j 1 (n j 1 ) k j 1n j k
• 如果不含常数项，可以在以上基础上多 引入1个虚拟变量；即当且仅当某个因素 的所有categories均引入1个虚拟变量。
• 根据前述说明回答：
• 如果在服装需求函数模型中必须包含3个 定性变量：季节（4种状态）、性别（2 种状态）、职业（5种状态），应该设置 多少虚变量？
– 11，但2=2 ，即两个回归的差异仅在其截距， 称为平行回归（Parallel Regressions）;
– 1=1，但22 ，即两个回归的差异仅在其斜率， 称为汇合回归(Concurrent Regressions)；
– 11，且22 ，即两个回归完全不同，称为相异 回归（Dissimilar Regressions）。
• 许多情况下，斜率发生变化，或斜率、截距同时 发生变化。
• 为反映斜率变化，可通过以乘法方式引入虚拟变 量来测度。

计量经济学分布滞后模型

计量经济学分布滞后模型

Yt 0 1Yt 1 2Yt 2 qYt q 0 X t 1 X t 1 s X t s t
q，s：滞后时间间隔
自 回 归 分 布 滞 后 模 型 （ autoregressive distributed lag model, ADL）：既含有Y对自身滞 后变量的回归，还包括着X分布在不同时期的滞 后变量。
例5.2.1 对一个分布滞后模型：
Y t 0 0 X t 1 X t 1 2 X t 2 3 X t 3 t
给定递减权数：1/2， 1/4， 1/6， 1/8 令
W 1t 1 1 1 1 X t X t 1 X t 2 X t 3 2 4 6 8
有限自回归分布滞后模型：滞后期长度有限 无限自回归分布滞后模型：滞后期无限
（1）分布滞后模型（distributed-lag model）
分布滞后模型：模型中没有滞后被解释变量， 仅有解释变量X的当期值及其若干期的滞后值：
Yt i 短 期 (short-run) 或 即 期 乘 数 (impact multiplier) ，表示本期 X 变化一单位对 Y 平均值 的影响程度。 i (i=1,2…,s)：动态乘数或延迟系数，表 示各滞后期X的变动对Y平均值影响的大小。
1. 滞后效应与与产生滞后效应的原因 因变量受到自身或另一解释变量的前几期值 影响的现象称为滞后效应。 表示前几期值的变量称为滞后变量。 如：消费函数 通常认为，本期的消费除了受本期的收入影 响之外，还受前1期，或前2期收入的影响： Ct=0+1Yt+2Yt-1+3Yt-2+t Yt-1，Yt-2为滞后变量。
(1)经验加权法
根据实际问题的特点、实际经验给各滞后变 量指定权数，滞后变量按权数线性组合，构成新 的变量。权数据的类型有：

§5.2 滞后变量模型

§5.2 滞后变量模型

................................ . ... ....... ... .. .
王中昭制作
滞后变量模型的一般形式
• • • • • • • • • • •
在模型中含有滞后变量的模型称为滞后变量模型。 滞后变量模型的一般形式（线性）： Yt=b0+b1Yt-1+…+bsYt-s+a0Xt+…+aq Xt-q+μt S,q分别称为滞后因变量和滞后解释变量的滞后期。 例如：消费函数：Ct= b0+b1Ct-1+b2It+μt （1）、分布滞后模型 只含有滞后解释变量的模型称为分布滞后模型。 Yt=b0+a0Xt+…+aq Xt-q+μt （2）、自回归模型 只含有解释变量和滞后因变量的模型称为自回归模型。 例如：Yt=b0+b1Yt-1+…+bsYt-s+a0Xt+μt
பைடு நூலகம்
王中昭制作
4、模型的参数含义
• （1）、对于分布滞后模型： • Yt=a0+b0Xt+b1Xt-1+…+bsXt-s+μt • 分布滞后模型的各系数体现了解释变量的当 期值和各期滞后值对被解释变量的不同影响程度。 因此称为乘数。 • b0称为短期（或即期）乘数，表示本期X变 化一单位对Y平均值的影响程度。 bi (i=1,2…,s)： 动态乘数或延迟系数，表示各滞后期X的变动对 Y平均值影响的大小。 • b0+b1+…+bs称为累计系数或长期或均衡乘 数，表示X变动一个单位，由于滞后效应而形成 的对Y平均值总累计影响的大小。
•
• 即把它化为分布滞后模型。各种参数的含义与 分布滞后模型相同。

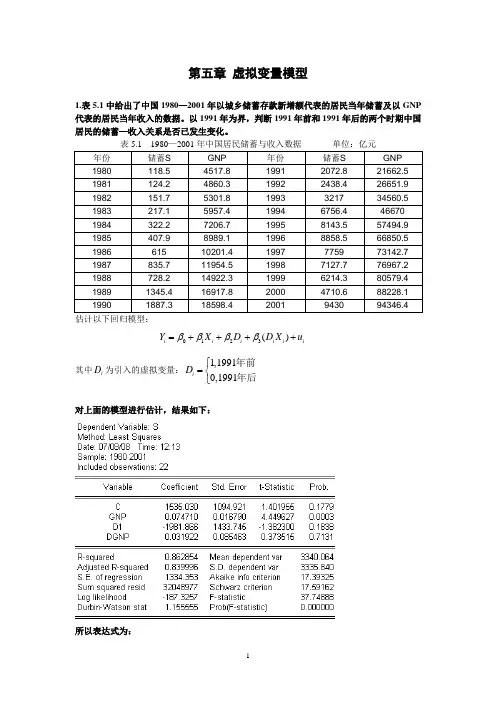
(精品)第五章-虚拟变量模型和滞后变量模型

(精品)第五章-虚拟变量模型和滞后变量模型

第五章虚拟变量模型1.表5.1中给出了中国1980—2001年以城乡储蓄存款新增额代表的居民当年储蓄及以GNP 代表的居民当年收入的数据。

以1991年为界，判断1991年前和1991年后的两个时期中国居民的储蓄—收入关系是否已发生变化。

年份储蓄S GNP 年份储蓄S GNP 1980 118.5 4517.8 1991 2072.8 21662.5 1981 124.2 4860.3 1992 2438.4 26651.9 1982 151.7 5301.8 1993 3217 34560.5 1983 217.1 5957.4 1994 6756.4 46670 1984 322.2 7206.7 1995 8143.5 57494.9 1985 407.9 8989.1 1996 8858.5 66850.5 1986 615 10201.4 1997 7759 73142.7 1987 835.7 11954.5 1998 7127.7 76967.2 1988 728.2 14922.3 1999 6214.3 80579.4 1989 1345.4 16917.8 2000 4710.6 88228.1 1990 1887.3 18598.4 2001 9430 94346.4 估计以下回归模型：0123()i i i i i iY X D D X uββββ=++++其中iD为引入的虚拟变量：1,19910,1991iD⎧=⎨⎩年前年后对上面的模型进行估计，结果如下：所以表达式为：15350.0751981.90.032()i i i i i Y X D D X =+-+(1.40) (4.45) (-1.38) (0.37)从2β和3β的t 检验值可以知道，这两个参数显著的为0，所以1991年前和1991年后两个时期的回归结果是相同的。

下面用邹式检验来验证上面对于两个时期的回归结果相同的结论是否正确。

计量经济学第五章 专门问题-滞后变量模型

计量经济学第五章 专门问题-滞后变量模型

•递减型： 即认为权数是递减的， X的近期值对Y的影响较 远期值大。 如消费函数中，收入的近期值对消费的影响作 用显然大于远期值的影响。 例如：滞后期为 3的一组权数可取值如下： 1/2， 1/4， 1/6， 1/8
则新的线性组合变量为：
W 1t 1 1 1 1 X t X t 1 X t 2 X t 3 2 4 6 8
《计量经济学》
《Econometrics》 《经济计量学》
1
5.2 滞后变量模型
一、滞后变量模型 二、分布滞后模型的参数估计 三、自回归模型的参数估计 四、格兰杰因果关系检验
一、滞后变量模型

在经济运行过程中，广泛存在时间滞后效应。某些经 济变量不仅受到同期各种因素的影响，而且也受到过 去某些时期的各种因素甚至自身的过去值的影响。 通常把这种过去时期的，具有滞后作用的变量叫做滞 后变量（Lagged Variable），含有滞后变量的模型称 为滞后变量模型。 滞后变量模型考虑了时间因素的作用，使静态分析的 问题有可能成为动态分析。含有滞后解释变量的模型 ，又称动态模型（Dynamical Model）。
有限自回归分布滞后模型：滞后期长度有限
无限自回归分布滞后模型：滞后期无限
（1）分布滞后模型（distributed-lag model）
分布滞后模型：模型中没有滞后被解释变量， 仅有解释变量X的当期值及其若干期的滞后值：
Yt i X t i t
i 0 s
0：短期(short-run)或即期乘数(impact multiplier)， 表示本期X变化一单位对Y平均值的影响程度。 i (i=1,2…,s)：动态乘数或延迟系数，表示各 滞后期X的变动对Y平均值影响的大小。

第5章滞后变量模型1

第5章滞后变量模型1
y=10+2*x+x(-1)+0.5*x(-2)+0.25*x(-3)+0.125*x(-4) +0.0625*x(-5)+0.03125*x(-6)
这里，假设X的系数按照：2、1、 0.5、 0.25、
0.125、 0.0625、 0.03125递减，表示距离现在越近， X的影响越大
作以下两个模拟试验
4
0.125
0.5 0.031496
3.875 0.976378
5 0.0625 0.3125 0.015748
3.9375 0.992126
6 0.03125 0.1875 0.007874 3.96875
1
总乘数＝3.96875，平均滞后时间=0.944882
有限分布滞后模型的估计
模型：
Y t a b 0 X t b 1 X t 1 b 2 X t 2 b sX t s u t t s 1 ,s 2 , ,n
内生滞后变量模型
外生滞后变量模型经过变换后往往成为 内生滞后变量模型。
Koyck变换模型 局部调整模型 适应性期望模型
1、Koyck变换模型
内生变量模型X的滞后期有时无法确定， 是无限的，模型的形式为
Y t a b 0 X t b 1 X t 1 b 2 X t 2 b s X t s u t
2.0
1.5
1.0
0.5
0.0 50 55 60 65 70 75 80 85 90 XX
15 14 13 12
11
10
9 50 55 60 65 70 75 80 85 90
Y
一般地，在模型
Yt a b0 X t b1 X t1 b2 X t2 t s 1, s 2, , n

eviews分布滞后和虚拟变量模型

eviews分布滞后和虚拟变量模型
一个远端约束限制 x 对 y 的作用在大于定义滞后的数目衰 减：
k1 1 2 (k 1 c) 3(k 1 c)2 p1(k 1 c) p 0
如果限制滞后算子的近端或远端，参数个数将减少一个来 解释这种约束。如果对近端和远端都约束，参数个数将减少二个。
EViews缺省不加任何约束。
2021/3/26
2021/3/26
第14页/共55页
14
二、在自回归模型中侦察自相关：德宾h检验
误差项 t 中可能的序列相关会使自回归模型 的估计变得复杂。如果原始模型中的误差项 ut 为 序列无关，则存量调整模型的误差项 t 就不会是 序列相关的。然而对于考伊克和适应性期望模型， 即使 序列ut 无关， 仍可t 能是序列相关。于是怎 样知道自相关模型中的误差项是否序列相关呢？
一、多项式分布滞后模型的估计方法
对于有限滞后长度的情形，分布滞后模型的一般形式如下
yt 0xt 1xt1 k xtk ut
(8.1.1)
其中系数 描述 x 对 y 作用的滞后。在模型中解释变量与
随机误差项不相关的情况下，可以直接使用OLS估计参数。 但是，一个显然的问题是解释变量之间，即 x 的当前和滞后 值之间具有高度共线性，而共线性问题的一个直接后果是参 数估计量失去意义，不能揭示 x 的各个滞后量对因变量的影 响，所以必须寻求另外的估计方法。
7
逐个观察，GDP滞后的系数统计上都不显著。但总体上讲回归具有一个合 理的R2 (尽管D—W统计量很低)。这是回归自变量中多重共线的典型现象，建 议拟合一个多项式分布滞后模型。估计一个无限制的3阶多项式滞后模型，输 入变量列表：INV c PDL(GDP, 3, 2)，窗口中显示的多项式估计系数，PDL01,

虚拟变量模型

虚拟变量模型

§5.2 滞后变量模型
§5.1
虚拟变量模型
一、虚拟变量的含义 二、虚拟变量的设置 三、虚拟变量的引入
一、虚拟变量的含义
•一种人为构造的、取值仅为“1”或“0”的变量
1. 定量变量和定性变量

定量变量：测度等级为间距（interval）或比率（ratio）尺度的变量，
如需求量、价格、收入、产量等
测度等级名义nominal或顺序ordinal尺度的变量如性别教育程度等其取值为类别或顺序可用数值表示但数值不具有实际含义仅是表示类别或序次的代码实际建模中考虑定性变量的影响是必要的但直接使用定性变量的取值则具有不合理性直接使用定性变量的不合理性例
第五章 经典单方程计量经济学模型专门问题
§5.1 虚拟变量模型
Yi 1 X i 2 E1i＋ 3 E2i 4 E3i i
大多数研究者认为 ，在一个含有截距的方程中，他们能更容易地处 理他们通常感兴趣的问题，是否有某个组与基准组有所不同以及有 多大不同，所以在方程中包括截距更方便。
——肯尼迪（Kennedy）
三、虚拟变量的引入

虚拟变量做为解释变量引入模型有两种基本方式： 加法方式和乘法方式。
◦ 其取值为具有实际含义的数据 ◦ 可以在建模过程中直接使用这些变量及其数据

定性变量：测度等级名义（nominal）或顺序（ordinal）尺度的变量，
如性别、教育程度等
◦ 其取值为类别或顺序，可用数值表示，但数值不具有实际含义，仅是表示
类别或序次的代码
性别（1－男；0－女）、教育程度（1－小学、2－初中、3－高中、4－大学）
• 其差异为：
E(男)－E(女)＝ 2
• 可以看出，虚拟变量对应的回归系数β2表示：虚拟变量取值为1所代表 的类别（男）相对于参照类别（取值为0，女）在因变量上的平均差异， 反映出定性变量取值的变化对因变量的影响 • 从回归模型上看，两个组上的回归模型的差异主要在于截距的不同

计量经济学第五章(新)

计量经济学第五章(新)

利用Eviews得回归方程为：
ˆ ln y 1.6524 0.3397 ln x1 0.9460 ln x2
t = (-2.73) p= (0.0144*) R2=0.995 (1.83) (0.085) (9.06) (0.000**)
对回归方程解释如下：斜率系数0.3397表示 产出对劳动投入的弹性，即表明在资本投入保持 不变的条件下，劳动投入每增加一个百分点，平 均产出将增加0.3397个百分点。同样地，在劳动 投入保持不变的条件下，资本投入每增加一个百 分点，产出将平均增加0.8640个百分点。两个弹 性系数相加为规模报酬参数，其数值等于1.1857 ，表明墨西哥经济的特征是规模报酬递增的（如 果数值等于1，属于规模报酬不变；小于1，则属 于规模报酬递减）。
20.5879 z 1 20.5879 x (4.6794 ) (4.3996 ** )
3、半对数模型和双对数模型
形式为：
ln y 0 1 x u y 0 1 ln x u
的模型称为半对数模型。 把形式为:
ln y 0 1 ln x u
即可利用多元线性回归分析的方法处理了。
例如，描述税收与税率关系的拉弗曲线：抛物线 t = a + b r + c r2 c<0
t：税收；
r：税率
设 z1 = r， z 2 = r2， 则原方程变换为 s = a + b z1 + c z 2 c<0
例 某生产企业在1981-1995年间每年的产量和总成本如下 表，试用回归分析法确定其成本函数。
表5-1 墨西哥的实际GDP、就业人数和实际固定资本
年份 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 GDP 114043 120410 129187 134705 139960 150511 157897 165286 178491 199457 212323 226977 241194 260881 277498 296530 306712 329030 354057 374977 就业人数 8310 8529 8738 8952 9171 9569 9527 9662 10334 10981 11746 11521 11540 12066 12297 12955 13338 13738 15924 14154 固定资产 182113 193749 205192 215130 225021 237026 248897 260661 275466 295378 315715 337642 363599 391847 422382 455049 484677 520533 561531 609825

计量经济学滞后变量模型

计量经济学滞后变量模型

• 矩型：
即认为权数是相等的，X的逐期滞后值对值 Y的影响相同。 如滞后期为3，指定相等权数为1/4，则新的 线性组合变量为：
W 2t 1 1 1 1 X t X t 1 X t 2 X t 3 4 4 4 4
• 倒V型
权数先递增后递减呈倒“V”型。 例如：在一个较长建设周期的投资中，历年 投资X为产出Y的影响，往往在周期期中投资对 本期产出贡献最大。
14 .70 X t 4 26 .94 X t 5 25 .42 X t 6
(-0.93) (1.09) F=42.54 (-1.12)
R 2 =0.9770
DW=1.03
（3）科伊克（Koyck）方法
科伊克方法是将无限分布滞后模型转换为自回 归模型，然后进行估计。
对于无限分布滞后模型：
给定递减权数：1/2， 1/4， 1/6， 1/8
令
W 1t 1 1 1 1 X t X t 1 X t 2 X t 3 2 4 6 8
原模型变为： Yt
ˆ 0 =0.5
0 1W1t t
该模型可用OLS法估计。假如参数估计结果为
ˆ 1 =0.8
则原模型的估计结果为：
(1.96) (1.10) (0.24)
为了比较，下面给出直接对滞后6期的模型进行 OLS估计的结果：
Yt 3361 .9 8.424 X t 11 .43 X t 1 15 .14 X t 2 4.71 X t 3
（12.43） (1.80) (-1.89) (1.21) (0.36)
• 产生滞后效应的原因 1、心理因素：人们的心理定势，行为方 式滞后于经济形势的变化，如中彩票的人 不可能很快改变其生活方式。 2、技术原因：如当年的产出在某种程度 上依赖于过去若干期内投资形成的固定资 产。 3、制度原因：如定期存款到期才能提取， 造成了它对社会购买力的影响具有滞后性。

滞后变量模型-PPT文档资料

滞后变量模型-PPT文档资料

2、滞后变量模型
一般形式：
Y Y Y Y X X X t 0 1 t 1 2 t 2 q t q 0 t 1 t 1 s t s t
q，s：滞后时间间隔 • 上述模型既含有 Y 对自身滞后变量的回归，还包括着 X分布在不同时 期 的滞后 变量 ，一般 称为 自回归 分布 滞后模 型 （ autoregressive distributed lag model, ADL）： ◎有限自回归分布滞后模型：滞后期长度有限 ◎无限自回归分布滞后模型：滞后期无限，
给定递减权数：1/2， 1/4， 1/6， 1/8 1 1 1 1 W X X X X 令: 1 t t t 1 t 2 t 3 2 4 6 8 原模型变为：
的过去值的影响。 • 以下原因可能导致滞后效应的产生 ◎心理原因：固有的心理定势和行为不可能马上改变 ◎技术原因：如当年的产出在某种程度上依赖于过去若干期内投资形 成的固定资产。
◎制度原因：如定期存款到期才能提取，造成了它对社会购买力的影
响具有滞后性。
• 滞后效应的存在要求在经济建模过程中，必须考虑过去因素的影响，
1、分布滞后模型估计的困难

无限期的分布滞后模型，由于样本观测值的有限性，使得无法直接对其
进行估计。

有限期的分布滞后模型，OLS会遇到如下问题： ◎没有先验准则确定滞后期长度； ◎如果滞后期较长，将缺乏足够的自由度进行估计和检验； ◎同名变量滞后值之间可能存在高度线性相关，即模型存在高度的多重
共线性。
的运动过程，使模型成为动态模型。动态模型（时间序列模型）已经成
为现代计量经济学的重要内容之一。
• 可以用滞后模型来模拟分析经济系统的变化调整过程。 例：投资者对利率调整的反应有多快？ 企业对营销策略的调整需要滞后多长时间才能产生影响？

5.2 滞后变量模型

5.2 滞后变量模型

• 矩型：
即认为权数是相等的，X的逐期滞后值对值 Y的影响相同。
如滞后期为3，指定相等权数为1/4，则新的 线性组合变量为：
W
2t
1 4
Xt
1 4
X t1
1 4
X t2
1 4
X t3
• 倒V型
权数先递增后递减呈倒“V”型。
例如：在一个较长建设周期的投资中，历年 投资X为产出Y的影响，往往在周期期中投资对 本期产出贡献最大。
滞后变量模型考虑了时间因素的作用，使静态 分析的问题有可能成为动态分析。含有滞后解释变 量的模型，又称动态模型（Dynamical Model）。
1、滞后效应与与产生滞后效应的原因
因变量受到自身或另一解释变量的前几 期值影响的现象称为滞后效应。
表示前几期值的变量称为滞后变量。 如：消费函数
通常认为，本期的消费除了受本期的收入影响 之外，还受前1期，或前2期收入的影响：
有限自回归分布滞后模型：滞后期长度有限
无限自回归分布滞后模型：滞后期无限，
（1）分布滞后模型（distributed-lag model） 分布滞后模型：模型中没有滞后被解释变量， 仅有解释变量X的当期值及其若干期的滞后值：
s
Yt i X ti t i0
0：短期(short-run)或即期乘数(impact multiplier)， 表示本期X变化一单位对Y平均值的影响程度。
主要步骤为：
第一步，阿尔蒙变换
对于分布滞后模型
令
W 1t
1 2
Xt
1 4
X t1
1 6
X t2
1 8
X t3
原模型变为：Yt 0 1W1t t
该模型可用OLS法估计。假如参数估计结果为

计量经济学习题与解答5.

计量经济学习题与解答5.

第五章经典单方程计量经济学模型：专门问题一、内容提要本章主要讨论了经典单方程回归模型的几个专门题。

第一个专题是虚拟解释变量问题。

虚拟变量将经济现象中的一些定性因素引入到可以进行定量分析的回归模型，拓展了回归模型的功能。

本专题的重点是如何引入不同类型的虚拟变量来解决相关的定性因素影响的分析问题，主要介绍了引入虚拟变量的加法方式、乘法方式以及二者的组合方式。

在引入虚拟变量时有两点需要注意，一是明确虚拟变量的对比基准，二是避免出现“虚拟变量陷阱”。

第二个专题是滞后变量问题。

滞后变量包括滞后解释变量与滞后被解释变量，根据模型中所包含滞后变量的类别又可将模型划分为自回归分布滞后模型与分布滞后模型、自回归模型等三类。

本专题重点阐述了产生滞后效应的原因、分布滞后模型估计时遇到的主要困难、分布滞后模型的修正估计方法以及自回归模型的估计方法。

如对分布滞后模型可采用经验加权法、Ａlmon多项式法、Koyck方法来减少滞项的数目以使估计变得更为可行。

而对自回归模型，则根据作为解释变量的滞后被解释变量与模型随机扰动项的相关性的不同，采用工具变量法或OLS法进行估计。

由于滞后变量的引入，回归模型可将静态分析动态化，因此，可通过模型参数来分析解释变量对被解释变量影响的短期乘数和长期乘数。

第三个专题是模型设定偏误问题。

主要讨论当放宽“模型的设定是正确的”这一基本假定后所产生的问题及如何解决这些问题。

模型设定偏误的类型包括解释变量选取偏误与模型函数形式选取取偏误两种类型，前者又可分为漏选相关变量与多选无关变量两种情况。

在漏选相关变量的情况下，OLS估计量在小样本下有偏，在大样本下非一致；当多选了无关变量时，OLS估计量是无偏且一致的，但却是无效的；而当函数形式选取有问题时，OLS估计量的偏误是全方位的，不仅有偏、非一致、无效率，而且参数的经济含义也发生了改变。

在模型设定的检验方面，检验是否含有无关变量，可用传统的t检验与F检验进行；检验是否遗漏了相关变量或函数模型选取有错误，则通常用一般性设定偏误检验（RESET检验）进行。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1. 表5.1中给出了中国1980—2001年以城乡储蓄存款新增额代表的居民当年储蓄及以GNP 代表的居民当年收入的数据。

以1991年为界，判断1991年前和1991年后的两个时期中国居民的储蓄—收入关系是否已发生变化。

表5.1 1980—2001年中国居民储蓄与收入数据 单位：亿元年份 储蓄S GNP 年份 储蓄S GNP 1980 118.5 4517.8 1991 2072.8 21662.5 1981 124.2 4860.3 1992 2438.4 26651.9 1982 151.7 5301.8 1993 3217 34560.5 1983 217.1 5957.4 1994 6756.4 46670 1984 322.2 7206.7 1995 8143.5 57494.9 1985 407.9 8989.1 1996 8858.5 66850.5 1986 615 10201.4 1997 7759 73142.7 1987 835.7 11954.5 1998 7127.7 76967.2 1988 728.2 14922.3 1999 6214.3 80579.4 1989 1345.4 16917.8 2000 4710.6 88228.1 19901887.318598.42001943094346.4估计以下回归模型：0123()i i i i i i Y X D D X u ββββ=++++其中i D 为引入的虚拟变量：1,19910,1991i D ⎧=⎨⎩年前年后对上面的模型进行估计，结果如下：所以表达式为：15350.0751981.90.032()i i i i i Y X D D X =+-+(1.40) (4.45) (-1.38) (0.37)从2β和3β的t 检验值可以知道，这两个参数显著的为0，所以1991年前和1991年后两个时期的回归结果是相同的。

下面用邹式检验来验证上面对于两个时期的回归结果相同的结论是否正确。

过程如下：输入要验证的突变点，本例为1991年。

输出结果如下：从伴随概率值可以看出，邹式检验的结果是接受原假设，即方程结构没有发生变化，1991年不是突变点。

与设定虚拟变量的结果是一样的。

2.表4是1982：1—1985：4中国季度酒销量（y，万吨）。

t画序列图如下得到序列图如下：这是一个季节时间序列数据，呈明显的季节变化特征，通过加入季节虚拟变量来描述季节特征建立模型。

表4 全国酒销量（t y ，万吨） 季节数据年月 Y D1 D2 D3 1982：1 92.7 1 0 0 1982：2 79.3 0 1 0 1982：3 80.1 0 0 1 1982：4 86.7 0 0 0 1983：1 104.1 1 0 0 1983：2 89.7 0 1 0 1983：3 90.2 0 0 1 1983：4 90.2 0 0 0 1984：1 107.9 1 0 0 1984：2 96.7 0 1 0 1984：3 97.8 0 0 1 1984：4 93.6 0 0 0 1985：1 111.5 1 0 0 1985：2 98.4 0 1 0 1985：3 97.7 0 0 1 1985：494 0 0 0定义虚拟变量1,1,1,1230,0,0,t t t D D D t t t ===⎧⎧⎧===⎨⎨⎨≠≠≠⎩⎩⎩第一季度第二季度第三季度，，第一季度第二季度第三季度Eviews 操作如下按上述过程依次定义D2和D3。

定义过虚拟变量后，建立模型，进行估计。

有上面的输出结果可以看出，D2和D3的相伴概率分别为0.3020和0.4939，可知，D2和D3的回归参数并不显著，所以从模型中剔除虚拟变量D2和D3。

重新进行参数估计：相应估计式为：80.94 1.2815.421t y t D =++(48.5) (7.3) (8.3)20.89,52,0.8R F DW ===1982年第二季度令t=1。

对于这组数据，只把第一季度区别于其他3个季度就可以了。

3. 表5.2给出了总过电力基本建设投资X 与发电量Y 的相关资料，拟建立一多项式分布滞后模型来考察两者的关系。

表5.2 中国电力工业基本建设投资与发电量年份基本建设投资（亿元）X 发电量（亿千瓦时）Y年份基本建设投资（亿元）X发电量（亿千瓦时）Y1975 30.65 1958 1986 161.6 4495 1976 39.98 2031 1987 210.88 4973 1977 34.72 2234 1988 249.73 5452 1978 50.91 2566 1989 267.85 5848 1979 50.99 2820 1990 334.55 6212 1980 48.14 3006 1991 377.75 6775 1981 40.14 3093 1992 489.69 7539 1982 46.23 3277 1993 675.13 8395 1983 57.46 3514 1994 1033.42 9218 1984 76.99 3770 1995 1124.15 10070 1985 107.86 4107由于无法预知电力行业基本建设投资对发电量影响的时滞期，需取不同的滞后期试算。

经过试算发现，在2阶阿尔蒙多项式变换下，滞后期数取到第6期，估计结果的经济意义比较合理。

估计过程如下：输出结果如下：输出结果的下边部分给出了分布滞后模型的各滞后期的参数。

最后得到分布滞后模型估计式为：1234563319.50.323 1.777 2.69 3.061 2.891 2.180.927t t t t t t t t Y X X X X X X X ------=+++++++(13.62) (0.19) (2.14) (1.88) (1.86) (1.96) (1.1) (0.24)4. 表5.3给出了中国1978—2000年按当年价测度的GDP 与居民消费CONS 数据，检验两者的因果关系。

表5.3 中国GDP与消费支出单位：亿元年份CONS GDP 年份CONS GDP 1978 1759.100 3605.600 1990 9113.200 18319.50 1979 2005.400 4074.000 1991 10315.90 21280.40 1980 2317.100 4551.300 1992 12459.80 25863.70 1981 2604.100 4901.400 1993 15682.40 34500.70 1982 2867.900 5489.200 1994 20809.80 46690.70 1983 3182.500 6076.300 1995 26944.50 58510.50 1984 3674.500 7164.400 1996 32152.30 68330.40 1985 4589.000 8792.100 1997 34854.60 74894.20 1986 5175.000 10132.80 1998 36921.10 79003.30 1987 5961.200 11784.70 1999 39334.40 82673.10 1988 7633.100 14704.00 2000 42911.90 89112.50 1989 8523.500 16466.00取两阶滞后，过程如下：输入要检验的变量。

输入滞后阶数。

输出结果如下：从上面的输出结果可以看出，根据伴随概率值知道，在5%的显著水平下：拒绝GDP不是CONS的格兰杰检验，即GDP是CONS的格兰杰检验。

接受CONS不是GDP的格兰杰检验。

5.以深圳成指（SZ）和上海综指（SH）序列为例进行非因果性检验步骤。

1999年1月4日—2001年10月15日深圳成指（SZ）和上海综指（SH）序列如下图：进行格兰杰检验，过程如下：建立工作文件，打开数据租窗口。

输入滞后期，本例选择滞后5期得到如下结果：对上述分析结果进行分析：由对应的概率可以看出：接受“上海综指不是深圳成指变化的原因”的假设；拒绝“深圳成指不是上海综指变化的原因”，即深圳成指是上海综指变化的原因。

分别进行滞后5，10，15，20，25期的检验，均得到上述结论。

6.已知1970—1991年美国制造业固定厂房设备投资Y和销售量X的相关数据如表5.4所示。

（1）假定销售量对厂房设备支出有一个分部滞后效应，使用4期滞后和2次多项式去估计此分布滞后模型。

（2）检验销售量与厂房设备支出的Granger因果关系，使用直至6期为止的滞后并评述结果。

表5.4 单位：10亿美元年份厂房开支Y 销售额X 年份厂房开支Y 销售额X 1970 36.99 52.805 1981 128.68 168.129 1971 33.6 55.906 1982 123.97 163.351 1972 35.42 63.027 1983 117.35 172.547 1973 42.35 72.931 1984 139.61 190.682 1974 52.48 84.79 1985 152.88 194.538 1975 53.66 86.589 1986 137.95 194.657 1976 68.53 98.797 1987 141.06 206.326 1977 67.48 113.201 1988 163.45 223.547 1978 78.13 126.905 1989 183.8 232.724 1979 95.13 143.936 1990 192.61 239.459 1980 112.6 154.391 1991 182.81 235.142估计分布滞后模型，过程如下：估计结果如下：对应的分布滞后模型的表达式为：123430.830.830.320.010.160.11t t t t t t Y X X X X X ----=-++---做格兰杰检验，以一阶滞后为例，过程如下：结果如下：从上面F检验的伴随概率值可以知道，X与Y互为因果关系。

按上述过程分别做从1直到6期滞后的Granger因果关系检验，结果分别如下：2阶：3阶：4阶：5阶：6阶：从上述结果可以看出，随着滞后期的增加，Y月X的Granger因果关系有所变化。

在不超过4期滞后的检验中，两者互为因果关系；而滞后期为5和6的检验结果说明，两者不互为因果关系。