D值法计算柱子侧移刚度

水平荷载作用下结构侧移计算（1）侧移刚度（2）风荷载作用下框架侧移计算6140081900T=1.7*0.8*根号下0.2094=0.6223Ⅲ类，特征周期为0.45s 0.08a1=0.060Fek=0.06*0.85*53459=2726.41117.0012219.432321.864424.296526.728641.508812.8388343600.7366302489.8314061378.9261821268.0209581176.0559893轴线6主梁线刚度i b计算框架柱的侧移刚度D值计算水平荷载作用下框架的层间侧移可按下式计算△μj= V j/ΣD j式中，V j—第j层的总剪力ΣD j——第j层所有柱的抗侧移刚度之和△μj——第j层的层间侧移风荷载作用下框架侧移计算内力计算为了简化计算，考虑如下几种受荷情况：○1恒载作用；○2活荷载满跨布置；○3风荷载作用（从左向右，或从右向左）；对于○1○2两种情况，框架在竖向荷载作用下，采用叠加法计算；对于○3，框架在水平荷载作用下，采用D值法计算。

1．恒荷载标准值作用下的内力计算（1）恒荷载引起的屋面梁的固端弯矩和不平衡弯矩M g Aw，Bw=M g Cw，Dw=-1/12×24.857×7.82=-126.025kN ·mg gM Bw，Cw-1/12-5/96=-23M g Aw，Bw=（2）标准层楼面的固端弯矩M g Bb，Ab=M g Db，Cb =-1/12×30.795×7.82= -156.13kN ·mM g Ab，Bb=M g Cb，Db =156.13kN ·mM g Bb，Cb =-1/12×12.96×3.62-5/96×5.51×3.62= -17.72 kN ·mM g Ab，Bb=（1）恒荷载引起的节点不平衡弯矩M Aw=M g Aw，+M g Aw，Bw =-126.025kN ·mM Bw=M g BwAw +M g Bw cw，=126.025-23=103.025 kN ·mM Cw=M g Cw，Bw +M g Cw Dw =23-126.025=-103.025 kN ·mM Dw，=M g Dw，+M g Dw，Cw =126.025 kN ·mM Ab=M g Ab +M g Ab，Bb =156.13kN ·mM Bb=M g Bb，Ab +M g Bb，C b = 156.13-17.72=138.41kN ·mM Cb=M g Cb，Bb +M g Cb，Db =17.72-156.13=-138.41kN ·mM Db=M g Db +M g Db Ab =156.13kN ·m1.活荷载标准值作用下的内力计算活荷载与恒荷载的比值小于1，故可采取满跨布置。

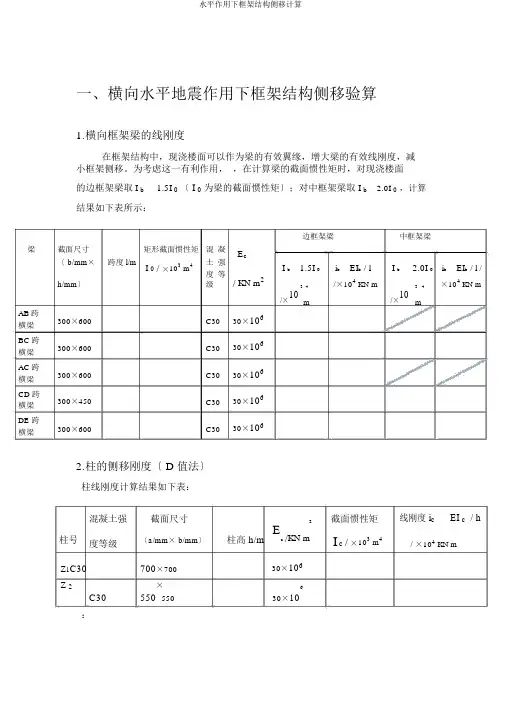
一、横向水平地震作用下框架结构侧移验算1.横向框架梁的线刚度在框架结构中，现浇楼面可以作为梁的有效翼缘，增大梁的有效线刚度，减小框架侧移。

为考虑这一有利作用， ，在计算梁的截面惯性矩时，对现浇楼面的边框架梁取 I b1.5I 0 〔 I 0 为梁的截面惯性矩〕；对中框架梁取 I b2.0I 0 ，计算结果如下表所示：边框架梁中框架梁梁截面尺寸矩形截面惯性矩 混 凝E c〔 b/mm ×跨度 l/m土 强i b EI b / li b EI b / l /I 0 / ×103 m4I b1.5I 0I b 2.0I 0h/mm 〕度 等/ KN m2/×104KN m×104KN m级3 4/×103 4/×10mmAB 跨 300×600C3030×106横梁BC 跨 300×600C3030×106横梁AC 跨 300×600C30 30×106横梁CD 跨 300×450C3030×106横梁DE 跨 300×600C3030×106横梁2.柱的侧移刚度〔 D 值法〕柱线刚度计算结果如下表：混凝土强 截面尺寸2截面惯性矩线刚度 i c EI c / h柱号度等级〔a/mm × b/mm 〕柱高 h/mEc/KN mIc / ×103 m 4/ ×104 KN mZ 1C30 700×70030×106Z 2C30 ×6550 55030×10：楼层横向框架柱侧移刚度〔 D 值〕计算如下表所示：Ki b K(一般层 )(一般层 )2i c K12柱类型Dic h 2根数i b/ 104KN / mK K(底层 )2(底层 )i c K一层其他层边框架边柱边框架中柱中框架边柱中框架中柱D边框架边柱边框架中柱中框架边柱中框架中柱DA 轴2E 轴2C 轴2D 轴2A 轴2B 轴4E 轴6B 轴2C 轴6D 轴6653520KN/mA 轴2E 轴2C 轴2D 轴2A 轴2B 轴4E 轴6B 轴2C 轴6D 轴6794540KN/m3.横向框架自振周期结构自振周期按顶点位移法计算，将各楼层面处的重力荷载代表值G i作为水平荷载作用在各楼层标高处，按弹性方法求得结构顶点的假想侧移，并考虑填充墙对框架的影响取折减系数r，计算结果如下表结构顶点的假想侧移G/KN nG i/KND i / KN m 1i / mm i / mm楼层V Gii 16999099907945405114582144879454041145832906794540311458443647945402114585582279454011241563237653520T1T T4.横向水平地震作用及楼层地震剪力计算本结构重量和刚度沿高度方向分布比拟均匀，高度不超过40m，变形以剪切变形为主，故水平地震作用采用底部剪力法计算。

•反弯点法得到的D值和D值法的D值得物理意义是什么？有何区别？分别在什么情况下使用？D值都是指柱子的抗侧移刚度，反弯点法中D值是指直接有结构力学确定的柱子的刚度，而D值法中的D值是指经过梁柱线刚度的比值修正过的，也就是在前者的基础上乘了一个修正系数（当然，这个修正系数由梁柱线刚度的比决定）。

其实反弯点法等于是d值法的一个特殊情况只是在计算层间位移的地方计算不同如果你发现的话反弯点法柱的弯矩为0的地方一般为1/3柱高的位置，便于计算而d值法的话就比较麻烦要计算弯矩分配情况明白吗？柱的抗侧移刚度不但与柱的线刚度和层高有关，而且还与梁的线刚度有关，另外，柱的反弯点高度也与梁柱线刚度比、上下层横梁的线刚度比，上下层层高的变化等因素有关。

日本武藤清教授在分析了上述影响因素的基础上，对反弯点法中柱的抗侧移刚度和反弯点高度进行了修正。

修正后，柱的抗侧移刚度以D表示，故此法又称“D值法”，也称为修正反弯点法。

D值法有四项假定：1.假定计算目标柱及与其上下相邻柱的线刚度均为ic2.假定计算目标柱及与其上下相邻柱的层间水平位移均为Δμ3.假定计算目标柱两端节点及与其上下左右相邻的各个节点的转角均为θ4.假定与目标柱相交的横梁的线刚度分别为i1，i2，i3，i4反弯点法适用于梁柱线刚度比大于3的情况，它不考虑由于层高的变化及梁柱截面尺寸的变化对反弯点高度的影响。

而D值法考虑了以上因素的影响并对反弯点高度进行修正。

2．D值的物理意义是什么？影响因素有哪些？具有相同截面的边柱和中柱的D值是否相同？具有相同截面及柱高的上层柱与底层柱的D 值是否相同（假定混凝土弹性模量相同）？3．物理意义：对反弯点法中柱的侧向刚度和反弯点高度的计算方法做了改进。

4．影响因素：具有相同截面的边住和中柱的D值不相同，因为边柱只有一根梁约束，中柱有两根梁约束；、具有相同截面及柱高的上层柱与底层柱的D值不相同，因为底层柱底端固定。

D值法中D值不但与柱刚度有关，而且跟与柱相连接的梁刚度也有关系。

•反弯点法得到得D值与Ｄ值法得D值得物理意义就是什么?有何区别？分别在什么情况下使用?Ｄ值都就是指柱子得抗侧移刚度,反弯点法中D值就是指直接有结构力学确定得柱子得刚度,而D值法中得Ｄ值就是指经过梁柱线刚度得比值修正过得,也就就是在前者得基础上乘了一个修正系数(当然,这个修正系数由梁柱线刚度得比决定)。

其实反弯点法等于就是ｄ值法得一个特殊情况只就是在计算层间位移得地方计算不同如果您发现得话反弯点法柱得弯矩为0得地方一般为１/3柱高得位置,便于计算而d值法得话就比较麻烦要计算弯矩分配情况明白不？柱得抗侧移刚度不但与柱得线刚度与层高有关,而且还与梁得线刚度有关,另外,柱得反弯点高度也与梁柱线刚度比、上下层横梁得线刚度比,上下层层高得变化等因素有关。

日本武藤清教授在分析了上述影响因素得基础上,对反弯点法中柱得抗侧移刚度与反弯点高度进行了修正。

修正后,柱得抗侧移刚度以Ｄ表示,故此法又称“D值法”,也称为修正反弯点法。

Ｄ值法有四项假定:1.假定计算目标柱及与其上下相邻柱得线刚度均为iｃ2ﻫ。

假定计算目标柱及与其上下相邻柱得层间水平位移均为Δμ3、假定计算目标柱两端节点及与其上下左右相邻得各个节点得转角均为θ4ﻫ。

假定与目标柱相交得横梁得线刚度分别为i1,i2,i3,i４反弯点法适用于梁柱线刚度比大于3得情况,它不考虑由于层高得变化及梁柱截面尺寸得变化对反弯点高度得影响。

而D值法考虑了以上因素得影响并对反弯点高度进行修正。

2．D值得物理意义就是什么？影响因素有哪些？具有相同截面得边柱与中柱得D值就是否相同？具有相同截面及柱高得上层柱与底层柱得D值就是否相同(假定混凝土弹性模量相同)？3．物理意义:对反弯点法中柱得侧向刚度与反弯点高度得计算方法做了改进。

4．影响因素:具有相同截面得边住与中柱得D值不相同,因为边柱只有一根梁约束,中柱有两根梁约束;、具有相同截面及柱高得上层柱与底层柱得Ｄ值不相同,因为底层柱底端固定。

主要内容：D 值法 内容分解：1） 两种计算方法的比较，引出较精确的 D 值法； 2） 具体计算步骤作用在框架上的水平荷载主要有风荷载和地震作用， 它们均可简化成作用在框架节点上的水平集中力。

由于水平荷载均可简化为水平集中力的形式， 所以高层多跨框架在水平荷载作用下 的弯矩图通常如图1所示。

各杆的弯矩图均为直线，且均有一弯矩为零的点，称为反弯 点。

该点弯矩为零，但有剪力，如 图1中所示的，。

如果能求出各柱的剪力及其反弯点 位置，则各柱端弯矩就可算出，进而根据节点力矩平衡可算出梁端弯矩。

因此必须确定 各柱间剪力的分配比和确定各柱的反弯点的位置一、反弯点法回顾反弯点法的适用条件为梁的线刚度 厂与柱的线刚度■之比大于3,其计算过程如下： （1） 反弯点位置的确定 由于反弯点法假定梁的线刚度无限大，则柱两端产生相 对水平位移时，柱两端无任何转角，且弯矩相等，反弯点在柱中点处。

因此反弯点法假 定：对于上部各层柱，反弯点在柱中点；对于底层柱，由于柱脚为固定端，转角为零， 但柱上端转角不为零，且上端弯矩较小，反弯点上移，故取反弯点在距固定端 2/3高度处。

（2） 柱的侧移刚度反弯点法中用侧移刚度 d 表示框架柱两端有相对单位侧移时 柱中产生的剪力，它与柱两端的约束情况有关。

由于反弯点法中梁的刚度非常大，可近似认为节点转角为零，则根据两端无转角但有单位水平位移时杆件的杆端剪力方程，最 后得,V 12i fd 三—匚歸占卅（1）式中，V 为柱中剪力，J 为柱层间位移，h 为层高（3）同一楼层各柱剪力的分配 根据力的平衡条件、变形协调条件和柱侧移刚度 的定义，可以得出第j 层第i 根柱的剪力为：式中，•为第j 层各柱的剪力分配系数，所有水平荷载的总和，即第j 层由外荷载引起的总剪力。

这里，需要特别强调的是，二亠‘ 与第j 层所承担的水平荷载是有所区别的。

由式（2）可以看出，在同一楼层内，各柱按侧移刚度的比例分配楼层剪力。

第六讲水平荷载作用下框架内力的计算——D值法主要内容：D值法内容分解：1）两种计算方法的比较，引出较精确的D值法；2）具体计算步骤作用在框架上的水平荷载主要有风荷载和地震作用，它们均可简化成作用在框架节点上的水平集中力。

由于水平荷载均可简化为水平集中力的形式，所以高层多跨框架在水平荷载作用下的弯矩图通常如图1所示。

各杆的弯矩图均为直线，且均有一弯矩为零的点，称为反弯点。

该点弯矩为零，但有剪力，如图1中所示的。

如果能求出各柱的剪力及其反弯点位置，则各柱端弯矩就可算出，进而根据节点力矩平衡可算出梁端弯矩。

因此必须确定各柱间剪力的分配比和确定各柱的反弯点的位置一、反弯点法回顾反弯点法的适用条件为梁的线刚度与柱的线刚度之比大于3，其计算过程如下：（1）反弯点位置的确定由于反弯点法假定梁的线刚度无限大，则柱两端产生相对水平位移时，柱两端无任何转角，且弯矩相等，反弯点在柱中点处。

因此反弯点法假定：对于上部各层柱，反弯点在柱中点；对于底层柱，由于柱脚为固定端，转角为零，但柱上端转角不为零，且上端弯矩较小，反弯点上移，故取反弯点在距固定端2/3高度处。

（2）柱的侧移刚度反弯点法中用侧移刚度d表示框架柱两端有相对单位侧移时柱中产生的剪力，它与柱两端的约束情况有关。

由于反弯点法中梁的刚度非常大，可近似认为节点转角为零，则根据两端无转角但有单位水平位移时杆件的杆端剪力方程，最后得（1）式中，V为柱中剪力，为柱层间位移，h为层高。

（3）同一楼层各柱剪力的分配根据力的平衡条件、变形协调条件和柱侧移刚度的定义，可以得出第j层第i根柱的剪力为：（2）式中，为第j层各柱的剪力分配系数，m为第j层柱子总数，为第j层以上所有水平荷载的总和，即第j层由外荷载引起的总剪力。

这里，需要特别强调的是，与第j层所受到的水平荷载是有所区别的。

由式（2）可以看出，在同一楼层内，各柱按侧移刚度的比例分配楼层剪力。

（4）柱端弯矩的计算由于前面已经求出了每一层中各柱的反弯点高度和柱中剪力，那么柱端弯矩可按下式计算：（3）式中，为第j层第i根柱的反弯点高度，为第j层的柱高。

24.3.2 D值法1．剪力分配在利用抗侧刚度作剪力分配时，作了以下两个假定：(1)忽略在水平荷载作用下柱的轴向变形及剪切变形，柱的剪力只与弯曲变形产生的水平位移有关；(2)梁的轴向变形很小，可以忽略，因而同一楼层处柱端位移相等。

假定在同一楼层中各柱端的侧移相等，则同层柱的相对位移都相等，由此可得到第j层各个柱子的剪力如下：式中i为柱编号，、分别为第j层第i根柱子的剪力及抗侧刚度，假定有m根柱，总剪力为，因为所以由此可得到将代入前面公式，可得；；上式即柱的剪力分配分式。

由上面推导过程可见，上式不限于一榀框架中各柱的剪力分配，而可适用于整个框架结构，这时上式中的为该框架结构第层的总剪力，m为该框架结构j层所有柱的总数。

在采用D值法时，将总剪力直接分配到柱往往更为方便而直接，不必经过先分配到每榀框架，再分配到柱这个过程。

2．反弯点高度比y反弯点到柱底距离与柱高度的比值称为反弯点高度比，令反弯点到柱底距离为yh。

在D值法中确定柱反弯点位置时，要考虑影响柱上下结点转角的各种因素，即柱上下端的约束条件。

由图24-10可见当两端约束相同时，，反弯点在中点，当两端约束不相同时，，反弯点则移向转角较大的一端，也就是移向约束刚度较小的一端，其极端情况见图24-10(c)，图中一端铰结，约束刚度为0，即反弯点与该端重合。

影响柱两端约束刚度的主要因素是：(1)结构总层数与该层所在位置；(2)梁柱线刚度比；(3)荷载形式；(4)上层与下层梁刚度比；(5)上、下层层高变化。

在D值法中，用下式计算反弯点高度比y式中，称为标准反弯点高度比，它是在假定各层层高相等、各层梁线刚度相等的情况下通过理论推导得到的。

、、则是考虑上、下梁刚度不同和上、下层层高有变化时反弯点位置变化的修正值。

24.3.3 反弯点法在实际工程中，如果梁的刚度比柱的线刚度大很多（），则梁柱结点的转角很小。

忽略此转角，把框架在水平荷载作用下的变形假设为如图24-13（a）所示情况，这时可按d值分配剪力，称为反弯点法。