平差数学模型

本节重点：（1）测量平差的函数模型定义，类型；测量平差的数学模型包括：条件平差法模型、间接平差法模型、附有参数的条件平差法模型、附有限制条件的间接平差法模型、综合平差模型；（2）测量平差的随机模型。

本节教学思路：首先说明平差的数学模型分两类：函数模型与随机模型，进而分别阐述其定义、分类及建立的方法和模型的具体形态。

教学内容：一、平差模型的定义与分类1 •从模型的性质分：函数模型、随机模型，函数模型连同随机模型称平差的数学模型；2 •函数模型又分为：条件平差法模型、间接平差法模型、附有参数的条件平差法模型、附有限制条件的间接平差法模型、综合平差模型；二、各类函数模型的建立（一）概述1 •函数模型定义：在科学技术领域，通常对研究对象进行抽象概括，用数学关系式来描述它的某种特征或内在的联系，这种数学关系式就称为函数模型。

2.函数模型的意义与特点函数模型是描述观测量与待求量之间的数学函数关系的模型。

对于一个平差问题，建立函数模型是测量平差中最基本、最重要的问题，模型的建立方法不同，与之相应就产生了不同的平差方法。

函数模型有线性与非线性之分，测量平差通常是基于线性函数模型，当函数模型为非线性时（如（2-1-4 ）式），总是要将其线性化。

（二）各种经典平差方法及其线性函数模型的建立方法。

1.条件平差法及其函数模型首先通过两个例子，来说明条件平差函数模型的建立方法。

A图2-2在图2-1中，观测了三个内角，n=3, t=2，贝U r=n-1=1,存在一个函数关系式（条件方程），可以表示为：L i L2 L3 -180 = 0令A13=[1 1 1]3 1 =[ L1 L2 L3 ] TA O=[-18O]则上式为AL A0 ~ 0（2-2-1 ）再如图2-2水准网，D为已知高程水准点，A、B、C均为待定点，观测值向量的真值为〜〜[h i6 1 1〜〜〜〜〜h2 h3 h4 h5 h6 ]其中n=6，t=3，则r=n-t=3，应列出3个线性无关的条件方程，它们可以是：F i（~） * -h2 -~4 =0F2（~）-~3 E = 0F3（~）=~ _忘 _~6 =0AL =0(2-2-2 )般而言，如果有 n 个观测值Ll ，必要观测个数为t ，则应列出r=n-t 个条件方程,(2-2-3)如果条件方程为线性形式，则可以直接写为A ~ A 0 = 0r :：n n 1 r 1 r 〉」1将［二L •厶代入（2-2-4 ）式，并令(2-2-4)则（2-2-4 ）式为W - -(AL A o )(2-2-5)(2-2-6)（2-2-4 ）或（2-2-6 ）式即为条件平差的函数模型。

平差计算的基本原理和方法平差计算是一种广泛应用于测量和工程领域的数学方法，用于解决数据观测值中的误差和偏差问题。

平差计算的基本原理是通过最小二乘法，以最小化观测值与计算值之间的残差平方和来确定最优解。

本文将介绍平差计算的基本原理和常用方法。

一、平差的概念和意义平差是指将不准确或不完整的观测数据进行修正和处理，使其达到最优解或近似最优解的过程。

在测量和工程领域中，由于各种误差和偏差的存在，观测数据往往具有一定的不确定性，因此需要进行平差计算来提高数据的精度和可靠性。

平差计算的结果可以用来进行工程设计、地图测绘、导航定位等各种应用。

二、平差计算的基本原理平差计算的基本原理是基于最小二乘法。

最小二乘法的核心思想是将观测值与计算值之间的残差平方和最小化，通过调整未知量的值来逼近最优解。

残差是指观测值与计算值之间的差异，而平差计算的目标就是使这些差异最小化。

平差计算的基本模型可以表示为以下方程组：A * x = L其中，A为系数矩阵，x为未知量向量，L为观测值向量。

通过解这个方程组，可以求得最优的未知量估计值x。

最小二乘法的优点是可以利用观测数据中的权重信息，将准确性较高的观测数据给予更大的权重，进一步提高计算结果的准确性。

此外，最小二乘法还具有数学上的良好性质，可以通过数学推导和求解得到闭式解，而不需要采用迭代方法。

三、平差计算的常用方法1. 三角形平差法三角形平差法是一种常用的平差计算方法，适用于测量角度和距离的观测数据。

该方法基于三角形的相似性原理，通过解析几何和三角函数等方法，将观测数据转化为方程组，并利用最小二乘法求解未知量。

2. 存储器平差法存储器平差法是一种适用于大规模观测数据的平差计算方法。

该方法通过将观测值按照一定规律存储在存储器中，然后通过循环迭代的方式逐步修正观测值和未知量的估计值，直到最终收敛。

3. 参数平差法参数平差法是一种广泛应用于工程测量领域的平差计算方法。

该方法将未知量表示为参数的形式，并利用最小二乘法求解最优的参数估计值。

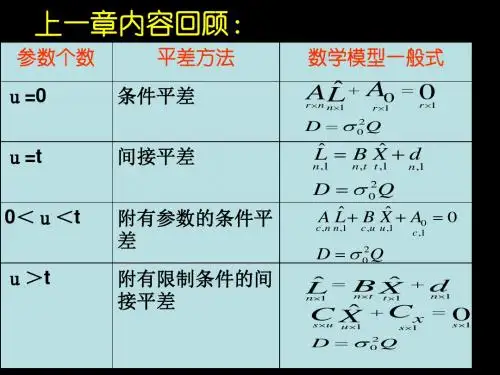
第八章 概括平差函数模型§8.1概述在已经介绍过的条件平差，间接平差，附有参数的条件平差以及附有限制条件的间接平差等四种基本平差方法，其差别就在于函数模型不同。

若将误差方程也视为参数形式的条件方程，以未知参数为纽带，可以对4种平差方法概括如下：（1）、条件平差：0)ˆ(=L F ，不选择未知参数，方程数等于多余观测数：c=t n r -= （2）、间接平差：)ˆ(ˆX F L=，选函数独立未知数t u =，方程数n t r u r c =+=+= （3）、附有参数的条件平差：0)ˆ,ˆ(=X LF ，选择t u <个函数独立参数，除应列出r 个条件方程外，还要附加u 个对未知参数的约束条件方程，所以必须列出u r c +=个条件方程。

（4）、附有限制条件的间接平差：)ˆ(ˆX F L =，0)ˆ(=ΦX 。

选择t u >个参数，参数间存在t u s -=个函数关系。

所以除列出n 个误差方程)ˆ(ˆX F L=（也可视为特殊形式的条件方程－参数方程形式的条件方程），还要列出s 个限制条件方程0)ˆ(=ΦX。

方程数c=n ＋s 。

由此可见，是否选择参数及如何选择参数决定着平差方法，即参数是联系各种平差方法的纽带。

另外可以看到，前三种函数模型中都含有观测量，或者同时包含观测量和未知参数，而后一种只含有未知参数而无观测量。

为了便于区别，将前三种统称为一般条件方程，而后者称为限制条件方程，并统称为条件方程。

在任何几何模型中，函数独立参数个数总是介于下列范围之内： t u ≤≤0。

也就是说，在任一平差问题中，最多只能列出t u =个函数独立的参数。

在不选择参数时，一般条件方程数c 等于多余观测数t n r -=，若又选用了u 个函数独立参数，则总共应当列出u r c +=个一般条件方程。

由于t u ≤，因此一般条件方程的个数总是介于n c r ≤≤范围，即一般条件方程总数不超过n 个。

哈代克罗斯法平差过程哈代克罗斯法平差过程哈代克罗斯法（Helmert-Kaeroids Method）是一种常见的平差方法，主要用于大型工程中的测量校正和误差分析。

其基本思想是将一组观测量转化为统一的参考系，然后根据参考系之间的差异，将观测量进行校正和调整，最终得到精确的结果。

本文将介绍一下哈代克罗斯法的平差过程，包括基本原理、数学模型、参数计算等。

希望能对有关测量校正和误差分析的工程师和学者们提供一些帮助和参考。

一、基本原理哈代克罗斯法的基本原理是将不同测量参考系之间的差异通过一个转换参数来表示和纠正，从而达到坐标和误差的精确校正。

这个转换参数包括七个自由度，即三个平移、三个旋转和一个比例因子。

通过测量实验或其他手段确定这些参数的大小和方向，就可以将不同参考系下的观测量转换为统一的标准参考系下的数据。

这样，就可以根据参考系之间的差异进行校正和调整，从而得到更为准确的结果。

二、数学模型哈代克罗斯法的数学模型可以表示为：i:表示第i个点X1i，Y1i，Z1i：观测量在第一参考系下的坐标X2i，Y2i，Z2i：在第二参考系下的坐标dx，dy，dz：平移参数wx，wy，wz：旋转参数K：比例因子其中，每个点的观测值都可以用一个观测方程来表示：X2i - X1i = dx + (1+K)*Y1i*wz - (1+K)*Z1i*wyY2i - Y1i = dy + (1+K)*Z1i*wx - (1+K)*X1i*wzZ2i - Z1i = dz + (1+K)*X1i*wy - (1+K)*Y1i*wx这些观测方程中包含了三个未知参数，即平移、旋转和比例因子。

通过求解这些未知数，就可以完成参考系之间的差异校正。

三、参数计算计算哈代克罗斯法的转换参数需要用到一组已知的观测量数据，这些数据可以通过GPS、卫星成像和其他测量技术获取。

首先，需要将这些数据转换到同一参考系下，然后利用上述数学模型和最小二乘法求解未知参数。

第4章平差数学模型与最小二乘原理测量———确定模型确定模型的必要元素(量、数据），其个数为t m个。

•必要元素的个数T只取决于模型本身•所有的必要元素都是彼此函数独立的量•模型中所有的量都是必要元素的函数•一个模型中函数独立的量最多只有T个•模型中作为必要元素的“量”不是唯一的必要元素分必要观测量(t 个）和必要起算数据(t o 个）。

一个测量问题中的总观测个数(n 个），则多余观测个数(r 个）相应的有总起算数据个数和多余起算数据个数。

必要观测数据个数：m o t t t =--多余起算数据个数控制网必要元素个数必要起算数据个数与类型水准网点数t=1一个点的高程测角三角网点数×2t=4一个点的坐标、一边边长和方位角⇦⇨两个已知点测边三角网点数×2t=3一个点的坐标、一边方位角边角三角网点数×2t=3一个点的坐标、一边方位角r=n-t当n＜t时，不能确定平差问题的模型n =t时，能确定模型，但无检核、有无粗差不知n＞t时，有多余观测，因观测误差使观测值间产生矛盾，使模型出现多解。

n＞t时，通过平差处理，让观测值的平差值之间满足相应的条件关系，消除矛盾，获取模型的唯一最优解。

4-2函数模型由于只能求出真误差的估值，即真值的估值，函数模型应为：ˆ0AL A +=平差值条件：0()AV W W AL A +==+改正数条件选择t 个函数独立的参数：，这些参数刚好能够确定模型。

则函数模型为：12(,,,)t X X X1()n L F X ⨯=线性情况下111n n t t n L B X d⨯⨯⨯⨯=+ 误差方程：111111()n t t n n n n n V B X l l d L ⨯⨯⨯⨯⨯⨯⨯=+=- o o1111()n t n t n n V B x ll BX d L L L ⨯⨯⨯⨯⨯=+=+-=-附有参数的条件平差法模型在具体平差问题中，观测次数n ，必要观测次数t ，则多余观测次数r ，再增加u 个独立参数，且0 ＜u ＜t ，则总共有r +u = c 个条件方程，一般形式是：线性情况下01111c n n c u u c c A L B X A ⨯⨯⨯⨯⨯⨯++=改正数条件方程：01111()c n c u n u c c A V B x W W AL BX A ⨯⨯⨯⨯⨯⨯++==++1(,)0c F L X ⨯=具有约束条件的间接平差法的函数模型选择u 个参数：，u＞t ，且包含t 个函数独立的参数。