一个数乘以分数的意义

《一个数乘分数意义》教学反思
这节课是本单元的教学重点及难点，是在学习了分数乘整数的意义和计算方法的基础上进行教学的，同分数乘整数的意义不完全相同，需要加以扩展。

计算方法上一个数乘分数的计算方法推导过程比较复杂，学生较难理解。

它也是今后学习分数除法的意义和计算方法以及分数乘除法应用题的基础，所以这部分内容是教学的重点也是难点。

教材编排重视学生全面参与教学过程，扶放结合。

理解意义和方法时，都是由感性认识到理性认识，让学生自己得出结论。

围绕教学重点，以探究为主线组织课堂学习过程。

通过观察、对比、讨论、交流，理解一个数乘分数的意义探究一个数乘分数的计算方法。

学生原有的基础是已经理解分数乘整数的意义，掌握了计算方法。

同时需要对分数的意义有较熟练的口述基础。

学生通过第一课时的学习，对分数乘法有了一定认识，所以，本课教学中继续让学生讨论、交流、试做，发挥学生的主体性，理解一个数乘分数的意义，探究一个数乘分数的计算方法。

但相对有了一定难度，因此学生的综合分析能力尤为重要，这一点也是班上学生比较弱势的，尤其是对于学困生，如果对意义都不理解，算式都列不正确更不要说计算了，因此巩固练习中，从基本练习到稍有难度的练习，并加以指导。

总之，在今后的教学中我将对于自己的不足进一步改进。

小学六年级数学知识点归纳六年级上册知识点概念总结1.分数乘法：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算。

2.分数乘法的计算法则：分数乘整数，用分数的分子和整数相乘的积作分子，分母不变；分数乘分数，用分子相乘的积作分子，分母相乘的积作分母。

但分子分母不能为零.。

3.分数乘法意义分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

一个数与分数相乘，可以看作是求这个数的几分之几是多少。

4.分数乘整数：数形结合、转化化归5.倒数：乘积是1的两个数叫做互为倒数。

6.分数的倒数找一个分数的倒数，例如3/4 把3/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是4/3。

3/4是4/3的倒数，也可以说4/3是3/4的倒数。

7.整数的倒数找一个整数的倒数，例如12，把12化成分数，即12/1 ，再把12/1这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是1/12 ，12是1/12的倒数。

8.小数的倒数：普通算法：找一个小数的倒数，例如0.25 ，把0.25化成分数，即1/4 ，再把1/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是4/19.用1计算法：也可以用1去除以这个数，例如0.25 ，1/0.25等于4 ，所以0.25的倒数4 ，因为乘积是1的两个数互为倒数。

分数、整数也都使用这种规律。

10.分数除法：分数除法是分数乘法的逆运算。

11.分数除法计算法则：甲数除以乙数（0除外），等于甲数乘乙数的倒数。

12.分数除法的意义：与整数除法的意义相同，都是已知两个因数的积与其中一个因数求另一个因数。

13.分数除法应用题：先找单位1。

单位1已知，求部分量或对应分率用乘法，求单位1用除法。

14.比和比例：比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括：比，等同于算式中等号左边的式子，是式子的一种（如：a:b）；比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同（如：a:b=c:d）。

分数乘分数的意义和计算方法以分数乘分数的意义和计算方法为标题，本文将详细讨论分数乘法的意义、计算方法以及相关概念。

首先，我们需要明确分数的概念。

在数学中，分数是用来表示部分数量的数，它由一个分子和一个分母组成，分子表示部分的数量，分母表示整体的数量。

现在让我们来探讨一下分数乘法的意义和计算方法。

一、分数乘法的意义分数乘法的意义可以从几个方面来理解。

首先，分数乘法表示了两个部分数量的相乘。

例如，如果我们有一块蛋糕，将其分成4份，每份各占1/4，如果我们想要将其中的一份再平均分成2份，则可以用分数乘法来表示：1/4 × 1/2。

这个乘法运算的结果就是将蛋糕的一份再分成8份，即1/8。

所以，分数乘法可以帮助我们计算部分数量的乘积。

分数乘法还可以表示比例的乘积。

比例是用来表示两个或多个数量之间的关系的数学概念。

如果我们要计算两个比例的乘积，可以使用分数乘法。

例如，如果甲乙两个人的身高比例分别为3/4和2/3，我们可以用分数乘法计算他们身高的比例：3/4 × 2/3。

这个乘法运算的结果是6/12，可以进一步化简为1/2。

所以，分数乘法还可以帮助我们计算比例的乘积。

二、分数乘法的计算方法分数乘法的计算方法相对简单，可以按照以下步骤进行：1. 将两个分数相乘的分子相乘，得到新的分子；2. 将两个分数相乘的分母相乘，得到新的分母；3. 化简分数，如果有必要。

让我们通过一个例子来说明分数乘法的计算方法。

假设我们要计算3/4 × 2/5。

按照上述步骤，我们可以进行如下计算：1. 将两个分数的分子相乘：3 × 2 = 6；2. 将两个分数的分母相乘：4 × 5 = 20；3. 化简分数：6/20可以进一步化简为3/10。

所以，3/4 × 2/5的结果是3/10。

三、分数乘法的相关概念在进行分数乘法计算时，还需要了解一些相关概念。

首先，乘法的交换律和结合律在分数乘法中同样适用。

本节教材是在同学们掌握了整数乘法，分数的意义和分数的基本性质，以及分数加、减法的计算等知识的基础上实行学习的。

本节内容属于分数中的基本知识和技能，利用这些知识不但能够解决相关的实际问题，而且也是后面学习分数除法，分数四则混合运算和应用题以及百分数的重要基础。

一、重要知识点1．分数乘以整数2．一个数乘以分数3．分数混合运算和整数乘法运算定律推广到分数乘法通过本节内容的学习，同学们要重点理解分数乘法的意义，熟练掌握分数乘法的计算法则；理解分数混合运算的顺序与整数的运算顺序相同,整数乘法运算定律对于分数乘法同样适用；能够准确灵活的实行分数乘、加、减混合运算.二、准确理解分数乘法的意义分数乘法包含两种情况，一种是分数乘以整数，另一种是一个数乘以分数。

分数乘以整数的计算法则比较容易, 一个数乘以分数的意义和计算法则既是本节的重点，又是难点。

1.分数和整数相乘，能够表示求几个相同加数的和的简便运算，这与整数乘法的意义是相同的；被乘数(这里指的是分数)表示相同的加数，乘数(这里指的是整数)表示相同的加数的个数 。

反之，求几个相同分数的和是多少能够用乘法计算。

例如：392⨯ 就表示求3个92的和是多少; 反之，求929292++的和是多少就能够列式为392⨯. 要注意：分数和整数相乘，还能够表示求一个整数的几分之几是多少，这与整数乘法的意义是不同的。

例如：392⨯ 还能够表示求3的92是多少. 2. 一个数乘以分数的意义就是求这个数的几分之几是多少。

这是整数乘法意义的扩展。

说明：这里的一个数能够是整数、小数、分数。

反之，求一个数的几分之几是多少能够用乘法计算。

例如： 5321⨯就表示求21的53是多少; 反之， 求21的53是多少就能够用乘法列式为： 5321⨯. 三、切实掌握分数乘法的计算法则 1. 分数乘以整数，用分数的分子和整数相乘的积作分子，分母不变。

这是因为同分母分数相加，分母不变，分子相加，相同的分子连加用乘法便于计算。

分数乘法的三种意义分数乘法是数学中的一种基本运算方法，它有着三种不同的意义，分别是乘法、比例和面积。

下面将对这三种意义进行详细的介绍。

一、乘法的意义在分数乘法中，乘法的意义是最基本的。

乘法是指将两个数相乘，得到它们的乘积。

在分数乘法中，我们可以将分数看作是真实世界中的一种实物，通过乘法来确定两个实物的总量。

比如，我们可以将1/2乘以3/4，得到的结果是3/8，这表示将1/2的实物乘以3/4的实物，最终得到的是3/8的实物。

可以看出，分数乘法的意义是描述两个实物相乘后得到的实物的总量。

二、比例的意义分数乘法还可以用来表示比例关系。

比例是指两个量之间的相对关系。

在分数乘法中，我们可以将分数看作是一种比例关系，通过乘法来确定两个比例之间的关系。

比如，当我们将1/2乘以2，得到的结果是1，这表示1/2与2之间存在着比例关系，即1/2是2的一半。

同样地，当我们将1/2乘以4，得到的结果是2，这表示1/2是4的四分之一。

可以看出，分数乘法的意义还可以用来表示两个量之间的比例关系。

三、面积的意义分数乘法还可以用来表示面积。

面积是指一个平面图形所占据的空间大小。

在分数乘法中，我们可以将分数看作是一种面积比例，通过乘法来确定一个平面图形相对于另一个平面图形的面积大小。

比如，当我们将1/2乘以3/4，得到的结果是3/8，这表示一个面积为1/2的图形相对于另一个面积为3/4的图形，其面积大小为3/8。

可以看出，分数乘法的意义还可以用来表示两个平面图形之间的面积比例关系。

分数乘法有着三种不同的意义，分别是乘法、比例和面积。

通过乘法，我们可以确定两个实物相乘后得到的实物的总量；通过比例，我们可以确定两个量之间的相对关系；通过面积，我们可以确定两个平面图形之间的面积比例关系。

分数乘法在数学和现实生活中都有着广泛的应用，它是我们理解和解决问题的重要工具之一。

分数乘法的三种意义一、分数乘法的基本意义分数乘法是数学中的一种基本运算，它有着独特的意义。

在分数乘法中，我们可以将其理解为“部分的部分”，即将一个数分成若干个相等的部分，再将其中的一部分取出来进行乘法运算。

这种意义在实际生活中有着广泛的应用。

举个例子来说明，假设小明要将一块长方形的蛋糕分成4份，每一份都要均匀一些。

这时，我们可以将蛋糕分成4列，每一列都是蛋糕的四分之一。

然后，小明需要从中的两列蛋糕中取出来，这样就相当于将四分之一的蛋糕乘以二。

这种分数乘法的意义在实际生活中经常出现，例如购物打折、比例缩放等。

二、分数乘法的几何意义分数乘法还有着几何的意义。

我们可以将其理解为“面积的比例”。

假设有一个矩形，它的长为a，宽为b，那么它的面积就是a*b。

现在，如果我们将矩形的宽度缩小为b的一半，即b/2，那么矩形的面积也会相应地减小为a*(b/2)。

这里，b/2可以理解为宽度的一半，即原来的宽度的四分之一。

所以，分数乘法在几何中可以表示面积的比例变化。

再举一个例子，假设有一个正方形，它的边长为1。

现在，我们将正方形的边长缩小为原来的一半，即1/2。

那么，新正方形的面积就是原来的面积的四分之一。

这是因为面积是边长的平方，所以新的面积就是(1/2)^2=1/4。

这种几何意义的分数乘法在比例问题中经常使用，例如图形的缩放、相似图形等。

三、分数乘法的比例意义分数乘法还有一种比例的意义。

我们可以将其理解为“数量的比例”。

假设有一个数a，现在要将其乘以一个小于1的分数b/c，那么相当于将a分成了c份，然后取其中的b份。

这种比例意义的分数乘法在实际问题中经常出现。

举个例子来说明，假设小明家有100个苹果，他要将其中的三分之一分给小红，那么小红将得到多少个苹果呢？这时，我们可以将100个苹果分成三份，每份约为33个苹果。

然后，小红将得到其中的一份，即33个苹果。

这种分数乘法可以理解为将100乘以1/3，即100*(1/3)=33。

一个数乘分数的意义课后反思一个数乘分数的意义课后反思在数学学习中，学生们经常会遇到一种情况，即一个数乘一个分数。

这种操作常常让学生感到迷惑和困惑，不知道如何处理。

所以，在这堂课上，老师详细讲解了一个数乘分数的意义，并提醒我们思考其背后的含义。

课后，我对这个问题进行了反思，以下是我对这个问题的一些思考。

首先，一个数乘一个分数意味着我们要将这个数乘以这个分数的分子和分母。

乘以分子是相对直观的，它表示我们要将这个数乘以这个数的数值部分。

例如，当我们计算 2 乘以1/4 时，我们将2 乘以1，结果是2。

这是因为1/4 的分子是1。

这种计算方法可以帮助我们理解一个数乘以一个分数的意义，并且得出准确的结果。

其次，一个数乘以一个分数还意味着我们要将这个数乘以这个分数的分母的倒数。

分母的倒数是一个分数的分母取倒数得到的数，即求倒数的操作。

例如，当我们计算 2 乘以1/4 时，我们需要计算 2 乘以1/4 的分母 4 的倒数。

4 的倒数是1/4，我们将 2 乘以1/4 的分母的倒数1/4，结果是1/2。

这是因为当我们将分母取倒数时，相当于分数的值变小了。

所以在计算中，我们要将这个数乘以这个分数的分母的倒数。

通过以上的思考，我发现了一个数乘以一个分数的意义。

这个操作可以用来帮助我们计算整数和分数的乘法，并得到准确的结果。

当我们计算一个数乘以一个分数时，首先将这个数乘以这个分数的分子，然后将这个数乘以这个分数的分母的倒数。

最后，我们将这两个结果相乘，得到的结果就是一个数乘以一个分数的准确结果。

例如，当我们计算 2 乘以1/4 时，我们计算出 2 乘以 1 和 2 乘以1/4 的分母的倒数，分别是2 和1/4，然后将这两个结果相乘得到2/4，即1/2。

这种思考方式让我深刻理解了一个数乘以一个分数的意义，并对如何处理这个操作有了更清晰的认识。

我意识到，在计算中，我们应该将这个数乘以分数的分子，并将这个数乘以分数的分母的倒数。

六年级数学知识点汇总1.分数乘法：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算。

2.分数乘法的计算法则：分数乘以整数，分数与整数相乘的乘积作为分子，分母不变；分数乘以分数，分子乘的积是分子，分母乘的积是分母。

但是分子和分母不能为零。

3.分数乘法意义整数的分数乘法和整数乘法的意思一样，都是求几个相同加数之和的简单运算。

一个数乘以一个分数可以看成是求这个数的一个分数。

4.分数乘整数：数形结合、转化化归5.倒数：乘积是1的两个数叫做互为倒数。

6.分数的倒数找一个分数的倒数，例如3/4 把3/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是4/3。

3/4是4/3的倒数，也可以说4/3是3/4的倒数。

7.整数的倒数找一个整数的倒数，例如12，把12化成分数，即12/1 ，再把12/1这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是1/12 ，12是1/12的倒数。

8.小数的倒数：普通算法：找一个小数的倒数，例如0.25 ，把0.25化成分数，即1/4 ，再把1/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是4/19.用1计算法：也可以用1去除以这个数，例如0.25 ，1/0.25等于4 ，所以0.25的倒数4 ，因为乘积是1的两个数互为倒数。

分数、整数也都使用这种规律。

10.分数除法:分数除法是分数乘法的逆运算。

11.分数除法计算法则：甲数除以乙数（0除外），等于甲数乘乙数的倒数。

12.分数除法的意义:与整数除法意义相同，是两个已知因子和其中一个求另一个因子的乘积。

13.分数除法应用题:先找单元1。

单元1已知。

乘法用来求部分量或对应的分数，除法用来求单位1。

14.比和比例：比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括：比，等同于算式中等号左边的式子，是式子的一种（如：a:b）；比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同（如：a:b=c:d）。

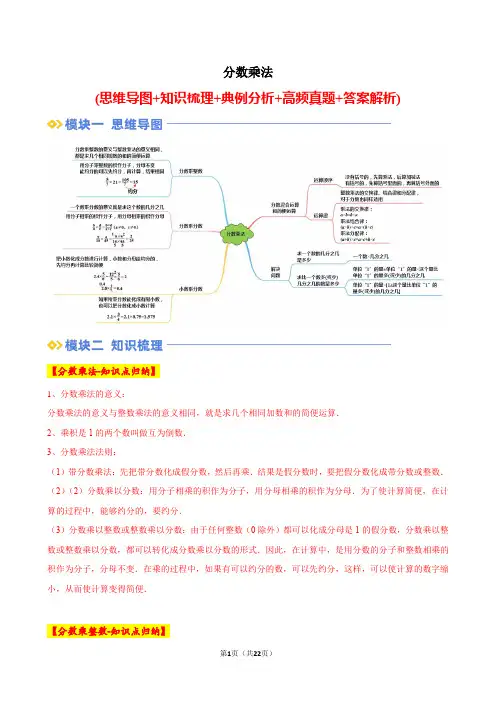
分数乘法(思维导图+知识梳理+典例分析+高频真题+答案解析)【分数乘法-知识点归纳】1、分数乘法的意义：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算．2、乘积是1的两个数叫做互为倒数．3、分数乘法法则：（1）带分数乘法：先把带分数化成假分数，然后再乘．结果是假分数时，要把假分数化成带分数或整数．（2）（2）分数乘以分数：用分子相乘的积作为分子，用分母相乘的积作为分母．为了使计算简便，在计算的过程中，能够约分的，要约分．（3）分数乘以整数或整数乘以分数：由于任何整数（0除外）都可以化成分母是1的假分数，分数乘以整数或整数乘以分数，都可以转化成分数乘以分数的形式．因此，在计算中，是用分数的分子和整数相乘的积作为分子，分母不变．在乘的过程中，如果有可以约分的数，可以先约分，这样，可以使计算的数字缩小，从而使计算变得简便．【分数乘整数-知识点归纳】1、分子乘整数，可以求出一共有多少个这样的分数单位，而分数单位的个数其实就是分子乘整数的积，因此整数乘分子作分子。

求几个分数单位的和，分数单位不变，也就是分母不变。

2、分数乘整数的意义：分数乘整数，也是表示几个相同加数相加，与整数乘法的意义相同。

3、分数乘整数的计算方法：分数乘整数，用分子乘整数的积作分子，分母不变。

其实就是计算分数单位的个数。

【整数乘分数-知识点归纳】1、一个数乘分数的意义就是求一个数的几分之几是多少。

2、“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）3、方法总结；（1）、整数与分数相乘，用分数的分子与整数相乘，分母不变；（2）、计算时能约分的可以先约分再计算出结果。

【分数乘分数-知识点归纳】分数乘法的计算法则1、整数和分数相乘：整数和分子相乘的积作分子，分母不变。

2、分数和分数相乘：分子相乘的积作分子，分母相乘的积作分母。

【典例1】在“世界无烟日”健康知识竞赛中，小星答对了50道题，小铭答对的题数比小星少15。

分数乘法的含义和意义分数乘法的含义和意义分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

一个数与分数相乘，可以看作是求这个数的几分之几是多少。

分数乘法的含义和意义1.分数乘以整数：和整数乘法意义相同,就是求几个相同加数的运算2.一个数乘以分数：是求一个数的几分之几是多少分数乘法的`含义和意义今年是我第四次教六年级数学。

与往年不同，今年的教材内容有所改变。

有些地方改变得很合理，例如：把原来分为三教时的利息、保险费、应缴税款合并为一教时。

以前我总是在新授利息之后让学生自学保险费和应缴税款，这三个内容本是一种类型。

教材做这样的改编，省时省力。

但有些地方改编的着实令人不解。

不仅学生糊涂，老师也不清楚。

例如分数乘法的意义。

老教材把分数乘法的意义分为两类：1、分数与整数相乘的意义：求几个相同加数的和的简便运算。

例：3/4×5表示5个3/5相加的和是多少?2、一个数与分数相乘的意义：求这个数的几分之几是多少?例：5×3/4表示5的3/4是多少?新教材在此作了旨在统一，减少分类麻烦的改革。

它在单元开头下了这样一句概念：分数乘法的意义与整数乘法的意义相同，也是求几个相同加数的和的简便运算。

言下之意所有的分数乘法都是这一条意义。

学生也欣然接受。

例题中既出现了1/4×3，又出现了3×1/4，还讲到“计算中，可以先约分再计算结果，这样比较简便”。

这是第一课时，接下来在第二课时中又重点指出“求一个数的几分之几是多少，就是求一个数的几倍是多少，用乘法计算。

”意思是随便什么式子都可以把它说成求()的()倍是多少?既然如此，何必分为两课时呢?专家在此做改动时，必然也斟酌再三，乘法是加法的简便运算这条意义不能不提。

总不能说3/4×1/5表示求1/5个3/4相加的和是多少。

所以只能摆出3/4的1/5是多少，为求统一，1/5和0.2都能说“倍”。

我的想法是把分数乘法的意义和计算方法分开教学，先学意义。

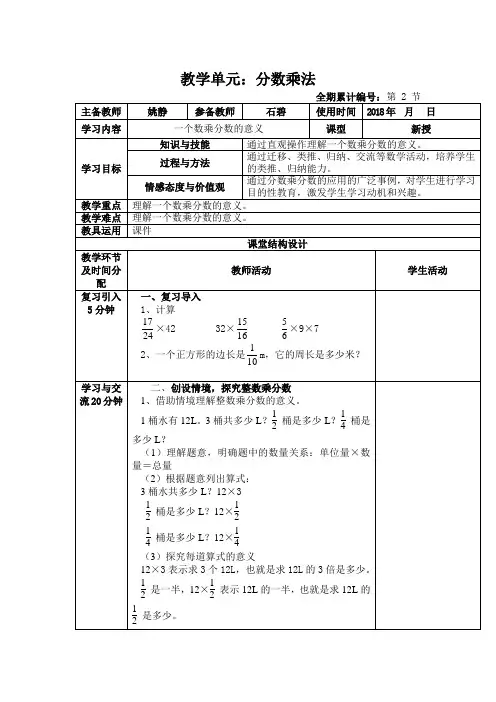
人教版数学五升六暑期精编专项讲义—新课衔接站第一单元《分数乘法》第2课《一个数乘分数》学习目标：1.使学生理解一个数乘分数的意义.掌握分数乘以分数的计算法则。

2.学会分数乘分数的简便计算。

3.通过一个数乘以分数应用的广泛性事例.对学生进行学习目的性教育.激发学生学习动机和兴趣。

新知讲解：【典例引入】（2020六上·侯马期末）先计算.并在图中涂色表示×。

× =【答案】×= .。

【解析】【分析】分数乘分数.用分子相乘的积作分子.分母相乘的积作分母.据此计算再涂色表示.图中画斜线部分即为所求。

【变式训练】【变式1】看图列式计算【答案】解：75×＝125(朵)答：玫瑰花有125朵.【解析】【分析】观察线段图可知.把菊花的朵数看作单位“1”.已知菊花的朵数.求比菊花朵数多是多少朵.用菊花的朵数×(1+)=玫瑰的朵数.据此列式解答.【变式2】水果批发商购进10吨水果.上午卖出了 .下午卖出了吨.一共卖出了多少吨水果？【答案】10×+=2+=（吨）答：一共卖出了吨水果.【解析】【分析】根据题意可知.先求出上午卖出的水果吨数.用购进的水果总质量×上午卖出的占总量的分率=上午卖出的水果质量.然后用上午卖出的水果质量+下午卖出的水果质量=一共卖出的水果质量.据此列式解答.【知识点总结】分数乘法计算法则：1.分数乘整数的运算法则是：分子与整数相乘.分母不变。

（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

（整数千万不能与分母相乘.计算结果必须是最简分数）。

2.分数乘分数的运算法则是：用分子相乘的积做分子.分母相乘的积做分母。

（分子乘分子.分母乘分母）（1）如果分数乘法算式中含有带分数.要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子.分母同时除以它们的最大公因数。

（3）在乘的过程中约分.是把分子.分母中.两个可以约分的数先划去.再分别在它们的上.下方写出约分后的数。

六年级上册数学的课堂笔记
一、分数乘法
1、分数乘法的意义：一个数乘以一个分数的意义是求这个数的几分之几。

2、分数乘法的计算方法：分子与分子相乘，分母与分母相乘，能约分的先约分。

3、分数乘法的应用：在解决实际问题时，可以把一个整体看作一个分数，用乘法计算。

二、分数除法
1、分数除法的意义：已知一个数的几分之几是多少，求这个数是多少。

2、分数除法的计算方法：除以一个数等于乘以这个数的倒数。

3、分数除法的应用：在实际生活中，我们经常用分数除法来计算一些问题，例如：速度、时间、路程等。

三、百分数
1、百分数的意义：表示一个数是另一个数的百分之几。

2、百分数的计算方法：把百分数转化为小数，再按照小数乘法的计算方法计算。

3、百分数的应用：在实际生活中，我们经常用百分数来表示一些数据的大小和比较，例如：增长率、占比等。

四、比例
1、比例的意义：表示两个量之间的比例关系。

2、比例的计算方法：根据比例关系，把两个量进行比较和计算。

3、比例的应用：在实际生活中，我们经常用比例来描述一些数据之间的关系和比较，例如：价格比例、人口比例等。

六年级上册数学分数乘法知识点总结六年级上册数学分数乘法知识点总结「篇一」关于小学六年级数学知识点的总结1.分数乘法：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算。

2.分数乘法的计算法则：分数乘整数，用分数的分子和整数相乘的积作分子，分母不变;分数乘分数，用分子相乘的积作分子，分母相乘的积作分母。

但分子分母不能为零。

3.分数乘法意义分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

一个数与分数相乘，可以看作是求这个数的几分之几是多少。

4.分数乘整数：数形结合、转化化归5.倒数：乘积是1的两个数叫做互为倒数。

6.分数的倒数找一个分数的倒数，例如3/4把3/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的'分母做分子。

则是4/3。

3/4是4/3的倒数，也可以说4/3是3/4的倒数。

7.整数的倒数找一个整数的倒数，例如12，把12化成分数，即12/1，再把12/1这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是1/12，12是1/12的倒数。

8.小数的倒数：普通算法：找一个小数的倒数，例如0.25，把0.25化成分数，即1/4，再把1/4这个分数的分子和分母交换位置，把原来的分子做分母，原来的分母做分子。

则是4/19.用1计算法：也可以用1去除以这个数，例如0.25，1/0.25等于4，所以0.25的倒数4，因为乘积是1的两个数互为倒数。

分数、整数也都使用这种规律。

10.分数除法：分数除法是分数乘法的逆运算。

11.分数除法计算法则：甲数除以乙数(0除外)，等于甲数乘乙数的倒数。

12.分数除法的意义：与整数除法的意义相同，都是已知两个因数的积与其中一个因数求另一个因数。

13.分数除法应用题：先找单位1。

单位1已知，求部分量或对应分率用乘法，求单位1用除法。

14.比和比例：比和比例一直是学数学容易弄混的几大问题之一，其实它们之间的问题完全可以用一句话概括：比，等同于算式中等号左边的式子，是式子的一种(如：a:b);比例，由至少两个称为比的式子由等号连接而成，且这两个比的比值是相同(如：a:b=c:d)。

人教版小学数学六年级上册1.2《一个数乘分数的意义及分数乘分数》教案一. 教材分析《一个数乘分数的意义及分数乘分数》是人教版小学数学六年级上册第一单元第二节的内容。

本节课主要让学生理解一个数乘分数的意义，掌握分数乘分数的计算法则，并能灵活运用。

通过本节课的学习，培养学生解决问题的能力，提高学生的数学素养。

二. 学情分析六年级的学生已经掌握了分数的基本知识，对分数的加减法有了一定的了解。

但学生在解决实际问题时，还不能很好地运用分数乘法。

因此，在教学过程中，教师需要结合学生的生活实际，引导学生理解分数乘法的意义，突破计算难关。

三. 教学目标1.理解一个数乘分数的意义，掌握分数乘分数的计算法则。

2.培养学生解决问题的能力，提高学生的数学素养。

3.激发学生学习数学的兴趣，培养学生的合作意识。

四. 教学重难点1.教学重点：理解一个数乘分数的意义，掌握分数乘分数的计算法则。

2.教学难点：分数乘分数的计算及在实际问题中的应用。

五. 教学方法1.情境教学法：通过生活实际问题，引导学生理解分数乘法的意义。

2.合作学习法：分组讨论，培养学生团队合作意识。

3.动手操作法：让学生亲自动手操作，加深对分数乘法计算的理解。

4.激励评价法：及时鼓励学生，提高学生学习数学的积极性。

六. 教学准备1.教学课件：制作课件，展示分数乘法的意义及计算方法。

2.练习题：准备不同难度的练习题，巩固学生所学知识。

3.教学道具：准备实物道具，帮助学生更好地理解分数乘法。

七. 教学过程导入（5分钟）教师通过展示一个实际问题：“小明有一块长方形蛋糕，长是8厘米，宽是3厘米，小明吃了蛋糕的12，小华吃了蛋糕的14，他们一共吃了这块蛋糕的几分之几？”引发学生思考，引出本节课的主题——分数乘法。

呈现（10分钟）1.教师通过讲解，呈现一个数乘分数的意义，如：“2乘以12表示2个12相加。

”2.教师引导学生观察、分析分数乘分数的计算法则，如：“23乘以12等于23乘以12等于13。

青岛版《一个数乘分数的意义及计算方法》说课稿青岛版《一个数乘分数的意义及计算方法》说课稿尊敬的各位专家、评委老师们，大家好!我说课的内容是义务教育课程标准实验教科书（青岛版）五年级数学上册第三单元信息窗2中的内容：《一个数乘分数的意义及计算方法》。

计算是数学学习的基础，本课学习内容十分抽象，是本单元学习的一个难点。

本节课的教学是在学生已经理解了分数乘整数的意义，掌握了分数乘整数的计算方法的基础上进行教学的。

这节课要理解一个数乘分数的意义，掌握计算方法并理解算理，本课学习也是后继学习分数四则混合运算及解答相应实际问题的重要基础。

根据对教材的分析，并结合课标的要求，我从知识与技能、过程与方法、情感态度价值观三个维度，制定本节课的教学目标为：（1）结合生活经验和直观图示，理解一个数乘分数的意义，探索计算方法。

（2）通过操作、观察，培养学生初步分析、推理能力。

（3）经历一个数乘分数的意义和计算方法的探索过程，渗透数形结合思想。

本节课的教学重点和难点都是理解一个数乘分数的意义。

让学生在大量的动手实践活动的基础上理解算理和计算方法，是突破本课重点和难点的关键所在。

在课堂上我让学生以折纸涂色活动为主线，给学生提供大量的动手操作的时间和观察交流、思考的空间，鼓励学生独立思考，从不同的角度去探究问题。

教学方法：五年级学生的思维处于由具体形象思维向抽象逻辑思维过渡的阶段。

与中低年级的学生相比，他们在动手操作、观察比较等方面能力更强。

想象的有意性迅速增长并逐渐符合客观现实，同时，创造性成分日益增多。

在教学中要充分利用学生已有经验和认知发展水平，结合本课知识内容抽象的特点,我采取数形结合的直观教学方法，让学生通过小组合作、折一折、画一画等手段帮助学生理解分数乘分数的意义，掌握分数乘分数的计算方法。

基于以上认识，在本节课主要采用了以下几种教学方法：（1）探究研讨法：当学生提出问题后，鼓励学生自己探究解决问题的方法，学生通过画一画、折一折、涂一涂，直观、形象地理解一个数乘分数的意义及计算方法，培养学生的观察、比较、分析、归纳、推理能力。