高一物理追击和相遇问题

高一物理追及相遇问题追及和相遇是高一物理中常见的运动学问题，这类问题涉及到两个或多个物体在同一时间或不同时间运动的情况。

解决这类问题的关键是掌握运动学的基本公式和定理，理解物体之间的相对运动关系，并运用数学工具进行计算和分析。

一、追及问题追及问题通常是指两个物体在同一时间开始运动，其中一个物体追赶另一个物体，直到追上或超过被追物体。

解决追及问题的关键是找出两个物体之间的位移差、速度差和时间关系。

定义变量设被追物体为A，追赶物体为B。

设t时刻A、B的位移分别为x1、x2，速度分别为v1、v2。

建立数学方程根据运动学公式，我们可以建立以下方程：(1) x1 = v1t + 1/2at^2（匀加速运动）(2) x2 = v2t（匀速运动）(3) 当A、B速度相等时，有v1 = v2 + at求解方程解方程组（1）（2）（3），可以求出t、x1、x2的值。

分析结果根据求出的t、x1、x2的值，可以判断A、B是否能够相遇，相遇时A、B的位移和速度关系。

二、相遇问题相遇问题是指两个物体在同一地点开始运动，其中一个物体迎向另一个物体，直到两个物体相遇或相离。

解决相遇问题的关键是找出两个物体之间的位移和速度关系。

定义变量设相遇的两个物体分别为A、B。

设t时刻A、B的位移分别为x1、x2，速度分别为v1、v2。

建立数学方程根据运动学公式，我们可以建立以下方程：(1) x1 + x2 = v1t + v2t（相对速度）(2) v1 - v2 = at（相对加速度）求解方程解方程组（1）（2），可以求出t、x1、x2的值。

分析结果根据求出的t、x1、x2的值，可以判断A、B是否能够相遇，相遇时A、B的位移和速度关系。

如果A、B不能相遇，还可以求出它们之间的距离。

高一物理 追击与相遇问题1.相遇和追击问题的实质研究的两物体能否在相同的时刻到达相同的空间位置的问题。

2. 解相遇和追击问题的关键画出物体运动的情景图，理清三大关系（1）时间关系 ：0t t t B A ±=（2）位移关系：0A B x x x =± （3）速度关系：两者速度相等。

它往往是物体间能否追上或（两者）距离最大、最小的临界条件，也是分析判断的切入点。

3. 相遇和追击问题剖析：(一)追及问题1、追及问题中两者速度大小与两者距离变化的关系。

甲物体追赶前方的乙物体，若甲的速度大于乙的速度，则两者之间的距离 。

若甲的速度小于乙的速度，则两者之间的距离 。

若开始甲的速度小于乙的速度过一段时间后两者速度相等，则两者之间的距离 （填最大或最小）。

2、追及问题的特征及处理方法：“追及”主要条件是：两个物体在追赶过程中处在同一位置，常见的情形有三种：⑴ 初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙，一定能追上，追上前有最大距离的条件：两物体速度 ，即v v =乙甲。

⑵ 匀速运动的物体甲追赶同向匀加速运动的物体乙，存在一个能否追上的问题。

判断方法是：假定速度相等，从位置关系判断。

①当甲乙速度相等时，甲的位置在乙的后方，则追不上，此时两者之间的距离最小。

②当甲乙速度相等时，甲的位置在乙的前方，则追上，此情况还存在乙再次追上甲。

③当甲乙速度相等时，甲乙处于同一位置，则恰好追上，为临界状态。

解决问题时要注意二者是否同时出发，是否从同一地点出发。

⑶ 匀减速运动的物体追赶同向的匀速运动的物体时，情形跟⑵类似。

3、分析追及问题的注意点：⑴ 要抓住一个条件，两个关系：一个条件是两物体的速度满足的临界条件，如两物体距离最大、最小，恰好追上或恰好追不上等。

两个关系是时间关系和位移关系，通过画草图找两物体的位移关系是解题的突破口。

⑵若被追赶的物体做匀减速运动，一定要注意追上前该物体是否已经停止运动。

专题追及与相遇问题一、追及问题1、追及与相遇的实质两物体能否在同一时刻到达同一位置。

2、两大关系：时间关系、位移关系。

3、巧用一个条件：两者速度相等；它往往是物体间能否追上或（两者）距离最大、最小的临界条件，也是分析判断的切入点。

4、三种常见情形种：⑴初速度比较小（包括为零）的匀加速运动的物体甲追赶同方向的匀速运动的物体乙，一定能追上。

a、追上前，当两者速度相等时有最大距离；b、当两者位移相等时，即后者追上前者。

⑵匀减速运动的物体追赶同向的匀速运动的物体时，存在一个能否追上的问题。

判断方法是：假定速度相等，从位置关系判断。

解决问题时要注意二者是否同时出发，是否从同一地点出发。

a、当两者速度相等时，若追者位移仍小于被追者，则永远追不上，此时两者间有最小距离；b、若两者速度相等时，两者的位移也相等，则恰能追上，也是两者避免碰撞的临界条件；c、若两者速度相等时，追者位移大于被追者，说明在两者速度相等前就已经追上；在计算追上的时间时，设其位移相等来计算，计算的结果为两个值，这两个值都有意义。

即两者位移相等时，追者速度仍大于被追者的速度，被追者还有一次追上追者的机会，其间速度相等时两者间距离有一个较大值。

⑶匀速运动的物体甲追赶同向匀加速运动的物体乙，情形跟⑵类似。

匀速运动的物体甲追赶同向匀减速运动的物体乙，情形跟⑴类似；被追赶的物体做匀减速运动，一定要注意追上前该物体是否已经停止运动。

5、解追及与相遇问题的思路（1）根据对两物体的运动过程分析，画出物体运动示意图（2）根据两物体的运动性质，（巧用“速度相等”这一条件）分别列出两个物体的位移方程，注意要将两物体的运动时间的关系反映在方程中（3）由运动示意图找出两物体位移间的关联方程（4）联立方程求解6、注意：⑴要抓住一个条件，两个关系：一个条件是两物体的速度满足的临界条件，如两物体距离最大、最小，恰好追上或恰好追不上等。

两个关系是时间关系和位移关系，通过画草图找两物体的位移关系是解题的突破口。

高中物理追击、追及和相遇问题一、追击问题追和被追的两物体的速度相等（同向运动）是能追上、追不上，两者距离有极值的临界条件：1、做匀减速直线运动的物体追赶同向做匀速直线运动的物体.（1）两物体的速度相等时，追赶者仍然没有追上被追者，则永远追不上，这种情况下当两者的速度相等时，它们间的距离最小.（2）两物体的速度相等时，如它们处在空间的同一位置，则追赶者追上被追者，但两者不会有第二次相遇的机会.（3）若追赶者追上被追者时，其速度大于被追者的速度，则被追者还可以再追上追赶者，两者速度相等时，它们间的距离最大.2、初速度为零的匀加速直线运动追赶同向做匀速直线运动的物体.（1）追上前，两者的速度相等时，两者间距离最大.（2）后者与前者的位移大小之差等于它们初始位置间的距离时，后者追上前者.二、相遇问题1、同向运动的两物体追及即相遇.2、相向运动的物体，当各自发生位移大小之和等于开始时两物体间的距离时即相遇.例1、两辆车同时同地同向做直线运动，甲以4m/s的速度做匀速运动，乙由静止开始以2m/s2的加速度做匀加速直线运动. 求：（1）它们经过多长时间相遇？相遇处离原出发地多远？（2）相遇前两物体何时距离最大？最大距离多少？解析：（1）经过t时间两物体相遇，位移为s，根据各自的运动规律列出方程：代入数据可得t=4s，s=16m.（2）甲乙经过时间t＇它们之间的距离最大，则从上面分析可知应该满足条件为：，，解得：此时它们之间最大距离为什么当时，两车间的距离最大？这是因为在以前，两车间距离逐渐变大，当以后，，它们间的距离逐渐变小，因此当时，它们间的距离最大.例2、羚羊从静止开始奔跑，经过50m的距离能加速到最大速度为25m/s，并能保持一段较长的时间；猎豹从静止开始奔跑，经过60m的距离能加速到最大速度30m/s，以后只能维持这一速度4.0s. 设猎豹距羚羊x时开始攻击，羚羊在猎豹开始攻击后1.0s才开始奔跑，假定羚羊和猎豹在加速阶段分别做匀加速运动，且均沿同一直线奔跑，则：（1）猎豹要在减速前追到羚羊，x值应在什么范围？（2）猎豹要在其加速阶段追到羚羊，x值应在什么范围？解析：解决这类题目，关键是要读懂题目，比如：猎豹在减速前一共用了多长时间，减速前的运动是何种运动等等.（1）由下图可知，猎豹要在减速前追到羚羊：对猎豹：，对羚羊同理可得：，即；当x≤55m时，猎豹能在减速前追上羚羊（2）猎豹要在其加速阶段追到羚羊，则：对猎豹：对羚羊：则：即：当x≤31.9m时，猎豹能在加速阶段追上羚羊.。

追及 相遇 问题反应时间：人从发现情况到采取相应行动经过的时间叫反应时间t 反。

反应距离：在反应时间内汽车保持原驾驶速度（相当于匀速）行驶所通过的距离s 1=v 0反刹车距离：制动刹车后开始做匀减速直线运动到汽车完全停止运动所通过的距离 停车距离：从驾驶员发现情况到汽车完全停下来的素所通过的距离.即 s 停=s 1+s 2安全距离：应该大于一定情况下的停车距离.即s 安>s 停两者速度速度大小与距离的关系：在两个物体的追及过程中，当追者的速度小于被追者的速度时，两者的距离_________；在两个物体的追及过程中，当追者的速度大于被追者的速度时，两者的距离_________；由此可知，追和被追的两者的_________常是能追上、追不上、两者之间的距离有极值的临界条，是最大值还是最小值，视实际情况而定。

知识点三：相遇问题相遇的定义：同向运动的两物体追及即相遇。

相向运动的两物体，当各自发生的_______大小之和等于开始时两物体的距离及相遇。

相遇问题的若干关系：相遇问题的主要条件是两物体在相遇处的位置相同。

1：列出两物体的位移方程，注意两个物体运动时间之间的关系。

2：利用两物体相遇时必处在同一位置，寻找两物体位移间的关系。

3：寻找问题中隐含的临界条件。

4：解析法、图像法和相对运动法是常用的方法。

例：1. 在经过某一个红绿灯时，一辆汽车以20m/s 的速度做匀速直线运动，同时停在旁边的一交警立即追赶，以2 m/s 2做匀加速直线运动，问:（1）交警和闯红灯者什么经过多长时候距离最远？ （2）交警和闯红灯者的最远距离是多少？2. 在同一直线上同方向运动的A 、B 两辆汽车，相距s=7m ，A 正以v A =4m/s 的速度向右做匀速直线运动，而B此时速度v B =10m/s ，并关闭油门，以2m/s 2的加速度大小做匀减速运动。

在追上之前A 、B 两者之间的最大距离是多少？知识点二：距离问题知识点一：概念辨析022o v s vt t +==⨯3.在经过某一个红绿灯时，一辆汽车以20m/s的速度做匀速直线运动，同时停在旁边的一交警立即追赶，以2 m/s2做匀加速直线运动，问:经过多长时间交警能追上闯红灯者？4.假设一辆轿车以20 m/s的速度行驶，在前50m处有辆客车以速度30 m/s做匀加速直线运动，如果轿车的加速度为1m/s2，则，请问，轿车经过多长时间追上客车？5.甲、乙两车从同一地点出发同向运动，其v-t图像如图所示．试计算：(1)从乙车开始运动多少时间后两车相遇?(2)相遇处距出发点多远?(3)相遇前两车的最大距离是多少?6.甲、乙两车相距10m，同时同向沿同一直线开始运动，甲在前面做初速度为零、加速度为2m/s2的匀加速直线运动，乙在后面做初速度为10m/s、加速度为1m/s2的匀加速直线运动，求甲乙两车可以相遇多少次？7.一个转弯路口，一辆轿车以15m/s行驶，突然发现前面20m远处有一辆卡车抛锚了停在前面，轿车司机立马开始刹车，假设轿车司机的反应时间为0.5s，问，要保证两车不相撞，轿车的加速度大小至少为多少？8.超载和超速是造成交通事故的隐患之一，有一辆执勤的警车停在公路边，突然发现从她旁边以15m/s的速度匀速行驶的汽车严重超载，他决定前去追赶，以防意外发生。

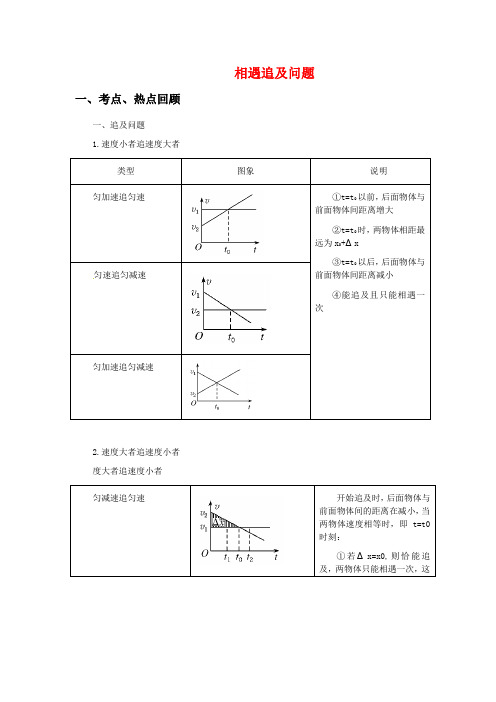
相遇追及问题一、考点、热点回顾一、追及问题1.速度小者追速度大者匀速追匀减速2.速度大者追速度小者度大者追速度小者次相遇，则①表中的Δx是开始追及以后，后面物体因速度大而比前面物体多运动的位移；②x0是开始追及以前两物体之间的距离；③t2-t0=t0-t1;④v1是前面物体的速度，v2是后面物体的速度.二、相遇问题这一类:同向运动的两物体的相遇问题,即追及问题.第二类:相向运动的物体,当各自移动的位移大小之和等于开始时两物体的距离时相遇.解此类问题首先应注意先画示意图,标明数值及物理量;然后注意当被追赶的物体做匀减速运动时,还要注意该物体是否停止运动了.求解追及问题的分析思路(1)根据追赶和被追赶的两个物体的运动性质，列出两个物体的位移方程，并注意两物体运动时间之间的关系．(2)通过对运动过程的分析，画出简单的图示，找出两物体的运动位移间的关系式．追及的主要条件是两个物体在追上时位置坐标相同．(3)寻找问题中隐含的临界条件．例如速度小者加速追赶速度大者，在两物体速度相等时有最大距离；速度大者减速追赶速度小者，在两物体速度相等时有最小距离，等等．利用这些临界条件常能简化解题过程．(4)求解此类问题的方法，除了以上所述根据追及的主要条件和临界条件解联立方程外，还有利用二次函数求极值，及应用图象法和相对运动知识求解．相遇问题相遇问题的分析思路：相遇问题分为追及相遇和相向运动相遇两种情形，其主要条件是两物体在相遇处的位置坐标相同．（1)列出两物体运动的位移方程、注意两个物体运动时间之间的关系． (2)利用两物体相遇时必处在同一位置，寻找两物体位移间的关系． (3)寻找问题中隐含的临界条件．(4)与追及中的解题方法相同．二、典型例题【例1】物体A 、B 同时从同一地点，沿同一方向运动，A 以10m/s 的速度匀速前进，B 以2m/s 2的加速度从静止开始做匀加速直线运动，求A 、B 再次相遇前两物体间的最大距离． 【解析一】 物理分析法A 做 υA ＝10 m/s 的匀速直线运动，B 做初速度为零、加速度a ＝2 m/s 2的匀加速直线运动．根据题意，开始一小段时间内，A 的速度大于B 的速度，它们间的距离逐渐变大，当B 的速度加速到大于A 的速度后，它们间的距离又逐渐变小；A 、B 间距离有最大值的临界条件是υA ＝υB ． ① 设两物体经历时间t 相距最远，则υA ＝at ② 把已知数据代入①②两式联立得t ＝5 s 在时间t 内，A 、B 两物体前进的距离分别为 s A ＝υA t ＝10×5 m＝50 ms B ＝12at 2＝12×2×52m ＝25 mA 、B 再次相遇前两物体间的最大距离为 Δs m ＝s A －s B ＝50 m －25 m ＝25 m 【解析二】 相对运动法因为本题求解的是A 、B 间的最大距离，所以可利用相对运动求解．选B 为参考系，则A 相对B 的初速度、末速度、加速度分别是υ0＝10 m/s 、υt ＝υA －υB ＝0、a ＝－2 m/s 2． 根据υt 2－υ0＝2as ．有0－102＝2×(-2)×s AB 解得Ａ、B 间的最大距离为s AB ＝25 m ． 【解析三】 极值法物体A 、B 的位移随时间变化规律分别是s A ＝10t ，s B ＝12at 2＝12×2×t 2 ＝t 5.则A 、B 间的距离Δs ＝10t －t 2，可见，Δs 有最大值，且最大值为Δs m ＝4×(－1)×0－1024×(－1) m ＝25 m【解析四】 图象法根据题意作出A 、B 两物体的υ-t 图象，如图1-5-1所示．由图可知，A 、B 再次相遇前它们之间距离有最大值的临界条件是υA ＝υB ，得t 1＝5 s ． A 、B 间距离的最大值数值上等于ΔO υA P 的面积，即Δs m ＝12×5×10 m＝25 m ．【答案】25 m【点拨】相遇问题的常用方法(1)物理分析法：抓好“两物体能否同时到达空间某位置”这一关键，按（解法一）中的思路分析．(2)相对运动法：巧妙地选取参考系，然后找两物体的运动关系．(3)极值法：设相遇时间为t ，根据条件列方程，得到关于t 的一元二次方程，用判别式进行讨论，若△＞0，即有两个解，说明可以相遇两次；若△＝0，说明刚好追上或相碰；若△＜0，说明追不上或不能相碰．(4)图象法：将两者的速度时间图象在同一个坐标系中画出，然后利用图象求解． 拓展如图1-5-2所示是甲、乙两物体从同一地点，沿同一方向做直线运动的υ－t 图象，由图象可以看出 （ 〕A ．这两个物体两次相遇的时刻分别是1s 末和4s 末B ．这两个物体两次相遇的时刻分别是2s 末和6s 末C ．两物体相距最远的时刻是2s 末D ．4s 末以后甲在乙的前面【解析】从图象可知两图线相交点1s 末和4s 末是两物速度相等时刻，从0→2s，乙追赶甲到2s 末追上，从2s 开始是甲去追乙，在4s 末两物相距最远，到6s 末追上乙．故选B ． 【答案】B【实战演练1】（2011·新课标全国卷）甲乙两辆汽车都从静止出发做加速直线运动，加速度方向一直不变。

高一物理追击相遇问题知识点总
结
1. 当两个物体在同一条直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距越来越大或越来越小时,就会涉及追及、相遇或避免碰撞等问题。

2. 追及问题的两类情况
(1) 若后者能追上前者,则追上时,两者处于同一位置,后者的速度一定不小于前者的速度。

(2) 若后者追不上前者,则当后者的速度与前者速度相等时,两者相距最近。

3.相遇问题的常见情况
(1)两个同向运动的物体追上时相遇。

(2)相向运动的两物体,当各自发生的位移大小之和等于开始时两物体的距离时即相遇。

4.追及相遇问题中的两个关系和一个条件
(1)两个关系:即时间关系和位移关系,这两个关系可通过画草图得到。

(2)一个条件:即两者速度相等,它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。

5.追及相遇问题常见的情况
物体a追物体b,开始时,两个物体相距s。

(1)a追上b时,必有s=s a-s b且v a≥v b;
(2)要使两物体恰好不相撞,必有s=s a-s b且v a≥v b;;
(3)若使物体肯定不相撞,则由v a=v b;时s a-s b≤s,且之后
v a≤v b。

三总结提升
速度小者追速度大者
速度大者追速度小者
说明：
(1)表中的δx是开始追赶以后,后面物体因速度大而比前面物体多运动的位移;
(2)x0是开始追赶以前两物体之间的距离;
(3)t2-t0=t0-t1
(4)v1是前面物体的速度,v2是后面物体的速度。

高一物理必修1 追及和相遇”问题两个物体同时在同一条直线上（或互相平行的直线上）做直线运动，可能相遇或碰撞，这一类问题称为“追及和相遇”问题。

(1)分析“追及”“相遇”问题时，一定要抓住一个条件，两个关系：①一个条件是两物体的速度满足的临界条件，如两物体距离最大、最小、恰好追上或恰好追不上等．②两个关系是时间关系和位移关系，其中通过画草图找到两物体位移之间的数量关系，是解题的突破口．(2)若被追赶的物体做匀减速运动，一定要注意追上前该物体是否停止运动．(3)仔细审题，应注意抓住题目中的关键字眼，充分挖掘题目中的隐含条件，如“刚好”“恰好”“最多”“至少”等，往往对应一个临界状态，满足相应的临界条件．“追及和相遇”问题的特点：（1）有两个相关联的物体同时在运动。

（2）“追上”或“相遇”时两物体同时到达空间同一位置。

“追及和相遇”问题解题的关键是：准确分析两个物体的运动过程，找出两个物体运动的三个关系：（1）时间关系（大多数情况下，两个物体的运动时间相同，有时运动时间也有先后）。

（2）位移关系。

（3）速度关系。

在“追及和相遇”问题中，要抓住临界状态：速度相同．．．．。

速度相同时，两物体间距离最小或最大。

如果开始前面物体速度大，后面物体速度小，则两个物体间距离越来越大，当速度相同时，距离最大；如果开始前面物体速度小，后面物体速度大，则两个物体间距离越来越小，当速度相同时，距离最小。

图象法解析追及、相遇问题[例1]：一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以3m/s2的加速度开始加速行驶，恰在这时一辆自行车以6m/s的速度匀速驶来，从后边超过汽车。

试求：汽车从路口开动后，在追上自行车之前经过多长时间两车相距最远？此时距离是多少？[解析]：[方法一]：临界状态法汽车在追击自行车的过程中，由于汽车的速度小于自行车的速度，汽车与自行车之间的距离越来越大；当汽车的速度大于自行车的速度以后，汽车与自行车之间的距离便开始缩小，很显然，当汽车的速度与自行车的速度相等时，两车之间的距离最大。

高一物理第二次培优试题追击和相遇问题知识梳理：两个物体同时在同一条直线上（或互相平行的直线上）做直线运动，可能相遇或碰撞，这一类问题称为“追及和相遇”问题。

“追及和相遇”问题解题的关键是准确分析两个物体的运动过程，找出两个物体运动的三个关系：（1）时间关系（大多数情况下，两个物体的运动时间相同，有时运动时间也有先后）。

（2）位移关系。

（3）速度关系。

在“追及和相遇”问题中，要抓住临界状态：速度相同．．．．。

速度相同时，两物体间距离最小或最大。

如果开始前面物体速度大，后面物体速度小，则两个物体间距离越来越大，当速度相同时，距离最大；如果开始前面物体速度小，后面物体速度大，则两个物体间距离越来越小，当速度相同时，距离最小。

1、甲、乙两车同时从同一地点出发,向同一方向运动,其中甲以8m/s的速度匀速行驶,乙以2m/s2的加速度由静止启动,求:(1)乙车追上甲车前与甲车的最大距离是多少?(2)乙车经过多长时间追上甲车,此时乙车的速度是多大?2、两辆完全相同的汽车，沿水平直路一前一后匀速行驶，速度均为v，若前车突然以恒定的加速度刹车，在它刚停住时，后车以前车刹车时的加速度开始刹车。

已知前车在刹车过程中所行的距离为x，若要保证两辆车在上述情况中不相撞，则两车在匀速行驶时保持的距离至少应为多大。

3、两辆游戏赛车a、b在两条平行的直车道上行驶．t＝0时两车都在同一计时线处，此时比赛开始．它们在四次比赛中的v－t图象如图所示．则下列图象对应的比赛中，有一辆赛车能够追上另一辆的是()4、甲、乙两辆汽车沿同一平直路面行驶，其v－t 图象如图3所示，下列对汽车运动状况的描述正确的是()A．在第10s 末，乙车改变运动方向B．在第10s 末，甲、乙两车相距150mC．在第20s 末，甲、乙两车相遇D．若开始时乙车在前，则两车可能相遇两次5、如图所示,为三个运动物体的v-t 图像,其中A,B 两物体是从不同地点出发,A,C 是从同一地点出发,则以下说法正确的是()A.A,C 两物体的运动方向相反B.t=4s 时,A,B 两物体相遇C.t=4s 时,A,C 两物体相遇D.t=2s 时,A,B 两物体相距最远6、设物体运动的加速度为a、速度为v、位移为s.现有四个不同物体的运动图象如下列选项所示，假设物体在t＝0时的速度均为零，则其中表示物体做单向直线运动的图象是()7、在平直公路上运动的汽车经过某位置时，从一辆同向匀速运动的自行车旁边经过。

专题三、匀变速直线运动的追及和相遇问题情况一速度大者减速（如匀减速直线运动）追速度小者（如匀速运动）：⑴当两者速度相等时，若追者仍未追上被追者，则永远追不上，此时两者有最小距离。

⑵若追上时，两者速度刚好相等，则称恰能相遇，也是两者避免碰撞的临界条件。

⑶若追上时，追者速度仍大于被追者的速度，（若不出现碰撞）则先前的被追者还有一次追上先前的追者的机会，其间速度相等时，两者相距最远。

情况二速度小者加速（如初速度为零的匀加速直线运动）追速度大者（如匀速运动）：⑴当两者速度相等时，有最大距离。

⑵若位移相等时，则追上。

例1：一小汽车从静止开始以3m/s2的加速度启动，恰有一自行车以6m/s的速度从车边匀速驶过，（1）试定性分析汽车从开动后至追上自行车前两车间的距离随时间变化的情况. （2）汽车在追上自行车前经过多长时间后两者距离最远？此时距离是多少？（3）什么时候追上自行车？此时汽车的速度是多少？例2、车从静止开始以1m/s2的加速度前进，车后相距x0为25m处，某人同时开始以6m/s的速度匀速追车，能否追上？如追不上，求人、车间的最小距离。

例3、甲车在前以10 m/s的速度匀速行驶，乙车在后以4 m/s的速度匀速行驶。

当两车相距7m时，甲车开始刹车，加速度大小为2m/s2。

问经多少时间乙车可追上甲车？在乙车追上甲车之前，二者之间的最大距离是多少？总结：一、解答追及，相遇问题时要特别注意明确两物体的位移关系、时间关系、速度关系，这些关系是我们根据相关运动学公式列方程的依据。

二、常用方法1、解析法2、临界状态分析法3、图像法4、相对运动法1、甲乙两车同时同向从同一地点出发，甲车以v1＝16m/s的初速度，a1＝－2m/s2的加速度作匀减速直线运动，乙车以v2＝4m/s的速度，a2＝1m/s2的加速度作匀加速直线运动，求两车相遇前两车相距最大距离和相遇时两车运动的时间。

2、一列火车以v1的速度直线行驶，司机忽然发现在正前方同一轨道上距车为x 处有另一辆火车正沿着同一方向以较小速度v2做匀速运动，于是他立即刹车，为使两车不致相撞，则a应满足什么条件？3、在一条公路上并排停着A、B两车，A车先启动，加速度a1＝20m/s2，B车晚3s启动，加速度a2＝30m/s2，以A启动为计时起点，问：在A、B相遇前经过多长时间两车相距最远？这个距离是多少？4、A、B两车在一条水平直线上同向匀速行驶，B车在前，车速v2＝10m/s，A 车在后，车速v1＝20m/s，当A、B相距100m时，A车用恒定的加速度a减速。