平面解析几何三角形与圆相关考前冲刺专题练习(二)附答案新高考高中数学
- 格式:doc
- 大小:178.50 KB
- 文档页数:4

高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.如图,已知PE 是圆O 的切线,直线PB 交圆O 于A 、B 两点,PA=4,AB=12,43AE =,则PE 的长为 ,ABE ∠的大小为 。
2.设12,,,n P P P 为平面α内的n 个点,在平面α内的所有点中,若点P 到12,,,n P P P 点的距离之和最小,则称点P 为12,,,n P P P 点的一个“中位点”.例如,线段AB 上的任意点都是端点,A B 的中位点.则有下列命题:
①若,,A B C 三个点共线,C 在线AB 上,则C 是,,A B C 的中位点;
②直角三角形斜边的点是该直角三角形三个顶点的中位点;
③若四个点,,,A B C D 共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是____________.(写出所有真命题的序号数学社区) (汇编年高考四川卷(理))。



高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.(选修4—1几何证明选讲)如图,AD 是⊙O 的切线,AC 是⊙O 的弦,过C 作AD 的垂 线,垂足为B ,CB 与⊙O 相交于点E ,AE 平分CAB ∠,且AE=2,则AC= .
2.如图,在ABC 中,090C ∠=, 0
60,20A AB ∠==,过C 作ABC 的外接圆的切线CD ,BD CD ⊥,BD 与外接圆交于点E ,则DE 的长为__________(汇编年普通高等学校招生统一考试重庆数学(理)试题(含答案))
评卷人
得分 二、解答题。
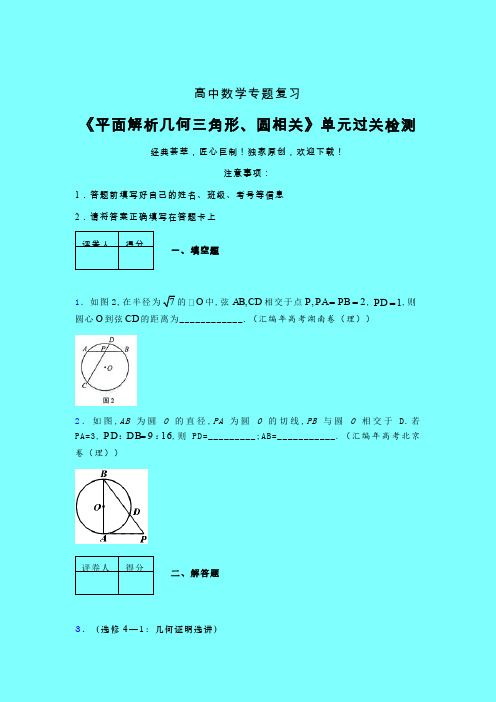
高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 评卷人得分一、填空题1.如图2,在半径为7的O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.(汇编年高考湖南卷(理))2.如图,已知圆O 的弦AB 交半径OC 于点D .若3=AD ,2=BD ,且D 为OC 的中点,则=CD .评卷人得分二、解答题3.如图,PA ,PB 是⊙O 的切线,切点分别为A ,B ,线段OP 交⊙O 于点C .若PA =12,PC =6,求AB 的长.4.已知 ABC ∆中,AC AB =,D 是ABC ∆外接圆劣弧AC 上的点(不与点C A ,重合),延长BD 至E . 求证:AD 的延长线平分CDE ∠.5.如图,⊙O 的半径OB 垂直于直径AC ,M 为AO 上一点,BM 的延长线交⊙O 于N ,过N 点的切线交CA 的延长线于P . (1)求证:2PM PA PC =⋅;(2)若⊙O 的半径为23,OA =3OM ,求MN 的长.ABPOC (第21题OC M NA PB(第1题)F ED ABC6.圆的两弦AB 、CD 交于点F ,从F 点引BC 的平行线和直线AD 交于P ,再从P 引这个圆的切线,切点是Q ,求证:PF =PQ .7.如图,四边形ABCD 内接于O ,AB AD =,过A 点的切线交CB 的延长线于E点。
求证:2AB BE CD =∙8.如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 的延长线交BC 于F . (1)求FCBF的值; (2)若△BEF 的面积为1S ,四边形CDEF 的面积为2S ,求21:S S 的值.ABCDE∙O【参考答案】***试卷处理标记,请不要删除评卷人得分一、填空题1.232.2评卷人得分二、解答题3.证明 如图,延长PO 交⊙O 于D ,连结AO ,BO .AB 交OP 于点E . 因为PA 与⊙O 相切, 所以PA 2=PC ·PD .设⊙O 的半径为R ,因为PA =12,PC =6,所以122=6(2R +6),解得R =9. …………………… 4分 因为PA ,PB 与⊙O 均相切,所以PA =PB .又OA =OB ,所以OP 是线段AB 的垂直平分线. …………………… 7分即AB ⊥OP ,且AB =2AE . 在Rt △OAP 中,AE =OA ·PA OP =365.所以AB=725. …………………… 10分 4.解(Ⅰ)设F 为AD 延长线上一点ABP OC (第21题DE∵D C B A ,,,四点共圆, ∴CDF ABC ∠=∠3分 又ACAB = ∴ACBABC ∠=∠,5分 且ACBADB ∠=∠, ∴CDFADB ∠=∠,7分对顶角ADB EDF ∠=∠, 故CDF EDF ∠=∠, 即AD的延长线平分CDE∠.10分 5.略6.(几何证明选讲)(本题满分10分)证明:证明:因为A ,B ,C ,D 四点共圆,所以∠ADF =∠ABC . 因为PF ∥BC ,所以∠AF P =∠ABC .所以∠AFP =∠FQP .因为∠APF =∠FPA ,所以△APF ∽△FPQ .所以PF PA =PDPF .………………5分 所以PF 2=PA ⋅PD .因为PQ 与圆相切,所以PQ 2=PA ⋅PD .所以PF 2=PQ 2.所以PF =PQ .……………………………………………10分 7.证明:连结AC . 因为EA 切O 于A , 所以∠EAB =∠ACB .因为AB AD =,所以∠ACD =∠ACB ,AB =AD .于是∠EAB =∠ACD . ……………………………………………4分 又四边形ABCD 内接于O ,所以∠ABE =∠D .所以ABE ∆∽CDA ∆.于是AB BE CD DA=,即AB DA BE CD ⋅=⋅.所以2AB BE CD =⋅. ……………………………10分 8.(选做题)(本小题满分8分)证明:(1)过D 点作DG ∥BC ,并交AF 于G 点, -------------------------2分AEBCDO· 第21AG F EDAB C∵E 是BD 的中点,∴BE=DE , 又∵∠EBF=∠EDG ,∠BEF=∠DEG , ∴△BEF ≌△DEG ,则BF=DG , ∴BF :FC=DG :FC ,又∵D 是AC 的中点,则DG :FC=1:2,则BF :FC=1:2;----------------------------------------------4分(2)若△BEF 以BF 为底,△BDC 以BC 为底, 则由(1)知BF :BC=1:3,又由BE :BD=1:2可知1h :2h =1:2,其中1h 、2h 分别为△BEF 和△BDC 的高, 则612131=⨯=∆∆BDC BEF S S ,则21:S S =1:5. -----------------------8分。
高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.如图,已知PE 是圆O 的切线,直线PB 交圆O 于A 、B 两点,PA=4,AB=12,43AE =,则PE 的长为 ,ABE ∠的大小为 。
2.设12,,,n P P P 为平面α内的n 个点,在平面α内的所有点中,若点P 到12,,,n P P P 点的距离之和最小,则称点P 为12,,,n P P P 点的一个“中位点”.例如,线段AB 上的任意点都是端点,A B 的中位点.则有下列命题:
①若,,A B C 三个点共线,C 在线AB 上,则C 是,,A B C 的中位点;
②直角三角形斜边的点是该直角三角形三个顶点的中位点;
③若四个点,,,A B C D 共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是____________.(写出所有真命题的序号数学社区) (汇编年高考四川卷(理))。
高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 评卷人得分一、填空题1.如图, AB 与CD 相交于点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知A C ∠=∠, PD = 2DA = 2, 则PE = ______. (汇编年高考陕西卷(文))(几何证明选做题)DBCEPA2.如图2,在半径为7的O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.(汇编年高考湖南卷(理))评卷人得分二、解答题3.如图,点D 为锐角ABC ∆的内切圆圆心,过点A 作直线BD 的垂线,垂足为F ,圆D 与边AC 相切于点E .若50C ∠=,FE D CBA(第21(A)图)求DEF ∠的度数.(选修4—1:几何证明选讲)(本小题满分10分)4.如图所示,已知PA 与O 相切,A 为切点,PBC 为割线,弦CD AP ∥,AD ,BC 相交于点E ,F 为CE 上一点,且P EDF ∠=∠.求证:2DE CE EF =⋅.5.如图,在梯形ABCD 中,AD ∥BC ,点E ,F 分别在边AB ,CD 上,设ED 与AF 相交于点G ,若B ,C ,F ,E 四点共圆,求证:AG GF DG GE ⋅=⋅.6.已知 ABC ∆中,AC AB =,D 是ABC ∆外接圆劣弧AC 上 的点(不与点C A ,重合),延长BD 至E .F ABPD E CGFEDCBA(第21—A.求证:AD的延长线平分CDE7.如图,AB为圆O的切线,A为切点,过线段AB上一点C作圆O的割线,CED(E在C、D之间),若∠ABE=∠BDE,求证:C为线段AB的中点。
8.自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C 两点.求证:∠MCP=∠MPB.【参考答案】***试卷处理标记,请不要删除评卷人得分一、填空题1. .62.23评卷人得分二、解答题3. (选修4—1:几何证明选讲)由圆D 与边AC 相切于点E ,得90AED ∠=︒,因为DF AF ⊥,得90AFD ∠=︒, 所以,,,A D F E 四点共圆,所以DEF DAF ∠=∠. ……………………………………5分又111()(180)90222ADF ABD BAD ABC BAC C C ∠=∠+∠=∠+∠=︒-∠=︒-∠,所以1902DEF DAF ADF C∠=∠=︒-∠=∠,由50C ∠=︒,得25DEF ∠=︒.……………10分 4.证明:CD PA∥ P C ∴∠=∠ …………(2分)又P EDF ∠=∠C EDF ∴∠=∠ …………(4分)又CED DEF ∠=∠CED DEF ∴∆∆ …………(8分)ED CEEF DE∴=2DE EF EC ∴=⋅.…………(10分)5.证明:连结EF ,∵B C F E ,,,四点共圆,∴ABC EFD ∠=∠……………2分F A BPDE C∵AD ∥BC ,∴BAD ABC ∠+∠=180°,∴BAD EFD ∠+∠=180° …………6分 ∴A D F E ,,,四点共圆…………8分∵ED 交AF 于点G ,∴AG GF DG GE ⋅=⋅……10分 6.解(Ⅰ)设F 为AD 延长线上一点 ∵D C B A ,,,四点共圆, ∴CDF ABC ∠=∠3分 又ACAB = ∴ACBABC ∠=∠,5分 且ACBADB ∠=∠, ∴CDFADB ∠=∠,7分对顶角ADB EDF ∠=∠, 故CDF EDF ∠=∠, 即AD的延长线平分CDE∠.10分 7.8.A .选修4-1:几何证明选讲, 证明:∵PA 与圆相切于A , ∴2MA MB MC =⋅,∵M 为PA 中点,∴PM MA =, ………………3分 ∴2PM MB MC =⋅,∴PM MBMC PM=. ……………5分 ∵BMP PMC ∠=∠, ∴△BMP ∽△PMC ,∴MCP MPB ∠=∠. ………………10分。
高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.如图,已知PE 是圆O 的切线,直线PB 交圆O 于A 、
B 两点,PA=4,AB=12,43AE =,则PE 的长为 ,ABE ∠的大小为 。
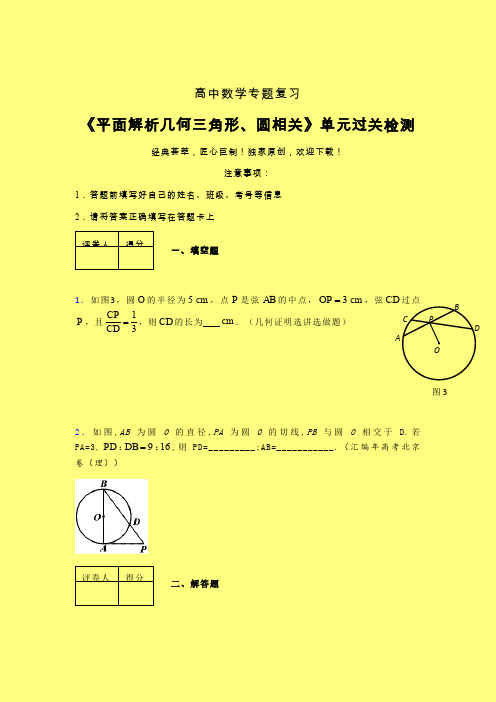
2.如图3,圆O 的半径为5cm ,点P 是弦AB 的中点,3OP =cm ,弦CD 过点P ,且13
CP CD =,则CD 的长为 cm .(几何证明选讲选做题)
评卷人
得分 二、解答题
3.如图,已知两圆交于A 、B 两点,过点A 、B 的直线分别与两圆
交于P 、Q 和M 、N .求证:PM //QN . P O A B C D 图3。