圆弧滑动面的边坡稳定计算方法

6.2 路基边坡稳定性分析6.2.1 概述根据对边坡发生滑坍现象的观察，边坡破坏时形成一滑动面。

滑动面的形状与土质有关。

对于粘性土，滑动土体有时像圆柱形，有时你碗形。

对于松散的砂性土及砂土，滑动面类似于平面。

在进行边坡稳定性分析时，大多采用近似的方法，并假设：（1）不考虑滑动土体本身内应力的分布；（2）认为平衡状态只在滑动面上达到，滑动土体成整体下滑；（3）极限滑动面位置要通过试算来确定。

路基边坡稳定性分析方法可分为两类，即力学分析法和工程地质法。

力学分析常用的边坡稳定性分析方法，根据滑动面形状分直线破裂面法和圆弧破裂面法，简称直线法和圆弧法。

直线法适用于砂类土，土的抗力以内摩擦力为主，粘聚力甚小。

边坡破坏时，破裂面近似平面。

圆弧法适用于粘性土，土的抗力以粘聚力为主，内摩擦力较小。

边坡破坏时，破裂面近似圆柱形。

下面着重讲圆弧法。

6.2.2 圆弧法（1）圆弧法的基本原理圆弧法假定滑动面为一圆弧，它适用于边坡有不同的土层、均质土边坡，部分被淹没、均质土坝，局部发生渗漏、边坡的折线或台阶形的粘性土的路堤与路堑。

圆弧法是将圆弧滑动面上的土体划分为若干竖向土条，依次计算每一土条沿滑动面的下滑力和抗滑力，然后叠加计算出整个滑动土体的稳定性。

圆弧法的计算精度主要与分段数有关。

分段愈多则计算结果愈精确，一般分8-10段。

小段的划分，还可结合横断面特性，如划分在边坡或地面坡度变化之处，以便简化计算。

用圆弧法进行边坡稳定性分析时，一般假定土为均质和各向同性；滑动面通过坡脚；不考虑土体的内应力分布及各土条之间相互作用力的影响，土条不受侧向力作用，或虽有侧向力，但与滑动圆弧的切线方向平行。

(2) 圆弧法的基本步骤（通过例子来讲解）取本设计中桩号K1+580的断面进行分析，其基本的数据为：左侧边坡高为5.572 “米，路基宽度为13.5米，路堤边坡坡度为1：1.5,其横断面如下图所示。

天然土为粘土，土的粘聚力10=,内摩擦角为22°（0.404c kP atgϕ=）,容重320/kN m γ=,设计荷载为汽-20（一辆车重力达300kN ）,验算荷载为挂-100。

6.3 极限平衡法•6.3.1 概述•6.3.2 简单（瑞典）条分法•6.3.3 简化毕肖甫法•6.3.4 Janbu法•6.3.5 Spencer方法•6.3.6 Morgenstern-Price方法•6.3.7 陈祖煜的通用条分法•6.3.8 总结•6.3.9 孔隙水压力的考虑•6.3.10 最小滑裂面的搜索6.3.1 概述•极限平衡法是建立在（刚体）极限状态时的静力平衡基础上；•不考虑变形协调条件与变形过程；•假设滑裂面（圆形或者任意）；•由于求解条件不足，需要一些假设；R M =∫()n n l σσ=其中是未知函数syxE 方程数：静力平衡＋力矩平衡＝3n滑动面上极限平衡条件＝n 未知数：条块间力＋水平力作用点位置＝2(n -1)+(n -1) ＝3n -3滑动面上的力＝2n 安全系数F＝14n5n -2未知数－方程数＝n-2q图6－64忽略土条体底部力N i 的作用点位置yE i i安全系数定义：条块底部：F c c =e ee e ef tg sec tg ϕαϕτi i i i i i N x c N l c l T +∆=+=⋅=Fϕϕtg tg e =en e f tg ϕστ+=c 极限平衡条件图6－65几种极限平衡法iq方程数：未知数：(5n -2)-3(n -1)=2n +14n图6－66h瑞典条分法0方程数：未知数：(5n-2)-(n -1)=4n -14nE iq图6－69毕肖普法(cos sin )(sin cos tg )(eee e =−∆−∆+∆−+∆+∆+∆∑∑∑R h Q x q W tg x c x q W i i i i i i i ααϕααϕFcc =e Fϕϕtg tg e =一个方程，一个未知数F ，可解，需试算。

6.3.4Janbu 法假定：假定各土条间推力作用点连线为光滑连续曲线↔“推力作用线”方程数：未知数：(5n -2)-(n -1)=4n -14ni qh i 即假定了条块间力的作用点位置Janbu 法)}tg()()]tg(tg 1[{eee=−∆−∆+∆+−+∆−∆∑ϕαϕααiiiiiiX x q W x c Q 此式可用于迭代求解安全系数F s ，但尚须先得到∆X i6.3.5 Spencer 法假定：假定土条间的切向力与法向力之比为常数，即方程数：未知数：(5n -2)-(n -1)+1=4n 4niqX i / E i = tg β= λSpencer 法补充一个方程：根据力矩平衡条件得到两个未知数：F 、β]cos sec )cos()sin()[sec(eeeee=∆−−∆+−∆−−∑ϕαϕαϕαϕβαiiiiiix c QW 1)(,0)()()(tan 1010==+=x f x f x f x f λβV 6.3.6 Morgenstern-Price 方法yxMorgenstern & Price 待求，f 1(x )为人为假定函数其中k 、m 为常数f 1(x )=1 Spencer 方法f 1(x )=0 Bishop 方法6－81Morgenstern-Price方法两个未知数F λ、两个方程，于是可以求解6.3.7yx假定：陈祖煜在Morgenstern & Price 方法的基础上，提出了更具一般性的方法其中λ待求，f 0(x )、f (x ) 为人为假定函数6.3.8 总结图6－97 几种计算方法小结极限平衡法边坡稳定分析的一些结论Duncan 关于边坡稳定分析方法的结论（1980、1996）：（1）瑞典条分法所得安全系数较小，在圆弧中心角较大和孔隙水压力较大时，安全系数的误差较大。

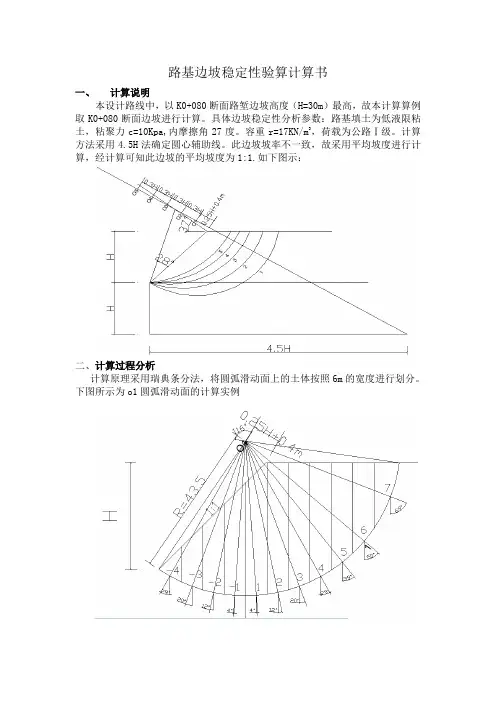
路基边坡稳定性验算计算书
一、计算说明
本设计路线中，以K0+080断面路堑边坡高度（H=30m）最高，故本计算算例取K0+080断面边坡进行计算。

具体边坡稳定性分析参数：路基填土为低液限粘土，粘聚力c=10Kpa,内摩擦角27度。

容重r=17KN/m3，荷载为公路Ⅰ级。

计算方法采用4.5H法确定圆心辅助线。

此边坡坡率不一致，故采用平均坡度进行计算，经计算可知此边坡的平均坡度为1:1.如下图示：
二、计算过程分析
计算原理采用瑞典条分法，将圆弧滑动面上的土体按照6m的宽度进行划分。

下图所示为o1圆弧滑动面的计算实例
采用计算表格可得计算结果：
L=
=R θπ
180
88.02m 则边坡稳定系数为： =
+=
∑∑i
hi b i
hi b cL Ks θγθϕγsin cos tan =⨯⨯⨯⨯⨯+⨯505
.9661701
.23927tan 61702.8810 1.35>1.25
按照上述方法一一计算出o2、o3、o4、o5处的稳定系数分别为1.32、1.29、1.33、1.37.故取Ks=1.29为最小的稳定系数，此时由于Ks>1.25,所以边坡稳定性满足要求。

第二节边坡稳定性分析方法力学验算法和工程地质法是路基边坡稳定性分析和验算方法常用的两种方法。

1．力学验算法(1)数解法假定几个不同的滑动面，按力学平衡原理对每个滑动面进行验算，从中找出最危险滑动面，按此最危险滑动面的稳定程度来判断边坡的稳定性。

此方法计算较精确，但计算繁琐。

(2)图解或表解法在图解和计算的基础上，经过分析研究，制定图表，供边坡稳定性验算时采用。

以简化计算工作。

2．工程地质法根据稳定的自然山坡或已有的人工边坡进行土类及其状态的分析研究，通过工程地质条件相对比，拟定出与路基边坡条件相类似的稳定值的参考数据，作为确定路基边坡值的依据。

一般土质边坡的设计常用力学验算法进行验算，用工程地质法进行校核；岩石或碎石土类边坡则主要采用工程地质法进行设计。

3．力学验算法的基本假定滑动土楔体是均质各向同性、滑动面通过坡脚、不考虑滑动土体内部的应力分布及各土条(指条分法)之间相互作用力的影响。

一、直线滑动面法松散的砂类土路基边坡，渗水性强，粘性差，边坡稳定主要靠其内摩擦力。

失稳土体的滑动面近似直线状态，故直线滑动面法适用于砂类土：如图2-2-4所示，验算时，先通过坡脚或变坡点假设一直线滑动面，将路提斜上方分割出下滑土楔体ABD，沿假设的滑动面AD滑动，其稳定系数K按下式计算(按边坡纵向单位长度计)：验算的边坡是否稳定，取决于最小稳定系数Kmin的值。

当Kmin＝1.0时，边坡处于极限平衡状态。

由于计算的假定，计算参数(r，Ψ，c)的取值都与实际情况存在一定的差异，为了保证边坡有足够的稳定性，通常以最小稳定系数Kmin≥1.25来判别边坡的稳定性。

但Kmin过大，则设计偏于保守，在工程上不经济。

当路堤填料为纯净的粗砂、中砂、砾石、碎石时，其粘聚力很小，可忽略不计，则式（2-2-3）变为：式(2-2-3)也适用于均质砂类土路堑边坡的稳定性验算。

二、圆弧滑动面法用粘性土填筑的路堤，边坡滑坍时的破裂面形状为一曲面，为简化计算，通常近似地假设为一圆弧状滑动面。

边坡稳定性分析方法简介介绍了边坡稳定性分析的极限平衡法：瑞典圆弧法、简化Bishop法、简化Janbu法、Morgenstern&Price法、Spencer法以及嚴格Janbu法；以及边坡稳定的可靠性分析方法：蒙特卡洛法、可靠指标法、统计矩法、模糊可靠度分析法以及随机有限元法。

标签：边坡稳定性滑坡极限平衡法可靠性分析方法一、引言滑坡是指人工或自然边坡在外界因素的诱发下丧失自身稳定性而发生滑移的地质现象，是一种严重的地质灾害，长期以来给人类造成了巨大的财产损失和人生伤害，是人类面临的三大自然灾害之一。

我国是滑坡多发国家之一，据《中国地质环境公报》有关数据显示，我国2012年全国共发生各类地质灾害18751起，全年共造成人员伤亡1021人，其中发生滑坡灾害8971起，造成人员伤亡379人，分别占地质灾害总数的47.8%和37.1%。

因此研究边坡稳定的影响因素及滑坡的发生机理，探索滑坡的防治技术具有极高的社会价值。

鉴于此，人类对边坡稳定的研究已有将近百年的历史，这使得边坡稳定性分析的方法也极大的丰富了起来。

二、边坡稳定的极限平衡分析方法极限平衡法假定边坡出现滑动面且处于极限平衡状态，然后将边坡离散成有垂直边界的土条，假设土条为刚体（即不考虑土条的变形），建立土条的静力平衡方程，通过求解静力平衡方程得到边坡的安全系数。

1776年法国工程师库仑提出了计算挡土墙土压力的方法，标志着土力学雏型的产生；1857年朗肯在假设墙后土体各点处于极限平衡状态的基础上，建立了计算主动和被动土压力的方法；库仑和朗肯在分析土压力时采用的方法后来被推广到边坡稳定分析中，形成了一个边坡稳定性评价体系，这就是极限平衡法。

在过去将近一个世纪中，这一方法逐步从一种经验性的简化方法发展成一个具有完整理论体系、较为成熟的分析方法。

（1）瑞典圆弧法。

瑞典人Fellenius提出了边坡稳定分析的圆弧滑动分析方法，即瑞典圆弧法，它是边坡稳定分析领域中最早的一种方法。

第四章堤防边坡失稳的除险加固汛期堤防边坡失稳包括临水坡的滑坡和崩岸与背水坡的滑坡，这些险情严重地威胁着堤防的安全，必须对其进行彻底的有效的治理。

堤防边坡失稳的原因是多方面的，在除险加固前必须对引起失稳的原因进行仔细地分析判断，找出原因，有针对性的采用相应的除险加固措施。

加固工作必须以《堤防工程设计规范》为依据，精心设计和施工。

加固后堤防必须达到设计标准。

本章就边坡失稳除险加固的有关技术问题做一系统的介绍，主要内容包括边坡失稳的成因与分类，滑坡的安全复核，边坡除险加固技术和崩岸除险加固技术。

第一节边坡失稳的成因与类型一、边坡失稳的成因堤防建成后，在运用中可能会遇到各种各样的情况，如汛期河湖水位涨、落、冲刷；台风季节风浪的袭击；暴雨时的浸水以及生物洞等等均会使堤防边坡失稳。

现分述如下：1.渗流原因在汛期，当河水位上涨到一定高度时，且持续时间又较长，堤身（在浸润线以下部分）将呈浸水的饱和状态，土体完全饱和后，抗剪强度降低，堤身的自重增加，相应的下滑力增大。

另外，渗流产生的渗透力，进一步增加了滑动体的滑动力。

综上所述，在渗流作用下堤身滑动体重量增加，抗剪强度降低和渗透力增加等均是导致滑坡产生的重要原因。

（二）水流冲刷浸袭原因水流冲刷浸袭岸坡主要发生在临水坡。

如在河流凹岸部分，往往主流逼岸。

受环流冲刷特别是急流顶冲的作用，岸坡淘刷通常较为严重。

一旦岸脚防护设施抵抗不住水流的冲刷力，护脚将被破坏，使岸脚的坡度逐渐变陡，直至失去平衡引起岸坡失稳破坏，即为通常所说的崩岸险情。

这种破坏多发生在河道弯曲河势复杂的凹岸堤段。

在汛期的涨水过程中或枯水期都有发生。

另外，当水位退至滩地地面高程以下并且堤身内渗水又不能及时排出时，将产生反向渗透力。

再加上浸水饱和堤身自重增加和强度降低，往往会发生坍塌。

如不及时处理，坍塌会逐步向堤防坡脚逼近，直到坡脚，引起岸坡失稳滑坡。

这种滑坡均发生在临水坡。

（三）堤防地基问题引起的滑坡堤防地基主要有两个问题，其一是地基的天然强度不够，其二是当截水设施失效时，由于大量渗水形成管涌而引起的堤防坍塌破坏。

5. 4 稳定性计算
5. 4. 1 地基稳定性可采用圆弧滑动面法进行验算。

最危险的滑动面上诸力对滑动中心所产生的抗滑力矩与滑动力矩应符合下式要求：
MＲ／MS≥1.2
(5.4.1) 式中：MS——滑动力矩（kN²m）；
MＲ——抗滑力矩（kN²m）。

5. 4. 2 位于稳定土坡坡顶上的建筑，应符合下列规定：
1 对于条形基础或矩形基础，当垂直于坡顶边缘线的基础底面边长小于或等于3m 时，其基础底面外边缘线至坡顶的水平距离（图5．4．2）应符合下式要求，且不得小于2.5m：条形基础
a≥3.5b – d/ tanβ (5.4.2-1)
矩形基础
a≥2.5b –d/ tanβ (5.4.2-2)
式中：a——基础底面外边缘线至坡顶的水平距离（m）；
b——垂直于坡顶边缘线的基础底面边长（m）；
d——基础埋置深度（m）；
β——边坡坡角（°）。

2 当基础底面外边缘线至坡顶的水平距离不满足式（5.4.2-1）、(5.4.2-2）的要求时，可根据基底平均压力按公式（5.4.1）确定基础距坡顶边缘的距离和基础埋深。

3 当边坡坡角大于 45°、坡高大于8m时，尚应按式（5.4.1）验算坡体稳定性。

边坡稳定性计算方法目前的边坡的侧压力理论，得出的计算结果，显然与实际情形不符。

边坡稳定性计算，有直线法和圆弧法，当然也有抛物线计算方法，这些不同的计算方法，都做了不同的假设条件。

当然这些先辈拿出这些计算方法之前，也曾经困惑，不做假设简化，基本无法计算。

而根据各种假设条件，是会得出理论上的结果，但与实际情况又不符。

倒是有些后人不管这些假设条件，直接应用其计算结果，把这些和实际不符的公式应用到现有的标准和理论中。

瑞典条分法，其中的一个假设条件破裂面为圆弧，另一个条件为假设的条间土之间，没有相互作用力，这样的话，对每一个土条在滑裂面上进行力学分解，然后求和叠加，最后选取系数最小的滑裂面。

从而得出判断结果。

其实，那两个假设条件对吗？都不对！第一、土体的实际滑动破裂面，不是圆弧。

第二、假设的条状土之间，会存在粘聚力与摩擦力。

边坡的问题看似比较简单，只有少数的几个参数，但是，这几个参数之间，并不是线性相关。

对于实际的边坡来讲，虽然用内摩擦角Ф和粘聚力C来表示，但对于不同的破裂面，破裂面上的作用力，摩擦力和粘聚力，都是破裂面的函数，并不能用线性的方法分别求解叠加，如果是那样，计算就简单多了。

边坡的破裂面不能用简单函数表达，但是，如果不对破裂面作假设，那又无从计算，直线和圆弧，是最简单的曲线，所以基于这两种曲线的假设，是计算的第一步，但由于这种假设与实际不符，结果肯定与实际相差甚远。

条分法的计算，是来源于微积分的数值计算方法，如果条间土之间，存在相互作用力，那对条状土的力学分解，又无法进行下去。

所以才有了圆弧破裂面的假设与忽略条间土的相互作用的假设。

其实先辈拿出这样与实际不符的理论，内心是充满着矛盾的。

实际看到的边坡的滑裂，大多是上部几乎是直线，下部是曲线形状，不能用简单函数表示，所以说，要放弃求解函数表达式的想法。

计算还是可以用条分法，但要考虑到条间土的相互作用。

用微分迭代的方法求解，能够得出近似破裂面，如果每次迭代，都趋于收敛，那收敛的曲线，就是最终的破裂面。

边坡稳定性计算方法和分析1、滑坡：土坡丧失其原有稳定性，一部分土体相对与另一部分土体滑动的现象。

2、土坡：具有倾斜坡面的土体。

3、边坡：具有倾斜坡面的岩土体。

4、土坡种类：天然土坡、人工土坡。

5、根本原因: 边坡中土体内部某个面上的剪应力达到了它的抗剪强度。

6、具体原因： a:滑面上的剪应力增加：如填土作用使边坡的坡高增加、渗流作用使下滑力产生渗透力、降雨使土体饱和，容重增加、地震作用等； b:滑面上的抗剪强度减小：如浸水作用使土体软化、含水量减小使土体干裂，抗滑面面积减小、地下水位上升使有效应力减小等。

7、假定：平面应变问题；8、滑动面形状无粘性土: 平面；均质粘性土: 光滑曲面、圆弧；非均质粘性土: 复合滑动面。

9、无粘性土的土坡稳定10、整体圆弧滑动稳定分析：粘性土颗粒之间存在粘结力，导致土坡整块下滑趋势。

11、边坡破坏形式：危险滑面位于土坡深处，对均匀土坡，平面应变条件下，滑面可近似为圆弧（圆柱面）。

12、稳定安全系数:滑动面上平均抗剪强度与平均剪应力之比。

对均质土坡、圆弧滑动面，稳定安全系数也可定义为：滑动面上最大抗滑力矩与滑动力矩之比13、最危险滑弧的寻找：手工计算，工作量大；计算机计算，程序容易实现 1、确定可能的圆心范围： 2、对每个圆心，选择不同滑弧半径，计算各滑弧安全系数； 3、比较所有安全系数，选最小值；14、条分法假定：土体为不变形刚体、滑面为连续面、极限平衡状态。

因为根据已知数不能求出未知数，所以条分法要简化：14、瑞典条分法的基本假定：滑动面为圆弧、不考虑条间力。

坡顶有荷载时：15、代替法：用浸润线以下，坡外水位以上所包围的同体积的水重对滑动圆心的力矩来代替渗流力对圆心的滑动力矩的方法。

16、毕肖普法：采用有效应力分析作用力有：土条自重；作用于土条底面的切向抗剪力、有效法向反力、孔隙水压力；在土条两侧分别作用有法向力和切向力。

17、杨布普遍条分法：假定条间力的作用点在土条底面以上1/3高度处。

求解边坡稳定安全系数两种方法的比较摘要：目前，边坡稳定性分析主要有刚体极限平衡法和有限元强度折减法，本文就理论基础、安全系数的定义及优缺点对以上两种方法进行了简要评述。

基于极限平衡法的发展起来的各种方法物理意义简单，便于计算，但是需要许多假设。

有限元强度折减法不需要假设，可以直接搜索临界滑动面并求出相应的安全系数，同时考虑了岩土体的弹塑性和边坡的破坏失稳过程。

通过对两种方法的认识比较，给岩土边坡工作者设计施工提供一定的参考价值。

关键词：边坡稳定性；极限平衡法；有限元法；安全系数引言边坡稳定分析是一个非常复杂的问题，从20世纪50年代以来，许多专家学者致力于这一研究，因此边坡稳定分析的内容十分丰富。

总体上来说，边坡稳定分析方法可分为两大类：定性分析方法和定量分析方法。

定性分析方法主要是通过工程地质勘探，可以综合考虑影响边坡稳定性的多种因素，对边坡岩土体的性质及演化史、影响边坡稳定性的主要因素、可能的变形破坏方式及失稳的力学机制等进行分析，从而给出边坡稳定性评价的定性说明和解释。

然而，人们更关心的是如何定量表示边坡的稳定性，即边坡稳定性分析的计算方法，定量方法将影响边坡稳定的各种因素都作为确定的量来考虑，通常以计算稳定安全系数为基础。

边坡稳定分析的定量方法有很多种，如条分法、数值分析方法、可靠度方法和模糊数学方法等[1-3]。

目前，边坡稳定分析方法中，人们较为熟知且广泛应用的有条分法和有限元方法。

条分法在边坡稳定分析中最早使用，因其力学模型概念清楚、简单实用，故广泛应用于实际工程中，已经逐渐成为边坡稳定分析的成熟方法。

随着计算机技术的发展，数值分析方法在工程领域应用越来越成熟，有限元方法考虑了土体的非线性应力－应变关系，同时弥补了条分法的不足，近年来有限元方法得到了极大的发展。

[4-6]刚体极限平衡法刚体极限平衡法是人们提出的最早的一类方法，是边坡分析的经典方法，只需要少许力学参数就能提供便于设计应用的稳定性指标即安全系数。

边坡稳定性计算方法一、边坡稳定性计算方法（三）毕肖普法从前述瑞典条分法可以看出，该方法的假定不是非常精确的，它是将不平衡的问题按极限平衡的方法来考虑并且未能考虑有效应力下的强度问题。

随着土力学学科的不断发展，不少学者致力于条分法的改进。

一是着重探索最危险滑位置的规律，二是对基本假定作些修改和补充。

但直到毕肖普（ A.N.Bishop ）于1955 年担出了安全系数新定义，条分法这五方法才发生了质的飞跃。

毕肖普将边坡稳定安全系数定义为滑动面上土的抗剪强度τ f 与实际产生的剪应力τ之比，即（9-7）这一安全系数定义的核心在于一是能够充分考虑有效应力下的抗剪总是；二是充分考虑了土坡稳定分析中土的抗剪强度部分发挥的实际情况。

这一概念不公使其物理意义更加明确，而且使用范围更广泛，为以后非圆弧滑动分析及土条分界面上条间力的各种考虑方式提供了有得条件。

由图 9 － 5 所示圆弧滑动体内取出土条i进行分析，则土条的受力如下：1.土条重W i 引起的切向反力T i 和法向反力N i ，分别作用在该分条中心处2.土条的侧百分别作用有法向力P i 、P i+1 和切向力H i 、H i+1 。

由土条的竖向静力平衡条件有∑ F z ，即图9-5 毕肖普法条块作用力分析（9-8）当土条未破坏时，滑弧上土的抗剪强度只发挥了一部分，毕肖普假定其什与滑面上的切向力相平衡，这里考虑安全系数的定义，且ΔH i =H i+1 -H i 即（9-9）将（9 －9 ）式代科（9 －8 ）式则有令（9-10）则(9-11)考虑整个滑动土体的极限平衡条件，些时条间力P i 和H i 成对出现，大小相等、方向相反，相互抵消。

因此只有重力W i 和切向力T i 对圆心产生力矩，由力矩平衡知(9-12)将（9 －11 ）式代入（9 －9 ）式再代入（9 －12 ）式，且d i =Rsinθ i ，此外，土条宽度不大时，b i =l i cosθ i ，经整理简化可行毕肖普边坡稳定安全系数的普遍公式(9-13)式中ΔH i 仍是未知量。