匀质粘性土体边坡稳定性计算
- 格式:doc
- 大小:4.72 MB
- 文档页数:7

边坡稳定性计算书计算依据:1、《建筑基坑支护技术规程》JGJ120-20122、《建筑边坡工程技术规范》GB50330-20023、《建筑施工计算手册》江正荣编著一、基本参数边坡稳定计算方式平面滑动法边坡工程安全等级三级边坡边坡土体类型粘性土土的重度γ(KN/m3) 20土的内摩擦角φ(°)15 土的粘聚力c(kPa) 12边坡高度H(m) 9 边坡斜面倾角α(°)40坡顶均布荷载q(kPa) 0.2二、边坡稳定性计算计算简图滑动体自重和顶部所受荷载:W= (1/2γH+q)×H×(ctgω-ctgα)=1/2(γH+2q)×H×sin(α-ω)/sinω/sinα边坡稳定性系数为:K s=(W×cosω×tanφ+H/sinω×c)/(W×sinω)=cotω×tanφ+2c/(γH+2q)×sinα/(sin(α-ω)×sinω)滑动面位置不同,Ks值亦随之而变,边坡稳定与否根据稳定性系数的最小值Ksmin 判断,相应的最危险滑动面的倾角为ω0。
求K smin值,根据dKs/dω=0,得最危险滑动面的倾角ω0的值:ctgω=ctgα+(a/(tanφ+a))0.5×cscα式中:a=2c/(γH+2q)= 2×12/(20×9+2×0.2)= 0.133ctgω=ctgα+(a/(tanφ+a))0.5×cscα= ctg(40°)+(0.133/(tan(15°)+0.133))0.5×csc(40°) = 2.088 则边坡稳定性最不利滑动面倾角为:ω0= 25.591°K smin=(2a+tanφ)×ctgα+2×(a(tanφ+a))0.5×cscα=(2×0.133+tan(15°))×ctg(40°)+2×(0.133×(tan(15°)+0.133) )0.5×csc(40°)=1.355≥1.25满足要求!。

一、边坡稳定性计算方法在边坡稳定计算方法中,通常采用整体的极限平衡方法来进行分析。
根据边坡不同破裂面形状而有不同的分析模式。
边坡失稳的破裂面形状按土质和成因不同而不同,粗粒土或砂性土的破裂面多呈直线形;细粒土或粘性土的破裂面多为圆弧形;滑坡的滑动面为不规则的折线或圆弧状。
这里将主要介绍边坡稳定性分析的基本原理以及在某些边界条件下边坡稳定的计算理论和方法。
(一)直线破裂面法化计算这类边坡稳定性分析采用直线破裂面法。
能形成直线破裂面的土类包括:均质砂性土坡;透水的砂、砾、碎石土;主要由内摩擦角控制强度的填土。
图 9 - 1 为一砂性边坡示意图,坡高 H ,坡角β,土的容重为γ,抗剪度指标为c、φ。
如果倾角α的平面AC面为土坡破坏时的滑动面,则可分析该滑动体的稳定性。
沿边坡长度方向截取一个单位长度作为平面问题分析。
图9-1 砂性边坡受力示意图已知滑体ABC重 W,滑面的倾角为α,显然,滑面 AC上由滑体的重量W= γ(ΔABC)产生的下滑力T和由土的抗剪强度产生的抗滑力Tˊ分别为:T=W · sina和则此时边坡的稳定程度或安全系数可用抗滑力与下滑力来表示,即为了保证土坡的稳定性,安全系数F s 值一般不小于 1.25 ,特殊情况下可允许减小到 1.15 。
对于C=0 的砂性土坡或是指边坡,其安全系数表达式则变为从上式可以看出,当α =β时,F s 值最小,说明边坡表面一层土最容易滑动,这时当 F s =1时,β=φ,表明边坡处于极限平衡状态。
此时β角称为休止角,也称安息角。
此外,山区顺层滑坡或坡积层沿着基岩面滑动现象一般也属于平面滑动类型。
这类滑坡滑动面的深度与长度之比往往很小。
当深长比小于 0.1时,可以把它当作一个无限边坡进行分析。
图 9-2表示一无限边坡示意图,滑动面位置在坡面下H深度处。
取一单位长度的滑动土条进行分析,作用在滑动面上的剪应力为,在极限平衡状态时,破坏面上的剪应力等于土的抗剪强度,即得式中N s =c/ γ H 称为稳定系数。

匀质粘性土体边坡稳定性计算边坡稳定性计算是土力学领域的一项重要内容,对于工程设计和施工具有重要的指导意义。
本文将对匀质粘性土体边坡稳定性计算方法进行详细介绍。
1.边坡稳定性计算的基本原理边坡稳定性计算是根据土体力学性质和力学平衡原理,对边坡的稳定性进行评价和判断。
边坡稳定性计算的基本原理包括力学平衡原理、摩擦角承载力理论、土体抗剪强度理论等。
2.边坡稳定性计算的步骤(1)确定边坡几何参数:包括边坡坡度、高度、底宽等几何参数,根据实际工程情况确定。
(2)确定土体力学参数:包括土体重度、内摩擦角、黏聚力等力学参数,通过室内试验或现场取样测试获得。
(3)计算边坡最大抗滑力:根据土体力学参数和边坡几何参数,使用土体力学理论计算边坡最大抗滑力。
(4)计算边坡滑动力:根据边坡上部土体的自重和外荷载,使用力学平衡原理计算边坡滑动力。
(5)判断边坡稳定性:比较边坡最大抗滑力与边坡滑动力的大小,判断边坡的稳定性。
3.土体力学参数的确定确定土体力学参数是边坡稳定性计算的重要基础,一般可以通过以下方法获得:(1)室内试验:如承压试验、剪切试验等,可以通过试验数据获得土体的内摩擦角、黏聚力等力学参数。
(2)现场取样测试:通过实际工程现场取样,并进行室内试验,获得土体力学参数。
(3)经验法:根据相似工程经验数据,利用统计分析方法获得土体力学参数的估计值。
4.边坡稳定性计算中的应力分析边坡稳定性计算中的应力分析是一个重要的环节,主要包括荷载分析和力的平衡分析。
荷载分析是指对边坡上的各种荷载进行分析,包括自重、活动荷载等。
力的平衡分析是指根据力学平衡原理,对边坡上部和下部的各种力进行分析,包括抗滑力、摩阻力、重力等。
5.边坡稳定性计算中的安全系数安全系数是衡量边坡稳定性的一个重要指标,一般通过比较抗滑力和滑动力的大小来确定。
安全系数的计算是边坡稳定性计算的最终结果,一般要求安全系数大于1,即抗滑力大于滑动力,以确保边坡的稳定。




一、边坡稳定性计算方法在边坡稳定计算方法中,通常采用整体的极限平衡方法来进行分析。
根据边坡不同破裂面形状而有不同的分析模式。
边坡失稳的破裂面形状按土质和成因不同而不同,粗粒土或砂性土的破裂面多呈直线形;细粒土或粘性土的破裂面多为圆弧形;滑坡的滑动面为不规则的折线或圆弧状。
这里将主要介绍边坡稳定性分析的基本原理以及在某些边界条件下边坡稳定的计算理论和方法。
(一)直线破裂面法所谓直线破裂面是指边坡破坏时其破裂面近似平面,在断面近似直线。
为了简化计算这类边坡稳定性分析采用直线破裂面法。
能形成直线破裂面的土类包括:均质砂性土坡;透水的砂、砾、碎石土;主要由内摩擦角控制强度的填土。
图 9 - 1 为一砂性边坡示意图,坡高 H ,坡角β,土的容重为γ,抗剪度指标为c、φ。
如果倾角α的平面AC面为土坡破坏时的滑动面,则可分析该滑动体的稳定性。
沿边坡长度方向截取一个单位长度作为平面问题分析。
已知滑体ABC重 W,滑面的倾角为α,显然,滑面 AC上由滑体的重量W= γ(Δ ABC)产生的下滑力T和由土的抗剪强度产生的抗滑力Tˊ分别为:T=W · sina和则此时边坡的稳定程度或安全系数可用抗滑力与下滑力来表示,即为了保证土坡的稳定性,安全系数F s 值一般不小于 1.25 ,特殊情况下可允许减小到 1.15 。
对于C=0 的砂性土坡或是指边坡,其安全系数表达式则变为从上式可以看出,当α =β时,F s 值最小,说明边坡表面一层土最容易滑动,这时图9-1 砂性边坡受力示意图当 F s =1时,β=φ,表明边坡处于极限平衡状态。
此时β角称为休止角,也称安息角。
此外,山区顺层滑坡或坡积层沿着基岩面滑动现象一般也属于平面滑动类型。
这类滑坡滑动面的深度与长度之比往往很小。
当深长比小于 0.1时,可以把它当作一个无限边坡进行分析。
图 9-2表示一无限边坡示意图,滑动面位置在坡面下H深度处。
取一单位长度的滑动土条进行分析,作用在滑动面上的剪应力为,在极限平衡状态时,破坏面上的剪应力等于土的抗剪强度,即得式中N s =c/ γ H 称为稳定系数。



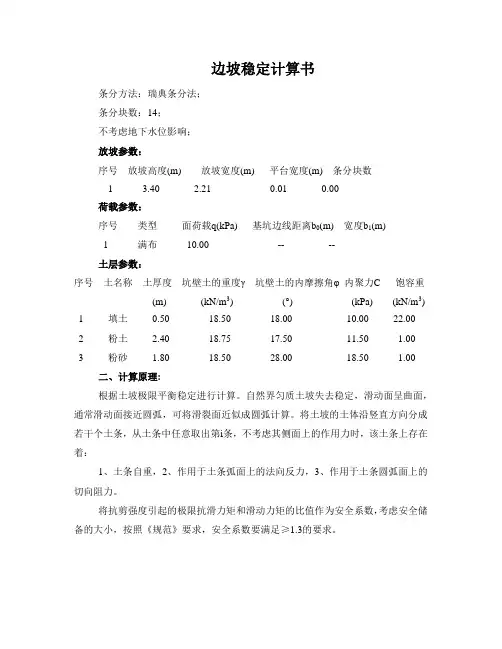
边坡稳定计算书条分方法:瑞典条分法;条分块数:14;不考虑地下水位影响;放坡参数:序号放坡高度(m) 放坡宽度(m) 平台宽度(m) 条分块数1 3.40 2.21 0.01 0.00荷载参数:序号类型面荷载q(kPa) 基坑边线距离b0(m) 宽度b1(m)1 满布10.00 -- --土层参数:序号土名称土厚度坑壁土的重度γ坑壁土的内摩擦角φ 内聚力C 饱容重(m) (kN/m3) (°) (kPa) (kN/m3)1 填土0.50 18.50 18.00 10.00 22.002 粉土 2.40 18.75 17.50 11.50 1.003 粉砂 1.80 18.50 28.00 18.50 1.00二、计算原理:根据土坡极限平衡稳定进行计算。
自然界匀质土坡失去稳定,滑动面呈曲面,通常滑动面接近圆弧,可将滑裂面近似成圆弧计算。
将土坡的土体沿竖直方向分成若干个土条,从土条中任意取出第i条,不考虑其侧面上的作用力时,该土条上存在着:1、土条自重,2、作用于土条弧面上的法向反力,3、作用于土条圆弧面上的切向阻力。
将抗剪强度引起的极限抗滑力矩和滑动力矩的比值作为安全系数,考虑安全储备的大小,按照《规范》要求,安全系数要满足≥1.3的要求。
三、计算公式:F s=∑{c i l i+[(γh1i+γ'h2i)b i+qb i]cosθi tanφi}/∑[(γh1i+γ'h2i)b i+qb i]sinθi 式子中:F s --土坡稳定安全系数;c i --土层的粘聚力;l i--第i条土条的圆弧长度;γ --土层的计算重度;θi --第i条土中线处法线与铅直线的夹角;φi --土层的内摩擦角;b i --第i条土的宽度;h i --第i条土的平均高度;h1i --第i条土水位以上的高度;h2i --第i条土水位以下的高度;γ' --第i条土的平均重度的浮重度;q --第i条土条土上的均布荷载;其中,根据几何关系,求得h i为:h i=(r2-[(i-0.5)×b i-l0]2)1/2-[r+l0-(i-0.5)×b i]tanα式子中:r --土坡滑动圆弧的半径;l0 --坡角距圆心垂线与坡角地坪线交点长度;α --土坡与水平面的夹角;h1i的计算公式h1i=h w-{(r-h i/cosθi)×cosθi-[rs in(β+α)-H]}当h1i≥h i时,取h1i = h i;当h1i≤0时,取h1i = 0;h2i的计算公式:h2i = h i-h1i;h w --土坡外地下水位深度;l i的几何关系为:l i={arccos[((i-1)×b i-l0)/r]-arccos[(i×b i-l0)/r]×2×r×π}/360θi=90-arccos[((i-0.5)×b i-l0)/r]四、计算安全系数:将数据各参数代入上面的公式,通过循环计算,求得最小的安全系数Fs:------------------------------------------------------------------------------------计算步数安全系数滑裂角(度) 圆心X(m) 圆心Y(m) 半径R(m)第1步 1.391 33.239 -0.019 5.024 5.024 示意图如下:--------------------------------------------------------------------------------------计算结论如下:第 1 步开挖内部整体稳定性安全系数Fs= 1.391>1.30 满足要求! [标高-3.400 m为开挖深度]。
土石坝边坡稳定分析与计算方法1 稳定性理论分析土坝的稳定性破坏有滑动、液化及塑性流动三种状态。
〔1〕坝坡的滑动是由于坝体的边坡太陡,坝体填土的抗剪强度太小,致使坍滑面以外的土体滑动力矩超过抗滑力矩,因此发生坍滑或由于坝基土的抗剪强度缺乏,因此坝体坝基一同发生滑动。
〔2〕坝体的液化是发生在用细砂或均匀的不够严密的砂料作成的坝体中,或由这种砂料形成的坝基中。
液化的原因是由于饱和的松砂受振动或剪切而发生体积收缩,这时砂土孔隙中的水分不能立即排出,局部或全部有效应力即转变为孔隙压力,砂土的抗剪强度减少或变为零,砂粒业就随着水的流动向四周流散了。
〔3〕土坝的塑性流动是由于坝体或坝基内的剪应力超过了土料实际具有的抗剪强度,变形超过了弹性限值,不能承受荷重,使坝坡或者坝脚地基土被压出或隆起,因此使坝体的坝基发生裂缝、沉陷等情况。
软粘性土的坝或坝基,假设设计不良,就容易产生这种破坏。
进展坝坡稳定计算时,应该杜绝以上三种破坏稳定的现象,尤其前两种,必须加以计算以及研究。
2 PC1500程序编制根据及计算方法2.1 编制根据及使用情况综述PC1500程序在计算方法方面采用了瑞典条分法和考虑土条程度侧向力的简化毕肖甫法。
从对土料物理力学指标的不同选用又可分为总应力法,有效应力法和简化有效应力法。
程序规定,计算公式中无孔隙水压力为总应力法;计入孔隙水压力为有效应力法;令孔隙水压力一项为零而将孔隙水压力包含在土体重量的计算之中,称为简化有效力法[1]。
分别考虑了稳定渗流期,施工期,水位降落期三种情况。
程序按照“水工建筑物抗震设计标准〞,“碾压土石坝设计标准〞编制。
2.2 计算方法所谓网格法,要计算假设干滑弧深度,对每一滑弧度计算过程如下:以给定滑弧圆心为中心,以大步长向四周由49个点,逐一计算,找出平安系数最小的点,以该点为中心,以小步长向四周布49个点,计算后就找出相应该滑弧深度的最小平安系数。
混合法是先用网格法。
将大步长布下的49个点算完后,找出平安系数最小的点,转入优选法计算。
一.边坡稳固性盘算办法在边坡稳固盘算办法中,平日采取整体的极限均衡办法来进行剖析.依据边坡不合决裂面外形而有不合的剖析模式.边坡掉稳的决裂面外形按土质和成因不合而不合,粗粒土或砂性土的决裂面多呈直线形;细粒土或粘性土的决裂面多为圆弧形;滑坡的滑动面为不规矩的折线或圆弧状.这里将重要介绍边坡稳固性剖析的基起源基本理以及在某些鸿沟前提下边坡稳固的盘算理论和办法.(一)直线决裂面法所谓直线决裂面是指边坡损坏时其决裂面近似平面,在断面近似直线.为了简化盘算这类边坡稳固性剖析采取直线决裂面法.能形成直线决裂面的土类包含:均质砂性土坡;透水的砂.砾.碎石土;重要由内摩擦角掌握强度的填土.图 9 - 1 为一砂性边坡示意图,坡高 H ,坡角β ,土的容重为γ ,抗剪度指标为c . φ .假如倾角α的平面AC面为土坡损坏时的滑动面,则可剖析该滑动体的稳固性.沿边坡长度偏向截取一个单位长度作为平面问题剖析.已知滑体ABC重 W ,滑面的倾角为α ,显然,滑图9-1 砂性边坡受力示意图面 AC上由滑体的重量W= γ(Δ ABC)产生的下滑力T和由土的抗剪强度产生的抗滑力Tˊ分离为:T=W · sina和则此时边坡的稳固程度或安然系数可用抗滑力与下滑力来暗示,即为了包管土坡的稳固性,安然系数F s 值一般不小于 1.25 ,特别情形下可许可减小到 1.15 .对于C=0 的砂性土坡或是指边坡,其安然系数表达式则变成从上式可以看出,当α =β时,F s 值最小,解释边坡概况一层土最轻易滑动,这时当 F s =1时,β=φ,标明边坡处于极限均衡状况.此时β角称为休止角,也称安眠角. 此外,山区顺层滑坡或坡积层沿着基岩面滑动现象一般也属于平面滑动类型.这类滑坡滑动面的深度与长度之比往往很小.当深长比小于 0.1时,可以把它当作一个无穷边坡进行剖析.图 9-2暗示一无穷边坡示意图,滑动面地位在坡面下H深度处.取一单位长度的滑动土条进行剖析,感化在滑动面上的剪应力为,在极限均衡状况时,损坏面上的剪应力等于土的抗剪强度,即得式中N s =c/ γ H 称为稳固系数.经由过程稳固因数可以肯定α和φ关系.当c=0 时,即无粘性土.α =φ ,与前述剖析雷同.二圆弧条法依据大量的不雅测标明,粘性土天然山坡.人工填筑或开挖的边坡在损坏时,决裂面的外形多呈近似的圆弧状.粘性土的抗剪强度包含摩擦强度和粘聚强度两个构成部分.因为粘聚力的消失,粘性土边坡不会像无粘性土坡一样沿坡面概况滑动.依据土体极限均衡理论,可以导出均质粘这坡的滑动面为对数螺线曲面,外形近似于圆柱面.是以,在工程设计中常假定滑动面为圆弧面.树立在这一假定上稳固剖析办法称为圆弧滑动法和圆弧条分法.1. 圆弧滑动法1915 年瑞典彼得森( K.E.Petterson )用圆弧滑动法剖析边坡的稳固性,今后该法在列国得到广泛运用,称为瑞典圆弧法.图 9 - 3 暗示一均质的粘性土坡. AC 为可能的滑动面, O为圆心, R 为半径.假定边坡损坏时,滑体ABC在自重W 感化下,沿AC绕O 点整体迁移转变.滑动面 AC 上的力系有:促使边坡滑动的滑动力矩 M s =W · d ;抵抗边坡滑动的抗滑力矩,它应当包含由粘聚力产生的抗滑力矩M r =c ·AC · R ,此外还应有由摩擦力所产生的抗滑力矩,这里假定φ= 0 .边坡沿AC的安然系数F s 用感化在 AC面上的抗滑力矩和下滑力矩之比暗示,是以有这就是整体圆弧滑动盘算边坡稳固的公式,它只实用于φ= 0 的情形.图9-3 边坡整体滑动 2. 瑞典条分法前述圆弧滑动法中没有斟酌滑面上摩擦力的感化,这是因为摩擦力在滑面的不合地位其偏向和大小都在转变.为了将圆弧滑动法运用于φ> 0 的粘性土,在圆弧法剖析粘性土坡稳固性的基本上,瑞典学者 Fellenius 提出了圆弧条剖析法,也称瑞典条分法.条会法就是将滑动土体竖向分成若干土条,把土条当成刚塑体,分离求感化于各土条上的力对圆心的滑动力矩和抗滑力矩,然后按式( 9-5 )求土坡的稳固安然系数.采取分条法盘算边坡的安然系数F ,如图 9 - 4 所示,将滑动土体分成若干土条.土条的宽度越小,盘算精度越高,为了防止盘算过于繁琐,并能知足设计请求,一般取宽为 2 ~ 6m 并应选择滑体外形变休和土层分界点作为分条的界线.于随意率性第 i条上的感化力如下.图9-4 瑞典条分法(1)土条的自.个中γ 为土的容得, 为土条的断面面积.将沿其断面积的形心感化至圆弧滑面上并分化成垂直滑面的法向分力和切于滑面的切向分力,由图 9 - 4 ( b )可知:显然, 是推进土体下滑的力.但假如第 i 条们于滑弧圆心铅垂线的载侧(坡脚一边),则起抗滑感化.对于起抗滑感化的切向分力采取符号 T ′暗示.因感化线能过滑弧圆心 O 点力矩为零,对边坡不起滑动感化,但决议着滑面上抗剪强度的大小.(2)滑面上的抗滑力 S ,偏向与滑动偏向相反.依据库仑公式应有S=N i tanφ+cl i .式中l i 为第i条的滑弧长.(3)土条的两个正面消失着条块间的感化力.感化在 i条块的力,除重力外,条块正面 ac和bd 感化有法向力P i . P i+1 ,切向力H i . H i+1 .假如斟酌这些条间力,则由静力均衡方程可知这是一个超静定问题.要使问题得解,由两个可能的门路:一是摈弃刚体均衡的概念,把土当做变形体,经由过程对土坡进行应力变形剖析,可以盘算出滑动面上的应力散布,是以可以不必用条分法而是用有限元办法.另一门路是仍以条分法为基本,但对条块间的感化力作一些可以接收的简化假定.Fellenius 假定不计条间力的影响,就是将土条两侧的前提力的合力近似地算作大小相等.偏向相反.感化在同感化面上.现实上,每一土条两侧的条间力是不服衡的,但经验标明,土条宽度不大时,在土坡稳固剖析中,疏忽条间力的感化对盘算成果的影响不明显.将感化在各段滑弧上的力对滑动圆心取矩,并分离将抗滑感化.下滑感化的力矩相加得出用在全部滑弧上的抗滑力矩以及滑动力矩的总和,即将抗滑力矩与下滑力矩之比界说为土坡的稳固安然系数,即这就是瑞典条分法稳固剖析的盘算公式.该法运用的时光很长,积聚了丰硕的工程经验,一般得到的安然系数偏低,即偏于安然,故今朝仍然是工程上经常运用的办法.(三)毕肖普法从前述瑞典条分法可以看出,该办法的假定不是异常准确的,它是将不服衡的问题按极限均衡的办法来斟酌并且未能斟酌有用应力下的强度问题.跟着土力学学科的不竭成长,许多学者致力于条分法的改良.一是侧重摸索最安全滑地位的纪律,二是对根本假定作些修正和填补.但直到毕肖普( A.N.Bishop )于 1955 年担出了安然系数新界说,条分法这五办法才产生了质的飞跃.毕肖普将边坡稳固安然系数界说为滑动面上土的抗剪强度τ f 与现实产生的剪应力τ之比,即(9-7)这一安然系数界说的焦点在于一是可以或许充分斟酌有用应力下的抗剪老是;二是充分斟酌了土坡稳固剖析中土的抗剪强度部分施展的现实情形.这一概念不公使其物理意义加倍明白,并且运用规模更广泛,为今后非圆弧滑动剖析及土条分界面上条间力的各类斟酌方法供给了有得前提.由图 9 - 5 所示圆弧滑动体内掏出土条i进行剖析,则土条的受力如下:1.土条重W i 引起的切向反力T i 和法向反力N i ,分离感化在该分条中间处2.土条的侧百分离感化有法向力P i . Pi+1 和切向力H i . H i+1 .由土条的竖向静力均衡前提有∑ F z ,即图9-5 毕肖普法条块感化力剖析(9-8)当土条未损坏时,滑弧上土的抗剪强度只施展了一部分,毕肖普假定其什与滑面上的切向力相均衡,这里斟酌安然系数的界说,且ΔH i =H i+1 -H i 即(9-9)将( 9 - 9 )式代科( 9 - 8 )式则有令(9-10)则(9-11)斟酌全部滑动土体的极限均衡前提,些时条间力P i 和 H i 成对消失,大小相等.偏向相反,互相抵消.是以只有重力W i 和切向力T i 对圆心产生力矩,由力矩均衡知(9-12)将( 9 - 11 )式代入( 9 - 9 )式再代入( 9 - 12 )式,且d i =Rsinθ i ,此外,土条宽度不大时, b i =l i cosθ i ,经整顿简化可行毕肖普边坡稳固安然系数的广泛公式(9-13)式中ΔH i 仍是未知量.毕肖普进一步假定ΔH i =0 于是上式进一步简化为(9-14)假如斟酌滑面上孔隙水压力 u 的影响并采取有用应力强度指标,则上式可改写为(9-15)从式中可以看出,参数m θi 包含有安然系数 F s ,是以不克不及接求出安然系数,而需采取试算法迭代求解F s 值.为了便于迭代盘算,已编制成m θ~θ关系曲线,如图 9 - 6 所示.试算时,可先假定 F s = 1.0 ,由图 9 - 6 查出各θ i所对应的值.代入( 9 - 14 )式中,求得边坡的安然系数 F s ′.若 F s ′与F s 之差大于划定的误差,用 F s ′查m θi ,再次盘算出安然系数 F s 值,如是重复迭代盘算,直至前后两次盘算出安然系数F s ′值,如是重复迭代盘算,直至前后两次盘算的安然系数异常接近,知足划定精度的请求为止.平日迭代老是收敛的,一般只要 3 ~ 4次即可知足精度.与瑞典条分法比拟,简化毕肖普法是在不斟酌条块间切向力的前提下,知足力多边形闭合前提,就是说,隐含着条块间有程度力的感化,固然在公式中程度感化力并未消失.所以它的特色是:(1)知足整体力矩均衡前提;(2)知足各条块力的多边形闭合前提,但不知足条块的力矩均衡前提;(4)假设条块间感化力只有法向力没有切向力;(4)知足极限均衡前提.毕肖普法因为斟酌了条块间程度力的感化,得到的安然系数较瑞典条分法略高一些.。
匀质粘性土体边坡稳定性计算中 极限平衡法与强度折减法数值分析比较1边坡的种类和滑面类型边坡按形成的原因大致可以分为三类:自然边坡、人工开挖边坡和人工填筑边坡;边坡按土层的种类也大致可以分为三种:匀质黏土边坡(人工填筑边坡一般为匀质边坡)、非匀质粘性土边坡(自然的黏砂性土边坡,或者人工开挖黏土边坡)和存在潜在软弱面或层面强度差异较大的边坡(如存在既有滑面的滑坡和上层为黏土层下为岩层的边坡)。
使边坡失稳的外因大致有:外荷载(地震、列车荷载、房屋和填土等)、重力和水的渗流、岩土的膨胀力等。
边坡失稳时滑动及滑面类型主要取决于边坡的外部荷载和边坡土层的类别,匀质粘土边坡的失稳滑面主要为圆弧型,非匀质边坡的失稳滑面主要是曲面型(复合型、对数螺旋型等),存在潜在软弱面或层面强度差异较大的边坡一般沿既有软弱面或者沿强度差异较大的两层面层间滑动(一般多为折线型,也有直线型)。
本将对匀质边坡进行有限差分强度折减法数值分析法和经典极限平衡法进行稳定性分析计算,并就安全系数的计算及粘性土边坡潜在滑动面的确定进行比较分析。
2匀质边坡的极限平衡法计算和数值模拟2.1匀质粘土边坡的极限平衡法概述粘性土边坡中,危险滑动面在土体的内部,常与圆弧面相似。
经典的基于圆弧滑动面的边坡稳定分析方法称为圆弧滑动法,属极限平衡法[1],本文对几种常用的经典分析方法进行简单概述如下。
(1)整体圆弧滑动法。
又称瑞典圆弧法,用于分析均质黏性土边坡的稳定性,即只能分析内摩擦角υ=0时的边坡稳定问题。
边坡稳定安全系数为抗滑力矩与滑动力矩之比,一般公式为:11(sin )nii r nsiii clM K M W α====∑∑(2)简单圆弧条分法。
又称瑞典条分法,仍假定滑动面为一个圆弧面。
为分析摩擦角υ>0时粘性土边坡的稳定性,将土坡分成若干个条块,但只考虑作用在条块上的重力、滑弧面上的法向力和切向抗滑力,忽略条块侧面法向力和切向力的作用。
一般公式为:11(cos tan )(sin )niii i r nsiii W cl M K M W αφα==+==∑∑(3)简化毕肖普(Bishop)法。
简化毕肖普法仍假设滑动面为圆弧,将滑动土体分为若干个条块。
在进行第i个条块的受力分析时,考虑条块侧面法向力的作用,但忽略切向力的作用。
一般公式为:1[tan ]sin i i i i iiii ic b W m K e W QRφα+=+∑∑∑,式中tan sin cos i ii i m Kφαα=+由以上简化毕肖普法的安全系数计算公式中可以看出,K 不是显函数,需采用试算迭代法求解。
(4)简布(Janbu )法。
简布法又称普遍条分法,其特点是对条块间正压力和切向力都给予考虑,由于滑动面不必是圆弧而可以是任何滑动面,其稳定安全系数也需要采用迭代方式求解(公式略)。
上面四种方法中,瑞典圆弧法和瑞典条分法由于不考虑条间力的影响,公式简单,计算速度快,但安全系数计算偏低10%~20%;后两种方法由于考虑条间力的作用,力学平衡较为合理,计算精度较高,但是计算公式较复杂,需要进行迭代试算,计算速度较慢。
本文采用Bishop 法进行匀质粘性土坡稳定性的极限平衡分析。
2.2粘性土边坡稳定性的Bishop 法分析Bishop 法作为一种条分法,发展了最初瑞典条分法将土坡按力与力矩极限平衡确定安全系数K 的思想,考虑了条间力的作用,并将土坡稳定安全系数确定为沿整个滑裂面的抗剪强度τf 与实际产生的剪应力τ之比,即:K=τ f /τ。
应用中还需要假定各土条之间的切向条间力均略去不计,即土条间的合力水平,这就是简化的Bishop 法。
Bishop 的公式推导及具体计算步骤请参见文献[2]。
现以新建铁路久长至永温线DK33+840~DK33+980段高填方路堤工点为例,采用 Bishop 法对铁路人工填筑路堤边坡进行稳定性分析: (1)工程地质概况DK33+840~DK33+980段路堤,长140m ,边坡填方最大高度25m ,站内为段内上覆坡残积(Q 4dl+el )红黏土,下伏基岩为寒武系中上统娄山关群(∈ol )白云岩夹泥质白云岩、角砾状白云岩。
地质建议基底岩土物理力学参数如下:岩土物理力学参数建议值(2)计算参数本工点选取填方边坡最高处DK33+970为代表断面,总填土高H=20m ,第一级填高12m 按1:1.75填筑,中间设2m 平台,第二级填高8m 按1:1.5填筑至坡顶,路基面宽度12.9m 。
坡脚换算角度 α=arctan(1/1.75)=29.74度,填土重度γ=20KN/m 3, υ=20度,c=10kpa ;填方基底为石灰岩地基(上部粘土考虑换填硬质岩W2),厚度为20m ,γ=25KN/m 3, 综合υ=60度。
荷载按铁路列车活载及轨道等静载换算为宽3.5m ,高3.2m 的土柱。
(3)计算过程边坡稳定性分析按照单线有列车荷载、双线有荷载、及双线均无列车荷载四种工况进行稳定性分析,将稳定性安全系数最小值作为设计值。
这里仅列出铁路双线均有列车行驶时的工况,计算简图如图1。
每条分宽度1m ,采用自动搜索最危险滑面的办法,搜索时的圆心步长0.5m ,半径步长0.5m 。
求得安全系数为1.01,最危险滑面滑动圆心O =(-0.040,51.700), 滑动半径R=51.7m ,最危险滑面见图2:Bishop 计算成果图。
从计算成果图上看,最危险滑面下部经过坡角附近,上部与第一个换算土柱结点相交。
X图2:Bishop 计算成果图2.2匀质边坡的数值模拟 边坡稳定的数值分析,可以得到到土体本身的全范围应力-应变关系,从微观上分析和计算边坡的稳定性。
基于有限差分的强度折减法,可以通过力和位移边界,应用合适的岩土模型和相应的屈服、破坏以及流动法则,能较准确的模拟匀质边坡的变形过程和应力分布,得到塑性位移等值线,根据塑性位移等值线图分析潜在滑移面及求得边坡安全系数。
这里利用2.1节所述算例进行数值模拟计算,填筑土体及下部岩石均采用摩尔-库仑屈服准则与非关联流动法则的弹塑性本构模型,应用世界著名的ITASCA 岩土咨询公司研发的Flac5.0进行建模分析。
Flac (fast lagrangian analysis for continus)是可以完成“拉格朗日分析”的“显式有限差分程序”,即使对准静态问题,FLAC 仍然求解完整的动力学方程,用局部阻尼及混合阻尼的方法吸收动能,以模拟系统的静态反应。
强度折减法简介强度折减法是有限元计算边坡稳定性的通用方法,计算时,首先选取初始折减系数Fs(通常为1),折减土体强度参数,将折减后的参数作为输入,进行有限元计算,若程序收敛,则土体仍处于稳定状态,然后再增加折减系数,直到不收敛为止,此时的折减系数即为边坡的稳定安全系数,此时的滑移面即为实际滑移面,这种方法称为土体强度折减系数法。
用折减系数摩擦角及粘聚力调整计算如下:折减的摩擦角υr=arctan(tan υ/Fs);折减的粘聚力Cr =C/Fs 。
其中υ和C 为土体初始力学参数。
但是目前有限元强度折减法中土体破坏的判断标准尚未统一,赵尚毅等人认为采用有限元计算时计算数值不收敛为判断土体破坏的依据,但是梁瑶等认为“有限元数值收敛时也不一定表明边坡处于安全状态,因此将计算的收敛性作为边坡失稳的判据不具有广泛的适用性”,另外还认为采用特征部位的位移突变性和塑性区的贯通性作为失稳判据受折减系数增幅的影响较大,会错过失稳的临界点。
采用Flac 的有限差分强度折减法计算时,由于系统本身求解的是动态方程,并采用双向折减系数进行逼近,较大值向下递减,较小值向上递增,当两个计算方向都收敛于同一数值时,认为该折减系数就是要求的安全系数。
这样就避免了上述各种失稳判据的不足和误差,计算结果是较为可信的。
根据《工程地质手册》第四版(以下简称《地质手册》)P160页表3-1-24,对照该填土层参数,取泊松比ν=0.3,压缩模量为Es=15Mpa ,推得弹性模量为022220.3(1)15110.3s E E νν⨯⨯=-⨯⨯)=(1---=0.743⨯15=11Mpa ,则土体弹性体积模量119.173(12)3(120.3)EK ν===⨯-⨯-⨯Mpa,土体弹性剪切模量G=112(1)2(10.3)Eν=⨯+⨯+=4.23Mpa ;根据《地质手册》P170页表3-1-43,对照石灰岩参数,取ν=0.3,静弹性模量为E=42.110⨯Mpa 。
根据Flac 的计算分析,求得边坡安全系数为1.08,图3及图4分别为边坡塑性剪切应变等值线图及塑性剪切应变率等值线图,图5为X 方向位移云图。
图3 边坡塑性剪切应变等值线图图4 边坡塑性剪切应变率等值线图图5 边坡X方向位移云图计算结果分析(1)从剪切变形等值线图及应变率等值线图上看,两等值线的脊线上应变及应变率最大,可以看成是填土最可能的滑移面。
该近似圆弧脊线与极限平衡法计算的最危险滑面基本相同,近一步验证了匀质边坡的圆弧型滑动类型及数值模拟强度折减法分析匀质边坡稳定性的有效性和合理性。
(2)从剪切变形等值线图及应变率等值线图上可以看出受影响的区域及受影响的大小。
但将两等值线图与X方向位移云图比较可以看出,边坡表层土体X方向发生的位移最大,但其应变值却较小,即剪切变形和X方向的位移相关性不大。
3结论及建议(1)极限平衡法和数值模拟强度折减法都是工程应用中可行的通用边坡稳定性定量分析方法,且极限平衡法在圆弧型滑动计算中安全系数的计算结果偏安全。
(2)极限平衡法由于本身力学分析上的限制,对某些边界力学条件进行假设或者忽略不计(如Bishop方法中的切向条间力),使得其力学方程本身不够准确,因此计算结果一般偏于安全。
(3)数值模拟强度折减法关注整个系统的力学平衡,且能够根据土体模型参数求得应力及应变结果,能够很好的反应土体应力破坏的影响区域和变形大小。
采用Flac进行边坡计算时,由于采用的是求解动态方程和双向强度系数法逼近,可以避免有限元强度折减法分析时各种失稳判据的不足和误差,计算结果是较为可信的。
(4)数值模拟强度折减法进一步验证了匀质边坡的圆弧型滑动类型。
(5)数值模拟计算时应注意土层本身的力学参数和模型的选用。
力学参数对数值模拟的影响很大(主要是粘聚力和内摩擦角),实际工程中需要通过现场及室内试验,求得相应工点所需的土层力学参数,并根据现场土层及外荷载对土层影响的实际情况选取适当的本构模型。
此外,数值模拟还受单元划分的大小,几何及位移边界条件等的影响。
所以,工程实践中应根据具体情况选择简布法、Bishop法及瑞典条分法等经典稳定性计算方法结合工程经验判断数值分析结果的合理性。