5第五章_离散傅里叶变换解析

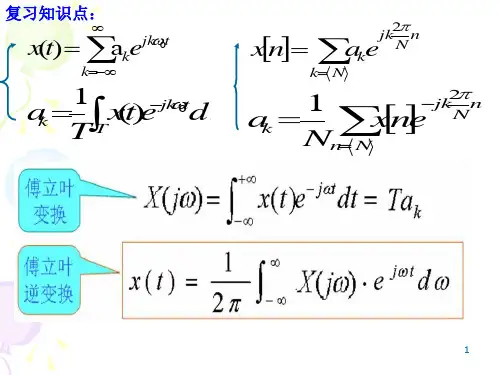
数字信号处理第五章离散傅里叶变换授课教师：胡双红联系QQ：79274544长沙理工大学计算机与通信工程学院DFT:离散傅里叶变换引言DFSDFTDFT性质DFT应用快速算法：FFT引言DTFT对绝对可加序列给出了频域（ω）表示 Z变换对任意序列给出了广义频域（z）表示 特点：变换都是对无限长序列定义的；变换都是连续变量（ω或z ）的函数；用MATLAB实现时必须将序列截断然后在有限点上求表达式。

即DTFT和ZT都不是数值可计算的变换数值可计算的变换DFT方法：通过在频域对DTFT采样获得。

步骤：通过分析周期序列来建立傅里叶级数(DFS)将DFS推广到有限长序列得DFT优点：适合计算机实现的数值可计算的变换缺点：对长序列的数值计算费时多改进方法：快速傅里叶变换（FFT）第一次课5.1 离散傅里叶级数定义MATLAB实例与Z变换和DTFT的关系Z域采样与重建~式中：x解：由题设可得基波周期~~令x周期，⎪⎧±±==−,2,,02N Lk j N N k L π"作出L=5和N=20的周期序列图>> x=[1,1,1,1,1,zeros(1,15)];>> xtilde=x'*ones(1,3);>> xtilde=xtilde(:);>> xtilde=xtilde';>> n=[-20:39];>> stem(n,xtilde)>> axis([-20,39,-0.5,1.5]);>> xlabel('n');ylabel('x(n)');title('周期方波序列')2）对L=5和N=20的MATLAB脚本如下------------------------MATLAB脚本--------------------->> L=5;N=20;k=[-N/2:N/2];% 方波参数>> xn=[ones(1,L),zeros(1,N-L)];% 方波序列x(n) >> Xk=dfs(xn,N);% DFS>> magXk=abs([Xk(N/2+1:N) Xk(1:N/2+1)]);% DFS幅度>> subplot(2,2,1);stem(k,magXk);>> axis([-N/2,N/2,-0.5,0.5]);>> subplot(2,2,1);stem(k,magXk);>> axis([-N/2,N/2,-0.5,5.5]);>> xlabel('k');ylabel('Xtilde(k)');>> title('L=5,N=20 的方波的DFS');3）结论：方波DFS的DFT包络为抽样函数"sinc"函数k=0时幅度为L，函数的零点在N/L的整数倍点 方波持续时间相同时，周期越大，其频谱越密设x(n)是一有限长的序列，长度为N,即：那么它的z 变换和DTFT 为：,01()0,n N x n n ≤≤−⎧=⎨⎩非零其余()()()()∑∑−=−−=−==1010N n jwnjw N n n e n x e X zn x z X 与Z 变换和DTFT 的关系（了解）~现在以周期3）在4）在解：序列x(n)不是周期的，但是有限长的在设x(n)任意序列N−∞1上式表明：单位圆上对X(z)采样，时域将得到一个周期序列，是原序列x(n)和它的无穷多个移位±rN 的副本的线性组合。

离散时间傅⾥叶变换1. 离散时间傅⾥叶变换的导出针对离散时间⾮周期序列，为了建⽴它的傅⾥叶变换表⽰，我们将采⽤与连续情况下完全类似的步骤进⾏。

考虑某⼀序列x[n]，它具有有限持续期；也就是说，对于某个整数N1和N2，在 −N1⩽以外，x[n]=0。

下图给出了这种类型的⼀个信号。

由这个⾮周期信号可以构成⼀个周期序列\tilde x[n]，使x[n]就是\tilde x[n]的⼀个周期。

随着N的增⼤，x[n]就在⼀个更长的时间间隔内与\tilde x[n]相⼀致。

⽽当N\to \infty，对任意有限时间值n⽽⾔，有\tilde x[n]=x[n]。

现在我们来考虑⼀下\tilde x[n]的傅⾥叶级数表⽰式\tag{1}\tilde x[n] = \sum_{k=(N)}a_ke^{jk{(2\pi/N)}n}\tag{2}a_k = \frac{1}{N} \sum_{n=(N)} \tilde x[n]e^{-jk{(2\pi/N)}n}因为在-N_1 \leqslant N \leqslant N_2区间的⼀个周期上\tilde x[n]=x[n]，因此我们将上式的求和区间就选在这个周期上\tag{3}a_k = \frac{1}{N} \sum_{n=-N_1}^{N_2} x[n]e^{-jk{(2\pi/N)}n} = \frac{1}{N} \sum_{n=-\infty}^{+\infty} x[n]e^{-jk{(2\pi/N)}n}现定义函数\tag{4}X(e^{j\omega})=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n}可见这些系数a_k正⽐于X(e^{j\omega})的各样本值，即\tag{5}a_k = \frac{1}{N}X(e^{jk\omega_0})式中，\omega_0=2\pi/N⽤来记作在频域中的样本间隔。

离散傅里叶变换系数离散傅里叶变换（Discrete Fourier Transform，DFT）是傅里叶变换在离散域上的一种形式。

它广泛应用于信号处理、图像处理、通信等领域。

离散傅里叶变换系数是对原始信号在频域上的表示，常用于分析信号的频谱特性、提取信号中的特征等。

离散傅里叶变换系数的计算可以通过快速傅里叶变换（Fast Fourier Transform，FFT）算法来高效地实现。

下面将介绍离散傅里叶变换系数的相关参考内容。

1. 基本定义：离散傅里叶变换系数可以用复数表示。

设原始信号为长度为N 的离散序列x(n)，其离散傅里叶变换系数为X(k)，则离散傅里叶变换的定义为：X(k) = ∑ [x(n) * e^(-j2πnk/N)]， n=0,1,2,...,N-1, k=0,1,2,...,N-1。

2. 离散傅里叶变换系数的物理意义：离散傅里叶变换系数表示了原始信号在不同频率分量上的能量分布。

离散傅里叶变换系数的模表示信号在该频率上的幅度，相位表示信号在该频率上的相位差。

3. FFT算法：离散傅里叶变换系数的计算可以通过FFT算法来高效地实现。

FFT算法将离散傅里叶变换的计算复杂度从O(N^2)降低到O(NlogN)。

FFT算法的基本思想是将信号分解成序列长度为2的幂次的子序列，然后利用蝶形结构的计算流程递归计算离散傅里叶变换。

4. 离散傅里叶变换系数的性质：离散傅里叶变换系数具有多种性质，包括线性性质、频率平移性质、频率抽样性质、能量守恒性质等。

这些性质可以用于信号处理的分析和计算。

5. 应用领域：离散傅里叶变换系数广泛应用于信号处理、图像处理、通信等领域。

在信号处理中，可以通过计算离散傅里叶变换系数来分析信号的频谱特性，如频率成分、频率间隔等。

在图像处理中，可以通过计算图像的二维离散傅里叶变换系数来进行图像压缩、图像滤波等操作。

在通信中，离散傅里叶变换系数可以用于信号的调制、解调、信道估计等。

离散时间傅里叶变换对介绍离散时间傅里叶变换（Discrete Fourier Transform, DFT）是信号处理中常用的一种变换方法，它将时域中的离散信号转换到频域中，通过分析信号在频域上的特性，可以揭示信号中隐藏的信息。

离散时间傅里叶变换对作为傅里叶变换对的一种形式，在数字图像处理、通信系统等领域有着广泛的应用。

一级标题DFT的定义离散时间傅里叶变换对将离散时间域序列x[n]（n为整数）转换为离散频率域序列X[k]（k为整数）。

其数学定义如下：其中，N为序列的长度，k为频率序列的索引。

DFT的计算复杂度较高，通常采用快速傅里叶变换（Fast Fourier Transform, FFT）算法来加速计算。

DFT的性质DFT具有一些重要的性质，它们对于理解和应用DFT至关重要。

1.线性性质：DFT是线性的，即对信号的线性组合的DFT等于DFT的线性组合。

2.循环移位性质：对于输入信号x[n]，将其向右循环移位m个单位，得到新的信号x_m[n]=x[(n-m) mod N]，则x_m[n]的DFT等于x[n]的DFT乘以旋转因子的m次幂。

3.对称性质：当输入信号x[n]是实数序列时，其DFT具有共轭对称性，即X[k]=X^*[N-k]。

4.周期性质：对于周期为N的信号，其DFT为离散频率域上的周期函数，频率分辨率为1/N。

DFT的应用DFT在信号处理中有着广泛的应用，如下所示：1.频谱分析：通过计算信号的DFT，可以将信号转换到频域中，从而分析信号中各个频率成分的强度和相位，揭示信号的频域特性。

2.信号压缩：DFT可以将时域信号转换为频域信号，在频域中进行处理，然后再通过逆变换将频域信号转换为时域信号，实现信号的压缩。

3.滤波器设计：DFT可以用来设计滤波器，通过将滤波器的频率响应转换为时域响应，从而得到滤波器的系数。

4.信号恢复：通过对信号的部分采样数据进行DFT，可以恢复出信号的完整信息，实现信号的恢复。

离散傅里叶变换逆变换推导1. 引言好吧，今天我们聊聊一个听起来有点复杂但其实很酷的东西——离散傅里叶变换（DFT）及其逆变换。

你可能会问：“这玩意儿是什么鬼？”别急，咱们慢慢捋清楚。

这就像是在一场音乐会上，乐队演奏的旋律和你脑海中回响的那段旋律之间的转换。

咱们一起来揭开这神秘的面纱，让你也能在这个数学的乐园里轻松翩翩起舞！2. 离散傅里叶变换的基础2.1 DFT的概念离散傅里叶变换，顾名思义，就是将一串离散的信号转化为频域的表示。

听起来复杂，其实就是把你的数据从时域（比如说，一个信号随时间的变化）转到频域（信号的频率成分）。

这就像把各种食材切成不同的形状，方便做出美味的菜肴。

对吧？2.2 数学公式好，咱们来看看公式。

DFT的公式是这样子的：X(k) = sum_{n=0^{N1 x(n) cdot e^{j2pi kn/N 。

这里，(X(k)) 是频域信号，(x(n)) 是时域信号，(N) 是信号的长度。

听起来像个外星语言，但其实它的意思就是每个频率成分都由所有时刻的信号通过一定的权重加权得到。

就像是调色盘上不同颜色的混合，最终变成一幅美丽的画！3. 逆变换的推导3.1 逆DFT的公式现在，我们说到逆变换。

逆离散傅里叶变换（IDFT）就是把频域信号再转换回时域信号。

它的公式长得有点像DFT，写出来是：x(n) = frac{1{N sum_{k=0^{N1 X(k) cdot e^{j2pi kn/N 。

这看起来是不是有点像“你来我往”的感觉？就像是跟朋友打乒乓球，你打回去，我再打回来。

通过这个公式，我们可以从频域的信号中提取出原始的时域信号。

3.2 推导过程推导过程其实没那么可怕。

我们从DFT的公式出发，想要得到时域的信号。

首先，把DFT的公式反过来用，就像把衣服翻过来一样。

接着，利用一些数学上的小技巧，比如换算和公式的变形。

虽然中间会遇到一些小麻烦，但只要耐心一点，慢慢捣鼓，总能把这些小怪兽一一击败，最终收获满意的成果。

第五章离散傅里叶变换及其快速算法 1离散傅里叶变换(DFT)的推导(1) 时域抽样：目的：解决信号的离散化问题。

效果：连续信号离散化使得信号的频谱被周期延拓。

⑵时域截断： 原因：工程上无法处理时间无限信号。

方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。

结果：时域乘以矩形脉冲信号，频域相当于和抽样函数卷积。

(3)时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。

方法：周期延拓中的搬移通过与 、：(t _nT s )的卷积来实现。

表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。

结果：周期延拓后的周期函数具有离散谱。

经抽样、截断和延拓后，信号时域和频域都是离散、周期的。

过程见图抽样后0 fJif-用于截断原函数J L<Z 用于抽样i4LJI Ji WWtin1 f=1 ----------> --------------t-------------- ►fVtt截断后有卷积波纹i------------- ►t0 I------------------ rfJL 」L延拓后7角ii t飞7Vtfft \ \ t \ f定义DFT用于延拓「ITf处理后信号的连续时间傅里叶变换:I'U N *|nT sr 0 N图1 DFT 推导过程示意图〜 oo "N 4l ~(f)=£ IS h(nTs)ek =^O「j2 飞n/Nn=0-kf o )(i) l~(f)是离散函数，仅在离散频率点f二kf o k—处存在冲激，强度为a k,其T o NT s余各点为0。

〜N N 1(ii) H(f)是周期函数，周期为Nf o == 工，每个周期内有N个不同的幅值。

T o NT s T s(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。

2 DFT及IDFT的定义DFT定义：设hnT s是连续函数h(t)的N个抽样值n=0,1,…,N J，这N个点的宽度为N 的DFT 为：DFT N h(nT s)]=^ h(nT s)e」2邢/N =H —— J (k =0,1,…，N _1)7 l NT s 丿IDFT定义：设H 上是连续频率函数H(f)的N个抽样值k =0,1，…，N J，这N个点(NT s 丿的宽度为N的IDFT为：DFT N1 H k丄7 H L e」2「nk/N厶nTs , (k =0,1,…，N —1)|L Ns N k 卫NT se^Rk/N称为N点DFT的变换核函数，e j2 flk/N称为N点IDFT的变换核函数。

离散信号傅里叶变换
离散信号傅里叶变换（DiscreteFourierTransform，DFT）是一种将离散信号转换为频域表示的数学工具。

它是傅里叶变换在离散信号上的推广，可以将一个N个采样点的离散信号转换为N个频率分量的复数表示，其中每个分量对应着信号中不同频率的成分。

DFT在数字信号处理、语音处理、图像处理、通信系统等领域得到了广泛应用。

DFT的基本原理是将一个离散信号分解成若干个正弦和余弦函数的和，每个函数都对应着一个频率分量。

这些分量的振幅和相位可以通过一组复数来表示，这组复数就是DFT的结果。

DFT可以通过快速傅里叶变换（FFT）算法来实现，该算法可以大大提高DFT的计算效率。

在实际应用中，需要对信号进行窗函数处理和零填充等预处理，以保证DFT结果的准确性和稳定性。

DFT在音频信号处理中的应用非常广泛。

例如，可以通过DFT将音频信号从时域转换为频域，以便于对音频信号进行滤波、降噪、谱分析、音乐合成等处理。

此外，DFT还可以用于数字通信中的调制解调、频率估计、信道均衡等方面的处理。

因此，掌握离散信号傅里叶变换的基本原理和应用方法，对于数字信号处理和通信系统的研究都具有重要的意义。

- 1 -。