最佳平方逼近多项式

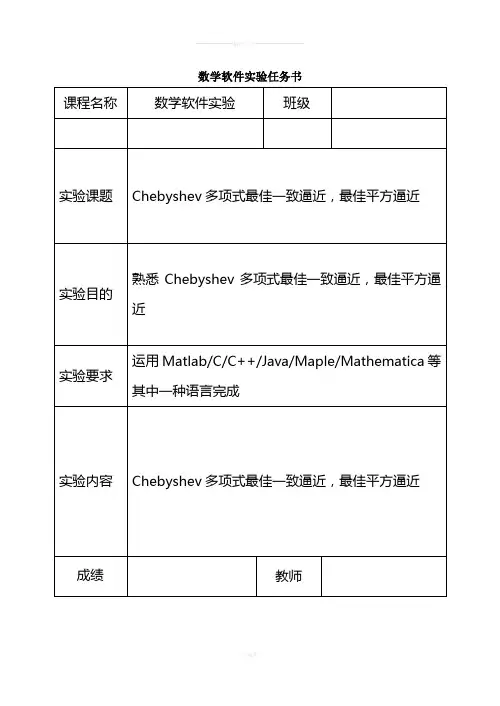
数学软件实验任务书实验1 Chebyshev 多项式最佳一致逼近1 实验原理设()f x 是定义在区间[,]a b 上的函数，寻求另一个构造简单，计算量小的函数()x ϕ来近似的代替()f x 的问题就是函数逼近问题。

通常我们会取一些线性无关的函数系来达到函数逼近的目的：对于给定的函数{()}j x ϕ，寻求函数0()()nj j j x c x ϕϕ==∑ 使()()0max lim n a x bf x x ϕ→∞<<-=的函数称为一致逼近。

使()()()0lim b pa n f x x W x dx ϕ→∞-=⎰ 的函数称为关于权()W x 的p L 逼近。

比较常用的p=2，称为平方逼近。

设()f x 是定义在区间[,]a b 上的函数，则任给定ε，存在一多项式P ε使不等式()f x P εε-<对所有[,]x a b ∈一致成立()()max n a x b f x P x ≤≤-则()n P x 称为()f x 的n 次最佳一致逼近多项式。

求最佳一次逼近多项式的一种方法是可以采用Chebyshev 节点插值，Chebyshev 节点为 1(21)[()cos _],0,1,2,,22(1)j j x b a b a j n n +=-++=+L 2 实验数据求函数()x f x xe =在区间[6,6]上的3，5和12次近似最佳逼近多项式（Chebyshev 插值多项式）3 实验程序function g=cheby(f,n,a,b)for j=0:ntemp1=(j*2+1)*pi/2/(n+1);temp2=(b-a)*cos(temp1)+b+a;temp3(j+1)=temp2/2;endx=temp3;y=f(x);g=lag(x,y);function s=lag(x,y,t)syms p;n=length(x);s=0;for(k=1:n)la=y(k);%构造基函数for(j=1:k-1)la=la*(p-x(j))/(x(k)-x(j)); end;for(j=k+1:n)la=la*(p-x(j))/(x(k)-x(j)); end;s=s+la;simplify(s);endif(nargin==2)s=subs(s,'p','x');s=collect(s);s=vpa(s,4);elsem=length(t);for i=1:mtemp(i)=subs(s,'p',t(i));ends=temp;endf=inline('x.*exp(x)','x');z1=cheby(f,3,-6,6)z2=cheby(f,5,-6,6)z3=cheby(f,12,-6,6)%作出逼近函数图形subplot(2,2,1),ezplot('x*exp(x)'),grid subplot(2,2,2),ezplot(z1),grid subplot(2,2,3),ezplot(z2),grid subplot(2,2,4),ezplot(z3),grid%改变背景为白色set(gcf,'color','white')4 实验结果z1 =-133.0+4.822*x^3+27.38*x^2-20.40*xz2 =.2001*x^5+1.359*x^4-2.020*x^3-18.56*x^2+6.126*x+40.2 5z3 =-.2405e-16+.5187e-7*x^12+.6439e-6*x^11+.1420e-5*x^1 0+.6201e-5*x^9+.2287e-3*x^8+.1813e-2*x^7+.8007e-2*x^6+.3709e-1*x^5+.1682*x^4+.520 9*x^3+.9981*x^2+.9729*x实验2 Chebyshev最佳平方逼近1 实验数据的5 次最佳求函数()arccos,(11)=-≤≤关于权函数f x x x平方逼近。

实验三 最佳平方逼近多项式的收敛性一、 实验目的若已知给定区间[a,b]上的连续函数f (x ),寻找一个简单、易于计算的函数P(x)来代替f (x )使用，即用P(x)去近似f (x )，这就是函数逼近所要研究的问题。

而逼近的方法很多，收敛速度也各有差异，本实验主要讨论最佳平方逼近，分别对Legendre 以及Chebychev 方法讨论其n 次截断多项式的问题，观察其收敛性，学习并掌握最佳平方逼近多项式的MATLAB 实验及精度比较。

二、 实验原理由教材定义有：对于给定的函数],[)(b a C x f ∈，如果存在使得则称S *(x )是f (x )在集合01{(),(),,()}n Span x x x ϕϕϕ中的最佳平方逼近函数。

显然，求最佳平方逼近函数)()(0**x a x S j n j j ϕ⋅=∑=的问题可归结为求它的系数**1*0,,,na a a ，使多元函数 取得极小值，也即点(**1*0,,,na a a )是I (a 0, …，a n )的极点。

由于I (a 0, a 1, …，a n )是关于a 0, a 1, …，a n 的二次函数，利用多元函数取得极值的必要条件，0=∂∂ka I (k = 0, 1, 2, …, n ) 即得方程组如采用函数内积记号 那么，方程组可以简写为0(,)(,)(0,1,2,,)n k j j k j a f k n ϕϕϕ===∑ (1)这是一个包含n + 1个未知元a 0, a 1, …, a n 的n + 1阶线性代数方程组，写成矩阵形式为0001000101111101(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)(,)n n n n n n n n a f a f a f ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭………（2） 此方程组叫做求a j (j = 0, 1, 2, …, n )的法方程组。

matlab采用勒让德正交多项式的方法求5次最佳平方逼近多项式摘要：一、勒让德正交多项式的基本概念二、MATLAB中求5次最佳平方逼近多项式的方法三、具体操作步骤及示例代码四、结果分析与实用性讨论正文：一、勒让德正交多项式的基本概念勒让德正交多项式（Legendre Polynomials）是一种重要的正交多项式，它在数学、物理等领域具有广泛的应用。

它们的定义如下：二、MATLAB中求5次最佳平方逼近多项式的方法在MATLAB中，可以使用polyfit函数来实现对给定数据的最佳平方逼近。

polyfit函数可以拟合任意次数的多项式，但这里我们关注的是5次最佳平方逼近多项式。

三、具体操作步骤及示例代码1.准备数据：首先，我们需要一组数据作为输入。

这里我们生成一个简单的数据集：```matlabx = linspace(0, 1, 100);y = sin(x);```2.求5次最佳平方逼近多项式：使用polyfit函数求解5次最佳平方逼近多项式：```matlabp5 = polyfit(x, y, 5);```3.绘制原始数据与5次逼近曲线：```matlabplot(x, y, "o", x, polyval(p5, x), "-");```4.输出5次逼近多项式的系数：```matlabdisp(p5);```四、结果分析与实用性讨论1.结果分析：通过MATLAB求得的5次最佳平方逼近多项式为：```p5 =1.0000 -0.4162 0.4162 -0.0707 0.0707```这意味着在给定数据集上，5次最佳平方逼近多项式的系数分别为1，-0.4162，0.4162，-0.0707和0.0707。

2.实用性讨论：勒让德正交多项式在许多实际应用中具有较好的性能，例如在数值积分、数值微分等方面。

在本示例中，我们使用MATLAB实现了5次最佳平方逼近多项式的求解，这对于逼近给定数据集具有较高的精度。

如何用MATLAB求解一次和二次最佳平方逼近多项式MATLAB是一款功能强大的科学计算软件，广泛应用于各个领域中。

在数学建模中，经常需要使用最佳平方逼近技术来找到最符合样本数据的多项式函数，而MATLAB正是一个能够高效求解最佳平方逼近问题的工具。

本文将详细介绍如何用MATLAB求解一次和二次最佳平方逼近多项式。

一、最佳平方逼近最佳平方逼近是一种拟合问题，其目的是找到一个多项式函数，使其能够最好地逼近给定的样本数据集合，即最小化其平方误差。

这个问题可以表示为以下形式：minimize f(x) = ||Ax - b||^2其中，x是待求解的多项式系数向量，A是输入数据集合的矩阵表示，而b则是对应的样本输出向量。

通过数学推导，可以得到最佳平方逼近问题的解析解为：x = (A^T A)^{-1} A^T b二、一次最佳平方逼近在一次最佳平方逼近中，我们需要找到一个一次多项式 y = ax + b，使其能够最好地逼近给定的样本数据集合。

首先，我们需要构建A 矩阵和b向量，并将其带入解析公式中求解。

具体步骤如下：步骤1：生成样本数据集合x = [1 2 3 4 5];y = [1.2 1.9 3.2 4.1 5];步骤2：构建A矩阵和b向量n = length(x);A = [x' ones(n, 1)];b = y';步骤3：求解多项式系数向量a_b = inv(A' * A) * A' * b;步骤4：绘制拟合曲线a = a_b(1);b = a_b(2);x_fit = linspace(min(x), max(x), 100);y_fit = a*x_fit + b;plot(x, y, 'o', x_fit, y_fit);三、二次最佳平方逼近在二次最佳平方逼近中，我们需要找到一个二次多项式 y = ax^2 + bx + c，使其能够最好地逼近给定的样本数据集合。

最佳三角多项式平方逼近最佳三角多项式平方逼近是一种数学方法，用于找到最接近给定数据集的三角多项式。

这种方法可以在各种领域中找到广泛的应用，包括信号处理、数据分析和图像处理。

下面将通过一个具体的例子来说明最佳三角多项式平方逼近的原理和应用。

假设我们有一组离散的数据点，表示某个周期性现象的变化趋势。

我们的目标是找到一个三角多项式，使得该多项式的平方与数据点的误差最小。

简单来说，我们希望找到一个函数，尽可能地逼近这些数据点，并且在逼近过程中最小化误差。

为了实现这个目标，我们可以使用最小二乘法。

最小二乘法是一种常见的数学方法，用于拟合数据和模型之间的关系。

它通过最小化残差平方和来找到最佳的拟合曲线。

在三角多项式平方逼近中，我们可以使用最小二乘法来找到最佳的三角多项式。

具体来说，我们可以使用三角函数的线性组合作为三角多项式的形式。

常见的三角函数包括正弦函数和余弦函数。

通过选择适当的系数，我们可以将这些三角函数进行线性组合，并得到一个逼近函数。

然后，我们可以使用最小二乘法来找到最佳的系数，使得逼近函数的平方与数据点的误差最小。

最佳三角多项式平方逼近的优点是可以适应不同类型的数据集。

它可以在周期性数据和非周期性数据中都得到良好的逼近效果。

此外，该方法还可以通过调整三角多项式的阶数来控制逼近的精度。

较高阶的三角多项式可以更精确地逼近数据，但也可能导致过拟合问题。

需要注意的是，最佳三角多项式平方逼近并不是万能的。

它的适用范围有一定限制，对于某些特殊的数据集可能效果不佳。

此外，该方法也需要一定的数学基础和计算能力才能正确应用。

总结来说，最佳三角多项式平方逼近是一种用于找到最接近给定数据集的三角多项式的数学方法。

它通过最小化平方误差来实现数据的逼近。

该方法在各种领域中都有广泛的应用，并且可以通过调整阶数来控制逼近的精度。

然而，需要注意该方法的适用范围和限制，并具备一定的数学基础和计算能力才能正确应用。