高考物理二轮复习专题

专题分层突破练2力与直线运动A组基础巩固练1.(2023浙江衢州模拟)北京冬奥会速滑馆内装有猎豹超高速4K轨道摄像机,让犯规无处遁形。

某次速度滑冰比赛中,摄像机和运动员的水平位移x随时间t变化的图像分别如图所示,下列说法正确的是()A.摄像机做直线运动,运动员做曲线运动B.0~t1时间内摄像机在前,t1~t2时间内运动员在前C.0~t2时间内摄像机与运动员的平均速度相同D.0~t2时间内任一时刻摄像机的速度都大于运动员的速度2.如图所示,甲、乙两辆汽车并排沿平直路面向前行驶,两车车顶O1、O2两位置都装有蓝牙设备,这两个蓝牙设备在5 m以内能够实现通信。

t=0时刻,甲、乙两车刚好位于图示位置,此时甲车的速度为5 m/s,乙车的速度为2 m/s,O1、O2的距离为3 m。

从该时刻起甲车以1 m/s2的加速度做匀减速直线运动直至停下,乙车保持原有速度做匀速直线运动。

忽略信号传递时间,从t=0时刻起,甲、乙两车能利用蓝牙通信的时间为()A.2.00 sB.4.75 sC.6.00 sD.6.25 s3.(2023河南安阳模拟)很多智能手机都有加速度传感器,能通过图像显示加速度情况,用手掌托着智能手机,打开加速度传感器,把手机向上抛出,然后又在抛出点接住手机,得到如图所示的加速度随时间变化的图像,图中t1=0.38 s,t2=0.55 s,t3=0.66 s,t4=1.26 s,重力加速度g取10 m/s2,由此可判断出()A.t1时刻手机的速度最大B.t2时刻手机离开手掌C.t3时刻手机处于超重状态D.手机离开手掌后上升的高度为0.45 m4.(2023全国乙卷)一同学将排球自O点垫起,排球竖直向上运动,随后下落回到O点。

设排球在运动过程中所受空气阻力大小和速度大小成正比,则该排球()A.上升时间等于下落时间B.被垫起后瞬间的速度最大C.达到最高点时加速度为零D.下落过程中做匀加速运动5.(2023山东日照模拟)如图所示,质量为2 kg的物体A静止于竖直的轻弹簧上,质量为2 kg的物体B 用细线悬挂,A、B间相互接触但无压力,重力加速度g取10 m/s2。

高三物理第二轮专题复习力与运动专题一、要点归纳(一)深刻理解牛顿第一、第三定律1．牛顿第一定律(惯性定律)一切物体总保持匀速直线运动状态或静止状态，直到有外力迫使它改变这种状态为止．(1)理解要点①运动是物体的一种属性，物体的运动不需要力来维持．②它定性地揭示了运动与力的关系：力是改变物体运动状态的原因，是使物体产生加速度的原因．(2)惯性：物体保持原来的匀速直线运动状态或静止状态的性质叫做惯性．①惯性是物体的固有属性，与物体的受力情况及运动状态无关．②质量是物体惯性大小的量度．2．牛顿第三定律作用力与反作用力一定是同种性质的力，作用效果不能抵消．懂得与一对平衡力区分。

(二)牛顿第二定律1．定律内容：物体的加速度a跟物体所受的合外力F合成正比，跟物体的质量m成反比．2．公式：F合＝ma理解要点①因果性：F合是产生加速度a的原因，它们同时产生，同时变化，同时存在，同时消失．②方向性：a与F合都是矢量，方向相同．③瞬时性和对应性：a为某时刻某物体的加速度，F合是该时刻作用在该物体上的合外力．3．应用牛顿第二定律解题的一般步骤：(1)确定研究对象；(2)分析研究对象的受力情况，画出受力分析图并找出加速度的方向；(3)建立直角坐标系，使尽可能多的力或加速度落在坐标轴上(4)分别沿x轴方向和y轴方向应用牛顿第二定律列出方程；(5)统一单位，计算数值．二、热点、重点、难点一、正交分解法在动力学问题中的应用当物体受到多个方向的外力作用产生加速度时，常要用到正交分解法．●例1如图甲所示，在风洞实验室里，一根足够长的细杆与水平面成θ＝37°固定，质量m＝1 kg的小球穿在细杆上静止于细杆底端O点．现有水平向右的风力F作用于小球上，经时间t1＝2 s后停止，小球沿细杆运动的部分v－t图象如图1－15乙所示．试求：(sin 37°＝0.6，cos 37°＝0.8)(1)小球在0～2 s内的加速度a1和2～4 s内的加速度a2．(2)风对小球的作用力F的大小．二、连接体问题(整体法与隔离法)高考卷中常出现涉及两个研究对象的动力学问题，整体法与隔离法是处理这类问题的重要手段．1．整体法是指当连接体内(即系统内)各物体具有相同的加速度时，可以把连接体内所有物体组成的系统作为整体考虑，分析其受力情况，运用牛顿第二定律对整体列方程求解的方法．2．隔离法是指当研究对象涉及由多个物体组成的系统时，若要求连接体内物体间的相互作用力，则应把某个物体或某几个物体从系统中隔离出来，分析其受力情况及运动情况，再利用牛顿第二定律对隔离出来的物体列式求解的方法．●例2 如图所示，在光滑的水平地面上有两个质量相等的物体，中间用劲度系数为k 的轻质弹簧相连，在外力F 1、F 2的作用下运动．已知F 1＞F 2，当运动达到稳定时，弹簧的伸长量为( )A ．F 1－F 2kB ．F 1－F 22kC ．F 1＋F 22kD ．F 1＋F 2k★同类拓展 如图所示，质量为m 的小物块A 放在质量为M 的木板B 的左端，B 在水平拉力的作用下沿水平地面匀速向右滑动，且A 、B 相对静止．某时刻撤去水平拉力，经过一段时间，B 在地面上滑行了一段距离x ，A 在B 上相对于B 向右滑行了一段距离L (设木板B 足够长)后A 和B 都停了下来．已知A 、B 间的动摩擦因数为μ1，B 与地面间的动摩擦因数为μ2，且μ2＞μ1，则x 的表达式应为( )A ．x ＝M m LB ．x ＝(M ＋m )L mC ．x ＝μ1ML (μ2－μ1)(m ＋M )D ．x ＝μ1ML (μ2＋μ1)(m ＋M )三、临界问题●例3 如图所示，滑块A 置于光滑的水平面上，一细线的一端固定于倾角为45°、质量为M 的光滑楔形滑块A 的顶端P 处，细线另一端拴一质量为m 的小球B ．现对滑块施加一水平方向的恒力F ，要使小球B 能相对斜面静止，恒力F 应满足什么条件？四、超重与失重问题●例4 为了测量某住宅大楼每层的平均高度(层高)及电梯的运行情况，甲、乙两位同学在一楼电梯内用电子体重计及秒表进行了以下实验：质量m ＝50 kg 的甲同学站在体重计上，乙同学记录电梯从地面一楼到顶层的过程中，体重计的示数随时间变化的情况，并作出了如图所示的图象．已知t ＝0时，电梯静止不动，从电梯内楼层按钮上获知该大楼共19层．求：(1)电梯启动和制动时的加速度大小．(2)该大楼的层高．三、经典考题在本专题中，正交分解、整体与隔离相结合是最重要也是最常用的思想方法，是高考中考查的重点．1．[2007年·上海物理卷]有一个直角支架AOB ，AO 水平放置，表面粗糙，OB 竖直向下，表面光滑．AO 上套有小环P ，OB 上套有小环Q ，两环质量均为m ，两环间由一根质量可忽略、不可伸长的细绳相连，并在某一位置平衡(如图所示)．现将P 环向左移一小段距离，两环再次达到平衡，那么将移动后的平衡状态和原来的平衡状态比较，AO 杆对P 环的支持力N 和细绳上的拉力T 的变化情况是 ( )A ．N 不变，T 变大B ．N 不变，T 变小C ．N 变大，T 变大D ．N 变大，T 变小2．[2004年·全国理综卷]如图所示，在倾角为α的固定光滑斜面上有一块用绳子拴着的长木板，木板上站着一只猫．已知木板的质量是猫的质量的2倍．当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变．则此时木板沿斜面下滑的加速度为 ( )A ．g 2sin α B ．g sin α C ．32g sin α D ．2g sin α3. [2010年海南卷]如图，粗糙的水平地面上有一斜劈，斜劈上一物块正在沿斜面以速度v0匀速下滑，斜劈保持静止，则地面对斜劈的摩擦力A.等于零B.不为零，方向向右C.不为零，方向向左D.不为零，v0较大时方向向左，v0较小时方向向右4．[2009年高考·山东理综卷]如图所示，某货场需将质量m 1＝100 kg 的货物(可视为质点)从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物由轨道顶端无初速度滑下，轨道半径R ＝1.8 m ．地面上紧靠轨道依次排放两块完全相同的木板A 、B ，长度均为l ＝2 m ，质量均为m 2＝100 kg ，木板上表面与轨道末端相切．货物与木板间的动摩擦因数为μ1，木板与地面间的动摩擦因数μ2＝0.2．(最大静摩擦力与滑动摩擦力大小相等，取g ＝10 m/s 2)(1)求货物到达圆轨道末端时对轨道的压力．(2)若μ1＝0.5，求货物滑到木板A 末端时的速度和在木板A 上运动的时间．5．[2009年海南卷]一卡车拖挂一相同质量的车厢，在水平直道上以012/v m s =的速度匀速行驶，其所受阻力可视为与车重成正比，与速度无关。

电场与磁场的理解一、选择题1．某平面区域内一静电场的等势线分布如图中虚线所示，相邻的等势线电势差相等，一负电荷仅在静电力作用下由a 运动至b ，设粒子在a 、b 两点的加速度分别为a a 、b a ，电势分别为a ϕ、b ϕ，该电荷在a 、b 两点的速度分别为a v 、b v ，电势能分别为p a E 、p b E ，则（ ）A ．a b a a >B ．b a v v >C ．p p a b E E >D ．a b ϕϕ>2．某静电场方向平行于x 轴，x 轴上各点电场强度随位置的变化关系如图所示，规定x 轴正方向为电场强度正方向。

若取x 0处为电势零点，则x 轴上各点电势随位置的变化关系可能为（ ）A ．B ．C ．D ．3．一匀强电场的方向平行于xOy 平面，平面内a 、b 、c 三点的位置如图所示，三点的电势分别为10V 、17V 、26V 。

下列说法正确的是（ ） A ．电场强度的大小为2.5V/cmB ．坐标原点处的电势为2VC ．电子在a 点的电势能比在b 点的小7eVD ．电子从b 点运动到O 点，电场力做功为16eV4．如图，空间中存在着水平向右的匀强电场，现将一个质量为m ，带电量为q +的小球在A 点以一定的初动能k E 竖直向上抛出，小球运动到竖直方向最高点C 时的沿场强方向位移是0x ，动能变为原来的一半（重力加速度为g ），下列说法正确的是（ ）A ．场强大小为22mgqB ．A 、C 竖直方向的距离为0x 的2倍C ．小球从C 点再次落回到与A 点等高的B 点时，水平位移是02xD ．小球从C 点落回到与A 点等高的B 点时，电场力做功大小为2k E5．如图，圆心为O 的圆处于匀强电场中，电场方向与圆平面平行，ab 和cd 为圆的两条直径，60aOc ∠=︒。

将一电荷量为q 的正点电荷从a 点移到b 点，电场力做功为W （0W >）；若将该电荷从d 点移到c 点，电场力做功也为W 。

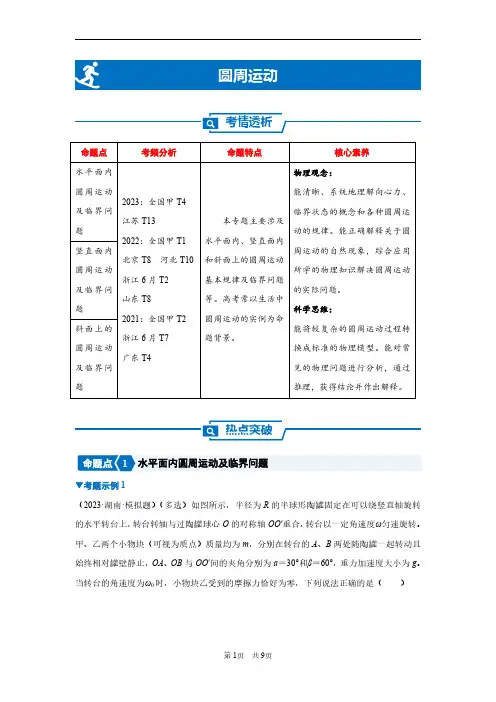
考情透析命题点考频分析命题特点核心素养水平面内圆周运动及临界问题2023：全国甲T4江苏T132022：全国甲T1北京T8河北T10浙江6月T2山东T82021：全国甲T2浙江6月T7广东T4本专题主要涉及水平面内、竖直面内和斜面上的圆周运动基本规律及临界问题等。

高考常以生活中圆周运动的实例为命题背景。

物理观念：能清晰、系统地理解向心力、临界状态的概念和各种圆周运动的规律。

能正确解释关于圆周运动的自然现象，综合应用所学的物理知识解决圆周运动的实际问题。

科学思维：能将较复杂的圆周运动过程转换成标准的物理模型。

能对常见的物理问题进行分析，通过推理，获得结论并作出解释。

竖直面内圆周运动及临界问题斜面上的圆周运动及临界问题热点突破1水平面内圆周运动及临界问题▼考题示例1（2023·湖南·模拟题）（多选）如图所示，半径为R的半球形陶罐固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合，转台以一定角速度ω匀速旋转。

甲、乙两个小物块（可视为质点）质量均为m，分别在转台的A、B两处随陶罐一起转动且始终相对罐壁静止，OA、OB与OO′间的夹角分别为a＝30°和β＝60°，重力加速度大小为g。

当转台的角速度为ω0时，小物块乙受到的摩擦力恰好为零，下列说法正确的是（）A ．ω0＝g RB ．当转台的角速度为ω0时，甲有上滑的趋势C ．当角速度从0.5ω0缓慢增加到1.5ω0的过程中，甲受到的摩擦力一直增大D ．当角速度从0.5ω0缓慢增加到1.5ω0的过程中，甲受到的支持力一直增大答案：BD解析：A 、小物块乙受到的摩擦力恰好为零，重力和支持力的合力提供向心力，即mg tan β＝mω02R sin β,解得：ω0＝2gR,故A 错误；B 、设转台角速度为ω时，物块甲受到的摩擦力为零，重力和支持力的合力提供向心力，mg tan α＝mω2R sin α,解得：ω＝2g3R＜ω0;所以当转速为ω0时，支持力和重力的合力不足以提供向心力，甲有沿内壁切线上滑的趋势，故B 正确；C 、甲的临界角速度ω＝2g3R＞0.5ω0，所以当角速度从0.5ω0缓慢增大到2g3R时，甲有沿内壁切线下滑的趋势，角速度从2g3R缓慢增大到1.5ω0时，甲有沿内壁切线上滑的趋势，摩擦力方向发生了变化，其大小先减小再反向增大，故C 错误；D 、将甲收到的力分解为水平方向和竖直方向，竖直方向的合力为0，即mg ＝N cos α＋f sin α，由C 可知，角速度从0.5ω0缓慢增加到1.5ω0的过程中，先减小再反向增大，则支持力一直在增大，故D 正确；故选：BD 。

机械振动和机械波一、单选题1．一列简谐横波沿x轴正方向传播，t=0时刻的波形如图中实线所示，t=0.1s时刻的波形如图中虚线所示。

波源不在坐标原点O，P是传播介质中离坐标原点xP=2.5m处的一个质点。

则以下说法中正确的是（）A．质点P的振幅为0.05mB．波的频率可能为7.5HzC．波的传播速度可能为50m/sD．在t=0.1s时刻与P相距5m处的质点一定沿y轴正方向运动2．如图所示，一质点做简谐运动，O点为平衡位置，质点先后以相同的速度依次通过M、N两点，历时1s，质点通过N点后再经过1s又第2次通过N点，在这2s内质点通过的总路程为12cm。

则质点的振动周期和振幅分别为（）A．3s，6cm B．4s，9cmC．4s，6cm D．2s，8cm3．两列振幅为A、波长相同的平面简谐横波，以相同的速率沿相反方向在同一介质中传播，如图所示为某一时刻的波形图，其中实线为向右传播的波，虚线为向左传播的波，a、b、c、d、e为介质中沿波传播路径上五个等间距的质点。

两列波传播的过程中，下列说法中正确的是（）A．质点b、d始终静止不动B．质点a、b、c、d、e始终静止不动C．质点a、c、e始终静止不动D．质点a、c、e以振幅A做简谐运动4．处于同一水平面的振源S1和S2做简谐运动，向四周分别发出两列振幅均为A的简谐横波，波在同一区域传播，形成如图所示稳定的干涉图样。

图中实线表示波峰，虚线表示波谷，N点为波峰与波谷相遇点，M点为波峰与波峰相遇点。

下列说法不正确的是（）A．两个振源S1和S2的振动频率一定相同B．M点为振动加强点，其振幅为AC．N点始终处在平衡位置D．从图示时刻开始经过四分之一周期，M、N两点竖直高度差为05．如图所示为某时刻的两列简谐横波在同种介质中沿相同方向传播的波形图，此时质点P的运动方向如图所示，已知质点P在a波上，质点Q在b波上，则下列说法错误的是（）A．两列波具有相同的波速B．此时质点Q正沿y轴正方向运动C．一个周期内，质点Q沿x轴前进的距离是质点P的1.5倍D．在质点P完成30次全振动的时间内质点Q可完成20次全振动6．如图所示，甲质点在x1轴上做简谐运动，O1为其平衡位置，A1、B1为其所能达到的最远处。

专题1“双基”篇所谓“双基”知识（基本概念、基本规律），就是能举一反三、以不变应万变的知识．只有掌握了“双基”，才谈得上能力的提高，才谈得上知识和能力的迁移．综合分析近几年的高考物理试卷不难看出，虽然高考命题已由“知识立意”向“能力立意”转变，但每年的试卷中总有一定数量的试题是着重考查学生的知识面的，试卷中多数试题是针对大多数考生设计的，其内容仍以基本概念、基本规律的内涵及外延的判断和应用为主．只要考生知道有关的物理知识，就不难得出正确的答案．以2003年我省高考物理试卷为例，属于对物理概念、规律的理解和简单应用考查的试题，就有15题，共90分，占满分的60％．如果考生的基本概念、基本规律掌握得好，把这90分拿到手，就已大大超过了省平均分．许多考生解题能力差，得分低，很大程度上与考生忽视对物理基础知识的理解和掌握有关，对基础知识掌握得不牢固或不全面，就会在解题时难以下手，使应得的分白白丢失． 如果说，我们要求学生高考时做到“该得的分一分不丢，难得的分每分必争”，那么，就要先从打好基础做起，抓好物理基本知识和规律的复习．复习中，首先要求学生掌握概念、规律的“内涵”（例如内容、条件、结论等），做到“理科文学”，对概念、规律的内容，该记该背的，还是要在理解的基础上熟记．其次，要掌握概念和规律的“外延”，例如，对机械能守恒定律，如果条件不满足，即重力或弹力以外的其他力做了功，系统的机械能将如何变化？等等．有一些情况我的感受特别深，一是有些试题看似综合性问题，而学生出错的原因实质是概念问题．二是老师以为很简单的一些概念问题，学生就是搞不清，要反复讲练．下面，就高中物理复习中常遇到的一些基本概念问题，谈谈我的看法．我想按照高中物理知识的五大板块来讲述．一些共同性的概念和规律：1．不能简单地从数学观点来理解用比值定义的物理量（一个物理量与另一个物理量成正比或反比的说法）．2．图线切线的斜率．3．变加速运动中，合力为零时，速度最大或最小．一、力学●物体是否一定能大小不变地传力？例1：两物体A 和B ，质量分别为m 1和m 2，互相接触放在光滑水平面上，如图所示．对物体A 施以水平的推力F ，则物体A 对物体B 的作用力等于 （ B ）A ．112m F m m + B ．212m F m m + C ．F D ．21m F m 拓展：如图，物体A 叠放在物体B 上，B 置于光滑水平面上．A 、B质量分别为m A ＝6kg ，m B ＝2kg ，A 、B 之间的动摩擦因数μ＝0.2．开始时水平拉力F ＝10N ，此后逐渐增加，在增大到45N的过程中，则 ( D )A ．只有当拉力F ＜12N 时，两物体才没有相对滑动B ．两物体开始没有相对运动，当拉力超过12N 时，开始相对滑动C ．两物体间从受力开始就有相对运动D ．两物体间始终没有相对运动●力、加速度、速度间的关系——拓展至与机械能的关系例2：如图所示，轻弹簧一端固定，另一端自由伸长时恰好到达O 点．将质量为m （视为质点）的物体P 与弹簧连接，并将弹簧压缩到A 由静止释放物体后，物体将沿水平面运动并能到达B 点．若物体与水平面间的摩擦力不能忽略，则关于物体运动的下列说法正确的是 （BC ）A ．从A 到O 速度不断增大，从O 到B 速度不断减小B ．从A 到O 速度先增大后减小，从O 到B 速度不断减小C ．从A 到O 加速度先减小后增大，从O 到B 加速度不断增大D ．从A 到O 加速度先减小后增大，从O 到B 加速度不断增大拓展1：（1991年）一物体从某一高度自由落下，落在直立于地面的轻弹簧上，如图所示．在A 点，物体开始与弹簧接触，到B 点时，物体速度为零，然后被弹回．下列说法正确的是 （ C ） A ．物体从A 下降到B 的过程中，动能不断变小B ．物体从B 上升到A 的过程中，动能不断变大C ．物体从A 下降到B ，以及从B 上升到A 的过程中，速率都是先增大，后减小D ．物体在B 点时，所受合力为零●矢量的合成或分解 1．认真画平行四边形例3：三段不可伸长的细绳OA 、OB 、OC 能承受的最大拉力相同，它们共同悬挂一重物，如图所示，其中OB 是水平的，A 端、B 端固定．若逐渐增加C 端所挂物体的质量，则最先断的绳 （ C ）A ．必定是OAB ．必定是OBC ．必定是OCD ．可能是OB ，也可能是OA2．最小值问题例4：有一小船位于60m 宽的河边，从这里起在下游80m 处河流变成瀑布．假设河水流速为5m/s ，为了使小船能安全渡河，船相对于静水的速度不能小于多少？3．速度的分解——孰合孰分？例5：如图所示，水平面上有一物体A 通过定滑轮用细线与玩具汽车B 相连，汽车向右以速度v 作匀速运动，当细线OA 、OB 与水平方向的夹角分别为α、β时，物体A 移动的速度为 （ D ）A ．v sin αcos βB ．v cos αcos βC ．v cos α/cos βD ．v cos β/cos α●同向运动的物体，距离最大（或最小）或恰好追上时，速度相等（但不一定为零）． 例6：如图所示，在光滑水平桌面上放有长为L 的长木板C ，在C 上左端和距左端s 处各放有小物块A 和B ，A 、B 的体积大小可忽略不计，A 、B 与长木板C 间的动摩擦因数为μ，A 、B 、C 的质量均为m ，开始时，B 、C 静止，A 以某一初速度v 0向右做匀减速运动，设物体B 与板C 之间的最大静摩擦力等于滑动摩擦力．求：A OBAB（1）物体A 运动过程中，物块B 和木板C 间的摩擦力．（2）要使物块A 、B 相碰，物块A 的初速度v 0应满足的条件． ●匀变速运动的规律及其推论的应用——注意条件例7：已知做匀加速直线运动的物体，第5s 末的速度为10m/s ，则该物体 （ BD ）A ．加速度一定为2m/s 2B ．前5s 内位移可能为25mC ．前10s 内位移一定为100mD ．前10s 内位移不一定为100m●匀速圆周运动、万有引力定律： 注意公式2r GMm F =①和r mv F 2=②中r 的含义． 例8：今年10月15日9时，中国自行研制的载人航天飞船“神舟”五号，从酒泉航天发射场升空，10分钟后进入预定轨道，绕地球沿椭圆轨道Ⅰ运行，如图．（1）当飞船进入第5圈后，在轨道Ⅰ上A 点加速，加速后进入半径为r 2的圆形轨道Ⅱ．已知飞船近地点B 距地心距离为r 1，飞船在该点速率为v 1，求：轨道Ⅱ处重力加速度大小．（2）飞船绕地球运行14圈后，返回舱与轨道舱分离，返回舱开始返回．当返回舱竖直向下接近距离地球表面高度h 时，返回舱速度约为9m/s ，为实现软着落（着地时速度不超过3m/s ），飞船向下喷出气体减速，该宇航员安全抗荷能力（对座位压力）为其体重的4倍，则飞船至少应从多高处开始竖直向下喷气？（g ＝10m/s 2）●惯性、离心运动和向心运动例9：如图（俯视图）所示，以速度v 匀速行驶的列车车厢内有一水平桌面，桌面上的A 处有一小球．若车厢中的旅客突然发现小球沿图中虚线从A 运动到B ，则由此可判断列车 （ A ）A ．减速行驶，向南转弯B ．减速行驶，向北转弯C ．加速行驶，向南转弯D ．加速行驶，向北转弯 例10：卫星轨道速度的大小及变轨问题．●一对作用力和反作用力的冲量或功例11：关于一对作用力和反作用力，下列说法中正确的是 （ D ）A ．一对作用力和反作用力大小相等，方向相反，作用在同一直线上，是一对平衡力B ．一对作用力和反作用力一定可以是不同种性质的力C ．一对作用力和反作用力所做功的代数和一定为零D ．一对作用力和反作用力的冲量的矢量和一定为零●对动量守恒定律的理解1．内涵——条件及结论2．对表达式的理解3．外延例12：对于由两个物体组成的系统，动量守恒定律可以表达为Δp 1＝－Δp 2．对此表达式，沈飞同学的理解是：两个物体组成的系统动量守恒时，一个物体增加了多少动量，另一AB个物体就减少了多少动量．你同意沈飞同学的说法吗？说说你的判断和理由（可以举例说明）．例13：总质量为M的小车，在光滑水平面上匀速行驶．现同时向前后水平抛出质量相等的两个小球，小球抛出时的初速度相等，则小车的速度将________（填“变大”、“变小”或“不变”）．●对机械能守恒定律的理解1．内涵——条件及结论2．外延——重力（若涉及弹性势能，还包括弹力）以外的其它力做的功，等于系统机械能的增量．例14：如图所示，质量为M＝1kg的小车静止在悬空固定的水平轨道上，小车与轨道间的摩擦力可忽略不计，在小车底Array部O点拴一根长L＝0.4m的细绳，细绳另一端系一质量m＝4kg的金属球，把小球拉到与悬点O在同一高度、细绳与轨道平行的位置由静止释放．小球运动到细绳与竖直方向成60°角位置时，突然撤去右边的挡板P，取g＝10m/s2，求：（1）挡板P在撤去以前对小车的冲量；（2）小球释放后上升的最高点距悬点O的竖直高度；（3）撤去右边的挡板P后，小车运动的最大速度．●功和能、冲量和动量的关系1．合外力的功＝动能的变化2．重力/弹力/分子力/电场力的功＝重力势能/弹性势能/分子势能/电势能变化的负值3．重力（或弹簧弹力）以外的其它力的功＝机械能的变化4．合外力的冲量＝动量的变化5．合外力＝动量的变化率例15：一物体静止在升降机的地板上，在升降机加速上升的过程中，地板对物体的支持力所做的功等于（ C ）A．物体势能的增加量B．物体动能的增量C．物体动能的增加量加上物体势能的增加量D．物体动能的增加量加上重力所做的功例16：一粒钢珠从静止状态开始自由下落,然后陷入泥潭中.若把在空中下落的过程称为过程Ⅰ,进入泥潭直到停住的过程称为过程Ⅱ，则（AC）A．过程Ⅰ中钢珠动量的改变量等于重力的冲量B．过程Ⅱ中阻力的冲量的大小等于过程Ⅰ中重力冲量的大小C．过程Ⅱ中钢珠克服阻力所做的功等于过程Ⅰ与过程Ⅱ中钢珠所减少的重力势能之和D．过程Ⅱ中损失的机械能等于过程Ⅰ中钢珠所增加的动能例17：在光滑斜面的底端静止一个物体，从某时刻开始有一个沿斜面向上的恒力F作用在物体上，使物体沿斜面向上滑去，经过一段时间突然撤去这个力，又经过4倍的时间又返回斜面的底端，且具有250J的动能，则恒力F对物体所做的功为J, 撤去F时物体具有J的动能．若该物体在撤去F后受摩擦力作用，当它的动能减少100J时，机械能损失了40J，则物体再从最高点返回到斜面底端时具有J的动能．例18：如图所示，分别用两个恒力F1和F2先后两次将质量为m的物体从静止开始，沿着同一个粗糙的固定斜面由底端推到顶端，第一次力F 1的方向沿斜面向上，第二次F 2的方向沿水平向右，两次所用时间相同．在这两个过程中 （ BD ）A ．F 1和F 2所做功相同B ．物体的机械能变化相同C ．F 1和F 2对物体的冲量大小相同D ．物体的加速度相同例19：在光滑斜面的底端静止一个物体，从某时刻开始有一个沿斜面向上的恒力F 作用在物体上，使物体沿斜面向上滑去，经过一段时间突然撤去这个力，又经过4倍的时间又返回斜面的底端，且具有250J 的动能，则恒力F 对物体所做的功为 J, 撤去F 时物体具有 J 的动能。

专题三运动学图像和动力学图像高频考点·能力突破考点一常规图像1．常规图像2.图像问题的解题思路例 1 [2022·河北卷]科学训练可以提升运动成绩，某短跑运动员科学训练前后百米全程测试中，速度v与时间t的关系图像如图所示．由图像可知( )A．0～t1时间内，训练后运动员的平均加速度大B．0～t2时间内，训练前、后运动员跑过的距离相等C.t2～t3时间内，训练后运动员的平均速度小D．t3时刻后，运动员训练前做减速运动，训练后做加速运动[解题心得]预测1 (多选)如图所示为甲、乙两物体在同一直线上运动的位移—时间图像，由图像可知( )A.甲、乙两物体开始运动时的速度方向相反B．甲、乙两物体同时同地开始运动C．甲物体在0～4 s内的平均速率比乙物体在1～4 s内的平均速率大D．两图线交点表示两物体速度相同预测2 (多选)2020东京奥运会田径男子4×100米接力比赛，由汤星强、谢震业、苏炳添和吴智强组成的中国队取得优异成绩．如图(a)所示，假设某接力比赛中甲、乙两运动员在直道交接棒过程的v－t图像大致如图(b)所示．设t1时刻为交接棒时刻，下列说法正确的是( )A．甲为交棒运动员，乙为接棒运动员B．0～t1过程中，甲在前，乙在后，二者距离越来越小C．t1～t2过程中，接棒运动员的加速度越来越小D．交接棒时的速度越大，因交接棒而损失的时间越少预测3 [2022·北京押题卷]很多智能手机都有加速度传感器，能通过图像显示加速度情况．用手掌托着手机，打开加速度传感器，手掌从静止开始迅速上下运动，得到如图所示的竖直方向上加速度随时间变化的图像，该图像以竖直向上为正方向．由此可判断出( )A．手机可能离开过手掌B．手机在t1时刻运动到最高点C．手机在t2时刻改变运动方向D．手机在t1～t3时间内，受到的支持力先减小再增大考点二非常规图像1．非常规图像a - F图像2.解决非常规图像的方法对于这类新型图像问题，关键是认清图像中横、纵轴所代表的物理量，找出它们的函数关系，并能迁移运用物理知识和方法清楚理解图像中的“点”“线”“斜率”“截距”和“面积”的物理意义．例2 [2022·河北押题卷]无人驾驶汽车在新冠疫情期间对疫情防控起到了积极作用．某自主品牌的一款无人驾驶汽车在直线测试时的速度平方与位移关系v2- x图像如图所示．从汽车经过x＝0位置时开始计时，则以下说法中正确的是( )A．汽车做匀加速直线运动B．汽车的加速度大小为10 m/s2C．该车在2 s内的位移大小为2.0 mD．该车在2 s内的位移大小为3.6 m[解题心得]预测4 一质点沿直线运动，如图所示是从t＝0时刻开始的质点的xt- t(式中x为位移)图像，可以推知( )A．质点做匀减速运动B．加速度的大小是1 m/s2C．t＝2 s时的速度是1 m/sD．t＝2 s时位移是3 m预测5 [2022·安徽示范高中皖北协作区联考](多选)如图1所示，足够长的木板B静置于光滑水平面上，其上放置小滑块A，滑块A受到随时间t变化的水平拉力F作用时，用传感器测出滑块A的加速度a，得到如图2所示的a- F图像，已知g取10 m/s2，则( )A．滑块A的质量为2 kgB．木板B的质量为6 kgC．当F＝12 N时，木板B的加速度为4 m/s2D．滑块A与木板B间的动摩擦因数为0.4素养培优·情境命题与体育运动、交通有关的v - t图像问题情境1 [2022·湖南株洲4月质检]为节约运行时间，设想一种高铁进站不停车模式．如图(a)所示，站台内铁路正上方有一固定轨道AB，高铁分为可分离的上下副、主车两部分，副车可在主车车顶轨道上滑行，主车保持匀速过站，需下车的乘客提前进入副车甲中，需上车的乘客已在静止于A端的副车乙中等待．车尾到B端瞬间，甲刚好完全滑上固定轨道AB，主、副车分离，副车甲立即减速，甲的车头到A端时刚好停下，乘客下车．当主车车头到A 端时，副车乙立即从固定轨道开始加速滑上车顶轨道，当乙的车尾与主车车尾对齐时主、副车刚好共速，锁死一起前进．设高铁以40 m/s 速度匀速驶来，副车长均为20 m，副车甲、乙运动的v - t图像如图(b)所示，则主车长为( )A．180 m B．200 mC．220 m D．820 m[解题心得]情境2 图(a)为2022年北京冬奥会冰壶比赛中的一个画面．比赛中，为了使冰壶滑行得更远，运动员可以用毛刷擦冰壶运行前方的冰面，使冰壶与冰面间的动摩擦因数减小．假设某运动员以初速度v0沿冰面将冰壶推出，冰壶做直线运动直到停止的过程中，其速度—时间(v - t)图像如图(b)所示，则下列判定正确的是( )A．0～t1和t2～t3时间内，运动员在用毛刷擦冰面B．t1～t2时间内，冰壶的加速度大小为v1−v2t2C．t1～t2时间内，冰壶的位移大小为1(v1＋v2)·(t2－t1)2(v0＋v1＋v2)D．0～t3时间内，冰壶的平均速度大小为13[解题心得]情境3 (多选)2021年7月31日，第二十届全国大学生机器人大赛ROBOCON圆满闭幕，本次大赛的主题项目为“投壶行觞”和“机器马术”．如图甲，在一次比赛中a、b两机器人从同一起跑线沿同一方向做直线运动，它们的速度—时间图像如图乙所示，则下列说法正确的是( )A．20 s时，a、b两机器人在运动方向上相距约500 mB．40 s时，a、b两机器人速度相等，在运动方向上相距最远，为400 mC．60 s时，b机器人在a机器人的前方，在运动方向上相距400 mD．a、b加速时，b机器人的加速度大于a机器人的加速度[解题心得]专题三 运动学图像和动力学图像高频考点·能力突破考点一例1 解析：根据v - t 图像的斜率表示加速度，及题图可知0～t 1时间内，训练后运动员的平均加速度比训练前的小，故A 错误；根据v - t 图像围成的面积表示位移，及题图可知0～t 2时间内，训练前运动员跑过的距离比训练后的大，故B 错误；根据v - t 图像围成的面积表示位移，及题图可知t 2～t 3时间内，训练后运动员的位移比训练前的位移大，根据平均速度等于位移与时间的比值，可知训练后运动员的平均速度大，故C 错误；由v - t 图像可直接看出，t 3时刻后，运动员训练前速度减小，做减速运动，运动员训练后速度增加，做加速运动，故D 正确．答案：D预测1 解析：甲物体开始运动时沿正向运动，乙物体开始运动时沿负向运动，A 正确；甲物体从0时刻在x ＝-5 m 位置开始运动，乙物体从1 s 时开始运动，开始运动的位置为x ＝0 m ，B 错误；x ­ t 图线的斜率的绝对值表示速度大小，则甲物体在0～4 s 内平均速率为v 甲＝5−(−5)4m/s ＝2.5 m/s ，乙物体在1～4 s 内平均速率为v 乙＝|−5|3m/s ＝53 m/s ，则甲物体在0～4 s 内的平均速率比乙物体在1～4 s 内的平均速率大，C 正确；x ­ t 图线的交点表示该时刻位置坐标相同，即两物体相遇，速度应看图线斜率，D 错误．答案：AC预测2 解析：由图(b)可知，交接棒过程中，接棒运动员在前，从静止开始向前加速运动，交棒运动员在后，开始时交棒运动员速度大于接棒运动员速度，二者之间的距离越来越小，当二者速度相等时，二者距离达到最小，此时要完成交接棒动作．交接棒完成后，接棒运动员继续加速直到达到最大速度，交棒运动员继续减速直到停下，综上分析，甲为交棒运动员，乙为接棒运动员，A 正确.0～t 1过程中，乙在前，甲在后，二者距离越来越小，B 错误．由图(b)可知，t 1～t 2过程中，接棒运动员乙做加速度逐渐减小的加速运动，C 正确．交接棒时的速度越大，移动相同位移所需时间越短，因交接棒而损失的时间越少，D 正确．答案：ACD预测3 解析：根据Δv ＝a Δt 可知，a - t 图像与坐标轴围成的面积表示速度变化量，可知手机在t 1时刻速度为正，还没有到最高点，故B 错误；根据Δv ＝a Δt 可知a ­ t 图像与坐标轴围成的面积表示速度变化量，可知手机在t 2时刻前后速度均为正，运动方向没有发生改变，故C 错误；由图可知t 1～t 2时间内加速度向上不断减小，根据牛顿第二定律得N -mg ＝ma ，即N ＝ma ＋mg .可知t 1～t 2时间内支持力不断减小，t 2～t 3时间内加速度向下，不断增大，根据牛顿第二定律得mg -N ＝ma ′得N ＝mg -ma ′，可得支持力还是不断减小，故D 错误；由图可知，手机的加速度某一段时间内等于重力加速度，则手机与手掌没有力的作用，手机可能离开过手掌，故A 正确．答案：A 考点二例2 解析：根据速度—位移关系v 2−v 02＝2ax ， 当x ＝0时，车的初速度为v 0＝6 m/s ， 将x ＝2 m ，v 2＝16 m 2/s 2代入可得a ＝-5 m/s 2.可知车做匀减速运动，则车的速度减小为零的时间为t ＝0−6−5s ＝1.2 s<2 s. 所以该车在2 s 内的位移大小为x ＝62×1.2 m＝3.6 m ，故D 正确，A 、B 、C 错误． 答案：D预测4 解析：由题分析可得图线的函数表达式为x t ＝1＋12t ，即x ＝t ＋12t 2，又因为匀变速直线运动中位移公式为x ＝v 0t ＋12at 2，根据对应关系得v 0＝1 m/s ，a ＝1 m/s 2>0，v 0与a 方向相同，则质点做匀加速运动，故A 项错误，B 项正确．当t ＝2 s 时，根据公式v ＝v 0＋at ，求出速度是3 m/s ，故C 项错误．当t ＝2 s 时，代入表达式x ＝t ＋12t 2，可得位移是4 m ，故D 项错误．答案：B预测5 解析：设滑块A 的质量为m ，木板B 的质量为M ，滑块A 与木板B 间的动摩擦因数为μ.由题图2可知，当F ＝F m ＝10 N 时，滑块A 与木板B 达到最大共同加速度a m ＝1ms 2，根据牛顿第二定律有F m ＝(M ＋m )a m ，解得M ＋m ＝10 kg.当F >10 N 时，A 与B 将发生相对滑动，对A 单独应用牛顿第二定律有F -μmg ＝ma ，整理得a ＝Fm -μg .根据题图2解得m ＝2 kg ，μ＝0.4，则M ＝8 kg ，故A 、D 正确，B 错误；当F ＝12 N 时，木板B 的加速度为a B ＝μmg M＝1ms 2，故C 错误．答案：AD 素养培优·情境命题情境1 解析：根据题意，对副车乙和主车的运动进行简化分析，如图所示．已知副车长20 m ，由v ­ t 图像可知，副车乙发生的位移为x 1＝12×(24.5-15.5)×40 m＝180 m ，在这一段时间内，主车做匀速直线运动，主车发生的位移为x 2＝(24.5-15.5)×40 m＝360 m ，故主车的长度为L ＝x 2-x 1＋20 m ＝360 m-180 m ＋20 m ＝200 m ，故选B 正确．答案：B情境2 解析：v ­ t 图线的斜率表示加速度，由图知t 1～t 2时间内图线斜率小，说明加速度小，由牛顿第二定律a ＝fm ＝μmg m＝μg ，知t 1～t 2时间内冰壶与冰面间的动摩擦因数小，说明运动员在用毛刷擦冰面；0～t 1和t 2～t 3时间内图线斜率大，动摩擦因数大，说明此时间段运动员没有用毛刷擦冰面，故A 错误；由加速度定义式a ＝ΔvΔt 知t 1～t 2时间内，冰壶的加速度大小为a ＝v 1−v2t 2−t 1，故B 错误；v ­ t 图线与坐标轴围的面积表示位移，在t 1～t 2时间内，冰壶的位移大小为x ＝12(v 1＋v 2)(t 2-t 1)，故C 正确；根据平均速度的定义式v ̅＝xt 知在0～t 3时间内，冰壶的平均速度大小为v̅＝x总t总＝12(v0+v1)t1+12(v1+v2)(t2−t1)+12v2(t3−t2)t3＝(v0−v2)t1+v1t2+v2t32t3，故D错误．答案：C情境3 解析：根据图像可知，t＝20 s时b车才出发，20 s时两者间距即为a在0～20 s内的位移；速度—时间图像与坐标轴围成的“面积”表示位移，则Δx＝x a＝10+402×20m＝500 m，故A正确；由图像所围面积可知：0～40 s内a比b多运动的位移S＝(10+402×20＋12×40×20)m＝900 m，故B错误；由a、b图像所围面积可知，60 s时二者的位移之差等于20 s时的位移差，由A选项分析可知，此时b机器人在a机器人的后方，在运动方向上相距500 m，故C错误；速度—时间图像图线的斜率表示加速度，由图像可知：a、b加速时，a图线的斜率小于b图线的斜率，说明b机器人的加速度大于a机器人的加速度，故D正确．答案：AD。

专题7 感应电荷量的应用1.安培力的冲量大小感应电流通过直导线时，直导线在磁场中要受到安培力的作用，当导线与磁场垂直时，安培力的大小为F=BIL。

方法1 微元法由于感应电流通常变化，所以安培力为变力，求时间t内安培力的冲量必须用微元法，在极短时间∆t内认为安培力为定值，则安培力冲量大小为I i=BI i L∆t = BLq i，求和可得全过程安培力冲量大小为I = BL∆q，其中∆q为此过程流过导体棒任意截面的电荷量。

方法2 平均电流法设此过程电流对时间的平均值为I，则∆q=It，所以安培力冲量通用表达式为：BILt BL q=∆，即感应电荷量与时间和安培力的冲量相联系。

2.感应电荷量在前面利用平均感应电流I=ER与和平均感应电动势E nt∆Φ=解得感应电荷量q=I t = nR∆Φ。

如果是由于导体棒切割产生的感应电荷量，则B S BLxq n nR R∆==，其中x为导体棒运动的距离，即感应电荷量与空间距离相联系。

3.感应电荷量的时空联系感应电荷量连接空间距离和安培力的冲量，因此在非匀变速运动中，如果题目求导体棒的位移，通常用感应电荷量和动量定理求解。

在分析电磁感应问题中，往往求解物体的初速度v0、末速度v、时间t、位移x、电荷量q 这5个物理量的时候，通常采用安培力的冲量，按此模型处理方法进行处理。

4.实例分析以2022年6月浙江选考19题第3问为例，如图1所示，用于推动模型飞机的动子（图中未画出）与线圈绝缘并固定，线圈带动动子，可在水平导轨上无摩擦滑动。

线圈位于导轨间的辐向磁场中，其所在处的磁感应强度大小均为B 。

开关S 与1接通，恒流源与线圈连接，动子从静止开始推动飞机加速，飞机达到起飞速度时与动子脱离；此时S 掷向2接通定值电阻R 0，同时施加回撤力F ，在F 和磁场力作用下，动子恰好返回初始位置停下。

若动子从静止开始至返回过程的v -t 图如图2所示，在t 1至t 3时间内F =(800-10v )N ，加速度不变恒为a =160m/s 2，t 3时撤去F 。

第1讲力与物体的平衡知识网络构建命题分类剖析命题点一静态平衡问题1．共点力平衡的常用处理方法(1)研究对象的选取：①整体法与隔离法(如图甲)；②转换研究对象法(如图乙)．(2)画受力分析图：按一定的顺序分析力，只分析研究对象受到的力．(3)验证受力的合理性：①假设法(如图丙)；②动力学分析法(如图丁)．例 1[2023·山东卷]餐厅暖盘车的储盘装置示意图如图所示，三根完全相同的弹簧等间距竖直悬挂在水平固定圆环上，下端连接托盘．托盘上叠放若干相同的盘子，取走一个盘子，稳定后余下的正好升高补平．已知单个盘子的质量为300 g，相邻两盘间距1.0 cm，重力加速度大小取10 m/s2.弹簧始终在弹性限度内，每根弹簧的劲度系数为( )A．10 N/m B．100 N/mC．200 N/m D．300 N/m例 2[2023·河北保定一模]质量为M的正方体A与质量为m的圆球B在水平向右的外力F作用下静止在墙角处，它们的截面图如图所示，截面正方形的对角线与截面圆的一条直径恰好在一条直线上，所有摩擦忽略不计，重力加速度为g.则( )A．F＝(M＋m)gB．F＝mgC．地面受到的压力为F N，F N<(M＋m)gD．地面受到的压力为F N，F N>(M＋m)g提升训练1. [2023·广东省中山市测试]如图甲为明朝《天工开物》记载测量“弓弦”张力的插图，图乙为示意图．弓的质量为m ＝5 kg ，弦的质量忽略不计，悬挂点为弦的中点．当在弓的中点悬挂质量为M ＝15 kg 的重物时，弦的张角为θ＝120°，g ＝10 m/s 2，则弦的张力为( )A ．50 NB ．150 NC ．200 ND ．200√3 N 2.[2023·浙江6月]如图所示，水平面上固定两排平行的半圆柱体，重为G 的光滑圆柱体静置其上，a 、b 为相切点，∠aOb ＝90°，半径Ob 与重力的夹角为37°.已知sin 37°＝0.6，cos 37°＝0.8，则圆柱体受到的支持力F a 、F b 大小为( )A ．F a ＝0.6G ，F b ＝0.4GB ．F a ＝0.4G ，F b ＝0.6GC ．F a ＝0.8G ，F b ＝0.6GD ．F a ＝0.6G ，F b ＝0.8G 3.[2023·河南省洛阳市模拟]如图所示，一光滑球体放在支架与竖直墙壁之间，支架的倾角θ＝60°，光滑球体的质量为m ，支架的质量为2m ，已知最大静摩擦力等于滑动摩擦力，整个装置保持静止，则支架和地面间的动摩擦因数至少为( )A ．√39B ．√34C ．√32 D ．√33命题点二 动态平衡问题(含临界、极值问题)1．解决动态平衡问题的一般思路化“动”为“静”，多个状态下“静”态对比，分析各力的变化或极值． 2．“缓慢”移动的三类经典模型图例分析求力F的最小值F min＝mg sin θ，结论：sin θ＝dLF＝mg，2cosθ绳子端点上下移动，力F不变N1、N2始终减小斜面对球的支持力F1逐渐减小，挡板对球的弹力F2先减小后增大考向1 共点力作用下的动态平衡例 1[2023·四川省成都市检测](多选)某中学举行趣味运动会时，挑战用一支钢尺取出深盒子(固定不动)中的玻璃球，该游戏深受大家喜爱，参与者热情高涨．游戏中需要的器材和取球的原理分别如图甲和图乙所示．若忽略玻璃球与盒壁、钢尺间的摩擦力，在不损坏盒子的前提下，钢尺沿着盒子上边缘某处旋转拨动(钢尺在盒内的长度逐渐变短)，使玻璃球沿着盒壁缓慢上移时，下列说法正确的是( )A．钢尺对玻璃球的弹力逐渐减小B．钢尺对玻璃球的弹力先增大后减小C．盒壁对玻璃球的弹力逐渐减小D．盒壁对玻璃球的弹力先减小后增大例 2[2023·河北唐山三模]如图所示，木板B放置在粗糙水平地面上，O为光滑铰链．轻杆一端与铰链O固定连接，另一端固定连接一质量为m的小球A.现将轻绳一端拴在小球A 上，另一端通过光滑的定滑轮O′由力F牵引，定滑轮位于O的正上方，整个系统处于静止状态．现改变力F的大小使小球A和轻杆从图示位置缓慢运动到O′正下方，木板始终保持静止，则在整个过程中( )A．外力F大小不变B．轻杆对小球的作用力变小C．地面对木板的支持力逐渐变小D．地面对木板的摩擦力逐渐减小思维提升三力作用下的动态平衡考向2 平衡中的极值或临界值问题例 3[2023·山东菏泽市模拟]将三个质量均为m的小球a、b、c用细线相连后(bc间无细线相连)，再用细线悬挂于O点，如图所示．用力F拉小球c，使三个小球都处于静止状态，且细线Oa与竖直方向的夹角保持为θ＝30°，则F的最小值为( ) A．1.5mg B．1.8mgC．2.1mg D．2.4mg例 4[2023·陕西省汉中市联考]在吊运表面平整的重型板材(混凝土预制板、厚钢板)时，如因吊绳无处钩挂而遇到困难，可用一根钢丝绳将板拦腰捆起(不必捆的很紧)，用两个吊钩勾住绳圈长边的中点起吊(如图所示)，若钢丝绳与板材之间的动摩擦因数为μ，为了满足安全起吊(不考虑钢丝绳断裂)，需要满足的条件是( )A．tan α>μ B．tan α<μC．sin α>μ D．sin α<μ提升训练1.[2023·湖南张家界模拟考](多选)利用物理模型对问题进行分析，是一种重要的科学思维方法．如图甲所示为拔河比赛时一位运动员的示意图，可以认为静止的运动员处于平衡状态．该情形下运动员可简化成如图乙所示的一质量分布均匀的钢管模型．运动员在拔河时身体缓慢向后倾倒，可以认为钢管与地面的夹角θ逐渐变小，在此期间，脚与水平地面之间没有滑动，绳子的方向始终保持水平．已知当钢管受到同一平面内不平行的三个力而平衡时，三个力的作用线必交于一点．根据上述信息，当钢管与地面的夹角θ逐渐变小时，下列说法正确的有( )A．地面对钢管支持力的大小不变B．地面对钢管的摩擦力变大C．地面对钢管作用力的合力变大D．地面对钢管作用力的合力大小不变2．(多选)在如图所示的装置中，两物块A、B的质量分别为m A、m B，而且m A>m B，整个系统处于静止状态，设此时轻质动滑轮右端的轻绳与水平面之间的夹角为θ，若小车向左缓慢移动一小段距离并停下来后，整个系统再次处于静止状态，则下列说法正确的是( )A．物块A的位置将变高B．物块A的位置将变低C．轻绳与水平面的夹角θ将变大D．轻绳与水平面的夹角θ将不变3．长沙某景区挂出32个灯笼(相邻两个灯笼由轻绳连接)，依次贴上“高举中国特色社会主义旗帜，为全面建设社会主义现代化国家而团结奋斗”，从高到低依次标为1、2、3、…、32.在无风状态下，32个灯笼处于静止状态，简化图如图所示．与灯笼“斗”右侧相连的轻绳处于水平状态，已知每一个灯笼的质量m＝0.5 kg，重力加速度g＝10 m/s2，悬挂灯笼的轻绳最大承受力T m＝320 N，最左端连接的轻绳与竖直方向的夹角为θ.下列说法正确的是( )A．θ最大为53°NB．当θ最大时最右端轻绳的拉力为F2＝160√33C．当θ＝53°时第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角为45°D．当θ＝37°时第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角为45°命题点三电场力、磁场力作用下的平衡问题1．电场力.(1)大小：F＝Eq，F＝kq1q2r2(2)方向：正电荷所受电场力的方向与电场强度的方向相同；负电荷所受电场力的方向与电场强度的方向相反．2．磁场力(1)大小：①安培力F＝BIL；②洛伦兹力F洛＝qv B.(2)方向：用左手定则判断．3．电磁学中平衡问题的处理方法处理方法与力学中平衡问题的分析方法一样，把方法和规律进行迁移应用即可．考向1 电场中的平衡问题例 1[2023·浙江模拟预测]如图所示，A、C为带异种电荷的带电小球，B、C为带同种电荷的带电小球．A、B被固定在绝缘竖直杆上，Q AQ B ＝3√38时，C球静止于粗糙的绝缘水平天花板上．已知L ACL AB＝√3，下列说法正确的是( )A．C处的摩擦力不为零B．杆对B的弹力为零C．缓慢将C处点电荷向右移动，则其无法保持静止D．缓慢将C处点电荷向左移动，则其一定会掉下来考向2 磁场中的平衡问题例 2 如图所示，竖直平面内有三根轻质细绳，绳1水平，绳2与水平方向成60°角，O为结点，绳3的下端拴接一质量为m、长度为l的导体棒，棒垂直于纸面静止，整个空间存在竖直向上、磁感应强度大小为B的匀强磁场．现向导体棒通入方向向里、大小由零缓慢增大到I0的电流，可观察到导体棒缓慢上升到与绳1所处的水平面成30°角时保持静止．已知重力加速度为g.在此过程中，下列说法正确的是( )A．绳1受到的拉力先增大后减小B．绳2受到的拉力先增大后减小C．绳3受到的拉力的最大值为√3mgD．导体棒中电流I0的值为√3mglB提升训练1.[2024·山西省翼城中学模拟预测]如图甲所示，一通电导体棒用两根绝缘轻质细线悬挂在天花板上并静止在水平位置．当导体棒所在空间加上匀强磁场，再次静止时细线与竖直方向成θ角，如图乙所示(图甲中从左向右看)．已知导体棒长度为L、质量为m、电流为I，重力加速度大小为g.关于图乙，下列说法正确的是( )A．当磁场方向斜向右上方且与细线垂直时磁感应强度最小B．磁感应强度的最小值为mg sinθILC．磁感应强度最小时，每根细线的拉力大小为mg2cosθD．当磁场方向水平向左时，不能使导体棒在图示位置保持静止2．如图所示，一绝缘细线竖直悬挂一小球A，在水平地面上固定一根劲度系数为k′的绝缘轻质弹簧，弹簧上端与小球C相连，在小球A和C之间悬停一小球B，当系统处于静止时，小球B处在AC两小球的中间位置．已知三小球质量均为m，电荷量均为q，电性未知．则下列判断正确的是( )A.相邻两小球之间的间距为q√kmgB．弹簧的形变量为11mg8k′C．细线对小球A的拉力大小为11mg8D．小球C受到的库仑力大小为5mg8素养培优·情境命题利用平衡条件解决实际问题联系日常生活，创新试题情境化设计，渗透实验的思想，考查考生分析解决实际问题的能力，引导学生实现从“解题”到“解决问题”的转变情境1 工人推车——科学思维[典例1] [2023·四川省成都市联测]如图甲所示，工人用推车运送石球，到达目的地后，缓慢抬起把手将石球倒出(图乙)．若石球与板OB、OA之间的摩擦不计，∠AOB＝60°，图甲中BO 与水平面的夹角为30°，则在抬起把手使OA 变得水平的过程中，石球对OB 板的压力大小N 1、对OA 板的压力大小N 2的变化情况是( )A ．N 1减小、N 2先增大后减小B ．N 1减小、N 2增大C ．N 1增大、N 2减小D ．N 1增大、N 2先减小后增大情境2 悬索桥——科学态度与责任[典例2] [2023·江苏省无锡市测试]图a 是一种大跨度悬索桥梁，图b 为悬索桥模型．六对轻质吊索悬挂着质量为M 的水平桥面，吊索在桥面两侧竖直对称排列，其上端挂在两根轻质悬索上(图b 中只画了一侧分布)，悬索两端与水平方向成45°，则一根悬索水平段CD 上的张力大小是( )A ．14Mg B ．16MgC ．112Mg D ．124Mg情境3 瓜子破壳器——科学探究[典例3] [2023·福建福州4月检测]有一种瓜子破壳器如图甲所示，将瓜子放入两圆柱体所夹的凹槽之间，按压瓜子即可破开瓜子壳．破壳器截面如图乙所示，瓜子的剖面可视作顶角为θ的扇形，将其竖直放入两完全相同的水平等高圆柱体A 、B 之间，并用竖直向下的恒力F 按压瓜子且保持静止，若此时瓜子壳未破开，忽略瓜子自重，不计摩擦，则( )A ．若仅减小A 、B 距离，圆柱体A 对瓜子的压力变大 B ．若仅减小A 、B 距离，圆柱体A 对瓜子的压力变小C ．若A 、B 距离不变，顶角θ越大，圆柱体A 对瓜子的压力越大D．若A、B距离不变，顶角θ越大，圆柱体A对瓜子的压力越小第1讲力与物体的平衡命题分类剖析命题点一[例1] 解析：由题知，取走一个盘子，稳定后余下的正好升高补平，则说明一个盘子的重力使弹簧形变量为相邻两盘间距，则有mg＝3·kx，解得k＝100 N/m，故选B.答案：B[例2] 解析：对圆球B受力分析如图，β＝45°A对B的弹力T＝mg，cosβ根据牛顿第三定律，B对A的弹力T′＝T＝mg，F＝T′sin β＝mg，故A错误，B正cosβcos β＝Mg＋mg，故C、D 确；对AB整体地面受到的压力为F N＝Mg＋T′cos β＝Mg＋mgcosβ错误．故选B.答案：B[提升训练]1．解析：整体法对弓和物体受力分析如图：＝(M＋m)g竖直方向上由受力平衡可得：2F cos θ2解得：F＝(M+m)g＝200 N，故C正确，A、B、D错误．2cosθ2答案：C2．解析：对光滑圆柱体受力分析如图由题意有F a＝G sin 37°＝0.6GF b＝G cos 37°＝0.8G故选D.答案：D3．解析：对光滑球体受力分析如图所示根据平衡条件可得N2cos θ＝mg对支架受力分析如图所示根据牛顿第三定律可知N3＝N2对支架由平衡条件可得N4＝2mg＋N3cos θ，f＝N3sin θ又f＝μN4联立解得μ＝√33.故选D.可知支架和地面间的动摩擦因数至少为√33答案：D命题点二[例1] 解析：对玻璃球的受力分析如图所示，玻璃球受重力G，左侧钢尺对玻璃球的弹力F1，盒壁对玻璃球的弹力F2，玻璃球在3个力作用下处于动态平衡，玻璃球沿着纸盒壁缓慢上移时，θ角变大，利用图解法可知，F1和F2均逐渐减小，A、C项正确，B、D项错误．故选AC.答案：AC[例2] 解析：对小球A进行受力分析，三力构成矢量三角形，如图所示根据几何关系可知两三角形相似，因此mgOO′＝FO′A＝F′OA，缓慢运动过程中，O′A越来越小，则F逐渐减小，故A错误；由于OA长度不变，杆对小球的作用力F′大小不变，故B 错误；由于杆对木板的作用力大小不变，方向向右下，但杆的作用力与竖直方向的夹角越来越小，所以地面对木板的支持力逐渐增大，地面对木板的摩擦力逐渐减小，故C错误，D正确．答案：D[例3] 解析：取整体为研究对象，当F垂直于Oa时，F最小，根据几何关系可得，拉力的最小值F＝3mg sin 30°＝1.5mg，故选A.答案：A[例4] 解析：要起吊重物，只需满足绳子张力T的竖直分量小于钢丝绳与板材之间的最大静摩擦力，一般情况认为最大静摩擦力等于滑动摩擦力，如图所示即T cos αμ>T sin α，化简可得tan α<μ，故B正确，A、C、D错误．故选B.答案：B[提升训练]1．解析：对钢管受力分析，钢管受重力mg、绳子的拉力T、地面对钢管竖直向上的支持力F N、水平向右的摩擦力F f，可知F N＝mg，F f＝T＝mgtanθ即随着钢管与地面夹角的逐渐变小，地面对钢管支持力的大小不变，地面对钢管的摩擦力变大，故A、B正确；对钢管受力分析，可认为钢管受到重力mg、绳子的拉力T和地面对钢管作用力的合力F 三个力，钢管平衡，三个力的作用线必交于一点，由此可知F方向沿钢管斜向上，与水平面夹角为α(钢管与水平面的夹角为θ)，根据共点力平衡条件可知F＝mgsinα，T＝mgtanα，当钢管与地面的夹角θ逐渐变小，同时α也减小，地面对钢管作用力的合力变大，C正确，D 错误．答案：ABC2．解析：以轻质动滑轮与轻绳的接触点O为研究对象，分析O点的受力情况，作出O 点的受力分析图，如图所示设绳子的拉力大小为F，动滑轮两侧绳子的夹角为2α，由于动滑轮两侧绳子的拉力关于竖直方向对称，则有2F cos α＝m B g，又小车向左缓慢移动一小段距离后，轻绳中的拉力大小与小车移动前相同，即F＝m A g保持不变，可知α角保持不变，由几何知识得，α＋θ＝90°，则θ保持不变，当小车向左缓慢移动一小段距离后，动滑轮将下降，则物块A 的位置将变高，故选项A、D正确，B、C错误．答案：AD3．解析：当最左端连接的轻绳的拉力大小为T m＝320 N时，θ最大，此时灯笼整体受力如图所示由平衡条件T m sin θm＝F2T m cos θm＝32mg解得θm＝60°，F2＝160√3 NA、B错误；当θ＝53°时，灯笼整体受力分析如图由平衡条件知，最右端轻绳的拉力F21＝32mg tan 53°＝6403N对第9个灯笼至第32个灯笼整体，其受力情况跟灯笼整体的受力情况类似，由平衡条件tan α＝F21(32−8)mg≠1则第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角α≠45°，C错误；当θ＝37°时，此时灯笼整体受力如图所示由平衡条件知，最右端轻绳的拉力F22＝32mg tan 37°＝120 N对第9个灯笼至第32个灯笼整体，其受力情况跟灯笼整体的受力情况类似，由平衡条件tan β＝F22(32−8)mg＝1则第8个灯笼与第9个灯笼间轻绳与竖直方向的夹角β＝45°，D正确．答案：D命题点三[例1] 解析：对C进行受力分析，A对C有吸引力，B对C有排斥力，及其重力，与水平天花板对C 可能有竖直向下的压力，如图所示由平衡条件，结合矢量合成法则，若不受摩擦力得F AC＝F BC cos θ由几何知识可得cos θ＝√32依据库仑定律有kQ A Q CL AC2＝√32kQ B Q CL BC2，Q AQ B＝3√38Q A Q B ＝3√38时恰好处于平衡状态；C球静止没有运动趋势，C处的摩擦力为零，故A错误；缓慢将C处点电荷向右移动，平衡状态被打破，其无法保持静止，故C正确；缓慢将C处点电荷向左移动，F BC变大，其竖直方向上的分量变大，C球一定不会掉下来，故D错误；B球如果不受杆的力，则C球给B球的排斥力在水平方向的分量无法平衡，因此杆对B 一定有弹力作用，故B错误．答案：C[例2] 解析：对整体分析，重力大小和方向不变，绳1、2弹力方向不变，根据左手定则，安培力水平向右且逐渐增大，由平衡条件得水平方向F1＝F2cos 60°＋BIl竖直方向F 2sin 60°＝mg电流逐渐变大，则F 1增大、F 2不变，故A 、B 错误；当电流增大到I 0时，安培力与重力的合力最大，即绳3的拉力最大sin 30°＝mg F 3最大值为F 3＝2mg ，故C 错误；对导体棒受力分析得tan 30°＝mg BI 0l ，得I 0＝√3mg Bl，故D 正确．答案：D [提升训练] 1．解析：对导体棒受力分析如图所示，导体棒在重力、拉力和安培力的作用下处于平衡状态．由平衡条件可知，导体棒所受拉力和安培力的合力与重力等大反向，拉力和安培力可能的方向如图所示，当安培力方向斜向右上方且与细线垂直时安培力最小，此时磁场方向沿着细线斜向左上方，A 错误；设磁感应强度大小为B ，由平衡条件得mg sin θ＝BIL ，解得B ＝mg sin θIL ，B 正确；设每条细线拉力大小为F T ，由平衡条件得mg cos θ＝2F T ，解得F T ＝12mg cos θ，C 错误；当磁场方向水平向左时，安培力竖直向上，如果安培力与重力大小相等，可以使导体棒在图示位置保持静止，D 错误．答案：B2．解析：如图甲所示，以小球B 为研究对象，小球A 和小球C 分别对小球B 的库仑力大小相等，且小球A 和小球C 对小球B 的合力与小球B 的重力等大反向，所以小球A 和小球B 带异种电荷，小球B 和小球C 带同种电荷，即小球A 和小球C 对小球B 的库仑力大小均为F A ＝F C ＝mg2，由库仑定律可得kq 2r 2＝12mg ，解得小球A 和小球B 之间距离为r ＝q √2kmg ，故A 错误；如图乙所示，以小球A 为研究对象，受到小球B 向下的库仑力为F B ＝mg 2，受到小球C向下的库仑力是受到小球B 的14，即为F C ′＝mg 8，所以小球A 受到的拉力为F T A ＝mg ＋F B ＋F ′C＝13mg 8，故C 错误；如图丙所示，以小球C 为研究对象，小球C 受到小球B 向下的库仑力为F ′B ＝mg2，受到A 向上的库仑力为F ′A ＝mg8，则小球C 对弹簧的压力为F 压＝F ′B －F ′A ＋mg＝11mg 8，小球C 受到向上的弹力为F 弹＝F 压＝11mg 8，由胡克定律得F 弹＝k ′x ，解得弹簧的形变量为x ＝11mg8k ′，故B 正确，D 错误．答案：B 素养培优·情境命题[典例1] 解析：在倒出石球的过程中，两个支持力的夹角是个确定值，为α＝120°，根据力的示意图可知N 1sin β＝N 2sin γ＝Gsin α，在转动过程中β从90°增大到180°，则sin β不断减小，N 1将不断减小；γ从150°减小到60°，其中跨过了90°，因此sin γ 先增大后减小，则N 2将先增大后减小，选项A 正确．答案：A[典例2] 解析： 对整体分析，根据平衡条件，2F T AC sin 45°＝Mg ，F T AC ＝√22Mg .对悬索左边受力分析，受A 左上绳的力F T AC ，CD 上水平向右的拉力为F T ，根据平衡条件，F T ＝F T AC cos 45°＝12Mg ，一根悬索水平段CD 上的张力大小是14Mg ，故选A.答案：A[典例3] 解析：瓜子处于平衡状态，若仅减小A 、B 距离，A 、B 对瓜子的弹力方向不变，则大小也不变，A 、B 错误；若A 、B 距离不变，顶角θ越大，则A 、B 对瓜子弹力的夹角减小，合力不变，则两弹力减小，C 错误，D 正确．故选D.答案：D。

高考二轮复习专题六：机械能守恒定律一、知识点综述：1. 在只有重力和弹簧的弹力做功的情况下，物体的动能和势能发生相互转化，但机械能的总量保持不变.2. 对机械能守恒定律的理解：（1）系统在初状态的总机械能等于末状态的总机械能.即 E 1 = E 2 或 1/2mv 12 + mgh 1= 1/2mv 22 + mgh 2（2）物体（或系统）减少的势能等于物体(或系统)增加的动能，反之亦然。

即 -ΔE P = ΔE K（3）若系统内只有A 、B 两个物体，则A 减少的机械能E A 等于B 增加的机械能ΔE B 即 -ΔE A = ΔE B 二、例题导航：例1、如图示，长为l 的轻质硬棒的底端和中点各固定一个质量为m 的小球，为使轻质硬棒能绕转轴O 转到最高点，则底端小球在如图示位置应具有的最小速度v= 。

解：系统的机械能守恒，ΔE P +ΔE K =0因为小球转到最高点的最小速度可以为0 ，所以，例2. 如图所示，一固定的楔形木块，其斜面的倾角θ=30°，另一边与地面垂直，顶上有一定滑轮。

一柔软的细线跨过定滑轮，两端分别与物块A 和B 连结，A 的质量为4m ，B 的质量为m ，开始时将B 按在地面上不动，然后放开手，让A 沿斜面下滑而B 上升。

物块A 与斜面间无摩擦。

设当A 沿斜面下滑S 距离后，细线突然断了。

求物块B 上升离地的最大高度H. 解：对系统由机械能守恒定律 4mgSsin θ – mgS = 1/2× 5 mv 2 ∴ v 2=2gS/5细线断后，B 做竖直上抛运动，由机械能守恒定律 mgH= mgS+1/2× mv 2 ∴ H = 1.2 S例3. 如图所示，半径为R 、圆心为O 的大圆环固定在竖直平面内，两个轻质小圆环套在大圆环上．一根轻质长绳穿过两个小圆环，它的两端都系上质量为m 的重物，忽略小圆环的大小。

（1）将两个小圆环固定在大圆环竖直对称轴的两侧θ=30°的位置上(如图)．在 两个小圆环间绳子的中点C 处，挂上一个质量M = m 的重物，使两个小圆环间的绳子水平，然后无初速释放重物M ．设绳子与大、小圆环间的摩擦均可忽略，求重物M 下降的最大距离．l mg l mg v m mv 22212122⋅+⋅=⎪⎭⎫⎝⎛+gl gl v 8.4524==∴2（2）若不挂重物M ．小圆环可以在大圆环上自由移动，且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略，问两个小圆环分别在哪些位置时，系统可处于平衡状态?解：(1)重物向下先做加速运动，后做减速运动，当重物速度 为零时，下降的距离最大．设下降的最大距离为h ，由机械能守恒定律得 解得（另解h=0舍去）(2)系统处于平衡状态时，两小环的可能位置为 a ． 两小环同时位于大圆环的底端． b ．两小环同时位于大圆环的顶端．c ．两小环一个位于大圆环的顶端，另一个位于大圆环的底端．d ．除上述三种情况外，根据对称性可知，系统如能平衡，则两小圆环的位置一定关于大圆环竖直对称轴对称．设平衡时，两小圆环在大圆环竖直对称轴两侧α角的位置上(如图所示)．对于重物，受绳子拉力与重力作用，有T=mg对于小圆环，受到三个力的作用，水平绳的拉力T 、竖直绳子的拉力T 、大圆环的支持力N.两绳子的拉力沿大圆环切向的分力大小相等，方向相反得α=α′, 而α+α′=90°，所以α=45 °例4.如图质量为m 1的物体A 经一轻质弹簧与下方地面上的质量为m 2的物体B 相连，弹簧的劲度系数为k ，A 、B 都处于静止状态。

高考物理二轮复习专题归纳—抛体运动（全国版）考点一运动的合成与分解例1(2022·辽宁卷·1)如图所示，桥式起重机主要由可移动“桥架”“小车”和固定“轨道”三部分组成．在某次作业中桥架沿轨道单向移动了8m，小车在桥架上单向移动了6m．该次作业中小车相对地面的位移大小为()A．6m B．8mC．10m D．14m答案C解析根据位移概念可知，该次作业中小车相对地面的位移大小为x＝x12＋x22＝82＋62m＝10m，故选C.例2(多选)(2022·广东省高三检测)如图所示，A、B两球分别套在两光滑无限长的水平直杆上，两球通过一轻绳绕过一定滑轮(轴心固定不动)相连，某时刻连接两球的轻绳与水平方向的夹角分别为α、β，A球向左的速度大小为v，下列说法正确的是()A．此时B球的速度大小为v cosαcosβB．此时B球的速度大小为v cosβcosαC．当β增大到等于90°时，B球的速度达到最大D．在β增大到90°的过程中，绳对B球的拉力一直做正功答案ACD解析将A球的速度分解为沿轻绳方向和垂直于轻绳的方向，在沿轻绳方向的分速度等于B球沿轻绳方向的分速度．A球在沿轻绳方向的分速度为v绳＝v cosα，所以v B＝v绳cosβ＝v cosαcosβ，A正确，B错误；当β增大到等于90°时，B球的速度在沿轻绳方向的分速度等于0，所以A沿绳子方向的分速度也是0，而cosα′不等于0，所以A球的速度为0；此时A的动能全部转化为B的动能，所以B球的速度达到最大，C正确；在β增大到90°的过程中，轻绳的方向与B球运动的方向之间的夹角始终是锐角，所以轻绳对B球的拉力一直做正功，D正确．把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解．常见的模型如图所示．考点二平抛运动1．平抛运动问题的求解方法已知条件情景示例解题策略已知速度方向从斜面外平抛，垂直落在斜面上，如图所示，已知速度的方向垂直于斜面.分解速度tan θ＝v 0v y ＝v 0gt从圆弧形轨道外平抛，恰好无碰撞地进入圆弧形轨道，如图所示，已知速度方向沿该点圆弧的切线方向.分解速度tan θ＝v y v 0＝gt v 0已知位移方向从斜面上平抛又落到斜面上，如图所示，已知位移的方向沿斜面向下.分解位移tan θ＝y x ＝12gt 2v 0t ＝gt 2v 0在斜面外平抛，落在斜面上位移最小，如图所示，已知位移方向垂直斜面.分解位移tan θ＝x y ＝v 0t 12gt 2＝2v 0gt2.平抛运动的两个推论(1)设做平抛运动的物体在任意时刻的速度方向与水平方向的夹角为θ，位移方向与水平方向的夹角为φ，则有tanθ＝2tanφ，如图甲所示．(2)做平抛运动的物体任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点，如图乙所示．例3(多选)(2022·湖南省高三学业质量第二次联合检测)投壶是从先秦延续至清末的中国传统礼仪和宴饮游戏，《礼记传》中提到：“投壶，射之细也．宴饮有射以乐宾，以习容而讲艺也．”如图所示，甲、乙两人在不同位置沿水平方向各射出一支箭，箭尖插入壶中时与水平面的夹角分别为37°和53°.已知两支箭的质量、竖直方向下落高度均相等，忽略空气阻力、箭长、壶口大小等因素的影响(sin37°＝0.6，cos37°＝0.8，sin53°＝0.8，cos53°＝0.6)，下列说法正确的是()A．甲、乙两人所射箭的初速度大小之比为16∶9B．甲、乙两人所射箭落入壶口时的速度大小之比为3∶4C．甲、乙两人投射位置与壶口的水平距离之比为9∶16D ．甲、乙两人所射箭落入壶口时的动能之比为16∶9答案AD 解析由题知甲、乙两人射箭高度相同，则两支箭在空中的运动时间相同，落入壶口时竖直方向的速度v y 相同．设箭尖插入壶中时与水平面的夹角为θ，箭射出时的初速度为v 0，则tan θ＝v y v 0，即v 0＝v y tan θ，故两支箭射出时的初速度大小之比为tan 53°∶tan 37°＝16∶9，A 正确；设箭尖插入壶中时的速度大小为v ，则v ＝v y sin θ，故两支箭落入壶口时的速度大小之比为sin 53°∶sin 37°＝4∶3，B 错误；因两支箭在空中的运动时间相同，甲、乙两人投射位置与壶口的水平距离之比等于初速度大小之比，为16∶9，C 错误；由E k ＝12mv 2可知，两支箭落入壶口时的动能之比为16∶9，D 正确．例4(2022·全国甲卷·24)将一小球水平抛出，使用频闪仪和照相机对运动的小球进行拍摄，频闪仪每隔0.05s 发出一次闪光．某次拍摄时，小球在抛出瞬间频闪仪恰好闪光，拍摄的照片编辑后如图所示．图中的第一个小球为抛出瞬间的影像，每相邻两个球之间被删去了3个影像，所标出的两个线段的长度s 1和s 2之比为3∶7.重力加速度大小取g ＝10m/s 2，忽略空气阻力．求在抛出瞬间小球速度的大小．答案255m/s 解析频闪仪每隔0.05s 发出一次闪光，每相邻两个球之间被删去3个影像，故相邻两球的时间间隔为t＝4T＝4×0.05s＝0.2s设抛出瞬间小球的速度大小为v0，每相邻两球间的水平方向上位移为x，竖直方向上的位移分别为y1、y2，根据平抛运动位移公式有x＝v0ty1＝12gt2＝12×10×0.22m＝0.2my2＝12g(2t)2－12gt2＝12×10×(0.42－0.22)m＝0.6m令y1＝y，则有y2＝3y1＝3y已标注的线段s1、s2分别为s1＝x2＋y2 s2＝x2＋3y2＝x2＋9y2则有x2＋y2∶x2＋9y2＝3∶7整理得x＝255y，故在抛出瞬间小球的速度大小为v0＝xt＝255m/s.例5(2022·浙江省名校协作体模拟)第24届冬季奥运会于2022年2月在北京召开，如图甲所示为运动员跳台滑雪运动瞬间，运动示意图如图乙所示，运动员从助滑雪道AB上由静止开始滑下，到达C点后水平飞出，落到滑道上的D点，运动轨迹上的E点的速度方向与轨道CD平行，设运动员从C到E与从E到D的运动时间分别为t1与t2，(忽略空气阻力，运动员可视为质点)下列说法正确的是()A．t1<t2B．t1>t2C ．若运动员离开C 点时的速度加倍，则落在斜面上的速度方向不变D ．若运动员离开C 点时的速度加倍，则落在斜面上距C 的距离也加倍答案C 解析以C 点为原点，以CD 为x 轴，以CD 垂直向上方向为y 轴，建立坐标系如图所示．对运动员的运动进行分解，y 轴方向上的运动类似竖直上拋运动，x 轴方向做匀加速直线运动．当运动员速度方向与轨道平行时，在y 轴方向上到达最高点，根据竖直上拋运动的对称性，知t 1＝t 2，A 、B 错误；将初速度沿x 、y 方向分解为v 1、v 2，将加速度沿x 、y 方向分解为a 1、a 2，则运动员的运动时间为t ＝2v 2a 2，落在斜面上的距离s ＝v 1t ＋12a 1t 2，离开C 点时的速度加倍，则v 1、v 2加倍，t 加倍，由位移公式得s 不是加倍关系，D 错误；设运动员落在斜面上的速度方向与水平方向的夹角为α，斜面的倾角为θ，则有：tan α＝v y v 0，tan θ＝y x ＝v y 2t v 0t ＝v y 2v 0，得tan α＝2tan θ，θ一定，则α一定，可知运动员落在斜面上的速度方向与从C 点飞出时的速度大小无关，C正确．考点三斜抛运动例6(2022·广东茂名市模拟)铅球运动员采用原地推和滑步推两种推铅球方式，如图为滑步推铅球．推力相同时，滑步推铅球比原地推铅球增加几米的成绩．两种方式铅球出手时相对地面的位置和速度方向都相同，忽略空气阻力，则()A．两种方式推出的铅球在空中运动的时间可能相同B．采用原地推铅球方式推出的铅球上升的高度更高C．两种方式推出的铅球在空中运动到最高点时的速度都相同D．滑步推铅球可以增加成绩，可能是延长了运动员对铅球的作用时间答案D解析两种方式铅球出手时相对地面的位置和速度方向都相同，滑步推铅球成绩更好，所以滑步推铅球初速度更大，竖直和水平方向的分速度更大，到达最高点的时间更长，故根据斜抛的对称性，铅球在空中运动的时间更长，上升的高度更高，在最高点速度更大，A、B、C错误；初速度都是0，滑步推时末速度大，根据动量定理有Ft＝mv－0，可知推力相同时，动量变化大的推力作用时间长，D 正确．例7(2022·山东潍坊市一模)在2月8日举行的北京2022年冬奥会自由式滑雪女子大跳台的比赛中，18岁的中国选手谷爱凌顶住压力，在关键的第三跳以超高难度动作锁定金牌，这也是中国女子雪上项目第一个冬奥会冠军．滑雪大跳台的赛道主要由助滑道、起跳台、着陆坡、停止区组成，如图所示．在某次训练中，运动员经助滑道加速后自起跳点C以大小为v C＝20m/s、与水平方向成α＝37°的速度飞起，完成空中动作后，落在着陆坡上，后沿半径为R＝40m的圆弧轨道EF自由滑行通过最低点F，进入水平停止区后调整姿势做匀减速滑行直到静止．已知运动员着陆时的速度方向与竖直方向的夹角为α＝37°，在F点运动员对地面的压力大小为所受重力(含装备)的2倍，运动员在水平停止区受到的阻力大小为所受重力(含装备)的二分之一，g 取10m/s 2，sin 37°＝0.6，忽略运动过程中的空气阻力．求：(1)水平停止区FG 的最小长度L ；(2)运动员完成空中动作的时间t (结果保留两位有效数字)．答案(1)40m (2)3.3s 解析(1)将运动员与装备看成一个质点，总质量为m 总，在F 点时，运动员对地面的压力大小为所受重力(含装备)的2倍，由牛顿第三定律知地面对该运动员整体的支持力大小F N ＝2m 总g此时支持力与总重力的合力为圆周运动提供向心力，则有F N －m 总g ＝m 总v 2R解得v ＝20m/s运动员到达F 点后，在水平停止区有F 阻＝0.5m 总g ＝m 总a ，做加速度大小为a 的匀减速直线运动，水平停止区FG 的最小长度L ＝v 22a＝40m (2)对运动员由C 点起跳的速度进行正交分解，水平方向做匀速直线运动，竖直方向做匀减速直线运动，水平方向速度v x ＝v C cos α竖直方向速度v y ＝v C sin α－gt着陆时竖直方向分速度与C 点的竖直方向分速度方向相反，由于运动员着陆时的速度方向与竖直方向的夹角为α，则有tan α＝v x －v y ＝v C cos αgt －v C sin α代入数值得t ≈3.3s.1.斜抛运动是匀变速曲线运动，可分解为水平方向上的匀速直线运动和竖直方向上的加速度为g 的匀变速直线运动，以斜上抛为例(如图所示)速度：v x ＝v 0cos θ，v y ＝v 0sin θ－gt位移：x ＝v 0cos θ·t ，y ＝v 0sin θ·t －12gt 22．当物体做斜上抛运动至最高点时，运用逆向思维，可转化为平抛运动．1．(2022·江苏省高考考前打靶卷)如图所示，一男孩欲拿石子击打苹果，第一次以抛射角(抛出时速度与水平方向的夹角)θ1抛出石子，第2次以θ2(图中未画出)抛出(θ2>θ1)，假设两次抛出时的位置相同，且初速度v 0大小相等，两次均击中苹果．不计空气阻力，则()A ．第一次石子在空中运动的时间比第二次长B ．若仅减小v 0，欲击中苹果，则抛射角θ1、θ2均变大C ．改变v 0大小和抛射角，石子不可能水平击中苹果D ．两次击中苹果前瞬间的速度大小相等答案D解析石子做斜抛运动，水平方向做匀速运动，则有v x＝v0cosθ，故石子在空中的运动时间t＝xv x＝xv0cosθ，所以t1t2＝cosθ2cosθ1，因为θ2>θ1，故cosθ2<cosθ1，所以t1<t2，第一次运动时间较短，A错误；石子竖直方向做竖直上抛运动，则有v y＝v0sinθ，竖直方向上升的高度为h＝v y t－12gt2，联立可得h＝x tanθ－gx22v02cos2θ，故只需要v0大小和抛射角满足上式即可击中苹果，C错误；由h＝x tanθ－gx22v02cos2θ可知，v0减小时，θ不一定增大，B错误；由动能定理有－mgh＝12mv2－12mv02，故两次击中苹果前瞬间的速度大小相等，D正确．2.(2022·北京市昌平区高三期末)运动的合成与分解是我们研究复杂运动时常用的方法．如图所示，一高度为h、内壁光滑的圆筒竖直放置，将一个小滑块在圆筒上端O点以水平初速度v0沿圆筒内壁切线方向抛出．小滑块沿圆筒内壁运动了一周后恰好从O′点离开圆筒．已知重力加速度为g，不计空气阻力．(1)求小滑块从抛出到离开圆筒所用的时间t.(2)如果沿虚线OO′将圆筒展开，以小滑块初始位置为坐标原点O，初速度v0方向为x轴正方向，竖直向下为y轴正方向，建立直角坐标系xOy，请在图中定性地画出小滑块在圆筒内表面的运动轨迹．答案(1)2h g(2)见解析图解析(1)由题意可知，小滑块竖直方向做自由落体运动，可得小滑块从抛出到离开圆筒所用的时间为h ＝12gt 2，解得t ＝2h g；(2)由题意可知，小滑块在圆筒内表面的运动轨迹如图所示．专题强化练[保分基础练]1．(2022·广东省模拟)《西游记》中，一只大龟浮水作舟，驮着唐僧师徒四人和白龙马渡过了通天河．已知大龟在静水中游动的速度大小与河水的流速大小之比为2∶1，出发点A 到正对岸B 点的距离为d ，河岸平直．若大家以最短的时间渡河，则大家上岸的地点与B 点的距离为()A.d 4B.d 2C ．2dD ．4d答案B解析要使渡河时间最短，大龟游动的速度方向应垂直河岸，渡河时间为t ＝dv 1，大家上岸的地点与B 点的距离x ＝v 2t ，又v 1∶v 2＝2∶1，联立解得x ＝d2，故B 正确．2.(2022·广东卷·6)如图所示，在竖直平面内，截面为三角形的小积木悬挂在离地足够高处，一玩具枪的枪口与小积木上P 点等高且相距为L .当玩具子弹以水平速度v 从枪口向P 点射出时，小积木恰好由静止释放，子弹从射出至击中积木所用时间为t .不计空气阻力．下列关于子弹的说法正确的是()A ．将击中P 点，t 大于L vB ．将击中P 点，t 等于L vC ．将击中P 点上方，t 大于L v D ．将击中P 点下方，t 等于L v答案B解析由题意知枪口与P 点等高，子弹和小积木在竖直方向上均做自由落体运动，当子弹击中积木时子弹和积木的运动时间相同，根据h ＝12gt 2，可知下落高度相同，所以将击中P 点；又由于初始状态子弹到P 点的水平距离为L ，子弹在水平方向上做匀速直线运动，故有t ＝Lv，故选B.3.(2022·江苏扬州市高三期末)如图所示，滑板爱好者先后两次从坡道A 点滑出，均落至B 点，第二次的滞空时间比第一次长，则()A．两次滑出速度方向相同B．两次腾空最大高度相同C．第二次滑出速度一定大D．第二次在最高点速度小答案D解析对滑板爱好者运动分析可知，从坡道A点滑出后，水平方向做匀速直线运动，竖直方向做竖直上抛运动，根据竖直上抛运动的对称性，即上升时间等于下降时间，由题知第二次的滞空时间比第一次长，所以第二次下降时间大于第一次，由h＝12gt2知，第二次腾空最大高度大于第一次，又因为两次水平位移相等，所以两次位移与水平方向的夹角不同，即两次滑出速度方向不相同，故A、B错误；因为第二次下降时间大于第一次，且两次水平位移相等，由x＝v x t知，第二次滑出后水平分速度小于第一次，即第二次在最高点速度小，又由v y＝gt可知，第二次滑出后竖直分速度大于第一次，所以第二次滑出速度不一定大，故C错误，D 正确．4.(多选)(2022·广西北海市一模)如图所示，直杆AB斜靠在墙角，∠ABO＝53°，∠AOB＝90°，AO＝5m．现从距A点正下方1.8m的C点以初速度v0水平抛出一小球(可视为质点)．已知重力加速度g取10m/s2，sin53°＝0.8，cos53°＝0.6，空气阻力不计．若使小球不能碰到杆AB，则v0的值可能为()A．4m/s B．4.4m/s C．5m/s D．6m/s答案AB解析若小球刚与杆接触时的末速度与水平方向夹角为53°，即小球运动轨迹与杆相切，设此时小球竖直方向下落高度为h，水平位移为x，则根据平抛运动相关推论有tan53°＝2hx，由几何关系可得tan53°＝h＋h ACx，联立解得h＝1.8m，x＝2.7m，则由v0<xt，t＝2hg，联立解得v0<4.5m/s，C、D错误，A、B正确．5．(2022·安徽合肥市质检)某校秋季运动会分为竞技组和健身组，健身组设置了定点投篮项目．某同学正在进行定点投篮，篮球在空中划出了一道漂亮的弧线．在篮球运动所在的竖直平面内建立坐标系xOy，如图所示，篮球由A点投出，A、B、C、D是篮球运动轨迹上的四点，C为篮球运动的最高点，A、B、D三点的坐标已在图中标出，重力加速度为g，空气阻力忽略不计．则下列说法正确的是()A．篮球经过C点时速度大小为gLB．篮球经过B点和D点的动量相同C．篮球由A到B和由B到C过程，动量的变化量相同D．篮球由B到C和由C到D过程，重力做功相同答案C解析依题意可知篮球抛出后做斜抛运动，利用逆向思维，将篮球从A到C的轨迹看作从C到A的平抛运动，设C点坐标为(0，y C)，C点到B点时间为t，由题图可得L＝v C t，y C＝12gt2,3L－y C＝gt2，联立解得y C＝L，v C＝gL2，故A错误；由题图知B点和D点在同一水平线上，则可知篮球在两点处的速度大小相等，但方向不同，所以两点处的动量不相同，故B错误；由题图知篮球由A到B和由B 到C过程水平方向上发生的位移相等，则所用时间相等，根据动量定理可得mgt ＝－Δp，所以动量的变化量相同，故C正确；篮球由B到C过程重力做负功，由C到D过程重力做正功，二者不相同，故D错误．6．(2022·广东梅州市一模)如图甲所示是网球发球机，某次室内训练时将发球机在距地面一定的高度的地方放置，然后向竖直墙面发射网球．假定网球水平射出，某两次射出的网球碰到墙面时与水平方向夹角分别为30°和60°，如图乙所示．若不考虑网球在空中受到的阻力，则()A．两次发射的初速度之比为3∶1B．碰到墙面前空中运动时间之比为1∶3C．下降高度之比为1∶3D．碰到墙面时动能之比为3∶1答案C解析在平抛运动过程中，有h ＝12gt 2，x ＝v 0t ，位移与水平方向夹角的正切值tanα＝h x ＝gt 2v 0，速度与水平方向夹角的正切值tan β＝v y v 0＝gtv 0，则tan β＝2tan α.在平抛运动中，h ＝xtan β2，所以h 1h 2＝tan 30°tan 60°＝13；由h ＝12gt 2可知，t 1t 2＝h 1h 2＝33；水平速度v ＝x t ，可得v 1v 2＝t 2t 1＝31；由v t ＝v 0cos β可知，v t 1v t 2＝v 1cos 60°v 2cos 30°＝11，所以碰到墙面时动能之比E k1E k2＝v t 12v t 22＝11，故A 、B 、D 错误，C 正确．[争分提能练]7.(2022·湖北武汉市高三期末)活塞带动飞轮转动可简化为如图所示的模型：图中A 、B 、O 三处都是转轴，当活塞在水平方向上移动时，带动连杆AB 运动，进而带动OB 杆以O 点为轴转动．若某时刻活塞的水平速度大小为v ，连杆AB 与水平方向夹角为α，AB 杆与OB 杆的夹角为β，此时B 点做圆周运动的线速度大小为()A.v sin αsin βB.v cos αsin βC.v cos αcos βD.v sin αcos β答案B解析设B 点做圆周运动的线速度大小为v ′，此速度为B 点的实际速度，根据运动合成与分解，可以分解为沿杆方向的分速度和垂直杆方向的分速度，如图，沿杆方向的分速度大小为v B ＝v ′cos(β－π2)＝v ′sin β，A 点速度为水平方向的v ，根据运动合成与分解，可以分解为沿杆方向的分速度和垂直杆方向的分速度，如图，沿杆方向的分速度为v A ＝v cos α，又有二者沿杆方向的分速度相等，即v ′sin β＝v cos α，则v ′＝v cos αsin β，故选B.8.(多选)(2022·山东卷·11)如图所示，某同学将离地1.25m 的网球以13m/s 的速度斜向上击出，击球点到竖直墙壁的距离4.8m ．当网球竖直分速度为零时，击中墙壁上离地高度为8.45m 的P 点．网球与墙壁碰撞后，垂直墙面速度分量大小变为碰前的0.75倍．平行墙面的速度分量不变．重力加速度g 取10m/s 2，网球碰墙后的速度大小v 和着地点到墙壁的距离d 分别为()A ．v ＝5m/sB ．v ＝32m/sC ．d ＝3.6mD ．d ＝3.9m答案BD解析设网球飞出时的速度为v 0，竖直方向v 0竖直2＝2g (H －h )，代入数据得v 0竖直＝2×10×8.45－1.25m/s ＝12m/s ，则v 0水平＝132－122m/s ＝5m/s ，网球击出点到P 点水平方向的距离x 水平＝v 0水平t ＝v 0水平·v 0竖直g ＝6m ，根据几何关系可得打在墙面上时，垂直墙面的速度分量v 0水平⊥＝v 0水平·45＝4m/s ，平行墙面的速度分量v0水平∥＝v0水平·35＝3m/s，反弹后，垂直墙面的速度分量v水平⊥′＝0.75·v0水平⊥＝3m/s，则反弹后的网球速度大小为v＝v水平＝v水平⊥′2＋v0水平∥2＝32m/s，网球落到地面的时间t′＝2Hg＝2×8.4510s＝1.3s，着地点到墙壁的距离d＝v水平⊥′t′＝3.9m，故B、D正确，A、C错误．9.(2022·安徽蚌埠市高三期末)如图为弹球游戏装置的简化示意图，两块平行挡板竖直固定在水平面上，右侧挡板下端有一小孔B，小亮将弹性小球自右侧挡板顶端A点以一定的水平速度向左抛出，小球经两个挡板多次碰撞最终恰好从B飞出，游戏获胜．已知两挡板的间距为L，A、B的高度差为h，小球直径略小于小孔的内径，小球与挡板碰撞前后的水平和竖直分速度大小均不变，且不与水平面相碰，重力加速度为g.则小球抛出时的速度v和它与两挡板碰撞总次数N分别为()A．v＝(N＋1)L2gh，N＝2n(n＝1,2,3，…)B．v＝(N＋1)L2gh，N＝2n－1(n＝1,2,3，…)C．v＝(N＋1)L g2h，N＝2n(n＝1,2,3，…)D．v＝(N＋1)L g2h，N＝2n－1(n＝1,2,3，…)答案B解析小球在两平行挡板间的运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动．设运动总时间为t，则水平方向、竖直方向分别有(N＋1)L＝vt，N＝2n－1(n＝1,2,3，…)，h＝12gt2，联立可得v＝(N＋1)L2gh，N＝2n－1(n＝1,2,3，…)，故A、C、D错误，B正确．10.(2022·山东日照市一模)跳台滑雪是冬奥会的重要项目之一．如图所示，某次比赛中，质量为m的运动员(包括滑雪板)以速度v0从跳台顶端水平飞出，经过一段时间后落在倾斜赛道上，赛道的倾角为θ，重力加速度为g，空气阻力忽略不计，运动员(包括滑雪板)视为质点．则运动员在空中运动的过程中()A．动量变化量的大小为mv0tanθB．位移的大小为v02tanθgC．距离赛道最远时的速度大小为v0tanθD．距离赛道最远时的竖直位移为总竖直位移的14答案D解析根据动量定理，动量变化量等于重力的冲量，即为竖直方向的动量变化，当运动员落至斜面时，分解其位移得tanθ＝hx＝12gt2v0t＝gt2v0，则落至斜面时的竖直分速度为v y＝gt＝2v0tanθ，因此动量变化量为Δp＝mΔv＝2mv0tanθ，故A错误；由A得运动员运动的时间为t＝2v0tanθg，则水平位移为x＝v0t＝2v02tanθg，则运动员实际位移大小为x实际＝xcosθ＝2v02tanθg cosθ，故B错误；将运动分解为沿斜面和垂直斜面两个方向，则垂直斜面方向的初速度方向垂直斜面向上，加速度方向垂直斜面向下，则垂直斜面的速度分量减小为零时运动员离斜面最远，即当运动员的速度方向与斜面平行时，距离赛道最远，在最远处分解其速度得cosθ＝v0v，则v＝v0cosθ，故C错误；垂直斜面方向的分运动类似于竖直上抛运动，根据竖直上抛运动的对称性，垂直斜面的速度分量减小为零时的运动时间为总时间的一半，再根据自由落体的公式h＝12gt2得，距离赛道最远时的竖直位移为总竖直位移的14，故D正确．11．(2022·河北保定市七校联考)如图所示，两人各自用吸管吹黄豆，甲黄豆从吸管末端P点水平射出的同时乙黄豆从另一吸管末端M点斜向上射出．经过一段时间后两黄豆在N点相遇，曲线1和2分别为甲、乙黄豆的运动轨迹．若M点在P 点正下方，M点与N点位于同一水平线上，且PM长度等于MN的长度，不计空气阻力，可将黄豆看成质点，则()A．两黄豆相遇时甲的速度与水平方向的夹角的正切值为乙的两倍B．甲黄豆在P点的速度与乙黄豆在最高点的速度不相等C．两黄豆相遇时甲的速度大小为乙的两倍D．乙黄豆相对于M点上升的最大高度为PM长度的一半答案A解析设甲黄豆做平抛运动的时间为t，那么乙黄豆做斜抛运动的时间也为t，根据斜抛运动的对称性可知，乙黄豆从M点运动至最高点的时间为t2，乙黄豆从M点运动至最高点的水平位移为MN的一半，设PM＝MN＝L，甲黄豆在P点的速度为v1，乙黄豆到达最高点的速度为v′，在水平方向上由运动学规律：对甲黄豆有L＝v1t，对乙黄豆从M点运动至最高点水平方向上有L2＝v′·t2，联立解得v1＝v′＝Lt，故B错误；对甲黄豆到达N点时，在竖直方向上有L＝12gt2，v1y＝gt＝2gL，在水平方向有v1＝Lt＝gL2，甲黄豆到达N点时的速度为v甲＝v12＋v1y2＝5gL2，对乙黄豆在从M点运动至最高点的过程中，由逆向思维得上升的最大高度为h＝12g(t2)2＝14·12gt2＝14L，所以乙黄豆相对于M点上升的最大高度为PM长度的14，乙黄豆在M点的竖直方向分速度为v2y2＝2g·L4，则v2y＝gL2，由运动的合成与分解得乙黄豆在N点的速度为v乙＝v′2＋v2y2＝gL，所以两黄豆相遇时甲的速度大小不是乙的两倍，故C、D错误；两黄豆相遇时甲的速度与水平方向的夹角正切值为tanα＝v1yv1＝2gLgL2＝2，乙的速度与水平方向的夹角正切值为tanβ＝v2yv′＝v2yv1＝gL2gL2＝1，所以两黄豆相遇时甲的速度与水平方向的夹角不是乙的两倍，甲的速度与水平方向的夹角的正切值为乙的两倍，故A正确．12．(2022·广东开平市模拟)2022年2月8日，18岁的中国选手谷爱凌在北京冬奥会自由式滑雪女子大跳台比赛中以绝对优势夺得金牌，这是中国代表团在北京冬奥会上的第三枚金牌，被誉为“雪上公主”的她赛后喜极而泣．现将比赛某段过程视为如图所示的质点小球的运动，小球从倾角为α＝30°的斜面顶端O 点以速度v 0飞出，已知v 0＝20m/s ，且与斜面夹角为θ＝60°.图中虚线为小球在空中的运动轨迹，且A 为轨迹上离斜面最远的点，B 为小球在斜面上的落点，C 是过A 作竖直线与斜面的交点，不计空气阻力，重力加速度取g ＝10m/s 2.求：(1)小球从O 点运动到A 点所用时间t ；(2)小球离斜面最远的距离L ；(3)O 、C 两点间距离x .答案(1)2s (2)103m (3)40m 解析(1)将小球在O 点的速度沿斜面和垂直斜面分解，如图所示，垂直斜面方向有v 1＝v 0sin θ，a 1＝g cos α，t ＝v 1a 1，联立解得t ＝2s(2)垂直斜面方向的速度匀减速至0时，有L ＝v 122a 1，代入数据得L ＝103m (3)解法1：由垂直斜面方向运动对称性可得，小球从O 到A 与从A 到B 所用时间相等，平行斜面方向有v 2＝v 0cos θ，a 2＝g sin α，则平行斜面方向有x OB ＝v 2·2t ＋12a 2(2t )2，小球在水平方向做匀速直线运动，C 为OB 中点，则x ＝12x OB。

专题二牛顿运动定律与直线运动高频考点·能力突破考点一匀变速直线运动规律的应用1．基本公式v＝v0＋at，x＝v0t+12at2，v2−v02＝2ax.2．重要推论v t2＝v0+v2＝v̅(利用平均速度求瞬时速度)；初、末速度平均值vt2＝√t02+t22；Δx＝aT2(用逐差法测加速度)．3．符号法则选定正方向，将矢量运算转化为代数运算．4．解决运动学问题的基本思路例 1 [2022·湖北卷]我国高铁技术全球领先，乘高铁极大节省了出行时间．假设两火车站W和G间的铁路里程为1 080 km，W和G之间还均匀分布了4个车站．列车从W站始发，经停4站后到达终点站G .设普通列车的最高速度为108 km /h ，高铁列车的最高速度为324 km /h .若普通列车和高铁列车在进站和出站过程中，加速度大小均为0.5 m /s 2，其余行驶时间内保持各自的最高速度匀速运动，两种列车在每个车站停车时间相同，则从W 到G 乘高铁列车出行比乘普通列车节省的时间为( )A ．6小时25分钟B ．6小时30分钟C ．6小时35分钟D ．6小时40分钟[解题心得]预测1 钢架雪车也被称为俯式冰橇，是2022年北京冬奥会的比赛项目之一．运动员需要俯身平贴在雪橇上，以俯卧姿态滑行．比赛线路由起跑区、出发区、滑行区及减速区组成．若某次运动员练习时，恰好在终点停下来，且在减速区AB 间的运动视为匀减速直线运动．运动员通过减速区时间为t ，其中第一个t 4时间内的位移为x 1，第四个t 4时间内的位移为x 2，则x 2:x 1等于( )A ．1∶16B ．1∶7C ．1∶5D ．1∶3预测2 [2022·福建泉州高三联考]如图为某轿车在行驶过程中，试图借用逆向车道超越客车的示意图，图中当两车相距L ＝4 m 时，客车正以v 1＝6 m /s 速度匀速行驶，轿车正以v 2＝10 m /s 的速度借道超车．客车长L 1＝10 m ，轿车长L 2＝4 m ，不考虑变道过程中车速的变化和位移的侧向变化．(1)若轿车开始加速并在3 s内成功超越客车L3＝12 m后，才能驶回正常行驶车道，其加速度多大？(2)若轿车放弃超车并立即驶回正常行驶车道，则至少要以多大的加速度做匀减速运动，才能避免与客车追尾？[试解]考点二动力学基本规律的应用动力学两类基本问题的解题思路温馨提示动力学中的所有问题都离不开受力分析和运动分析，都属于这两类基本问题的拓展和延伸．例2 [2022·浙江卷1月]第24届冬奥会在我国举办．钢架雪车比赛的一段赛道如图1所示，长12 m水平直道AB与长20 m的倾斜直道BC在B点平滑连接，斜道与水平面的夹角为15°.运动员从A点由静止出发，推着雪车匀加速到B点时速度大小为8 m/s，紧接着快速俯卧到车上沿BC匀加速下滑(图2所示)，到C点共用时5.0 s．若雪车(包括运动员)可视为质点，始终在冰面上运动，其总质量为110 kg，sin 15°＝0.26(取g＝10 m/s2)，求雪车(包括运动员)(1)在直道AB上的加速度大小；(2)过C点的速度大小；(3)在斜道BC上运动时受到的阻力大小．[试解]预测3 (多选)14岁的奥运冠军全红婵，在第14届全运会上再次上演“水花消失术”夺冠．在女子10 m 跳台的决赛中(下面研究过程将全红婵视为质点)，全红婵竖直向上跳离跳台的速度为5 m/s，竖直入水后到速度减为零的运动时间与空中运动时间相等，假设所受水的阻力恒定，不计空气阻力，全红婵的体重为35 kg，重力加速度大小为g＝10 m/s2，则( )A．跳离跳台后上升阶段全红婵处于失重状态B．入水后全红婵处于失重状态C．全红婵在空中运动的时间为1.5 sD．入水后全红婵受到水的阻力为612.5 N预测4 衢州市2022年5月1日起部分县、区超标电动车不得上道路行驶，新的电动自行车必须符合国标GB17761－2018的标准，新标准规定最高车速不能高于25 km/h，整车质量应当小于或等于55 kg，制动性能要符合如下规定：某人体重m＝50 kg，骑着符合新标准、质量M＝50 kg的电动自行车在水平路面行驶．电动自行车的刹车过程可简化为匀变速直线运动．(1)当遇到紧急情况时，若他同时使用前后车闸刹车，在干燥路面上该车的最小加速度是多少？此时受到的制动力是多大？(保留两位有效数字)(2)若此人私自改装电瓶输出功率，致使车速超标(其他条件不变)，当他以32 km/h速度在雨后的路面上行驶，遇见紧急情况，采取同时使用前后车闸方式刹车，则该车刹车后行驶的最大距离是多少？(3)根据你所学物理知识，分析电动自行车超速超载有什么危害？[试解]考点三连接体问题1．处理连接体问题的常用方法2.连接体问题中常见的临界条件例3 [2022·全国甲卷]如图，质量相等的两滑块P、Q置于水平桌面上，二者用一轻弹簧水平连接，两滑块与桌面间的动摩擦因数均为μ.重力加速度大小为g.用水平向右的拉力F拉动P，使两滑块均做匀速运动；某时刻突然撤去该拉力，则从此刻开始到弹簧第一次恢复原长之前( )A．P的加速度大小的最大值为2μgB．Q的加速度大小的最大值为2μgC．P的位移大小一定大于Q的位移大小D．P的速度大小均不大于同一时刻Q的速度大小[解题心得]预测5 如图所示，将一盒未开封的香皂置于桌面上的一张纸板上，用水平向右的拉力将纸板迅速抽出，香皂盒的移动距离很小，几乎观察不到，这就是大家熟悉的惯性演示实验(示意图如图所示)，若香皂盒和纸板的质量分别为m1和m2，各接触面间的动摩擦因数均为μ，重力加速度为g.若本实验中，m1＝100 g，m2＝5 g，μ＝0.2，香皂盒与纸板左端的距离d＝0.1 m，若香皂盒移动的距离超过l＝0.002 m，人眼就能感知，忽略香皂盒的体积因素影响，g取10 m/s2，为确保香皂盒移动不被人感知，纸板所需的拉力至少是( )A．1.41 N B．1.42 NC．1 410 N D．1 420 N预测6 [2022·全国乙卷]如图，一不可伸长轻绳两端各连接一质量为m的小球，初始时整个系统静置于光滑水平桌面上，两球间的距离等于绳长L.一大小为F的水平恒力作用在轻绳的中点，方向与两球连线垂直．当两球运动至二者相距35L时，它们加速度的大小均为( )A．5F8m B．2F5mC．3F8m D．3F10m预测7 如图所示，在倾角为θ＝30°的光滑固定斜面上端系有一劲度系数为k＝100 N/m的轻质弹簧，弹簧下端连一个质量为m＝8 kg的小球，球被一垂直于斜面的挡板A挡住，此时弹簧没有形变．从t＝0时刻开始挡板A以加速度a＝1 m/s2沿斜面向下匀加速运动，则：(g＝10 m/s2)(1)t＝0时刻，挡板对小球的弹力多大？(2)从开始运动到小球与挡板分离所经历的时间为多少？(3)小球向下运动多少距离时速度最大？[试解]素养培优·情境命题实际情境中的直线运动情境1 [2022·山东押题卷]高速公路的ETC电子收费系统如图所示，ETC通道的长度是识别区起点到自动栏杆的水平距离，总长为19.6 m．某汽车以5 m/s的速度匀速进入识别区，ETC用0.3 s的时间识别车载电子标签，识别完成后发出“滴”的一声，汽车又向前行驶了2 s司机发现自动栏杆没有抬起，于是紧急刹车，汽车恰好没有撞杆．已知司机的反应时间和汽车系统的反应时间之和为0.8 s．则刹车的加速度大小约为( )A．2.52 m/s2B．3.55 m/s2C．3.75 m/s2D．3.05 m/s2[解题心得]情境2 驾驶员看见过马路的人，从决定停车，直至右脚刚刚踩在制动器踏板上经过的时间，叫反应时间，在反应时间内，汽车按一定速度匀速行驶的距离称为反应距离；从踩紧踏板(抱死车轮)到车停下的这段距离称为刹车距离；司机从发现情况到汽车完全停下来，汽车所通过的距离叫做停车距离．如图所示，根据图中内容，下列说法中正确的是( )A．根据图中信息可以求出反应时间B．根据图中信息可以求出汽车的制动力C．匀速行驶的速度加倍，停车距离也加倍D．酒后驾车反应时间明显增加，停车距离不变[解题心得]情境3 [2022·浙江6月]物流公司通过滑轨把货物直接装运到卡车中，如图所示，倾斜滑轨与水平面成24°角，长度l1＝4 m，水平滑轨长度可调，两滑轨间平滑连接．若货物从倾斜滑轨顶端由静止开始下滑，其与滑轨间的动摩擦因数均为μ＝2，货物可视为质点(取9cos 24°＝0.9，sin 24°＝0.4)．(1)求货物在倾斜滑轨上滑行时加速度a1的大小；(2)求货物在倾斜滑轨末端时速度v的大小；(3)若货物滑离水平滑轨末端时的速度不超过2 m/s，求水平滑轨的最短长度l2.[试解]情境4 疫情期间，为了减少人与人之间的接触，一餐厅推出了一款智能送餐机器人进行送餐(如图甲)．该款机器人的最大运行速度为4 m/s，加速度大小可调节在1 m/s2≤a≤3 m/s2范围内，要求：送餐过程托盘保持水平，菜碟与托盘不发生相对滑动，机器人到达餐桌时速度刚好为0.现把送餐过程简化为如图乙的直线情境图，已知机器人恰好以最大运行速度v＝4 m/s通过O处，O与餐桌A相距x0＝6 m，餐桌A和餐桌F相距L＝16 m，机器人、餐桌都能看成质点，送餐使用的菜碟与托盘之间的动摩擦因数为μ＝0.2，最大静摩擦力等于滑动摩擦力，重力加速度g＝10 m/s2.(1)在某次从O到餐桌A的过程中，机器人从O开始匀减速恰好到A停下，求机器人在此过程加速度a的大小．(2)完成(1)问中的送餐任务后，机器人马上从A继续送餐到F，若要求以最短时间从A 送餐到F，求机器人运行的最大加速度a m和加速过程通过的位移x加．[试解]专题二 牛顿运动定律与直线运动高频考点·能力突破考点一例1 解析：108 km/h ＝30 m/s ，324 km/h ＝90 m/s由于中间4个站均匀分布，因此节省的时间相当于在任意相邻两站间节省的时间的5倍，为总的节省时间，相邻两站间的距离x ＝1 080×1035m ＝2.16×105m普通列车加速时间t 1＝v1a＝300.5 s ＝60 s加速过程的位移x 1＝12at 12＝12×0.5×602m ＝900 m根据对称性可知加速与减速位移相等，可得匀速运动的时间t 2＝x −2x 1v＝2.16×105−2×90030s ＝7 140 s同理高铁列车加速时间t ′1＝v 1′a＝900.5s ＝180 s加速过程的位移x ′1＝12at1′2＝12×0.5×1802m ＝8 100 m根据对称性可知加速与减速位移相等，可得匀速运动的时间t ′2＝x −2x 1′v 1′＝2.16×105−2×8 10090s ＝2 220 s相邻两站间节省的时间Δt ＝(t 2＋2t 1)－(t ′2＋2t ′1)＝4 680 s ，因此总的节省时间Δt 总＝5Δt ＝4 680×5 s＝23 400 s ＝6小时30分，B 正确．答案：B预测1 解析：由题意知，在减速区AB 间的运动视为匀减速直线运动，且最终减为零，将此减速过程由逆向思维，可看作初速度为零的匀加速直线运动，则根据初速度为零的匀加速直线运动，连续相等时间内位移之比为1∶3∶5…可知，x 2∶x 1之比即为初速度为零的匀加速直线中第一个t4时间内的位移与第四个t4时间内的位移之比，即x 2∶x 1＝1∶7，故选B.答案：B预测2 解析：(1)设轿车的加速度大小为a ，经过t 1＝3 s ，客车和轿车位移分别为s 1、s 2，由运动学公式得s 1＝v 1t 1，s 2＝v 2t 1+12at 12，s 2＝s 1＋L 1＋L 2＋L ＋L 3，解得a ＝4 m/s 2.(2)设轿车减速的加速度大小为a ′，经过时间t 2，轿车、客车达到共同速度，则v 2－a ′t 2＝v 1，客车和轿车位移分别为s ′1、s ′2，满足s ′2＝v 2t 2−12a ′t 22， s ′1＝v 1t 2， s ′2＝s ′1＋L ，解得a ′＝2 m/s 2，即轿车至少以2 m/s 2的加速度做匀减速运动，才能避免与客车追尾． 答案：(1)4 m/s 2(2)2 m/s 2考点二例2 解析：(1)设雪车从A →B 的加速度大小为a 、运动时间为t ，根据匀变速直线运动的规律有2al AB ＝v B 2、v B ＝at解得t ＝3 s 、a ＝83 m/s 2.(2)方法一 由题知雪车从A →C 全程的运动时间t 0＝5 s ，设雪车从B →C 的加速度大小为a 1、运动时间为t 1，故t 1＝t 0－t ，根据匀变速直线运动的规律有l BC ＝v B t 1+12a 1t 12v C ＝v B ＋a 1t 1代入数据解得a 1＝2 m/s 2、v C ＝12 m/s.方法二 由于雪车在BC 上做匀变速运动，故l BC ＝v BC ̅̅̅̅·t 1＝v B +v C 2(t 0－t )解得v C ＝12 m/s.(3)方法一 设雪车在BC 上运动时受到的阻力大小为f ，根据牛顿第二定律有mg sin 15°－f ＝ma 1代入数据解得f ＝66 N方法二 对雪车在BC 上的运动过程由动量定理有 (mg sin 15°－f )(t 0－t )＝mv C －mv B 代入数据解得f ＝66 N.方法三 对雪车从B →C 由动能定理有(mg sin 15°−f )l BC ＝12tt t 2−12tt t 2解得f＝66 N.答案：(1)83m/s2(2)12 m/s (3)66 N预测3 解析：跳离跳台后上升阶段，加速度向下，则全红婵处于失重状态，A正确；入水后全红婵的加速度向上，处于超重状态，B错误；以向上为正方向，则根据－h＝v0t－12gt2，可得t＝2 s，即全红婵在空中运动的时间为2 s，C错误；入水时的速度v1＝v0－gt＝5 m/s－10×2 m/s＝－15 m/s，在水中的加速度大小a＝0−v1t＝7.5 m/s2，方向竖直向上，根据牛顿第二定律可得f＝ma＋mg＝35×10 N＋35×7.5 N＝612.5 N，D正确．答案：AD预测4 解析：(1)根据匀变速运动公式2ax＝t2−t02解得t＝t2−t022t＝－3.4 m/s2根据牛顿第二定律得：制动力F＝(M＋m)a＝340 N.(2)根据匀变速运动公式2a1x1＝v12，2a1x2＝v22，x1x2＝t12t22联立解得x2＝36 m.(3)超速时，加速度不变但刹车距离变大，超载时，质量变大，减速的加速度变小，刹车距离变大．答案：(1)－3.4 m/s2340 N (2)36 m (3)见解析考点三例3 解析：撤去力F后到弹簧第一次恢复原长之前，弹簧弹力kx减小，对P有μmg＋kx＝ma P，对Q有μmg－kx＝ma Q，且撤去外力瞬间μmg＝kx，故P做加速度从2μg减小到μg的减速运动，Q做加速度从0逐渐增大到μg的减速运动，即P的加速度始终大于Q的加速度，故除开始时刻外，任意时刻P的速度大小小于Q的速度大小，故P的平均速度大小必小于Q的平均速度大小，由x＝v̅t可知Q的位移大小大于P的位移大小，可知B、C错误，A、D正确．答案：AD预测5 解析：香皂盒与纸板发生相对滑动时，根据牛顿第二定律可得μm1g＝m1a1解得a1＝2 m/s2对纸板，根据牛顿第二定律可得F－μm1g－μ(m1＋m2)g＝m2a2为确保实验成功，即香皂盒移动的距离不超过l＝0.002 m，纸板抽出时香皂盒运动的最大距离为x1＝12a1t12纸板运动距离为d＋x1＝12a2t12纸板抽出后香皂盒运动的距离为x2＝12a3t22则l＝x1＋x2由题意知a1＝a3，a1t1＝a3t2代入数据联立得F＝1.42 N，故B正确，A、C、D错误．答案：B预测6解析：如图可知sin θ＝12×3L5L2＝35，则cos θ＝45，对轻绳中点受力分析可知F＝2T cos θ，对小球由牛顿第二定律得T＝ma，联立解得a＝5F8m，故选项A正确．答案：A预测7 解析：解答本题的关键是要能分析得出板和小球分离时，板对小球的作用力为零；当球的速度最大时，球的加速度为零．(1)因开始时弹簧无形变，故对小球，根据牛顿第二定律得mg sin 30°－F1＝ma解得F1＝32 N.(2)当挡板和小球分离时，根据牛顿第二定律得mg sin 30°－kx＝ma，其中x＝12at2解得t＝0.8 s，x＝0.32 m.(3)当小球的速度最大时，加速度为零，此时mg sin 30°＝kx1解得x1＝0.4 m.答案：(1)32 N (2)0.8 s (3)0.4 m素养培优·情境命题情境1 解析：设刹车的加速度大小为a，则有x＝t0(t1+t2+tt)+t022t代入数据有19.6＝5×(0.3＋2＋0.8)＋522a解得a＝3.05 m/s2，所以D正确；A、B、C错误．答案：D情境2 解析：图中知道汽车速度，反应距离，根据x＝v0t可以求出反应时间，故A 正确；由于不知汽车质量，则无法求出汽车的制动力，故B错误；设停车距离为x，反应时间为t0.则x＝t0t0+t022t，可知匀速行驶的速度加倍，停车距离不是简单的加倍，故C错误；除了反应时间，其他条件不变的情况下，根据公式x＝t0t0+t022t，酒后驾车反应时间明显增加，停车距离增加，故D错误．答案：A情境3 解析：(1)根据牛顿第二定律mg sin 24°－μmg cos 24°＝ma1a1＝2 m/s2(2)在倾斜滑轨上运动过程为匀加速直线运动v2＝2a1l1v＝4 m/s(3)在水平滑轨上的运动过程为匀减速直线运动v12－v2＝2a2l2a2＝－μgl2＝2.7 m答案：(1)2 m/s2(2)4 m/s (3)2.7 m情境4 解析：(1)从O点到A点，由运动公式0－v2＝2ax0，解得a＝0−v22x0＝－422×6m/s2＝－43m/s2，机器人在此过程加速度a的大小为43m/s2.(2)要想用时最短，则机器人先以最大加速度加速，然后匀速一段时间，再以最大加速度做减速到零．最大加速度为a m＝μg＝2 m/s2，加速的位移为x加＝v22a m＝4 m.答案：(1)43m/s2(2)2 m/s2 4 m。

微元法本专题主要讲解利用微元法解决动力学问题、变力做功问题、电场和电磁感应等问题，主要分为时间微元和位移微元两大类。

微元法在近几年高考中考查频率较高，出现了分值高、难度较大的计算题。

微元法是一种非常有效的解题方法，将研究对象或研究过程分解为众多细小的“微元”，分析这些“微元”，进行必要的数学推理或物理思想处理，能够有效的简化复杂的物理问题。

考查学生的分析推理能力，应用数学方法解决物理问题能力。

时间微元微元思想是中学物理中的重要思想。

所谓微元思想，是将研究对象或者物理过程分割成无限多个无限小的部分，先取出其中任意部分进行研究，再从局部到整体综合起来加以考虑的科学思维方法。

如图所示，两根平行的金属导轨MN和PQ放在水平面上，左端连接阻值为R的电阻。

导轨间距为L，电阻不计。

导轨处在竖直向上的匀强磁场中，匀强磁场的磁感应强度为B。

一根质量为m、阻值为r的金属棒放置在水平导轨上。

现给金属棒一个瞬时冲量，使其获得一个水平向右的初速度v0后沿导轨运动。

设金属棒运动过程中始终与导轨垂直且接触良好，导轨足够长，不计一切摩擦。

求：（1）金属棒的速度为v时受到的安培力是多大？（2）金属棒向右运动的最大距离是多少？物理学研究问题一般从最简单的理想情况入手，由简入繁，逐渐贴近实际。

在研究真实的向上抛出的物体运动时，我们可以先从不受阻力入手，再从受恒定阻力研究，最后研究接近真实的、阻力变化的运动情形。

现将一个质量为m的小球以速度v0竖直向上抛出，重力加速度为g。

（1）若忽略空气阻力对小球运动的影响，求物体经过多长时间回到抛出点；（2）若空气阻力大小与小球速度大小成正比，已知小球经t时间上升到最高点，再经一段时间匀速经过抛出点时，速度大小为v1，求小球抛出后瞬间的加速度和上升的最大高度。

涉及时间微元问题的一般解题步骤：（1）本方法一般用来处理变加速直线运动的情况且物体所受的变力与速度成正比。

（2）找微元：对于这类变速运动，通常选取极短的一段时间∆t，在这段极短的时间内可认为物体的受力、速度等物理量不变。

专题01 力与直线运动一、单选题1．（2022·河南·洛宁县第一高级中学模拟预测）意大利物理学家伽利略在《关于两门新科学的对话》一书中，对自由落体运动的研究，是科学实验和逻辑思维的完美结合。

如图所示，这可以大致表示实验过程，图中各个小球位置之间的时间间隔可以认为相等，对这一过程的分析，下列说法正确的是（ ）A ．运用图甲的实验，可“减弱”重力的作用，放大时间，便于观察B ．只要测量出图丁中相邻两小球球心位置之间的距离，就可以计算出重力加速度大小C ．该实验中将自由落体运动改为在斜面上运动是为了缩短时间，便于测量位移D ．从图甲到图丁，通过逐渐增大斜面倾角，最后合理外推到自由落体运动，从而说明自由落体运动是初速度不为零的匀加速直线运动（ ） 【答案】A【详解】A ．运用图甲的实验，可“减弱”重力的作用，放大时间，便于观察，A 正确； B ．只有测量出图丁中相邻两小球球心位置之间的距离和各个小球位置之间的时间间隔T ，才能利用2x gT ∆=计算出重力加速度大小，只测量出图丁中相邻两小球球心位置之间的距离，不能计算出重力加速度大小，B 错误；C ．该实验中将自由落体运动改为在斜面上运动的设计思想是为了“放大”时间，便于测量时间，C 错误；D ．从图甲到图丁通过逐渐增大斜面倾角，最后合理外推到自由落体运动，从而说明自由落体运动是初速度为零的匀加速直线运动，D 错误。

故选A 。

2．（2022·新疆·博乐市高级中学（华中师大一附中博乐分校）模拟预测）将一乒乓球竖直向上抛出，乒乓球在运动过程中，它的动能随时间变化的关系的图线如图所示。

已知乒乓球运动过程中，受到的空气阻力与速率平方成正比，重力加速度为g 。

则乒乓球在整个运动过程中加速度的最小值、最大值为（ ）A ．0，4gB ．0，5gC ．g ，4gD ．g ，5g121mg kv =此时的动能m 5a g =故选B 。