小专题(一) 三角形三条重要线段的应用

第七章三角形本章小结小结1 本章概述三角形是几何知识中的重要内容，也是几何学的基础．本章从三角形出发，先学习与三角形有关的线段和角再到多边形，其中包括三角形的内角和、外角和及多边形的内角和等知识，最后到多边形的实际应用．小结2 本章学习重难点【本章重点】了解三角形的有关概念(内角、外角、中线、高、角平分线)；会画出任意三角形的角平分线、中线和高．【本章难点】通过探索平面图形的镶嵌，知道任意一个三角形、四边形或六边形可以镶嵌平面，并能运用这几种图形进行简单的镶嵌设计．【学习本章应注意的问题】正确理解三角形的有关概念，掌握有关性质．在学习中，要注意观察，搜集资料，多交流，注重新旧知识的联系，学会将新知识转化到已学的知识上去，再进行归纳、整理、分析，要深刻理解并掌握归纳、类比的方法．学习中，还要多注意结合图形，理解用多边形镶嵌图案的道理，欣赏丰富多彩的图案，体验数学美，提高审美情趣．小结3 中考透视本章知识在中考中所占比重较大，一方面以填空题、选择题形式出现，以考查对基本概念、基本定理的理解为主；另一方面以综合题形式出现，主要考查对知识的灵活运用及综合运用的能力，利用本章知识解决实际问题的题目也越来越多地出现在中考试题中，还有平面图形的镶嵌内容也是近年来的热点考题，备受关注．由于镶嵌问题具有较强的实用性，对知识的运用要求灵活性较高，所以要得到这类问题的分数也不是太容易的，分值占3～4分．知识网络结构图专题总结及应用一、知识性专题专题1 三角形的三条重要线段【专题解读】三角形的中线、角平分线和高是三角形的三条重要线段，它们具有十分重要的性质，三角形的高构造了垂直的条件，三角形的中线隐含线段相等，通过三角形的中线可以把三角形的面积分成相等的两部分，三角形的角平分线提供了角相等的条件.掌握这些概念,对解与三角形有关的问题十分重要.例1 如图7-64所示,D为△ABC中AC边上一点,AD=1,DC=2,AB=4,E是AB上一点,且△DEC的面积等于△ABC的面积的一半,求EB.分析已知△DEC的面积等于△ABC的面积的一半,在图形中, △DEC与△ABC既不同底也不等高,因此需寻找桥梁△AEC来建立二者之间的关系,因为△AEC既与△DEC等高也与△ABC等高.解:作EF⊥AC于F,则122132DECAECDC EFS DCS ACAC EF===,作CG⊥AB于点G,则12142AECABCAE CGS AE AES ABAB CG===,∴234DEC AECAEC ABCS S AES S=⨯,即6DECABCS AES=.又∵12DECABCSS=,∴162AE=,∴AE=3,∴BE=AB-AE=1,即BE的长为1.【解题策略】等高的两个三角形的面积比等于底边长的比,它是面积问题中常用的解题策略.专题2 多边形的内角和及外角和【专题解读】用三角形的内角和定理可以推出多边形的内角和定理及外角和定理,在推导的过程中体现了转化思想,在解有关多边形的问题时,如求多边形的内角、外角、边数及对角线等问题，这两个定理都很重要.例2 已知一个多边形的内角和与某个外角的度数的总和为1350°,求这个多边形的边数.分析应充分利用多边形每个外角在0°～180°间和等式的性质巧解此题.解:设这个多边形的这个外角为x,它的边数为n,则(n-2)·180°+x=1350°, ∴(n-2) ·180°=8×180°-(90°+x),由此可得90°+x是180°的倍数. ∵0°＜x＜180°,∴x=180°-90°=90°,∴(n-2) ·180°=7×180°,∴n=9.【解题策略】灵活运用多边形的内角和定理及外角和定理是解决此类问题的关键.二、规律方法专题专题3 用公式法解有关对角线的条数问题【专题解读】用n边形的对角线有(3)2n n-条来解决相关问题.例3 若一个多边形有77条对角线,求它的内角和.分析由(3)2n n-=77,求n.解:设这个多边形的边数为n,由题意,得(3)2n n-=77.解得n=14,即这个多边形是十四边形,十四边形的内角和为(14-2) ×180°=2160°,即内角和为2160°.【解题策略】根据对角线条数的公式(3)2n n -,即已知边数可求对角线的条数,反之已知对角线的条数,可求出边数.三、思想方法专题 专题4 转化思想 【专题解读】转化思想在本章中有很多的应用,主要体现在探索有关多边形的问题时经常转化为三角形的问题进行解决.例4 填表.分析 先由三角形的内角和为180°及外角和为360°逐一推广,将4,5,…,n 边形分割成若干个三角形,易得答案.解:填表如下.2011中考真题精选（2011陕西，12，3分）如图，AC ∥BD ，AE 平分∠BAC 交BD 于点E ，若︒=∠641， 则=∠2 ．考点：平行线的性质。

专题01三角形的三边、高线、中线及角平分线考点一三角形的稳定性考点二三角形的三边关系考点三三角形的高线考点四三角形的中线考点五三角形的角平分线考点一三角形的稳定性例题：（2021·广西·南宁十四中七年级期末）下列图形中没有运用三角形稳定性的是（）A．B．C．D．【答案】B【解析】【分析】利用三角形的稳定性解答即可．【详解】解：对于A、C、D选项，都含有三角形，故利用了三角形的稳定性；而B选项中，用到了四边形的不稳定性.故选B．【点睛】本题主要考查了三角形的稳定性，需理解稳定性在实际生活中的应用；明确能体现出三角形的稳定性，则说明物体中必然存在三角形是解题关键．【变式训练】1．（2022·吉林吉林·二模）如图，人字梯中间设计一“拉杆”，在使用梯子时，固定拉杆会增加安全性．这样做蕴含的数学道理是（）A．三角形具有稳定性B．两点之间线段最短C．经过两点有且只有一条直线D．垂线段最短【答案】A【解析】【分析】人字梯中间设计一“拉杆”后变成一个三角形，稳定性提高．【详解】三角形的稳定性如果三角形的三条边固定，那么三角形的形状和大小就完全确定了，三角形的这个特征，叫做三角形的稳定性.故选A【点睛】本题考查三角形的稳定性，理解这一点是本题的关键．2．（2022·广东·佛山市惠景中学七年级期中）如图所示的自行车架设计成三角形，这样做的依据是三角形具有___．【答案】稳定性【解析】【分析】根据是三角形的稳定性，即可求解．【详解】解：自行车的主框架采用了三角形结构，这样设计的依据是三角形具有稳定性，故答案为：稳定性．【点睛】本题考查的是三角形的性质，掌握三角形具有稳定性是解题的关键．考点二三角形的三边关系例题：（2022·黑龙江·哈尔滨市风华中学校七年级期中）下列各组长度的线段为边，能构成三角形的是（）．A．1，2，3B．3，4，5C．4，5，11D．6，3，3【答案】B【解析】【分析】比较三边中两较小边之和与较大边的大小即可得到解答．【详解】解：A、1+2=3，不符合题意；B、3+4>5，符合题意；C、4+5<11，不符合题意；D、3+3=6，不符合题意；故选B．【点睛】本题考查构成三角形的条件，熟练掌握三角形的三边关系是解题关键．【变式训练】1．（2022·黑龙江·哈尔滨市第六十九中学校七年级期中）下列各组长度的三条线段能够组成三角形的是（）A．3，4，8B．5，6，11C．5，6，10D．10，7，3【答案】C【解析】【分析】根据三角形三边关系可直接进行排除选项．【详解】解：A、3+4＜8，不符合三角形三边关系，故不能构成三角形；B、5+6=11，不符合三角形三边关系，故不能构成三角形；C、5+6＞10，符合三角形三边关系，故能构成三角形；D、3+7=10，不符合三角形三边关系，故不能构成三角形；故选C．【点睛】本题主要考查三角形三边关系，熟练掌握三角形三边关系是解题的关键．2．（2022·海南·海口市第十四中学七年级阶段练习）在△ABC中，三条边长分别为3和6，第三边长为奇数，那么第三边的长是()A．5或7B．7或9C．3或5D．9【答案】A【解析】【分析】先求出第三边长的取值范围，再根据条件具体确定符合条件的值即可．【详解】解：因为三条边长分别为3和6，所以6-3＜第三边＜6+3，所以3＜第三边＜9，因为第三边长为奇数，∴第三边的长为5或7，故选：A．【点睛】本题考查了三角形的三边关系，掌握三角形任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．3．（2022·江苏·南师附中新城初中七年级期中）已知三角形三边长分别为3，x，14，若x为正整数，则这样的三角形个数为（）A．4B．5C．6D．7【答案】B【解析】【分析】直接根据三角形的三边关系求出x的取值范围，进而可得出结论．【详解】解：三角形三边长分别为3，x，14，x<<．x143143∴-<<+，即1117x为正整数，12x=，13，14，15，16，即这样的三角形有5个．故选：B．【点睛】本题考查的是三角形的三边关系，熟知三角形两边之和大于第三边，两边之差小于第三边是解答此题的关键．考点三三角形的高线例题：（2022·重庆市育才中学七年级阶段练习）下列各组图形中，BD是ABC的高的图形是（）A．B．C．D．【答案】B【解析】【分析】三角形的高即从三角形的顶点向对边引垂线，顶点和垂足间的线段．根据概念即可得到答案．【详解】解：根据三角形高的定义可知，只有选项B中的线段BD是∴ABC的高，故选：B．【点睛】考查了三角形的高的概念，掌握高的作法是解题的关键．【变式训练】1．（2022·浙江杭州·中考真题）如图，CD ∴AB 于点D ，已知∴ABC 是钝角，则（ ）A ．线段CD 是ABC 的AC 边上的高线B ．线段CD 是ABC 的AB 边上的高线 C ．线段AD 是ABC 的BC 边上的高线D ．线段AD 是ABC 的AC 边上的高线【答案】B【解析】【分析】根据高线的定义注意判断即可．【详解】∴ 线段CD 是ABC 的AB 边上的高线，∴A 错误，不符合题意；∴ 线段CD 是ABC 的AB 边上的高线，∴B 正确，符合题意；∴ 线段AD 是ACD 的CD 边上的高线，∴C 错误，不符合题意；∴线段AD 是ACD 的CD 边上的高线，∴D 错误，不符合题意；故选B ．【点睛】 本题考查了三角形高线的理解，熟练掌握三角形高线的相关知识是解题的关键．2．（2022·湖南怀化·七年级期末）如图，在直角三角形ABC 中，90ACB ∠=︒，AC ＝3，BC ＝4，AB ＝5，则点C 到AB 的距离为______．【答案】125【解析】【分析】根据面积相等即可求出点C 到AB 的距离．【详解】解：∴在直角三角形ABC 中，90ACB ∠=︒， ∴1122AC BC AB CD ⨯=⨯， ∴AC ＝3，BC ＝4，AB ＝5， ∴1134522CD ⨯⨯=⨯⨯， ∴CD =125， 故答案为：125． 【点睛】本题考查求直角三角形斜边上的高，用面积法列出关系式是解题关键．3．（2022·重庆·七年级期中）如图，点A 、点B 是直线l 上两点，10AB =，点M 在直线l 外，6MB =，8MA =，90AMB ∠=︒，若点P 为直线l 上一动点，连接MP ，则线段MP 的最小值是______．【答案】4.8【解析】【分析】根据垂线段最短可知：当MP AB ⊥时，MP 有最小值，再利用三角形的面积可列式计算求解MP 的最小值．【详解】解：当MP AB ⊥时，MP 有最小值，10AB =，6MB =，8MA =，90AMB ∠=︒，AB MP AM BM ∴⋅=⋅，即1068MP =⨯，解得 4.8MP =．故答案为：4.8．【点睛】本题主要考查垂线段最短，三角形的面积，找到MP 最小时的P 点位置是解题的关键．考点四 三角形的中线例题：（2021·广西·靖西市教学研究室八年级期中）如图，已知BD 是∴ABC 的中线，AB ＝5，BC ＝3，且∴ABD 的周长为12，则∴BCD 的周长是_____．【答案】10【解析】【分析】先根据三角形的中线、线段中点的定义可得AD CD =，再根据三角形的周长公式即可求出结果．【详解】 解：BD 是ABC 的中线，即点D 是线段AC 的中点，AD CD ∴=，5AB =，ABD △的周长为12，12AB BD AD ∴++=，即512BD AD ++=，解得：7BD AD +=，7BD CD ∴+=，则BCD △的周长是3710BC BD CD ++=+=．故答案为：10．【点睛】本题主要考查了三角形的中线、线段中点的定义等知识点，掌握线段中点的定义是解题关键．【变式训练】1．（2022·陕西·西安市曲江第一中学七年级期中）在ABC 中，BC 边上的中线AD 将ABC 分成的两个新三角形的周长差为5cm ，AB 与AC 的和为11cm ，则AC 的长为________．【答案】3cm 或8cm【解析】【分析】根据三角形的中线的定义可得BD CD =，然后求出ABD △与ADC 的周长差是AB 与AC 的差或AC 与AB 的差，然后代入数据计算即可得解．【详解】如图1，图2，∴AD 是BC 边上的中线，∴BD CD =，∴中线AD 将ABC 分成的两个新三角形的周长差为5cm ，∴()()5AB BD AD AC CD AD ++-++=或()()5AC CD AD AB BD AD ++-++=，∴5AB AC -=或者5AC AB -=，∴AB 与AC 的和为11cm ，∴11AB AC +=，∴83AB AC =⎧⎨=⎩或38AB AC =⎧⎨=⎩， 故答案为：3cm 或8cm ．【点睛】本题考查了三角形的中线，熟记概念并求出两个三角形的周长的差等于两边长的差是解题的关键． 2．（2022·江苏·泰州市第二中学附属初中七年级阶段练习）如图，D ，E 分别是∴ABC 边AB ，BC 上的点，AD =2BD ，BE =CE ，设∴ADF 的面积为S 1，∴FCE 的面积为S 2，若S △ABC =16，则S 1－S 2的值为_________．【答案】8 3【解析】【分析】S△ADF−S△CEF＝S△ABE−S△BCD，所以求出三角形ABE的面积和三角形BCD的面积即可，因为AD＝2BD，BE＝CE，且S△ABC＝16，就可以求出三角形ABE的面积和三角形BCD的面积.【详解】解：∴BE＝CE，∴BE＝12BC，∴S△ABC＝16，∴S△ABE＝12S△ABC＝8．∴AD＝2BD，S△ABC＝16，∴S△BCD＝13S△ABC＝163，∴S△ABE−S△BCD＝（S1＋S四边形BEFD）−（S2＋S四边形BEFD）＝S1−S2＝83，故答案为83．【点睛】本题考查三角形的面积，关键知道当高相等时，面积等于底边的比，据此可求出三角形的面积，然后求出差．3．（2022·江苏·苏州市相城实验中学七年级期中）如图，AD 是∴ABC 的中线，BE 是∴ABD 的中线，EF ⊥BC于点F．若24ABCS=，BD =4，则EF 长为___________．【答案】3【解析】【分析】因为S △ABD =12S △ABC ，S △BDE =12S △ABD ；所以S △BDE =14S △ABC ，再根据三角形的面积公式求得即可． 【详解】解：∴AD 是∴ABC 的中线，S △ABC =24，∴S △ABD =12S △ABC =12，同理，BE 是∴ABD 的中线，612BDE ABD SS ==，∴S △BDE =12BD •EF ，∴12BD •EF =6，即1462EF ⨯⨯= ∴EF =3．故答案为：3．【点睛】此题考查了三角形的面积，三角形的中线特点，理解三角形高的定义，根据三角形的面积公式求解，是解题的关键．考点五 三角形的角平分线 例题：（2022·全国·八年级）如图，在ABC 中，90CAB ∠=︒，AD 是高，CF 是中线，BE 是角平分线，BE 交AD 于G ，交CF 于H ，下列说法正确的是（ ）①AEG AGE ∠=∠；②BH CH =；③2EAG EBC ∠=∠；④ACF BCF S S =A．①③B．①②③C．①③④D．②③④【答案】C【解析】【分析】①根据∴CAB=90°，AD是高，可得∴AEG=90°−∴ABE，∴DGB=90°−∴DBG，又因为BE是角平分线，可得∴ABE=∴DBE，故能得到∴AEG=∴DGB，再根据对顶角相等，即可求证该说法正确；②因为CF是中线，BE是角平分线，得不到∴HCB=∴HBC，故该说法错误；③∴EAG+∴DAB=90°，∴DBA+∴DAB=90°，可得∴EAG=∴DBA，因为∴DBA=2∴EBC，故能得到该说法正确；④根据中线平分面积，可得该说法正确．【详解】解：①∴∴CAB=90°，AD是高，∴∴AEG=90°−∴ABE，∴DGB=90°−∴DBG，∴BE是角平分线，∴∴ABE=∴DBE，∴∴AEG=∴DGB，∴∴DGB=∴AGE，∴∴AEG=∴AGE，故该说法正确；②因为CF是中线，BE是角平分线，得不到∴HCB=∴HBC，故该说法错误；③∴∴EAG+∴DAB=90°，∴DBA+∴DAB=90°，∴∴EAG=∴DBA，∴∴DBA=2∴EBC，∴∴EAG=2∴EBC，故该说法正确；④根据中线平分面积，可得S△ACF=S△BCF，故该说法正确．故选：C．【点睛】本题考查了三角形的高，中线，角平分线的性质，解题的关键是熟练掌握各线的特点和性质．【变式训练】1．（2022·全国·八年级）如图，在∴ABC中，∴C＝90°，D，E是AC上两点，且AE＝DE，BD平分∴EBC，那么下列说法中不正确的是（）A．BE是∴ABD的中线B．BD是∴BCE的角平分线C．∴1＝∴2＝∴3D．S△AEB＝S△EDB【答案】C【解析】【分析】根据三角形中线、角平分线的定义逐项判断即可求解．【详解】解：A、∴AE＝DE，∴BE是∴ABD的中线，故本选项不符合题意；B、∴BD平分∴EBC，∴BD是∴BCE的角平分线，故本选项不符合题意；C、∴BD平分∴EBC，∴∴2＝∴3，但不能推出∴2、∴3和∴1相等，故本选项符合题意；D、∴S△AEB＝12×AE×BC，S△EDB＝12×DE×BC，AE＝DE，∴S△AEB＝S△EDB，故本选项不符合题意；故选：C【点睛】本题主要考查了三角形中线、角平分线的定义，熟练掌握三角形中，连接一个顶点和它的对边的中点的线段叫做三角形的中线；三角形的一个角的平分线与这个角的对边相交，连接这个角的顶点和交点的线段叫三角形的角平分线是解题的关键．2．（2022·全国·八年级）如图，AD，BE，CF依次是ABC的高、中线和角平分线，下列表达式中错误的是（ ）A ．AE ＝CEB ．∴ADC ＝90° C ．∴CAD ＝∴CBE D ．∴ACB ＝2∴ACF【答案】C【解析】【分析】 根据三角形的高、中线和角平分线的定义（1）三角形的角平分线定义：三角形的一个角的平分线与这个角的对边相交，连接这个角的顶点和交点的线段叫做三角形的角平分线；（2）三角形的中线定义：在三角形中，连接一个顶点和它所对边的中点的连线段叫做三角形的中线；（3）三角形的高定义：从三角形一个顶点向它的对边（或对边所在的直线）作垂线，顶点和垂足间的线段叫做三角形的高线，简称为高．求解即可．【详解】解：A 、BE 是△ABC 的中线，所以AE ＝CE ，故本表达式正确；B 、AD 是△ABC 的高，所以∴ADC ＝90，故本表达式正确；C 、由三角形的高、中线和角平分线的定义无法得出∴CAD ＝∴CBE ，故本表达式错误；D 、CF 是△ABC 的角平分线，所以∴ACB ＝2∴ACF ，故本表达式正确．故选：C ．【点睛】本题考查了三角形的高、中线和角平分线的定义，是基础题，熟记定义是解题的关键．3．（2021·全国·八年级课时练习）填空：（1）如图（1）,,AD BE CF 是ABC 的三条中线，则2AB =______，BD =______，12AE =______． （2）如图（2）,,AD BE CF 是ABC 的三条角平分线，则1∠=______，132∠=______，2ACB ∠=______．【答案】 AF 或BF CD AC 2∠ ABC ∠ 4∠【解析】【分析】（1）根据三角形的中线定义：三角形一边的中点与此边所对顶点的连线叫做三角形的中线可得E 、F 、D 分别是AC 、AB 、BC 上的中点，进而得到答案．（2）根据角平分线定义，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线即可解答．【详解】解：（1）∴CF 是AB 边上的中线，∴AB ＝2AF ＝2BF ；∴AD 是BC 边上的中线，∴BD ＝CD ，∴BE 是AC 边上的中线，∴AE ＝12AC ，（2）∴AD 是BAC ∠的角平分线，∴12∠=∠ ，∴BE 是ABC ∠的角平分线， ∴132∠=ABC ∠， ∴CF 是ACB ∠的角平分线，∴2ACB ∠=4∠．故答案为：AF 或BF ；CD ；AC ；2∠；ABC ∠；4∠【点睛】此题主要考查了三角形的中线、角平分线，解题的关键是掌握三角形的中线及角平分线的定义．一、选择题1．（2022·黑龙江·哈尔滨市风华中学校七年级期中）画ABC的BC边上的高，正确的是（）A．B．C．D．【答案】A【解析】【分析】利用三角形的高线的定义判断即可．【详解】解：画△ABC的BC边上的高，即过点A作BC边的垂线．∴只有选项A符合题意，故选：A．【点睛】本题考查了三角形高线的画法，从三角形的一个顶点向对边作垂线，顶点与垂足间的线段，叫做三角形的高线，锐角三角形的三条高线都在三角形的内部，钝角三角形的高有两条在三角形的外部．直角三角形的高线有两条是三角形的直角边．2．（2022·山东潍坊·七年级期末）在数学实践课上，小亮经研究发现：在如图所示的ABC中，连接点A和BC上的一点D，线段AD等分ABC的面积，则AD是ABC的（）．A．高线B．中线C．角平分线D．对角线【答案】B【解析】【分析】直接利用三角形中线的性质即可得出结果．【详解】解：∴线段AD等分∴ABC的面积，∴∴ABD的面积等于∴ACD的面积，∴两个三角形的高为同一条高，∴BD=CD，∴AD为∴ABC的中线，故选：B．【点睛】题目主要考查三角形中线的性质，理解三角形中线将三角形分成两个面积相同的三角形是解题关键．3．（2022·河北保定外国语学校一模）能用三角形的稳定性解释的生活现象是（）A．B．C．D．【答案】C【解析】【分析】根据各图所用到的直线、线段有关知识，即可一一判定【详解】解：A、利用的是“两点确定一条直线”，故该选项不符合题意；B、利用的是“两点之间线段最短”，故该选项不符合题意；C、窗户的支架是三角形，利用的是“三角形的稳定性”，故该选项符合题意；D、利用的是“垂线段最短”，故该选项不符合题意；故选：C【点睛】本题考查了两点确定一条直线、两点之间线段最短、三角形的稳定性、垂线段最短的应用，结合题意和图形准确确定所用到的知识是解决本题的关键．4．（2022·山东青岛·七年级期末）如图，BD是ABC的边AC上的中线，AE是ABD△的边BD上的中线，BF 是ABE△的边AE上的中线，若ABC的面积是32，则阴影部分的面积是（）A．9B．12C．18D．20【答案】B【解析】【分析】利用中线等分三角形的面积进行求解即可．【详解】∴BD是ABC的边AC上的中线，∴11321622ABD BCD ABCS S S===⨯=△△，∴AE是ABD△的边BD上的中线，∴1116822ABE ADE ABDS S S===⨯=，又∴BF 是ABE △的边AE 上的中线，则CF 是ACE 的边AE 上的中线， ∴118422BEF ABF ABE S S S ===⨯=，182CEF ACF ADE CED ACE S S S S S =====，则4812BEF CEF S SS =+=+=阴影，故选：B ．【点睛】 本题考查了中线的性质，清晰明确三角形之间的等量关系，进行等量代换是解题的关键．5．（2021·江苏·无锡市侨谊实验中学三模）如图为一张锐角三角形纸片ABC ，小明想要通过折纸的方式折出如下线段：①BC 边上的中线AD ，②BC 边上的角平分线AE ，③BC 边上的高AF ．根据所学知识与相关活动经验可知：上述三条线中，所有能够通过折纸折出的有（ ）A ．①②B ．①③C ．②③D ．①②③【答案】D【解析】【分析】 根据三角形中线，角平分线和高的定义即可判断．【详解】沿着A 点和BC 中点的连线折叠，其折痕即为BC 边上的中线，故①符合题意；折叠后使B 点在AC 边上，且折痕通过A 点，则其折痕即为BC 边上的角平分线，故②符合题意； 折叠后使B 点在BC 边上，且折痕通过A 点，则其折痕即为BC 边上的高，故③符合题意；故选D ．【点睛】本题考查三角形中线，角平分线和高的定义．掌握各定义是解题关键．二、填空题6．（2022·湖南邵阳·八年级期末）若ABC 的三条边长分别为3cm ，xcm ，4cm ，则x 的取值范围______．【答案】17x <<##71x >>【解析】【分析】根据三角形的三边关系进行求解即可.【详解】解：根据“三角形任意两边之和大于第三边，任意两边之差小于第三边”可得到4343x －＜＜＋，∴17x ＜＜.故答案为：17x ＜＜.【点睛】本题主要考查三角形三边关系，熟记“三角形任意两边之和大于第三边，任意两边之差小于第三边”是解答此类题目的关键.7．（2022·云南红河·八年级期末）已知a b c 、、是ABC ∆的三边长，a b 、满足()2610a b -+-=，c 为偶数，则c =_______．【答案】6【解析】【分析】根据非负数的性质列式求出a 、b 的值，再根据三角形的任意两边之和大于第三边，两边之差小于第三边求出c 的取值范围，再根据c 是偶数求出c 的值．【详解】解：∴a ，b 满足()2610a b -+-=，∴a -6=0，b -1=0，解得a =6，b =1，∴6-1=5，6+1=7，∴5＜c ＜7，又∴c 为偶数，∴c =6，故答案为：6【点睛】本题考查非负数的性质：偶次方，解题的关键是明确题意，明确三角形三边的关系．8．（2021·北京市陈经纶中学分校八年级期中）随着人们物质生活的提高，手机成为一种生活中不可缺少的东西，手机很方便携带，但唯一的缺点就是没有固定的支点．为了解决这一问题，某工厂研制生产了一种如图所示的手机支架．把手机放在上面就可以方便地使用手机，这是利用了三角形的______.【答案】三角形的稳定性【解析】【分析】利用三角形的稳定性的性质直接回答即可．【详解】解：把手机放在上面就可以方便地使用手机，这是利用了三角形的稳定性，故答案为：三角形的稳定性．【点睛】本题考查了三角形的稳定性，解题的关键是掌握三角形具有稳定性．9．（2022·北京市师达中学七年级阶段练习）如图，AB∴BD 于点B，AC∴CD 于点C，且AC 与BD 交于点E，已知AE=10，DE=5，CD=4，则AB 的长为_________．【答案】8【解析】【分析】根据三角形高的定义可判断出边上的高，然后利用三角形面积求解即可．【详解】解：∴AB∴BD，AC∴CD，∴AB是∴ADE的边DE上的高，CD是边AE上的高，∴S △AED =1122DE AB AE CD ⋅=⋅， ∴10485AE CD AB DE ⋅⨯===， 故答案为：8．【点睛】本题考查三角形高的定义，三角形的面积等知识，掌握基本概念是解题关键，学会用面积法求线段的长． 10．（2022·全国·八年级专题练习）如图，在ABC 中，2AB AC ==，P 是BC 边上的任意一点，PE AB ⊥于点E ，PF AC ⊥于点F .若ABC S =PE PF +=______．【解析】【分析】 根据1122ABC ABP APC S S S AB PE AC PF =+=⋅+⋅，结合已知条件，即可求得PE PF +的值． 【详解】解：如图，连接APPE AB ⊥于点E ，PF AC ⊥于点F1122ABC ABP APC S S S AB PE AC PF ∴=+=⋅+⋅2AB AC ==，ABC S ∴1122AB PE AC PF ⋅+⋅PE PF =+【点睛】本题考查了三角形的高，掌握三角形的高的定义是解题的关键．三、解答题11．（2022·全国·八年级）在∴ABC中，BC＝8，AB＝1；(1)若AC是整数，求AC的长；(2)已知BD是∴ABC的中线，若∴ABD的周长为17，求∴BCD的周长．【答案】(1)8(2)24【解析】【分析】（1）根据三角形三边关系“两边之和大于第三边，两边之差小于第三边”得7＜AC＜9，根据AC是整数得AC＝8；（2）根据BD是∴ABC的中线得AD＝CD，根据∴ABD的周长为17和AB＝1得AD+BD＝16，即可得．(1)解：由题意得：BC﹣AB＜AC＜BC+AB，∴7＜AC＜9，∴AC是整数，∴AC＝8．(2)解：如图所示，∴BD是∴ABC的中线，∴AD＝CD，∴∴ABD的周长为17，∴AB+AD+BD＝17，∴AB ＝1，∴AD +BD ＝16，∴∴BCD 的周长＝BC +BD +CD ＝BC +AD +CD ＝8+16＝24．【点睛】本题考查了三角形，解题的关键是掌握三角形三边的关系和三角形的中线．12．（2022·全国·八年级专题练习）已知：a 、b 、c 满足2(|0a c +-=求：(1)a 、b 、c 的值；(2)试问以a 、b 、c 为边能否构成三角形？若能构成三角形，求出三角形的周长；若不能构成三角形，请说明理由．【答案】(1)a =5b =，c =(2)能构成三角形，周长为(51【解析】【分析】（1）根据非负数之和等于零，则每个非负数等于零，分别建立方程求解即可；（2）先比较长三边的大小，再用较小两边之和与最大边比较即可判断能够构成三角形；然后计算三角形的周长即可．(1)解：∴(20a ≥0，0c -≥，a 、b 、c 满足(20a c -=，∴0a =，50b -=，0c -，解得a =5b =，c =；(2)解：∴81825<<，∴5，即a c b <<，∴5=>，∴能构成三角形，三角形的周长)5551a b c =++===． 【点睛】 本题考查了非负数的性质，二次根式有意义的条件和构成三角形的条件，解题的关键是根据非负数之和等于零的条件分别建立方程和如何判定三边能否构成三角形．13．（2022·四川·威远中学校七年级期中）（1）已知一个三角形的两边长分别是4cm 、7cm ，则这个三角形的周长的取值范围是什么？（2）在等腰三角形ABC 中，AB ＝AC ，周长为14cm ，BD 是AC 边上的中线，△ABD 比△BCD 周长长4cm ，求△ABC 各边长．【答案】（1）14<c <22；（2）AB =6，AC =6，BC =2．【解析】【分析】（1）根据三角形三边关系，先求出三角形第三边长的范围，即可求出周长范围．（2）根据三角形中线的定义可得,AD CD =，从而可得4,AB BC -=再根据ABC 的周长是14，，以及,AB AC ＝，可得214AB BC +=进行计算即可解答．【详解】解：（1）设第三边长为x ，根据三角形的三边关系得7474,x ∴-<<+3,x ∴<<11∴三角形的周长C 的取值范围为：1422.c <<（2）如图所示：∴BD 是AC 边上的中线，,AD CD ∴=∴△ABD比△BCD周长长4cm，()()4,AB AD BD BC CD BD∴++-++=4,AB BC∴-=4,BC AB∴=-ABC的周长是14，14,AB AC BC∴++=,AB AC＝214,AB BC∴+=2414,AB AB∴+-=6,AB∴=6,AB AC∴==2.BC∴=【点睛】本题主要考查了三角形三边关系，等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．14．（2022·河北邯郸·七年级阶段练习）如图，在直角三角形ABC中，∴BAC＝90°，AD是BC边上的高，CE 是AB边上的中线，AB＝12cm，BC＝20cm，AC＝16cm，求：（1）AD的长；（2）∴BCE的面积．【答案】（1）485；（2）48．【解析】【分析】（1）利用面积法得到12AD•BC＝12AB•AC，然后把AB＝12cm，BC＝20cm，AC＝16cm代入可求出AD的长；（2）由于三角形的中线将三角形分成面积相等的两部分，所以S△BCE＝12S△ABC．【详解】解：（1）∴∴BAC ＝90°，AD 是BC 边上的高， ∴12AD •BC ＝12AB •AC ，∴AD ＝121620⨯＝485（cm ）；（2）∴CE 是AB 边上的中线，∴S △BCE ＝12S △ABC ＝12×12×12×16＝48（cm 2）．【点睛】本题考查三角形中线的性质，涉及等积法，是重要考点，掌握相关知识是解题关键．15．（2022·黑龙江·哈尔滨市风华中学校七年级期中）如图，在6×10的网格中，每一小格均为正方形且边长是1，已知∴ABC 的每个顶点都在格点上．(1)画出∴ABC 中BC 边上的高线AE ；(2)在∴ABC 中AB 边上取点D ，连接CD ，使3BCD ACD S S =△△；(3)直接写出∴BCD 的面积是__________．【答案】(1)画图见解析(2)画图见解析(3)7.5【解析】【分析】（1）利用网格线过A 作BC 的垂线即可；（2）利用网格线的特点，取格点D ，满足3BD AD =，则D 即为所求作的点；（3）利用三角形的面积公式直接计算即可．(1)解：如图，AE 即为BC 上的高．(2)如图，利用网格特点，可得3BD AD =，∴D 即为所求作的点，满足3BCD ACD S S =△△．(3)1537.52BCD S =⨯⨯=． 【点睛】本题考查的是画三角形的高，三角形的面积的计算，熟悉等高的两个三角形的面积之间的关系是解本题的关键．16．（2022·江苏·沭阳县怀文中学七年级阶段练习）如图，在ABC 中，CD 、CE 分别是ABC 的高和角平分线，,()BAC B ∠α∠βαβ==>．(1)若70,40αβ=︒=︒，求DCE ∠的度数；(2)试用α、β的代数式表示DCE ∠的度数_________．【答案】(1)15DCE ∠=︒(2)2αβ-【解析】【分析】（1）根据三角形的内角和定理求出∴ACB 的值，再由角平分线的性质以及直角三角形的性质求出∴DCE ． （2）由（1）的解题思路即可得正确结果．(1) 解：70BAC ∠=︒，40B ∠=︒∴()180()180704070ACB BAC B ∠=︒-∠+∠=︒-︒+︒=︒，CE 是ACB ∠的平分线，∴1352ACE ACB ∠=∠=︒． CD 是高线，∴90ADC ∠=︒，∴9020ACD BAC ∠=︒-∠=︒，∴352015DCE ACE ACD ∠=∠-∠=︒-=︒︒．(2) 解：BAC α∠=，B β∠=∴()180()180ACB BAC B αβ∠=︒-∠+∠=︒-+，CE 是ACB ∠的平分线，∴()1118090222ACE ACB αβαβ+∠=∠=⨯︒-+=︒-⎡⎤⎣⎦． CD 是高线，∴90ADC ∠=︒，∴9090ACD BAC α∠=︒-∠=︒-， ∴909022DCE ACE ACD αβαβα+-∠=∠-∠=︒--︒+=．【点睛】本题主要考查角平分线，高线以及角的转换，掌握角平分线，高线的性质是解题的关键．17．（2022·上海·八年级专题练习）如图，∴ABC 中，∴BAC ＝60º，AD 平分∴BAC ，点E 在AB 上，EG ∴AD ， EF ∴AD ，垂足为F ．(1)求∴1和∴2的度数．(2)联结DE ，若S △ADE ＝S 梯形EFDG ，猜想线段EG 的长和AF 的长有什么关系？说明理由．【答案】(1)30º；60º(2)相等，理由见解析【解析】【分析】(1)利用角平分线的定义求得BAD ∠，然后在直角三角形中利用两锐角互余即可求得∴2，再利用平行线的性质即可求得∴1的度数．(2)根据S △ADE ＝S 梯形EFDG 可得AD =DF +EG ，结合图形即可求解．(1)∴∴BAC ＝60º，AD 平分∴BAC ， ∴1302BAD BAC ∠=∠=︒， 又∴EF ∴AD ，∴29060BAD ∠=︒-∠=︒， ∴EG ∴AD ，∴130BAD ∠=∠=︒．(2)相等． 理由如下： ∴EF ∴AD ，∴S △ADE =12AD EF ⋅，S 梯形EFDG =1()2DE EG EF +⋅ ∴S △ADE = S 梯形EFDG ∴12AD EF ⋅=1()2DE EG EF +⋅∴AD =DF +EG ，∴AD =AF +DF ，∴DF +EG =AF +DF ，即AF =EG ．【点睛】本题考查了平行线的性质，角平分线的定义以及三角形和梯形的面积公式，熟练掌握平行线的性质和角平分线的定义是解题的关键．18．（2021·安徽省六安皋城中学八年级期中）如图，AD 是∴ABC 的边BC 上的中线，已知AB =5，AC =3． （1）边BC 的取值范围是 ；（2）∴ABD 与∴ACD 的周长之差为 ；（3）在∴ABC 中，若AB 边上的高为2，求AC 边上的高．【答案】（1）28BC <<；（2）2；（3）103h =． 【解析】【分析】 （1）直接根据三角形三边关系进行解答即可；（2）根据三角形中线将∴ABD 与∴ACD 的周长之差转换为AB 和AC 的差即可得出答案；（3）设AC 边上的高为h ，根据三角形面积公式列出方程求解即可．【详解】解：（1）∴∴ABC 中AB =5，AC =3，∴5353BC -<<+，即28BC <<，故答案为：28BC <<；（2）∴∴ABD 的周长为AB AD BD ++，∴ACD 的周长为AC AD CD ++，∴AD 是∴ABC 的边BC 上的中线，∴BD CD =，∴AB AD BD ++-(AC AD CD ++)=532AB AC -=-=，故答案为：2；（3）设AC 边上的高为h ， 根据题意得：11222AB AC h ⨯=⨯, 即1152322h ⨯⨯=⨯⨯， 解得103h =． 【点睛】本题考查了三角形三边关系，三角形的中线，三角形的高等知识点，熟练掌握基础知识是解本题的关键．。

八上同步跟踪复习专题1：三角形三边关系的应用我们知道：三角形任意两边之和大于第三边；三角形任意两边之差小于第三边。

上面结论证明的依据是：两点之间，线段最短。

利用这两个关系有如下应用，现举例说明：一、基本应用（一）确定三条线段能否构成三角形（常用技巧：先确定最大边，看两短线段和是否大于较长线段）例1 下列长度的三根木棒首尾相接，不能做成三角形框架的是（）A.5cm、7cm、10cmB.7cm、10cm、13cmC.5cm、7cm、13cmD.5cm、10cm、13cm例2 已知五条线段的长分别为1cm，2cm，3cm，4cm，5cm，以其中三条线段为边长可以组成个三角形。

例3 有下列长度的三条线段能否组成三角形？（1）a－3，a，3(其中a＞3)；（2）a，a＋4，a＋6(其中a＞0)；（3）a＋1，a＋1，2a(其中a＞0)。

（二）已知两边，确定三角形第三边的取值范围（常用技巧：另两边的差<任一边<另两边的和）例4 用三条绳子打结成三角形(不考虑结头长)，已知其中两条长分别是3m和7m，问第三条绳子的长有什么限制？例5 （1）已知三角形的三边长分别是2，x，13，则这样的三角形个数为（）A.2B.3C.5D.13（2）三角形的三边分别为3，a21 ，8，求a的取值范围。

（三）求三角形某一边的长度（或周长）问题（注意此类问题中往往有陷阱）例6 （1）一个等腰三角形的两边分别是2厘米和9厘米，则第三边长为厘米。

（2）已知等腰三角形的一边等于5，另一边等于6，则它的周长等于。

例7 已知等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分，求这个三角形的腰长。

简析：如图1，设腰AB=xcm，底BC=ycm，D为AC边的中点.根据题意，得x+12x＝12，且y+12x＝21；或x+12x ＝21，且y+12x ＝12。

解得x ＝8，y ＝17；或x ＝14，y ＝5。

显然当x=8，y=17时，8＋8＜17不符合定理，应舍去。

期中考点专题01 三角形的基础重点突破三角形的概念：由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。

三角形特性三角形用符号“”表示，顶点是A、B、C的三角形记作“ABC”，读作“三角形ABC”。

三角形按边分类：等腰三角形：有两条边相等的三角形叫做等腰三角形，其中相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰与底边的夹角叫做底角。

等边三角形：底边与腰相等的等腰三角形叫做等边三角形，即三边都相等。

三角形三边的关系（重点（1）三角形的随意两边之和大于第三边。

三角形的随意两边之差小于第三边。

（这两个条件满意其中一个即可）用数学表达式表达就是：记三角形三边长分别是a，b，c，则a＋b＞c或c－b＜a。

（2）已知三角形两边的长度分别为a，b，求第三边长度的范围：|a－b|＜c＜a＋b三角形的分类：三角形按边的关系分类如下：三角形按角的关系分类如下：三角形的稳定性➢三角形具有稳定性➢四边形及多边形不具有稳定性要使多边形具有稳定性，方法是将多边形分成多个三角形，这样多边形就具有稳定性了。

考查题型考查题型一三角形的个数问题典例1．（2024·西林县期中）如图所示，其中三角形的个数是（）A．2个B．3个C．4个D．5个【答案】D【提示】依据三角形的定义解答即可，由不在同始终线上的三条线段首尾顺次相接所组成的图形叫做三角形.【详解】图中的三角形有：△ABC，△BCD，△BCE，△ABE，△CDE共5个.故选D.【名师点拨】本题考查了三角形的概念，由不在同始终线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边，相邻边的公共端点叫做三角形的顶点.相邻两条边组成的角，叫做三角形的内角，简称为三角形的角.变式1-1．（2024·秦皇岛市期中）图中三角形的个数是（）A．3个B．4个C．5个D．6个【答案】D【解析】图中的三角形有: △ABD, △ADE, △AEC, △ABE, △ADC, △ABC,共6个.故选D.变式1-2．（2024·洛阳市期末）图中三角形的个数是（）A．4个B．6个C．8个D．10个【答案】C【提示】依据三角形的定义即可得．【详解】图中的三角形是，共8个故选：C．【名师点拨】本题考查了三角形的定义，驾驭理解三角形的概念是解题关键．变式1-3．（2024·恩施市期中）如图，图中三角形的个数有（）A．6个B．8个C．10个D．12个【答案】B【解析】试题解析：以O为一个顶点的有△CBO、△CDO、△ABO、△ADO，不以O为顶点的三角形有△CAD、△CBA、△BCD、△BAD，共有8个．故选B.考查题型二三角形的分类典例2（2024·石家庄市期末）在△ABC中，∠A=20°，∠B=60°，则△ABC的形态是（）A．等边三角形 B．锐角三角形C．直角三角形 D．钝角三角形【答案】D【解析】试题提示：依据三角形的内角和定理求出∠C，即可判定△ABC的形态．解：∵∠A=20°，∠B=60°，∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°，∴△ABC是钝角三角形．故选D．变式2-1．（2024·黄冈市期中）一个三角形三个内角的度数之比为1：2：3，则这个三角形肯定是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰直角三角形【答案】B【解析】试题提示：依据三角形的内角和为180°，可知最大角为90°，因式这个三角形是直角三角形.故选B.变式2-2．（2024·深圳市期中）在△ABC中，若∠A：∠B：∠C＝1：3：5，则△ABC是（）A．锐角三角形B．直角三角形C．钝角三角形D．形态不确定【答案】C【提示】依据∠A：∠B：∠C=1：3：5，可设∠A=x°，∠B=3x°，∠C=5x°，再依据三角形内角和为180°可得方程x+3x+5x=180，解方程算出x的值，即可推断出△ABC的形态．【详解】解：∵∠A：∠B：∠C=1：3：5，∴设∠A=x°，∠B=3x°，∠C=5x°，∴x+3x+5x=180，解得：x=20，∴∠C=5×20°=100°，∴△ABC是钝角三角形．故选：C．【名师点拨】本题考查三角形内角和定理，关键是利用方程思想列出三个角的关系式．变式2-3．（2024·石家庄市期末）下面给出的四个三角形都有一部分被遮挡，其中不能确定三角形类型的是（）A．B．C．D．【答案】A【提示】依据三角形按角分类的方法一一推断即可．【详解】视察图象可知：选项B，D的三角形是钝角三角形，选项C中的三角形是锐角三角形，选项A中的三角形无法判定三角形的类型．故选A．【名师点拨】本题考查了三角形的分类，解题的关键是娴熟驾驭基本学问，属于中考常考题型．考查题型三构成三角形的条件典例3．（2024·宜兴市期末）下列各组线段不能组成三角形的是 ( )A．4cm、4cm、5cm B．4cm、6cm、11cmC．4cm、5cm、6cm D．5cm、12cm、13cm【答案】B【提示】依据三角形的随意两边之和大于第三边对各选项提示推断后利用解除法求解.【详解】A 、4485+=>，∴445cm cm cm 、、能组成三角形，故本选项错误；B 、461011+=<，∴4611cm cm cm 、、不能组成三角形，故本选项正确；C 、5496+=>，∴456cm cm cm 、、能组成三角形，故本选项错误；D 、5121713+=>，∴51213cm cm cm 、、能组成三角形，故本选项错误.故选：B .【名师点拨】本题考查了三角形的三边关系，是基础题，熟记三边关系是解题的关键.变式3-1．（2024·太仓市）等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（ ）A ．12B ．15C ．12或15D ．18【答案】B【解析】试题提示：依据题意，要分状况探讨：①、3是腰；②、3是底．必需符合三角形三边的关系，随意两边之和大于第三边．解：①若3是腰，则另一腰也是3，底是6，但是3+3=6，∴不构成三角形，舍去．②若3是底，则腰是6，6．3+6＞6，符合条件．成立．∴C=3+6+6=15．故选B ．变式3-2．（2024·兰州市期末）等腰三角形的一边长为4，另一边长为9，则这个三角形的周长为( )A ．22B ．17C ．13D ．17或22【答案】A【提示】分4是腰长和底边两种状况探讨求解即可．【详解】解：4是腰长时，三角形的三边分别为4、4、9，∵4+4=8＜9，∴不能组成三角形，4是底边时，三角形的三边分别为4、9、9，能组成三角形，周长=4+9+9=22，综上所述，该等腰三角形的周长为22．故选A ．【名师点拨】本题主要考查了三角形三边关系，难点在于分状况探讨并利用三角形的三边关系推断是否能组成三角形．cm cm长的两根木棒首尾相接成一个三角形的变式3-3．（2024·哈尔滨市期中）下列长度的四根木棒中，能与49，是（）A．4cm B．5cm C．9cm D．13cm【答案】C【提示】依据三角形三边关系：三角形随意两边之和大于第三边，逐一推断选项，即可.【详解】∵4+4<9，cm cm长的木棒首尾相接，不能组成三角形，∴4cm，49，∴A错误；∵5+4=9，cm cm长的木棒首尾相接，不能组成三角形，∴5cm，49，∴B错误；∵9+4>9，cm cm长的木棒能组成三角形，∴9cm，49，∴C正确；∵4+9=13，cm cm长的木棒，不能组成三角形，∴13cm，49，∴D错误；故选C.【名师点拨】本题主要考查三角形的三边关系，驾驭“三角形随意两边之和大于第三边”，是解题的关键.m-=，且m，n恰好是等腰△ABC的两条边的边长，变式3-4．（2024·濮阳市期末）若实数m，n满意20则△ABC的周长是( )A．12 B．8 C．10 D．10或8【答案】C【提示】依据非负数的性质求出,m n的值，依据等腰三角形的性质求解即可.m-=【详解】20m n∴==2,4,当三角形的腰长为2时，224+=，构不成三角形；++=.当三角形的腰长为4时，三角形的周长为：44210故答案选：C.【名师点拨】考查非负数的性质以及等腰三角形的性质，驾驭三角形的三边关系是解题的关键.考查题型四三角形第三边的取值范围典例4．（2024·三明市期末）已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）A．1 B．2 C．8 D．11【答案】C【提示】依据三角形两边之和大于第三边，两边之差小于第三边可确定出第三边的范围，据此依据选项即可推断. 【详解】设第三边长为x，则有7-3<x<7+3，即4<x<10，视察只有C选项符合，故选 C.【名师点拨】本题考查了三角形三边的关系，娴熟驾驭三角形三边之间的关系是解题的关键.a的三条线段能组成一个三角形，则a的值可以是（）变式4-1．（2024·龙岩市期中）若长度分别为,3,5A．1 B．2 C．3 D．8【答案】C【提示】依据三角形三边关系可得5﹣3＜a＜5+3，解不等式即可求解．【详解】由三角形三边关系定理得：5﹣3＜a＜5+3，即2＜a＜8，由此可得，符合条件的只有选项C，故选C．【名师点拨】本题考查了三角形三边关系，能依据三角形的三边关系定理得出5﹣3＜a＜5+3是解此题的关键，留意：三角形的两边之和大于第三边，三角形的两边之差小于第三边．变式4-2．（2024·齐齐哈尔市期末）已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为A．2 B．3 C．5 D．13【答案】B【提示】依据“三角形两边之和大于第三边, 两边之差小于第三边”，可得x的取值范围，一一推断可得答案. 【详解】解：依据“三角形两边之和大于第三边, 两边之差小于第三边”可得:13-2<x<13+2,即11<x<15,因为取正整数,故x的取值为12、13、14,即这样的三角形共有3个.故本题正确答案为B.【名师点拨】本题主要考查构成三角形的三边的关系.变式4-3．（2024·广州市期中）一个三角形的两边长为3和8，第三边长为奇数，则第三边长为（）A ．5或7B ．7或9C ．7D ．9【答案】B 【详解】依据三角形三边关系可得：5＜第三边＜11，依据第三边长为奇数，则第三边长为7或9．故选B.考查题型五 三角形三边关系的应用典例5．（2024·德州市期末）已知三角形的两边分别为1和4，第三边长为整数 ，则该三角形的周长为（ ）A ．7B ．8C ．9D ．10【答案】C【提示】依据三角形的三边关系“第三边大于两边之差，而小于两边之和”，求得第三边的取值范围；再依据第三边是整数，从而求得周长．【详解】设第三边为x ，依据三角形的三边关系，得：4-1＜x ＜4+1，即3＜x ＜5，∵x 为整数，∴x 的值为4．三角形的周长为1+4+4=9．故选C.【名师点拨】此题考查了三角形的三边关系．关键是正确确定第三边的取值范围．变式5-1．（2024·汕头市期中）已知a b c 、、是ABC ∆的三边长，化简a b c b a c +----的值是（ ）A ．2c -B ．22b c -C ．22a c -D ．22a b - 【答案】B【提示】依据三角形的三边关系“随意两边之和大于第三边，随意两边之差小于第三边”，得到a+b-c ＞0，b -a -c ＜0，再依据肯定值的性质进行化简计算.【详解】依据三角形的三边关系，得a+b-c>0，b -a -c <0.∴原式= a+b-c −(a +c −b)= 22b c -.故选择B 项.【名师点拨】本题考查三角形三边关系和肯定值，解题的关键是娴熟驾驭三角形三边关系.变式5-2．（2024·保定市期末）如图，为估计池塘岸边A ，B 的距离，小明在池塘的一侧选取一点O ，测得OA=15米，OB=10米，A ，B 间的距离可能是（ ）A．30米B．25米C．20米D．5米【答案】C【解析】设A，B间的距离为x．依据三角形的三边关系定理，得：15-10＜x＜15+10，解得：5＜x＜25，所以，A，B之间的距离可能是20m．故选C．变式5-3．（2024·滨州市期末）若（a﹣3）2+|b﹣6|＝0，则以a、b为边长的等腰三角形的周长为（）A．12 B．15 C．12或15 D．18【答案】B【提示】依据非负数的和为零，可得每个非负数同时为零，可得a、b的值，依据等腰三角形的判定，可得三角形的腰，依据三角形的周长公式，可得答案．【详解】由（a﹣3）2+|b﹣6|＝0，得a﹣3＝0，b﹣6＝0．则以a、b为边长的等腰三角形的腰长为6，底边长为3，周长为6+6+3＝15，故选B．【名师点拨】本题考查了非负数的性质，利用非负数的和为零得出每个非负数同时为零是解题关键．变式5-4．（2024·南开区期末）假如一等腰三角形的周长为27，且两边的差为12，则这个等腰三角形的腰长为（）A．13 B．5 C．5或13 D．1【答案】A【详解】设等腰三角形的腰长为x，则底边长为x﹣12或x+12，当底边长为x﹣12时，依据题意，2x+x﹣12=27，解得x=13，∴腰长为13；当底边长为x+12时，依据题意，2x+x+12=27，解得x=5，因为5+5＜17，所以构不成三角形，故这个等腰三角形的腰的长为13，故选A．考查题型六三角形的稳定性典例6．（2024·路北区期中）下列图形具有稳定性的是（）A．B．C．D．【答案】A【提示】依据三角形具有稳定性，四边形具有不稳定性进行推断即可得．【详解】A、具有稳定性，符合题意；B、不具有稳定性，故不符合题意；C、不具有稳定性，故不符合题意；D、不具有稳定性，故不符合题意，故选A．【名师点拨】本题考查了三角形的稳定性和四边形的不稳定性，正确驾驭三角形的性质是解题关键．变式6-1．（2024·乌鲁木齐市期末）为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是（）A．两点之间，线段最短B．垂线段最短C．三角形具有稳定性D．两直线平行，内错角相等【答案】C【解析】试题提示：三角形具有稳定性，其它多边形不具有稳定性，把多边形分割成三角形则多边形的形态就不会变更．解：这样做的道理是三角形具有稳定性．故选：C．变式6-2．（2024·安阳市期末）王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（）．A．0根B．1根C．2根D．3根【答案】B【解析】三角形具有稳定性，连接一条对角线，即可得到两个三角形，故选B变式6-3．（2024·济南市期末）如图，窗户打开后，用窗钩AB可将其固定，其所运用的几何原理是（）A．三角形的稳定性B．垂线段最短C．两点确定一条直线D．两点之间，线段最短【答案】A【提示】依据点A、B、O组成一个三角形，利用三角形的稳定性解答．【详解】解：一扇窗户打开后，用窗钩将其固定，正好形成三角形的形态，所以，主要运用的几何原理是三角形的稳定性．故答案选A.【名师点拨】本题考查三角形稳定性的实际应用．三角形的稳定性在实际生活中有着广泛的应用．变式6-4．（2024·深圳市期末）如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的依据是( )A．两点之间的线段最短B．长方形的四个角都是直角C．三角形有稳定性D．长方形是轴对称图形【答案】C【详解】用木条EF固定长方形门框ABCD，使其不变形的依据是三角形具有稳定性．故选：C．【名师点拨】本题考查了三角形具有稳定性在实际生活中的应用，是基础题．变式6-5．（2024·抚顺市期中）人字梯中间一般会设计一“拉杆”，这样做的道理是（）A．两点之间，线段最短B．垂线段最短C．两直线平行，内错角相等D．三角形具有稳定性【答案】D【提示】依据三角形的稳定性解答即可．【详解】解：人字梯中间一般会设计一“拉杆”，是为了形成三角形，利用三角形具有稳定性来增加其稳定性，故选：D．【名师点拨】此题考查三角形的性质，关键是依据三角形的稳定性解答．。

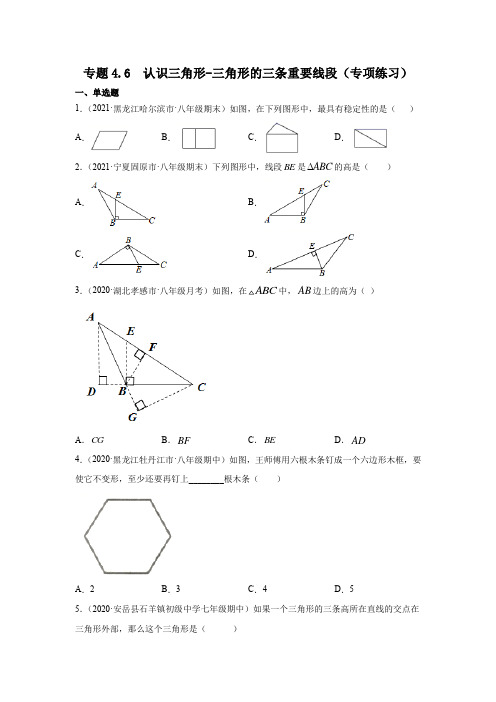
专题4.6 认识三角形-三角形的三条重要线段（专项练习）一、单选题1．（2021·黑龙江哈尔滨市·八年级期末）如图，在下列图形中，最具有稳定性的是（）A．B．C．D．的高是（）2．（2021·宁夏固原市·八年级期末）下列图形中，线段BE是ABCA．B．C．D．3．（2020·湖北孝感市·八年级月考）如图，在ABC中，AB边上的高为（）A．CG B．BF C．BE D．AD 4．（2020·黑龙江牡丹江市·八年级期中）如图，王师傅用六根木条钉成一个六边形木框，要使它不变形，至少还要再钉上________根木条（）A．2B．3C．4D．5 5．（2020·安岳县石羊镇初级中学七年级期中）如果一个三角形的三条高所在直线的交点在三角形外部，那么这个三角形是（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等边三角形 6．（2020·辽宁抚顺市·）如图，CE 是ABC 的外角ACD ∠的平分线，若30B ∠=︒，50ACE ∠=︒，则A ∠=（ ）A ．40︒B ．50︒C ．60︒D ．70︒7．（2021·上海崇明区·九年级一模）已知点G 是ABC 的重心，如果连接AG ，并延长AG 交边BC 于点D ，那么下列说法中错误的是（ ）A ．BD CD =B ．AG GD =C ．2AG GD = D ．2BC BD = 8．（2020·安徽阜阳市·八年级月考）如图，在ABC 中，D 、E 、F 分别是BC 、AC 、AD 的中点，若ABC 的面积是40，则四边形BDEF 的面积是（ ）A ．10B ．12.5C ．15D ．209．（2019·山东临沂市·八年级期中）如图，在△ABC 中，点D ，E ，F 分别是BC ，AD ，CE 的中点，若S △ABC =16，则S △BEF 的值为（ ）A ．1B ．4C ．6D ．810．（2020·内蒙古赤峰市·八年级期中）如图所示，在ABC 中，AD BC ⊥于D ，E 是BC 边上的一点，连结AE ，则线段AD 是（ ）个三角形的高A．3B．4C．5D．6 11．（2020·广西八年级月考）如图，盖房子时，在窗框没有安装之前，木工师傅常常先在窗框上斜钉一根木条，使其不变形，这种做法的根据是（）A．两点之间线段最短B．长方形的对称性C．长方形四个角都是直角D．三角形的稳定性的边AC上的高是（）12．（2021·北京丰台区·八年级期末）如图所示，ABCA．线段AE B．线段BA C．线段BD D．线段DA 13．（2021·湖南娄底市·八年级期末）如图，在△ABC中，AD是BC边上的中线，BE是△ABD 中AD边上的中线，若△ABC的面积是40，则△ABE的面积是( )A．25B．20C．15D．10 14．（2020·浙江省开化县第三初级中学八年级期中）如图，工人师傅砌门时，常用一根木条EF来固定长方形门框ABCD，使其不变形，这样做的根据是（）A ．两点之间线段最短B ．长方形的四个角都是直角C ．长方形是轴对称图形D ．三角形具有稳定性15．（2020·四川绵阳市·东辰国际学校八年级月考）如图，在△ABC 中，已知点D 、E 、F 分别为边BC 、AD 、CE 的中点，且23S cm =阴影，则△ABC 的面积为（ ）平方厘米A ．9B ．12C ．15D ．18二、填空题 16．（2020·广西柳州市·八年级期中）如图，BE 、CF 是ABC 的角平分线，80,60ABC ACB ︒︒∠=∠=，BE 、CF 相交于D ，则CDE ∠的度数是_____________．17．（2020·安徽合肥市五十中学西校八年级期中）如图所示，AD 、CE 、BF 是△ABC 的三条高，AB ＝6，BC ＝5，AD ＝4，则CE ＝_____．18．（2020·湖北孝感市·八年级月考）如图所示，则α=__________．19．（2021·全国九年级专题练习）如图，△ABC中，AD是BC边上的中线，BE是△ABD中AD边上的中线，若△ABC的面积是24，则△ABE的面积________．20．（2020·甘州中学七年级月考）OB是△AOC内部的一条射线，把三角形的角的顶点放在点O处，转动三角尺，当三角尺的边OD平分△AOB，三角尺的另一边OE也正好平分△BOC，则△AOC的度数为________21．（2019·广东广州市白云区六中珠江学校八年级期中）如图，在ABC中，AD、AE分AE=，ABC的面积为25，则CD的长为________．别是边BC上的中线与高，522．（2021·肥东县第四中学七年级期末）如图，已知AD 是ABC 的中线，CE 是ADC 的中线，ABC 的面积为8，则CDE △的面积为______．23．（2020·吉林吉林市·八年级期末）大桥钢架、索道支架等为了坚固，都采用三角形结构．这样做的根据是__________________．24．（2021·河南商丘市·八年级期末）如图，在△ABC 中，△ABC 和△ACB 的角平分线交于点O ，延长BO 与△ACB 的外角平分线交于点D ，若△BOC ＝130°，则△D ＝_____25．（2021·上海九年级专题练习）已知点G 是ABC ∆的重心，连接BG 、GC ，那么BGC ABCS S ∆∆=_________． 26．（2021·全国九年级专题练习）如图，、、A B C 分别是线段1A B 、1B C 、1C A 的中点，若ABC 的面积是1，那么111A B C △的面积为____．27．（2020·东营市实验中学七年级月考）如图，若//AB CD ，BF 平分ABE ∠，DF 平分CDE ∠，90BED ∠=，则BFD ∠=______．28．（2020·宁津县育新中学八年级期中）如图，在△ABC 中，△A=64°，△ABC 与△ACD 的平分线交于点A 1，△A 1BC 与△A 1CD 的平分线相交于点A 2，得△A 2；…；△A n -1BC 与△A n -1CD 的平分线相交于点A n ，要使△A n 的度数为整数，则n 的值最大为______．29．（2020·天津市河西区新华圣功学校八年级月考）如图，已知AE 是ABC 的边BC 上的中线，若8AB cm =，ACE △的周长比AEB △的周长多2cm ，则AC =______cm ．30．（2020·宜春市宜阳学校八年级月考）如图，在ABC 中，点D 、E 、F 分别是边BC 、AD 、CE 上的中点，则6ABC S =，则BEF S =△______．31．（2021·全国八年级）如图，在ABC 中，点,,D E F 分别在三边上，点E 是AC 的中点，,,AD BE CF 交于一点,283BGD AGE G BD DC S S ===，，，则ABC 的面积是________．32．（2021·全国八年级）如图，ABC 的三边的中线AD ，BE ，CF 的公共点为G ，且21AG GD =：：．若12ABC S =△，则图中阴影部分的面积是________．33．（2020·上海宝山区·九年级月考）如图，△ABC 的两条中线AD 、BE 相交于点G ，如果S △ABG ＝2，那么S △ABC ＝_____．34．（2021·菏泽市定陶区第一实验中学八年级月考）如图，在△ABC 中，△A ＝θ，△ABC 和△ACD 的平分线交于点A 1，得△A 1，△A 1BC 和△A 1CD 的平分线交于点A 2，得△A 2；…；△A 2020BC 和△A 2020CD 的平分线交于点A 2021，则△A 2021＝________．（用θ表示）35．（2021·庆云县第二中学八年级期末）如图，ACD ∠是ABC 的外角，ABC ∠的平分线与ACD ∠的平分线交于点1A ，1A BC ∠的平分线与1A CD ∠的平分线交于点2A ，…，1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A ，设=A θ∠，则2=A ∠___________，=n A ∠___________．36．（2020·黑龙江牡丹江市·八年级期中）如图，点D，E，F分别是边BC，AD，AC上的中点，若图中阴影部分的面积为3，则ABC的面积是________．37．（2020·龙湾区永中中学九年级月考）如图1，ABC纸片面积为24，G为ABC纸片）连结CG，DG，并将纸片剪去GDC，的重心，D为BC边上的一个四等分点（BD CD则剩下纸片（如图2）的面积为__________．38．（2021·四川绵阳市·八年级期末）如图，在△ABC中E是BC上的一点，BC=3BE，点D 是AC的中点，设△ABC，△ADF，△BEF的面积分别为S△ABC，S△ADF，S△BEF，且S△ABC=12，则S△ADF﹣S△BEF=____．三、解答题39．（2020·贵州省施秉县第二中学八年级期末）如图，在△ABC中，BE△AC，BC＝5cm，AC＝8cm，BE＝3cm．（1）求△ABC的面积；（2）画出△ABC中BC边上的高AD，并求出AD的长．40．（2021·福建三明市·八年级期末）如图，在△ABC中，△A＝30°，△ACB＝80°，△ABC 的外角△CBD的平分线BE交AC的延长线于点E．（1）求△CBE的度数；DF BE，交AC的延长线于点F，求△F的度数．（2）过点D作//41．（2021·全国八年级）如图，在△ABC中，CD是AB边上的高，BE是AC边上的中线，且BD＝CE．（1）求证：点D在BE的垂直平分线上；（2）若△ABE＝20°，请求出△BEC的度数．42．（2021·山东济南市·八年级期末）△ABC中，AD是△BAC的角平分线，AE是△ABC的高．（1）如图1，若△B＝40°，△C=60°，求△DAE的度数；（2）如图2，△B＜△C，则DAE、△B，△C之间的数量关系为___________；（3）如图3，延长AC到点F，△CAE和△BCF的角平分线交于点G，求△G的度数．43．（2021·四川绵阳市·东辰国际学校七年级期末）如图，两个形状、大小完全相同的含有30°、60°的直角三角板如图△放置，PA、PB与直线MN重合，且三角板PAC、三角板PBD 均可绕点P逆时针旋转（1）试说明△DPC=90°；（2）如图△，若三角板PBD保持不动，三角板PAC绕点P逆时针旋转旋转一定角度，PF 平分△APD，PE平分△CPD，求△EPF；（3）如图△．在图△基础上，若三角板PAC开始绕点P逆时针旋转，转速为5°/秒，同时三角板PBD绕点P逆时针旋转，转速为1°/秒，（当PA转到与PM重合时，两三角板都停止转动），在旋转过程中，PC、PB、PD三条射线中，当其中一条射线平分另两条射线的夹角时，请求出旋转的时间．参考答案1．D【分析】根据三角形的稳定性进行解答即可．【详解】解：根据三角形具有稳定性可得选项D具有稳定性，其余的都具有不稳定性，故选：D．【点拨】此题主要考查了三角形的稳定性，关键是掌握当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性．2．D【分析】根据三角形高的定义可得结论【详解】在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高．故选：D【点拨】熟记三角形高的定义是解决本题的关键．3．A【分析】在ABC中，过C点向AB所在的直线作垂线，顶点与垂足之间的线段是AB上的高，由此可得答案．【详解】CG解：ABC中，AB边上的高为：.故选：.A【点拨】本题考查的是三角形的高的含义，掌握钝角三角形的高是解题的关键．4．B【分析】根据三角形的稳定性，要使它不变形，只需每一条边都分别在一个三角形之中即可【详解】解：要使六边形木框不变形，则需每一条边都分别在一个三角形之中，观察图形可得，至少还需要再钉上3根木条故选：B【点拨】本题考查了三角形的稳定性，观察图形如何使每一条边都分别在一个三角形之中是解决本题的关键5．C【分析】直接根据钝角三角形的三条高线交于三角形的外部解答即可．【详解】解：钝角三角形的三条高线交于三角形的外部，故选：C ．【点拨】本题考查了三角形的三条高线交点的位置与三角形的形状的关系，即：锐角三角形的三条高线交于三角形的内部，直角三角形的三条高线交于三角形的直角的顶点，钝角三角形的三条高线交于三角形的外部．6．D【分析】根据角平分线的定义以及三角形外角的性质，即可求解．【详解】△CE 是ABC 的外角ACD ∠的平分线，50ACE ∠=︒，△△ACD =2△ACE=100°，△△A=△ACD -△B=100°-30°=70°，故选D【点拨】本题主要考查角平分线的定义以及三角形外角的性质，熟练掌握“三角形的外角等于不相邻的两个内角之和”是解题的关键．7．B【分析】根据三角形重心的定义和性质解答即可．【详解】解：△点G 是ABC 的重心，△BD CD =，2AG GD =，2BC BD =，△A 、C 、D 正确，B 错误，故选B ．【点拨】本题考查的是三角形的重心的概念和性质，三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．8．C【分析】要求四边形面积，可以转化为两个三角形面积之和，把三角形面积计算中的底与高转化为大三角形ABC 的底与高即可求解．【详解】△ABC 的面积是40， △1402BC h ⨯⨯=， △D 、E 、F 分别是BC 、AC 、AD 的中点，△EF 平行且等于12CD ，CD BD =， 以BD 为底，设BDF 的高为h '，以EF 为底，DEF 的高为h ''， △//BC EF ，△h h '''=， 11=22BDF DEF BDEF S S S BD h EF h ''+=⨯⨯+⨯⨯四边形， △F 是AD 的中点，△12h h '=， △111111=10515222422BDEF S BC h BC h ⨯⨯⨯+⨯⨯⨯=+=四边形， 故选：C ．【点拨】本题主要考查的是三角形中线的性质求面积问题，熟练掌握三角形中线求面积的性质是解答本题的关键．9．B【分析】根据三角形中线把三角形分成面积相等的两部分可以得解．【详解】解：由题意可得：BEC BED DEC SS S =+=()12ABD ACD S S + =12ABC S =8， △142BEF BEC S S ==， 故选：B ．【点拨】本题考查三角形中线的应用，熟练掌握三角形中线把三角形分成面积相等的两部分的性质是解题关键 ．10．D【分析】由AD BC ⊥，结合线段BC （包括端点）共有4个已知点，从而可得线段AD 是三角形以,,,,,BE BD BC ED EC DC 为边上的高，于是可得答案．【详解】解：,AD BE ⊥AD ∴是ABE △的高，,AD BD ⊥AD ∴是ABD △的高，AD BC ⊥，AD ∴是ABC 的高，AD DE ⊥,AD ∴是ADE 的高，,AD CE ⊥AD ∴是ACE △的高，,AD CD ⊥AD ∴是ACD △的高，∴ 线段AD 是6个三角形的高故选：.D【点拨】本题考查的是三角形高的含义，分类讨论的数学思想，掌握以上要点是解题的关键． 11．D【分析】在窗框未安装之前，木工师傅常常先在窗框上斜钉一根木条，则分成了两个三角形，据此即可判断是利用了三角形的稳定性．【详解】在窗框未安装之前，木工师傅常常先在窗框上斜钉一根木条，则分成了两个三角形，利用了三角形的稳定性，D 正确．故答案选D ．【点拨】本题比较简单主要考查三角形稳定性的实际应用，通常要使一些图形具有稳定的结构，往往是将其转化为三角形而获得．12．C【分析】根据三角形的高解答即可，三角形的一个顶点到它的对边所在直线的垂线段叫做这个三角形的高．A.线段AE是△ABC的边BC上的高，故不符合题意；B.线段BA不是任何边上的高，故不符合题意；C.线段BD是△ABC的边AC边上的高，故符合题意；D.线段DA是△ABD的边BD上的高，故不符合题意；故选C．【点拨】本题考查了三角形的高线，熟练掌握三角形高线的定义是解答本题的关键．13．D【分析】根据三角形的中线把三角形分成面积相等的两部分，求出面积比，即可解答．【详解】解：△AD是BC上的中线，△12ABD ACD ABCS S S==△△△，△BE是△ABD中AD边上的中线，△12ABE BED ABDS S S==△△△，△14ABE ABCS S=△△，△△ABC的面积是40，△144010ABES，故选：D．【点拨】本题主要考查了三角形面积的求法，掌握三角形的中线将三角形分成面积相等的两部分，是解答本题的关键．14．D【分析】根据三角形具有稳定性解答．用木条EF 固定长方形门框ABCD ，使其不变形，这样做的根据是三角形具有稳定性， 故选：D ．【点拨】此题考查三角形的稳定性，正确理解题意即可解决实际问题．15．B【分析】由点D 为BC 的中点，可得△ABD 、△ACD 与△ABC 的面积之比，继而由点E 为AD 的中点，可得△ABC 与△BCE 的面积之比，同理可得△BCE 和△EFB 的面积之比，据此可解答．【详解】解：如图，△D 为BC 的中点，△S △ABD = S △ACD = 12S △ABC ， △E 为AD 的中点， △S △BDE =12 S △ABD ，S △CDE = 12S △ACD ， △S △BDE + S △CDE = 12S △ABD + 12 S △ACD = 12 S △ABC ， △S △BEC = 12 S △ABC ， △F 为EC 的中点，△S △BEF = 12 S △BEC = 14S △ABC ， △S △BEF =3，△S △ABC =12．故选：B ．【点拨】本题主要考查了三角形面积及三角形面积的等积变换，三角形的中线将三角形分成面积相等的两部分．16．70【分析】利用角平分线的定义求得CBE FCB ∠∠、的度数，然后利用三角形外角的性质求解【详解】解：△BE 、CF 是ABC 的角平分线，80,60ABCACB ∠=∠=， △1140,3022CBE ABC FCB ACB ∠=∠=∠=∠=， △70CDE CBE FCB ∠=∠+∠=． 故答案为：70．【点拨】本题考查三角形外角的性质，掌握三角形外角等于不相邻的两个内角和是解题关键． 17．103【分析】 利用三角形面积公式得到12×AB ×CE ＝12×BC ×AD ，然后将已知条件代入求解即可． 【详解】解：△S △ABC ＝12×AB ×CE ＝12×BC ×AD ， △CE ＝BC AD AB⨯＝546⨯＝103． 故答案为103． 【点拨】本题主要考查了三角形面积公式，利用三角形的面积公式列出方程是解答本题的关键． 18．114︒【分析】根据三角形外角性质解答即可．【详解】如图所示:由三角形外角性质可得:1245882︒︒∠=+︒=1328232114α︒︒︒︒=∠+=+=故答案为: 114︒．【点拨】此题考查三角形外角性质，关键是根据三角形外角性质解答．19．6【分析】根据三角形的中线把三角形分成面积相等的两部分，即可解答．【详解】解：△AD是BC上的中线，△ABC的面积是24，△S△ABD=S△ACD=12S△ABC=12，△BE是△ABD中AD边上的中线，△S△ABE=S△BED=12S△ABD=6，故答案为：6．【点拨】本题主要考查了三角形面积的求法，掌握三角形的中线将三角形分成面积相等的两部分，是解答本题的关键．20．120°【分析】根据角平分线是定义得到△BOD=12△AOB，△BOE=12△COB,则△DOE=12△AOB+12△COB=12△AOC，然后把△DOE=60°代入计算即可．【详解】△OD平分△AOB，OE平分△COB，△△BOD1=2△AOB，△BOE=12△COB，△△DOE=12△AOB+12△COB=12△AOC，△△DOE=60°，△△AOC=260=120⨯．故答案为：120°【点拨】本题主要考查了角之间的和差关系及角平分线的定义．正确理解角的和差倍分关系是解题的关键．21．5.【分析】由三角形的面积为：25，求解,BC 再利用三角形的中线的概念求解CD 即可得到答案． 【详解】 解： AD 、AE 分别是边BC 上的中线与高，1,,2BD CD BC AE BC ∴==⊥ 1252BC AE ∴=， 5AE =，550BC ∴=，10BC ∴=，152CD BC ∴==， 故答案为：5.【点拨】本题考查的是三角形的中线，高的含义，三角形的面积，掌握以上知识是解题的关键． 22．2【分析】根据三角形的中线把三角形的面积分成相等的两部分直接进行求解即可．【详解】 解：AD 是ABC 的中线，ABC 的面积为8， ∴142ADC ABC S S ==△△， CE 是ADC 的中线， ∴122CDE ADC S S △△；故答案为：2．【点拨】本题主要考查三角形的中线，熟练掌握三角形的中线把三角形的面积分成相等的两部分是解题的关键．23．三角形具有稳定性【分析】三角形的形状是固定的，三角形的这个性质叫三角形的稳定性，利用三角形的稳定性即可解释．【详解】△三角形具有稳定性，△大桥钢架、索道支架等为了坚固，都采用三角形结构．这样做的根据是三角形的稳定性．故答案为：三角形的稳定性．【点拨】本题考查三角形的稳定性，掌握三角形是固定不变的，不会变形，即三角形的稳定性，生活中需要稳定的东西一般都制成三角形的形状．24．40°【分析】根据角平分线的定义结合三角形外角的性质即可得到结论．【详解】解：△△ABC和△ACB的角平分线交于点O，△△ACO=12△ACB，△CD平分△ACE，△△ACD=12△ACE，△△ACB+△ACE=180°，△△OCD=△ACO+△ACD=12（△ACB+△ACE）=12×180°=90°，△△BOC＝130°，△△D=△BOC-△OCD=130°-90°=40°，故答案为：40°．【点拨】本题考查了三角形的外角性质，角平分线的定义，熟练掌握相关性质和概念正确推理计算是解题的关键．25．13【分析】直接根据三角形重心的性质进行解答即可．【详解】解：连接AG 并延长交BC 于D△点G 为△ABC 的重心，△AG=2DG ，△△DGC 的面积等于△ADC 面积的13， △DGB 的面积等于△ADB 面积的13， △△DGC 的面积+△DGB 的面积=13（△ADC 的面积+△ADB 的面积） △△BCG 的面积=13△ABC 的面积 △13∆∆=BGC ABC S S 故答案为：13【点拨】本题考查的是三角形的重心，熟知三角形的重心是三角形三边中线的交点是解答此题的关键．26．7【分析】连接111,,AB BC CA ，根据等底等高的三角形的面积相等求出1ABB △，11A AB △的面积，从而求出11A BB 的面积，同理可求11B CC 的面积，11A AC △的面积，然后相加即可得解．【详解】解：如下图，连接111,,AC B A C B ，△B 是线段1B C 的中点，△1B B BC =， ABC 和1AB B 等底同高，△根据等底同高的两个三角形面积相等可得11B AB ABC S S ==△△；同理可得：1111A B A AB B S S ==△△；△11111112A B B A B A AB B S S S =+=+=；同理可得112C CB S =△，112C AA S =△，△11111111122217A B C A BB C CB C AA ABC S S S S S =+++=+++=．故答案为：7．【点拨】本题考查了与三角形中线有关的面积计算，主要利用了等底等高的三角形的面积相等，作辅助线把三角形进行分割是解题的关键．27．45°【分析】如图，作射线BF 与射线BE ，根据平行线的性质和三角形的外角性质可得△ABE +△EDC ＝90°，然后根据角平分线的定义和三角形的外角性质即可求出答案．【详解】解：如图，作射线BF 与射线BE ，△AB △CD ，△△ABE ＝△4，△1＝△2，△△BED＝90°，△BED＝△4+△EDC，△△ABE+△EDC＝90°，△BF平分△ABE，DF平分△CDE，△△1+△3＝12△ABE+12△EDC＝45°，△△5＝△2+△3，△△5＝△1+△3＝45°，即△BFD＝45°，故答案为：45°．【点拨】本题考查了平行线的性质、角平分线的定义和三角形的外角性质，属于常考题型，熟练掌握上述知识是解题的关键．28．6【分析】根据三角形的一个外角等于与它不相邻的两个内角的和得到△A＝2△A1，同理可得△A1＝2△A2，即△A＝22△A2，因此找出规律．【详解】由三角形的外角性质得，△ACD＝△A＋△ABC，△A1CD＝△A1＋△A1BC，△△ABC的平分线与△ACD的平分线交于点A1，△△A1BC＝12△ABC，△A1CD＝12△ACD，△△A1＋△A1BC＝12（△A＋△ABC）＝12△A＋△A1BC，△A1B、A1C分别平分△ABC和△ACD，△△ACD＝2△A1CD，△ABC＝2△A1BC，而△A1CD＝△A1＋△A1BC，△ACD＝△ABC＋△A，△△A＝2△A1，△△A1＝12△A，同理可得△A1＝2△A2，△△A2＝14△A，△△A＝2n△A n，△△A n＝（12）n△A＝642n，△△A n的度数为整数，△n＝6．故答案为：6．【点拨】本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记性质并准确识图然后求出后一个角是前一个角的12是解题的关键．29．10【分析】依据AE是△ABC的边BC上的中线，可得CE=BE，再根据AE=AE，△ACE的周长比△AEB 的周长多2cm，即可得到AC的长．【详解】解：△AE是△ABC的边BC上的中线，△CE=BE，又△AE=AE，△ACE的周长比△AEB的周长多2cm，△AC-AB=2cm，即AC-8=2cm，△AC=10cm，故答案为：10；【点拨】本题考查了三角形的角平分线、中线和高，求出两个三角形的周长的差等于两边的差是解题的关键．30．3 2【分析】利用三角形的中线把三角形分成面积相等的两部分解决问题即可．【详解】解：△BD=DC ，△S △ABD =S △ADC =12×6=3（cm 2）， △AE=DE ，△S △AEB =S △AEC =12×3=32（cm 2）， △S △BEC =6-3=3（cm 2），△EF=FC ，△S △BEF =12×3=32（cm 2）， 故答案为32． 【点拨】本题考查三角形的面积，三角形的中线等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．31．30【分析】根据部分三角形的高相等，由这些三角形面积与底边的比例关系可求三角形ABC 的面积．【详解】解：在BDG 和GDC 中，△2BD DC =,△2BDG GDC SS =，8BGD S =△， △4GDC S =,△点E 是AC 的中点，3AGE S = △ 3.GEC AGE SS == △84315BEC BDG GDC GEC SS S S =++=++=， △230.ABC BEC S S ==故答案为：30．【点拨】本题中由于部分三角形的高相等，可根据这些三角形面积的比等于底边的比例关系来求三角形ABC的面积是解题关键．32．4【分析】根据三角形的中线把三角形的面积分成相等的两部分，知△ABC的面积即为阴影部分的面积的3倍．【详解】解：△△ABC的三条中线AD、BE，CF交于点G，AG：GD=2：1，△AE=CE，△S△CGE=S△AGE=13S△ACF，S△BGF=S△BGD=13S△BCF，△S△ACF=S△BCF=12S△ABC=12×12=6，△S△CGE=13S△ACF=13×6=2，S△BGF=13S△BCF=13×6=2，△S阴影=S△CGE+S△BGF=4．故阴影部分的面积为4．故答案为：4．【点拨】本题考查了三角形的面积，三角形中线的性质，正确的识别图形是解题的关键．33．6【分析】根据D，E分别是三角形的中点，得出G是三角形的重心，再利用重心的概念可得：2GD ＝AG进而得到S△ABG：S△ABD＝2：3，再根据AD是△ABC的中线可得S△ABC＝2S△ABD进而得到答案．【详解】解：△△ABC的两条中线AD、BE相交于点G，△2GD＝AG，△S△ABG＝2，△S△ABD＝3，△AD是△ABC的中线，△S△ABC＝2S△ABD＝6．故答案为：6．此题主要考查了重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的两倍．34．20212θ【分析】根据三角形的一个外角等于与它不相邻的两个内角的和，可得ACD A ABC ∠=∠+∠，111ACD A A BC ∠=∠+∠，根据角平分线的定义可得112A BC ABC ∠=∠，112ACD ACD ∠=∠，然后整理得到112A A ∠=∠，同理可得2112A A ∠=∠，⋯从而判断出后一个角是前一个角的一半，然后表示出n A ∠即可．【详解】解：1A B 平分ABC ∠，1A C 平分ACD ∠，112A BC ABC ∴∠=∠，112ACA ACD ∠=∠， 111ACD A A BC ∠=∠+∠， ∴11122ACD A ABC ∠=∠+∠， 11()2A ACD ABC ∴∠=∠-∠， A ABC ACD ∠+∠=∠，A ACD ABC ∴∠=∠-∠，112A A ∴∠=∠， 1221122A A A ∠=∠=∠，⋯， 以此类推，12n n A A ∠=∠， 202120212021122A A θ∴∠=∠=． 故答案为：20202θ．本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记性质并准确识图然后求出后一个角是前一个角的一半是解题的关键．35．4θ 2n θ 【分析】根据三角形的外角性质可得△ACD=△A+△ABC ，△A 1CD=△A 1+△A 1BC ，根据角平分线的定义可得△A 1BC=12△ABC ，△A 1CD=12△ACD ，整理得到△A 1=12△A ，同理可得△A 2=12△A 1，从而判断出后一个角是前一个角的12，然后表示出△A n 即可得答案． 【详解】△ACD ∠是ABC 的外角，△A 1CD 是△A 1BC 的外角，△△ACD=△A+△ABC ，△A 1CD=△A 1+△A 1BC ，△ABC ∠的平分线与ACD ∠的平分线交于点1A ，△△A 1BC=12△ABC ，△A 1CD=12△ACD ， △△A 1=12△A ， 同理可得△A 2=12△A 1=14△A ， △△A=θ，△△A 2=4θ， 同理：△A 3=12△A 2=382θθ=， △A 4=12△A 3=4162θθ= ……△△A n =2n θ． 故答案为：4θ，2nθ 【点拨】 本题考查了三角形的外角性质及角平分线的定义，三角形的一个外角等于与它不相邻的两个内角的和；熟记性质并准确识图，求出后一个角是前一个角的12是解题的关键．36．8【分析】利用三角形的中线将三角形分成面积相等的两部分，S△ABD=S△ACD=12S△ABC，S△BDE=12S△ABD，S△ADF=12S△ADC，再得到S△BDE=14S△ABC，S△DEF=18S△ABC，所以S△ABC=83S阴影部分．【详解】解：△D为BC的中点，△12ABD ACD ABCS S S==△△△，△E，F分别是边,AD AC上的中点，△111,,222 BDE ABD ADF ADC DEF ADFS S S S S S===，△111,448 BDE ABC DEF ADC ABCS S S S S===，△113488BDE DEF ABC ABC ABCS S S S S S=+=+=阴影部分，△888333ABCS S⨯===阴影部分，故答案为：8．【点拨】本题考查了三角形的面积：三角形的面积等于底边长与高线乘积的一半，即S△=12×底×高．三角形的中线将三角形分成面积相等的两部分．37．18【分析】连接BG，根据重心的性质得到△BGC的面积，再根据D点是BC的四等分点得到△GDC的面积，故可求解．【详解】连接BG，△G为ABC纸片的重心，△S△BGC=13S△ABC=8△D为BC边上的一个四等分点（BD CD）△S△DGC=34S△BGC=6△剪去GDC，则剩下纸片的面积为24-6=18故答案为：18．【点拨】此题主要考查重心的性质，解题的关键是熟知重心的性质及面积的换算关系．38．2【分析】S△ADF-S△BEF=S△ABD-S△ABE，所以求出三角形ABD的面积和三角形ABE的面积即可，因为BC=3BE，点D是AC的中点，且S△ABC=12，就可以求出三角形ABD的面积和三角形ABE 的面积．【详解】解：△点D是AC的中点，△AD=12 AC，△S△ABC=12，△S△ABD=12S△ABC=12×12=6．△BC=3BE，△S△ABE=13S△ABC=13×12=4，△S△ABD-S△ABE=（S△ADF+S△ABF）-（S△ABF+S△BEF）=S△ADF-S△BEF，即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2，故答案为：2．【点拨】本题考查三角形的面积，解题的关键是要能根据已知条件求出三角形的面积并对要求的两个三角形的面积之差进行变化．39．（1）212cm ；（2）作图见解析，245cm 【分析】（1）结合题意，根据三角形面积计算公式分析，即可得到答案；（2）过点A 作AD BC ⊥交BC 于点D ，结合三角形面积公式计算，即可得到答案．【详解】（1）△BE△AC ， AC ＝8cm ，BE ＝3cm △211=831222ABC S AC BE cm ⨯=⨯⨯=△ （2）如图，过点A 作AD BC ⊥交BC 于点D△211=1222ABC S AC BE BC AD cm ⨯=⨯=△ △22122455ABC S AD BC ⨯===△cm ． 【点拨】本题考查了三角形的知识；解题的关键是熟练掌握三角形高的性质，从而完成求解． 40．（1）55CBE ∠=︒；（2）25.F ∠=︒【分析】（1）由30,80,A ACB ∠=︒∠=︒ 利用三角形的外角的性质求解,CBD ∠ 再利用角平分线的含义求解CBE ∠即可得到答案；（2）先由三角形的外角的性质求解,CEB ∠ 再利用平行线的性质求解F ∠即可得到答案．【详解】解：（1）30,80,A ACB ∠=︒∠=︒3080110,CBD A ACB ∴∠=∠+∠=︒+︒=︒ BE 平分,CBD ∠1111055.22CBE CBD ∴∠=∠=⨯︒=︒ （2）80,55,ACB CBE ∠=︒∠=︒805525,CEB ACB CBE ∴∠=∠-∠=︒-︒=︒//,BE DF25.F CEB ∴∠=∠=︒【点拨】本题考查的是三角形的外角的性质，平行线的性质，掌握以上知识是解题的关键．41．（1）见解析；（2）60°．【分析】（1）连接DE ，根据垂直定义得到△ADC ＝△BDC ＝90°，根据直角三角形的性质可得DE ＝CE ，根据线段垂直平分线的性质可得结论；（2）根据等边对等角的性质和三角形外角的性质及角的和差倍数关系即可求证结论．【详解】（1）证明：连接DE ，△CD 是AB 边上的高，△△ADC ＝△BDC ＝90°，△BE 是AC 边上的中线，△AE ＝CE ，△DE ＝CE ，△BD ＝CE ，△BD ＝DE ，△点D 在BE 的垂直平分线上；（2）解：△DE ＝AE ，△△A ＝△ADE ，△△ADE ＝△DBE+△DEB ，△BD ＝DE ，△△DBE ＝△DEB ，△△A ＝△ADE ＝2△ABE ，△△BEC ＝△A+△ABE ，△△BEC＝3△ABE，△△ABE＝20°，△△BEC＝60°．【点拨】本题考查线段垂直平分线的性质、直角三角形斜边中线定理、等边对等角的性质、三角形外角和性质，解题的关键是熟练掌握上述所学知识．42．（1）10°；（2）△DAE＝12(△C−△B)；（3）45°．【分析】（1）根据三角形的内角和定理可求得△BAC＝80°，由角平分线的定义可得△CAD 的度数，利用三角形的高线可求△CAE得度数，进而求解即可得出结论；（2）根据（1）的推理方法可求解△DAE、△B、△C的数量关系；（3）设△ACB＝α，根据角平分线的定义得△CAG＝12△EAC＝12（90°−α）＝45°−12α，△FCG＝12△BCF＝12（180°−α）＝90°−12α，再利用三角形外角的性质即可求得结果．【详解】解：（1）△△B＝40°，△C＝60°，△BAC＋△B＋△C＝180°，△△BAC＝80°，△AD平分△BAC，△△CAD＝△BAD＝12△BAC＝40°，△AE是△ABC的高，△△AEC＝90°，△△C＝60°，△△CAE＝90°−60°＝30°，△△DAE＝△CAD−△CAE＝10°；（2）△△BAC＋△B＋△C＝180°，△△BAC＝180°−△B−△C，△AD平分△BAC，。

专题一 三角形三边关系的常见应用一. 专题目标1.了解和掌握三角形的定义和三角形的三边关系 2.通过例题学习，学会用三边关系解决“能否构成三角形”类型的题目 3.通过例题学习，学会用三边关系解决“第求三边长或可能性”类型的题目 4.通过例题学习，学会用三边关系解决“三角形中和边长之间的关系”类型的题目 5.通过例题学习，学会用三边关系解决“绝对值化简”类型的题目 二. 专题环节三角形的三边关系：1. 在一个三角形中，任意两边之和大于第三边2. 在一个三角形中，任意两边之差小于第三边三角形的定义：由不在同一直线上的三条线段首尾依次连结所组成的图形叫做三角形。

一． 能否构成三角形例1，1、若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为_____.分析：根据线段MN 平行于Y 轴，MN=M N y y -，分别讲M 点所在二次函数解析式和N 点所在AB 直线解析式求得代入即可得到MN 关于x 的函数关系式。

详解：设直线AB 的解析式为y 2＝kx ＋b ，由y 1＝－x 2＋2x ＋3求得B 点的坐标为(0，3)．把A (3，0)，B (0，3)代入y 2＝kx ＋b ，解得k ＝－1 b ＝3．∴直线AB 的解析式为y 2＝－x ＋3．∵MN ∥y 轴，M （x,－x 2＋2x ＋3）,N(x,－x ＋3)∴MN=M N y y -=－x 2＋2x ＋3-（－x ＋3）=－x 2＋3x=-（x-32）2 +94(0≤x ≤3)∵a=-1<0 ∴当x=32时，线段MN 最大值为94关键词：二次函数表示线段长一 图形问题：周长例2，如图，已知二次函数245y x x =--的图像与坐标轴交于点A （-1,0）和B （0，-5）对称轴存在一点P ，使得△ABP 的周长最小，请求出P 的坐标分析：二次函数中的周长最小值，往往是用利用轴对称求线段最值的办法来获得的：即：△ABP 周长为AB+BP+AP ，由于AB 是定线段，所以周长最小值转化为PA+PB 最小，所以可以做A 关于对称轴的对称点C ，连接BC,和对称轴的交点P .此时PA+PB 获得最小值BC ， 此时只需要将对称轴的横坐标代入BC 所在直线解析式，就可以求出P 点坐标。

专题02 三角形的高、中线、角平分线重点突破知识点一三角形的高概念：从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。

知识点二三角形的中线概念：在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。

性质：三角形三条中线的交于一点，这一点叫做“三角形的重心”。

重心到顶点的距离是它到对边中点距离的2倍。

（选学）三角形的中线可以将三角形分为面积相等的两个小三角形。

知识点三三角形的角平分线概念：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。

考查题型考查题型一画三角形的高典例1（2020·泉州市期中）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．【答案】A【提示】经过一个顶点作对边所在的直线的垂线段，叫做三角形的高，根据概念即可得出.【详解】根据定义可得A是作BC边上的高，C是作AB边上的高，D是作AC边上的高.故选A.变式1-1．（2018·梁平区期末）在数学课上，同学们在练习过点B作线段AC所在直线的垂线段时，有一部分同学画出下列四种图形，请你数一数，错误的个数为( )A．1个B．2个C．3个D．4个【答案】D【解析】试题解析：从左向右第一个图形中，BE不是线段，故错误；第二个图形中，BE不垂直AC，所以错误；第三个图形中，是过点E作的AC的垂线，所以错误；第四个图形中，过点C作的BE的垂线，也错误.故选D.变式1-2．（2020·海淀区期末）用直角三角板，作△ABC的高，下列作法正确的是（）A．B．C．D．【答案】D【解析】详解：三角形的高必须是从三角形的一个顶点向对边或对边的延长线作的垂线段.可以判断A,B,C虽然都是从三角形的一个顶点出发的，但是没有垂直对边或对边的延长线.故选D.变式1-3．（2020·苏州市期中）如图，∠ACB＞90°，AD⊥BC，BE⊥AC，CF⊥AB，垂足分别为点D、点E、点F，△ABC中AC边上的高是（）A．CF B．BE C．AD D．CD【答案】B【解析】试题提示：根据图形，BE是△ABC中AC边上的高．故选B．变式1-4．（2019·杭州市期中）如图AD⊥BC于点D，那么图中以AD为高的三角形的个数有（）A．3 B．4 C．5 D．6【答案】D【解析】结合三角形高的定义可知，以AD为高的三角形有：△ABD，△ABE，△ABC，△ADE，△ADC，△AEC，共6个.故选D考查题型二与三角形高有关的计算典例2．（2019·济南市期中）如图，在直角三角形ABC中，点B沿CB所在直线远离C点移动，下列说法错误的是( )A．三角形面积随之增大B．∠CAB的度数随之增大C．BC边上的高随之增大D．边AB的长度随之增大【答案】C【提示】根据三角形的面积公式、角和线段大小的比较以及三角形高的定义进行解答即可．【详解】解：A、在直角三角形ABC中，S△ABC=12BC•AC，点B沿CB所在直线远离C点移动时BC增大，则该三角形的面积越大．故A正确；B、如图，随着点B的移动，∠CAB的度数随之增大．故B正确；C、BC边上的高是AC，线段AC的长度是不变的．故C错误．D、如图，随着点B的移动，边AB的长度随之增大．故D正确；故选：C．【名师点拨】本题考查了三角形的面积，角和线段大小的比较以及三角形高的定义，解题时要注意“数形结合”数学思想的应用．变式2-1．（2020·毕节市期末）如图，△ABC 中，D ，E 分别是BC 上两点，且BD=DE=EC ，则图中面积相等的三角形有（ ）A ．4对B ．5对C ．6对D ．7对【答案】A 【提示】根据三角形的面积公式，知：只要同底等高，则两个三角形的面积相等，据此可得面积相等的三角形．【详解】由已知条件，得△ABD ，△ADE ，△ACE ，3个三角形的面积都相等，组成了3对，还有△ABE 和△ACD 的面积相等，共4对.故选A.【名师点拨】本题考查了三角形的相关知识，解题的关键是熟练的掌握三角形面积公式与运用.变式2-2．（2020·龙岩市期中）如图，AD ，CE 是△ABC 的两条高，已知AD=10，CE=9，AB=12，则BC 的长是（ ）A ．10B ．10.8C ．12D ．15【答案】B 【解析】∵AD ，CE 是△ABC 的两条高，AD=10，CE=9，AB=12，∴△ABC 的面积=12×12×9=12BC ⋅AD=54， 即12BC ⋅10=54，解得BC=10.8.故选B.变式2-3．（2018·合肥市期中）如图所示，AD CE BF 、、是ABC ∆的三条高，654AB BC AD ===，，，则CE =（ ）A ．245B ．152C ．103D ．3【答案】C【提示】根据三角形的面积公式解答即可． 【详解】解：因为AD 、CE 、BF 是△ABC 的三条高，654AB BC AD ===，，，所以可得：12BC•AD=12AB•CE ， 可得：CE=•BC AD AB ＝546⨯＝103． 故选C ．【名师点拨】此题考查三角形的面积，关键是根据同一三角形面积相等来提示．变式2-4．（2018·烟台市期末）如图，在△ABC 中，CD 、BE 分别是AB 、AC 边上的高，并且CD 、BE 交于点P ，若∠A=50°，则∠BPC 等于（ ）A ．90°B ．130°C ．270°D ．315°【答案】B 【详解】根据∠A=50°可得∠ABC+∠ACB=130°，根据CD ⊥AB ，BE ⊥AC 可得∠ABE=40°，∠ACD=40°，则∠PBC+∠PCB=130°－40°－40°=50°，则∠BPC=180°－50°=130°. 故选：B.变式2-5．（2019·荆门市期末）如图，三角形ABC ，∠BAC =90︒，AD 是三角形ABC 的高，图中相等的是（ ）．A ．∠B =∠CB ．∠BAD=∠BC ．∠C =∠BAD D ．∠DAC=∠C【答案】C 【提示】根据直角三角形的性质可得∠B +∠C =90︒，由AD 是三角形ABC 的高，可得∠BDA=∠ADC =90︒，再运用三角形内角和定理依次判断即可.【详解】∵∠BAC =90︒，∴∠B +∠C =90︒，故选项A 错误；∵AD 是三角形ABC 的高，∴∠BDA=90︒，∴∠BAD+∠B=90︒，故选项B 错误；∵∠BAC =90︒，∴∠BAD+ ∠DAC=90︒，又∵∠ADC =90︒，∴∠DAC+ ∠C=90︒，∴∠C=∠BAD，故选项C正确，选项D错误.故选C.【名师点拨】本题考查了三角形的高线以及三角形的内角和定理，属于基础题型.变式2-6．（2019·济南市期中）如图△ABC中，分别延长边AB，BC，CA，使得BD＝AB，CE＝2BC，AF＝3CA，若△ABC的面积为1，则△DEF的面积为( )A．12 B．14 C．16 D．18【答案】D【提示】连接AE和CD，要求三角形DEF的面积，可以分成三部分（△FCD+△FCE+△DCE）来分别计算，三角形ABC是一个重要的条件，抓住图形中与它同高的三角形进行提示计算，即可解得△DEF的面积．【详解】解：连接AE和CD，∵BD=AB，∴S△ABC=S△BCD=1，S△ACD=1+1=2，∵AF=3AC，∴FC=4AC，∴S△FCD=4S△ACD=4×2=8，同理可以求得：S△ACE=2S△ABC=2，则S△FCE=4S△ACE=4×2=8；S△DCE=2S△BCD=2×1=2；∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18．故选：D．【名师点拨】本题考查三角形面积及等积变换的知识，注意高相等时三角形的面积与底成正比的关系，并在实际问题中的灵活应用，有一定难度．考查题型三三角形中线有关的长度计算典例3．（2018·秦皇岛市期中）如图，AE 是ABC 的中线，已知EC 4=，DE 2=，则BD 的长为( )A ．2B ．3C ．4D ．6【答案】A【解析】试题解析：∵AE 是△ABC 的中线，EC=4，∴BE=EC=4，∵DE=2，∴BD=BE-DE=4-2=2．故选A ．变式3-1．（2019·肇庆市期中）已知AD 是△ABC 的中线，且△ABD 比△ACD 的周长大3cm ，则AB 与AC 的差为( ) A ．2cm B ．3cm C ．4cm D ．6cm【答案】B【提示】根据三角形中线的定义可得BD=CD ，然后根据三角形的周长公式列式计算即可得解．【详解】解：∵AD 是△ABC 的中线，∴BD=DC ，∴△ABD 与△ACD 的周长之差=（AB+AD+BD ）-（AC+AD+CD ）=AB-AC ，∵△ABD 比△ACD 的周长大3cm ，∴AB 与AC 的差为3cm ．故选B ．【名师点拨】本题考查了三角形的中线，熟记概念并求出两三角形周长的差等于AB-AC 是解题的关键．变式3-2．（2020·哈尔滨市期中）如图，三角形ABC 中，D 为BC 上的一点，且S △ABD =S △ADC ，则AD 为（ ）A ．高B ．角平分线C ．中线D ．不能确定【答案】C【解析】解：设BC边上的高为h，∵S△ABD=S△ADC，∴，故BD=CD，即AD是中线．故选C．变式3-3．（2019·临清市期末）如图，在△ABC中，AD是BC边上的中线，△ADC的周长比△ABD的周长多5cm，AB 与AC的和为13cm，那么AC的长为（）A．8cm B．9cm C．10cm D．11cm【答案】B【提示】根据中线的定义知CD=BD．结合三角形周长公式知AC-AB=5cm；又AC+AB=13cm．易求AC的长度．【详解】∵AD是BC边上的中线，∴D为BC的中点，CD=BD．∵△ADC的周长-△ABD的周长=5cm．∴AC-AB=5cm．又∵AB+AC=13cm，∴AC=9cm．即AC的长度是9cm．故选B.【名师点拨】本题考查了三角形的中线，根据周长的差表示出AC-AB=5cm，是解题的关键．考查题型四三角形中线有关的面积计算典例4．（2020·渠县期中）如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE 的中点，且△ABC的面积为4cm2，则△BEF的面积等于（）A．2cm2B．1cm2C．0．5 cm2D．0．25 cm2【答案】B【提示】依据三角形的面积公式及点D 、E 、F 分别为边BC ，AD ，CE 的中点，推出14BEF ABC SS ∆=从而求得△BEF 的面积．【详解】解：∵点D 、E 、F 分别为边BC ，AD ，CE 的中点， 1111,,,2222ABD ABC BDE ABD CDE ADC BEF BEC S S S S S S S S ∆∆∆∆∆∆∆∆∴==== 14BEF ABC S S ∆∆∴= ∵△ABC 的面积是4，∴S △BEF =1．故选：B【名师点拨】本题主要考查了与三角形的中线有关的三角形面积问题，关键是根据三角形的面积公式S=12×底×高，得出等底同高的两个三角形的面积相等．变式4-1．（2018·鄂尔多斯市期中）如图，△ABC 的面积为12cm 2，点D 在BC 边上，E 是AD 的中点，则△BCE 的面积是（ ）A ．4cm 2B ．6cm 2C ．8cm 2D ．6cm 2【答案】B 【解析】∵E 是AD 的中点，∴S △BDE =12S △ABD ，S △DEC =12S △ADC ， ∴△BCE 的面积=S △BDE +S △DEC =12×（S △ABD +S △ADC ）=12×△ABC 的面积=6， 故选B ．名师点拨：本题考查的是三角形的面积的计算，掌握三角形的一条中线把三角形分为面积相等的两部分是解题的关键．变式4-2．（2019·沧州市期末）如图，D ，E ，F 分别是边BC ，AD ，AC 上的中点，若S 阴影的面积为3，则△ABC 的面积是（ ）A ．5B ．6C ．7D ．8【答案】D【提示】利用三角形中线将三角形分成面积相等的两部分，111222ABD ACD ABC BDE ABD ADF ADC SS S S S S S ====，，，再得到1148BDE ABC DEF ABC S S S S ==，，所以83ABC S S =阴影部分即可得出. 【详解】∵D 为BC 的中点 ∴1122BDE ABD ADF ADC S S S S ==，，12DEF ADF S S =∴1148BDE ABC DEF ABC S S S S ==， ∴BDE S △+DEF S △=14ABC S +18ABC S =38ABC S ∴ABC S =83S 阴影部分=83×3=8 故选：D【名师点拨】三角形的中线将三角形分成两个面积相等的三角形，根据中线找出图中三角形的面积关系是解决本题的关键.变式4-3．（2019·温州市期中）如图，在△ABC 中，点D 是BC 边上的一点，E ，F 分别是AD ，BE 的中点，连结CE ，CF ，若S △CEF ＝5，则△ABC 的面积为（ ）A ．15B ．20C ．25D ．30【答案】B 【提示】根据题意，利用中线分的三角形的两个图形面积相等，便可找到答案【详解】解：根据等底同高的三角形面积相等，可得∵F 是BE 的中点，S △CFE ＝S △CFB ＝5，∴S △CEB ＝S △CEF +S △CBF ＝10，∵E 是AD 的中点，∴S △AEB ＝S △DBE ，S △AEC ＝S △DEC ，∵S △CEB ＝S △BDE +S △CDE∴S △BDE +S △CDE ＝10∴S △AEB +S △AEC ＝10∴S △ABC ＝S △BDE +S △CDE +S △AEB +S △AEC ＝20故选：B．【名师点拨】熟悉三角形中线的拓展性质：分其两个三角形的面积是相等的，这样便可在实际问题当中家以应用. 考查题型五三角形重心的有关性质典例5．（2019·北京市期中）如图，小明用铅笔可以支起一张质地均匀的三角形卡片，则他支起的这个点应是三角形的（）A．三边高的交点B．三条角平分线的交点C．三边垂直平分线的交点D．三边中线的交点【答案】D【提示】根据题意得：支撑点应是三角形的重心．根据三角形的重心是三角形三边中线的交点．【详解】解：∵支撑点应是三角形的重心，∴三角形的重心是三角形三边中线的交点，故选D．【名师点拨】考查了三角形的重心的概念和性质．注意数学知识在实际生活中的运用．变式5-1．（2019·泉州市期中）如图，在△ABC中，D，E分别是BC，AC的中点，AD和BE相交于点G，若AD=6，则AG的长度为（）A．2 B．3 C．4 D．5【答案】C【提示】根据D、E分别是边BC，AC的中点，AD、BF相交于G，即可得出G为三角形的重心，利用重心的性质得出AG的长即可.【详解】∵D、E分别是边BC，AC的中点，AD、BF相交于G∴G为△ABC的重心∴AG=2DG∵AD=6∴AG=4故选C.【名师点拨】本题考查的是三角形的重心性质，能够判断出点G 是三角形的重心是解题的关键.考查题型六 三角形的角平分线典例6．（2019·滨州市期末）如图，△ABC 中，AD 为△ABC 的角平分线，BE 为△ABC 的高，∠C=70°，∠ABC=48°，那么∠3是（ ）A ．59°B ．60°C ．56°D ．22°【答案】A 【详解】根据题意可得，在△ABC 中，70,48︒︒∠=∠=C ABC ，则62︒∠=CAB ，又AD 为△ABC 的角平分线，1262231︒︒∴∠=∠=÷=又在△AEF 中，BE 为△ABC 的高∴90159359︒︒︒∠=-∠=∴∠=∠=EFA EFA变式6-1．（2019·宁德市期末）如图，已知AE 是ΔABC 的角平分线，AD 是BC 边上的高．若∠ABC=34°，∠ACB=64°，则∠DAE 的大小是（ ）A ．5°B ．13°C ．15°D ．20°【答案】C 【提示】由三角形的内角和定理，可求∠BAC=82°，又由AE 是∠BAC 的平分线，可求∠BAE=41°，再由AD 是BC 边上的高，可知∠ADB=90°，可求∠BAD=56°，所以∠DAE=∠BAD-∠BAE ，问题得解．【详解】在△ABC 中，∵∠ABC=34°，∠ACB=64°, ∴∠BAC=180°−∠B−∠C=82°，∵AE 是∠BAC 的平分线，∴∠BAE=∠CAE=41°. 又∵AD 是BC 边上的高，∴∠ADB=90°，∵在△ABD中∠BAD=90°−∠B=56°，∴∠DAE=∠BAD −∠BAE =15°.【名师点拨】在本题中，我们需要注意到已知条件中已经告诉三角形的两个角，所以利用内角和定理可以求出第三个角，再有已知条件中提到角平分线和高线，所以我们可以利用角平分线和高线的性质计算出相关角，从而利用角的和差求解，在做几何证明题时需注意已知条件衍生的结论.变式6-2．（2019·信阳市期中）如图，在△ABC中，AD是角平分线，DE⊥AB于点E，△ABC的面积为7，AB=4，DE=2，则AC的长是（）A．4 B．3 C．6 D．5【答案】B【解析】过点D作DF⊥AC于F，∵AD是△ABC的角平分线，DE⊥AB，∴DE=DF=2，∴S△ABC=×4×2+AC×2=7，解得AC=3.故选B.变式6-3．（2019·合肥市期中）如图所示，AD、AE分别是△ABC的高和角平分线，且∠B=76°，∠C=36°，则∠DAE 等于（）A．20°B．18°C．45°D．30°【答案】A【提示】根据高线的定义以及角平分线的定义分别得出∠BAD=14°，∠CAD=54°，进而得出∠DAE的度数，进而得出答案．【详解】∵AD ，AE 分别是△ABC 的高和角平分线，且∠B=76°，∠C=36°，∴∠BAD=14°，∠CAD=54°，∴∠BAE=12∠BAC=12×68°=34°， ∴∠DAE=34°-14°=20°．故选：A ．【名师点拨】此题主要考查了高线以及角平分线的性质，得出∠DAE 的度数是解题关键．变式6-4．（2020·泰兴市期中）如图，BE 、CF 是△ABC 的角平分线，∠A=50°，BE 、CF 相交于D ，则∠BDC 的度数是（ ）A ．115°B ．110°C ．100°D ．90°【答案】A【提示】由于∠A=50°，根据三角形的内角和定理，得∠ABC 与∠ACB 的度数和，再由角平分线的定义，得∠DBC+∠DCB 的度数，进而求出∠BDC 的度数．【详解】∵∠A=50°，∴∠ABC+∠ACB=180°﹣50°=130°，∵BE 、CF 是△ABC 的角平分线，∴1122EBC ABC FCB ACB ∠=∠∠=∠，，∴()1652EBC FCB ABC ACB ∠+∠=⨯∠+∠=︒，∴∠BDC=180°﹣65°=115°，故选A ．【名师点拨】考查三角形内角和定理以及角平分线的性质，熟练掌握角平分线的性质是解题的关键.变式6-5．（2019·西安市期末）如图，点O 在ABC 内，且到三边的距离相等，若∠A=60°，则∠BOC 的大小为()A ．135°B ．120°C ．90°D ．60°【答案】B【提示】由条件可知O为三角形三个内角的角平分线的交点，则可知∠OBC+∠OCB=12（∠ABC+∠ACB）=12（180°-∠A），在△BOC中利用三角形的内角和定理可求得∠BOC．【详解】∵O到三边的距离相等∴BO平分∠ABC，CO平分∠ACB∴∠OBC+∠OCB=12(∠ABC+∠ACB)=12(180°−∠A)∵∠A=60°∴∠OBC+∠OCB=60°∴∠BOC=180°−(∠OBC+∠OCB)=180°−60°=120°故选B.【名师点拨】本题考查了角平分线的性质，熟练掌握角平分线把一个角分成两个相等的角是解题的关键．。

专题17 三角形基础【专题目录】技巧1：三角形三边关系的巧用技巧2：三角形的三种重要线段技巧3：三角形内角和与外角的几种常见应用类型【题型】一、三角形的分类【题型】二、构成三角形三边的条件【题型】三、确定三角形第三边的取值范围【题型】四、与三角形高有关的相关计算问题【题型】五、与三角形重心有关的计算【题型】六、与三角形内角和定理的有关的计算【题型】七、利用直角三角形两个锐角互余进行相关计算【题型】八、利用三角形外角性质进行相关计算【考纲要求】1、了解三角形和全等三角形有关的概念，掌握三角形的三边关系．2、理解三角形内角和定理及推论．3、理解三角形的角平分线、中线、高的概念及画法和性质．【考点总结】一、三角形的概念【考点总结】二、三角形中的重要线段和有关的角【技巧归纳】技巧1：三角形三边关系的巧用【类型】一、判断三条线段能否组成三角形1．下列每组数分别表示三根木棒的长度，将它们首尾连接后，不能摆成三角形的一组是()A．4，4，8 B．5，5，1C．3，7，9 D．2，5，42．有四条线段，长度分别为4 cm，8 cm，10 cm，12 cm，选其中三条组成三角形，试问可以组成多少个三角形？分别写出来．【类型】二、求三角形第三边的长或取值范围3．一个三角形的两边长分别为5 cm和3 cm，第三边的长是整数，且周长是偶数，则第三边的长是() A．2 cm或4 cm B．4 cm或6 cm C．4 cm D．2 cm或6 cm4．如果三角形的两边长分别为3和5，则周长l的取值范围是()A．6＜l＜15 B．6＜l＜16C．11＜l＜13 D．10＜l＜165．若三角形的三边长是三个连续的自然数，其周长m满足10＜m＜22，则这样的三角形有________个．【类型】三、三角形的三边关系在等腰三角形中的应用6．等腰三角形的一条边长为6，另一条边长为13，则它的周长为()A．25 B．25或32C．32 D．197．已知等腰三角形ABC的底边BC＝8 cm，|AC－BC|＝2 cm，则AC＝________．8．若等腰三角形的底边长为4，且周长小于20，则它的腰长b的取值范围是____________．【类型】四、三角形的三边关系在代数中的应用9．已知三角形三边长分别为a，b，c，且|a＋b－c|＋|a－b－c|＝10，求b的值．10．已知a，b，c是△ABC的三边长，b，c满足(b－2)2＋|c－3|＝0，且a为方程|x－4|＝2的解，求△ABC的周长．【类型】五、利用三角形的三边关系说明边的不等关系11．如图，已知D，E为△ABC内两点，说明：AB＋AC＞BD＋DE＋CE.技巧2：三角形的三种重要线段【类型】一、三角形的高题型1：找三角形的高1．如图，已知AB⊥BD于点B，AC⊥CD于点C，AC与BD交于点E.△ADE的边DE上的高为________，边AE上的高为________．题型2：作三角形的高2．(动手操作题)画出图中△ABC的三条高．(要标明字母，不写画法)题型3：应用三角形的高3．如图，在△ABC中，BC＝4，AC＝5，若BC边上的高AD＝4.(1)求△ABC的面积及AC边上的高BE的长；(2)求AD∶BE的值．4．如图，在△ABC中，AB＝AC，DE⊥AB，DF⊥AC，BG⊥AC，垂足分别为点E，F，G.试说明：DE＋DF＝BG.【类型】二、三角形的中线题型1：利用中线求长度5．如图，AE是△ABC的中线，已知EC＝4，DE＝2，则BD的长为()A．2 B．3 C．4 D．66．如图，已知BE＝CE，ED为△EBC的中线，BD＝8，△AEC的周长为24，则△ABC的周长为()A．40B．46C．50D．567．在等腰三角形ABC中，AB＝AC，一腰上的中线BD将这个三角形的周长分成15 cm和6 cm两部分，求这个等腰三角形的三边长．题型2：利用中线求面积8．图，△ABC的三边的中线AD，BE，CF的公共点为G，且AG∶GD＝2∶1，若S△ABC＝12，则图中阴影部分的面积是________．9．操作与探索：在图①～③中，△ABC的面积为a.(1)如图①，延长△ABC的边BC到点D，使CD＝BC，连接DA，若△ACD的面积为S1，则S1＝________(用含a的代数式表示)；(2)如图②，延长△ABC的边BC到点D，延长边CA到点E，使CD＝BC，AE＝CA，连接DE，若△DEC的面积为S2，则S2＝________(用含a的代数式表示)，请说明理由；(3)如图③，在图②的基础上延长AB到点F，使BF＝AB，连接FD，FE，得到△DEF，若阴影部分的面积为S3，则S3＝________(用含a的代数式表示)．【类型】三、三角形的角平分线题型1：三角形角平分线定义的直接应用10．(1)如图，在△ABC中，D，E，F是边BC上的三点，且∠1＝∠2＝∠3＝∠4，以AE为角平分线的三角形有__________；(2)如图，若已知AE平分∠BAC，且∠1＝∠2＝∠4＝15°，计算∠3的度数，并说明AE是△DAF的角平分线．题型2：三角形的角平分线与高线相结合求角的度数11．如图，在△ABC中，AD是高，AE是∠BAC的平分线，∠B＝20°，∠C＝60°，求∠DAE的度数．题型3：求三角形两内角平分线的交角度数12．如图，在△ABC中，BE，CD分别为其角平分线且交于点O.(1)当∠A＝60°时，求∠BOC的度数；(2)当∠A＝100°时，求∠BOC的度数；(3)当∠A＝α°时，求∠BOC的度数．技巧3：三角形内角和与外角的几种常见应用类型【类型】一、直接计算角度1．如图，在△ABC中，∠A＝60°，∠B＝40°，点D，E分别在BC，AC的延长线上，则∠1＝________．2．在△ABC中，三个内角∠A，∠B，∠C满足∠B－∠A＝∠C－∠B，则∠B＝________．【类型】二、三角尺或直尺中求角度3．把一个直尺与一块三角尺按如图所示的方式放置，若∠1＝40°，则∠2的度数为()A．125°B．120°C．140°D．130°4．一副三角尺ABC和DEF如图放置(其中∠A＝60°，∠F＝45°)，使点E落在AC边上，且ED∥BC，则∠CEF的度数为________．5．一副三角尺如图所示摆放，以AC为一边，在△ABC外作∠CAF＝∠DCE，边AF交DC的延长线于点F，求∠F的度数．【类型】三、与平行线的性质综合求角度6．如图，AB ∥CD ，∠ABE ＝60°，∠D ＝50°，求∠E 的度数．【类型】四、与截角和折叠综合求角度7．如图，在△ABC 中，∠C ＝70°，若沿图中虚线截去∠C ，则∠1＋∠2等于( )A ．360°B ．250°C ．180°D ．140°8．△ABC 是一个三角形的纸片，点D ，E 分别是△ABC 边AB ，AC 上的两点．(1)如图①，如果沿直线DE 折叠，则∠BDA′与∠A 的关系是____________；(2)如果折成图②的形状，猜想∠BDA′，∠CEA′和∠A 的关系，并说明理由；(3)如果折成图③的形状，猜想∠BDA′，∠CEA′和∠A 的关系，并说明理由．【题型讲解】【题型】一、三角形的分类例1、已知①ABC 中::3:4:7A B C ∠∠∠=，则①ABC 一定是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定【题型】二、构成三角形三边的条件例2、三角形的两边长分别为3cm 和6cm ，则第三边长可能为（ ）A ．2cmB ．3cmC ．6cmD ．9cm【题型】三、确定三角形第三边的取值范围例3、如图，ABCD 的对角线AC ，BD 交于点O ，若6AC =，8BD =，则AB 的长可能是（ ）A ．10B ．8C ．7D ．6【题型】四、与三角形高有关的相关计算问题例4、如图，在ABC ∆中，90ACB ∠=︒，过点C 作CD AB ⊥于点D ，已知12AC =，13AB =，则CD 的长是（ ）A ．5B ．6013C ．6D ．6512【题型】五、与三角形重心有关的计算例5、如图，在①ABC 中，AD ，BE 分别是BC ，AC 边上的中线，且AD①BE ，垂足为点F ，设BC ＝a ，AC ＝b ，AB ＝c ，则下列关系式中成立的是（ ）A ．a 2+b 2＝5c 2B ．a 2+b 2＝4c 2C ．a 2+b 2＝3c 2D ．a 2+b 2＝2c 2【题型】六、与三角形内角和定理的有关的计算例6、如图所示，直线EF //GH ，射线AC 分别交直线EF 、GH 于点B 和点C ，AD ①EF 于点D ，如果①A ＝20°，则①ACG ＝（ ）A ．160°B ．110°C ．100°D ．70°【题型】七、利用直角三角形两个锐角互余进行相关计算例7、如图，在四边形ABCD 中，CD①AB ，AC①BC ，若①B ＝50°，则①DCA 等于（ ）A ．30°B ．35°C ．40°D ．45°【题型】八、利用三角形外角性质进行相关计算例8、如图，已知//,AB CD 直线AC 和BD 相交于点,E 若70,40ABE ACD ∠=︒∠=︒，则AEB ∠等于（ ）A ．50︒B ．60︒C ．70︒D ．80︒三角形基础（达标训练）一、单选题1．如图，在①ABC 中，D 为BC 的延长线上一点，若①B =70°，①1=110°，则①A =（ ）A ．35°B ．40°C ．55°D ．70°2．如图，已知直线AE ①BD ，且①C ＝15°，①1＝110°，则①2的度数是（ ）A ．45°B ．55°C ．65°D ．75°3．数学课上，同学们在作ABC 中AC 边上的高时，共画出下列四种图形，其中正确的是（ ）．A ．B ．C ．D ．4．某班级计划在耕读园里搭三角形围栏，可以选择三种长度的木条组合是（ ）A ．3、4、8B ．4、4、8C ．3、5、6D ．5、6、115．如图，人字梯中间设计一“拉杆”，在使用梯子时，固定拉杆会增加安全性．这样做蕴含的数学道理是（ ）A ．三角形具有稳定性B ．两点之间线段最短C ．经过两点有且只有一条直线D ．垂线段最短二、填空题6．如图，点B 、C 、D 在同一直线上，AB ①CE ，若①A ＝55°，①ACB ＝65°，则①1为___°．7．如图，在Rt ABC 中，90C ∠=︒，点E 、F 分别是边AB AC 、上，且AF EF =．若72CFE ∠=︒，则B ∠=_________°．三、解答题8．如图，在四边形ABCD 中，AB CD ∥，130BCD ∠=︒，BE 平分ABC ∠交AD 于点E ，交CD 的延长线于点F ．(1)求ABE ∠的大小；(2)若48ADC ∠=︒，求DEF ∠的大小．三角形基础（提升测评）一、单选题1．如图，点C ，D 在直线AB 上，OC OD ⊥，若120ACO ∠=，则①BDO 的大小为（ ）A ．120B ．140C ．150D ．1602．一把直尺和一块三角板ABC （含45°角）如图所示摆放，直尺一边与三角板的两直角边分别交于点D 和点E ，另一边与三角板的两直角边分别交于点F 和点A ，①CED =25°，则①BF A 的大小为（ ）A ．105°B ．110°C ．115°D ．125°3．如图，BE 是ABC 的中线，AD BC ⊥交BE 于点F ，且BD AE =，50∠︒=EAD ，则EBC ∠的度数为（ ）A ．30°B ．25°C ．20°D ．15°4．如图，在ABC 中，BD 为AC 边上的中线，已知8BC =，5AB =，BCD △的周长为20，则ABD △的周长为（ ）A ．17B ．23C ．25D ．285．如图，Rt ①ABC 中，①C ＝90°，BD 平分①ABC 交AC 于点D ，点E 为AB 的中点，若AB ＝12，CD ＝3，则①DBE 的面积为（ ）A ．10B ．12C ．9D ．6二、填空题6．如图，在ABC ∆ 中，AD 平分CAB ∠ ，AB AC CD =+ ，若81CAB ∠=︒ ，则B ∠ 度数为______．7．如图，在ABC 中，AB AC =，点D 在边BC 上，AD BD =，如果102∠=︒DAC °，那么BAD ∠=___________度．三、解答题8．如图，在Rt ABC △中，90BAC ∠=︒，将Rt ABC △绕点A 旋转一定的角度得到Rt ADE △，且点E 恰好落在边BC 上．(1)求证：AE 平分CED ∠；(2)连接BD ，求证：90DBC ∠=︒．。

专题01 三角形的基本概念和性质知识对接考点一、三角形的概念及其性质1．三角形的概念由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2．三角形的分类(1)按边分类：(2)按角分类：3．三角形的内角和外角(1)三角形的内角和等于180°.(2)三角形的任意一个外角等于和它不相邻的两个内角之和；三角形的一个外角大于任何一个和它不相邻的内角.4．三角形三边之间的关系三角形任意两边之和大于第三边，任意两边之差小于第三边.5．三角形内角与对边对应关系在同一个三角形内，大边对大角，大角对大边；在同一三角形中，等边对等角，等角对等边.6．三角形具有稳定性.专项训练一、单选题1．（2021·福建九年级其他模拟）如图是由18根完全相同的火柴棒摆成的图形，如果拿掉其中的3根，剩下的图形中恰好有7个三角形，那么拿掉的3根火柴棒可能是（）A．GD，EI，MH B．GF，EF，MF C．DE，GH，MI D．AD，AG，GD 【答案】A【分析】根据各选项画出相应图形，再数三角形的个数即可得．【详解】A、拿掉GD，EI，MH后，剩下的图形如下：图形中恰好有7个三角形，此项符合题意；B、拿掉GF，EF，MF后，剩下的图形如下：图形中有4个三角形，此项不符题意；C、拿掉DE，GH，MI后，剩下的图形如下：图形中有6个三角形，此项不符题意； D 、拿掉AD ，AG ，GD 后，剩下的图形如下：图形中有9个三角形，此项不符题意； 故选：A ． 【点睛】本题考查了三角形的概念，正确画出剩下的图形是解题关键．2．（2021·黑龙江九年级三模）有长度分别为1,2,3cm cm cm 的小木棒若干，从中任取三根首尾顺次相接组成三角形，则能组成形状不同的三角形（ ） A ．4种 B ．5种C ．6种D ．7种【答案】B 【分析】根据三角形三边的关系任意两边之和大于第三边与任意两边之差小于第三边进行分类讨论即可． 【详解】 解：∵1+2=3，∵三边长只能组成等边三角形或者等腰三角形，∵长度分别为1,1,1cm cm cm ，2,2,2cm cm cm ，3,3,3m cm cm 组成等边三角形，边长不等，但形状相同，则为一种；∵当两边长相等时有：2,2,1cm cm cm ，3,3,1cm cm cm ，2,2,3cm cm cm ，3,3,2cm cm cm ，4种形状不同的三角形； 因此共有5种，故选：B．【点睛】本题考查了三角形的三边关系，关键在于根据任意两边之和大于第三边与任意两边之差小于第三边进行分析．3．（2021·陕西西安·交大附中分校九年级其他模拟）锐角∵ABC中，∵B＝45°，BC则AC的长可以是（）A．1B C D【答案】D【分析】作CD∵AB于D，先利用等腰直角三角形的性质和三角函数求出BD=CD=1，然后利用勾股定理进行逐一判断四个选项是否满足题意即可.【详解】解：作CD∵AB于D，如图所示：∵∵B＝45°，∵∵BCD是等腰直角三角形，∵BD＝CD＝sin=1BC B，∵BCD＝45°，当AC＝1时，点D与A重合，∵ABC是直角三角形，选项A不符合题意；当AC1AD CD==，则∵ACD是等腰直角三角形，∵ACD＝45°，∵∵ACB＝90°，∵ABC是直角三角形，选项B不符合题意；当AC AC＜CD，∵∵ACD＞∵A，则∵ABC是钝角三角形，选项C不符合题意；当AC时，12AD CD ==<∵∵ACD＜∵A，则∵ABC是锐角三角形；选项D符合题意，故选D．【点睛】本题主要考查了等腰直角三角形的性质，解直角三角形，勾股定理，三角形角与边的关系，解题的关键在于能够熟练掌握相关知识进行求解.4．（2021·连云港市新海实验中学九年级二模）如图，在Rt ABC 中，∵ACB =90°，BC =2，∵BAC =30°，将ABC 绕顶点C 逆时针旋转得到∵A 'B 'C '， M 是BC 的中点，P 是A 'B '的中点， 连接PM ，则线段PM 的最大值是（ ）A ．4B ．2C ．3D．【答案】C 【分析】连接PC ，分别求出PC ，CM 的长，然后根据PM MC PC ≤+即可得到答案． 【详解】解：如图所示，连接PC ， ∵∵ACB =90°，BC =2，∵BAC =30°， ∵AB =2BC =4，由旋转的性质可知：=90A CB ACB ''=∠∠，4A B AB ''==， ∵P 、M 分别是A B ''、BC 的中点， ∵122PC A B ''==，112CM BC ==，∵3PM MC PC ≤+=，∵PM 的最大值为3，且此时P 、C 、M 三点共线， 故选C ．【点睛】本题主要考查了旋转的性质，直角三角形斜边的中线，三角形三边的关系，解题的关键在于能够熟练掌握相关知识进行求解．5．（2021·福建省同安第一中学）下列长度的三条线段能组成三角形的是（ ） A ．3，4，8 B ．5，6，11C ．4，4，8D ．8，8，8【答案】D 【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析． 【详解】解：A 、3+4＜8，不能构成三角形； B 、5+6=11，不能构成三角形； C 、4+4=8，不能构成三角形； D 、8+8＞8，能构成三角形． 故选：D ． 【点睛】此题主要考查了三角形三边关系，根据第三边的范围是：大于已知的两边的差，而小于两边的和是解决问题的关键．6．（2021·福建九年级其他模拟）若某三角形的两边长分别为5和9，则该三角形第三边的长可能是（ ） A ．4 B ．5C ．14D ．15【答案】B 【分析】根据三角形的三边关系即可得． 【详解】设该三角形第三边的长为a ，由三角形的三边关系得：9559a -<<+，即414a <<， 观察四个选项可知，只有选项B 符合， 故选：B ．【点睛】本题考查了三角形的三边关系，熟练掌握三角形的三边关系是解题关键． 本号资料皆来源于微信公众号：数学第六*感7．（2021·辽宁）如图，在3×3的网格中，每个小正方形的边长均为1，点A ，B ，C 都在格点上，则S ∵ABC 的面积为（ ）A ．52B ．3C ．72D ．4【答案】C 【分析】利用割补法求∵ABC 面积等于大正方形面积-三个三角形面积即可． 【详解】解：在网格中添加字母如图， S ∵AEB =1112122AE BE ⋅=⨯⨯=， S ∵AFC =1123322AF FC ⋅=⨯⨯=， S ∵BGC =11313222BG GC ⋅=⨯⨯=，S 正方形=9EF FC ⋅=，∵S ∵ABC = S 正方形- S ∵AEB - S ∵AFC - S ∵BGC =9-1-3-3722=． 故选择C ．【点睛】本题考查网格三角形面积，掌握用割补法求网格三角形面积的方法是解题关键． 8．（2021·福建宁德市·）下列长度的三条线段，能组成三角形的是（ ）A ．2，3，4B ．2，3，5C ．2，2，4D ．2，2，5【答案】A 【分析】根据三角形的三边关系进行分析判断． 【详解】解：根据三角形任意两边的和大于第三边，得 A 中，3+2＞4，能够组成三角形； 符合题意 B 中，2+3＝5，不能组成三角形；不符合题意 C 中，2+2＝4，不能组成三角形；不符合题意 D 中，2+2＜5，不能组成三角形．不符合题意 故选：A ． 【点睛】本题考查了能够组成三角形三边的条件：用两条较短的线段相加，如果大于最长的那条线段就能够组成三角形．9．（2021·陕西咸阳市·九年级一模）如图，CM 是ABC ∆的中线，BCM 的周长比ACM ∆的周长大3cm ，8cm BC =，则 AC 的长为（ ）A ．3cmB ．4cmC ．5cmD ．6cm【答案】C 【分析】根据三角形中线的特点进行解答即可． 【详解】解：∵CM 为∵ABC 的AB 边上的中线， ∵AM =BM ，∵∵BCM 的周长比∵ACM 的周长大3cm ， ∵（BC +BM +CM ）-（AC +AM +CM ）=3cm ， ∵BC -AC =3cm ， ∵BC =8cm ， ∵AC =5cm ， 故选：C ．【点睛】本题考查的是三角形的中线，熟知三角形一边的中点与此边所对顶点的连线叫做三角形的中线是此题的关键． 本号资*料皆来源于微信公众号：数学第六感10．（2021·福建省厦门第六中学九年级三模）如图，在ABC 中，BC 边上的高是（ ）A ．CDB ．AEC ．AFD ．AH【答案】C 【分析】根据从三角形顶点向对边作垂线，顶点和垂足之间的线段叫做三角形的高，即可得出结论． 【详解】由图可知，过点A 作BC 的垂线段AF ， 则ABC 中，BC 边上的高是AF ， 故选：C ． 【点睛】本题主要考查了三角形高的定义，熟练掌握定义是解题的关键． 二、填空题11．（2021·内蒙古包头市·）在ABC 中，,A B ∠∠都是锐角，且满足2sin cos 0A B ⎫+=⎪⎪⎝⎭，则三角形的形状是__． 【答案】钝角三角形 【分析】根据题意非负数之和为零，只有一种情况，即零加零等于零；利用特殊角锐角三角函数值分别求出,A B ∠∠,再根据三角形内角和定理求得C ∠,判断三角形的形状即可． 【详解】2sin 0cos 0A B ⎫≥≥⎪⎪⎝⎭∴sin0A=cos0B=45,30A B∴∠=︒∠=︒1804530105C∴∠=︒-︒-︒=︒∴ABC是钝角三角形．故答案为：钝角三角形．【点睛】本题考查了特殊角的锐角三角函数值，三角形的分类，绝对值的非负性，实数平方的非负性，熟练特殊角的锐角三角函数值是解题的关键．12．（2021·浙江九年级专题练习）现有下列长度的五根木棒：3，5，8，10，13，从中任取三根，可以组成三角形的概率为________．【答案】2 5【分析】求出任取三根木棒的所有情况，再求出能组成三角形的所有情况，利用概率公式直接计算即可.【详解】五根木棒，任意取三根共有10种情况：3、5、83、5、103、5、133、8、103、8、133、10、135、10、135、8、105、8、138、10、13其中能组成三角形的有：∵3、8、10，由于8-3<10<8+3,所以能构成三角形；∵5、10、13，由于10-5<13<10+5，所以能构成三角形；∵5、8、10，由于8-5<10<8+5，所以能构成三角形；∵8、10、13，由于10-8<13<10+8，所以能构成三角形；所以有4种方案符合要求，故能构成三角形的概率是P=410=25，故答案为：2 5 .【点睛】此题考查三角形的三边关系，列举法求事件的概率，列举法求概率的关键是在列举所有情况时考虑要全面，不能重复也不能遗漏.13．（2021·扬州市梅岭中学）判断命题“若ABC的边a、b、c满足22a b ac bc-=-，则ABC 是等腰三角形”的真假，答：_________．（选填“真命题”或“假命题”或“无法判断”）【答案】真命题【分析】根据22a b ac bc-=-变形即可求得,,a b c的关系，再进行判断即可【详解】22a b ac bc-=-()()()a b a b c a b∴+-=-a b c+≠a b∴-=a b∴=∴ABC是等腰三角形故答案为：真命题【点睛】本题考查了命题，因式分解，三角形三边关系，等腰三角形的定义，因式分解后根据三角形三边关系判断是解题的关键．14．（2021·内蒙古包头市·）如图，在边长为4的正方形ABCD中，点E是BC的中点，点F 在CD上，且CF=3DF，AE，BF相交于点G ，则AGF的面积是________．【答案】5611．【分析】延长AG交DC延长线于M，过G作GH∵CD，交AB于N，先证明∵ABE∵∵MCE，由CF=3DF，可求DF =1，CF =3，再证∵ABG ∵∵MFG ，则利用相似比可计算出GN ，再利用两三角形面积差计算S ∵DEG 即可． 【详解】解：延长AG 交DC 延长线于M ，过G 作GH ∵CD ，交AB 于N ，如图， ∵点E 为BC 中点， ∵BE =CE ，在∵ABE 和∵MCE 中， ABE MCE BE CEAEB MEC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∵∵ABE ∵∵MCE （ASA ）， ∵AB =MC =4，∵CF =3DF ，CF +DF =4，∵DF =1，CF =3，FM =FC +CM =3+4=7， ∵AB∥MF ，∵∵ABG =∵MFG ，∵AGB =∵MGF ， ∵∵ABG ∵∵MFG ， ∵47AB GN MF GH ==， ∵4GN GH +=， ∵1628,1111GN GH ==， S ∵AFG =S ∵AFB -S ∵AGB =1111165644422221111AB HN AB GN ⋅-⋅=⨯⨯-⨯⨯=， 故答案为5611．【点睛】本题考查了正方形的性质，三角形全等判定与性质，三角形相似判定与性质，割补法求三角形面积，掌握正方形的性质，三角形全等判定与性质，三角形相似判定与性质，割补法求三角形面积，熟练运用相似比计算线段的长是解题关键．15．（2021·四川省宜宾市第二中学校九年级三模）如图，在Rt∵ABC中，AB＝AC，D、E 是斜边BC上两点，且∵DAE＝45°，将∵ADC绕点A顺时针旋转90°后，得到∵AFB，连接EF，下列结论：∵∵AED∵∵AEF；∵AE ADBE CD=；∵∵ABC的面积等于四边形AFBD的面积；∵BE2+DC2＝DE2；∵BE＝EF﹣DC；其中正确的选项是_____________（填序号）【答案】∵∵∵【分析】∵根据旋转的性质知∵CAD=∵BAF，AD=AF，因为∵BAC=90°，∵DAE=45°，所以∵CAD+∵BAE=45°，可得∵EAF=45°=∵DAE，由此即可证明∵AEF∵∵AED；∵当∵ABE∵∵ACD时，该比例式成立；∵根据旋转的性质，∵ADC∵∵ABF，进而得出∵ABC的面积等于四边形AFBD的面积；∵据∵知BF=CD，EF=DE，∵FBE=90°，根据勾股定理判断．∵根据∵知道∵AEF∵∵AED，得CD=BF，DE=EF；由此即可确定该说法是否正确．【详解】解：∵根据旋转的性质知∵CAD=∵BAF，AD=AF．本号资料皆来源于微@信公众号：数学第*六感∵∵BAC=90°，∵DAE=45°，∵∵CAD+∵BAE=45°，∵∵EAF=45°，∵∵AED∵∵AEF；故本选项正确；∵∵AB=AC，∵∵ABE=∵ACD；∵当∵BAE=∵CAD时，∵ABE∵∵ACD，∵AE AD BE CD=；当∵BAE≠∵CAD时，∵ABE与∵ACD不相似，即AE AD BE CD≠；∵此比例式不一定成立，故本选项错误； ∵根据旋转的性质知∵ADC ∵∵AFB ，∵S ∵ABC =S ∵ABD +S ∵ABF =S 四边形AFBD ，即三角形ABC 的面积等于四边形AFBD 的面积，故本选项正确；∵∵∵FBE =45°+45°=90°， ∵BE 2+BF 2=EF 2．∵∵ADC 绕点A 顺时针旋转90°后，得到∵AFB ， ∵∵AFB ∵∵ADC ， ∵BF =CD ． 又∵EF =DE ，∵BE 2+DC 2=DE 2，故本选项正确；∵根据∵知道∵AEF ∵∵AED ，得CD =BF ，DE =EF ，∵BE +DC =BE +BF ＞DE =EF ，即BE +DC ＞FE ，故本选项错误．综上所述：正确的说法是∵∵∵． 本@号资料皆来源于微信公众号：数学@第六#感 故答案为：∵∵∵．【点睛】本题考查了图形的旋转变换以及全等三角形的判定等知识，三角形三边的关系，相似三角形的性质与判定，解题时注意旋转前后对应的相等关系． 三、解答题16．（2021·浙江）如图，在84⨯的正方形网格中，按ABC 的形状要求，分别找出格点C ，且使5BC =，并且直接写出对应三角形的面积．【答案】见解析；10S =；252S =；12S =【分析】根据全等三角形的性质，勾股定理，角的分类去求解即可【详解】解：钝角三角形时，如图，∵BC∵BD，BC=5，∵∵ABC是钝角三角形，根据平行线间的距离处处相等，得BC边上高为BD=4,∵11=45=10 22S BC BD=⨯⨯⨯；直角三角形时，如图，取格点F使得BF=4，FC=3，根据勾股定理，得BC，∵AE=BF=4，EB=FC=3，∵AEB=∵BFC=90°，∵∵AEB∵∵BFC，∵∵EAB=∵FBC，∵∵EAB+∵EBA=90°，∵∵FBC+∵EBA=90°，∵∵ABC =90°，∵∵ABC是直角三角形，根据勾股定理，得AB，∵11=5522S BA BC=⨯⨯⨯252=；锐角三角形时，如图，取格点M使得BM=3，CM=4，根据勾股定理，得BC，根据直角三角形时的作图，知道∵ABN=90°，本号资料皆来源于微信公众号：#数学第六感∵∵ABC＜∵ABN，∵∵ABC＜90°∵AB=BC，∵∵ABC是等腰三角形，∵∵A=∵C＜90°，∵∵ABC是锐角三角形，∵1462S=⨯⨯=12；【点睛】本题考查了网格上的作图，等腰三角形的性质，勾股定理，三角形全等的性质和判定，平行线间的距离处处相等，根据题意，运用所学构造符合题意的格点线段是解题的关键．17．（2021·四川省宜宾市第二中学校九年级一模）如图，分别过点C、B作ABC的BC边上的中线AD及其延长线的垂线，垂足分别为E、F．（1）求证：BF CE=；（2）若ACE的面积为4，CED的面积为3，求∵ABF的面积．本号资料#皆#来源于微信公众号：数学第*六感【答案】（1）见解析；（2）10【分析】（1）根据垂直，中线的性质，证明∵CDE∵∵BDF即可；（2）根据三角形全等，确定∵BDF和∵CDE的面积相等，根据中线的性质，得∵ABD和∵ACD 的面积相等，计算即可．【详解】（1）证明：∵AD 是BC 边上的中线， ∵BD =CD ，∵CE ∵AF ，BF ∵AF ， ∵∵CED =∵F =90°， ∵∵CDE =∵BDF , ∵CED F CDE BDF DC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵CDE ∵∵BDF , ∵CE =BF ；（2）解：∵AD 是BC 边上的中线， ∵BD =CD ，∴ΔΔABD ACD S S =，Δ4ACE S =，3CEDS=∴ΔΔACD ACE CEDS S S =+43=+7=∴7ABDS=由（1）已证：∵CDE ∵∵BDF ,∴ΔΔ3BDF CDE S S == ∴ΔΔΔABF ABD BDF S S S =+73=+10=． 【点睛】本题考查了三角形中线的性质，三角形的全等的判定和性质，三角形的面积，熟练掌握三角形全等的判定方法，灵活运用三角形中线与三角形面积的关系是解题的关键．18．（2021·吉林九年级其他模拟）图∵、图∵、图∵均是33⨯的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，线段AB的端点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求以AB为边画ABC．要求：（1）在图∵中画一个钝角三角形，在图∵中画一个直角三角形，在图∵中画一个锐角三角形；（2）三个图中所画的三角形的面积均不相等；（3）点C在格点上．【答案】见详解（答案不唯一）【分析】因为点C在格点上，故可将直尺的一角与线段AB点A重合，直尺边长所在直线经过33正方形网格左上角第一个格点，继而以点A为旋转中心，逆时针旋转直尺，当直尺边长所在直线与正方形格点相交时，确定点C的可能位置，顺次连接A、B、C三点，按照题目要求排除不符合条件的C点，作图完毕后可根据三角形面积公式判断其面积是否相等．【详解】经计算可得下图中：图∵面积为12；图∵面积为1；图∵面积为32，面积不等符合题目要求（2），且符合题目要求（1）以及要求（3）．故本题答案如下：【点睛】本题考查三角形的分类及其作图，难度较低，按照题目要求作图即可．19．（2021·江苏九年级月考）如图，在Rt ∵ABC 中，∵C =90°，点D 是AB 的中点，AC ＜BC ． (1)试用无刻度的直尺和圆规．．．．．．．．．，在BC 上作一点E ，使得直线ED 平分ABC 的周长；(不要求写作法，但要保留作图痕迹)．(2)在(1)的条件下，若DE 分Rt ∵ABC 面积为1﹕2两部分，请探究AC 与BC 的数量关系．【答案】(1)作图见解析；(2)BC=3AC 【分析】（1）在BC 上用圆规截取BF=AC ，然后再作FC 的垂直平分线，其与BC 的交点即为E 点，最后连接DE 即可．（2）连接DC ，由点D 是AB 的中点，则S ∵ADC =S ∵BCD ;设S ∵ADC =S ∵BCD =x ，S ∵DEC =y ，则有（x+y ）：（x -y ）=2:1，解得x=3y ，即E 为BC 的三等分点，即可说明BC=3EC;有EC=EF=BF=AC,即BC=3AC ． 【详解】解：（１）如图：DE 即为所求；（2）连接DC ∵点D 是AB 的中点 ∵S ∵ADC =S ∵BCD设S ∵ADC =S ∵BCD =x ，S ∵DEC =y ， ∵S ∵BDC :S 四边形CADE =1:2∵(S ∵BDC -S ∵DCE ):( S ∵ADC +S ∵DCE )=1:2, ∵2（x -y ）=x+y ，即x=3y∵点E 为BC 的三等分点, 即BC=3EC ∵EC=EF=BF=AC ∵BC=3AC ．【点睛】本题考查了尺规作图、三角形中线的性质、三角形n 等分点的性质等知识点，其中根据题意完成（1）是解答本题的关键．20．（2021·广东）若a,b,c 为∵ABC 的三边长 （1）化简：-+2+-||a b c a b c b a c -+---（2）若a,b ()220b -=，且c 是整数，求c 的值. 【答案】（1）2a ；（2）1<c<5． 【分析】（1）由a ，b ，c 为三角形ABC 的三边，利用三角形的两边之和大于第三边列出关系式，判断出绝对值里边式子的正负，利用绝对值的代数意义化简，去括号合并即可得到结果． （2）根据非负数的性质列式求出a 、b ，再根据三角形的任意两边之和大于第三边，两边之差小于第三边求解即可． 【详解】（1）∵a ，b ，c 为∵ABC 的三边， ∵a+b>c ，即−a−b+c<0，a+c>b ，即a−b+c>0，b−a−c<0，则|−a−b+c|+2|a−b+c|−|b−a−c|=a+b−c+2(a−b+c)+b−a−c=a+b−c+2a−2b+2c+b−a−c=2a ； （2）由题意得，a−3=0，b−2=0， 解得a=3，b=2， ∵3−2=1，3+2=5， ∵1<c<5． 【点睛】此题考查二次根式的性质，绝对值，三角形三边关系的应用，解题关键在于利用两边之和大于第三边.21．（2021·河南省淮滨县第一中学九年级一模）先阅读下面的内容，再解决问题， 例题：若2222690m mn n n ++-+=，求m 和n 的值． 解：∵2222690m mn n n ++-+=∵2222690m mn n n n +++-+=∵22()(3)0m n n ++-= ∵0,30,m n n +=-=∵3, 3.m n =-=问题（1）若∵ABC 的三边长a b c 、、都是正整数，且满足22661830a b a b c +--++-=，请问∵ABC 是什么形状?说明理由.（2）若224212120x y xy y +-++=，求y x 的值．（3）已知24,6130a b ab c c -=+-+=，则a b c ++= ．【答案】（1）∵ABC 是等边三角形，理由见解析；（2）14；（3）3 【分析】（1）先把a 2+b 2-6a -6b +18+|3-c |=0，配方得到（a -3）2+|3-c |=0，根据非负数的性质得到a =b =c =3，得出三角形的形状即可；（2）首先把x 2+4x 2-2xy +12y +12=0，配方得到（x -y ）2+3(y +2)2=0，再根据非负数的性质得到x =-2，代入求得值即可；（3）首先根据a -b =8，ab +c 2-16c +80=0，应用因式分解的方法，判断出（a -4）2+（c -8）2=0，求出A 、B 、C 的值各是多少；然后把a 、b 、c 的值求和，求出a +b +c 的值是多少即可.【详解】解：（1）∵ABC 是等边三角形，理由如下：由题意得()()223330a b c -+-+-=∵3a b c ===∵∵ABC 是等边三角形．（2）由题意得()()22320x y y -++=∵2x y ==-． ∵14y x =． （3）∵24,6130a b ab c c -=+-+=，即a =b +4，（b +4)b +c 2 –6c +13=0，∵（b 2+4b +4 ）+（c 2 –6c +9）=0，∵b +2=0，c –3=0，∵b = –2，c =3，a =2，∵a +b +c =3．【点睛】此题主要考查了因式分解的应用，要熟练掌握，解答此题的关键是要明确：用因式分解的方法将式子变形时，变形的可以是整个代数式，也可以是其中的一部分.此题还考查了三角形的三条边之间的关系，要熟练掌握，解答此题的关键是要明确：任意两边之和大于弟三边；任意两边之差小于第三边.22．（2021·江西九年级其他模拟）如图，在正方形网格中，ABC的顶点均在格点上，请仅用无刻度直尺完成以下作图．（保留作图痕迹）（1）在图1中，作ABC的高AM；（2）在图2中，作ABC的高AN．（提示：三角形的三条高所在的直线交于一点）【答案】（1）见解析；（2）见解析【分析】（1）格点ABC中AB=AC且垂直，以AB、AC为边作正方形，连接对角线AM即可得到BC的高AM；（2）在正方形网格中，m×n格的对角线与n×m格的对角线互相垂直，AB是1×4格的对角线，那么4×1格的对角线与之垂直，又需过点C，所以如图所示的CF∵AB交AB与点H，同理AC是4×3格的对角线，那么3×4格的对角线与之垂直，又需过点B，所以如图所示的BE∵AC交AC与点D，又三角形的三条高所在的直线交于一点，所以连接AG并延长交BC 与点N，即AN为所求．【详解】（1）如图1，∵格点ABC中AB=AC且垂直，∵以AB、AC为边作正方形，连接对角线AM即AM∵BC（2）如图2，∵AB是1×4格的对角线∵过点C 且是4×1格的对角线即为如图所示的CF ，∵CF ∵AB同理AC 是4×3格的对角线，∵过点B 且是3×4格的对角线即为如图所示的BE∵BE ∵AC∵三角形的三条高所在的直线交于一点∵连接AG 并延长交BC 与点N ，即AN 为所求．【点睛】本题主要考查了求作格点三角形的高线问题，主要方法有：构造特殊形状，如：正方形，菱形，利用对角线垂直的性质作高；正方形网格中，m ×n 格的对角线与n ×m 格的对角线互相垂直；三角形的三条高所在的直线交于一点，掌握以上的作图方法是解题的关键． 23．（2021·福建省福州咨询有限公司九年级其他模拟）如图，在ABC 中，按以下步骤作图：∵以点B 为圆心，任意长为半径作弧，分别交边AB ，BC 于点D ，E ；∵分别以点D ，E 为圆心，大于12DE 的相同长度为半径作弧，两弧交于点F ； ∵作射线BF 交AC 于点G ．（1）根据上述步骤补全作图过程（要求：规作图，不写作法，保留作图痕迹）； （2）如果8AB =，12BC =，那么ABG 的面积与CBG 的面积的比值是________．【答案】（1）见解析；（2）23【分析】 （1）根据尺规作图要求,按给定的步骤与作法画图即可；（2）根据角分线性质，两三角形的AB 与BC 边上的高相等，可得面积比为底的比即可．【详解】解：（1）根据步骤（1）得弧线交AB ，BC 于点D ，E ，根据步骤（2）得两弧交点F ，根据步骤（3）得射线BG ，根据作图的步骤与图形结合得BG 平分∵ABC ；如图所示，即为所求．（2）过点G 作GH ∵BC 于H ，GM ∵射线AB 于M ，∵BG 平分∵ABC ，∵GM =GH ，S ∵ABG =118422AB GM GM GM ⋅=⨯⨯=， S ∵BCG =1112622BC GH GH GH ⋅=⨯⨯=， S ∵ABG : S ∵BCG =4:64:62:3GM GH GH GH ==，故答案为：23． 【点睛】本题考查尺规作图，角平分线性质，三角形面积，掌握尺规作图步骤与要求，角平分线性质，三角形面积，利用角平分线性质得出两三角。

小专题(一) 三角形三条重要线段的应用类型1 三角形的高的应用1．如图,在△ABC 中,AB ＝AC,DE ⊥AB,DF ⊥AC,BG ⊥AC,垂足分别为点E,F,G.求证：DE ＋DF ＝BG.证明：连接AD,∵S △ABC ＝S △ABD ＋S △ADC , ∴12AC·BG＝12AB·DE＋12AC·D F. 又∵AB ＝AC,∴BG ＝DE ＋DF.类型2 三角形的中线的应用2．如图,已知BE ＝CE,ED 为△EBC 的中线,BD ＝8,△AEC 的周长为24,则△ABC 的周长为(A )A ．40B ．46C ．50D ．563．(广东中考改编)如图,△ABC 的三边的中线AD,BE,CF 的公共点为G,且AG ∶GD ＝2∶1,若S △ABC ＝12,则图中阴影部分的面积是4．4．在等腰三角形ABC 中,AB ＝AC,一腰上的中线BD 将这个三角形的周长分成15 cm 和6 cm 两部分,求这个等腰三角形的三边长．解：设AD ＝CD ＝x cm ,则AB ＝2x cm ,BC ＝(21－4x)cm .依题意,有AB ＋AD ＝15 cm 或AB ＋AD ＝6 cm ,则有2x ＋x ＝15或2x ＋x ＝6,解得x ＝5或x ＝2.当x ＝5时,三边长为10 cm ,10 cm ,1 cm ；当x＝2时,三边长为4 cm,4 cm,13 cm,而4＋4＜13,故不成立．∴这个等腰三角形的三边长分别为10 cm,10 cm,1 cm.类型3三角形的角平分线的应用5．(1)如图,在△ABC中,D,E,F是边BC上的三点,且∠1＝∠2＝∠3＝∠4,以AE为角平分线的三角形有△ABC和△ADF；(2)如图,若已知AE平分∠BAC,且∠1＝∠2＝∠4＝15°,计算∠3的度数,并说明AE是△DAF的角平分线．解：∵AE平分∠BAC,∴∠BAE＝∠CAE.又∵∠1＝∠2＝15°,∴∠BAE＝∠1＋∠2＝15°＋15°＝30°.∴∠CAE＝∠BAE＝30°,即∠CAE＝∠4＋∠3＝30°.又∵∠4＝15°,∴∠3＝15°.∴∠2＝∠3＝15°,∴AE是△DAF的角平分线．6．如图,在△ABC中,BE,CD分别为其角平分线且交于点O.(1)当∠A＝60°时,求∠BOC的度数；(2)当∠A＝100°时,求∠BOC的度数；(3)当∠A＝α°时,求∠BOC的度数．解：(1)∵∠A ＝60°,∴∠ABC ＋∠ACB ＝120°.∵BE,CD 为△ABC 的角平分线,∴∠EBC ＋∠DCB ＝60°,∴∠BOC ＝180°－(∠EBC ＋∠DCB)＝180°－60°＝120°.(2)∵∠A ＝100°,∴∠ABC ＋∠ACB ＝80°.∵BE,CD 为△ABC 的角平分线,∴∠EBC ＋∠DCB ＝40°,∴∠BOC ＝180°－(∠EBC ＋∠DCB)＝180°－40°＝140°.(3)∵∠A ＝α°,∴∠ABC ＋∠ACB ＝180°－α°.∵BE,CD 为△ABC 的角平分线,∴∠EBC ＋∠DCB ＝90°－12α°, ∴∠BOC ＝180°－(∠EBC ＋∠DCB)＝180°－(90°－12α°)＝90°＋12α°.。

专题01三角形（突破核心考点）【聚焦考点+题型导航】考点一三角形三边关系考点二三角形的稳定性考点三三角形中的高线、中线、角平分线考点四三角形的内角、外角考点五多边形的对角线、内角和【知识梳理+解题方法】一、三角形的定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形．要点诠释：（1）三角形的基本元素：①三角形的边：即组成三角形的线段；②三角形的角：即相邻两边所组成的角叫做三角形的内角，简称三角形的角；③三角形的顶点：即相邻两边的公共端点.（2）三角形的定义中的三个要求：“不在同一条直线上”、“三条线段”、“首尾顺次相接”.（3）三角形的表示：三角形用符号“△”表示，顶点为A、B、C的三角形记作“△ABC”，读作“三角形ABC”，注意单独的△没有意义；△ABC的三边可以用大写字母AB、BC、AC来表示，也可以用小写字母a、b、c来表示，边BC用a表示，边AC、AB分别用b、c表示．二、三角形的三边关系定理：三角形任意两边之和大于第三边.推论：三角形任意两边的之差小于第三边.要点诠释：（1）理论依据：两点之间线段最短.（2）三边关系的应用：判断三条线段能否组成三角形，若两条较短的线段长之和大于最长线段的长，则这三条线段可以组成三角形；反之，则不能组成三角形．当已知三角形两边长，可求第三边长的取值范围．（3）证明线段之间的不等关系．三、三角形的分类1.按角分类：ìïìííïîî直角三角形三角形锐角三角形斜三角形钝角三角形要点诠释：①锐角三角形：三个内角都是锐角的三角形;②钝角三角形：有一个内角为钝角的三角形.2.按边分类：ìïìííïîî不等边三角形三角形底边和腰不相等的等腰三角形等腰三角形等边三角形要点诠释：①不等边三角形：三边都不相等的三角形；②等腰三角形：有两条边相等的三角形叫做等腰三角形，相等的两边都叫做腰，另外一边叫做底边，两腰的夹角叫顶角，腰与底边夹角叫做底角;③等边三角形：三边都相等的三角形.四、三角形的三条重要线段三角形的高、中线和角平分线是三角形中三条重要的线段，它们提供了重要的线段或角的关系，为我们以后深入研究三角形的一些特征起着很大的帮助作用，因此，我们需要从不同的角度弄清这三条线段，列表如下：线段名称三角形的高三角形的中线三角形的角平分线文字语言从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段．三角形中，连接一个顶点和它对边中点的线段．三角形一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段．图形语言作图语言过点A 作AD ⊥BC 于点D ．取BC 边的中点D ，连接AD ．作∠BAC 的平分线AD ，交BC 于点D ．标示图形符号语言1．AD是△ABC的高．2．AD是△ABC中BC边上的高．3．AD⊥BC于点D．4．∠ADC＝90°，∠ADB＝90°．(或∠ADC＝∠ADB＝90°)1．AD是△ABC的中线．2．AD是△ABC中BC边上的中线．3．BD＝DC＝12BC4．点D是BC边的中点．1．AD是△ABC的角平分线．2．AD平分∠BAC，交BC于点D．3．∠1＝∠2＝12∠BAC．推理语言因为AD是△ABC的高，所以AD⊥BC．(或∠ADB＝∠ADC＝90°)因为AD是△ABC的中线，所以BD＝DC＝12BC．因为AD平分∠BAC，所以∠1＝∠2＝12∠BAC．用途举例1．线段垂直．2．角度相等．1．线段相等．2．面积相等．角度相等．注意事项1．与边的垂线不同．2．不一定在三角形内．—与角的平分线不同．重要特征三角形的三条高(或它们的延长线)交于一点．一个三角形有三条中线，它们交于三角形内一点．一个三角形有三条角平分线，它们交于三角形内一点．五、三角形的稳定性三角形的三条边确定后，三角形的形状和大小就确定不变了，这个性质叫做三角形的稳定性。

专题一三角形的高、中线与角平分线剖析一、三角形的高1.三角形的高定义：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形这边上的高，简称三角形的高。

如图，线段AD是BC边上的高。

注意：高与垂线不同，高是线段，垂线是直线。

2.表示：1.AD是△ABC的BC上的高线；2.AD⊥BC于D；3.∠ADB=∠ADC=90°。

3.三角形高的交点位置：锐角三角形的三条高的交点在三角形的内部，直角三角形三条高的交点在角直角顶点，钝角三角形的三条高的交点在三角形的外部。

如下图所示。

图1 图2 图34.三角形的三条高的特性二、三角形的中线1.三角形的中线定义：在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形这边上的中线。

2.表示：1.AD是△ABC的BC上的中线；2.BD=DC=12 BC.3.三角形的重心：三角形的三条中线相交于一点。

三角形三条中线的交点叫做三角形的重心。

重心一定在三角形内。

三、三角形的角平分线1.三角形的角平分线定义：在三角形中，一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫三角形的角平分线。

2.表示：1.AD是△ABC的∠BAC的平分线；2.∠1=∠2=12∠BAC.3.三角形的角平分线的位置：三角形的三条角平分线都在三角形的内部，并且三条角平分线交于三角形内一点。

1．（2020·重庆南开中学期末）如图，在ABC 中，D 是BC 的中点，E 在AC 上，且:=1:3AE EC ，连接AD ，BE 交于点F ，若=40ABC S △，则=DCEF S 四边形（ ）.A ．14B ．15C ．18D ．202．（2020·重庆南开中学）如图，ABC ∆中，点D E F 、、分别在三边上，AD BE CF 、、交于一点,G E 是AC 的中点，2,6,4GDC GEC BD CD S S ∆∆===则ABC S ∆=（ ）A ．1785B ．1985C ．40D ．423．（2020·河南宛城期末）如图在ABC 中，AD 是高，AE 是角平分线，AF 是中线，则下列说法中错误的是（ ）A ．BF CF =B ．12EAD B C ∠=∠-∠ C ．C BAD ∠=∠ D ．2ABC ABF S S =△△4．（2020·江苏海州期末）如图，D、E、F是△ABC内的三个点，且D在AF上，F在CE上，E在BD上，若CF=12EF，AD=13FD，BE=14DE，△DEF的面积是12，则△ABC的面积是（）A．24.5 B．26 C．29.5 D．305．（2020·陕西渭滨期末）如图，AE是△ABC的角平分线，AD⊥BC于点D，点F为BC 的中点，若∠BAC＝104°，∠C＝40°，则有下列结论：①∠BAE＝52°；②∠DAE＝2°；③EF＝ED；④S△ABF＝12S△ABC.其中正确的个数有( )A．1个B．2个C．3个D．4个6．（2019·广东深圳外国语学校期末）如图，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，若CM＝3，则CE2+CF2的值为( )A．6 B．9 C．18 D．367．（2020·江苏江阴·河塘中学月考）如图，在△ABC中，D是AB的中点，E是BC上的一点，且BE＝4EC，CD与AE相交于点F．若△CEF的面积为1，则△ABC的面积为（）A．24 B．25 C．30 D．328．（2020·长春市第四十七中学）如图，△ABC中，点D是AC边上的中点，点E是AB 边上的中点，若S∆ABC=12 ，则图中阴影部分的面积是（）A．6 B．4 C．3 D．29．（2020·江西南昌月考）如图，AD是△ABC的中线，已知△ABD的周长为22 cm，AB 比AC长3 cm，则△ACD的周长为（）A．19 cm B．22 cm C．25 cm D．31 cm10．（2020·安徽安庆期中）如图，AE 是△ABC 的中线，D 是BE 上一点，若BE =5，DE =2，则CD 的长为（ ）A ．7B ．6C ．5D ．411．（2019·湖北蔡甸）如图，若ABC ∆的三条角平分线AD 、BE 、CF 交于点G ，则与EGC ∠互余的角是( )A ．CGD ∠B ．FAG ∠C ．ECG ∠D ．FBG ∠12．（2019·四川宜宾期末）在直角三角形ABC 中，=90C ∠︒，AD 平分BAC ∠交BC 于点D ，BE 平分ABC ∠交AC 于点E ，AD 、BE 相交于点F ，过点D 作DG AB ∥，过点B作BG DG ⊥交DG 于点G .下列结论：①135AFB ∠=︒；②2BDG CBE ∠=∠；③BC 平分ABG ∠；④BEC FBG ∠=∠.其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个13．（2020·广东龙岗·龙岭初级中学期中）如图△ABC中，分别延长边AB、BC、CA，使得BD=AB，CE=2BC，AF=3CA，若△ABC的面积为1，则△DEF的面积为________.14．（2019·四川绵阳月考）如图，已知△ABC的周长为21cm，AB＝6cm，BC边上中线AD ＝5cm，△ABD的周长为15cm，则AC长为_____．15．（2019·山东牡丹期末）如图ABC中，AD是BC边上的中线，BE是ABC中AD 边上的中线，若ABC的面积是24，6AE ，则点B到ED的距离是___．16．（2019·广东佛山）如图，G为△ABC的重心，点D在CB延长线上，且BD＝12 BC，过D、G的直线交AC于点E，则AEAC＝_____．17．（2020·江西全国月考）如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E，当P点在线段AD上运动时，∠E与∠B，∠ACB的数量关系为________18．（2020·江苏姜堰期末）如图，在△ABC中，AD⊥BC，垂足为D，AE平分∠BAC交BC于E，若∠C=80°，∠B=40°则∠DAE的度数为______．19．（2020·江苏张家港期末）如图，已知∠BDC＋∠EFC＝180°，∠DEF＝∠B．（1）求证：ED∥BC；（2）若D，E，F分别是AB，AC，CD边上的中点，四边形ADFE的面积为6．①求△ABC的面积；②若G是BC边上一点，C G＝2B G，求△FC G的面积．20．（2020·江苏姜堰期中）如图，在△ABC中，AE为边BC上的高，点D为边BC上的一点，连接AD．（1）当AD为边BC上的中线时．若AE=4，△ABC的面积为24，求CD的长；（2）当AD为∠BAC的角平分线时．①若∠C=65°，∠B=35°，求∠DAE的度数；②若∠C-∠B=20°，则∠DAE= °．21．（2020·四川达川期末）如图，在△ABC中，AM是中线，AD是高线．（1）若AB比AC长4 cm，则△ABM的周长比△ACM的周长多__________ cm．（2）若△AMC的面积为12 cm2，则△ABC的面积为__________cm2．（3）若AD又是△AMC的角平分线，∠AMB=130°，求∠ACB的度数．（写过程）22．（2019·昆明市官渡区第一中学月考）（1）如图1，在△ABC中，BD、CD分别是△ABC 两个内角∠ABC、∠ACB的平分线．①若∠A＝70°，求∠BDC的度数．②∠A＝α，请用含有α的代数式表示∠BDC的度数．(直接写出答案)（2）如图2，BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线．若∠A＝α，请用含有α的代数式表示∠BEC的度数．23．（2019·江苏宜兴期中）如图①，AD 平分BAC ∠，AE ⊥BC ，∠B =450,∠C =730．（1） 求DAE ∠的度数；（2） 如图②，若把“AE ⊥BC ”变成“点F 在DA 的延长线上，FE BC ⊥”，其它条件不变，求DFE ∠ 的度数；（3） 如图③，若把“AE ⊥BC ”变成“AE 平分BEC ∠”，其它条件不变，DAE ∠的大小是否变化，并请说明理由．24．（2020·江苏泰州市凤凰初级中学月考）如图，已知在△ABC中，△ABC的外角∠ABD 的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．求证：（1）MO=MB；（2）MN=CN﹣BM．专题二三角形内角和与外角和定理剖析【技巧解析】1.三角形内角和定理（1）三角形三个内角的和180°.（2）在三角形中，已知任意两个角的度数，可求出第3个角的度数；（3）已知三角形中三个内角关系，可利用三角形内角和等于180°，列方程求出各内角的度数.2.三角形外角性质（1）三角形的外角等于与它不相邻的两个内角的和.（2）三角形内角和的另一个推论：三角形外角大于任何一个与它不相邻的内角.3.三角形外角和定理（1）在三角形的每个顶点处取一个外角，三个不同顶点处的外角的和叫做三角形的外角和. （2）三角形外角和为360°.1．（2020·阳江市阳东区大八镇大八初级中学月考）如图，已知AB∥CD，∠A=60°，∠C =25°，则∠E等于（）A．60°B．25°C．35°D．45°2．（2020·浙江西湖期末）如图,直线l 1∥l 2,线段AB 交l 1,l 2于D ,B 两点,过点A 作AC ⊥AB ,交直线l 1于点C ,若∠1＝15︒,则∠2＝（ ）A ．95︒B ．105︒C ．115︒D ．125︒3．（2020·辽宁丹东期末）如图，//AB CD ，90ACB ︒∠=，CE AB ⊥，垂足为E ，图中与CAB ∠互余的角有（ ）A ．1个B ．2个C ．3个D ．4个4．（2020·全国）如图，在CEF △中，80E ∠=︒，50F ∠=︒，AB CF ，AD CE ，连接BC ，CD ，则A ∠的度数是（ ）A ．45°B ．50°C ．55°D ．80°5．（2020·银川月考）如图，在直角三角形ABC 中，AC ≠AB ，AD 是斜边上的高，DE ⊥AC ，DF ⊥AB ，垂足分别为E 、F ，则图中与∠C (∠C 除外)相等的角的个数是( )A ．3个B ．4个C ．5个D ．6个6．（2020·山东芝罘期中）如图，△ABC中，∠BAC＝60°，∠C＝80°，∠BAC的平分线AD交BC于点D，点E是AC上一点，且∠ADE＝∠B，则∠CDE的度数是（）A．20°B．30°C．40°D．70°7．（2020·枣庄市市中区实验中学月考）如图，AD是△ABC的高，BE是△ABC的角平分线，BE，AD相交于点F，已知∠BAD＝42°，则∠BFD＝( )A．45°B．54°C．56°D．66°8．（2020·四川省营山中学校期中）如图，将△ABC纸片沿DE折叠，点A的对应点为A’，若∠B=60°，∠C=80°，则∠1+∠2等于( )A．40°B．60°C．80°D．140°9．（2020·江苏东台月考）如图，∠ABD、∠ACD的角平分线交于点P，若∠A= 50°,∠D =10°，则∠P的度数为( )A．15°B．20°C．25°D．30°10．（2020·南通市八一中学）如图，BP平分∠ABC交CD于点F，DP平分∠ADC交AB 于点E，若∠A＝40°，∠P＝38°，则∠C的度数为（）A．36°B．39°C．38°D．40°11．（2019·四川江油期中）如图，AB⊥BC，AE平分∠BAD交BC于点E，AE⊥DE，∠1+∠2=90°，M、N分别是BA、CD延长线上的点，∠EAM和∠EDN的平分线交于点F，∠F的度数为（）A．120°B．135°C．150°D．不能确定12．（2020·全国）如图，在ABC ∆中，A ABC CB =∠∠，BD 是ABC ∆内角ABC ∠的平分线，AD 是ABC ∆外角EAC ∠的平分线，CD 是ABC ∆外角ACF ∠的平分线，以下结论不正确的是（ ）A ．//AD BCB ．2ACB ADB ∠=∠C ．90ADC ABD ∠=-∠ D ．BD 平分ADC ∠13．（2020·博兴县吕艺镇中学月考）如图，△ABC 的∠ABC 和∠ACB 的平分线BE ，CF 相交于点G ，∠A =100°，则∠B G C =_________°．14．（2020·辽宁中山期末）如图，AE 平分,BAC BE AE ∠⊥于,//E ED AC ，,BAC a ∠=则BED ∠的度数为________________．(用含α的式子表示)15．（2020·福建新罗期末）一副三角尺如图摆放，D 是BC 延长线上一点，E 是AC 上一点，90B EDF ∠=∠=︒，30A ∠=︒，45F ∠=︒，若EF ∥BC ，则CED ∠等于_________度．16．（2020·江苏张家港期末）如图，在四边形ABCD 中，∠B ＝120°，∠B 与∠ADC 互为补角，点E 在BC 上，将△DCE 沿DE 翻折，得到△DC ′E ，若AB ∥C ′E ，DC ′平分∠ADE ，则∠A 的度数为______°．17．（2019·温州外国语学校期中）如图1，已知长方形坻带ABCD ，//AD CD ，//AD BC ．将纸带沿EF 折叠后，点B 、C 分别落在H 、G 的位置．再沿GF 折叠成图2．点A 、D 分别落在Q 、H 的位置，已知24108QHG GFH ∠=∠-︒，则∠=EFC _______．18．（2020·哈尔滨市第四十七中学期中）在四边形ABCD 中，ADC ∠与BCD ∠的角平分线交于点E ，115DEC ∠=︒，过点B 作//BF AD 交CE 于点F ，2CE BF =，54CBF BCE ∠=∠，连接BE ，Δ4BCE S =，则CE =__________．19．（2020·江苏工业园区期末）如图，AD、AE分别是△ABC的高和角平分线，∠B＝50°，∠ACB＝80°．点F在BC的延长线上，F G⊥AE，垂足为H，F G与AB相交于点G．（1）求∠A G F的度数；（2）求∠DAE的度数．20．（2020·福建惠安期末）在△ABC中，∠ACB的平分线CD与外角∠EAC的平分线AF 所在的直线交于点D．（1）如图1，若∠B＝60°，求∠D的度数；（2）如图2，把△ACD沿AC翻折，点D落在D′处．①当AD′⊥AD时，求∠BAC的度数；②试确定∠DAD′与∠BAC的数量关系，并说明理由．21．（2020·江苏邳州期中）如图，△ABC中，AE是△ABC的角平分线，AD是BC边上的高．（1）若∠B＝35°，∠C＝75°，求∠DAE的度数；（2）若∠B＝m°，∠C＝n°，（m＜n），则∠DAE＝°（直接用m、n表示）．22．（2020·湖北武汉期末）如图，四边形ABCD中，AB∥CD，∠B＝∠D，点E为BC延长线上一点，连接AE，AE交CD于H．∠DCE的平分线交AE于G．（1）求证：AD∥BC；（2）若∠BAC＝∠DAE，∠A G C＝2∠CAE．求∠CAE的度数；（3）（2）中条件∠BAC＝∠DAE仍然成立，若∠A G C＝3∠CAE，直接写出∠CAE的度数．23．（2019·洛阳市第五十四中学月考）如图，在ABC 中，AD 是高，AE ，BF 是角平分线，它们相交于点O ．（1）若60ABC ∠=︒，70C ∠=︒，求DAE ∠的度数． （2）若70C ∠=︒，求∠BOE 的度数．（3）若ABC α∠=，()C βαβ∠=<，则DAE =∠______用含α、β的式子表示)24．（2020·北京朝阳期末）线段AB与线段CD互相平行，P是平面内的一点，且点P不在直线AB，CD上，连接P A，PD，射线AM，DN分别是∠BAP和∠CDP的平分线．（1）若点P在线段AD上，如图1，①依题意补全图1；②判断AM与DN的位置关系，并证明；（2）是否存在点P，使AM⊥DN？若存在，直接写出点P的位置；若不存在，说明理由．专题三 角平分线的性质与判定强化1.角的平分线的性质（1）角的平分线的性质：角的平分线上的点到角两边的距离相等. （2）用符号语言表示角的平分线的性质定理：若CD 平分∠ADB ，点P 是CD 上一点，且PE ⊥AD 于点E ，PF ⊥BD 于点F ，则PE ＝PF .2.角的平分线的判定（1）角平分线的判定：角的内部到角两边距离相等的点在角的平分线上.（2）用符号语言表示角的平分线的判定若PE ⊥AD 于点E ，PF ⊥BD 于点F ，PE ＝PF ，则PD 平分∠ADB3.角的平分线的尺规作图角平分线的尺规作图（1）以O 为圆心，适当长为半径画弧，交OA 于D ，交OB 于E . （2）分别以D 、E 为圆心，大于DE 的长为半径画弧，两弧在∠AOB 内部交于点C . （3）画射线OC . 射线OC 即为所求.124.三角形角平分线的性质（1）三角形三条角平分线交于三角形内部一点，此点叫做三角形的内心且这一点到三角形三边的距离相等.（2）三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示：△ABC 的内心为，旁心为，这四个点到△ABC 三边所在直线距离相等.1．（2020·南通市通州区平潮初级中学期中）如图，在△ABC 中，E 为AC 的中点，AD 平分∠BAC ，BA ：CA =2：3，AD 与BE 相交于点O ，若△OAE 的面积比△BOD 的面积大1，则△ABC 的面积是（ ）A ．8B ．9C ．10D ．111P 234,,PPP2．（2020·兴仁市真武山街道办事处黔龙学校月考）如图，已知CD⊥AB于D，现有四个条件：①AD=ED②∠A=∠BED③∠C=∠B④AC=EB，那么不能得出△ADC≌△EDB的条件是（）.A．①③B．②④C．①④D．②③3．（2020·吉林长春外国语学校月考）如图，在△ABC中，∠C=90°，AB=10，AD是△ABC 的一条角平分线．若CD=3，则△ABD的面积为（）A．13 B．14 C．15 D．214．（2020·聊城市茌平区教育和体育局教研室期末）如图所示，12∠=∠，34∠=∠，则下列结论正确的有（ ）①AD 平分BAF ∠；②AF 平分BAC ∠；③AE 平分DAF ∠；④AF 平分DAC ∠；⑤AE 平分BAC ∠．A ．4个B ．3个C ．2个D ．1个5．（2020·辽宁北镇期末）如图，//AB CD ，BE 和CE 分别平分ABC ∠和BCD ∠，AD 过点E ，且与AB 互相垂直，点P 为线段BC 上一动点，连接PE ．若8AD ＝，则PE 的最小值为( )A ．8B ．6C ．5D ．46．（2020·陕西商州·期末）如图，已知AB∥CD，直线EF分别交AB、CD于点E、F，F G平分∠EFD交AB于点G，若∠BEF＝70°，则∠A G F的度数为（）A．35°B．45°C．55°D．65°7．（2020·辽宁凌海期末）在正方形网格中，∠AOB的位置如图所示，则点P、Q、M、N 中在∠AOB的平分线上是（）A．P点B．Q点C．M点D．N点8．（2020·云南昭通期末）如图，OP 平分AOB ∠，PD OA ⊥于点D ，点E 是射线OB 上的一个动点，若3PD =，则PE 的最小值（ ）A ．等于3B ．大于3C ．小于3D ．无法确定9．（2019·贵州遵义）如图，已知AEF DFE EH FH ∠=∠⊥,于点H ，EG 平分AEF ∠，平移EH 恰好到GF ，连接EG ，则下列结论：①//AB CD ；②EG HF =；③EH 平分BEF FH ∠，平分EFD ∠；④90GFH ∠=︒．其中正确的结论个数是（ ）A ．1个B ．2个C ．3个D ．4个10．（2020·贵州赫章期末）如图，在△ABC中，∠C＝90°，以点B为圆心，以适当长为半径画弧交AB、BC于P、Q两点，再分别以点P，Q为圆心，大于12P Q的长为半径画弧，两弧相交于点N，射线BN交AC于点D．若AB＝10，AC＝8，则CD的长是（）A．2 B．2.4 C．3 D．411．（2020·湖北襄城期末）若两条直线被第三条直线所截，有一对同位角相等，则其中一对同旁内角的角平分线()A．互相垂直B．互相平行C．相交或平行D．不相等12．（2020·湖北省直辖县级单位·中考真题）如图，已知ABC 和ADE 都是等腰三角形，90BAC DAE ∠=∠=︒，,BD CE 交于点F ，连接AF ，下列结论：①BD CE =；②BF CF ⊥；③AF 平分CAD ∠；④45AFE ∠=︒．其中正确结论的个数有（ ）A ．1个B ．2个C ．3个D ．4个13．（2019·广西玉林期末）如图，△ABC 的三边AB ，BC ，CA 的长分别为14，12，8，其三条角平分线的交点为O ，则::ABOBCOCAOSSS=_____．14．（2020·山东牡丹期末）如图所示，在ABC ∆中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥于E ，8BC cm =，则DE DB +=________．15．（2020·南京外国语学校期中）如图，BD平分∠ABC，DE⊥AB于E，DF⊥BC于F，AB＝6，BC＝8.若S△ABC＝21，则DE＝________．16．（2019·江苏高邮期中）如图，AB∥CD，O为∠BAC、∠ACD的平分线的交点，OE⊥AC 于E，且OE=1，则AB与CD之间的距离等于____．17．（2019·深圳实验学校中学部期中）如图,在△ABC中,∠BAC=40°,∠ACB=60°，D为△ABC外一点，DA平分∠BAC，且CBD=50°，则∠DCB的度数是_______.18．（2020·宜春市第三中学期末）如图，OP平分∠AOB，∠AOP＝15°，PC∥OA，PC＝4，点D是射线OA上的一个动点，则PD的最小值为_____．19．（2020·山东日照期末）如图，点D为线段BC上的一点，点F在BA的延长线上，点E在线段CD上，EF与AC相交于点G，∠BDA+∠CE G=180°．（1）AD与EF平行吗，请说明理由：（2）若点H在FE的延长线上，且∠ED H=∠C，∠F=∠H，那么AD平分∠BAC吗，请说明理由．20．（2020·山东期末）如图所示，直线AB∥CD，直线AB、CD被直线EF所截，E G平分∠BEF，F G平分∠DFE，(1)若∠AEF＝50°，求∠EF G的度数．(2)判断E G与F G的位置关系，并说明理由．21．（2019·广东郁南期末）如图，直线AB 、CD 与MN 相交于M 、N ，∠1=105°，∠2=75°，E 、F 、O 分别在AB 、CD 、MN 上，OE OF ⊥．（1）求证：//AB CD ； （2）求34∠+∠的度数；（3）若分别在OE 、CD 上取点G 、H ，使得FO 平分CFG ∠，OE 平分AEH ∠，求证：//FG EH ．22．（2020·广西覃塘期末）如图，D ，E ，G 分别是AB ，AC ，BC 边上的点，12180∠+∠=︒，3B ∠=∠．（1）请说明//DE BC 的理由；（2）若DE 平分ADC ∠，22B ∠=∠，判断CD 与EG 的位置关系，并说明理由．AB CD，直线EF与AB、CD分别交于点E、F，23．（2019·广东中山期末）如图，已知//点P是射线EB上一点(与点E不重合)．FM、FN分别平分∠PFE和∠PFD，FM、FN交直线AB于点M、N，过点N作N H⊥FM于点H．（1）若∠BEF=64°，求∠FN H的度数；（2）猜想∠BEF和∠FN H之间有怎样的数量关系，并加以证明．。

1.三角形的三线：（1）在三角形中，连接一个顶点与它对边中点的________，叫做这个三角形的中线，三角形的三条中线_____________交于一点，这点称为三角形的__________．（2）在三角形中，一个角的角平分线与它的对边相交，这个角的顶点与交点之间的______叫做三角形的角平分线，三角形的三条角平分线________________交于一点，这点称为三角形的_________．（3）从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的________叫做三角形的高线（简称三角形的高），三角形的三条高________________交于一点，这点称为三角形的________；锐角三角形的三条高线及垂心都在其________，直角三角形的垂心是________，钝角三角形的垂心和两条高线在其________．一．选择题（共9小题）1．如图，在△ABC中，BC边上的高是、在△BCE中，BE边上的高、在△ACD中，AC边上的高分别是（）A．A F、CD、CEB．A F、CE、CDC．A C、CE、CDD．A F、CD、CE2．下列说法中正确的是（）A．三角形三条高所在的直线交于一点B．有且只有一条直线与已知直线平行C．垂直于同一条直线的两条直线互相垂直D．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离3．△ABC中BC边上的高作确的是（）A．B．C．D．4．如果一个三角形两边上的高的交点在三角形的部，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．任意三角形5．不一定在三角形部的线段是（）A．三角形的角平分线B．三角形的中线C．三角形的高D．以上皆不对6．已知AD是△ABC的中线，且△ABD比△ACD的周长大3cm，则AB与AC的差为（）A．2cm B．3cm C．4cm D．6cm7．下列说法中正确的是（）A．三角形的角平分线、中线、高均在三角形部B．三角形中至少有一个角不小于60°C．直角三角形仅有一条高D．三角形的外角大于任何一个角8．三角形的①中线、角平分线、高都是线段；②三条高必交于一点；③三条角平分线必交于一点；④三条高必在三角形．其中正确的是（）A．①②B．①③C．②④D．③④9．（2015春•校级月考）下列说确的是（）①三角形的角平分线是射线；②三角形的三条角平分线都在三角形部，且交于同一点；③三角形的三条高都在三角形部；④三角形的一条中线把该三角形分成面积相等的两部分．A．①②B．②③C．③④D．②④二．填空题（共2小题）10．如图，在△ABC中，BE是边AC上的中线，已知AB=4cm，AC=3cm，BE=5cm，则△ABC的周长是cm．11．如图，在△ABC中，BD平分∠ABC，BE是AC边上的中线，如果AC=10cm，则AE= cm，如果∠ABD=30°，则∠ABC= ．三．解答题（共10小题）12．已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC 交射线OE于点D．设∠OAC=x°．（1）如图1，若AB∥ON，则①∠ABO的度数是；②当∠BAD=∠ABD时，x= ；当∠BAD=∠BDA时，x= ．（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB 中有两个相等的角？若存在，求出x的值；若不存在，说明理由．13．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，BE=2，AF=3，填空：（1）BE= =．（2）∠BAD= =．（3）∠AFB= = ．（4）S△AEC= ．14．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？15．如图，AD是△ABC的BC边上的高，AE是∠BAC的角平分线，（1）若∠B=47°，∠C=73°，求∠DAE的度数．（2）若∠B=α°，∠C=β°（α＜β），求∠DAE的度数（用含α、β的代数式表示）16．如图，△ABC的周长为9，AD为中线，△ABD的周长为8，△ACD的周长为7，求AD的长．17．已知：如图，△ABC中，AD、AE分别是△ABC的高和角平分线，BF是∠ABC的平分线，BF与AE交于O，若∠ABC=40°，∠C=60°，求∠DAE、∠BOE的度数．18．如图（1），AD是△ABC的高，如图（2），AE是△ABC的角平分线，如图（3），AF是△ABC的中线，完成下列填空：（1）如图（1），∠=∠=90°；S△ABC= ；（2）如图（2），∠BAE=∠=∠；（3）如图（3），BF= =；S△ABF= ．19．如图，完成下面几何语言的表达．①∵AD是△ABC的高（已知）；∴AD⊥BC，∠= = °．②∵AE是△ABC的中线（已知），∴= =，=2 =2 ；③∵AF是△ABC的角平分线（已知），∴∠=∠=∠，∠=2∠=2∠．20．在△ABC中，D为BC的中点，E为AC上任一点，BE交AD 于O，某学生在研究这一问题时，发现了如下事实：（1）当==时，有=；（2）当==时，有=；（3）当==时，有=；①当=时，按照上述的结论，请你猜想用n表示AO/AD的一般性结论（n为正整数）；②若=，且AD=18，求AO．点评：本题考查了三角形的中线能把三角形的面积平分，等高三角形的面积的比等于底的比，熟练掌握这个结论是解题的关键．已知△ABC的面积是60，请完成下列问题：（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积△ACD的面积（填“＞”“＜”或“=”）（2）如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD=DB得：S△ADO=S△BDO，同理：S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=x，S△AEO=y由题意得：S△ABE=S△ABC=30，S△ADC=S△ABC=30，可列方程组为：，解得，通过解这个方程组可得四边形ADOE的面积为．（3）如图3，AD：DB=1：3，CE：AE=1：2，请你计算四边形ADOE的面积，并说明理由．答案一．选择题（共9小题）1．（2015•州校级模拟）如图，在△ABC中，BC边上的高是、在△BCE中，BE边上的高、在△ACD中，AC边上的高分别是（）A．A F、CD、CE B．A F、CE、CD C．A C、CE、CD D．A F、CD、CE考点：三角形的角平分线、中线和高．分析：根据从三角形顶点向对边作垂线，顶点和垂足之间的线段叫做三角形的高，确定出答案即可．解答：解：在△ABC中，BC边上的高是AF；在△BCE中，BE边上的高CE；在△ACD中，AC边上的高分别是CD；故选B点评：本题考查了三角形的角平分线、中线、高线，是基础题，熟记三角形高的定义是解题的关键．2．（2015春•东平县校级期末）下列说法中正确的是（）A．三角形三条高所在的直线交于一点B．有且只有一条直线与已知直线平行C．垂直于同一条直线的两条直线互相垂直D．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离考点：三角形的角平分线、中线和高．分析：A正确，即三角形的垂心；B应有无数条因此错误；C在平面几何中垂直于同一条直线的两条直线互相平行所以错误；D中语言错误线段不能叫距离．解答：解：B中应为：有无数条直线与已知直线平行，故B错；C中应为：在平面几何中垂直于同一条直线的两条直线互相平行，故C错，D中应写成垂线段长度；A 正确．故选A．点评：本题考查了三角形的垂心知识和一些几何基础知识，做题时注意严格对比概念．3．（2015春•期末）△ABC中BC边上的高作确的是（）A．B．C．D．考点：三角形的角平分线、中线和高．分析：根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答．解答：解：为△ABC中BC边上的高的是D选项．故选D．点评：本题考查了三角形的角平分线、中线、高线，熟记高线的定义是解题的关键．4．（2015春•昌乐县期末）如果一个三角形两边上的高的交点在三角形的部，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．任意三角形考点：三角形的角平分线、中线和高．分析：根据三角形高的定义知，若三角形的两条高都在三角形的部，则此三角形是锐角三角形．解答：解：利用三角形高线的位置关系得出：如果一个三角形两边上的高的交点在三角形的部，那么这个三角形是锐角三角形．故选：A．点评：此题主要考查了三角形的高线性质，了解不同形状的三角形的位置：锐角三角形的三条高都在三角形的部；直角三角形的三条高中，有两条是它的直角边，另一条在部；钝角三角形的三条高有两条在外部，一条在部．5．（2015春•沙河市期末）不一定在三角形部的线段是（）A．三角形的角平分线B．三角形的中线C．三角形的高D．以上皆不对考点：三角形的角平分线、中线和高．分析：根据三角形的角平分线、中线、高线的定义解答即可．解答：解：三角形的角平分线、中线一定在三角形的部，直角三角形的高线有两条是三角形的直角边，钝角三角形的高线有两条在三角形的外部，所以，不一定在三角形部的线段是三角形的高．故选C．点评：本题考查了三角形的角平分线、中线和高，是基础题，熟记概念是解题的关键．6．（2015春•莘县期末）已知AD是△ABC的中线，且△ABD比△ACD的周长大3cm，则AB与AC的差为（）A．2cm B．3cm C．4cm D．6cm考点：三角形的角平分线、中线和高．分析：根据三角形中线的定义可得BD=CD，然后根据三角形的周长公式列式计算即可得解．解答：解：∵AD是△ABC的中线，∴BD=DC，∴△ABD与△ACD的周长之差=（AB+AD+BD）﹣（AC+AD+CD）=AB﹣AC，∵△ABD比△ACD的周长大3cm，∴AB与AC的差为3cm．故选B．点评：本题考查了三角形的角平分线、中线和高线，熟记概念并求出两三角形周长的差等于AB﹣AC是解题的关键．7．（2015春•崇安区期中）下列说法中正确的是（）A．三角形的角平分线、中线、高均在三角形部B．三角形中至少有一个角不小于60°C．直角三角形仅有一条高D．三角形的外角大于任何一个角考点：三角形的角平分线、中线和高；三角形角和定理；三角形的外角性质．分析：根据三角形的角平分线、中线、高的定义及性质判断A；根据三角形的角和定理判断B；根据三角形的高的定义及性质判断C；根据三角形外角的性质判断D．解答：解：A、三角形的角平分线、中线与锐角三角形的三条高均在三角形部，而直角三角形有两条高与直角边重合，另一条高在三角形部；钝角三角形有两条高在三角形外部，一条高在三角形部，故本选项错误；B、如果三角形中每一个角都小于60°，那么三个角的和小于180°，与三角形的角和定理相矛盾，故本选项正确；C、直角三角形有三条高，故本选项错误；D、三角形的一个外角大于和它不相邻的任何一个角，故本选项错误；故选B．点评：本题考查了三角形的角平分线、中线、高的定义及性质，三角形的角和定理，三角形外角的性质，熟记定理与性质是解题的关键．8．（2015春•校级期中）三角形的①中线、角平分线、高都是线段；②三条高必交于一点；③三条角平分线必交于一点；④三条高必在三角形．其中正确的是（）A．①②B．①③C．②④D．③④考点：三角形的角平分线、中线和高．分析：根据三角形的中线、角平分线、高的定义对四个说法分析判断后利用排除法求解．解答：解：①三角形的中线、角平分线、高都是线段，说确；②三角形的三条高所在的直线交于一点，三条高不一定相交，故三条高必交于一点的说法错误；③三条角平分线必交于一点，说确；④锐角三角形的三条高在三角形部；直角三角形有两条高与直角边重合，另一条高在三角形部；钝角三角形有两条高在三角形外部，一条高在三角形部．故三条高必在三角形的说法错误；故选：B．点评：本题考查了三角形的角平分线、中线、高线，从三角形的一个顶点向它的对边作垂线，垂足与顶点之间的线段叫做三角形的高；三角形一个角的平分线与这个角的对边交于一点，则这个角的顶点与所交的点间的线段叫做三角形的角平分线；三角形一边的中点与此边所对顶点的连线叫做三角形的中线．熟记概念与性质是解题的关键．9．（2015春•校级月考）下列说确的是（）①三角形的角平分线是射线；②三角形的三条角平分线都在三角形部，且交于同一点；③三角形的三条高都在三角形部；④三角形的一条中线把该三角形分成面积相等的两部分．A．①②B．②③C．③④D．②④考点：三角形的角平分线、中线和高．分析：根据三角形的角平分线的定义与性质判断①与②；根据三角形的高的定义及性质判断③；根据三角形的中线的定义及性质判断④即可．解答：解：①三角形的角平分线是线段，说法错误；②三角形的三条角平分线都在三角形部，且交于同一点，说确；③锐角三角形的三条高都在三角形部；直角三角形有两条高与直角边重合，另一条高在三角形部；钝角三角形有两条高在三角形外部，一条高在三角形部．说法错误；④三角形的一条中线把该三角形分成面积相等的两部分，说确．故选D．点评：本题考查了三角形的角平分线、中线和高的定义及性质，是基础题．从三角形的一个顶点向它的对边作垂线，垂足与顶点之间的线段叫做三角形的高；三角形一个角的平分线与这个角的对边交于一点，则这个角的顶点与所交的点间的线段叫做三角形的角平分线；三角形一边的中点与此边所对顶点的连线叫做三角形的中线．二．填空题（共2小题）10．（2014•模拟）如图，在△ABC中，BE是边AC上的中线，已知AB=4cm，AC=3cm，BE=5cm，则△ABC的周长是cm．考点：三角形的角平分线、中线和高．分析：根据三角形的中线定理：AB2+BC2=2（BE2+AE2），来求出BC的长度，然后再来求△ABC的周长．解答：解：∵在△ABC中，BE是边AC上的中线，∴AB2+BC2=2（BE2+AE2），AE=AC，∵AB=4cm，AC=3cm，BE=5cm，∴BC=（cm），∴AB+BC+AC=（cm），即△ABC的周长是cm．点评：本题主要考查了三角形的中线定理．11．（2014春•合川区校级期中）如图，在△ABC中，BD平分∠ABC，BE是AC边上的中线，如果AC=10cm，则AE= 5 cm，如果∠ABD=30°，则∠ABC= 60°．考点：三角形的角平分线、中线和高．分析：根据题意，E是边AC的中点，所以AE=AC，代入数据计算即可；根据角平分线的定义，∠ABC=2∠ABD，然后代入数据计算即可．解答：解：∵BE是AC边上的中线，AC=10cm，∴AE=AC=×10=5cm，∵BD平分∠ABC，∠ABD=30°，∴∠ABC=2∠ABD=2×30°=60°．故答案为：5；60°．点评：本题主要考查了三角形中线的定义以及三角形角平分线的定义，熟记定义并灵活运用是解题的关键，是基础题．三．解答题（共10小题）12．（2015春•期末）已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．（1）如图1，若AB∥ON，则①∠ABO的度数是20°；②当∠BAD=∠ABD时，x= 120°；当∠BAD=∠BDA时，x= 60°．（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．考点：三角形的角平分线、中线和高；平行线的性质；三角形角和定理．专题：计算题．分析：利用角平分线的性质求出∠ABO的度数是关键，分类讨论的思想．解答：解：（1）①∵∠MON=40°，OE平分∠MON∴∠AOB=∠BON=20°∵AB∥ON∴∠ABO=20°②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°∵∠BAD=∠BDA，∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°故答案为：①20 ②120，60（2）①当点D在线段OB上时，若∠BAD=∠ABD，则x=20若∠BAD=∠BDA，则x=35若∠ADB=∠ABD，则x=50②当点D在射线BE上时，因为∠ABE=110°，且三角形的角和为180°，所以只有∠BAD=∠BDA，此时x=125．综上可知，存在这样的x的值，使得△ADB中有两个相等的角，且x=20、35、50、125．点评：本题考查了三角形的角和定理和三角形的外角性质的应用，注意：三角形的角和等于180°，三角形的一个外角等于和它不相邻的两个角之和．13．（2014秋•剑川县期末）如图，在△ABC中，AE是中线，AD是角平分线，AF是高，BE=2，AF=3，填空：（1）BE= CE =BC ．（2）∠BAD= ∠DAC =∠BAC ．（3）∠AFB= ∠AFC = 90°．（4）S△AEC= 3 ．考点：三角形的角平分线、中线和高；三角形的面积．分析：分别根据三角形的中线、角平分线和高及三角形的面积公式进行计算即可．解答：解：（1）∵AE是中线，∴BE=CE=BC．故答案为：CE，BC；（2）∵AD是角平分线，∴∠BAD=∠DAC=∠BAC．故答案为：∠DAC，∠BAC；（3）∵AF是高，∴∠AFB=∠AFC=90°．故答案为：∠AFC，90°；（4）∵AE是中线，AF是高，BE=2，AF=3，∴BE=CE=2，∴S△AEC=CE•AF=×2×3=3．故答案为：3．点评：本题考查的是三角形的中线、角平分线和高，熟知三角形的中线、角平分线和高的性质是解答此题的关键．14．（2012春•桑日县校级期中）如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？考点：三角形的角平分线、中线和高；角平分线的定义；垂线；三角形角和定理．专题：动点型．分析：（1）先根据三角形角和定理求出∠BAC的度数，再根据角平分线的定义求得的度数，在△ADC中，利用三角形角和求出∠ADC的度数，从而可得∠DAE的度数．（2）结合第（1）小题的计算过程进行证明即可．（3）利用三角形的外角等于与它不相邻的两个角之和先用∠B和∠C表示出∠A′DE，再根据三角形的角和定理可证明∠DA′E=（∠C﹣∠B）．解答：解：（1）在△ABC中，∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣80°=50°；∵AD是角平分线，∴∠DAC=∠BAC=25°；在△ADC中，∠ADC=180°﹣∠C﹣∠DAC=75°；在△ADE中，∠DAE=180°﹣∠ADC﹣AED=15°．（2）∠DAE=180°﹣∠ADC﹣AED=180°﹣∠ADC﹣90°=90°﹣∠ADC=90°﹣（180°﹣∠C﹣∠DAC）=90°﹣（180°﹣∠C﹣∠BAC）=90°﹣[180°﹣∠C﹣（180°﹣∠B﹣∠C）]=（∠C﹣∠B）．（3）（2）中的结论仍正确．∠A′DE=∠B+∠BAD=∠B+∠BAC=∠B+（180°﹣∠B﹣∠C）=90°+∠B﹣∠C；在△DA′E中，∠DA′E=180°﹣∠A′ED﹣∠A′DE=180°﹣90°﹣（90°+∠B﹣∠C）=（∠C﹣∠B）．点评：本题考查了三角形的角平分线和高，三角形的角和定理，垂线等知识，注意综合运用三角形的有关概念是解题关键．15．（2012春•都江堰市校级期中）如图，AD是△ABC的BC边上的高，AE是∠BAC的角平分线，（1）若∠B=47°，∠C=73°，求∠DAE的度数．（2）若∠B=α°，∠C=β°（α＜β），求∠DAE的度数（用含α、β的代数式表示）考点：三角形的角平分线、中线和高；三角形角和定理．分析：（1）根据三角形的角和定理求出∠BAC的度数，再根据角平分线的定义求出∠BAE的度数，根据直角三角形两锐角互余求出∠BAD的度数，然后根据∠DAE=∠BAD﹣∠BAE计算即可得解；（2）根据（1）的思路，把度数换为α、β，整理即可得解．解答：解：（1）∵∠B=47°，∠C=73°，∴∠BAC=180°﹣47°﹣73°=60°，∵AD是△ABC的BC边上的高，∴∠BAD=90°﹣47°=43°，∵AE是∠BAC的角平分线，∴∠BAE=∠BAC=30°，∴∠DAE=∠BAD﹣∠BAE=43°﹣30°=13°；（2））∵∠B=α°，∠C=β°，∴∠BAC=180°﹣α°﹣β°，∵AD是△ABC的BC边上的高，∴∠BAD=90°﹣α°，∵AE是∠BAC的角平分线，∴∠BAE=∠BAC=（180°﹣α°﹣β°），∴∠DAE=∠BAD﹣∠BAE=90°﹣α°﹣（180°﹣α°﹣β°），=90°﹣α°﹣90°+α°+β°，=（β﹣α）°．点评：本题考查了三角形的角平分线，三角形的高线，以及三角形的角和定理，仔细分析图形，观察出∠DAE=∠BAD﹣∠BAE，然后分别表示出∠BAD与∠BAE是解题的关键．16．如图，△ABC的周长为9，AD为中线，△ABD的周长为8，△ACD的周长为7，求AD的长．考点：三角形的角平分线、中线和高．分析：先根据三角形的中线的定义求出BC=2BD=2CD，再根据三角形周长的定义得出AB+BC+AC=9，AB+BD+AD=8，AC+CD+AD=7，进而求出即可．解答：解：∵AD是△ABC的中线，∴BC=2BD=2CD，∵△ABC的周长为9，AD为中线，△ABD的周长为8，△ACD的周长为7，∴AB+BC+AC=9，AB+BD+AD=8，AC+CD+AD=7，∴（AB+BD+AD）+（AC+CD+AD）﹣（AB+BC+AC）=8+7﹣9，∴2AD=6，∴AD=3．点评：本题考查了三角形的中线，三角形的周长，关键是求出2AD=（AB+BD+AD）+（AC+CD+AD）﹣（AB+BC+AC）=6．17．已知：如图，△ABC中，AD、AE分别是△ABC的高和角平分线，BF是∠ABC的平分线，BF与AE交于O，若∠ABC=40°，∠C=60°，求∠DAE、∠BOE的度数．考点：三角形的角平分线、中线和高．分析：先根据三角形的角和定理得到∠BAC的度数，再利用角平分线的性质可求出∠DAC=∠BAC，而∠EAC=90°﹣∠C，然后利用∠DAE=∠DAC﹣∠EAC进行计算即可．由三角形外角的性质求得∠AFO=80°，利用三角形角和定理得到∠AOF=50°，所以对顶角相等：∠BOE=∠AOF=50°．解答：解：①在△ABC中，∵∠ABC=40°，∠C=60°，∴∠BAC=180°﹣∠B﹣∠C=80°．∵AE是的角平分线，∴∠EAC=∠BAC=40°．∵AD是△ABC的高，∴∠ADC=90°∴在△ADC中，∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣60°=30°∴∠DAE=∠EAC﹣∠DAC=40°﹣30°=10°．②∵BF是∠ABC的平分线，∠ABC=40°，∴∠FBC=∠ABC=20°，又∵∠C=60°，∴∠AFO=80°，∴∠AOF=180°﹣80°﹣50°=50°，∴∠BOE=∠AOF=50°．点评：考查了三角形的角和定理：三角形的角和为180°．也考查了三角形的高线与角平分线的性质．18．如图（1），AD是△ABC的高，如图（2），AE是△ABC的角平分线，如图（3），AF是△ABC的中线，完成下列填空：（1）如图（1），∠ADB =∠ADC =90°；S△ABC= ；（2）如图（2），∠BAE=∠EAC =∠BAC ；（3）如图（3），BF= FC =BC ；S△ABF= S△AFC．．考点：三角形的角平分线、中线和高；三角形的面积；三角形角和定理．分析：（1）根据三角形的高的概念即可完成填空；（2）根据三角形的角平分线的概念即可完成填空；（3）根据三角形的中线的概念即可完成填空．解答：解：（1）如图（1），∠ADB=∠ADC=90°；S△ABC=；（2）如图（2），∠BAE=∠EAC=∠BAC；（3）如图（3），BF=FC=BC；S△ABF=S△AFC．故答案为：ADB；ADC；；EAC；BAC；FC；BC；S△AFC．点评：此题考查三角形的角平分线、中线、高问题，能够根据三角形的中线、角平分线和高的概念得到线段、角之间的关系．19．如图，完成下面几何语言的表达．①∵AD是△ABC的高（已知）；∴AD⊥BC，∠ADB = ∠ADC = 90 °．②∵AE是△ABC的中线（已知），∴BE = CE =BC ，BC =2 BE =2 CE ；③∵AF是△ABC的角平分线（已知），∴∠BAF =∠CAF =∠BAC ，∠BAC =2∠BAF =2∠CAF ．考点：三角形的角平分线、中线和高．分析：①根据三角形的定义和垂直的定义解答；②根据三角形的中线的定义和线段的中点的定义解答；③根据三角形的角平分线和角平分线的定义解答．解答：解：①∵AD是△ABC的高（已知）；∴AD⊥BC，∠ADB=∠ADC=90°．②∵AE是△ABC的中线（已知），∴BE=CE=BC，BC=2BE=2CE；③∵AF是△ABC的角平分线（已知），∴∠BAF=∠CAF=∠BAC，∠BA=2∠BAF=2∠CAF．故答案为：ADB，∠ADC，90，BE，CE，BC，BC，BE，CE，BAF，CAF，BAC，BCA，BAF，CAF．点评：本题考查了三角形的角平分线，中线，高，熟记各定义是解题的关键．20．在△ABC中，D为BC的中点，E为AC上任一点，BE交AD于O，某学生在研究这一问题时，发现了如下事实：（1）当==时，有=；（2）当==时，有=；（3）当==时，有=；①当=时，按照上述的结论，请你猜想用n表示AO/AD的一般性结论（n为正整数）；②若=，且AD=18，求AO．考点：三角形的角平分线、中线和高．专题：规律型．分析：①过D作DF∥BE，即求AE：AD，因为当=时，可以根据平行线分线段成比例，及线段相互间的关系即可得出．②利用①中方法得出AE：（AE+2EF）=1：8，进而得出AE：EF=2：7，以及==得出答案即可．解答：解：①过D作DF∥BE，∴AO：AD=AE：AF．∵D为BC边的中点，∴CF=EF=0.5EC．∵=，∴AE：（AE+2EF）=1：（1+n）．∴AE：EF=2：n．∴AE：AF=2：（n+2）．∴=；②过D作DF∥BE，∴AO：AD=AE：AF．∵D为BC边的中点，∴CF=EF=0.5EC．∵=，∴AE：（AE+2EF）=1：8，∴AE：EF=2：7，∴==，∵AD=18，∴AO=4．点评：此题主要考查了平行线分线段成比例定理性质，根据已知熟练将比例是变形得出是解题关键．21．（2015春•迁安市期末）已知△ABC的面积是60，请完成下列问题：（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积= △ACD的面积（填“＞”“＜”或“=”）（2）如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD=DB得：S△ADO=S△BDO，同理：S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=x，S△AEO=y由题意得：S△ABE=S△ABC=30，S△ADC=S△ABC=30，可列方程组为：，解得，通过解这个方程组可得四边形ADOE的面积为20 ．（3）如图3，AD：DB=1：3，CE：AE=1：2，请你计算四边形ADOE的面积，并说明理由．考点：三角形的面积．分析：（1）根据等底等高的两个三角形面积相等知，三角形的中线把三角形的面积分为相等的两部分，所以S△ABD=S△ACD；（2）根据三角形的中线能把三角形的面积平分，等高三角形的面积的比等于底的比，即可得到结果；（3）连结AO，由AD：DB=1：3，得到S△ADO=S△BDO，同理可得S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=3x，S△AEO=2y，由题意得列方程组即可得到结果．解答：解：（1）如图1，过A作AH⊥BC于H，∵AD是△ABC的BC边上的中线，∴BD=CD，∴，，∴S△ABD=S△ACD，故答案为：=；（2）解方程组得，∴S△AOD=S△BOD=10，∴S四边形ADOB=S△AOD+S△AOE=10+10=20，故答案为：得，20；（3）如图3，连结AO，∵AD：DB=1：3，∴S△ADO=S△BDO，∵CE：AE=1：2，∴S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=3x，S△AEO=2y，由题意得：S△ABE=S△ABC=40，S△ADC=S△ABC=15，可列方程组为：，解得：，∴S四边形ADOE=S△ADO+S△AEO=x+2 y=13．点评：本题考查了三角形的中线能把三角形的面积平分，等高三角形的面积的比等于底的比，熟练掌握这个结论是解题的关键．。

三角形三条重要线段测试姓名：1、下列说法中正确的是（）A．三角形三条高所在的直线交于一点B．有且只有一条直线与已知直线平行C．垂直于同一条直线的两条直线互相垂直D．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离2、三角形的三条高所在的直线相交于一点，这个交点的位置在（）A．三角形内B．三角形外C．三角形边上D．要根据三角形的形状才能定3、．三角形三条高所在直线的交点一定在（）A．三角形的内部B．三角形的外部C．三角形的内部或外部D．三角形的内部、外部或顶点4、．△ABC中，AD是BC边上的中线，下列五种说法：①AD把∠BAC分成相等的两部分；②AD 是线段BC分成相等的两部分；③AD把△ABC分成形状相同的两个三角形；④AD把△ABC分成周长相等的两个三角形；⑤AD把△ABC分成面积相等的两个三角形．其中正确的说法有个5、．在△ABC中，AB=AC，AD是中线，△ABC的周长为34cm，△ABD的周长为30cm，求AD的长．6、在△ABC中，AB=AC，DB为△ABC的中线，且BD将△ABC周长分为12cm与15cm两部分，求三角形各边长．7、如图，（1）在△ABC中，∠A=52°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C的度数是．（2）在△ABC中，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，∠ABD2与∠ACD2的角平分线交于点D3，若∠BD3C的度数是n°，则∠A的度数是（用含n的代数式表示）．8、如图①路与②路公交车都是从体育馆到少年宫．（1）比较①路和②路这两条线路的长短；（2）小利坐出租车由体育馆去少年宫．假设出租车的收费标准为：起步价为7元，3千米后每千米为1.8元，用式子表示出租车的收费p（元）与行驶路程s（千米s＞3）之间的关系；（3）若这段路程有4.5千米，小利身上有10元钱，够不够付车费？9、北京市为治理交通拥堵状况，鼓励市民乘坐公交车出行，从4月1日开始，北京市三环内的停车费第一小时为10元，比原先的每小时2元上涨8元，此后每小时15元，比之前上涨13元．设在这样的停车场停车x小时，需付费y元．（假定每辆车的停车时间均是整数小时）．分别写出4月1日前和4月1日后y与x间的函数关系式．概率专题测试姓名：1、一个不透明的袋中装有红、黄、白三种颜色球共100个，它们除颜色外都相同，其中黄球个数是白球个数的2倍少5个．已知从袋中摸出一个球是红球的概率是（1）求袋中红球的个数；（2）求从袋中摸出一个球是白球的概率；（3）取走10个球（其中没有红球）后，求从剩余的球中摸出一个球是红球的概率2、“五•一”期间，某书城为了吸引读者，设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：读者每购买100元的书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么读者就可以分别获得45元、30元、25元的购书券，凭购书券可以在书城继续购书，如果读者不愿意转转盘，那么可以直接获得10元的购书券．（1）写出转动一次转盘获得45元购书券的概率；（2）转转盘和直接获得购书券，你认为哪种方式对读者更合算？请说明理由．3、桌面上有4张背面相同的卡片，正面分别写着数字“1”、“2”、“3”、“4”．先将卡片的背面朝上洗匀．（1）如果让小唐从中任意抽取一张，抽到奇数的概率是；（2）如果让小唐从中任意抽取两张，游戏规则规定：抽到的两张卡片上的数字之和为奇数，则小唐胜，否则小谢胜．你认为这个游戏公平吗？说出你的理由．4、一个布袋中有8个红球和16个白球，它们除颜色外都相同．（1）求从袋中摸出一个球是红球的概率；（2）现从袋中取走若干个白球，并放入相同数量的红球．搅拌均匀后，要使从袋中摸出一个球是红球的概率是，问取走了多少个白球？（要求通过列式或列方程解答）5、如图所示，转盘被等分成八个扇形，并在上面依次标有数字1，2，3，4，5，6，7，8．（1）自由转动转盘，当它停止转动时，指针指向的数正好能被8整除的概率是多少（2）请你用这个转盘设计一个游戏，当自由转动的转盘停止时，指针指向的区域的概率为．（注：指针指在边缘处，要重新转，直至指到非边缘处）。

经典《三角形》专题训练知识点梳理考点一、三角形1、三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、三角形的分类.⎪⎩⎪⎨⎧钝角三角形直角三角形锐角三角形⎪⎪⎩⎪⎪⎨⎧)(等边三角形等腰三角形不等边三角形 3、三角形的三边关系：三角形任意两边之和大于第三边,任意两边之差小于第三边. 4、三角形的重要线段①三角形的中线：顶点与对边中点的连线,三条中线交点叫重心②三角形的角平分线：内角平分线与对边相交,顶点和交点间的线段,三个角的角平分线的交点叫内心③三角形的高：顶点向对边作垂线,顶点和垂足间的线段.三条高的交点叫垂心(分锐角三角形,钝角三角形和直角三角形的交点的位置不同)5、三角形具有稳定性6、三角形的内角和定理及性质 定理：三角形的内角和等于180°. 推论1：直角三角形的两个锐角互补。

推论2：三角形的一个外角等于不相邻的两个内角的和。

推论3：三角形的一个外角大于与它不相邻的任何一个内角。

7、多边形的外角和恒为360° 8、多边形及多边形的对角线①正多边形：各个角都相等，各条边都相等的多边形叫做正多边形．②凸凹多边形：画出多边形的任何一条边所在的直线，若整个图形都在这条直线的同一侧，这样的多边形称为凸多边形；，若整个多边形不都在这条直线的同一侧，称这样的多边形为凹多边形。

③多边形的对角线的条数:A.从n 边形的一个顶点可以引（n-3）条对角线，将多边形分成（n-2）个三角形。

B.n 边形共有2)3(-n n 条对角线。

9、边形的内角和公式及外角和①多边形的内角和等于（n-2）×180°(n ≥3)。

②多边形的外角和等于360°。

三角形 (按角分)三角形 (按边分)10、平面镶嵌及平面镶嵌的条件。

①平面镶嵌：用形状相同或不同的图形封闭平面，把平面的一部分既无缝隙，又不重叠地全部覆盖。

②平面镶嵌的条件：有公共顶点、公共边；在一个顶点处各多边形的内角和为360°。

小专题(一)三角形三边关系的巧用“三角形任意两边之和大于第三边,任意两边之差小于第三边”是常考的重要知识点之一.解题时注意方程思想和分类讨论思想的应用,注意根据题意列方程(组)或不等式(组)进行求解,解题时容易忽视检验所得的三角形是否存在,巧用三角形的三边关系往往能化难为易,起到事半功倍的解题效果.类型1判断三条线段能否组成三角形1.判断下列所给的三条线段能否围成三角形?(1)5,5,a(0<a<10);(2)a+1,a+2,a+3;(3)三条线段的长度之比为2∶3∶5.解:(1)∵0<a<10,∴5+5>a,因而能构成三角形.(2)当a=0时,a+1+a+2=2a+3=3,因而不能组成三角形.(3)∵三条线段之比为2∶3∶5,∴设三条线段为2k,3k,5k,∵2k+3k=5k,因而不能组成三角形.类型2确定三角形的个数2.以长度为5 cm,7 cm,9 cm,13 cm的线段中的三条为边,能组成三角形的情况有(B)A.2种B.3种C.4种D.5种3.边长为整数并且最大边长是5的三角形共有9个.4.现有长为7 cm,3 cm的木棒各一根,另有一堆长短不等的木棒若干,请在这堆木棒里选取长为偶数且能与原两根木棒钉成三角形的木棒,则符合条件的木棒有几种?解:设符合条件的木棒的长为x cm,则4<x<10,又x为偶数,则x可取6和8,故符合条件的木棒有两种.类型3确定第三边或字母的取值范围5.若三角形三条边长分别是3,1-2a,8,则a的取值范围是(B)A.a>-5B.-5<a<-2C.-5≤a≤-2D.a>-2或a<-56.一个三角形有两边长为2和5,则第三边长x的取值范围是3<x<7.若它的周长是偶数,则第三边的长为5.类型4确定等腰三角形的边长7.已知有两边相等的三角形的两边长分别为6 cm,4 cm,则该三角形的周长是16 cm或14 cm.8.在△ABC中,AB=AC,边AC上的中线BD把三角形的周长分为10 cm和18 cm两部分,求△ABC 各边的长.解:设等腰三角形的腰长AB=AC=2x cm,BC=y cm,∵BD是腰上的中线,∴AD=DC=x cm.若AB+AD=10 cm,则解得此时组不成三角形,应舍去.若AB+AD=18 cm,则解得∴AB=AC=12 cm,BC=4 cm,即△ABC各边的长分别为12 cm,12 cm和4 cm.类型5在代数中的应用9.已知等腰△ABC的周长为10,求腰长x的取值范围.解:设腰长为x,则底边长为10-2x,依题意得解得<x<5.故腰长的取值范围为<x<5.10.已知a,b,c是△ABC的三边,a,b满足|a-4|+(b-2)2=0,c为奇数,求△ABC的周长.解:∵|a-4|+(b-2)2=0,∴a-4=0且b-2=0,∴a=4,b=2,∴2<c<6.∵c为奇数,∴c=3或5,∴△ABC的周长为4+2+3=9或4+2+5=11.11.已知a,b,c为△ABC的三边长,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|.解:∵a,b,c是△ABC的三边长,∴a+b+c>0,a-b-c<0,a-b+c>0,a+b-c>0,∴|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|=(a+b+c)-[-(a-b-c)]-(a-b+c)-(a+b-c)=a+b+c+a-b-c-a+b-c-a-b+c=0.类型6证明线段之间的不等关系12.如图,点P是△ABC内任意一点.试说明:PB+PC<AB+AC.证明:延长BP交AC于点D,在△ABD中,PB+PD<AB+AD,①在△PCD中,PC<PD+CD,②①+②得PB+PD+PC<AB+AD+PD+CD,即PB+PC<AB+AC.13.如图,P为△ABC中任意一点.证明:AB+BC+CA>PA+PB+PC>(AB+BC+CA).证明:延长BP交AC于点D,∵在△ABD中,AB+AD>PB+PD,在△DPC中,DP+DC>PC,∴AB+AD+DP+DC>PB+PD+PC,∴AB+CA>PB+PC.同理AC+BC>PA+PB,AB+BC>PA+PC,∴2AB+2AC+2BC>2PA+2PB+2PC,即AB+BC+CA>PA+PB+PC.又∵PA+PB>AB,PB+PC>BC,PC+PA>CA,∴2(PA+PB+PC)>AB+BC+CA,∴PA+PB+PC>(AB+BC+CA),∴AB+BC+CA>PA+PB+PC>(AB+BC+CA).。

专题02 三角形中线段的问题知识对接考点一、三角形中的线段三角形中的四条特殊的线段是：高线、角平分线、中线、中位线.1．内心：三角形角平分线的交点，是三角形内切圆的圆心，它到各边的距离相等.2．外心：三角形三边垂直平分线的交点，是三角形外接圆的圆心，它到三个顶点的距离相等. 3．重心：三角形三条中线的交点，它到每个顶点的距离等于它到对边中点距离的2倍.4．垂心：三角形三条高线的交点.5．三角形的中位线：连结三角形两边中点的线段是三角形的中位线.中位线定理：三角形的中位线平行于第三边且等于第三边的一半.要点补充：(1)三角形的内心、重心都在三角形的内部.(2)钝角三角形的垂心、外心都在三角形的外部.(3)直角三角形的垂心为直角顶点，外心为直角三角形斜边的中点.(4)锐角三角形的垂心、外心都在三角形的内部.专项训练一、单选题1．（2021·湖南长沙·）如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）A ．两点确定一条直线B ．两点之间线段最短C ．三角形的稳定性D ．垂线段最短2．（2021·浙江）如图，在矩形ABCD 中，点F 为边AD 上一点，过F 作//EF AB 交边BC 于点E ，P 为边AB 上一点，PH DE ⊥交线段DE 于H ，交线段EF 于Q ，连接DQ ．当AF AB =时，要求阴影部分的面积，只需要知道下列某条线段的长，该线段是（ ）A ．EFB ．DEC ．PHD ．PE3．（2021·上海金山·九年级二模）已知三条线段长分别为2cm 、4cm 、acm ，若这三条线段首尾顺次联结能围成一个三角形，那么a 的取值可以是（ ）A ．1cmB ．2cmC ．4cmD ．7cm4．（2021·青海西宁·九年级一模）下列事件中，属于必然事件的是（ ）A ．某个数的绝对值大于0B ．a -一定是负数C ．五边形的外角和等于540︒D ．长分别为3,4,6的三条线段能围成一个三角形5．（2021·江苏九年级专题练习）下列说法正确的是（ ）．A ．方差越大，数据波动越小B ．两直线平行，同旁内角相等C ．长为3cm ，3cm ，5cm 的三条线段可以构成一个三角形* 本号资料皆来源于微信公众号：数学第六感D ．学校在初三3100名同学中随机抽取300名同学进行体考成绩调查，300名同学为样本 6．（2021·江苏九年级一模）下列长度的三条线段，不能组成三角形的是（ ） 本号资料皆来源于微信@公众号：数学第六感A ．3，7，5B ．4，8，5C ．5，12，7D ．7，13，8 7．（2021·全国）如图，已知在Rt ABC 中，90C ∠=︒，点G 是ABC 的重心，GE AC ⊥，垂足为E ，如果8CB =，则线段GE 的长为（ ）A．53B．73C．83D．1038．（2021·山东）现有4条线段，长度依次是2、4、6、7，从中任选三条，能组成三角形的概率是（）A．14B．12C．35D．349．（2021·全国）若平行四边形的两条对角线长为6 cm和16 cm，则下列长度的线段可作为平行四边形边长的是( )A．5cm B．8cm C．12cm D．16cm 10．（2021·福建）如图，AD经过ABC的重心，点E是AC的中点，过点E作//EG BC交AD 于点G，若12BC ，则线段GE的长为（）A．6B．4C．5D．3二、填空题11．（2021·靖江市靖城中学九年级一模）过△ABC的重心G作GE△BC交AC于点E，线段BC＝12，线段GE长为________．12．（2021·沙坪坝·重庆一中九年级三模）从长度分别为1，3，5，6的四条线段中，随机抽取两条线段，与长度为8的线段恰好能围成三角形的概率是______．13．（2021·扬州中学教育集团树人学校）如图，在Rt△ABC中，AC＝BC＝2，△ACB＝90°，正方形BDEF BDEF绕点B旋转一周，连接AE，点M为AE的中点，连接FM，则线段FM的最大值是___．14．（2021·浙江杭州市·九年级模拟预测）如果从长度分别为2、4、6、7的四条线段中随机抽取三条线段，那么抽取的三条线段能构成三角形的概率是_______．15．（2021·湖北襄阳市·）从长度分别为1、3、5、7的四条线段中任选三条作边，能构成三角形的概率为_______________．三、解答题16．（2021·江苏泰州中学附属初中九年级三模）如图，已知抛物线2y x mx n =-++和直线y x =，抛物线顶点为A ，与y 轴交点为B ，直线y x =与抛物线对称轴交于点C ．（1）抛物线顶点坐标为 （用m ，n 表示），（2）当抛物线的顶点落在直线21y x =+上时，求n 的最大值．（3）若四边形ABOC 为平行四边形△求m 的值．△若直线y x =与抛物线在对称轴右侧部分的交点为D ，当BOD 为直角三角形时，求n 的值．△过C 点作线段CE AC ⊥，设CE=a ，是否存在实数a 值使ACE 的重心恰好落在抛物线上，若存在直接写出a 和n 的关系式，若不存在，请说明理由．17．（2021·广西南宁十四中九年级）如图，在平面直角坐标系中，已知ABC 的三个顶点坐标分别是()2,2A 、()4,0B 、()4,4C -．（1）请画出ABC 绕点A 顺时针旋转90 得到的11AB C △；（2）若点D 在线段11B C 上，且直线AD 将11AB C △分成面积相等的两部分，请画出线段AD ，并写出D 的坐标．18．（2021·陕西西安·）问题提出（1）如图△，在Rt △ABC 中，△A ＝90°，AB ＝3，AC ＝4，在BC 上找一点D ，使得AD 将△ABC分成面积相等的两部分，作出线段AD ，并求出AD 的长度； 本号资料@皆来源于微信公众号：数#学第六感问题探究（2）如图△，点A 、B 在直线a 上，点M 、N 在直线b 上，且a △b ，连接AN 、BM 交于点O ，连接AM 、BN ，试判断△AOM 与△BON 的面积关系，并说明你的理由；解决问题（3）如图△，刘老伯有一个形状为筝形OACB 的养鸡场，在平面直角坐标系中，O （0，0）、A （4，0）、B （0，4）、C （6，6），是否在边AC 上存在一点P ，使得过B 、P 两点修一道笔直的墙（墙的宽度不计），将这个养鸡场分成面积相等的两部分？若存在，请求出直线BP 的表达式；若不存在，请说明理由．19．（2021·陕西九年级一模）问题提出：（1）如图1，在△ABC 中，已知AB ＝AC ＝5，BC ＝4，在BC 上找一点D ，使得线段AD 将△ABC 分成面积相等的两部分，画出线段AD ，并写出AD 的长为 ．问题探究：（2）如图2，点D是△ABC边AC上一定点，在BC上找一点E，使得线段DE将△ABC 分成面积相等的两部分，并说明理由．问题解决：（3）如图3，四边形ABCD是西安市高新区新近改造过程中的一块不规则空地，为了美化环境，市规划办决定在这块地里种植两种花卉，打算过点C修一条笔直的通道，以便市民出行观赏花卉，要求通道两侧种植花卉的面积相等，经测量AB＝20米，AD＝100米，△A ＝60°，△ABC＝150°，△BCD＝120°，若将通道记为CF，请你画出通道CF，并求出通道CF的长．20．（2021·泗水县教育和体育局教学研究中心）（数学经验）三角形的中线的性质：三角形的中线等分三角形的面积．（经验发展）面积比和线段比的联系：（1）如图1，M为△ABC的AB上一点，且BM=2AM．若△ABC的面积为a，若△CBM的面积为S，则S=_______(用含a的代数式表示)．（结论应用）（2）如图2，已知△CDE的面积为1，14CDAC=，13CECB=，求△ABC的面积．（迁移应用）（3）如图3．在△ABC中，M是AB的三等分点(13AM AB=)，N是BC的中点，若△ABC的面积是1，请直接写出四边形BMDN的面积为________．21．（2021·江苏南京·）已知线段AB与点O，利用直尺和圆规按下列要求作△ABC（不写作法，保留作图痕迹）．（1）在图△中，点O是△ABC的内心；（2）在图△中，点O是△ABC的重心．22．（2021·陕西九年级二模）（1）如图1，AB是△○的弦，点P在△○上，当△P AB是直角三角形时，请在图1中画出点P的位置；（2）如图2，△○的半径为4，A、B为△○外固定两点（O、A、B三点不在同一直线上），OA=，P为△○上的一个动点（点P不在直线AB上），以PA和AB为邻边作平行四边形且8P ABC，求BC最小值；（3）如图3，A、B是△○上的两个点，过A点作射线AM AB⊥，AM交△○于点C，若3AB=，AC=，点D是平面内的一个动点，且24CD=，E为BD的中点，在点D的运动过程中，求线段AE长度的最大值与最小值．23．（2021·黑龙江九年级一模）如图，网格中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．（1）在图中确定点C，点C在小正方形的顶点上，请你连接CA，CB，BC＝；（2）在（1）确定点C后，在网格内确定点D，点D在小正方形的顶点上，请你连接CD，BD，CD△AB，△CDB的面积为6，直接写出△CBD的正切值．。