下载文档原格式
第14章 本征函数展开法一、本征函数法的基本概念研究线性算子方程Lu g = (14-1)例如，对于波动方程()∇+=-22k u f ，则L k g f =-∇+=(),22 。
我们的目标是已知算子L 、源g ，求解函数u 。
引入本征方程Lu u =λ (14-2)其中，λ称为本征值，u 称为对应于λ的本征函数矢量。
一般来说，若边界有限，则本征值λ为离散谱。
若边界无界，则本征值λ为连续谱。
所以对于有限边界Lu u n n n n ==λ12,, (14-3) 设{}λn为本征值谱，{}u n为本征函数系。
如果{}u n 完备，则g 可以用本征函数系{}u n 展开为g u n n n=∑β (14-4)如果{}u n 还为正交归一系，即u u m nm n m n mn,==≠=⎧⎨⎩δ01 (14-5) 式中，<>a b ,表示a 与b 的内积。
对(14-4)式两边关于u n 取内积，可得 βn n u g =<>, (14-6) 未知解函数u 也可以用{}u n 展开为u u n n n=∑α (14-7)于是求u 的问题转化为求αn 的问题。
将(14-7)和(14-4)代入算子方程(14-1)，得∑∑∞=∞==11n nn n nn nuu L βα (14-8)将(14-3)代入，得()αλβnn n n n u -==∞∑01(14-9)根据正交归一性，有 αβλn nn= (14-10)本征函数展开理论认为，带激励的算子方程可以分解为两部分，一部分由算子自身特性(包括区域边界几何特性、媒质特性)决定，它将给出一切可能的潜在解，即本征函数系及其展开。
另一部分则是激励，它决定激励哪些特殊解。
前者为内因，后者为外因，就如同一只鼓，当它做成以后，所有可能的音域已经确定，敲鼓的点和方式不同，声音不同，但都是可能音域中的某些成分或组合。
大鼓绝对发不出高音来。
因此，如果我们把问题的本征函数搞清楚了，一切激励均迎刃而解。
引言——物理学是什么？“物理学是探讨物质的结构和运动基本规律的学科”——赵凯华，罗蔚茵，《新概念物理教程·力学》 研究对象：物质 → 可观测的东西 ＊ 物理学→现象学Physical ：源于希腊语，意为“自然的、肉体的” ＊ 观测不到的东西（如上帝、阿弥陀佛……）不是物理学不是（或不完全是）一个层面的知识 ＊ 科学不是万能的：有触及不到的地方 基石：实验 伽利略（Galileo Galilei ，1564-1642） 分析工具＊ 数学：牛顿（I. Newton ，1642-1727）《自然哲学之数学原理》，1687 ＊ （基于实验的）思辨 套路第一篇 力学“研究机械运动及其规律的物理学分支”（狭义） Mechanical ：机械的、力学的广义的力学：电动力学、热力学、统计力学、量子力学…… 经典力学：＊ 牛顿力学：动力学核心为“力”→ 矢量力学＊ 理论力学：动力学核心为“能量”，包含拉格朗日（J. Lagrange, 1735-1813）力学和哈密顿（W.R. Hamilton ，1805-1865）力学《力学》教学内容：＊ 牛顿定律{动量定理→动量守恒定律机械能定理→机械能守恒定律角动量定理→角动量守恒定律＊ 应用：刚体；振动与波；流体实验合理假设（模型）数学推演及推论实验验证 NOYES第一章质点运动学✍第一章作业：2、4、6、10、12、14、19{运动学：如何描述运动动力学：（特定）运动形成的原因运动：“物体及物体中的各个点部位的空间位置随时间的变化”（舒幼生，《力学（物理类）》）✓芝诺（Zeno，约490B.C.——425B.C.）悖论：“飞矢不动”飞行的箭每时刻占据固定的空间范围、具有相同的形状，如何称之为“动”✓运动关涉位置随时间的变化：无穷小时间间隔≠0 ⇒微积分的引入✓惠施（390B.C.——317B.C.）：“飞鸟之景，未尝动也”✓经典力学质点某时刻运动状态的完备描述：给定{r⃑(t); v⃑(t)}1.1时间和空间空间：事物排列的相对方位和次序时间：事物发生的先后顺序1.1.1时空观宗教的时空观：如神创时空观、唯识时空观等哲学上的时空观：如康德（I. Kant，1724-1804）的“先验时空观”时空先于经验存在，是人们“整理感性材料的先天直观形式”（康德，《纯粹理性批判》，1781）物理的时空观：测量的时空观空间是用尺测量的东东；时间是用表测量的东东物理学中的时空观：* 绝对时空观：与观察者、物质及其运动无关→ 与物理无关物理/数学实现：经典力学/平直欧式空间+时间（假定！）* 相对时空观：与观察者、物质及其运动无关（马赫）物理/数学实现（爱因斯坦）·狭义相对论/平直闵氏时空·广义相对论/黎曼弯曲时空“物质告诉时空如何弯曲，时空告诉物质如何运动”——惠勒1.1.2时空的度量时间的度量：* 满足一定规律的物理过程可看作是“钟”：如人的相貌* 周期性的物理过程：天体运动，钟摆振动，原子钟* 秒的定义：1s为铯133原子基态两个超精细能级之间跃迁相对应的辐射周期的9 192 631 770倍。
第一章静电场作业：2，7，9，12，14，16，18，19，22，24，25其中1.25题补充条件：取O点处为电势零点。
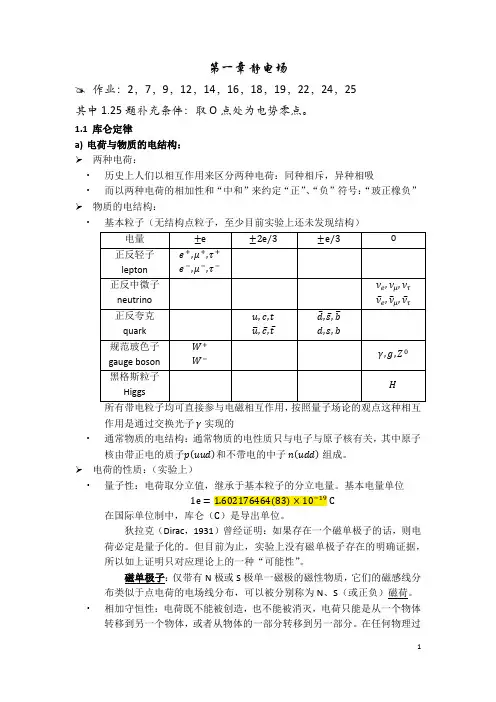
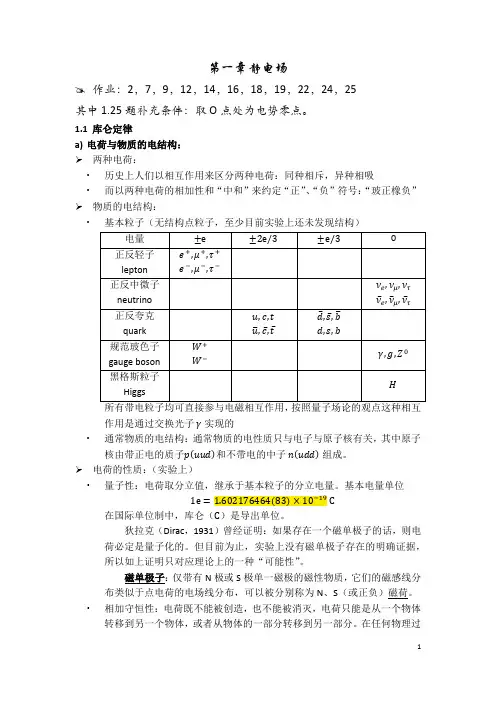
1.1库仑定律a)电荷与物质的电结构：两种电荷：∙历史上人们以相互作用来区分两种电荷：同种相斥，异种相吸∙而以两种电荷的相加性和“中和”来约定“正”、“负”符号：“玻正橡负” 物质的电结构：∙基本粒子（无结构点粒子，至少目前实验上还未发现结构）作用是通过交换光子 γ 实现的∙通常物质的电结构：通常物质的电性质只与电子与原子核有关，其中原子核由带正电的质子p(uud)和不带电的中子 n(udd)组成。
电荷的性质：（实验上）∙量子性：电荷取分立值，继承于基本粒子的分立电量。
基本电量单位1e=1.602176464(83)×10−19 C在国际单位制中，库仑（C）是导出单位。
狄拉克（Dirac，1931）曾经证明：如果存在一个磁单极子的话，则电荷必定是量子化的。
但目前为止，实验上没有磁单极子存在的明确证据，所以如上证明只对应理论上的一种“可能性”。
磁单极子：仅带有N极或S极单一磁极的磁性物质，它们的磁感线分布类似于点电荷的电场线分布，可以被分别称为N、S（或正负）磁荷。
∙相加守恒性：电荷既不能被创造，也不能被消灭，电荷只能是从一个物体转移到另一个物体，或者从物体的一部分转移到另一部分。
在任何物理过程中(从宏观到微观)，电荷的代数和守恒。
∙相对论不变性：是严格的量子性与相加守恒性的内在要求实验证据：宏观物体的稳定性（如上三点均为稳定性的内在要求） b) 库仑定律： 历史回顾： ∙富兰克林（Franklin ，1755）发现带电小球在带电金属桶内几乎不受力，普里斯特利（Priestley ，1767）通过类比万有引力定律猜想电力满足平方反比律。
∙卡文迪什（Cavendish ，1772）利用导体壳静电平衡的性质，即当f~r −(2±|δ|) |δ|越小，内表面带电量越小以内表面电量的“示零实验”测得 |δ|<2×10−2 ，其结果为麦克斯韦（Maxwell ，1870’s ）整理发表，并进一步将精度提高到 |δ|<5×10−5 ，目前的精度为|δ|<2.7×10−16 （Williams et. al.，1971） ∙库仑（Coulomb ，1785）以设计精巧的“扭称”直接验证了平方反比定律（|δ|<4×10−2） 库仑定律表述：如图，两个真空静止点电荷{ F ⃑21=10Q 1Q 2r ⃑21213=10Q 1Q 2212r ⃑̂21F ⃑12=14πε0Q 1Q 2r ⃑12r 123=14πε0Q 1Q 2r 122r ⃑̂12其中，真空介电常数ε0=8.85×10−12 C 2/(N ∙m 2)库仑定律的适用条件及其拓展：1. 真空：如果有物质（注意：物质都有电结构，如导体和电介质），物质中的电结构会在外电场的影响下发生改变，稳定后每个电荷微元（可看作为点电荷）激发的电场仍然满足（真空）库仑定律。
电磁场导论孟昭敦【电磁场导论】练习1：两点电荷之间的距离R的计算 Example 1.1 已知点电荷q1位于坐标原点，点电荷q2位于点（3，4，0）m处，计算两点电荷之间的距离R。
解答 R2 =（x2）2 +（y2）2 +（z2）2 =（3）2 +（4）2 +（0）2 = 25 R= 5 m 第二种情况点电荷q1位于坐（x1，y1，z1）标原点，点电荷q2位于点（x2，y2，z2）讨论画图求解距离R Example 1.2 已知点电荷q1位于点（0，1，2）m处；点电荷q2位于点（2，0，0）m处，计算两点电荷之间的距离R 讨论画图求解解答 R2 =（x1-x2）2 +（y1-y2）2 +（z1-z2）2 R2 =（0-2）2 +（1-0）2 +（2-0）2 = 22+12+22 = 9 R=3 m 练习2：表示作用力F的方向的e21 和e12 方法1 作用力F的方向的直接确定法：优点：简单、有效。
适用：两个点电荷之间的库仑力计算。
1). 同号点电荷之间的库仑力是排斥力，因此 F12的方向由q2指向q1; F21的方向由q1 指向q2 。
2). 异号点电荷之间的库仑力是吸引力，因此 F12的方向由q1指向q2; F21的方向由q2指向q1 。
方法2 矢量表示法 e12 = R12 / R e21 = R21 / R 式中 R12为由q1 指向q2的距离矢量；R21为由q2指向q1的距离矢量。
R为两个点电荷之间的距离关键 * 距离矢量R12、R21 距离R R12=（x1-x2）ex+（y1-y2）ey+（z1-z2）ez R21 =（x2- x1）ex+（y2- y1）ey+（z2- z1）ez = - R12 Example 1.3 已知点电荷q1位于点（0，1，2）m处；点电荷q2位于点（2，0，0）m处，计算e12 与e21。
讨论画图求解解答 q1位置 R1 = 0 ex + 1ey+ 2ez q2位置 R2 = 2 ex + 0ey+ 0ez R12 = R2 - R1 = （2 ex + 0ey+ 0ez）-（0 ex + 1ey+ 2ez） =（x2-x1）ex+（y2-y1）ey+（z2-z1）ez = 2 ex- 1 ey- 2 ez R2 =（x1-x2）2 +（y1-y2）2 +（z1-z2）2 =（0-2）2 +（1-0）2 +（2-0）2 = 22+12+22 = 9 R=3 m e12 = R12 / R = (2 ex- 1 ey- 2 ez )/ 3 R21= - R12 = -2 ex+ 1 ey+ 2 ez e21 = -e12 Example 1.4 已知已知点电荷q1位于点（0，1，2）m处；点电荷q2位于点（2，0，0）m处，讨论库仑力F12与 F21。
