当前位置：文档之家 › 第四节阶跃函数和冲激函数

第四节阶跃函数和冲激函数

  • 格式：ppt
  • 大小：208.50 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

阶跃函数和冲激函数

阶跃函数和冲激函数

பைடு நூலகம்
控制系统的性能优化
阶跃函数用于测试控制系统的 性能，通过观察系统对阶跃输 入的响应速度和超调量，可以
评估系统的性能。
冲激函数可用于分析系统的 频率响应，了解系统在不同 频率下的性能表现，为系统
性能优化提供依据。
通过调整控制系统的参数，结 合阶跃函数和冲激函数的特性， 可以优化控制系统的性能指标。
控制系统的故障诊断与修复
在图形上，冲激函数看起来像一个非 常窄的矩形脉冲。
应用场景
在信号处理中，冲激函数常被 用作单位冲激信号，用于表示 某一事件的发生或开始。
在物理学中，冲激函数可以用 于描述瞬间作用或力的作用， 例如碰撞或冲击。
在电路分析中，冲激函数可以 用于描述电路中的瞬态响应或 冲激响应。
03
阶跃函数与冲激函数的 比较
05
阶跃函数和冲激函数在 控制系统中的应用
控制系统的稳定性分析
01
阶跃函数用于分析控制系统的稳定性，通过观察系统
对阶跃输入的响应，可以判断系统是否稳定。
02
冲激函数可用于分析系统的零点和极点，进一步确定
系统的稳定性。
03
通过计算系统的传递函数，结合阶跃函数和冲激函数
的性质，可以判断系统在不同频率下的稳定性。
阶跃函数和冲激函数可用于检测控制系统的故障，通过观察系统对输入信号的响应变化，可以判断系 统是否存在故障。
阶跃函数和冲激函数还可以用于定位故障，通过分析系统在不同输入下的响应特性，可以确定故障发生 的位置。
在故障诊断的基础上，可以利用阶跃函数和冲激函数的特性，制定相应的修复措施，恢复控制系统的正 常运行。
04
阶跃函数和冲激函数在 信号处理中的应用
信号的分离与提取
3-4单位阶跃函数和单位冲激函数

3-4单位阶跃函数和单位冲激函数


解：
i L ( t ) I s ( t )
diL ( t ) d (t ) uL ( t ) L LI s LI s (t ) dt dt
如果电感电流发生跳变，必然有冲激电压施 加在电感两端，电感中的磁通量发生跳变。
电感磁通的跳变量为：
uL ( t )dt LI s ( t )dt LI s
0 0 0 0
解二
L[iL (0 ) iL (0 )] LI s
解：
i (t ) ( t ) 2 t 2 t 2
4.阶跃函数的作用：
(1)阶跃函数可以作为开关的数学模型，所以有
时也称为开关函数。
(2)表示某些分段函数。 (3)起到分解波形的作用。
二、单位冲激函数
1.定义
(t ) 0 t0 ( t )dt 1
§34 单位阶跃函数和单位冲激函数
一、单位阶跃函数:
1. 定义
1 t 0 (t ) 0 t 0
t = 0，函数值不确定
(t 0 ) 0 (t 0 ) 1
(t )等效表示电路的输入示例
直流电压源和任意网络接通
(t ) 表示的等效电路模型
t 0 t 0
t 0 t 0
f ( t ) ( t t 0 )dt
f ( t0 )
( t )dt f ( t0 )
单位冲激函数的采样性质 (sampling property)
三. 单位冲激函数和单位阶跃函数之间的关系
lim f ( t ) ( t )
0
lim f ( t ) ( t )


A ( t )dt A
阶跃函数和冲激函数

阶跃函数和冲激函数

阶跃函数和冲激函数阶跃函数和冲激函数在分析线性电路过渡过程时，常使用一些奇异函数来描述电路中的激励或响应。

阶跃函数和冲激函数是两个最常用最重要的函数。

一、单位阶跃函数。

单位阶跃函数定义为：（式8-2-1）图8-2-1其波形如图8-2-1所示。

单位阶跃函数在处有跳变，是一个不连续点。

将单位阶跃函数乘以常数，就得到阶跃函数，又称为开关函数。

因为它可以用来描述电路中的开关动作，如图8-2-2所示。

图8-2-2所示电路在时刻开关S从1切换至2，那么一端口网络的入端电压就可用阶跃函数表示为：，如图8-2-2所示。

图8-2-2延时的单位阶跃函数定义为：（式8-2-2）其波形如图8-2-3所示，同样以图8-2-2为例，若时刻将开关S 从1切换至2，那么一端口网络的入端电压就可用延时阶跃函数表示为：。

二、单位冲激函数单位冲激函数定义为：（式8-2-3）其波形如图8-2-5所示。

为了更好地理解单位冲激函数，先来看单位脉冲函数。

单位脉冲函数定义为：（式8-2-4）图8-2-5其波形如图8-2-5所示。

单位脉冲函数的宽度是，高度是，面积为1。

当脉冲宽度减小，其高度将增大，而面积仍保持为1。

当脉冲宽度趋于无限小时，其高度将趋于无限大，但面积仍然为1。

当脉冲宽度趋于零时，这时脉冲函数就成为单位冲激函数。

将单位冲激函数乘以常数K，就得到冲激强度为K的冲激函数，表示为。

延时的单位冲激函数定义为：（式8-2-5）其波形如图8-2-6所示。

图8-2-6冲激函数不是一般函数，属于广义函数，其更严格的定义可参阅有关数学书中的论述。

知识点1第一章第4节阶跃函数和冲激函数

知识点1第一章第4节阶跃函数和冲激函数

知识点1第一章第4节阶跃函数和冲激函数阶跃函数和冲激函数是控制工程和信号处理中常用的数学函数。

它们在描述系统的动态响应以及信号的特性时起到了重要的作用。

本文将详细介绍阶跃函数和冲激函数的定义、性质以及在实际应用中的意义。

一、阶跃函数的定义和性质阶跃函数（Step Function）是一类常见的跃变函数，它在数学上用于描述其中一时刻突然跃变的情况。

阶跃函数通常被表示为u(t)，其中t 为自变量。

阶跃函数的定义如下：1,t≥0u(t)=0,t<0在定义中，当t≥0时，阶跃函数的取值为1；当t<0时，阶跃函数的取值为0。

阶跃函数的图像呈现为一个从0跃变到1的过程。

阶跃函数具有以下性质：1.阶跃函数u(t)在t=0的时刻不可导，因为它在该点没有斜率。

2.在t<0时，阶跃函数的值恒为0；在t>0时，阶跃函数的值恒为13.阶跃函数可用于表示信号的开关状态，如电路的打开和关闭。

二、冲激函数的定义和性质冲激函数（Impulse Function）是另一种重要的数学函数，它在数学上用于描述一个瞬间产生的脉冲信号。

冲激函数通常被表示为δ(t)，其中t为自变量。

冲激函数的定义如下：无穷,t=0δ(t)=0,t≠0在定义中，只有当t=0时，冲激函数的取值为无穷大；其余时刻冲激函数的取值都为0。

冲激函数的图像呈现为在t=0时的一个尖峰。

冲激函数具有以下性质：1.冲激函数δ(t)在t≠0的时刻都为0，只有在t=0时取值为无穷大。

2. 冲激函数是一个特殊的函数，它的积分等于1，即∫δ(t)dt=13.冲激函数可用于描述系统对瞬变信号的响应。

三、阶跃函数和冲激函数在实际应用中的意义阶跃函数和冲激函数在控制工程和信号处理中具有广泛的应用，主要包括以下方面：1.系统响应：阶跃函数和冲激函数可用于描述系统对不同类型输入信号的响应。

通过对系统在不同时刻的输出特性进行测量，可以得到系统的传递函数或冲激响应等重要参数。

1.4 阶跃函数和冲激函数

1.4 阶跃函数和冲激函数


(t 2) 2 (t ) d t
板书：例1.4-1，例1.4-2，
d [(t 2) 2 ] t 0 2(t 2) t 0 4 dt
13
通信与信息工程学院基础教学部
练习
通信与信息工程学院基础教学部
14
练习答案
通信与信息工程学院基础教学部
15
5.复合函数形式的冲激函数 实际中有时会遇到形如δ[f(t)]的冲激函数，其中f(t)是普通函 数。并且f(t) = 0有n个互不相等的实根 ti ( i=1，2，…，n)
1, k 0 (k ) 0, k 0
def
ε (k)
1 -1 o1 2 3 … k
3.ε(k)与δ(k)的关系 δ(k) = ε(k) –ε(k –1)
(k )
或
i
(i)
j 0
k
ε(k) = δ(k)+ δ(k – 1)+…
(k ) (k j )
通信与信息工程学院基础教学部
19
小结：
• • • 单位阶跃信号的定义 单位冲激信号的定义、性质 西电精品课程视频（来源于网络）
通信与信息工程学院基础教学部
20
冲激信号尺度变换的证明 从 ( t ) 定义看：
pt 1
pat 1




2 t

2
O



2a
O

a

2a
t
t 强度为1 p(t)面积为1，
2
注意：如果f(t)=0有重根，δ[f(t)]无意义。
通信与信息工程学院基础教学部
17
三、序列δ(k)和ε(k)
阶跃信号和冲激信号

阶跃信号和冲激信号


t0 O
t
宗量>0 函数值为1 宗量<0 函数值为0
3．用单位阶跃信号描述其他信号
门函数：也称窗函数
ftutut
2 2
其他函数只要用门函数处理(乘以 门函数)，就只剩下门内的部分。
符号函数：(Signum)
f t
1
Gτ t
O
2
t
2
sgn t
sgtn )( 11
t0 t0
O
t
st ) g u ( t ) n u ( t ) 2 ( u ( t ) 1 u(t)1[sgt)n 1(] 2
一．单位斜变信号
1． 定义
0 t0 R(t)t t0
2．有延迟的单位斜变信号
0 R (tt0) tt0
tt0 tt0
由宗量t -t0=0 可知起始点为 t 0 3．三角形脉冲
f(t) K R(t)
0
0t
其它
R(t) 1
O1
t
R(t t0 ) 1
O t0 t0 1 t
f (t) K
O
t
二．单位阶跃信号
四.总结： R(t)，u(t)， (t) 之间的关系R(t )来自u(t )1 1
t
O1
O
R(t) 求 ↓↑积
u(t) 导 ↓↑分
(t)
(t)
(1)
t
t
O
(-<t< )
冲激函数的性质总结
（1）抽样性
f(t)(t) f(0 )(t)
（5）冲激偶
( t) (t)
f (t)(t)dtf(0)
(t)dt0
（2）奇偶性
(t)(t)
t (t)dt(t)
§1.4 阶跃函数和冲激函数

§1.4 阶跃函数和冲激函数

●阶跃函数●冲激函数是两个典型的奇异函数。

●阶跃序列和单位样值序列§1.4 阶跃函数和冲激函数函数本身有不连续点(跳变点)或其导数与积分有不连续点的一类函数统称为奇异信号或奇异函数。

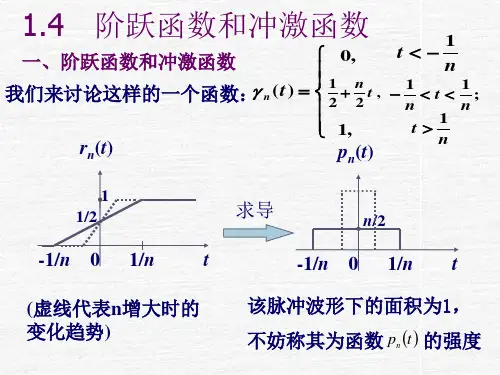
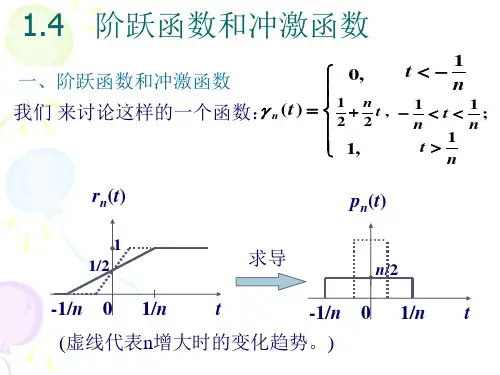
§1.4 阶跃函数和冲激函数一、单位阶跃函数二．单位冲激函数三．冲激函数的性质四. 序列δ(k)和ε(k)一、单位阶跃函数ton1-n11γn21⎪⎩⎪⎨⎧>=<==∞→0,10,21,0)(lim )(def t t t t t n n γε下面采用求函数序列极限的方法定义阶跃函数。

选定一个函数序列γn (t)如图所示。

t)(t εO11. 定义2. 延迟单位阶跃信号t)(0t t +εO10t -t)(0t t -εO10t 0,1)(0000>⎩⎨⎧><=-t t t t t t t ε0, 1 0)(000>⎩⎨⎧->-<=+t t t t t t t εt)(t εO 13. 阶跃函数的性质f (t )o2t12-1（1）可以方便地表示某些信号f (t ) = 2ε(t )-3ε(t -1) +ε(t -2)（2）用阶跃函数表示信号的作用区间(a)(b)f (t )f (t )ε(t )oottot(c)f (t )[ε(t -t 1)-ε(t -t 2)]t 1t 2（3）积分)(d )(t t tεττε=⎰二．单位冲激函数单位冲激函数是个奇异函数，它是对强度极大，作用时间极短一种物理量的理想化模型。

●狄拉克(Dirac)定义●函数序列定义δ(t)●冲激函数与阶跃函数关系1. 狄拉克(Dirac )定义()⎪⎩⎪⎨⎧=≠=⎰∞+∞- 1d )(0 0)(t t t t δδ⎰⎰+∞∞-+-=00d )(d )(tt t t δδ➢函数值只在t = 0时不为零；➢积分面积为1；➢t =0 时，，为无界函数。

()∞→t δto(1)δ(t )2.函数序列定义δ(t )t on1-n11γn21top n (t )n1n1-2n )(lim )(deft p t n n ∞→=δ对γn (t )求导得到如图所示的矩形脉冲p n (t ) 。

1-2冲击信号

1-2冲击信号


3 系统框图 连续基本单元：积分器、加法器、数乘器、延时器等。 连续基本单元：积分器、加法器、数乘器、延时器等。 离散基本单元：加法器、数乘器、延迟器等。 离散基本单元：加法器、数乘器、延迟器等。
连续系统基本单元 积分器
f (t )
f1 (t )
离散系统基本单元
∫
y (t ) =
∫
t
−ω
f ( x)dx
Aε (t )
u = Aε (t )
2. 定义
1 ε (t ) = 0
ε (t )
t >0 t<0
延时阶跃函数： 延时阶跃函数：
1 ε (t − t 0 ) = 0
(t )
t > t0 t < t0
O
t0
3. 阶跃函数是可积函数
r (t ) = tε (t ) = ε (τ )dτ
三. 冲激函数
1.工程背景 工程背景 力学中瞬间作用的作用力；电学中的雷击电闪等。 力学中瞬间作用的作用力；电学中的雷击电闪等。 2.定义 2.定义 狄拉克（Dirac） 狄拉克（Dirac）定义 极限方式定义 严格数学定义：分配函数（广义函数） 严格数学定义：分配函数（广义函数）定义
δ (t )
与任意函数相乘
+ω
f (t )δ ' (t ) = f (0)δ ' (t ) − f ' (0)δ (t )
f (t )δ ' (t − t 0 ) = f (t 0 )δ ' (t − t 0 ) − f ' (t 0 )δ (t − t 0 )
抽样性
∫
−ω
f (t )δ ' (t ) dt = − f ' (0)
阶跃函数和冲激函数

阶跃函数和冲激函数


f ( t ) ( t t1 ) f (t1 ) (t t1 ) f (t ) (t t1 )dt f (t1 ) (t t1 )dt f (t1 ) ' f (t ) (t t1 )dt f ' (t1 )
0 r (t ) t
t0 t0
εxdx r t tεt
t
三、有延迟的单位冲激和单位阶跃信号 若冲激不是发生在原点,而是在 t t 0 则记为 ( t t 0 )
(t t0 ) 时移的冲激函数
1
0
t0
t
( t t 0 ) 0 , t t 0 t t 0 dt 1
例如：如图所示的函数：
f t
1
可表示为：
1
0
1
2
t
f t t 1 t 1 t t 1 t t 2
例如：如下图所示的函数：
f t
1
1 0 1 2 t
可表示为：
f t t 1 2 t t 2
0 单位冲激函数
sgnt
符号函数：(Signum)—奇异函数例
1 sgn( t ) 1 t 0 t0
1 (t ) [sgn( t ) 1] 2
O
t
sgn( t ) (t ) (t ) 2 (t ) 1
冲激函数的导数
s(t )
1 1
1/n
t
(虚线代表n增大时的 变化趋势)
该脉冲波形下的面积为1， 不妨称其为函数 pn t 的强度
rn(t)
1 1/2
(t)
阶跃信号与冲激信号

阶跃信号与冲激信号


0
t0
t
延时的阶跃信号
信号与系统
二.单位阶跃信号
门函数的定义
G (t)
G
(t
)
u
(t
2
)
u(t
2
)
1
用单位阶跃函数来表达分段区间函数
0
t
atb
f (t) f (t)[u(t a) u(t b)]
2
2
门函数
t t0
f (t) f (t)u(t t0)
t t1
f (t) f (t)[1 u(t t1)] f (t)u(t t1)
例：利用冲激函数的性质求下列积分
(1) (t 1)sin( t)dt
4
(2) e 3 2t (t 2k)dt
0
k
解：
(t
1 ) sin( t )dt
4
sin( t )
t1 4
sin
4
2 2
e 3 2t (t 2k)dt e 3 2t (t) (t 2) dt
0
k
0
t2
2 (t) sin(t) dt lim 2 sin(t) 2
t
t 0
t
信号与系统
三．单位冲激信号
例：化简函数 d 2 [sin(t )u(t)]
dt 2
4
解：
d2 dt 2
[sin(t
4
)u(t)]
d dt
[cos(t
4
)u(t)
sin(t
4
)
(t)]
d [cos(t )u t sin( ) (t)]
f (t)
f (t)
f (t)
0a
b
第一章(2)阶跃函数和冲激函数

第一章(2)阶跃函数和冲激函数


2、移位 在t
= t1
处的冲激函数为 δ ( t − t 1 ) 则：
f ( t )δ ( t − t 1 ) = f ( t 1 )δ ( t − t 1 ) ∞ ∞ ∫−∞ f (t )δ (t − t1 )dt = f (t1 )∫−∞ δ (t − t1 )dt = ∞ ' f ( t ) δ ( t − t1 )dt = − f ' ( t1 ) ∫− ∞
1.4 阶跃函数和冲激函数
0, 1 n γ n (t ) = + t , − 1 < t < 1 ; 我们 来讨论这样的一个函数： n n 2 2 1 1, t > n
一、阶跃函数和冲激函数
1 t < − n
rn(t)
1 1/2
pn(t) 求导 1/n t -1/n 0
n/2
ε(t)
1
t ε(t) = ∫−∞δ (τ )dτ
可见它们不同于普通函数。 可见它们不同于普通函数。
0 单位阶跃函数
t
δ(t)
(1)
0 单位冲激函数
t
ε (t )与 (t )之 的 系 δ 间 关 ：
dε (t ) δ (t ) = dt
ε(t)
1
t ε(t) = ∫−∞δ (τ )dτ
乘积。 乘积。 解： t δ ( t ) = 0
f (t )δ ' (t ) = f (0 )δ ' (t ) − f ' (0 )δ (t )
f (t )δ (t ) = f (0 )δ (t )
e −αtδ ( t ) = δ ( t )
tδ ' ( t ) = − δ ( t ) e − α t δ ' ( t ) = δ ' ( t ) + αδ ( t )

阶跃响应与冲激响应的关系

阶跃响应与冲激响应的关系1. 引言嘿，大家好！今天咱们来聊聊“阶跃响应”和“冲激响应”这两位老兄。

这两个概念在信号处理和系统分析里可是风头正劲的角色。

可能你听过它们，却不知道它们之间到底有什么关系。

别急，咱们慢慢来，保证让你听得津津有味。

2. 什么是冲激响应？2.1 冲激响应的定义首先，咱得了解一下“冲激响应”。

可以把它想象成一个超级短暂的信号，就像是你在派对上对朋友大喊“嗨！”然后瞬间安静下来了。

这种瞬间的信号就叫做冲激信号，而系统对这个信号的响应就是冲激响应。

听起来是不是很简单？2.2 冲激响应的特性而且，冲激响应的一个特性就是它能完全描述一个线性时不变系统的行为。

也就是说，只要你知道了冲激响应，你就能推导出系统对任何输入信号的响应，简直是信号处理界的万金油！所以，冲激响应就像是一张藏宝图，指引我们找到信号处理的宝藏。

3. 阶跃响应的魅力3.1 阶跃响应的定义接下来，咱们来看看“阶跃响应”。

它是系统对一个阶跃信号的响应，就像你突然把一个开关打开，整个房间立刻亮起来。

阶跃信号的特点就是它在某一时刻突然变得不一样，从0到1的变化就好比一瞬间的蜕变。

3.2 阶跃响应的重要性阶跃响应在很多实际应用中可是大显身手的，尤其是在控制系统中。

比如说，想象一下你在开车，突然踩下油门，车辆的加速反应就是阶跃响应在起作用。

通过阶跃响应，你可以了解系统的稳定性和动态特性，简直是开车必备的“老司机技巧”。

4. 冲激响应与阶跃响应的关系4.1 从冲激响应到阶跃响应那么，冲激响应和阶跃响应之间又是怎样的关系呢？简单来说，阶跃响应可以通过冲激响应“推导”出来。

你可以把冲激响应看作是一种基本的“调味料”，而阶跃响应就是这道菜的成品。

通过数学上的卷积操作，我们能把冲激响应变成阶跃响应，没错，就像把原料变成美味佳肴！4.2 直观的理解想象一下，你在做蛋糕。

冲激响应就像是准备蛋糕的面糊，而阶跃响应就是烤好的蛋糕，香喷喷的出炉了！当然，不同的配方会让蛋糕的味道有所不同，但最终都是通过面糊这个基础材料变成的。

§1.4阶跃函数和冲激函数

（1）
0
t0
t
▲
■
11 /31
2.用极限定义δ(t)
对γn(t)求导得到如图所示的矩形脉冲pn(t) 。
γn 11
n pn(t)
2
2
1 o 1
n
n
求导
t def
1 o 1 t
n
n

(t)

lim
n
pn
(t)
演示
高度无穷大，宽度无穷小，面积为1的对称窄脉冲。
▲
■
12 /31
我们从物理概念上理解如何产生冲激信号 (t)
例如，各次谐波的正弦与余弦信号构成的三角函数集就是正 交函数集。任何周期信号f(t)只要满足狄里赫利条件，就可以由 这些三角函数的线性组合来表示，称为f(t)的三角形式的傅里叶 级数。同理， f(t)还可以展开成指数形式的傅里叶级数。
▲
■
26 /31
1.4 信号的分解
（1）任意信号分解为偶分量与奇分量之和 ？？
偶分量定义为 f e (t ) f e (t )
奇分量定义为 f o (t ) f o (t )
任意信号可分解为偶分量与奇分量之和，即
f (t) fe (t) fo (t)
Even: 偶 Odd: 奇
（3）比例性
(at) 1 t
a
（4）微积分性质
(t) d (t) dt
t
( ) d (t)

（5）冲激偶 f (t ) (t ) f (0) (t ) f (0) (t )

f (t) (t)d t f (0) t (t)d t (t) (t) (t) (t)d t 0

5-2冲激函数与阶跃函数的关系

冲激函数与阶跃函数的关系
冲激函数与阶跃函数互为微积分的关系【微分与积分---积分跟积分变量没有关系】
冲激函数变上限积分就是阶跃函数（2）、阶跃函数的导数就是冲激函数：
对阶跃函数求导，是冲激函数。

阶跃函数的波形图
如右图示，在高数中，对
函数求导，就是求该函数
的变化率，从右图中的阶
跃函数的波形可知，当时
间0
<
t，阶跃函数恒等于
0，函数没有任何变化；当
>
t，阶跃函数恒大于0，
函数也没有任何变化。

当
函数没有变化时，也不不
存在变化率，也就是不存
在导数问题。

在阶跃函数中，当时间t从0
<
t变化为0
=
t时，函数从0变化为1，由于函数值从0变为1，而自变量变化量t∆持续的时间很短【自变量变化量t∆趋于0】，所以其导数趋于无穷大，即∞
=
dt
t
du)(
，而这个无穷大就是冲激函数的幅值。

（3）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

t
x
dx
0,
t,
t<0 t>0
t
t
t
t
x
dx
t
t
'x
dx
tdt 1
'tdt 0
• 四.冲激函数的性质：
• 1.与普通函数的乘积： f t t f 0 t
筛选特性
f
t tdt
f
0 tdt
f
0
f t ' t f 0 ' t f ' 0 t
f
t
' t dt
f
' 0
• 而一些广义函数间乘积无定义如：δ(t)ε(t);δ(t)δ(t);δ(t)δ’(t)等。
第四节 阶跃函数和冲激函数
• 一. 阶跃函数和冲激函数
rn(t)
1
1 .阶跃函数 ：（引入）若有一个函数： 2
n 1
1
t
n
• rn(t)=
0
, t<-1/n 即信号从(-1/n,1/n)区间内从0幅度升高到1。
•
½+nt/2 , -1/n<t<1/n
•
1
, t>1/n
• 若所用时间很短 0，即在0- 0+的时间内由0 1，则定义为单位阶跃函数
波形如图:
t
t 0,t 0
• 冲激函 t
dt
t
t
x
dx
• 二.冲激函数的广义定义
• <1>δ(t)广义定义：对一个性能良好的函数φ(t)（检验函数）有以下定义
则δ(t) 为冲激函数：
(t ) (t )dt
，(0φ)(t)为一般函数，性能良好
•
2.移位：
t
t1
f
t dt
f
t1
f
t
' t
t1 dt
f
' t1
f(t)
• 例：如图函数求其导数
4
• 解：ƒ(t)= 0
t<0,t<3
•
2+
2 3
t
0≤t≤ 3
2
t
3
•
=(2+
2 3
t)[ε(t)-ε(t-3)
]
•
f
't
2
2 3
t
t
t
3'
2
2 3
t
'
t
t
3
2
2 3
t
t
t
3'
2 t t 3 2 2 t 't 't 3
具有任意阶导数，φ(t)及各高阶导数在无限远处急剧下降。该式包含筛
选特性，即冲激函数δ(t)与检验函数φ(t)作用效果是从φ(t)中选出t=0的值。
δ(t)还有其他的广义定义。
• •
<1.2冲>冲激激函函数数的的导导数数定和义积：分：1 t
d t
dt
nt
d n t
dt n
叫冲激偶，波形：
n (t)
偶函数
•
nt 1n t n为偶数时为偶函数
•
n为奇数时为奇函数
• 5.复合函数形式的冲激函数：
•
n
f t i1
f
1
' ti
t
ti
ti为ƒ(t)=0的单根时，重根无意义
•
例.
4t 2 1 1 t 1 1 t 1
4 2 4 2
根t1=
1 2
,t2=
1 2
3
3
2 tt 3 2 t 2 t t 2 t 3 2 t t 3
3
3
3
2 t t 3 2 t 4 t 3
3
• •
3.尺度变换：
at 1
a
a为常数
t
推论
at b
1 a
t
b a
1at 1 1 1t
aa
nat
1 a
1 an
n
t
• 4.奇偶性： t t
•
0 t<0
•
t def
lim
n
rn
t
1/2
t=0
•
1 t>0
• 2.冲激函数：若有一个函数 •
Pn(t) Pn(t)= 0 t<-1/n t n/2 -1/n<t<1/n
•
-1/n 1/n
• 当信号宽度 0 ,而面积保持不变而形成 一个冲激叫单位冲激函数。
•
δ(t)
t def
lim
n
Pn t
t
• 阶跃函数ε(t)的导数有：ε’(t)=δ(t).
• 可利用阶跃函数和冲激函数广义定义证明：
•
' (t) (t)dt
t ' t dt
0
'
t
dt
0
•
而 (t) (t)dt 0
比较两式得ε’(t)=δ(t)
• 2.冲激函数的积分
•
•
先定义一种函数，斜坡函数r(t)=
则
r
t