冲激函数
- 格式:ppt
- 大小:58.00 KB
- 文档页数:1

冲激信号是偶函数,冲激偶信号是奇函数
冲激函数既不是偶函数也不是奇函数.是一个非正常函数,某种极限函数。
冲激偶函数是奇函数,关于原点对称,在全时域对其积分为零,即正、负两个冲激的面积相互抵消。
所以说冲激函数是偶函数,冲激偶就是奇函数
信号的分解,可以分解为冲激函数和阶跃函数的卷积,只不过对于阶跃函数而言会有一个初值的问题,这个初值产生原因就在于其对信号分解可以看成冲激函数与信号卷积的微分和积分(微分分配给f,积分分配给冲激函数),无论是先微分或者先积分,都会存在一个常数是无法确切表示的,需要有初值条件,从频域分析时,是因为存在微分性质使用时要保证是没有直流分量
在频域分析时,同样我们可以的得到一个有趣的结论,可以将任意信号分解为该信号的基函数的幅频特性曲线必没有0点,进一步拓展,一个有限长的信号,一定不能作为基函数表示任意信号(在时域来看这是显然的)。
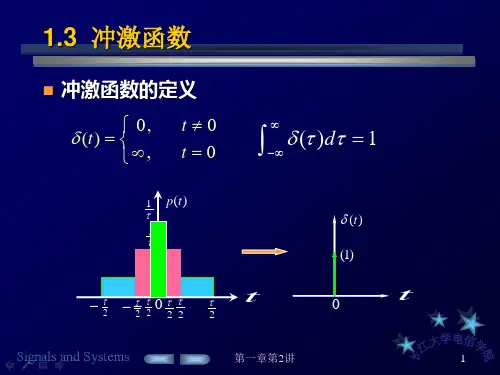

离散数学冲激函数冲击函数是离散数学中的一种重要函数,也称为脉冲响应函数或单位脉冲函数。
它常用符号δ(n)或δ[n]表示。
冲激函数具有以下特点:1.冲激函数在离散时间n=0时取值为1,其他时刻取值为0。
即δ(0)=1,δ(n)=0,n≠0。
2.冲激函数的取值是一个理想化的信号,它在瞬间时间内具有无限大的振幅和无限短的时间宽度。
冲激函数的定义可以通过极限的方式来理解。
当我们得到一个脉冲宽度为0、振幅趋近于无穷大的函数时,我们可以将其逼近为冲激函数。
冲激函数在离散时间系统中具有重要的作用,可以用于描述信号的性质、系统的响应以及信号的滤波特性。
它可以用来表示信号的单位样本,在系统的输入中起到触发输出的作用。
在信号处理中,冲激函数通常被用来表示单位冲激信号,即在一些特定时间发生的瞬时脉冲。
通过将冲激信号与待处理的信号进行卷积运算,我们可以得到系统对输入信号的响应。
此外,冲激函数还可以用于构造信号的频谱表示。
根据频谱分析理论,任意一个信号都可以表示为一系列冲激函数的叠加。
这种表示方式被广泛应用于数字信号处理、图像处理等领域。
在离散控制系统中,冲激函数用于描述系统的动态性能。
通过对冲激函数进行观测和分析,我们可以得到系统的传递函数、阶跃响应以及频率特性等关键参数。
总结起来,冲激函数在离散数学中具有重要的意义。
它是描述信号和系统性质的重要工具,可以用于构造信号的频谱表示,描述系统的动态性能,以及解决各种实际问题。
在实际应用中,冲激函数被广泛应用于数字信号处理、图像处理、控制系统和通信系统等领域。

冲激函数的特解范文冲激函数是数学中的一种特殊函数,通常记为δ(t),也称为Dirac函数。
它在数学分析和工程应用中非常有用,尤其在处理信号问题时。
冲激函数的特解即是求解线性时不变系统微分方程的一个方法,下面将详细介绍冲激函数的特解的基本原理和应用。
首先,我们来了解一下冲激函数的基本性质。
冲激函数δ(t)在t=0的时刻取无穷大,并且在其他时刻都为零。
在数学上,可以将冲激函数定义为满足以下两个性质的极限函数:1.函数在t=0时的值为无穷大,即δ(0)=∞。
2.对任意的t≠0,函数的值为零,即δ(t)=0。
在实际应用中,由于冲激函数的定义非常特殊,它不是一个常用函数,而是作为一种数学工具来使用。
因此,我们通常可以将冲激函数理解为一个脉冲信号,它的幅值非常短暂且极大,然后迅速衰减为零。
这种特性使得冲激函数成为处理信号问题的重要工具。
接下来,我们来探讨冲激函数的特解的应用。
在信号处理和系统分析中,我们经常遇到线性时不变系统的微分方程,例如:d^n y(t) / dt^n + a_(n-1) d^(n-1) y(t) / dt^(n-1) + ... +a_0 y(t) = b_(n-1) d^(n-1) x(t) / dt^(n-1) + ... + b_0 x(t)其中,y(t)表示系统的响应,x(t)表示系统的输入信号,a_i和b_i表示系统的系数。
我们可以通过冲激函数的特解来求解这个微分方程。
假设系统的零状态响应为y_p(t),那么系统的总响应为y(t)=y_p(t)+y_c(t),其中y_c(t)是系统的零输入响应。
根据线性时不变系统的性质,我们可以将输入信号x(t)拆解为冲激函数的线性组合,即:x(t)=∫x(τ)δ(t-τ)dτ带入微分方程,我们可以得到:d^n y_p(t) / dt^n + a_(n-1) d^(n-1) y_p(t) / dt^(n-1) + ...+ a_0 y_p(t) = ∫ b_(n-1) d^(n-1) x(τ) / dt^(n-1) δ(t - τ)dτ + ... + b_0 x(t)根据冲激函数的性质,除了t=τ处的δ(t-τ)项之外,其他的冲激函数都为零。

冲激函数的卷积冲激函数(impulse function)是一种在数学和工程中经常出现的函数。
形式上,冲激函数是一个极小化了宽度但有无限高度的正态分布函数,通常表示为δ(t)。
冲激函数的主要特点是在t=0的地方等于无限值,且在其他地方都等于0。
当两个函数f(t)和g(t)做卷积运算时,结果可以写成下面的形式:f(t)*g(t) = ∫f(t-τ)g(τ)dτ在这个公式中,f(t)和g(t)可以是任何类型的函数,而τ是一个积分变量。
这个公式中包含的信息是f(t)的形状要和位于τ处的g(τ)的形状结合起来,可以想象它们的相对位置在不断地变化。
卷积运算的物理解释是将一个函数和一个滤波器(另一个函数)相乘,然后在一定时间内积分,得到的结果是输出信号。
在实际中,经常使用冲激函数来描述信号系统的行为。
因为冲激函数的一个重要特性是可以用来表示单位冲激响应函数(impulse response),即系统对单位冲激响应的输出。
另一个重要的特性是冲击函数具有筛选性质(selectivity property),即对于输入序列的每个分量,只有在t=0时能够对输出产生影响。
所以,当使用冲激函数对一个系统进行调试时,只需要生成一个单位冲激输入信号,通过观察系统的输出能够得到系统对每个分量响应的确认。
在卷积运算中,冲激函数具有独特的作用。
假设有一个函数f(t),我们将它和冲激函数做卷积运算,可以得到下面的形式:f(t)*δ(t) = ∫f(t-τ)δ(τ)dτ根据冲激函数的定义,只有在τ=0时δ(τ)才会取得其最大值。
再根据卷积运算的定义,当τ=t时f(t-τ)等于f(0),所以上式需要简化为:f(t)*δ(t) = f(0)这个结果非常有用。
它表示当一个信号与冲激函数做卷积运算时,得到的结果就是原始信号在t=0处的值。
这个性质在信号处理和控制系统设计中经常被用到。
举个例子,设有一个跃阶函数(step function)f(t),其表达式为:f(t) = 1,t>=0; f(t) = 0,t<0将f(t)和冲击函数δ(t)做卷积计算,可以得到下面的公式:f(t)*δ(t) = ∫f(t-τ)δ(τ)dτ = ∫1δ(τ)dτ = 1结果是1,这意味着在t=0处,f(t)的值为1。

冲激函数的定义冲激函数是一种特殊的函数,它在数学和工程领域有着广泛的应用。
冲激函数在信号处理、控制理论、线性系统、微积分和物理学等领域都起着重要的作用。
本文将对冲激函数进行详细的定义和解释,以便读者更好理解其概念和应用。
1、什么是冲激函数冲激函数是数学中的一种特殊函数,也称为Dirac函数或Dirac delta函数。
冲激函数是在除零点外均为0,在零点附近无限大的函数。
冲激函数通常表示为δ(x),其中x为自变量。
冲激函数在x=0处的值无限大,但在除零点外的其他点的值都为0。
在物理学和工程领域,冲激函数可以通过一个实验来理解它的概念。
如果我们在时间轴上以极短的时间间隔内向电路中输入一个短暂的电压脉冲,那么电路将会产生一个极短的电流脉冲,这个电流脉冲就可以用一个冲激函数来描述。
2、冲激函数的重要性冲激函数在数学中的重要性很大。
它可以用在微积分、偏微分方程、傅里叶分析、抽象代数和泛函分析等领域。
在控制系统和信号处理领域,冲激函数也是非常重要的。
它可以用来描述系统的 impulse response(冲击响应)函数,冲激响应是控制系统和信号处理中非常常见的一种概念。
冲激函数还可以用来分析和设计滤波器和信号处理系统。
在物理学中,冲激函数可以用来描述质点、电荷或电流的瞬间变化情况。
冲激函数也可以用来描述物理学中的波函数,比如在量子力学中,波函数可以在测量时间点上采用Delta函数的形式。
冲激函数有一些非常重要的性质。
下面我们将对其中的一些最主要的进行介绍。
3.1 奇异性冲激函数在所有除零点外的点上取值为0,但在零点处取值为无穷大。
冲激函数在数学上是一个奇异函数,可能常常忽略它在除零点外的任何部分。
3.2 瞬时能量3.3 单位冲激函数3.4 积分性质冲激函数的积分性质十分重要。
因为冲激函数在所有除零点外的点上都为0,所以对于任意函数f(x),有:∫f(x)δ(x)dx=f(0)这意味着冲激函数的积分可以用来计算f(x)在零点处的值。



冲激函数的特解冲激函数是一种在数学和工程领域常用的特殊函数,它具有许多独特的性质和广泛的应用。
它的特解可谓是独具一格,发人深省。
冲激函数,顾名思义,形似一个瞬间突然增长到无穷大,然后迅速回到零的函数。
它可以用来描述一瞬间发生的现象,例如,当一个球体从高楼上自由下落时,撞到地面时的冲击力就可以用冲激函数来表示。
如果将这种冲击力视为一个“冲激”,那么在数学上,我们可以用冲激函数来模拟这个过程。
冲激函数在控制论、信号处理和物理学等领域有广泛的应用。
在控制论中,我们经常需要对系统的冲击响应进行分析和设计,例如自动驾驶汽车中的碰撞检测系统。
在信号处理中,冲激函数常常被用来描述信号的时域特性,例如在音频处理中,我们可以利用冲激函数来实现音频信号的均衡和滤波。
在物理学中,冲激函数可以用来描述电荷的分布、介质的传导和波的传播等现象。
冲激函数的特解与其它函数的特解有些不同之处。
在通常的微分方程中,我们需要给定一些初始条件来求解方程的特解,但对于冲激函数而言,其特解在冲激函数出现的瞬间即可得到。
这是因为冲激函数在出现瞬间的那一刻,它的值变为无穷大,而在其他时刻,它的值均为零。
因此,冲激函数的特解在出现时刻的性质决定了整个特解的形式。
冲激函数的特解具有高频调制和窄带性的特点。
高频调制意味着在时间轴上,冲激函数的特解的波峰和波谷之间的时间间隔非常短,从而可以观察到短时的冲击力。
窄带性意味着冲激函数的频率范围较窄,因此它对频率较低的信号有较强的敏感性,而对频率较高的信号则不敏感。
冲激函数的特解在工程实际中起到了重要的作用。
例如,在声学中,我们可以利用冲激函数的特解来精确测量音响系统的频率响应。
在通信中,我们可以使用冲激函数的特解来计算信道的冲击响应,从而实现可靠的信号传输。
在控制系统中,我们可以通过冲激函数的特解来设计控制器的增益和时间响应,从而实现系统的稳定性和性能优化。
总之,冲激函数的特解是一种生动而全面的数学工具,它在数学和工程领域发挥着重要的作用。
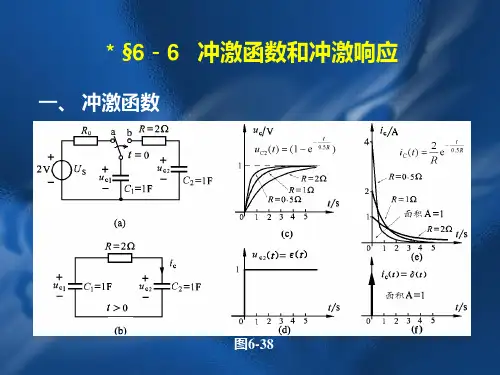
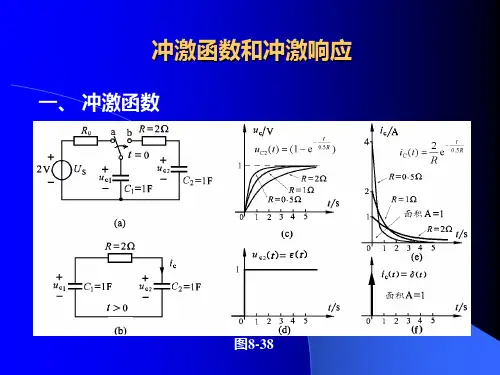
冲激函数主要内容由理想电路引入冲激函数12单位冲激函数的定义及波形任意冲激函数的定义及波形3如图所示用理想元件组成的电路,求电容电压、电容电流。
v C (t )=Eu (t )解电容电压0vC (t )tE注意:电容电压突变!−+E i C (t )。
v C (t )+−a。
bk 当t =0时,开关k 由a→b ,1、由理想电路引入冲激函数d v C (t)i C (t )=Cd t电容电流当t > 0或t < 0时,i C (t )=00v C (t )tE t = 0时,i C (t )=?电容电压1v C (t )=i C (τ) d τC⎰−∞t在t =0时,电容电压可导吗?在t =0时,电容电压v C (t )突变的原因是什么?问:在t =0时,电容电压可导吗?在t =0时,电容电压v C (t )突变的原因是什么?这样的物理现象可引入什么数学模型来描述?的时间积分有限的物理现象可以用冲激函数描述。
这种电流持续时间为零,电流幅度为无穷大,但电流问:答:2、单位冲激函数的定义及波形单位冲激函数的符号—— (t )单位冲激函数可由矩形脉冲面积保持为1,宽度τ→0的极限表示δ(t )=lim τ→0τ1u (t+) −u (t −)τ2τ20f (t )τ2τ21τ2−τ1τ11−τ11/τ−τ2τ2t单位冲激函数一般定义为δ(t )t(1)∞t = 00t ≠0δ(t ) =⎰∞−∞δ(t ) d t = 1幅度强度3、任意冲激信号(函数)的定义及波形任一时刻t = t 0、强度为A 的冲激函数记为A δ(t −t 0)∞t = t 00t ≠t 0A δ(t −t 0)(A )t 0tA δ(t −t 0) d t = A⎰∞−∞冲激函数由t −t 0=0→t=t 0A δ(t −t 0) =。