当前位置：文档之家 › 04非线性回归模型的线性化 (3)

04非线性回归模型的线性化 (3)

  • 格式：docx
  • 大小：259.33 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

非线性回归模型的线性化

非线性回归模型的线性化

k 1 beatut yt
k 1 beatut yt
ln
k yt
1
ln b at
ut
令yt
ln
k yt
1
,
b
ln b
yt b at ut
此时可用最小二乘法估计b*和a。
钉螺存活率曲线 （生长曲线模型）
把一批钉螺埋入土中，以后每隔一个月取出部分钉螺，检 测存活个数，计算存活率。数据见表。
FOOD
3000
2000
1000
0 0
4000
8000
12000
INCOME 16000 20000
9.0 LOG(FOOD)
8.5
8.0
7.5
7.0
6.5
6.0 LOG(LOG(INCOME))
5.5 1.80 1.85 1.90 1.95 2.00 2.05 2.10 2.15 2.20 2.25 2.30
以1为例
1
yt xt1
线性模型中的回归系数（边际系数）是对数线性回归模型中弹性
系数的一个分量。
应用柯布-道格拉斯生产函数模型评价台湾省农业生产 效率。利用台湾省1958-1972年农业生产总值yt、劳动力 投入xt1、资本投入xt2的数据估计模型如下：
Yˆt
0.035X
1.5 t1
X
0.49 t2
yt ke be at
yt ke be at
曲线的上限和下限分别为k和0 。
当a 0, Limyt k, 当a 0,b 0 , Limyt 0
t
t
曲线有拐点，坐标为 Lnb , k
a e
, 但曲线不对称于拐点。
一般情形，上限值k可事先估计，有了k值，龚伯斯曲线才 可以用最小二乘法估计参数。

计量经济学基础-非线性回归模型

计量经济学基础-非线性回归模型

第四节 非线形回归模型一、 可线性化模型在非线性回归模型中，有一些模型经过适当的变量变换或函数变换就可以转化成线性回归模型，从而将非线性回归模型的参数估计问题转化成线性回归模型的参数估计，称这类模型为可线性化模型。

在计量经济分析中经常使用的可线性化模型有对数线性模型、半对数线性模型、倒数线性模型、多项式线性模型、成长曲线模型等。

1．倒数模型我们把形如:u xb b y ++=110；u x b b y ++=1110 （3.4.1） 的模型称为倒数(又称为双曲线函数)模型。

设：xx 1*=，y y 1*=，即进行变量的倒数变换，就可以将其转化成线性回归模型。

倒数变换模型有一个明显的特征：随着x 的无限扩大，y 将趋于极限值0b (或0/1b )，即有一个渐进下限或上限。

有些经济现象(如平均固定成本曲线、商品的成长曲线、恩格尔曲线、菲利普斯曲线等)恰好有类似的变动规律，因此可以由倒数变换模型进行描述。

2．对数模型模型形式：u x b b y ++=ln ln 10 （3.4.2）(该模型是将ub e Ax y 1=两边取对数，做恒等变换的另一种形式，其中A b ln 0=)。

上式lny 对参数0b 和1b 是线性的，而且变量的对数形式也是线性的。

因此，我们将以上模型称为双对数(double-log)模型或称为对数一线性(log-liner)模型。

令：x x y y ln ,ln **==代入模型将其转化为线性回归模型： u x b b y ++=*10* （3.4.3）变换后的模型不仅参数是线性的，而且通过变换后的变量间也是线性的。

模型特点：斜率1b 度量了y 关于x 的弹性：xdx y dy x d y d b //)(ln )(ln 1== （3.4.4） 它表示x 变动1%，y 变动了多少，即变动了1b %。

模型适用对象：对观测值取对数，将取对数后的观测值（lnx ，lny ）描成散点图，如果近似为一条直线，则适合于对数线性模型来描述x 与y 的变量关系。

计量经济学非线性回归模型的线性化

计量经济学非线性回归模型的线性化
1. 非标准线性回归模型的线性化方法
变量替换法
Y 0 1 f1 ( X 1 , X 2 ,, X k ) 2 f 2 ( X 1 , X 2 ,, X k ) p f k ( X 1 , X 2 ,, X k ) u
变量替换公式为 Z1 f1 ( X 1 , X 2 ,, X k )
第一节 变量间的非线性关系
第二类：可线性化的非线性回归模型
此类模型可通过适当的变换化为标准的线性回归模型。 如，柯布—道格拉斯（Cobb-Dauglas）生产函数模型，简 称C-D生产函数模型：
Y AK L e

u
其中，Y 表示产出量，K 表示资金投入量，L 表示劳动投入 量，A 为效率系数， 和 非别为K 和 L的产出弹性，A、 和 均为待估未知参数。 取对数后：
第四章 非线性回归模型的线性化
第一节：变量间的非线性关系 第二节：线性化方法 第三节：案例分析
第一节 变量间的非线性关系
1. 线性回归模型与非线性回归模型的形式有何不同？
线性模型
Y 0 1 X 1 2 X 2 k X k u
非线性模型 Y f ( X 1 , X 2 ,, X k ; 0 , 1 ,, p ) u
ln Y ln A
Z f ( X , X ,, X ) 2 2 1 2 k Z k f k ( X 1 , X 2 , , X k )
则
Y 0 1 Z1 p Z p u
第二节 线性化方法
（1）多项式函数模型
Yi 0 1 X i 2 X i k X k ui
就可以得到线性回归模型的一组新的最小二乘估计量。 第三步：将非线性函数 f 在这组新的参数估计值 附近作泰勒级数展开，线性化后得到一个新的标准线性回 归模型。对这个新的标准线性回归模型再应用普通最小二

（整理）计量经济学第四章非线性回归模型的线性化

（整理）计量经济学第四章非线性回归模型的线性化

（整理）计量经济学第四章⾮线性回归模型的线性化第四章⾮线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是⾮线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述⾮线性回归模型是⽆法⽤最⼩⼆乘法估计参数的。

可采⽤⾮线性⽅法进⾏估计。

估计过程⾮常复杂和困难，在20世纪40年代之前⼏乎不可能实现。

计算机的出现⼤⼤⽅便了⾮线性回归模型的估计。

专⽤软件使这种计算变得⾮常容易。

但本章不是介绍这类模型的估计。

另外还有⼀类⾮线性回归模型。

其形式是⾮线性的，但可以通过适当的变换，转化为线性模型，然后利⽤线性回归模型的估计与检验⽅法进⾏处理。

称此类模型为可线性化的⾮线性模型。

下⾯介绍⼏种典型的可以线性化的⾮线性模型。

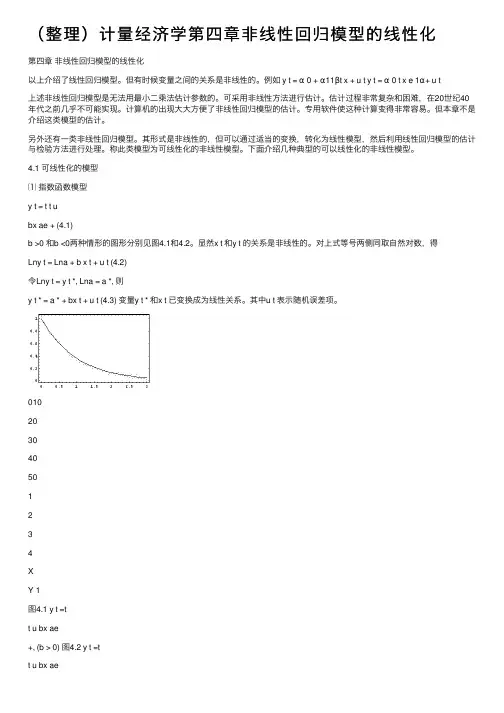
4.1 可线性化的模型⑴指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是⾮线性的。

对上式等号两侧同取⾃然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表⽰随机误差项。

010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =t+, (b < 0)⑵对数函数模型y t = a + b Ln x t+ u t(4.4)b>0和b<0两种情形的图形分别见图4.3和4.4。

x t和y t的关系是⾮线性的。

令x t* = Lnx t, 则y t = a + b x t* + u t(4.5)变量y t和x t* 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6) b取不同值的图形分别见图4.5和4.6。

4 第四章 非线性回归模型

4 第四章 非线性回归模型

解：根据经济理论，二者之间的关系可以用双曲线模 型来表示
1 y = β 0 + β1 + µ x
令 则
z = 1 x
y = β 0 + β1 z + µ
运用Eviews进行回归, 操作步骤为：quickempty groupprocsmake equation, 输出结果如下： 输出结果如下4.1.2
即可利用多元线性回归分析的方法处理了。
例如，描述税收与税率关系的拉弗曲线 例如， 拉弗曲线：抛物线 拉弗曲线 s = a + b r + c r2 c<0 s：税收； r：税率 设 z1 = r， z2 = r2， 则原方程变换为 s = a + b z1+ c z2 c<0
例4.1.1 某生产企业在1981-1995年间每年的产量和 总成本如下表（表4.1.1），试用回归分析法确定其 成本函数。 表4.1.1
∧
∧
即

1 x
s = (1.0086)（4.6794) t = (−0.2572)（4.3996**)
3、半对数模型和双对数模型 、 把函数形式为
ln y = β0 + β1x + µ
（4.1.5） (4.16)
y = β + β ln x + µ
称为半对数模型。 把函数形式为
ln y = ln β0 + β1 ln x + µ
第四章 非线性 回归模型
前面我们讨论的经济问题，都是假定作为因变量的经 济变量与作为解释变量的经济变量之间存在着线性关 系。由此建立线性回归模型进行线性回归分析。这里 所说的线性是指：（1）解释变量线性。（2）参数线 性。但是，在众多的经济现象中，分析经济变量之间 的关系，根据某种经济理论和对实际经济问题的分析， 所建立的经济模型往往不符合上面的线性要求，即模 型是非线性的，称为非线性模型(Non-linear Model)。 非线性模型的参数如何进行估计，如何进行分析，是 本章所要讨论的问题。

浅谈非线性回归模型的线性化

浅谈非线性回归模型的线性化

浅谈非线性回归模型的线性化广东省惠州市惠阳区崇雅中学高中部 卢瑞勤(516213)回归分析在各个领域中都有十分重要的作用，比如：在财务中可以用回归分析进行财务预测；在医疗检验中可以用回归分析进行病理预报等等。

高中新课标教材就在《必修3》和《选修2-3》中分别增加了《线性回归》和《回归分析》的内容，介绍了求线性回归方程的方法。

但在实际问题中，变量间的关系并非总是线性关系，本文结合本人的教学实践，对教材中的这两部分内容进行适当延伸，谈谈对一些可线性化的非线性回归模型的线性化问题，供各位同行在教学时参考。

一、什么是可线性化的非线性回归模型线性回归模型的基本特征是预报变量可以表示成解释变量和一个系数相乘的和，即预报变量y 可以表示成解释变量i x (i =1，2，3，……)的如下形式：0112233y a a x a x a x =++++，其中变量ix 是以其原型(而不是以ni x 或其它)的形式出现，变量y 是各变量i x 的线性函数。

而有些回归模型不具备这个特点，但是可以通过适当的代数变换转化成这种形式，我们称这类回归模型为可线性化的回归模型。

在本文中，我们只讨论只有一个解释变量可线性化的非线性回归模型的线性化。

二、非线性回归模型的线性化的基本思路非线性回归模线性化的基本思路是：由已知数据，确定解释变量和预报变量，作出散点图，根据经验，确定回归曲线的类型，然后作适当的代数变换，若变换后散点图体现较好的线性关系，即可将其化成线性形式求解，最后还原到原来的回归曲线。

如果回归曲线可用多种形式表示，可以各自将其线性化后求解，再用相关系数2R 进行拟合效果分析，2R 越大，拟合效果越好，所求的回归方程也就越精确。

三、非线性回归模型的线性化的常用方法可线性化的非线性回归模型有以下几种常见类型：(1)双曲线型，其形式为1a b y x =+，其变换为1y y '=， 1x x'=，变换后的形式为y b ax ''=+ (2)幂函数型，其形式为by ax = ，可以变形为ln ln ln y a b x =+，作变换ln y y '= ，ln x x '= ，变换后的形式为y a bx ''=+(3)指数函数型，其形式为bxy ae = ，以变形为ln ln y a bx =+，作变换ln y y '=，ln a a '= ，变换后的形式为y a bx ''=+(4)对数函数型，其形式为ln y a b x =+，作变换ln x x '=，变换后的形式为y a bx '=+ 下面以高中新课标数学教材《选修2-3》一道习题为例加以说明【例】在某地区的一段时间内观察到的不小于某震级x 的地震个数y 数据如下表，试建立回归方程表述二者之间的关系。

04-非线性回归模型的线性化

04-非线性回归模型的线性化
t
i l
2 t
2
2016/3/29
6
4.2、线性化方法
1、 被解释变量与解释变量之间不存在线性关系，与
未知参数之间存在线性关系的模型，其线性化的方法 为：变量替换法；然后利用OLS估计参数。 2、被解释变量与解释变量、未知参数之间不存在线性 关系，但可线性化的模型的线性化方法为：对数法和 变量替换法；然后利用OLS估计参数。 3、真正意义上的非线性模型，需要进行线性化处理。
2016/3/29 5
4.1.3、非线性回归模型的基本假定
1．扰动项零均值： E(u ) 0, t 1, 2,..., n 2．无自相关性： E(u u ) 0; i, l 1, 2,..., n; i l 3．同方差性： E(u ) , t 1, 2,..., n ，其中为有限常 数。 4．解释变量为非随机变量 5．函数性质：一般情况下，假设 f (xt , β)为二阶连 续可微函数。 6．模型参数可识别 7．分布假定：零均值、同方差。在极大似然估 计中，需要对扰动项的分布做出假设，一般假 设其服从正态分布。
ˆ ˆ) log(a 1 ˆ ˆ b
2
ˆ e ) (a
ˆ 1
应当指出，在这种情况下，线性模型估计量
的性质（如 BLUE, 正态性等）只适用于变换后的参 ˆ 和 ˆ ，而不一定适用于原模型参数的估 数估计量 1 2 计量 a ˆ 。 ˆ和 b
2016/3/29 16
CES生产函数模型的线性化回归
最小二乘法
t
ˆ ) min S (β) S (β

min (Yt f (xt , β))2

t
2016/3/29 21
非线性最小二乘法的正规方程组

非线性回归模型的线性化

非线性回归模型的线性化

p f p ( X1, X 2 , , X k ) ＋u
令
Z1 f1(X1, X2, Z2 f2(X1, X2,
, Xk) , Xk)
Zp fp(X1, X2, , Xk )
则可以把原模型转化为一个标准的多元线性回归模型
Y 0 1Z1 2Z2 pZ p u
6
下面介绍在经济问题时经常遇到的几种非标准线性 回归模型
p fp(X1, X2, , Xk )
2024/10/17
5
4.2线性化方法
1、非标准线性回归模型的线性化方法 非标准线性回归模型的线性化方法是变量替换法。
非标准线性回归模型的一般形式为：
Y 0 1 f1( X1, X 2 , , X k ) 2 f2 ( X1, X 2 , , X k )
Yi* bX i ui
2024/10/17
16
（2）幂函数模型（全对数模型）
幂函数模型的一般形式为：
Yi
AX
1 1i
X
2 2i
X e k ui ki
对上式两边取对数得到：
ln Yi ln A 1 ln X1i 2 ln X 2i k ln X ki ui
令
Yi*
ln Y , 0
在这样一些非线性关系中，有些可以通过代数 变换变为线性关系处理，另一些则不能。下面我们 通过一些例子来讨论这个问题。
2024/10/17
1
线性模型的含义
线性模型的基本形式是:
Y 0 1X1 2 X 2 ...... k X k u
线性模型的线性包含两重含义：
（1）变量的线性
变量以其原型出现在模型之中，而不是以 X 2 或
（1）多项式函数模型 多项式函数模型的一般形式为：

非线性回归模型的线性化讲解

非线性回归模型的线性化讲解

( b1>0, b2>0)
(b1<0, b2 <0
（2） 双曲函数模型
1 1 ui 双曲函数模型的一般形式为： Yi Xi 1 1 令 * * Yi , Xi Yi Xi
则可将原模型化为标准的线性回归模型
Yi X ui
* * i
双曲线函数还有另一种表达方式，
ln GDP i ln A ln Ki ln Li ui
Yi ln GDP i , X 1i ln Ki , X 2i ln Li
0 ln A, 1 , 2 则可将C-D生产函数模型转换成标准的二元线性回归模型
Yi 0 1 X1i 2 X 2i ui

Z p f p ( X1, X 2 ,, X k )
Y 0 1Z1 2 Z2 p Z p u
7
下面介绍在经济问题时经常遇到的几种非标准线性 回归模型 （1）多项式函数模型
多项式函数模型的一般形式为：
Yi 0 1 X i 2 X i2 k X ik ui
首先对上式做倒数变换得：
1 e X i ui Yi
令
1 Yi , X i* e X i Yi
*
则可将原模型化为标准的线性回归模型
Yi* X i* ui
15
2 可线性化的非线性回归模型的线性化方法
下面几种在研究经济问题时经常遇到的可线性化的非线性 回归模型 （1）指数函数模型
yt = b0 +b1 x 1t + b2 x 2t + b3 x 3t + ut 这是一个三元线性回归模型。如经济学中的总成本与产 品产量曲线与左图相似。

04-非线性回归模型的线性化.

04-非线性回归模型的线性化.

对此方程采用对数变换 logM=loga+blog(r-2)
令Y=logM, X=log(r-2), β1= loga, β2=b
则变换后的模型为：
β β Y = + X + u 2020/10/1
t 1 2t t
15
将OLS法应用于此模型，可求得β1和β2的估计
值 ˆ1, ˆ2，从而可通过下列两式求出a和b估计值：
log(aˆ) ˆ1 (aˆ eˆ1 ) bˆ ˆ2
应当指出，在这种情况下，线性模型估计量 的性质（如BLUE,正态性等）只适用于变换后的参 数估计量 ˆ1和ˆ2 ，而不一定适用于原模型参数的估
计量 aˆ 和 bˆ 。
是重要的，因为变量的非线性可通过适当的重新
定义来解决。例如，对于
Y 1X12 2
X2
3
X3 X4
...
只需定义
Z1
X
2 1
,
Z2
X2 ,
Z3
X3 X4
...
该关系即可以重写为：
Y 1Z1 2Z2 3Z3 ... 此方程的变量和参数都是线性的。
2020/10/1
13
参数的非线性是一个严重得多的问题，因为它不
（2）参数的线性
因变量Y是各参数的线性函数。
2020/10/1
3
4.1.2. 非线性模型中变量间的关系
非线性模型的一般形式是 Yt f ( X1t , X 2t ,..., X kt ; 1, 2 ,..., m ) ut
其中f是关于解释变量和未知参数的一个非线性函
数。
上式中解释变量的个数k与参数个数m不一定相 等，
模型形式：
2表020示/10什/1 么意义呢？（思考）

第四章 非线性回归模型的线性化讲解

第四章 非线性回归模型的线性化讲解
第四章 非线性回归模型的线性化
线性回归模型 最小二乘法求解 若不是线性回归模型，又该如何求解呢？
（一）变量关系非线性问题：
若：(1)、变量

Y 和
X 1 , X K
之间不存在
多元线性随机函数关系
Y 0 1 X 1 K X K

那么我们如何估计出模型中的未知参数呢？
Dependent Variable: Y Method: Least Squares Date: 10/08/08 Time: 13:51 Sample: 1980 1996 Included observations: 17 Variable Coefficient C -10.46551 X1 1.021132 X2 1.472202 R-squared Adjusted R-squared S.E. of regression
(2)可线性化的非线性回归模型： 虽然被解释变量Y与解释变量X1X 2 .....X k以及与未知 参数 0 1...... k 之间都不存在线性关系，但是可以转化 为线性函数。例如： 生产函数模型： Y AK L e 转化为： ln Y LnA LnK LnL (3)不可线性化的非线性回归模型： 被解释变量Y与解释变量X1X 2 .....X k以及与未知 参数 0 1...... k 之间都不存在线性关系，而且无法转化 为线性函数。 例如：Y 0 1e 1x1 2 e 2 x2
0.99841 S.D. dependent var 0.029873 Akaike info criterion
变量间的非线性关系
(1)非标准线性回归模型： 虽然被解释变量Y与解释变量X1X 2 .....X k 之间 不存在线性关系，但与未知参数 0 1...... k 之间 存在线性关系。例如： 根据平均成本与产量为U型曲线理论，总成本C 可以用产量X的三次多项式来近似表示，得到总成 本函数模型如下： C 0 1 X 2 X 2 3 X 3

计量经济学习题含答案

计量经济学习题含答案

计量经济学习题含答案第1章绪论习题一、单项选择题1．把反映某一总体特征的同一指标的数据，按一定的时间顺序和时间间隔排列起来，这样的数据称为（ B ）A. 横截面数据B. 时间序列数据C. 面板数据D. 原始数据2．同一时间、不同单位按同一统计指标排列的观测数据称为（B ）A．原始数据 B．截面数据C．时间序列数据 D．面板数据3．用计量经济学研究问题可分为以下四个阶段（B）A．确定科学的理论依据、建立模型、模型修定、模型应用B．建立模型、估计参数、检验模型、经济预测C．搜集数据、建立模型、估计参数、预测检验D．建立模型、模型修定、结构分析、模型应用4．下列哪一个模型是计量经济模型( C )A.投入产出模型B.数学规划模型C.包含随机变量的经济数学模型D.模糊数学模型二、问答题1．计量经济学的定义2．计量经济学的研究目的3．计量经济学的研究内容1．答：计量经济学是统计学、经济学、数学相结合的一门综合性学科，是一门从数量上研究物质资料生产、交换、分配、消费等经济关系和经济活动规律及其应用的科学2．答：计量经济学的研究目的主要有三个：（1）结构分析。

指应用计量经济模型对经济变量之间的关系作出定量的度量。

（2）预测未来。

指应用已建立的计量经济模型求因变量未来一段时期的预测值。

（3）政策评价。

指通过计量经济模型仿真各种政策的执行效果，对不同的政策进行比较和选择。

3．答：计量经济学在长期的发展过程中逐步形成了两个分支：理论计量经济学和应用计量经济学。

理论计量经济学主要研究计量经济学的理论和方法。

应用计量经济学将计量经济学方法应用于经济理论的特殊分支，即应用理论计量经济学的方法分析经济现象和预测经济变量。

2一元线性回归模型习题一、单项选择题1．最小二乘法是指（D）A. 使达到最小值B. 使达到最小值C. 使达到最小值D. 使达到最小值2．在一元线性回归模型中，样本回归方程可表示为（C ）A. B.C． D.3．线设OLS法得到的样本回归直线为，以下说法不正确的是(B ) A． B．C．D．在回归直线上4．对样本的相关系数，以下结论错误的是（A）A.越接近0，与之间线性相关程度高B.越接近1，与之间线性相关程度高C.D、，则与相互独立二、多项选择题1．最小二乘估计量的统计性质有（ ABC ）A. 无偏性B. 线性性C. 最小方差性D. 不一致性E. 有偏性2．利用普通最小二乘法求得的样本回归直线的特点（ACD）A. 必然通过点B. 可能通过点C. 残差的均值为常数D.的平均值与的平均值相等E. 残差与解释变量之间有一定的相关性3．随机变量（随机误差项）中一般包括那些因素（ABCDE ）A回归模型中省略的变量B人们的随机行为C建立的数学模型的形式不够完善。

第四章非线性回归模型的线性化

第四章非线性回归模型的线性化
L
1 0 ln A, 1 m , 2 m(1 ), 3 m (1 ) 2
• 得到一个简单的线性回归模型
Z 0 1 X1 2 X 2 3 X 3
1、CES函数的参数估计
• 其中：
ˆ ˆ Ae 0
ˆ
ˆ ˆ 1 2
(1)多项式函数模型
• 多项式函数模型的一般形式：
Yi 0 1 X i 2 X i 2 ... k X k k
令：
Z1i X i ,...Zki X ik
则原模型化为标准的线性回归模型：
Yi 0 1Z1i 2 Z2i ... k Zki
第四章 非线性回归模型的线性化
第一节 变量间的非线性关系 第二节 线性化方法 第三节 案例分析
第一节 变量间的非线性关系
1、第一种类型（非标准线性回归模型） 2、第二种类型（可线性化的非线性回归模型） 3、第三种类型（不可线性化的非线性回归模型）
第一节 变量间的非线性关系
在实际经济活动中，经济变量的关系是复杂的，直 接表现为线性关系的情况并不多见。 如著名的恩格尔曲线(Engle curves)表现为幂函数曲线 形式、宏观经济学中的菲利普斯曲线（Pillips cuves）表现 为双曲线形式等。 但是，大部分非线性关系又可以通过一些简单的数学 处理，使之化为数学上的线性关系，从而可以运用线性回 归的方法进行计量经济学方面的处理。
1、第一种类型（非标准线性回归模型）
• 非标准线性回归模型一般可以表示成如下形式：
Z1 f1 ( X 1 , X 2 ,... X K ) Z 2 f 2 ( X 1 , X 2 ,... X K ) ...... Z f ( X , X ,... X ) P 1 2 K p Y 0 f1 ( X 1 , X 2 ,... X K

4 非线性回归模型

4 非线性回归模型

0.0000
0.0000 0.0000 27.61000 6.581363 0.900560 1.021594 1202.220 0.000000
4.4 多项式模型
对总成本函数求导，得到边际成本函数的估计式为：
ˆ dy dx
0.634777 0.025924 x 0.000272 x
2
Included observations: 12
Variable X C Coefficient -0.788293 8.014701 Std. Error 0.241772 1.240188 t-Statistic -3.260479 6.462492 Prob. 0.0086 0.0001
R-squared
4.5 成长曲线模型
逻辑（Logistic）成长曲线模型因其
函数图形如S形状（如右图所示），
又称为S曲线模型，其一般表达式 为
yt K 1 e
f t
K
其中
2
O
y
t
f t a0 a1t a2t ... ak t
k
4.5 成长曲线模型 逻辑成长曲线模型经过应用而逐渐简化，目前
（总固定成本不变），最终
接近β0。
4.3 倒数模型 该类型的重要应用就是 恩 格 尔 消 费 曲 线 （ Engel
0 0 1 0
y β0
expenditure curve），表明消 费者在某一商品上的支出与
x
0 1
0
其总收入或总消费支出的关 系。
4.3 倒数模型 若y表示消费者在某一商 品上的消费支出，x表示消费
β1衡量了y的年均增长率。
4.3 倒数模型 倒数模型的函数形式
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

非线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是非线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述非线性回归模型是无法用最小二乘法估计参数的。

可采用非线性方法进行估计。

估计过程非常复杂和困难，在20世纪40年代之前几乎不可能实现。

计算机的出现大大方便了非线性回归模型的估计。

专用软件使这种计算变得非常容易。

但本章不是介绍这类模型的估计。

另外还有一类非线性回归模型。

其形式是非线性的，但可以通过适当的变换，转化为线性模型，然后利用线性回归模型的估计与检验方法进行处理。

称此类模型为可线性化的非线性模型。

下面介绍几种典型的可以做线性化处理的非线性模型。

⑴ 指数函数模型y t = t t u bx ae + (4.1) b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是非线性的。

对上式等号两侧同取自然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表示随机误差项。

图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =tt u bx ae +, (b < 0)⑵ 对数函数模型y t = a + b Ln x t + u t (4.4)b >0和b <0两种情形的图形分别见图4.3和4.4。

x t 和y t 的关系是非线性的。

令x t * = Lnx t , 则y t = a + b x t * + u t (4.5)变量y t 和x t * 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6)b取不同值的图形分别见图4.5和4.6。

x t和y t的关系是非线性的。

对上式等号两侧同取对数，得Lny t = Lna + b Lnx t + u t(4.7) 令y t* = Lny t, a* = Lna, x t* = Lnx t, 则上式表示为y t* = a* + b x t* + u t(4.8) 变量y t* 和x t* 之间已成线性关系。

其中u t表示随机误差项。

(4.7) 式也称作全对数模型。

图4.5 y t = a x t b t u e图4.6 y t = a x t b t u e⑷双曲线函数模型1/y t = a + b/x t+ u t(4.9)也可写成，y t = 1/ (a + b/x t+ u t) (4.10) b>0情形的图形见图4.7。

x t和y t的关系是非线性的。

令y t* = 1/y t, x t* = 1/x t，得y t* = a + b x t* + u t已变换为线性回归模型。

其中u t表示随机误差项。

图4.7 y t = 1/ (a + b/x t ), (b > 0) 图4.8 y t = a + b/x t , (b > 0) 双曲线函数还有另一种表达方式，y t = a + b/x t + u t(4.11) b>0情形的图形见图4.8。

x t和y t的关系是非线性的。

令x t* = 1/x t，得y t = a + b x t* + u t上式已变换成线性回归模型。

⑸多项式方程模型一种多项式方程的表达形式是y t = b0 +b1 x t + b2 x t2 + b3 x t3 + u t(4.12)其中b1>0, b2>0, b3>0和b1<0, b2>0, b3<0情形的图形分别见图4.9和4.10。

令x t 1 = x t，x t 2 = x t2，x t 3 = x t3，上式变为y t = b0 +b1 x t 1 + b2 x t 2 + b3 x t 3 + u t(4.13)这是一个三元线性回归模型。

如经济学中的总成本曲线与图4.9相似。

图4.9 y t = b0 +b1 x t + b2 x t2 + b3 x t3 + u t图4.10 y t = b0 + b1 x t + b2 x t2 + b3 x t3 + u t 另一种多项式方程的表达形式是y t = b0 + b1 x t + b2 x t2 + u t(4.14)其中b1>0, b2>0和b1<0, b2<0情形的图形分别见图4.11和4.12。

令x t 1 = x t，x t 2 = x t 2，上式线性化为，y t = b0 + b1 x t1 + b2 x t2 + u t(4.15)如经济学中的边际成本曲线、平均成本曲线与图4.11相似。

图4.11 y t = b 0 +b 1x t + b 2x t 2 + u t 图4.12 y t = b 0 + b 1x t + b 2x t 2 + u t⑹ 生长曲线 (logistic) 模型y t = tu t f e k++)(1 (4.16)一般f (t ) = a 0 + a 1 t + a 2 t 2 + … + a n t n ，常见形式为f (t ) = a 0 - a ty t = u u at a e k +-+)(01= tu at be k+-+1 (4.17) 其中b = 0a e 。

a > 0情形的图形分别见图4.13和4.14。

美国人口统计学家Pearl 和Reed 广泛研究了有机体的生长，得到了上述数学模型。

生长模型（或逻辑斯谛曲线，Pearl-Reed 曲线）常用于描述有机体生长发育过程。

其中k 和0分别为y t 的生长上限和下限。

∞→t t Limy = k ,-∞→t t Limy = 0。

a , b 为待估参数。

曲线有拐点，坐标为（a Lnb ,2k），曲线的上下两部分对称于拐点。

图4.13 y t = k / (1 +tu at be+-) 图4.14 y t = k / (1 +tu at be +)为能运用最小二乘法估计参数a , b ，必须事先估计出生长上极限值k 。

线性化过程如下。

当k 给出时，作如下变换，k /y t = 1 + t u at be +- 移项， k /y t - 1 = t u at be +-取自然对数，Ln ( k /y t - 1) = Lnb - a t + u t (4.18) 令y t * = Ln ( k /y t - 1), b * = Lnb , 则y t * = b * - a t + u t (4.19)此时可用最小二乘法估计b *和a 。

图4.15 内地5月1日至28日每天非典数据一览⑺ 龚伯斯（Gompertz ）曲线英国统计学家和数学家最初提出把该曲线作为控制人口增长的一种数学模型，此模型可用来描述一项新技术，一种新产品的发展过程。

曲线的数学形式是，y t =at be ke --图4.15 y t =atbeke --曲线的上限和下限分别为k 和0，∞→t t Limy = k , -∞→t t Limy = 0。

a , b 为待估参数。

曲线有拐点，坐标为（a Lnb ,ek ），但曲线不对称于拐点。

一般情形，上限值k 可事先估计，有了k 值，龚伯斯曲线才可以用最小二乘法估计参数。

线性化过程如下：当k 给定时，y t / k = at be e --，k /y t = at be e -Ln (k /y t ) = at be -， Ln [Ln (k /y t )] = Lnb - a t令y *= Ln [Ln (k /y t )], b * = Lnb ，则y * = b * - a t上式可用最小二乘法估计b * 和 a 。

Cobb-Douglas 生产函数下面介绍柯布−道格拉斯（Cobb-Douglas ）生产函数。

其形式是Q = k L α C 1- α (4.24)其中Q 表示产量；L 表示劳动力投入量；C 表示资本投入量；k 是常数；0 < α < 1。

这种生产函数是美国经济学家柯布和道格拉斯根据1899-1922年美国关于生产方面的数据研究得出的。

α的估计值是0.75，β的估计值是0.25。

更习惯的表达形式是y t =t u t t e x x 21210βββ (4.25)这是一个非线性模型，无法用OLS 法直接估计，但可先作线性化处理。

上式两边同取对数，得：Lny t = Ln β0 + β1 Lnx t 1 + β2 Lnx t 2 + u t (4.26)取 y t * = Lny t , β0* = Ln β0, x t 1* = Ln x t 1, x t 2* = Ln x t 2，有y t *= β0* +β1 x t 1* + β2 x t 2* + u t (4.27)上式为线性模型。

用OLS 法估计后，再返回到原模型。

若回归参数 β1 + β2 = 1，称模型为规模报酬不变型（新古典增长理论）； β1 + β2 > 1，称模型为规模报酬递增型； β1 + β2 < 1，称模型为规模报酬递减型。

对于对数线性模型，Lny = Ln β0 + β1 Lnx t 1 + β2 Lnx t 2 + u t ，β1和β2称作弹性系数。

以β1为例，β1 = 1t t Lnx Lny ∂∂= 1111t t t t x x y y ∂∂--= 11//t t tt x x y y ∂∂= 11t t t t x y y x ∂∂ (4.28) 可见弹性系数是两个变量的变化率的比。

注意，弹性系数是一个无量纲参数，所以便于在不同变量之间比较相应弹性系数的大小。

对于线性模型，y t = α0 + α1 x t 1 + α2 x t 2 + u t ，α1和 α2称作边际系数。

以α1为例，α1 =1t tx y ∂∂ (4.29) 通过比较(4.28)和(4.29)式，可知线性模型中的回归系数（边际系数）是对数线性回归模型中弹性系数的一个分量。

例1：此模型用来评价台湾农业生产效率。

用台湾1958-1972年农业生产总值（y t ），劳动力（x t 1），资本投入（x t 2）数据（见表4.1）为样本得估计模型， ∧t Lny = -3.4 + 1.50 Lnx t 1 + 0.49 Lnx t 2 (4.30) (2.78) (4.80) R 2 = 0.89, F = 48.45 还原后得，t yˆ= 0.713 x t 11.50 x t 20.49 (4.31) 因为1.50 + 0.49 = 1.99，所以，此生产函数属规模报酬递增函数。