非线性回归分析(常见曲线及方程)

判断多元非线性回归经验公式的精读什么是多元非线性回归分析多元非线性回归分析是指包含两个以上变量的非线性回归模型。

对多元非线性回归模型求解的传统做法，仍然是想办法把它转化成标准的线性形式的多元回归模型来处理。

有些非线性回归模型，经过适当的数学变换，便能得到它的线性化的表达形式，但对另外一些非线性回归模型，仅仅做变量变换根本无济于事。

属于前一情况的非线性回归模型，一般称为内蕴的线性回归，而后者则称之为内蕴的非线性回归。

多元非线性回归分析方程如果自变数与依变数Y皆具非线性关系，或者有的为非线性有的为线性，则选用多元非线性回归方程是恰当的。

例如，二元二次多项式回归方程为：令,及于是上式化为五元一次线性回归方程：这样以来，便可按多元线性回归分析的方法，计算各偏回归系数，建立二元二次多项式回归方程。

多元非线性回归分析模型一、常见的内蕴多元性回归模型只要对模型中的变量进行数学变换，比如自然对数变换等，就可以将其转化具有标准形式特征的多元线性回归模型。

1.多重弹性模型是一组对的样本观察资料，则称存在下列关系的非线性回归模型为多重弹性模型(1)上述模型中的各解释变量的幂，能够说明解释变量的相对变化对被解释变量产生的相对影响，我们正式从这一角度说它是多重弹性模型的。

2.Cobb-Dauglas生产函数模型(2)其中，yi表示产出总量，Ki为资本要素，Li为劳动力要素，A、α、β为参数。

比较式(1)和(2)，不难看出C-D生产函数模型实际是多重弹性模型的简化或特殊形式。

3.总成本函数模型用yi表示总成本，xi表示产出规模，则称具有如下关系的回归模型为总成本函数模型,i=1,2,…,n(3) 总成本函数是多项式函数的特殊形式，更为一般的情况就是多项式回归模型：,i=1,2,…,n(4) 多项式回归模型从宽松的角度讲，可以不把它看成是非线性回归模型，在这里主要是用来说明一下问题，把它看成内蕴的线性回归模型也无妨。

二、内蕴的非线性回归模型内蕴非线性回归模型的形式有很多种，大部分难以根据经济含义进行称呼，下面，列出几个以帮助大家增加认识。

非线性回归问题两个变量不呈线性关系，不能直接利用线性回归方程建立两个变量的关系，可以通过变换的方法转化为线性回归模型。

分析非线性回归问题的具体做法是：〔1〕假设问题中已给出经验公式，这时可以将变量x 进行置换〔换元〕，将变量的非线性关系转化为线性关系，将问题化为线性回归分析问题来解决． 〔2〕假设问题中没有给出经验公式，需要我们画出数据的散点图，通过与各种函数〔如指数函数、对数函数、幂函数等〕的图象作比拟，选择一种与这些散点拟合得最好的函数，然后采用适当的变量置换，将问题化为线性回归分析问题来解决． 下面举例说明非线性回归分析问题的解法．例1 在彩色显影中，由经验可知：形成染料光学密度y 与析出银的光学密度x 由公式e b xy A =〔b <0〕表示，现测得实验数据如下：试求对的回归方程．分析：该例是一个非线性回归分析问题，由于题目中已给定了要求的曲线为eb xy A =〔b <0〕类型，我们只要通过所给的11对样本数据求出A 和b ，即可确定x 与y 的相关关系的曲线方程．解：由题意可知，对于给定的公式e bxy A =〔b <0〕两边取自然对数，得ln ln b y A x=+． 与线性回归方程对照可以看出，只要取1u x=，ln v y =，ln a A =，就有v a bu =+，这是v 对u 的线性回归直线方程，对此我们再套用相关性检验，求回归系数b 和a ． 题目中所给数据由变量置换1u =，ln v y =变为如表所示的数据：由于｜r ｜=0.998>0.602，可知u 与v 具有很强的线性相关关系． 再求得0.146b =-，0.548a =，∴v =0.5480.146u -，把u 和v 置换回来可得0.146ln 0.548y x=-， ∴0.1460.1460.1460.5480.548e1.73xxxy eee---===，∴回归曲线方程为0.1461.73exy -=．点评：解决此题的思路是通过适当的变量置换把非线性回归方程转化为线性回归方程，然后再套用线性回归分析的解题步骤．例2 为了研究某种细菌随时间x 变化的繁殖个数，收集数据如下：天数x 1 2 3 4 5 6 繁殖个数y612254995190〔1〕作出这些数据的散点图； 〔2〕求出y 对x 的回归方程． 解析：〔1〕作出散点图如图1所示．〔2〕由散点图看出样本点分布在一条指数型曲线e bxy c =〔c ＞0〕的周围，那么ln ln y bx c =+．令ln ln z y a c ==，，那么z bx a =+．x1 2 3 4 5 6 z相应的散点图如图2． 从图2可以看出，变换后的样本点分布在一条直线附近，因此可以用线性回归方程来拟合．由表中数据得到线性回归方程为0.69 1.115z x =+．因此 细菌的繁殖个数对温度的非线性回归方程为0.69 1.115e x y +=．点评：通过作散点图看出，此题是一个非线性回归问题，通过变量置换转化为线性回归问题求解的．值得注意的是，此题的数据与回归曲线是拟合得相当好的，这说明确定性关系〔如公式、函数关系式〕和相关关系之间并没有一条不可逾越的鸿沟．由于有实验误差、测量误差等存在，变量之间确实定性关系往往通过相关关系表现出来；反过来，在有些问题中，可以研究相关关系来深入了解变量变化的内在规律，从而找到它们确实定性关系．。

非线性回归分析常见曲线及方程Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】非线性回归分析回归分析中，当研究的因果关系只涉及和一个时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。

此外，回归分析中，又依据描述自变量与因变量之间因果关系的表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。

通常线性回归分析法是最基本的分析方法，遇到非线性回归问题可以借助数学手段化为线性回归问题处理两个现象变量之间的相关关系并非线性关系，而呈现某种非线性的曲线关系，如：双曲线、二次曲线、三次曲线、幂函数曲线、指数函数曲线(Gompertz)、S型曲线(Logistic) 对数曲线、指数曲线等，以这些变量之间的曲线相关关系，拟合相应的回归曲线，建立非线性回归方程，进行回归分析称为非线性回归分析常见非线性规划曲线1.双曲线1bay x =+2.二次曲线3.三次曲线4.幂函数曲线5.指数函数曲线(Gompertz)6.倒指数曲线y=a/e b x其中a>0，7.S型曲线(Logistic)1e x ya b-=+8.对数曲线y=a+b log x,x>09.指数曲线y=a e bx其中参数a>01．回归：（1）确定回归系数的命令[beta，r，J]=nlinfit（x,y,’model’,beta0）（2）非线性回归命令：nlintool（x，y，’model’, beta0，alpha）2．预测和预测误差估计：[Y，DELTA]=nlpredci（’model’, x，beta，r，J）求nlinfit 或lintool所得的回归函数在x处的预测值Y及预测值的显着性水平为1-alpha的置信区间Y，DELTA.例2 观测物体降落的距离s与时间t的关系，得到数据如下表，求s关于t的回归方程2ˆct=.+btas+解：1. 对将要拟合的非线性模型y=a/e b x，建立M文件如下：function yhat=volum(beta,x)yhat=beta(1)*exp(beta(2)./x);2．输入数据：x=2:16;y=[ 10];beta0=[8 2]';3．求回归系数：[beta,r ,J]=nlinfit(x',y','volum',beta0)； beta即得回归模型为：1.064111.6036e x y-=4．预测及作图：[YY,delta]=nlpredci('volum',x',beta,r ,J)； plot(x,y,'k+',x,YY,'r')2．非线性函数的线性化曲线方程曲线图形变换公式变换后的线性函数by ax＝ln ln ln c a v x u y＝＝＝ u c bv +＝bx y ae ＝ln ln c a u y＝＝u c bv +＝b xe y a＝1ln ln x c a v u y=＝＝u c bv +＝ln y a b x +＝ln v x u y＝＝ u bv +＝a。

（整理）计量经济学第四章⾮线性回归模型的线性化第四章⾮线性回归模型的线性化以上介绍了线性回归模型。

但有时候变量之间的关系是⾮线性的。

例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述⾮线性回归模型是⽆法⽤最⼩⼆乘法估计参数的。

可采⽤⾮线性⽅法进⾏估计。

估计过程⾮常复杂和困难，在20世纪40年代之前⼏乎不可能实现。

计算机的出现⼤⼤⽅便了⾮线性回归模型的估计。

专⽤软件使这种计算变得⾮常容易。

但本章不是介绍这类模型的估计。

另外还有⼀类⾮线性回归模型。

其形式是⾮线性的，但可以通过适当的变换，转化为线性模型，然后利⽤线性回归模型的估计与检验⽅法进⾏处理。

称此类模型为可线性化的⾮线性模型。

下⾯介绍⼏种典型的可以线性化的⾮线性模型。

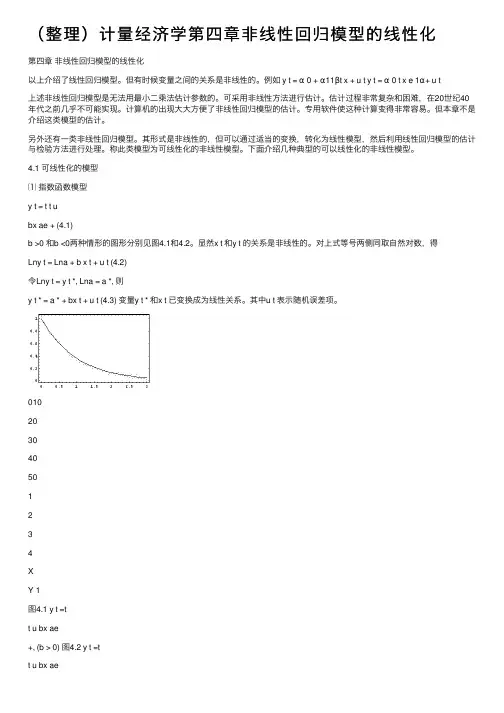
4.1 可线性化的模型⑴指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。

显然x t 和y t 的关系是⾮线性的。

对上式等号两侧同取⾃然对数，得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。

其中u t 表⽰随机误差项。

010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =t+, (b < 0)⑵对数函数模型y t = a + b Ln x t+ u t(4.4)b>0和b<0两种情形的图形分别见图4.3和4.4。

x t和y t的关系是⾮线性的。

令x t* = Lnx t, 则y t = a + b x t* + u t(4.5)变量y t和x t* 已变换成为线性关系。

图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6) b取不同值的图形分别见图4.5和4.6。

非线性回归常见模型一．基本内容模型一xc e c y 21=，其中21,c c 为常数.将xc ec y 21=两边取对数，得x c c e c y xc 211ln )ln(ln 2+==，令21,ln ,ln c b c a y z ===，从而得到z 与x 的线性经验回归方程a bx z +=，用公式求即可，这样就建立了y 与x 非线性经验回归方程.模型二221c x c y +=，其中21,c c 为常数.令a c b c x t ===212,,，则变换后得到y 与t 的线性经验回归方程a bt y +=，用公式求即可，这样就建立了y 与x 非线性经验回归方程.模型三21c x c y +=，其中21,c c 为常数.a cbc x t ===21,,，则变换后得到y 与t 的线性经验回归方程a bt y +=，用公式求即可，这样就建立了y 与x 非线性经验回归方程.模型四反比例函数模型：1y a b x=+令xt 1=，则变换后得到y 与t 的线性经验回归方程a bt y +=，用公式求即可，这样就建立了y 与x 非线性经验回归方程.模型五三角函数模型：sin y a b x=+令x t sin =，则变换后得到y 与t 的线性经验回归方程a bt y +=，用公式求即可，这样就建立了y 与x 非线性经验回归方程.二．例题分析例1．用模型e kx y a =拟合一组数据组()(),1,2,,7i i x y i =⋅⋅⋅，其中1277x x x ++⋅⋅⋅+=；设ln z y =，得变换后的线性回归方程为ˆ4zx =+，则127y y y ⋅⋅⋅=（）A．70e B．70C．35e D．35【解析】因为1277x x x ++⋅⋅⋅+=，所以1x =，45z x =+=，即()127127ln ...ln ln ...ln 577y y y y y y +++==，所以35127e y y y ⋅⋅⋅=.故选：C例2．一只红铃虫产卵数y 和温度x 有关，现测得一组数据()(),1,2,,10i i x y i =⋅⋅⋅，可用模型21e c x y c =拟合，设ln z y =，其变换后的线性回归方程为4zbx =- ，若1210300x x x ++⋅⋅⋅+=，501210e y y y ⋅⋅⋅=，e 为自然常数，则12c c =________.【解析】21e c x y c =经过ln z y =变换后，得到21ln ln z y c x c ==+，根据题意1ln 4c =-，故41e c -=，又1210300x x x ++⋅⋅⋅+=，故30x =，5012101210e ln ln ln 50y y y y y y ⋅⋅⋅=⇒++⋅⋅⋅+=，故5z =，于是回归方程为4zbx =- 一定经过(30,5)，故ˆ3045b -=，解得ˆ0.3b =，即20.3c =，于是12c c =40.3e -.故答案为：40.3e -.该景点为了预测2023年的旅游人数，建立了模型①：由最小二乘法公式求得的数据如下表所示，并根据数据绘制了如图所示的散点图.。

非线性回归分析回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。

此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。

通常线性回归分析法是最基本的分析方法，遇到非线性回归问题可以借助数学手段化为线性回归问题处理两个现象变量之间的相关关系并非线性关系，而呈现某种非线性的曲线关系，如：双曲线、二次曲线、三次曲线、幂函数曲线、指数函数曲线(Gompertz)、S型曲线(Logistic)对数曲线、指数曲线等，以这些变量之间的曲线相关关系，拟合相应的回归曲线，建立非线性回归方程，进行回归分析称为非线性回归分析常见非线性规划曲线1.双曲线1b a yx2.二次曲线3.三次曲线4.幂函数曲线5.指数函数曲线(Gompertz)6.倒指数曲线y=ab/xe其中a>0，7.S型曲线(Logistic) y1 abex8.对数曲线y=a+blogx,x>0bx9.指数曲线y=ae其中参数a>01．回归：（1）确定回归系数的命令[beta，r，J]=nlinfit（x,y,’model’,beta0）（2）非线性回归命令：nlintool（x，y，’model’,beta0，alpha）2．预测和预测误差估计：[Y，DELTA]=nlpredci（’model’,x，beta，r，J）求nlinfit或lintool所得的回归函数在x处的预测值Y及预测值的显著性水平为1-alpha的置信区间Y，DELTA.例2观测物体降落的距离s与时间t的关系，得到数据如下表，求s关于t的回归方程s?a btct2.t(s)1/302/303/304/305/306/307/30s(cm)11.8615.6720.6026.6933.7141.9351.13t(s)8/309/3010/3011/3012/3013/3014/30s(cm)61.4972.9085.4499.08113.77129.54146.48解：b/x，建立M文件volum.m如下：e1.对将要拟合的非线性模型y=afunctionyhat=volum(beta,x)yhat=beta(1)*exp(beta(2)./x);2．输入数据：x=2:16;y=[6.428.209.589.59.7109.939.9910.4910.5910.6010.8010.6010.9010.76];beta0=[82]';3．求回归系数：[beta,r,J]=nlinfit(x',y','volum',beta0)；beta2.y11.6036ex即得回归模型为：4．预测及作图：[YY,delta]=nlpredci('volum',x',beta,r,J)；plot(x,y,'k+',x,YY,'r')2．非线性函数的线性化曲线方程曲线图形变换公式变换后的线性函数b y＝ax c＝lnavlnx＝u＝ylnu＝cbvbx y＝ae c＝alnu＝ylnu＝cbvc＝alny＝a1bvxxeu＝ylnu＝cbvy＝abxvlnxln＝＝u＝abvuy。

非线性回归分析与曲线拟合方法回归分析是一种常见的统计分析方法，用于研究自变量与因变量之间的关系。

在实际应用中，很多数据并不符合线性关系，而是呈现出曲线形式。

这时，我们就需要使用非线性回归分析和曲线拟合方法来更好地描述数据的规律。

一、非线性回归分析的基本原理非线性回归分析是一种通过拟合非线性方程来描述自变量与因变量之间关系的方法。

与线性回归不同，非线性回归可以更准确地反映数据的特点。

在非线性回归分析中，我们需要选择适当的非线性模型，并利用最小二乘法来估计模型的参数。

二、常见的非线性回归模型1. 多项式回归模型：多项式回归是一种常见的非线性回归模型，它通过多项式方程来拟合数据。

多项式回归模型可以描述数据的曲线特征，但容易出现过拟合问题。

2. 指数回归模型：指数回归模型适用于自变量与因变量呈指数关系的情况。

指数回归模型可以描述数据的增长或衰减趋势，常用于描述生物学、物理学等领域的数据。

3. 对数回归模型：对数回归模型适用于自变量与因变量呈对数关系的情况。

对数回归模型可以描述数据的增长速度，常用于描述经济学、金融学等领域的数据。

4. S形曲线模型：S形曲线模型适用于自变量与因变量呈S形关系的情况。

S形曲线模型可以描述数据的增长或衰减过程，常用于描述市场营销、人口增长等领域的数据。

三、曲线拟合方法曲线拟合是一种通过选择合适的曲线形状来拟合数据的方法。

在曲线拟合过程中，我们需要根据数据的特点选择适当的拟合方法。

1. 最小二乘法：最小二乘法是一种常用的曲线拟合方法，通过最小化观测值与拟合值之间的残差平方和来确定拟合曲线的参数。

2. 非线性最小二乘法：非线性最小二乘法是一种用于拟合非线性模型的方法，它通过最小化观测值与拟合值之间的残差平方和来确定模型的参数。

3. 曲线拟合软件：除了手动选择拟合方法，我们还可以使用曲线拟合软件来自动拟合数据。

常见的曲线拟合软件包括MATLAB、Python的SciPy库等。

四、应用实例非线性回归分析和曲线拟合方法在实际应用中有着广泛的应用。

应用MATLAB进行非线性回归分析摘要早在十九世纪，英国生物学家兼统计学家高尔顿在研究父与子身高的遗传问题时，发现子代的平均高度又向中心回归大的意思，使得一段时间内人的身高相对稳定。

之后回归分析的思想渗透到了数理统计的其他分支中。

随着计算机的发展，各种统计软件包的出现，回归分析的应用就越来越广泛。

回归分析处理的是变量与变量间的关系。

有时，回归函数不是自变量的线性函数，但通过变换可以将之化为线性函数，从而利用一元线性回归对其进行分析，这样的问题是非线性回归问题。

下面的第一题：炼钢厂出钢水时用的钢包，在使用过程中由于钢水及炉渣对耐火材料的侵蚀，使其容积不断增大。

要找出钢包的容积用盛满钢水时的质量与相应的实验次数的定量关系表达式，就要用到一元非线性回归分析方法。

首先我们要对数据进行分析，描出数据的散点图，判断两个变量之间可能的函数关系，对题中的非线性函数，参数估计是最常用的“线性化方法”，即通过某种变换，将方程化为一元线性方程的形式，接着我们就要对得到的一些曲线回归方程进行选择，找出到底哪一个才是更好一点的。

此时我们通常可采用两个指标进行选择，第一个是决定系数，第二个是剩余标准差。

进而就得到了我们想要的定量关系表达式。

第二题：给出了某地区1971—2000年的人口数据，对该地区的人口变化进行曲线拟合。

也用到了一元非线性回归的方法。

首先我们也要对数据进行分析，描出数据的散点图，然后用MATLAB编程进行回归分析拟合计算输出利用Logistic模型拟合曲线。

关键词：参数估计，Logistic模型，MATLAB正文一、一元非线性回归分析的求解思路：•求解函数类型并检验。

•求解未知参数。

可化曲线回归为直线回归，用最小二乘法求解；可化曲线回归为多项式回归。

二、回归曲线函数类型的选取和检验1、直接判断法2、作图观察法，与典型曲线比较，确定其属于何种类型，然后检验。

3、直接检验法（适应于待求参数不多的情况）4、表差法（适应于多想式回归，含有常数项多于两个的情况）三、化曲线回归为直线回归问题用直线检验法或表差法检验的曲线回归方程都可以通过变量代换转化为直线回归方程，利用线性回归分析方法可求得相应的参数估计值。

非线性回归分析回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。

此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。

通常线性回归分析法是最基本的分析方法，遇到非线性回归问题可以借助数学手段化为线性回归问题处理 两个现象变量之间的相关关系并非线性关系，而呈现某种非线性的曲线关系，如：双曲线、二次曲线、三次曲线、幂函数曲线、指数函数曲线(Gompertz)、S 型曲线(Logistic) 对数曲线、指数曲线等，以这些变量之间的曲线相关关系，拟合相应的 回归曲线，建立非线性回归方程，进行回归分析称为非线性回归分析常见非线性规划曲线1. 双曲线1b a y x =+2.二次曲线 3.三次曲线 4.幂函数曲线 5.指数函数曲线(Gompertz) 6.倒指数曲线y=a /e b x 其中a>0， 7.S 型曲线(Logistic) 1e x y a b -=+ 8.对数曲线 y=a+b log x,x >0 9. 指数曲线y =a e bx 其中参数a >01．回归：（1）确定回归系数的命令[beta ，r ，J]=nlinfit （x,y,’model’,beta0）（2）非线性回归命令：nlintool （x ，y ，’model’, beta0，alpha ）2．预测和预测误差估计：[Y ，DELTA]=nlpredci （’model’, x，beta ，r ，J ）求nlinfit 或lintool 所得的回归函数在x 处的预测值Y 及预测值的显著性水平为1-alpha 的置信区间Y ，DELTA.例2 观测物体降落的距离s 与时间t 的关系，得到数据如下表，求s关于t 的回归方程2ˆct bt a s++=. 解：1. 对将要拟合的非线性模型y=a /e b x ，建立M 文件volum.m 如下：function yhat=volum(beta,x)yhat=beta(1)*exp(beta(2)./x);2．输入数据：x=2:16;y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.5910.60 10.80 10.60 10.90 10.76];beta0=[8 2]';3．求回归系数：[beta,r ,J]=nlinfit(x',y','volum',beta0)； beta即得回归模型为：1.064111.6036e x y-=4．预测及作图：[YY,delta]=nlpredci('volum',x',beta,r ,J)； plot(x,y,'k+',x,YY,'r')2．非线性函数的线性化。

非线性回归分析简介非线性回归分析是一种用于建立非线性关系模型的统计方法。

与线性回归不同，非线性回归可以更好地拟合非线性数据，提供更准确的预测结果。

在许多实际问题中，数据往往呈现出非线性的趋势，因此非线性回归分析在实际应用中具有广泛的应用价值。

一、非线性回归模型的基本形式非线性回归模型的基本形式可以表示为：y = f(x, β) + ε其中，y是因变量，x是自变量，β是模型参数，f(x, β)是非线性函数，ε是误差项。

非线性函数可以是任意形式的函数，如指数函数、对数函数、幂函数等。

二、非线性回归模型的参数估计与线性回归不同，非线性回归模型的参数估计不能直接使用最小二乘法。

常见的非线性回归参数估计方法有以下几种：1. 非线性最小二乘法（NLS）非线性最小二乘法是一种常用的参数估计方法，它通过最小化残差平方和来估计模型参数。

具体而言，通过迭代的方式不断调整参数，使得残差平方和最小化。

2. 非线性广义最小二乘法（GNLS）非线性广义最小二乘法是对非线性最小二乘法的改进，它在最小化残差平方和的同时，还考虑了误差项的方差结构。

通过引入权重矩阵，可以更好地处理异方差性的数据。

3. 非线性加权最小二乘法（WNLS）非线性加权最小二乘法是对非线性广义最小二乘法的进一步改进，它通过引入加权矩阵，对不同数据点赋予不同的权重。

可以根据数据的特点，调整权重矩阵，提高模型的拟合效果。

三、非线性回归模型的评估指标在进行非线性回归分析时，需要对模型进行评估，以确定模型的拟合效果。

常见的评估指标有以下几种：1. 残差分析残差分析是一种常用的评估方法，通过分析残差的分布情况，判断模型是否符合数据的分布特征。

如果残差呈现随机分布，说明模型拟合效果较好；如果残差呈现一定的规律性，说明模型存在一定的问题。

2. 决定系数（R-squared）决定系数是衡量模型拟合优度的指标，其取值范围为0到1。

决定系数越接近1，说明模型对数据的解释能力越强；决定系数越接近0，说明模型对数据的解释能力越弱。

非线性回归一、可化为线性回归的曲线回归在实际问题当中，有许多回归模型的被解释变量y 与解释变量x 之间的关系都不是线性的，其中一些回归模型通过对自变量或因变量的函数变换可以转化为线性关系，利用线性回归求解未知参数，并作回归诊断。

如下列模型。

εββ++=x e y 10-------（1） εββββ+++++=p p x x x y 2210--------（2） εe ae y bx =--------------------（3） ε+=bx ae y -------------（4）对于（1）式，只需令x e x ='即可化为y 对x '是线性的形式εββ+'+=x y 10，需要指出的是，新引进的自变量只能依赖于原始变量，而不能与未知参数有关。

对于（2）式，可以令1x =x ,2x =2x ,…, p x =p x ,于是得到y 关于1x ,2x ,…, p x 的线性表达式εββββ+++++=p p x x x y 22110对与（3）式，对等式两边同时去自然数对数，得ε++=bx a y ln ln ,令 y y ln =',a ln 0=β,b =1β，于是得到y '关于x 的一元线性回归模型： εββ++='x y 10。

对于（4）式，当b 未知时，不能通过对等式两边同时取自然数对数的方法将回归模型线性化，只能用非线性最小二乘方法求解。

回归模型（3）可以线性化，而（4）不可以线性化，两个回归模型有相同的回归函数bx ae ，只是误差项ε的形式不同。

（3）式的误差项称为乘性误差项，（4）式的误差项称为加性误差项。

因而一个非线性回归模型是否可以线性化，不仅与回归函数的形式有关，而且与误差项的形式有关，误差项的形式还可以有其他多种形式。

乘性误差项模型和加性误差项模型所得的结果有一定差异，其中乘性误差项模型认为t y 本身是异方差的，而t y ln 是等方差的。