第一节二重积分的概念与性质

二重积分极坐标与直角坐标系转换二重积分是微积分中的重要概念，它在数学和物理等领域中有广泛的应用。

在求解二重积分时，可以选择使用直角坐标系或极坐标系进行计算。

本文将介绍二重积分的概念和性质，并对直角坐标系和极坐标系下的二重积分进行转换和计算。

第一部分：二重积分的概念和性质二重积分是对二元函数在某个区域上的积分。

可以将二重积分看作是在平面上对函数进行求和的过程。

在直角坐标系下，二重积分的计算可以通过分割区域为小矩形，并对每个小矩形的面积乘以函数值进行求和来实现。

而在极坐标系下，二重积分的计算可以通过分割区域为小扇形，并对每个小扇形的面积乘以函数值进行求和来实现。

二重积分具有以下性质：1. 线性性质：二重积分具有线性性质，即对于常数a和b，有∬(af(x, y) + bg(x, y))dxdy = a∬f(x, y)dxdy + b∬g(x, y)dxdy。

2. 区域可加性：如果将一个区域分割成两个不相交的子区域，则二重积分可以分别在这两个子区域上进行计算，然后将结果相加。

3. 积分交换性：如果被积函数f(x, y)在闭区域D上连续，那么可以交换积分次序，即∬f(x, y)dxdy = ∫[a,b]∫[c,d]f(x, y)dydx = ∫[c,d]∫[a,b]f(x, y)dxdy。

第二部分：直角坐标系和极坐标系下的二重积分转换在实际计算中，有时候在直角坐标系下计算二重积分比较复杂，而在极坐标系下计算则相对简单。

因此，我们可以将直角坐标系下的二重积分转换为极坐标系下的二重积分来简化计算。

对于直角坐标系和极坐标系下的二重积分转换，有如下关系：1. 直角坐标系到极坐标系的转换：x = rcosθy = rsinθdxdy = rdrdθ2. 极坐标系到直角坐标系的转换：r = √(x^2 + y^2)θ = arctan(y/x)dxdy = r dr dθ通过以上转换，我们可以将直角坐标系下的二重积分转换为极坐标系下的二重积分，从而简化计算。

第⼀节⼆重积分的概念与性质第⼀节⼆重积分的概念与性质学习指导１．教学⽬的：使读者理解⼆重积分的概念与性质。

２．基本练习：熟悉⼆重积分的⼏何、物理背景。

熟悉⼆重积分的性质。

3．应注意的事项：⼆重积分是⼆元函数乘积和式的极限，是定积分的推⼴，因此从引例到研究⽅法，从定义到性质都是类似的，读者要善于⽐较，触类旁通，温故⽽知新。

第⼀节⼆重积分的概念与性质⼀、⼆重积分的概念1. 曲顶柱体的体积（1）曲顶柱体（2）曲顶柱体的体积现在我们来讨论如何定义并计算上述曲顶柱体的体积V。

平顶柱体的体积2. 平⾯薄⽚的质量(1) 问题的提出(2) 均匀薄⽚的质量(3) ⾮均匀薄⽚质量的计算⽅法(4) ⼆重积分的定义上⾯两个问题的实际意义虽然不同，但所求量都归结为同⼀形式的和的极限。

在物理、⼒学、⼏何和⼯程技术中，有许多物理量或⼏何量都可以归结为这⼀形式的和的极限。

因此我们要⼀般的研究这种和的极限，并抽象出下述⼆重积分的定义。

定义设是有界闭区域上的有界函数.将闭区域任意分成个⼩闭区域其中表⽰第个⼩闭区域，也表⽰它的⾯积。

再每个上任取⼀点，作乘积，并作和。

如果当个⼩闭区域的直径中最⼤值趋于零时，这和的极限总存在。

则称此极限为函数在闭区域上的⼆重积分，记作，即。

（1）叫做被积函数，叫做被积表达式，叫做⾯积元素，与叫其中积分变量，叫做积分区域，叫做积分和。

(5) 直⾓坐标系中的⾯积元素在⼆重积分的定义中对闭区域的划分是任意的，如果在直⾓坐标系中⽤平⾏于坐标轴的直线⽹来划分，那么除了包含边界点的⼀些⼩闭区域外，其余的⼩闭区域都是矩形闭区域。

设矩形闭区域的边长为和，则。

因此在直⾓坐标系中，有时也把⾯积元素记作。

⽽把⼆重积分记作其中叫做直⾓坐标系中的⾯积元素。

(6) ⼆重积分的存在性这⾥我们要指出，当在闭区域上连续时，式右端的和的极限必定存在，也就是说，函数在上的⼆重积分必定存在。

我们总假定函数在闭区域上连续，所以在上的⼆重积分都是存在的，以后就不在每次加以说明了。

二重积分知识点一、引言二重积分是高等数学中的重要内容，是对二元函数在有限区域上的积分运算。

二重积分的概念与求解技巧是深入理解、掌握多元函数的必备工具，也为解决实际问题提供了数学方法。

本文将从二重积分的概念、性质、计算方法和应用等方面，全面详细地介绍二重积分的知识点。

二、概念1. 二重积分的定义设f (x,y )在闭区域D 上有定义，D 由有向闭曲线C 围成，且f (x,y )在D 上有界。

若存在数I ，对于任意给定的正数ε，都存在正数δ，使得对于D 内任意满足Δσ<δ的任意分割σ，对应的任意代点ξij ，总有|∑∑f mj=1n i=1(ξij )Δσij −I|<ε则称I 为函数f (x,y )在闭区域D 上的二重积分，记作I =∬f D(x,y )dσ其中，Δσij 表示第(i,j )个小区域的面积，Δσ表示整个区域D 的面积。

2. 二重积分的几何意义二重积分的几何意义是对二元函数在闭区域上的面积进行逐点求和，即将闭区域D 分割成无穷多个小面积区域，并对每个小面积区域上的函数值进行乘积再求和，最终得到二重积分。

三、性质1. 线性性质设闭区域D上有二重积分∬fD(x,y)dσ，若c为常数，则有∬(cf(x,y)) D dσ=c∬fD(x,y)dσ∬(f(x,y)±g(x,y)) D dσ=∬fD(x,y)dσ±∬gD(x,y)dσ2. 区域可加性设闭区域D可分为非重叠的两部分D1和D2，则有∬fD (x,y)dσ=∬fD1(x,y)dσ+∬fD2(x,y)dσ3. Fubini定理（累次积分）设函数f(x,y)在闭区域D上连续，则有∬f D (x,y)dσ=∫(∫fβ(x)α(x)(x,y)dy)badx=∫(∫fδ(y)γ(y)(x,y)dx)dcdy其中，(x,y)∈D,α(x)≤y≤β(x),γ(y)≤x≤δ(y)。

4. 值定理设函数f(x,y)在闭区域D上一致连续，则存在(ξ,η)∈D，使得∬fD (x,y)dσ=f(ξ,η)∬dDσ=f(ξ,η)σ(D)其中，σ(D)表示闭区域D的面积。

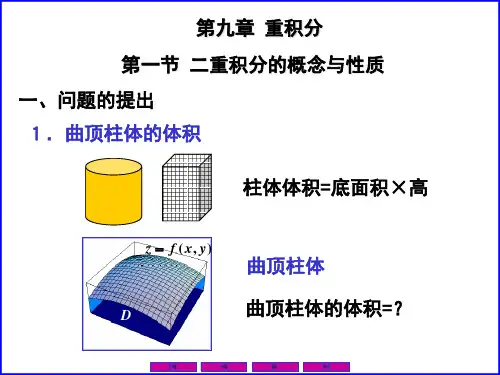
第九章 重积分大纲要求1．理解二重积分、三重积分的概念，了解重积分的性质，了解二重积分的中值定理2．掌握二重积分（直角坐标、极坐标）的计算方法，会计算三重积分（直角坐标、柱面坐标、球面坐标）3．会用重积分求一些几何量与物理量（平面图形的面积、体积、质量、重心、转动惯量等）第一节 二重积分的概念与性质㈠ 本课的基本要求掌握二重积分的定义和性质㈡ 本课的重点、难点二重积分的定义本课的重点，二重积分的几何意义为本课的难点㈢ 教学内容一．两个实际问题1．曲顶柱体的体积曲顶柱体是指底为xoy 平面上的有界闭区域D ，侧面是以D 的边界曲线为准线而母线平行于z 轴的柱面，顶是由二元连续函数）（假定0),(),(≥=y x f y x f z 表示的曲面围成的立体。

问题：求曲顶柱体的体积V ？ 图① 分割 将区域D 任意分成n 个小区域n i i ,2,1}{=∆σ，i σ∆表示第i 个小区域的面积，以每个小区域i σ∆为底，以它的边界线为准线作母线平行于z 轴的小曲顶柱体。

这样整个曲顶柱体就相应地分割成n 个小曲顶柱体，它们的体积分别证为1σ∆，2σ∆，…，n σ∆。

② 近似代替 取),(),(i i i i i f ηξσηξ，以∆∈为高，i σ∆为底的平顶柱体的体积i i i f σηξ∆),(近似i V ∆),(y x f),,2,1(),(n i f V i i i i =∆≈∆σηξ③ 求和 ∑∑==∆≈∆=n i i ii n i i f V V 11),(σηξ④ 取极限 ∑=→∆=n i i i i f V 10),(lim σηξλ，λ表示n 个小区域中的最大直径2．平面薄片的质量设有一质量非均匀分布的薄片，在xoy 平面上占有区域D ，面密度ρ(x,y)是D 上的ct 函数，且ρ(x,y)>0，求M 。

),,2,1(),(n i M i i i =∆≈∆σηξρ 图∑=∆≈n i i ii M 1),(σηξρ ∑=→∆=ni i i i M 10),(lim σηξρλ (n →∞，λ→0，小区域的最大直径)二．二重积分的概念引入定义：设),(y x f z =是定义在有界区域D 上的有界函数，将D 任意地分成n 个小区域 1σ∆，2σ∆，…，n σ∆，小区域i σ∆的面积仍记为i σ∆，在i σ∆内任取一点),(i i ηξ，作和式∑=∆=n i i ii n f S 1),(σηξ，若当),,2,1(n i i =∆σ的最大直径n S 时，0→λ极限存在，则称此极限值为函数),(y x f z =在区域D 上的二重积分，记为⎰⎰Dd y x f σ),(，即\ ⎰⎰D d y x f σ),(=∑=→∆n i i i i f 10),(lim σηξλ 其中),(y x f 称为被积函数，σd y x f ),(称为被积表达式，D 叫做积分区域，σd 称为面积元素，⎰⎰为重积分号，x ，y 为积分变量，∑=∆=n i i ii n f S 1),(σηξ称为积分和。

第九章 重积分第一节 二重积分的概念及性质一．二重积分的概念 1．引例引例1 曲顶柱体的体积设有一立体的底是xy 面上的有界闭区域D ，侧面是以D 的边界曲线为准线、母线平行于z 轴的柱面，顶是有二元非负连续函数),(y x f z =所表示的曲面，如图9—1所示，这个立体称为D 上的曲顶柱体，试求该曲顶柱体的体积。

图9—1 图9—2 图9—3解 对于平柱体的体积底面积高⨯=V ，然而，曲顶柱体不是平顶柱体，那么具体作法如下(1)分割把区域D 任意划分成n 个小闭区域nσσσ∆∆∆,,,21Λ，其中iσ∆表示第i 个小闭区域，也表示它的面积。

在每个小闭区域内，以它的边界曲线为准线、母线平行于z 轴的柱面，如图9—2所示。

这些柱面就那原来的曲顶柱体分割成n 个小曲顶柱体。

(2)近似在每一个小闭区域iσ∆上任取一点),(i i ηξ，以),(i i f ηξ为高，iσ∆为底的平顶柱体的体积i i i f σηξ∆),(近似代替第i 个小曲顶柱体的体积。

i i i f V σηξ∆≈∆),((3)求和这n 个小平顶柱体的体积之和即为曲顶柱体体积的近似值∑=∆≈∆=ni i i i f V V 1),(σηξ(4)取极限将区域D 无限细分，且每个小闭区域趋向于或说缩成一点，这个近似值趋近于曲顶柱体的体积。

即∑=→∆=ni i i i f V 10),(lim σηξλ其中λ表示这n 个小闭区域iσ∆直径中最大值的直径（有界闭区域的直径是指区域中任意两点间的距离）。

引例2 平面薄片的质量设有一平面薄片占有xy 面上的有界闭区域D ，它的密度为D 上的连续函数),(y x z ρ=，试求平面薄片的质量。

解 对于均匀平面薄片的质量薄片面积密度⨯=m ，然而，平面薄片并非均匀，那么具体作法如下(1)分割将薄片（即区域D ）任意划分成n 个小薄片nσσσ∆∆∆,,,21Λ，其中iσ∆表示第i 个小小薄片，也表示它的面积，如图9—3所示。