二重积分及三重积分的计算
- 格式:doc
- 大小:763.00 KB
- 文档页数:13




重积分知识点总结(一)前言重积分是高等数学中的重要知识点,是对多重积分进行研究的内容。
它在物理学、工程学和计算机科学等领域都有广泛的应用。
本文将针对重积分的知识点进行总结,以帮助读者更好地理解和掌握这部分知识。
正文一、重积分的定义与性质1.重积分的定义:对于二重积分来说,可以将其理解为将被积函数在某个有界闭区域上的“总体积”。
而对于三重积分来说,则是将被积函数在某个有界闭区域上的“总体积”。
2.交换积分次序:在某些情况下,交换积分次序可以简化重积分计算的复杂程度。
3.重积分的性质:包括线性性质、保号性质、次可加性质等。
这些性质在进行重积分计算时非常重要。
二、二重积分的计算方法1.二重积分的计算方法主要有面积法、直角坐标法和极坐标法。
在具体的计算过程中,可以根据题目要求和被积函数的形式选择合适的计算方法。
2.面积法:将被积函数看做是一片平面上每一点的贡献,通过对整个区域的累加求和来计算二重积分。
3.直角坐标法:根据被积函数在直角坐标系内的表达式,利用基本积分计算公式进行计算。
4.极坐标法:将被积函数用极坐标系表示,通过变量代换进行计算。
对于具有旋转对称性的问题,极坐标法可以简化计算过程。
三、三重积分的计算方法1.三重积分的计算方法主要有体积法、直角坐标法和柱坐标法。
在具体的计算过程中,同样需要根据题目要求和被积函数的形式选择合适的计算方法。
2.体积法:将被积函数看做是空间内每一点的贡献,通过对整个区域的累加求和来计算三重积分。
3.直角坐标法:根据被积函数在直角坐标系内的表达式,利用基本积分计算公式进行计算。
4.柱坐标法:将被积函数用柱坐标系表示,通过变量代换进行计算。
对于具有旋转对称性的问题,柱坐标法可以简化计算过程。
结尾重积分是数学中重要而复杂的知识点,在实际应用中具有广泛的价值。
通过本文的总结,希望读者们能够对重积分的定义、性质和计算方法有更深入的理解,从而更好地应对相关问题的解决和应用。
前言重积分是高等数学中的重要知识点,是对多重积分进行研究的内容。

多重积分的方法总结多重积分是微积分的重要内容之一,在物理、工程、经济等学科中有广泛的应用。
它是定积分的推广,主要用于计算二重积分、三重积分以及更高维度的积分。
一、二重积分的求解方法1.直角坐标求解法:根据被积函数的形式,选择适当的积分次序,将二重积分转化为两次一重积分求解。
2.换元法:将二重积分转化为在转化后的坐标系中的积分。
常见的换元法有极坐标法、参数方程法等。
3.极坐标法:对于具有圆形对称性的被积区域和被积函数,可以使用极坐标进行求解。
极坐标的变换公式为:x = r*cosθy = r*sinθ面积元素dA = r*dr*dθ4.矩形法:对于长方形区域上的二重积分,可以使用矩形法进行计算。
将整个被积区域划分为若干个小矩形,然后对每个小矩形上的被积函数进行近似计算,最后将所有小矩形的结果相加得到最终的结果。
二、三重积分的求解方法1.直角坐标求解法:根据被积函数的形式,选择适当的积分次序,将三重积分转化为三次一重积分求解。
2.柱坐标法:对于具有柱面对称性的被积区域和被积函数,可以使用柱坐标进行求解。
柱坐标的变换公式为:x = r*cosθy = r*sinθz=z体积元素dV = r*dr*dθ*dz3.球坐标法:对于具有球面对称性的被积区域和被积函数,可以使用球坐标进行求解。
球坐标的变换公式为:x = r*sinφ*cosθy = r*sinφ*sinθz = r*cosφ体积元素dV = r^2*sinφ*dφ*dθ*dr应用题解析:多重积分在物理、工程和经济学等学科中有广泛应用,常用于计算质量、体积、中心、质心、转动惯量、质量矩等物理量。
在应用题中,需要根据具体问题确定积分的次序、被积函数和被积区域,并利用常见的求解方法进行求解。
例如,计算一个半径为R的球体的体积。
由于球体具有球面对称性,我们可以使用球坐标进行求解。
将球体划分为若干个体积元素,并对每个体积元素进行积分,最后将所有体积元素的体积相加得到球体的总体积。

二重积分与多重积分及其应用总结知识要点。
(1) 二重积分(2) 三重积分(3) 多重积分的应用。
(4) 三重积分的总结。
一、二重积分(1) 直角坐标系下的二重积分。
(重点)直角坐标系下的二重积分,积分区域为二维平面。
⎰⎰=Ddxdy y x f I ),(。
这种形式的积分要让x 、y 取遍所有D 上的点(Ω为积分区域)。
所以要先让x 为常量,取遍y ,然后在上面的基础上再取遍x 。
或者先让y 为常量,取遍x ,然后在上面的基础上再取遍y 。
(点动成线,线动成面。
与这类似。
)针对不同的题目选择不同的方式。
而这其中的关键就是要找对积分区域D 和正确的目标函数表达式),(y x f 。
(2) 极坐标系下的二重积分。
(理解,计算是重点)极坐标系下的二重积分,积分区域同样为二维平面。
⎰⎰=Dd d f I θθ ),(。
这种形式的积分要先取长度 的线,然后变角度,就像是扫地一样。
或者是角度确定,变长度 一样就像是水波的扩散一样。
两种不同的方式一样可以取遍积分区域D 上的所有点。
但是单独拿出来的很少理解即可。
(3)直角坐标系下的二重积分与极坐标系下的二重积分之间的转换(重点)。
积分区域D 为圆或圆的一部分是,直角坐标下的积分有时候很难计算,但是化为极坐标会很简单。
这就需要极坐标与直角坐标的相互转换。
转换公式如下:ϑcos =x ϑsin =y ⎰⎰⎰⎰=DD d d f dxdy y x f ϑϑϑ )sin ,cos (),(额略长。
不过这是省掉积分上下限的。
如果在圆域内(尤其是那种圆的一部分),在直角坐标下积分的上下限异常麻烦,而且计算量相当之大。
但在极坐标系下将很容易。
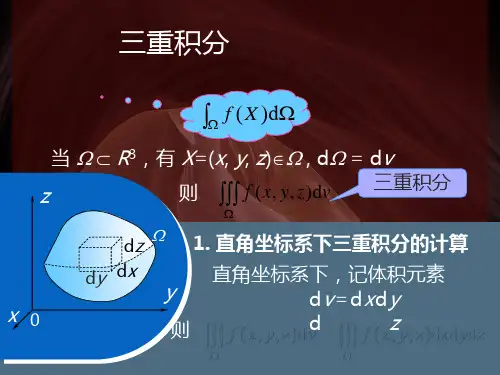
3/16.二、三重积分(1) 直角坐标系下的三重积分。
(重点)。
直角坐标系下的三重积分,积分区域为三维立体。
⎰⎰⎰=Ddxdydz z y x f I ),,( 。
计算方式与二重积分无异。
就是先固定两个动一个。
再固定原先固定的一个,动另一个。


[【原创】] 一般区域二重、三重积分MATLAB计算方法这里讨论的计算方法指的是利用现有的MATLAB函数来求解,而不是根据具体的数值计算方法来编写相应程序。
目前最新版的2009a有关于一般区域二重积分的计算函数quad2d(详细介绍见/viewthread.php?tid=873479),但没有一般区域三重积分的计算函数,而NIT工具箱似乎也没有一般区域三重积分的计算函数。
本贴的目的是介绍一种在7.X版本MATLAB(不一定是2009a)里求解一般区域二重三重积分的思路方法。
需要说明的是,上述链接里已经讨论了一种求解一般区域二重三重积分的思路方法,就是将被积函数“延拓”到矩形或者长方体区域,但是这种方法不可避免引入很多乘0运算浪费时间。
因此,新的思路将避免这些。
由于是调用已有的MATLAB函数求解,在求一般区域二重积分时,效率和2009a的quad2d相比有一些差距,但是相对于"延拓"函数的做法,效率大大提高了。
下面结合一些简单例子说明下计算方法。
譬如二元函数f(x,y) = x*y,y从sin(x)积分到cos(x),x从1积分到2,这个积分可以很容易用符号积分算出结果1.syms x y2.int(int(x*y,y,sin(x),cos(x)),1,2) ]结果是-1/2*cos(1)*sin(1)-1/4*cos(1)^2+cos(2)*sin(2)+1/4*cos(2)^2 = -0.635412702399943复制代码如果你用的是2009a,你可以用1.quad2d(@(x,y) x.*y,1,2,@(x)sin(x),@(x)cos(x),'AbsTol',1e-12)复制代码得到上述结果。
如果用的不是2009a,那么你可以利用NIT工具箱里的quad2dggen函数。
那么我们如果既没有NIT工具箱用的也不是2009a,怎么办呢?答案是我们可以利用两次quadl函数,注意到quadl函数要求积分表达式必须写成向量化形式,所以我们构造的函数必须能接受向量输入。


二重积分与三重积分区别都是递进关系,从一重积分开始,只说几何意义吧。
一重积分(定积分):只有一个自变量y = f(x)当被积函数为1时,就是直线的长度(自由度较大)∫(a→b) dx = L(直线长度)被积函数不为1时,就是图形的面积(规则)∫(a→b) f(x) dx = A(平面面积)另外,定积分也可以求规则的旋转体体积,分别是盘旋法(Disc Method):V = π∫(a→b) f2(x) dx圆壳法(Shell Method):V = 2π∫(a→b) xf(x) dx计算方法有换元积分法,极坐标法等,定积分接触得多,不详说了∫(α→β) (1/2)[A(θ)]2 dθ = A(极坐标下的平面面积)二重积分:有两个自变量z = f(x,y)当被积函数为1时,就是面积(自由度较大)∫(a→b) ∫(c→d) dxdy = A(平面面积)当被积函数不为1时,就是图形的体积(规则)、和旋转体体积∫(a→b) ∫(c→d) dxdy = V(旋转体体积)计算方法有直角坐标法、极坐标法、雅可比换元法等极坐标变换:{ x = rcosθ{ y = rsinθ{ α≤θ≤β、最大范围:0 ≤θ≤ 2π∫(α→β) ∫(h→k) f(rcosθ,rsinθ) r drdθ三重积分:有三个自变量u = f(x,y,z)被积函数为1时,就是体积、旋转体体积(自由度最大)∫(a→b) ∫(c→d) ∫(e→f) dxdydz = V(旋转体体积)当被积函数不为1时,就没有几何意义了,有物理意义等计算方法有直角坐标法、柱坐标切片法、柱坐标投影法、球面坐标法、雅可比换元法等极坐标变化(柱坐标):{ x = rcosθ{ y = rsinθ{ z = z{ h ≤ r ≤ k{ α≤θ≤β、最大范围:0 ≤θ≤ 2π∫(α→β) ∫(h→k) ∫(z?→z?) f(rcosθ,rsinθ,z) r dzdrdθ极坐标变化(球坐标):{ x = rsinφcosθ{ y = rsinφsinθ{ z = rcosφ{ h ≤ r ≤ k{ a ≤φ≤ b、最大范围:0 ≤φ≤π{ α≤θ≤β、最大范围:0 ≤θ≤ 2π∫(α→β) ∫(a→b) ∫(h→k) f(rsinφcosθ,rsinφsinθ,rcosφ) r2sin2φ drdφdθ所以越上一级,能求得的空间范围也越自由,越广泛,但也越复杂,越棘手,而且限制比上面两个都少,对空间想象力提高了。
三重积分及其计算法二重积分的被积函数是一个二元函数,它的积分域是—平面区域.如果考虑三元函数f(x,y,z)在一空间区域(V)上的积分,就可得到三重积分的概念。
三重积分的概念设函数u=f(x,y,z)在空间有界闭区域(V)任意划分成n 个子域(△V 1),(△V 2),(△V 3),…,(△V n ),它们的体积分别记作△V k (k=1,2,…,n).在每一个子域上任取一点,并作和数如果不论△V k 怎样划分,点怎样选取,当n→+∞而且最大的子域直径δ→0时,这个和数的极限都存在,那末此极限就称为函数在域(V)上的三重积分,记作:即:如果f(x,y,z)在域(V)上连续,那末此三重积分一定存在。
对于三重积分没有直观的几何意义,但它却有着各种不同的物理意义。
直角坐标系中三重积分的计算方法这里我们直接给出三重积分的计算公式,具体它是怎样得来的,请大家参照有关书籍。
直角坐标系中三重积分的计算公式为:此公式是把一个三重积分转化为一个定积分与一个二重积分的问题,根据我们前面所学的结论即可求出。
例题:求,其中(V)是由平面x=0,y=0,z=0及x+y+z=1所围成的区域.解答:把I 化为先对z 积分,再对y 和x 积分的累次积分,那末应把(V)投影到xOy 平面上,求出投影域(σ),它就是平面x+y+z=1与xOy 平面的交线和x 轴、y 轴所围成的三角区域.我们为了确定出对z 积分限,在(σ)固定点(x,y),通过此点作一条平行于z 的直线,它与(V)上下边界的交点的竖坐标:z=0与z=1-x-y,这就是对z积分的下限与上限,于是由积分公式得:其中(σ)为平面区域:x≥0,y≥0,x+y≤1,如下图红色阴影部分所示:再把(σ)域上的二重积分化成先对y后对x的累次积分,得:柱面坐标系中三重积分的计算法我们先来学习一下空间中的点用极坐标的表示方法。
平面上点P可以用极坐标(ρ,θ)来确定,因此空间中的点P可用数组(ρ,θ,z)来表示.显然,空间的点P与数组(ρ,θ,z)之间的对应关系是一一对应关系,数组(ρ,θ,z)称为空间点P的柱面坐标.它与直角坐标的关系为:构成柱面坐标系的三族坐标面分别为:ρ=常数:以z轴为对称轴的同轴圆柱面族,θ=常数:通过z轴的半平面族,z=常数:与z轴垂直的平面族.因此,每三个这样的坐标面确定着空间的唯一的一点,由于利用了圆柱面,所以称为柱面坐标。
重积分知识点总结重积分是微积分中的一个重要概念,用于求解曲面、体积、质量等问题。
重积分包括二重积分和三重积分,分别对应二维和三维空间中的曲面和体积。
一、二重积分二重积分是对二维区域上的函数进行积分,常用于求解平面区域的面积、重心、质心等问题。
求解二重积分的方法有直接计算和变量代换两种。
1. 直接计算:将二重积分转化为累次积分,先对一个变量积分再对另一个变量积分。
需要注意的是积分的次序可能会影响结果。
2. 变量代换:通过变量代换,将原积分转化为更简单的形式。
常用的变量代换有极坐标代换、参数方程代换等。
二、三重积分三重积分是对三维空间内的函数进行积分,常用于求解空间区域的体积、质量、重心等问题。
求解三重积分的方法有直接计算和变量代换两种。
1. 直接计算:将三重积分转化为累次积分,先对一个变量积分再对另一个变量积分,最后再对剩下的变量积分。
同样,积分的次序可能会影响结果。
2. 变量代换:通过变量代换,将原积分转化为更简单的形式。
常用的变量代换有柱面坐标代换、球面坐标代换等。
三、重积分的应用重积分在物理学、工程学、经济学等领域中有广泛的应用。
1. 物理学:重积分可以用于计算物体的质量、质心、转动惯量等物理量。
例如,可以通过三重积分计算物体的质量分布情况,进而求解物体的质心位置。
2. 工程学:重积分可以用于计算三维物体的体积、表面积等。
例如,在建筑设计中,可以通过三重积分计算建筑物的体积,帮助设计师合理规划空间。
3. 经济学:重积分可以用于计算经济领域的总产出、总消费等指标。
例如,在城市规划中,可以通过二重积分计算城市的总人口、总收入等。
四、重积分的性质重积分具有一些重要的性质,如线性性、保号性、保序性等。
1. 线性性:重积分具有线性性质,即对于常数a和函数f(x, y)、g(x, y),有∬(af(x, y) + bg(x, y))dxdy = a∬f(x, y)dxdy + b∬g(x, y)dxdy。
第一部分 定积分的计算一、定积分的计算例1 用定积分定义求极限.)0(21lim 1>++++∞→a nn a a a a n . 解 原式=⎰∑=⋅⎪⎭⎫ ⎝⎛=∞→1011lim aani n x n n i dx =a a x a +=++11111.例2 求极限 ⎰+∞→1021lim xx n n dx . 解法1 由10≤≤x ,知nn x x x ≤+≤210,于是⎰+≤1210x x n ⎰≤1n x dx dx .而⎰10nx ()∞→→+=+=+n n n x dx n 0111101,由夹逼准则得⎰+∞→1021lim xx n n dx =0.解法2 利用广义积分中值定理()()x g x f ba⎰()()⎰=bax g f dx ξdx (其中()x g 在区间[]b a ,上不变号),().101111212≤≤+=+⎰⎰n n nn dx x dx xx ξξ由于11102≤+≤nξ,即211nξ+有界,()∞→→+=⎰n n dx x n01110,故⎰+∞→1021lim x x nn dx =0. 注 (1)当被积函数为()22,x a x R +或()22,a x x R -型可作相应变换.如对积分()⎰++3122112xxdx,可设t x tan =;对积分()02202>-⎰a dx x ax x a,由于()2222a x a x a x --=-,可设t a a x s i n =-.对积分dx e x ⎰--2ln 021,可设.sin t e x =-(2)()0,cos sin cos sin 2≠++=⎰d c dt td t c tb t a I π的积分一般方法如下:将被积函数的分子拆项,[分子]=A[分母]+B[分母]',可求出22d c bdac A ++=,22dc adbc B +-=. 则积分 ()220cos sin ln 2cos sin cos sin πππtd t c B A dt td t c t d t c B A I ++=+'++=⎰.ln2dc B A +=π例3 求定积分()dx x x x ⎰-1211arcsin分析 以上积分的被积函数中都含有根式,这是求原函数的障碍.可作适当变换,去掉根式. 解法1 ()dxx x x ⎰-1211arcsin 2t x xt ==12121211212arcsin arcsin arcsin 21arcsin 2tt d t dt tt ==-⎰⎰.1632π= 解法2 ()dx x x x⎰-1211arcsin .163cos sin cos sin 2sin 2242242πππππ==⋅=⎰u du u u uu u u x 小结 (定积分的换元法)定积分与不定积分的换元原则是类似的,但在作定积分换元()t x ϕ=时还应注意:(1)()t x ϕ=应为区间[]βα,上的单值且有连续导数的函数; (2)换限要伴随换元同时进行;(3)求出新的被尽函数的原函数后,无需再回代成原来变量,只要把相应的积分限代入计算即可.例4 计算下列定积分(1)⎰+=2031cos sin sin πx x xdx I , dx xx x I ⎰+=2032cos sin cos π; (2).1cos 226dx e xx ⎰--+ππ解 (1)⎰+=2031cos sin sin πxx xdxI)(sin cos cos 2023du uu uu x -+-=⎰ππ=.sin cos cos 223⎰=+πI dx xx x故dx xx xx I I ⎰++==203321cos sin cos sin 21π=()41cos cos sin sin 212022-=+-⎰ππdx x x x x . (2)=I .1cos 226dx e xx ⎰--+ππ()dxe xdu e uu x x u ⎰⎰--+=-+-=2262261cos 1cos ππππ⎥⎦⎤⎢⎣⎡+++=⎰⎰--2222661cos 1cos 21ππππdx e x dx e x e I x xx.3252214365cos cos 21206226πππππ=⨯⨯⨯===⎰⎰-xdxxdx这里用到了偶函数在对称取间上的积分公式以及公式:dx xdx n n⎰⎰=2020cos sin ππ()()()()()()⎪⎪⎩⎪⎪⎨⎧=⋅⨯-⨯--=⨯-⨯--=偶数奇数n n n n n n n n n n ,22421331,1322431π小结 (1)常利用线性变换把原积分化为可抵消或可合并的易于积分的形式。
积分区间为[0,a]时,设x a u =-;积分区间为[-a,a]时,设x u =-。
可使新的积分区间与原积分区间相同,以利于合并或产生原积分。
(2)利用例10.6(2)中同样的方法易得()()()()()()⎰⎰+=+2020cos sin cos cos sin sin ππdx x f x f x g dx x f x f x g例5 设()x f 在[]π,0上具有二阶连续导数,()3='πf ,且()()[]2cos 0=''+⎰xdx x f x f π,求().0f '解 ()()[]xdx x f x f cos 0⎰''+π()()()()()()()()20sin cos sin sin cos sin 00000='-'-='⋅+'+'⋅-='+=⎰⎰⎰⎰f f dx x f x x f x dx x f x x xf x f xd x d x f πππππππ故 ()().53220-=--='--='πf f小结 (1)定积分与不定积分的分部积分法有同样的选择dv u ,的原则; (2)当被积函数中含有抽象函数的导数形式时,常用分部积分法求解.例6 计算定积分xdx n ⎰π206sin (n 为自然数).解 x 6sin 是以π为周期的偶函数..8522143654sin 4sin 2sin 220622606πππππππn xdx n xdx n xdx n =⨯⨯⨯⋅====⎰⎰⎰-原式例7 证明积分()()⎰+∞++=0211αxx dxI 与α无关,并求值. 解 ()()⎰+∞++=0211αxx dxI ()()()()⎰⎰∞+∞+++=++=020211111ααααxx dxx t t dt t x t,于是 ()()()()⎥⎦⎤⎢⎣⎡+++++=⎰⎰∞+022111121αααx x dxx x x dx I .4arctan 21121002π==+=∞++∞⎰x xdx ┃ 小结 收敛的广义积分的计算和证明依据与定积分完全类似的换元积分法和分部积分法.二、含定积分的不等式的证明例8 证明(1)222121212≤≤⎰---dx e e x ;()*20sin 2sin >⎰+tdt e x xt π.证 (1)()2x ex f -=在⎥⎦⎤⎢⎣⎡-21,21上连续,令()()022=-='-x e x f x ,得0=x .比较212121-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-e f f 与()10=f 的大小,知在⎥⎦⎤⎢⎣⎡-21,21上的最大值为()10==f M ,最小值为2121-=⎪⎭⎫⎝⎛=e f m ,故.22121212122121212=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--≤≤⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎰---M dx e m ex (2)由于t e t sin sin 以π2为周期, ()tdt e tdt ex F t x xtsin sin 20sin 2sin ⎰⎰=∆+ππ.sin sin 2sin 0sin tdt e tdt e t t ⎰⎰+=πππ而 udu e t u tdt e u t sin 2sin 0sin 2sin ⎰⎰---=ππππ令tdt e t sin 0sin ⎰--=π,因为 ()0sin sin sin >--t e e t t ,().,0π∈t所以 ()()0sin 0sin sin >-=⎰-tdt e e x F t t π ┃事实上,(2)中所给变上(下)限定积分与x 无关,仅为取正值的常数. 例9 设()x f 是[]1,0上单调减少的正值连续函数,证明 ()()dx x f dx x f ⎰⎰>βαααβ0().10<<<βα证 利用积分中值定理,()()dx x f dx x f ⎰⎰-βαααβ0()()()21ηαβαηαβf f --⋅= ()1,021<≤≤≤≤βηααη()()[]()02221>+-=ηαηηαβf f f (因为()x f 递减取正值).即 ()()dx x f dx x f ⎰⎰>βαααβ0().10<<<βα ┃例10 设()x f 在[]b ,0上连续且单调递增,证明:当b a ≤<0时,有 ()()().2200dx x f a dx x f b dx x xf ab ba ⎰⎰⎰-≥(10.1) 分析 将定积分不等式(10.1)视为数值不等式,可利用相应的函数不等式的证明方法证明。
将要证的不等式两端做差,并将b 换成u ,作辅助函数()u F ,即需证().0≥b F证 作()()()()dx x f a dx x f u dx x xf u F u aua ⎰⎰⎰+-=0022 ()b u a ≤≤, 则 ()()()()dx x f u uf u uf u F u⎰--='02121()()[]0210≥-=⎰udx x f u f (因为()x f 递增,()()0≥-x f u f ) 于是,由拉格朗日中值公式,有()()()()()().0≥-'=-'+=a b F a b F a F b F ζζ ().b a <<ζ即式(10.1)成立.例11 设()x f '在[]b a ,上连续,且()0=a f ,证明()()().max ,22x f M a b M dx x f b x a ba'=-≤≤≤⎰分析 利用条件,生成改变量,借助于拉格朗日中值公式估计().x f证 因为()x f '在[]b a ,上连续,故有界,即存在0>M ,使()M x f ≤',[]b a x ,∈ ()()()()()(),a x M f a x a f x f x f -≤'-=-=ξ 故()()dx x f dx x f bab a⎰⎰≤()().22a b M dx a x M ba-⋅=-≤⎰ ┃ 例12 设()x f 在[]a ,0上二阶可导,且()0≥''x f ,证明().20⎪⎭⎫⎝⎛≥⎰a af dx x f a分析 已知()x f 二阶可导,可考虑利用()x f 的一阶泰勒公式估计()x f ;又所证的不等式中出现了点2a ,故考虑使用20ax =处的泰勒公式. 证 ()x f 在2a处的一阶泰勒公式为 ()()222222⎪⎭⎫ ⎝⎛-''+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛'+⎪⎭⎫ ⎝⎛=a x f a x a f a f x f !ξ,其中,ξ在x 与2a之间.利用条件()0≥''x f ,可得 ()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛'+⎪⎭⎫ ⎝⎛≥222a x a f a f x f ,两边从0到a 取积分,得().222200⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛'+⎪⎭⎫ ⎝⎛≥⎰⎰a af dx a x a f a af dx x f a a┃小结 关于含定积分的不等式的证明,常用的有两种方法: (1) 利用定积分的保序性; (2) 利用积分上限函数的单调性.三、定积分的应用例13 求由曲线()0>=a a xy 与直线a x a x 2,==及0=y 所围成的图形分别绕x 轴、y 轴及1=y 旋转一周所成的旋转体的体积.xy=a图11—8yxOF G BAC(2a,0.5)D(a,1)解 (1)绕x 轴旋转,积分变量为[]a a x x 2,,∈ .2122a dx x a V aaππ=⎪⎭⎫⎝⎛=⎰(2)绕y 轴旋转 (3)绕y =1旋转解法1 取y 为积分变量,[]1,0∈y ,直线a x =及a x 2=和双曲线a xy =的交点D 及C 的纵坐标分别为1=y 和21=y .设平面图形CDFG ,BCGO 及ADFO (见图11—8)绕y 轴旋转而成的立体的体积分别为21,V V 和3V ,则所求旋转体的体积为 321V V V V -+=().2222221212a a a dy y a ππππ=-+⎪⎪⎭⎫ ⎝⎛=⎰ 解法2 取y 为积分变量,[]1,0∈y ,将[]1,0分成两部分区间:⎥⎦⎤⎢⎣⎡21,0和⎥⎦⎤⎢⎣⎡1,21.在⎥⎦⎤⎢⎣⎡21,0上,体积元素为 ()()[].322221dy a dy a a dV ππ=-=在⎥⎦⎤⎢⎣⎡1,21上,体积元素为 .1122222dy y a dy a a dV ⎪⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=πππ 故所求体积为dy y a dy a V ⎪⎪⎭⎫ ⎝⎛-+=⎰⎰11321212212ππ.22123222a a a πππ=+=解法3 选x 为积分变量,[]a a x 2,∈.将旋转体分割成以y 轴为中心的圆柱形薄壳,以薄壳的体积作为体积元素,这一方法称为柱壳法.对应于区间[]x x x ∆+,的窄曲边梯形可近似地看做高为xay =,宽为dx 的举矩形,它绕y 轴旋转而成的圆柱形薄壳的体积,即体积元素为.2dx xax dV ⋅=π因此有 .222222a adx dx xax V a a a a πππ==⋅=⎰⎰(3)绕1=y 旋转选x 为积分变量,[]a a x 2,∈.体积元素为 dx x a dV ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=2211π所求体积为 ⎰⎰⎪⎪⎭⎫⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=a a aadx x a x a dx x V 2222222911ππ .212ln 21ln 222⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⋅+=a x a x a aa π小结 (1)在直角坐标系中求旋转体体积时,被积函数总是正的,定限时要注意积分下限一定小于上限.(2)选取哪个变量作为积分变量,才能使运算更为简便,要根据具体问题,灵活选取.一般地若xOy 平面中的平面图形D 是由曲线()()x y x y 21,ϕϕ==()()()x x 12ϕϕ>与直线b x a x ==,所围成,则分别绕x 轴、y 轴旋转所得旋转体体积为()()[]()()[]⎰⎰-=-=bay bax xdx x x V dxx x V .2122122ϕϕπϕϕπ第二部分 二重(三重)积分一、重积分的计算及技巧总结计算二重积分的基本方法是化为二次积分,其关键是确定积分次序和确定积分限.所遵循的原则是:1. 直角坐标系下确定积分次序的原则(1)函数原则内层积分能够求出的原则.例如()()2,y e x g y x f =一定应先对x 积分,后对y 积分.例如()()y g xyy x f cos ,=一定应先对y 积分,后对x 积分.(2)区域原则若积分区域为Y 型(即用平行于x 轴的直线穿过区域D ,它与D 的边界曲线相交最多为两个点),应先对x 积分,后对y 积分.若积分区域为X 型(即用平行于y 轴的直线穿过区域D ,它与D 的边界曲线相交最多为两个点),应先对y 积分,后对x 积分.若积分区域既为X 型区域,又为Y 型区域,这时在函数原则满足的前提下,先对x 积分或先对y 积分均可以;在这种情况下,先对哪个变量积分简单,就先采用该积分顺序.(3)少分块原则在满足函数原则的前提下,要使分块最少,从而计算简单. 2.直角坐标系下化二重积分为二次积分时,确定积分限的原则 (1)每层积分的下限都应小于上限.(2)一般而言,内层积分限可以是外层积分变量的函数,也可以是常数. (3)外层积分限必须为常数.3.当二重积分的积分域D 为圆域、扇形域或圆环域,被积函数具有22y x +的函数形式,即()()22,y x f y x g +=时,可考虑用极坐标计算该二重积分.用极坐标计算二重积分一般均采用先r 后θ的积分次序. 4.极坐标下积分限的确定 当极点在积分域D 之外时 ()()()()⎰⎰⎰⎰=θθβαθθθσ21.sin ,cos ,r r Drdr r r f d d y x f当极点在积分域D 的边界曲线上时 ()()()⎰⎰⎰⎰=θβαθθθσr Drdr r r f d d y x f 0.sin ,cos ,当极点在积分域D 内时 ()()()⎰⎰⎰⎰=θπθθθσr Drdr r r f d d y x f 020.sin ,cos ,()()()()⎰⎰⎰⎰=θθπθθθσ21.sin ,cos ,20r r Drdr r r f d d y x f小结化二重积分为二次积分的关键在于确定二次积分的上、下限.确定积分限采用穿线法,若先对y后对x积分,则将积分区域投影在x轴上,可得x的变化范围.再过固定的x点作一平行于y轴的直线从下向上穿过区域D,则可得到y的变化范围.从而可将积分域D用不等式组表示出来,这种确定上、下限的方法比较直观.二重积分化为二次积分,一般而言,内层积分的上、下限是外层积分变量的函数或者常数,而外层积分的上、下限一定为常数.小结极坐标系下化二重积分为二次积分一般选择的积分次序是先r后θ,定限时仍采用“穿线法”。