10.第6章-空间问题

第四节实用艺术学习建议1．结合自己的亲身经历，理解建筑艺术的民族性与时代性特征。

2．在欣赏园林艺术时，不但要欣赏园林的自然美与建筑美，更应欣赏蕴藏其中的文化美。

3．认识工艺美术品是中华民族文化艺术宝库的重要组成部分。

4．了解现代设计在当代社会生产与生活中的重要作用。

一、实用艺术实用艺术，指实用与审美相结合的表现性空间艺术，主要包括建筑艺术、园林艺术、工艺美术与现代设计等。

实用艺术最基本的特征就是实用原则与美观原则相结合，既有实用价值，又有审美价值。

实用性与审美性紧密地结合在一起的艺术，它具有物质生产与艺术创作相统一的特征，实用的、材料的、结构的特点与装饰的、美化的、观赏的特点交融在一起，既具有物质的实用功能，又具有精神的愉悦功能，二者密不可分。

如果二者缺少了其中的任何因素，就不能称之为实用艺术。

在人类发展史上，最古老的原始艺术都是实用艺术。

随着物质技术的发展和社会的进步，实用物品越来越具有审美的性质，直至使少数实用艺术发展成为纯艺术品，另一部分实用艺术的装饰、美化、观赏、审美的特征也愈加明显。

物质生活与艺术创作的统一，技术（技巧）与艺术的统一，实用价值与审美价值的统一，这是实用艺术的基本特征，也是实用艺术与其他艺术根本区别之所在。

实用艺术属于视觉艺术空间艺术、静态艺术和表现艺术，有时又划属广义的造型艺术实用艺术通常有狭义和广义之分：狭义的专指那些运用一定造型手段和艺术技巧，对生活实用品和陈设品进行艺术加工的装饰艺术，如染织工艺、家具工艺、陶瓷工艺、装饰绘画、象牙雕刻、商业广告艺术等；广义的则指那些既能满足人们的实用需求，又能满足人们的审美需求，融科学与美学、技术与艺术于一体的作品，一般包括建筑、园林艺术、工艺（或工艺美术）、书法等。

在美学和艺术学里，人们常用后一种即广义的实用艺术的概念。

当然，广义的实用艺术包含了狭义的实用艺术在内。

实用艺术大多为劳动人民所直接创造，同人们的物质生活和精神生活息息相关。

第一章测试1.无线电波在自由空间中的传播速度与光速一样，都是大约_3*10°m/s 。

（）A:对B:错答案:A2.最常用和最基本的无线通信网络是（）。

A:星状网B:网状网C:环状网D:对等网答案:A3.半双工系统由于使用同一信道进行双向通信，因此节省了带宽。

（）。

A:错B:对答案:B4.无线电波在自由空间传播时不存在能量损耗，但是会因波的扩展而产生衰减。

（）A:错B:对答案:B5.单工通信只有从发射嚣到接收嚣一个方向，即消息只能单方向传输A:对B:错答案:A第二章测试1.我国附地公用峰窝数字移动通信网GSM，采用（）MHz频段。

A:1200B:900C:600D:1500答案:B2.下列（）是5G定义的新场景。

A:高清电视及视频业务场景B:海量机器类通信业务场景C:高可靠低延时连接业务场景D:增强型移动宽带业务场景答案:BCD3.下列（）是指第五代移动通信。

A:IMT-AdvancedB:IMT-2000C:LTE答案:B4.下列（）组织负责管理和协调国际无线电频资源的分配。

A:ITU-DB:ITU-RC:IETFD:ITU-T答案:B5.移动通信利用无线电波进行信息传输A:对B:错答案:A第三章测试1.LDPC具有（）特性A:很好的随机性B:复杂度低C:容易实现D:复杂度较高答案:ABC2.移动通信系统采用信道编码技术是为降低（）。

A:信道突发和随机差错B:网络编码差错C:语音编码差错答案:A3.通信是指消息由一地向另一地进行有效传输，为了提高数字通信抗干扰能力的编码统称为信源编码。

（）A:错B:对答案:A4.5G信道编码技术主要采用哪些?（）。

A:LDPCB:卷积码C:PolarD:Turbo答案:AC5.信道编码的特点包括发现和纠正差错，以提高信息码元传输的可靠性A:对B:错答案:A第四章测试1.下列（）不是多载波调制技术。

A:F-OFDMB:SCMAC:CDMAD:OFDMA答案:C2.5G新波形的选择方面出现了各种新的波形设计方案，主要包括基于滤波器的正交频分复用（F-OFDM）调制方案、基于滤波器组的多载波（FilterBank MultiCarrier，FBMC）调制方案、通用滤波器组多载波（UniversalFiltered MultiCarrier，UFMC）调制方案等。

西安市人民政府关于印发西安市地下空间开发利用管理办法的通知正文：---------------------------------------------------------------------------------------------------------------------------------------------------- 西安市人民政府关于印发西安市地下空间开发利用管理办法的通知（市政发〔2014〕10号）各区、县人民政府，市人民政府各工作部门，各直属机构：《西安市地下空间开发利用管理办法》已经2014年2月10日市政府第77次常务会议研究同意，现印发你们，请遵照执行。

西安市人民政府2014年3月17日西安市地下空间开发利用管理办法第一章总则第一条为合理开发利用地下空间资源，引导城市建设向立体空间发展，依据《中华人民共和国物权法》、《中华人民共和国城乡规划法》、《中华人民共和国土地管理法》、《中华人民共和国建筑法》、《中华人民共和国城市房地产管理法》、《中华人民共和国人防法》及《城市地下空间开发利用管理规定》等法律、法规，结合本市实际，制定本办法。

第二条本办法适用于西安市规划区内，地表以下的空间。

主要包括同一主体结合地面建筑一并开发建设的地下工程（以下简称“结建地下工程”），独立开发建设的地下工程（以下简称“单建地下工程”），以及管线敷设、道路交通、桩基等利用地下空间的建设工程。

城市轨道交通所涉及的地下空间，遵照《西安市城市轨道交通条例》执行。

城市地下交通干线、地下营业性设施、地下停车场、地下过街通道等城市地下空间的开发建设，其使用空间和设施应当兼顾人民防空工程的防护要求。

第三条地下空间的开发利用应坚持统一规划、综合开发、合理利用、以人为本、协调发展、依法管理的原则，坚持社会效益、经济效益和环境效益相结合，并充分考虑安全、防灾、应急避难等需要。

地下空间开发利用应当优先发展地下交通、市政共同沟、地下公共停车场等城市基础设施和公共服务设施，鼓励竖向分层、横向连通的立体综合开发。

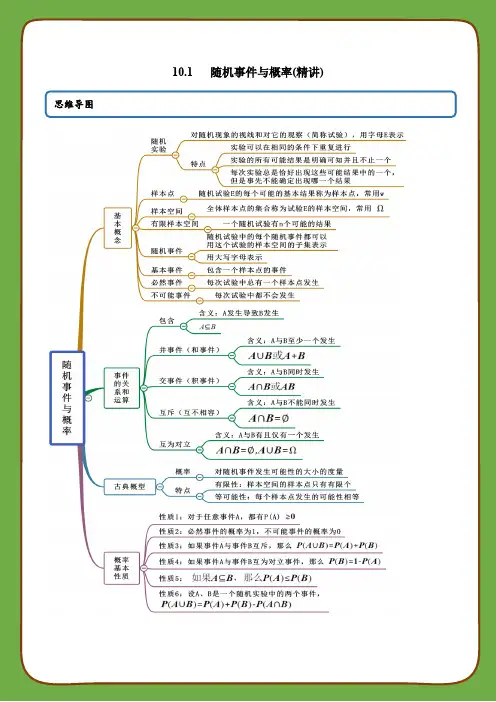
10.1 随机事件与概率(精讲)思维导图考法一 有限样本空间与随机事件【例1-1】(2021·全国高一)给出下列四个命题：①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件；②“当x 为某一实数时，可使x 2≤0”是不可能事件；③“明天天津市要下雨”是必然事件；④“从100个灯泡(含有10个次品)中取出5个，5个全是次品”是随机事件．其中正确命题的个数是( )A ．0B ．1C ．2D ．3 【答案】C【解析】对于①，三个球全部放入两个盒子，有两种情况：1+2和3+0，故必有一个盒子有一个以上的球，所以该事件是必然事件，①正确；对于②，x =0时x 2=0，所以该事件不是不可能事件，②错误； 对于③，“明天天津市要下雨”是偶然事件，所以该事件是随机事件，③错误；对于④，“从100个灯泡(含有10个次品)中取出5个，5个全是次品”，发生与否是随机的，所以该事件是随机事件，④正确．故正确命题有2个.故选：C ．【例1-2】(2020·全国高一)袋子中有4个大小和质地相同的球，标号为1，2，3，4，从中随机摸出一个球，记录球的编号，先后摸两次.(1)若第一次摸出的球不放回，写出试验的样本空间；(2)若第一次摸出的球放回，写出试验的样本空间.【答案】(1)详见解析(2)详见解析 【解析】m 表示第一次摸出球的编号，用n 表示第二次摸出球的编号，则样本点可用(),m n ，{},1,2,3,4m n ∈表示.(1)若第一次摸出的球不放回，则m n ≠，此时的样本空间可表示为()()()()()()()()()()()(){}1,2,1,3,1,4,2,1,,2,3,2,4,3,1,3,2,3,4,4,1,4,2,4,3Ω=，共有12个样本点.(2)若第一次摸出的球放回，则m ，n 可以相同.此时试验的样本空间可表示为(){}{},,1,2,3,4m n m n Ω=∈，常见考法共有16个样本点.【举一反三】1．(2021·全国高一课时练习)下列事件中，随机事件的个数为( )①连续两次抛掷一枚骰子，两次都出现2点向上；②13个人中至少有两个人生肖相同；③某人买彩票中奖；④在标准大气压下，水加热到90℃会沸腾.A ．1个B ．2个C ．3个D ．4个【答案】B【解析】抛掷一枚骰子，每一面出现都是随机的，所以①是随机事件；一年只有12生肖，所以13个人中至少有两个人生肖相同是必然事件，所以②是必然事件；购买彩票号码是随机的，某人买彩票中奖也是随机的，所以③是随机事件；在标准大气压下，水加热到100℃才会沸腾.故④是不可能事件故选：B2．(多选)(2020·全国高一单元测试)下列事件中，是随机事件的是( )A ．2021年8月18日，北京市不下雨B ．在标准大气压下，水在4C 时结冰C ．从标有1，2，3，4的4张号签中任取一张，恰为1号签D ．若x ∈R ，则20x ≥【答案】AC【解析】A 选项与C 选项为随机事件，B 为不可能事件，D 为必然事件．故选：AC ．3．(2020·全国高一课时练习)写出下列各随机试验的样本空间：(1)采用抽签的方式，随机选择一名同学，并记录其性别；(2)采用抽签的方式，随机选择一名同学，观察其ABO 血型；(3)随机选择一个有两个小孩的家庭，观察两个孩子的性别；(4)射击靶3次，观察各次射击中靶或脱靶情况；(5)射击靶3次，观察中靶的次数.【答案】(1)详见解析(2)详见解析(3)详见解析(4)详见解析(5)详见解析【解析】解：(1)一名同学的性别有两种可能结果：男或女.故该试验的样本室间可以表示为Ω={男，女}；(2)一名同学的血型有四种可能结果：A 型、B 型、AB 型、O 型.故该试验的样本空间可表示为{},,,A B AB O Ω=；(3)每个小孩的性别有男或女两种可能，两个小孩的性别情况有四种可能，故该试验的样本空间可表示为{(男、男)，(男，女)，(女，男)，(女，女)}；(4)每次射击有中靶或脱靶两种可能，射击3次有八种可能，用1表示中靶，用0表示脱靶，该试验的样本空间可表示为()()()()()()()(){}0,0,0,0,1,0,0,0,1,0,1,1,1,0,0,1,1,0,1,0,1,1,1,1N =；(5)射击3次，中靶的次数可能是0，1，2，3，故该试验的样本空间可以表示为{}0,1,2,3N =.4．(2021·全国高一)写出下列试验的样本空间：(1)设袋中装有4个白球和6个黑球，从中不放回逐个取出，直到白球全部取出为止，记录取球的次数；(2)甲、乙、丙三位同学参加演讲比赛，通过抽签确定演讲的顺序，记录抽签的结果.【答案】(1)详见解析(2)详见解析【解析】(1)从中不放回逐个取出，直到白球全部取出为止，则取球次数为{}4,5,6,7,8,9,10N =；(2)由抽签确定演讲的顺序，抽签的结果即样本空间可表示为{(甲，乙，丙)，(甲，丙，乙)，(丙，甲，乙)，(丙，乙，甲)，(乙，甲，丙)，(乙，丙，甲)}.考法二 事件的关系与运算【例2-1】(2020·全国高一课时练习)盒子里有6个红球，4个白球，现从中任取3个球.设事件A =“1个红球和2个白球”，事件B =“2个红球和1个白球”，事件C =“至少有1个红球”，事件D“既有红球又有白球”，则：(1)事件D 与事件,A B 是什么关系？(2)事件C 与事件A 的交事件与事件A 是什么关系？【答案】(1)D A B =⋃.(2)事件C 与事件A 的交事件与事件A 相等.【解析】(1)对于事件D ,可能的结果为1个红球和2个白球或2个红球和1个白球,故D A B =⋃.(2)对于事件C ,可能的结果为1个红球和2个白球,2个红球和1个白球或3个红球,故C A A ⋂=,所以事件C 与事件A 的交事件与事件A 相等.【例2-2】(2021·全国高一)掷一枚骰子，给出下列事件：A =“出现奇数点”，B =“出现偶数点”，C =“出现的点数小于3”. 求：(1)A B ，B C ⋂；(2)A B ，B C ⋃.【答案】(1)A B =∅，B C ⋂=“出现2点”. (2)A B =“出现1，2，3，4，5或6点”，B C =∪“出现1，2，4或6点”.【解析】由题意知：A =“出现奇数点”{}1,3,5=，B =“出现偶数点”{}2,4,6=，C =“出现的点数小于3”{}1,2=，(1)AB =∅，{}2BC ⋂==出现2点”； (2){}1,2,3,4,5,6A B ==“出现1，2，3，4，5或6点”，{}1,2,4,6B C ⋃==“出现1，2，4或6点”.【举一反三】1．(2020·全国高一课时练习)用红、黄、蓝三种不同的颜色给大小相同的三个圆随机涂色，每个圆只涂一种颜色.设事件A =“三个圆的颜色全不相同”，事件B =“三个圆的颜色不全相同”，事件C =“其中两个圆的颜色相同”，事件D“三个圆的颜色全相同”.(1)写出试验的样本空间.(2)用集合的形式表示事件,,,A B C D .(3)事件B 与事件C 有什么关系？事件A 和B 的交事件与事件D 有什么关系？并说明理由.【答案】(1)见解析；(2)见解析；(3)事件B 包含事件C ，事件A 和B 的交事件与事件D 互斥.见解析【解析】(1)由题意可知3个球可能颜色一样,可能有2个一样,另1个异色,或者三个球都异色.则试验的样本空间Ω={(红,红,红),(黄,黄,黄),(蓝,蓝,蓝),(红,红,黄),(红,红,蓝),(蓝,蓝,红),(蓝,蓝,黄),(黄,黄,红),(黄,黄,蓝),(红,黄,蓝)}.(2)A ={(红,黄,蓝)} B ={(红,红,黄),(红,红,蓝),(蓝,蓝,红),(蓝,蓝,黄),(黄,黄,红),(黄,黄,蓝),(红,黄,蓝)}C ={(红,红,黄),(红,红,蓝),(蓝,蓝,红),(蓝,蓝,黄),(黄,黄,红),(黄,黄,蓝)}.D {(红,红,红),(黄,黄,黄),(蓝,蓝,蓝)}.(3)由(2)可知事件B 包含事件C ,事件A 和B 的交事件与事件D 互斥.2．(2021·全国高一)记某射手一次射击训练中，射中10环、9环、8环、7环分别为事件A ，B ，C ，D ，指出下列事件的含义：(1)A B C ；(2)B C ∩；(3)B C D ∪∪.【答案】(1)射中10环或9环或8环.(2)射中9环.(3)射中10环或6环或5环或4环或3环或2环或1环或0环.【解析】(1)A=射中10环，B=射中9环，C=射中8环，∴A B C=∪∪射中10环或9环或8环. (2)C=射中8环，∴C=射中环数不是8环，则B C=∩射中9环.(3)B C D=∪∪射中9环或8环或7环，则B C D=∪∪射中10环或6环或5环或4环或3环或2环或1环或0环.3．(2021·全国高一)在试验“甲、乙、丙三人各射击1次，观察中靶的情况”中，事件A表示随机事件“甲中靶”，事件B表示随机事件“乙中靶”，事件C表示随机事件“丙中靶”，试用A，B，C的运算表示下列随机事件：(1)甲未中靶；(2)甲中靶而乙未中靶；(3)三人中只有丙未中靶；(4)三人中至少有一人中靶；(5)三人中恰有两人中靶.【答案】(1)A(2)AB(3)ABC(4)ABC(5)()()() ABC ABC ABC【解析】(1)甲未中靶：A.(2)甲中靶而乙未中靶：A B⋂,即AB.(3)三人中只有丙未中靶：A B C,即ABC.(4)三人中至少有一人中靶ABC.(5)三人中恰有两人中靶()()()ABC ABC ABC.考法三互斥与对立【例3】(多选)(2020·全国高一课时练习)袋中有红球3个，白球2个，黑球1个，从中任取2个，则互斥的两个事件是( )A．至少有一个白球与都是白球B．恰有一个红球与白、黑球各一个C．至少一个白球与至多有一个红球D．至少有一个红球与两个白球【答案】BD【解析】袋中装有红球3个、白球2个、黑球1个，从中任取2个，在A中，至少有一个白球和都是白球两个事件能同时发生，不是互斥事件，故A不成立.在B 中，恰有一个红球和白、黑球各一个不能同时发生，是互斥事件，故B 成立；在C 中，至少一个白球与至多有一个红球，能同时发生，故C 不成立；在D 中，至少有一个红球与两个白球两个事件不能同时发生，是互斥事件，故D 成立；故选：BD.【举一反三】1．(多选)(2020·全国高一课时练习)一个人连续射击2次，则下列各事件关系中，说法正确的是( )A ．事件“两次均击中”与事件“至少一次击中”互为对立事件B ．事件“恰有一次击中”与事件“两次均击中”互为互斥事件C ．事件“第一次击中”与事件“第二次击中”互为互斥事件D ．事件“两次均未击中”与事件“至少一次击中”互为对立事件【答案】BD【解析】对于A ，事件“至少一次击中”包含“一次击中”和“两次均击中“，所以不是对立事件，A 错误 对于B ，事件“恰有一次击中”是“一次击中、一次不中”它与事件“两次均击中”是互斥事件，B 正确 对于C ，事件“第一次击中”包含“第一次击中、第二次击中”和“第一次击中、第二次不中”，所以与事件“第二次击中”不是互斥事件，C 错误 对于D ，事件“两次均未击中”的对立事件是“至少一次击中”，D 正确故选：BD2．(多选)(2020·全国高一课时练习)下面结论正确的是( )A ．若()()1P A PB +=，则事件A 与B 是互为对立事件B ．若()()()P AB P A P B =，则事件A 与B 是相互独立事件C ．若事件A 与B 是互斥事件，则A 与B 也是互斥事件D ．若事件A 与B 是相互独立事件，则A 与B 也是相互独立事件【答案】BD【解析】对于A 选项，要使,A B 为对立事件，除()()1P A P B +=还需满足()0P AB =，也即,A B 不能同时发生，所以A 选项错误.对于C 选项，A 包含于B ，所以A 与B 不是互斥事件，所以C 选项错误.对于B 选项，根据相互独立事件的知识可知，B 选项正确.对于D 选项，根据相互独立事件的知识可知，D 选项正确.故选：BD3．(2020·全国高一课时练习)在试验E “连续抛掷一枚骰子2次，观察每次掷出的点数”中，事件A 表示随机事件“第一次掷出的点数为1”，事件j A 表示随机事件“第一次掷出的点数为1，第二次掷出的点数为j ，事件B 表示随机事件“2次掷出的点数之和为6”，事件C 表示随机事件“第二次掷出的点数比第一次的大3”，(1)试用样本点表示事件A B 与A B ；(2)试判断事件A 与B ，A 与C ，B 与C 是否为互斥事件；(3)试用事件j A 表示随机事件A .【答案】(1)详见解析(2)事件A 与事件B ，事件A 与事件C 不是互斥事件，事件B 与事件C 是互斥事件.(3)123456A A A A A A A =【解析】由题意可知试验E 的样本空间为Ω=()()()()()(){1,1,1,2,1,3,1,4,1,5,1,6,()()()()()()2,1,2,2,2,3,2,4,2,5,2,6,()()()()()()3,1,3,2,3,3,3,4,3,5,3,6,()()()()()()4,1,4,2,4,3,4,4,4,5,4,6,()()()()()()5,1,5,2,5,3,5,4,5,5,5,6,()()()()()()}6,1,6,2,6,3,6,4,6,5,6,6. (1)因为事件A 表示随机事件“第一次掷出的点数为1”,所以满足条件的样本点有()()()()()()1,1,1,2,1,3,1,4,1,5,1,6,即()()()()()(){}1,1,1,2,1,3,1,4,1,5,1,6A =.因为事件B 表示随机事件“2次掷出的点数之和为6”,所以满足条件的样本点有()()()()()1,5,2,4,3,3,4,2,5,1,即()()()()(){}1,5,2,4,3,3,4,2,5,1B =.所以(){}1,5A B =,()()()()()()()()()(){}1,1,1,2,1,3,1,4,1,5,1,6,2,4,3,3,4,2,5,1A B =.(2)因为事件C 表示随机事件“第二次掷出的点数比第一次的大3”,所以()()(){}1,4,2,5,3,6C =.因为(){}1,5A B =≠∅,(){}1,4A C =≠∅,B C =∅,所以事件A 与事件B ,事件A 与事件C 不是互斥事件,事件B 与事件C 是互斥事件.(3)因为事件j A 表示随机事件“第一次掷出的点数为1,第二次掷出的点数为j ”,所以(){}(){}(){}(){}(){}(){}1234561,1,1,2,1,3,1,4,1,5,1,6A A A A A A ======, 所以123456A A A A A A A =.考法四 古典概型【例4】(2020·全国高一课时练习)在一次语文考试的阅卷过程中，两位老师对一篇作文打出的分数都是两位的正整数，且十位数字都是5，则两位老师打出的分数之差的绝对值小于或等于1的概率为( )A ．0.18B ．0.2C ．0.28D ．0.32 【答案】C【解析】用(),x y 表示两位老师的打分，则(),x y 的所有可能情况有1010100⨯=种.当50x =时，y 可取50，51，共2种；当51x =，52，53，54，55，56，57，58时，y 的取值均有3种；当59x =时，y 可取58，59，共2种；综上可得两位老师打出的分数之差的绝对值小于或等于1的情况有28种，由古典概型的概率公式可得所求概率280.28100P ==故选：C. 【举一反三】1．(2020·全国高一课时练习)从数字1，2，3，4中任取两个数，则这两个数中其中一个数为另一个数的整数倍的概率为( )A ．14B ．12C ．13D ．23【答案】D【解析】基本事件为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6个，其中符合条件的基本事件为(1,2),(1,3),(1,4),(2,4)共4个，所求概率为4263P ==.故选：D 2．(2021·全国高一)把分别写有1，2，3，4的四张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么2，3连号的概率为( )A ．23B ．13C ．35D ．14【答案】B【解析】分三类情况，第一类1，2连号，则甲、乙、丙三个人拿到的卡片可能为()12,3,4，()12,4,3，()3,12,4，()4,12,3，()3,4,12，()4,3,12，有6种分法；第二类2，3连号，则甲、乙、丙三个人拿到的卡片可能为()1,23,4，()4,23,1，()23,1,4，()23,4,1，()1,4,23，()4,1,23，有6种分法；第三类3，4连号，则甲、乙、丙三个人拿到的卡片可能为()1,2,34，()2,1,34，()34,1,2，()34,2,1，()1,34,2，()2,34,1，有6种分法；共有18种分法，则2，3连号的概率为61183P ==. 故选：B .3．(2021·全国高一)为了更好了解某年入伍新兵的身高情况，解放军某部随机抽取100名新兵，分别对他们的身高进行了测量，并将测量数据分为以下五组：[160,165)，[165,170)，[170,175)，[175,180)，[180,185]进行整理，如下表所示：组号分组 频数 第1组 [160,165)5 第2组[165,170) 35 第3组 [170,175)30 第4组 [175,180)20 第5组 [180,185]10 合计 100(1)在下面的图纸中，画出频率分布直方图；(2)若在第4，5两组中，用分层抽样的方法抽取6名新兵，再从这6名新兵中随机抽取2名新兵进行体能测试，求这2名新兵来自不同组的概率．【答案】(1)直方图见解析；(2)815.【解析】(1)频率分布直方图如下图所示：（2）因为第4，5组共有30名新兵，所以利用分层抽样从中抽取6名，每组应抽取的人数分别为：4组：206430⨯=名，第5组：106230⨯=名，设第4组抽取的4名新兵分别为1A，2A，3A，4A，第5组抽取的2名新兵分别为1B，2B．从这6名新兵中随机抽取2名新兵，有以下15种情况：12{,}A A，13{,}A A，14{,}A A，11{,}A B，12{,}A B，23{,}A A，24{,}A A，21{,}A B，22{,}A B，34{,}A A，31{,}A B，32{,}A B，41{,}A B，42{,}A B，12{,}B B，这2名新兵来自不同组的情况有以下8种：11{,}A B，12{,}A B，21{,}A B，22{,}A B，31{,}A B，32{,}A B，41{,}A B，42{,}A B，故所求的概率P=815．考法五概率的基本性质【例5-1】(2020·全国高一课时练习)老师讲一道数学题，李峰能听懂的概率是0.8，是指( )A ．老师每讲一题，该题有80%的部分能听懂，20%的部分听不懂B ．老师在讲的10道题中，李峰能听懂8道C ．李峰听懂老师所讲这道题的可能性为80%D ．以上解释都不对 【答案】C【解析】概率的意义就是事件发生的可能性大小，即李峰听懂老师所讲这道题的可能性为80%.故选：C 【例5-2】(2020·全国高一课时练习)在学校运动会开幕式上，100名学生组成一个方阵进行表演，他们按照性别(M (男)、F (女))及年级(1G (高一)、2G (高二)、3G (高三))分类统计的人数如下表：1G2G3GM 18 20 14 F17247若从这100名学生中随机选一名学生，求下列概率：()P M =____________，()P F =____________，()P MF =____________，()P MF =____________，()1P G =____________，()2P M G =____________，()3P FG =____________【答案】0.52 0.48 1 0 0.35 0.76 0.07 【解析】()()123182014520.52100100100100P M P MG MG MG ==++==； ()()10.48P F P M =-=； ()1P MF =；()()0P MF P =∅=；()()11118170.35100100P G P MG FG ==+=； ()()()()2220.520.440.200.76P MG P M P G P MG =+-=+-=；()370.07100P FG == 故答案为：(1)0.52；(2)0.48；(3)1；(4)0；(5)0.35；(6)0.76；(7)0.07 【举一反三】1．(2020·全国高一课时练习)在北京消费季活动中，某商场为促销举行购物抽奖活动，规定购物消费每满200元就可以参加一次抽奖活动，中奖的概率为110.那么以下理解正确的是( ) A ．某顾客抽奖10次，一定能中奖1次 B ．某顾客抽奖10次，可能1次也没中奖 C ．某顾客消费210元，一定不能中奖 D ．某顾客消费1000元，至少能中奖1次 【答案】B 【解析】中奖概率110表示每一次抽奖中奖的可能性都是110，故不论抽奖多少次，都可能一次也不中奖， 故选：B.2．(2020·全国高一课时练习)某射击运动员平时训练成绩的统计结果如下： 命中环数 6 7 8 9 10 频率0.10.150.250.30.2如果这名运动员只射击一次，以频率作为概率，求下列事件的概率； (1)命中10环；(2)命中的环数大于8环； (3)命中的环数小于9环； (4)命中的环数不超过5环.【答案】(1)0.2 (2)0.5 (3)0.5 (4)0 【解析】用x 表示命中的环数，由频率表可得. (1)(10)0.2P x ==；(2)(8)P x P >=(9x =或10x =)(9)(10)0.30.20.5P x P x ==+==+=； (3)(9)(6)(7)(8)0.10.150.250.5P x P x P x P x <==+=+==++=； (4)(5)1(6)1(0.10.150.250.30.2)0P x P x =-=-++++=.3．(2021·全国高一课时练习)判断下列说法是否正确，若错误，请举出反例 (1)互斥的事件一定是对立事件，对立事件不一定是互斥事件； (2)互斥的事件不一定是对立事件，对立事件一定是互斥事件；(3)事件A 与事件B 中至少有一个发生的概率一定比A 与B 中恰有一个发生的概率大；(4)事件A 与事件B 同时发生的概率一定比A 与B 中恰有一个发生的概率小.【答案】(1)错误，举例见解析；(2)正确；(3)错误，举例见解析；(4)错误，举例见解析. 【解析】(1)错误；(2)正确；(3)错误：(4)错误. 设某试验的样本空间为{1,2,3,4}Ω=.(1)中反例，取{1},{2}A B ==，则A ,B 互斥但不对立. (2)由互斥事件与对立事件的定义可知(2)正确(3)中反例，取{1},A B ==∅,则1()()4P A B P A ⋃==1()()()4P AB AB P AB P A ⋃===. (4)中反例，取{1},{1,2}A B ==,则1()()4P AB P A ==,1()()4P AB AB P AB ⋃==.4．(2020·全国高一课时练习)甲、乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，乙的中靶概率为0.9，求下列事件的概率： (1)两人都中靶； (2)恰好有一人中靶； (3)两人都脱靶； (4)至少有一人中靶.【答案】(1)0.72 (2)0.26 (3)0.02 (4)0.98【解析】设A =“甲中靶”, B =“乙中靶”,则A =“甲脱靶”,B =“乙脱靶”,由于两个人射击的结果互不影响,所以A 与B 相互独立,A 与B ,A 与B ,A 与B 都相互独立 由已知可得,()()()()0.8,0.9,0.2,0.1P A P B P A P B ====. (1)AB = “两人都中靶”,由事件独立性的定义 得()()()0.80.90.72P AB P A P B =⋅=⨯= (2)“恰好有一人中靶” ABAB =,且AB 与AB 互斥根据概率的加法公式和事件独立性定义,得()()()P ABAB P AB P AB=+()()()()P A P B P A P B =⋅+⋅ 0.80.10.20.90.26=⨯+⨯=(3)事件“两人都脱靶”AB =, 所以()()()P AB P A P B =⋅()()10.810.90.02=-⨯-=(4)方法1：事件“至少有一人中靶”AB ABAB =,且AB ,AB 与AB 两两互斥,所以()P ABAB AB()()()P AB P AB P AB =++ ()()P AB P ABAB =+0.720.260.98=+=方法2：由于事件“至少有一人中靶”的对立事件是“两人都脱靶” 根据对立事件的性质,得事件“至少有一人中靶”的概率为()110.020.98P AB -=-=5．(2020·全国高一课时练习)已知n 是一个三位正整数，若n 的个位数字大于十位数字，十位数字大于百位数字，则称n 为“三位递增数”(如135，256，345等)现要从甲乙两名同学中，选出一个参加某市组织的数学竞赛，选取的规则如下：从由1，2，3，4，5，6组成的所有“三位递增数”中随机抽取1个数，且只抽取1次，若抽取的“三位递增数”是偶数，则甲参加数学竞赛；否则，乙参加数学竞赛.(1)由1，2，3，4，5，6可组成多少“三位递增数”？并一一列举出来. (2)这种选取规则对甲乙两名学生公平吗？并说明理由. 【答案】(1)见解析；(2)不公平，理由见解析.【解析】(1)由题意知，所有由1，2，3，4，5，6组成的“三位递增数共有20个.分别是123，124，125，126，134，135，136，145，146，156，234，235，236，245，246，256，345，346，356，456.(2)不公平由(1)知，所有由1，2，3，4，5，6组成的“三位递增数”有20个，记“甲参加数学竟赛”为事件A ，记“乙参加数学竞赛”为事件B.则事件A 含有基本事件有：124，134，234，126，136，146，156，236，246，256，346，356，456共13个. 由古典概型计算公式，得13()20A P A ==事件含有的基本事件的个数试验所有基本事件的总数，又A 与B 对立，所以137()1()12020P B P A =-=-=， 所以()()P A P B >.故选取规则对甲、乙两名学生不公平.。

绪论单元测试1.数据在计算机存储器内表示时，物理地址与逻辑地址相同并且是连续的，称这为( )。

A:顺序存储结构B:链式存储结构C:存储结构D:逻辑结构答案:A2.算法的时间复杂度取决于（）。

A:问题的可解性B:待处理数据的初态C:问题的复杂度D:问题的规模答案:BD3.从逻辑上可以把数据结构分为( )。

A:非线性结构B:物理结构C:线性结构D:静态结构答案:AC4.除了考虑存储数据结构本身所占用的空间外,实现算法所用辅助空间的多少称为算法的( )。

A:空间效率B:软件效率C:硬件效率D:时间效率答案:A5.链式存储的存储结构所占存储空间( )。

A:分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针B:只有一部分,存储表示结点间关系的指针C:分两部分,一部分存放结点值,另一部分存放指向下一结点的地址D:只有一部分,存放结点值答案:AC6.设语句X++的时间是单位时间,则语句。

for(I=1;I＜=n;I++)x++;的时间复杂度为( )A:O(n3)B:O(n2)C:O(n)D:O(1)答案:C7.对一个算法的评价，不包括如下（）方面的内容。

A:时空复杂度B:健壮性和可读性C:计算性D:并行性答案:CD8.以下数据结构中哪一个是非线性结构 ( )A:二叉树B:队列C:线性表D:栈答案:A9.逻辑结构与数据元素本身的内容和形式无关（）A:对B:错答案:A10.基于某种逻辑结构之上的基本操作，其实现是唯一的。

（）A:对B:错答案:B第一章测试1.非空的循环单链表head的尾结点（由p指向）满足（）。

A:p→next==headB:p==NULLC:p==headD:p→next==NULL答案:A2.带头结点head的单链表为空的判定条件是（）。

A:head-＞next==headB:head-＞next==NULLC:head!==NULLD:head==NULL答案:B3.在长度为n的顺序表的第i个位置上插入一个元素（1≤ i ≤n+1），元素的移动次数为（）。

第一章测试1【判断题】(10分)传统大地测量方法可以建立地心坐标系A.错B.对2【判断题】(10分)传统大地测量无法建立全球统一的坐标框架A.错B.对3【判断题】(10分)传统大地测量方法可以同时测定点的三维坐标A.对B.错4【判断题】(10分)采用日夜对称观测的方法可以消除旁遮光的影响A.错B.对5【单选题】(10分)下面反映地球自转轴在本体内的运动状况的是A.岁差B.章动C.格林尼治真恒星时角D.极移值6【多选题】(10分)下面属于空间大地测量范畴的是A.VLBIB.卫星测高C.GNSSD.遥感成像7【判断题】(10分)卫星测高不属于空间大地测量范畴A.错B.对8【判断题】(10分)利用空间大地测量技术不能确定精确的大地水准面差距A.错B.对9【判断题】(10分)空间大地测量技术能够确定地心坐标A.错B.对10【单选题】(10分)利用下面卫星数据解算重力场模型解算精度最低的是A.GRACEB.测高卫星C.CHAMPD.GOCE第二章测试1【判断题】(10分)地球自转是建立世界时的时间基准A.对B.错2【判断题】(10分)在常用的时间系统中，原子时最精确A.对B.错3【单选题】(10分)在常用的时间系统中，最精确的时间系统为A.历书时B.原子时C.太阳时D.世界时4【判断题】(10分)频率准确度反映时钟的系统性误差A.错B.对5【判断题】(10分)频率稳定度反映了钟的系统误差A.对B.错6【多选题】(10分)下列属于太阳时的时间系统包括A.平太阳时B.真太阳时C.民用时D.世界时7【判断题】(10分)协调世界时与世界时之间时刻差需要保持在0.9s以内，否则将采取闰秒进行调整A.对B.错8【判断题】(10分)GLONASS时属于原子时，不需要闰秒A.错B.9【多选题】(10分)下面不需要闰秒的时间系统为A.TALB.UTCC.GLONASSD.GPS时10【多选题】(10分)各国使用的历法主要包括A.阴历B.阴阳历C.儒略日D.阳历第三章测试1【判断题】(10分)赤道岁差可以使春分点的位置西移A.错B.对2【判断题】(10分)固定平纬由于采用了周期为6天的数据来计算点的纬度，因此要比历元平纬稳定A.错B.对3【判断题】(10分)固定平极由于采用了固定平纬来计算极移位置，因此要比历元平极稳定A.错B.对4【判断题】(10分)瞬时天球赤道坐标系的三个坐标轴都是固定的A.对B.错5【判断题】(10分)协议天球坐标系现有两个，分别是J1950.0和J2000.0A.错B.对6【判断题】(10分)J2000.0为现在用的空固系，将来也有可能被淘汰A.错B.对7【单选题】(10分)在进行卫星轨道积分时所采用的坐标系统为A.地心天球坐标系B.国际地球坐标系C.参心坐标系D.站心天球坐标系8【判断题】(10分)CGCS2000是一个基于GPS定位技术建立起来的全球性的地心坐标系A.错B.对9【多选题】(10分)下列属于地心坐标系的是A.WGS84B.BJ54C.ICRSD.CGCS200010【单选题】(10分)从观测瞬间的真地球坐标系转换到观测瞬间的真天球坐标系，需要进行的转换是A.极移矩阵B.旋转GST角C.岁差矩阵D.章动矩阵第四章测试1【判断题】(10分)射电望远镜进行天体测量时的角分辨率和射电望远镜的口径成正比A.错B.对2【判断题】(10分)射电望远镜进行天体测量时的角分辨率和无线电信号的波长成正比A.对B.错3【单选题】(10分)下面需要将射电望远镜用电缆连接起来的是A.空间甚长基线干涉测量B.联线干涉测量C.e-VLBID.甚长基线干涉测量4【判断题】(10分)甚长基线干涉测量不需要电缆将两望远镜连接起来A.错B.对5【判断题】(10分)VLBI观测所需的时间和频率信号由各自独立的氢原子钟提供A.对B.错6【判断题】(10分)延迟量和延迟率的观测精度与系统的信噪比成正比A.错B.对7【判断题】(10分)目前世界上最大的单口径射电望远镜在中国贵州A.对B.错8【判断题】(10分)馈源质量的好坏影响天线的噪声A.错B.对9【单选题】(10分)VLBI系统的接收机的混频器的主要作用是将射频信号转换为A.低频信号B.高频信号C.中频信号D.基频信号10【判断题】(10分)VLBI不能用来进行人造飞行器定轨A.对B.错第五章测试1【判断题】(10分)目前部分SLR跟踪站可以在白天工作A.错B.对2【多选题】(10分)专门用于地球动力学应用和大地测量的专用卫星包括A.Etalon-2B.Lageos-1C.Etalon-1D.Lageos-23【单选题】(10分)我国的SLR数据处理中心在A.长春B.上海C.武汉D.北京4【判断题】(10分)SLR跟踪站在全球的分布相对于GPS较均匀A.错B.对5【判断题】(10分)在IERS官网不能查到SLR跟踪站的坐标A.错B.6【判断题】(10分)在利用SLR进行卫星定轨时，太阳辐射压也是一重要摄动因素，辐射压的大小和卫星的面质比成正比A.错B.对7【判断题】(10分)在利用SLR进行卫星定轨时，大气阻力的大小和卫星的面质比成正比A.对B.错8【判断题】(10分)人卫激光测距不能用来测定地球质心的位置A.B.对9【判断题】(10分)用于测月的激光测距仪的指向精度要比用于测卫星的激光测距仪的指向精度要低A.错B.对10【单选题】(10分)下面月球表面放置的SLR激光反射器不能工作的是A.Apollo15B.Lunakhod1C.Apollo14D.Lunakhod2第六章测试1【多选题】(10分)在卫星轨道误差中，需要考虑的误差源主要包括A.大气传播延迟B.跟踪站坐标误差C.海洋潮汐D.太阳光压E.固体潮汐F.重力场模型2【判断题】(10分)在进行测高数据误差改正时，卫星质心改正不用考虑A.对B.错3【判断题】(10分)在进行海面高的框架转换时，需要有四个参数A.对B.错4【判断题】(10分)在进行海面高的框架转换时，三个平移参数和一个偏差因子可以通过最小二乘的方法求得A.错B.对5【判断题】(10分)卫星从南半球向北半球运行在地面的投影轨迹称为降弧A.错B.对6【判断题】(10分)测高卫星每一周期相对应的弧的地面轨迹严格吻合A.对B.错7【判断题】(10分)利用测高数据可以计算垂线偏差A.对B.错8【判断题】(10分)利用测高数据不能反演海洋重力异常A.对B.错9【判断题】(10分)测高数据不能用来建立海洋大地水准面的数学模型A.对B.错10【单选题】(10分)一般把其他测高卫星的海面高都转换到下面哪颗卫星的框架下来A.T/PB.HY-2AC.Jason-3D.Jason-1第七章测试1【多选题】(10分)下面属于卫星重力探测任务的是A.GOCEB.GRACEA和GRACEBC.CHAMPD.GRACEFollow-on2【判断题】(10分)利用动力法测定地面点的重力属于重力力学反演问题A.错B.对3【判断题】(10分)利用卫星技术确定地球重力场属于重力力学正演问题A.错B.对4【判断题】(10分)解算的重力场模型的最高阶次与卫星的轨道高度没有关系A.对B.错5【多选题】(10分)卫星能量守恒法确定地球重力场包括A.基于单星的能量守恒法B.利用动力学法C.重力梯度测量D.基于双星的能量守恒法6【判断题】(10分)对于GRACE低-低卫星跟踪卫星任务，两颗卫星间的瞬时位差是恢复地球重力场的重要观测数据A.错B.对7【判断题】(10分)GOCE卫星不是采用重力梯度测量方式来确定地球重力场A.错B.对8【判断题】(10分)重力梯度测量不能利用差分加速度计测出重力位的二阶导数A.对B.错9【判断题】(10分)短波分量是重力场谱结构的主分量，精确确定重力场模型中的短波分量，就是为模型提供牢固和精密的框架A.对B.错10【判断题】(10分)GRACE双星计划能够反演重力场，但是由于其数据量稀少，因此不能提供短期至一天的时变重力场信息A.错B.对第八章测试1【单选题】(10分)下面不属于多普勒方式进行定位或定轨的系统为A.DORIS系统B.子午卫星C.GPSD.CICADA2【判断题】(10分)当信号源与信号接收器之间作背向运动时，接收的信号频率减小A.错B.对【判断题】(10分)当信号源与信号接收器之间作相向运动时，接收的信号波长压缩A.错B.对4【判断题】(10分)多普勒测量又称距离差测量A.错B.对5【判断题】(10分)利用多普勒计数不能确定两时刻的接收机与信标机之间的距离差A.对B.错6【判断题】(10分)DORIS系统的信标机在地面上，发射的信号由安装在卫星上的接收机接收。

高等代数例题第一章 多项式1．44P 2 （1）m 、p 、q 适合什么条件时，有231x mx x px q +-++2．45P 7 设32()(1)22f x x t x x u =++++，3()g x x tx u =++的最大公因式是一个二次多项式，求t 、u 的值。

3．45P 14 证明：如果((),())1f x g x =，那么(()(),()())1f x g x f x g x += 4．45P 18 求多项式3x px q ++有重根的条件。

5．46P 24 证明：如果(1)()n x f x -，那么(1)()n n x f x -6．46P 25 证明：如果23312(1)()()x x f x xf x +++，那么1(1)()x f x -，2(1)()x f x - 7．46P 26 求多项式1nx -在复数域内和实数域内的因式分解。

8．46P 28 （4）多项式1p x px ++ （p 为奇素数）在有理数域上是否可约？9．47P 1 设1()()()f x af x bg x =+，1()()()g x cf x dg x =+，且0ad bc -≠。

求证：11((),())((),())f x g x f x g x =。

10．48P 5 多项式()m x 称为多项式()f x ，()g x 的一个最小公倍式，如果（1）()()f x m x ，()()g x m x ； （2）()f x ，()g x 的任意一个公倍式都是()m x 的倍式。

我们以[(),()]f x g x 表示首项系数为1的那个最小公倍式。

证明：如果()f x ，()g x 的首项系数都为1，那么()()[(),()]((),())f xg x f x g x f x g x =。

11．设 m 、n 为整数，2()1g x x x =++除33()2mn f x xx =+-所得余式为 。

有限空间10项典型隐患清单
1.未对有限空间作业场所进行辨识，多处未设置明显安全警示标志，未建立健全有限空间台账并及时更新。

2.未落实作业审批制度，擅自进入有限空间作业。

3.实施有限空间作业前未在醒目位置设置警示标志，警示作业人员，防止无关人员进入。

4.未严格遵守“先通风、再检测、后作业”的原则。

未对有限空间采取通风措施，未对有限空间氧浓度、易燃易爆物质浓度、有毒有害气体浓度等指标进行检测并合格便开展作业。

5.作业过程中未采取通风措施，保持空气流通，未对作业场所中的危险有害因素进行定时检测或者连续监测。

当作业中断超过30分钟，未重新通风、检测合格后便进入作业。

6.作业人员未正确佩戴和使用劳动防护用品，未始终与监护人员保持联系。

未在发现有限空间内氧含量浓度过低或者有毒有害气体浓度过高时，立即停止作业，并撤离作业现场。

7.未落实有限空间作业安全管理特别措施要求。

8.未对有限空间进行分类分级管理。

9.未开展有限空间培训教育及应急演练。

10.涉及有毒有害和易燃易爆物质的有限空间，必须实行锁闭管理制度。

（锁闭管理对象不包括：法律法规标准中明令禁止锁闭的场所及锁闭后可能产生其他风险的场所）。

- 1 -。

一年级上册数学全册教案(西师)第一章：认识数字1-5教学目标：1. 让学生通过观察、操作、交流等活动，认识数字1-5。

2. 培养学生数数、识数的能力。

教学内容：1. 学习数字1-5的读写。

2. 通过实物、图片等引导学生理解数字1-5的意义。

3. 进行数数练习，培养学生数数的能力。

教学重点：1. 数字1-5的读写。

2. 理解数字1-5的意义。

教学难点：1. 数字5的写法。

2. 理解数字1-5的意义。

教学准备：1. 数字卡片。

2. 实物、图片等。

教学过程：1. 引导学生观察数字卡片，学习数字1-5的读写。

2. 通过实物、图片等引导学生理解数字1-5的意义。

3. 进行数数练习，培养学生数数的能力。

第二章：认识数字6-10教学目标：1. 让学生通过观察、操作、交流等活动，认识数字6-10。

2. 培养学生数数、识数的能力。

教学内容：1. 学习数字6-10的读写。

2. 通过实物、图片等引导学生理解数字6-10的意义。

3. 进行数数练习，培养学生数数的能力。

教学重点：1. 数字6-10的读写。

2. 理解数字6-10的意义。

教学难点：1. 数字10的写法。

2. 理解数字6-10的意义。

教学准备：1. 数字卡片。

2. 实物、图片等。

教学过程：1. 引导学生观察数字卡片，学习数字6-10的读写。

2. 通过实物、图片等引导学生理解数字6-10的意义。

3. 进行数数练习，培养学生数数的能力。

第三章：比较大小1. 让学生通过观察、操作、交流等活动，学会比较数字的大小。

2. 培养学生识数、比较的能力。

教学内容：1. 学习比较数字的大小。

2. 运用比较方法，解决实际问题。

教学重点：1. 学会比较数字的大小。

2. 运用比较方法，解决实际问题。

教学难点：1. 理解数字大小的概念。

2. 运用比较方法，解决实际问题。

教学准备：1. 数字卡片。

2. 实物、图片等。

教学过程：1. 引导学生观察数字卡片，学习比较数字的大小。

2. 通过实物、图片等引导学生运用比较方法，解决实际问题。

§10.1空间几何体的直观图、三视图及其应用对应学生用书第134页1.简单多面体的结构特征名称特征棱柱侧棱都互相平行,上下底面是全等的多边形棱锥底面是任意多边形,侧面是有一个公共顶点的三角形棱台由平行于底面的平面截棱锥得到,其上下底面是相似多边形2.旋转体的结构特征名称特征圆柱由矩形绕一边所在直线旋转一周得到圆锥由直角三角形绕一条直角边所在直线旋转一周得到圆台由直角梯形绕直角腰所在直线旋转一周或等腰梯形绕上下底边中心所在直线旋转半周得到,也可由平行于底面的平面截圆锥得到球由半圆面绕直径旋转一周或圆面绕直径旋转半周得到3.简单几何体的三视图简单几何体的三视图是用平行投影得到,这种投影下,与投影面平行的平面图形留下的影子,与平面图形的形状和大小是全等和相等的,三视图包括正(主)视图、侧(左)视图、俯视图.4.简单几何体的直观图简单几何体的直观图常用斜二测画法来画,基本步骤如下:画几何体的底在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x'轴、y'轴,两轴相交于点O',且使∠x'O'y'= 45°或135°,已知图形中平行于x轴、y轴的线段,在直观图中平行于x'轴、y'轴.已知图形中平行于x轴的线段,在直观图中长度不变,平行于y轴的线段,长度变为原来的一半面 画几何体的高在已知图形中过O 点作z 轴垂直于xOy 平面,在直观图中对应的z'轴,也垂直于x'O'y'平面,已知图形中平行于z 轴的线段,在直观图中仍平行于z'轴且长度 不变1.按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积的关系:S 直观图=√24S 原图形,S 原图形=2√2S 直观图.2.记住旋转体的一些常见结论 (1)球的三视图都是半径相等的圆.(2)水平放置的圆锥的正(主)视图和侧(左)视图均为全等的等腰三角形.(3)水平放置的圆台的正(主)视图和侧(左)视图均为全等的等腰梯形.(4)水平放置的圆柱的正(主)视图和侧(左)视图均为全等的矩形.3.正方体的截面情况:三角形,四边形(有菱形、矩形、梯形等),五边形,六边形.(1)三视图的长度特征:“长对正,宽相等,高平齐”,即正(主)视图和侧(左)视图一样高,正(主)视图和俯视图一样长,侧(左)视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法. (2)台体可以看成是由锥体截得的,但一定要强调截面与底面平行.(3)注意空间几何体的不同放置对三视图的影响. (4)几何体的展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.【概念辨析】1.关于空间几何体的结构特征,判断下面结论是否正确.(对的打“√”,错的打“×”)(1)棱柱的侧棱长都相等. ( ) (2)棱锥的侧棱长都相等.( ) (3)三棱台的上、下底面是相似三角形. ( ) (4)有的棱台的侧棱长都相等.( )答案 (1)√ (2)× (3)√ (4)√【对接教材】2.(人教A版必修2P15T2改编)下列几何体各自的三视图中,有且仅有两个视图相同的是().A.①②B.①③C.①④D.②④答案 D解析正方体的三视图都相同,而三棱台的三视图各不相同,圆锥和正四棱锥的正(主)视图和侧(左)视图相同,故选D.3.(人教A版必修2P8A组T1改编)下列说法中正确的是().A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有几何体的表面都能展开成平面图形D.棱柱的各条棱都相等答案 B解析棱柱的侧面都是四边形,A不正确;正方体和长方体都是特殊的四棱柱,B正确;不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;棱柱的各条棱并不是都相等,但棱柱的侧棱都相等,所以D不正确.【易错自纠】4.(2021江西南昌模拟)如图,在正四棱柱ABCD-A1B1C1D1中,P是平面A1B1C1D1内一点,则三棱锥P-BCD 的正(主)视图与侧(左)视图的面积之比为().A.1︰1B.2︰1C.2︰3D.3︰2答案 A解析根据题意,三棱锥P-BCD的正(主)视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高;侧(左)视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高.故三棱锥P-BCD的正(主)视图与侧(左)视图的面积之比为1∶1.故选A.5.某几何体的三视图如图所示(单位: cm),则该几何体的体积(单位: cm3)是().A.2B.4C.6D.8答案 C解析由三视图知该几何体是底面为直角梯形的直四棱柱,即如图所示的四棱柱A1B1C1D1-ABCD.×(1+2)×2=3.直四棱柱的高为2,所以体积V=3×2=6.故选C.由三视图可知S底面=12【真题演练】6.(2020年北京卷)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为().A.6+√3B.6+2√3C.12+√3D.12+2√3答案 D解析由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表×2×2×sin60°)=12+2√3.故选D.面积S=3×(2×2)+2×(12对应学生用书第136页空间几何体的结构特征【题组过关】1.给出下列四个命题:①有两个侧面是矩形的棱柱是直棱柱;②侧面都是等腰三角形的棱锥是正棱锥;③侧面都是矩形的直四棱柱是长方体;④若有两个侧面垂直于底面,则该四棱柱为直四棱柱.其中所有错误命题的序号是().A.②③④B.①②③C.①②④D.①②③④答案 D解析认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析,故①③错误,对等腰三角形的腰是否为侧棱未作说明,故②错误,平行六面体的两个相对侧面也可能与底面垂直且互相平行,故④错误,故选D.2.给出下列结论:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④用一个平面截圆锥,得到一个圆锥和一个圆台;⑤用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是球.其中正确结论的序号是.答案⑤解析①中这条边若是直角三角形的斜边,则得不到圆锥,①错误;②中这条腰若不是垂直于两底的腰,则得到的不是圆台,②错误;圆柱、圆锥、圆台的底面都是圆面,③错误;④中如果用不平行于圆锥底面的平面截圆锥,那么得到的不是圆锥和圆台,④错误;只有球满足任意截面都是圆面,⑤正确.3.如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正(主)视图是().答案 C解析可先作出三棱柱的正(主)视图,再删去三棱锥,只有选项C满足.点拨解决与空间几何体结构特征有关问题的技巧(1)紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.(2)通过反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.空间几何体的三视图【考向变换】考向1由几何体的直观图识别三视图(2018年全国Ⅲ卷)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是().答案 A解析两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A.故选A.点拨由几何体的直观图求三视图,注意正(主)视图、侧(左)视图和俯视图的观察方向,注意看到的部分用实线,不能看到的部分用虚线表示.【追踪训练1】(2021辽宁沈阳模拟)在正方体ABCD-A1B1C1D1中,E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧(左)视图为().答案 C解析过点A,E,C1的截面为AEC1F,如图,则剩余几何体的侧(左)视图为选项C中的图形.故选C.考向2已知三视图,判断几何体某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为().A.1B.2C.3D.4答案 C解析将三视图还原为直观图,几何体是底面为直角梯形,且一条侧棱和底面垂直的四棱锥,如图所示.易知,BC∥AD,BC=1,AD=AB=PA=2,AB⊥AD,PA⊥平面ABCD,故△PAD,△PAB为直角三角形,因为PA⊥平面ABCD,BC⊂平面ABCD,所以PA⊥BC,又BC⊥AB,且PA∩AB=A,所以BC⊥平面PAB,又PB⊂平面PAB,所以BC⊥PB,所以△PBC为直角三角形,容易求得PC=3,CD=√5,PD=2√2,故△PCD不是直角三角形,故选C.点拨由几何体的三视图还原几何体的形状,要熟悉柱、锥、台、球体的三视图,明确三视图的形成原理,结合空间想象将三视图还原为直观图.其步骤如下:(1)定底面:根据俯视图确定;(2)定棱及侧面:根据正(主)视图、侧(左)视图确定几何体的侧棱与侧面特征,调整实线、虚线对应棱的位置;(3)定形状:确定几何体的形状.【追踪训练2】一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则截去的几何体是().A.三棱锥B.三棱柱C.四棱锥D.四棱柱答案 B解析由三视图还原几何体如图所示,可知剩余几何体为直四棱柱ABEA1-DCFD1,截去的部分为三棱柱BB1E-CC1F.故选B.考向3已知几何体的某些视图,判断其他视图(2021唐山五校联考)如图所示的是一个空间几何体的正(主)视图和俯视图,则它的侧(左)视图为().答案 A解析由正(主)视图和俯视图可知,该几何体是由一个圆柱挖去一个圆锥构成的,结合正(主)视图的宽及俯视图的直径可知侧(左)视图应为A,故选A.点拨由几何体的部分视图画出剩余的视图,先根据已知的一部分视图,还原、推测其直观图的可能形式,然后再找其剩下部分视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分视图是否符合.【追踪训练3】(2021江西赣州模拟)在一个几何体的三视图中,正(主)视图和俯视图如图如示,则相应的侧(左)视图可以为().答案 D解析由正(主)视图和俯视图可以推测几何体为半圆锥和三棱锥的组合体(大致图形如图所示),且顶点在底面的射影恰好是底面半圆的圆心,可知侧(左)视图为等腰三角形,且轮廓线为实线,排除C.故选D.空间几何体的直观图【典例迁移】已知正三角形ABC的边长为a,那么△ABC的平面直观图△A'B'C'的面积为().A.√34a2B.√38a2C.√68a2D.√616a2答案 D解析如图①,②所示的分别是实际图形和直观图.由②可知,A'B'=AB=a ,O'C'=12OC=√34a ,在图②中作C'D'⊥A'B'于点D', 则C'D'=√22O'C'=√68a.所以S △A'B'C'=12A'B'·C'D'=12×a×√68a=√616a 2.【变式设问】本例改为“已知△ABC 的平面直观图△A 1B 1C 1是边长为a 的正三角形”,则原△ABC 的面积为 .答案√62a 2解析 如图,在△A 1D 1C 1中,由正弦定理a sin45°=xsin120°,得x=√62a ,所以S △ABC =12×a×√6a=√62a 2.点拨 (1)在斜二测画法中,要确定关键点及关键线段的位置,注意“三变”与“三不变”;平面图形的直观图,其面积与原图形的面积的关系是S 直观图=√24S 原图形.(2)在原图形中与x 轴或y 轴平行的线段,在直观图中与x'轴或y'轴平行,原图中不与坐标轴平行的线段可以先画出线段的端点再连线,原图中的曲线段可以通过取一些关键点,作出在直观图中的相应点后,用平滑的曲线连接而画出.【追踪训练4】已知梯形ABCD 是直角梯形,按照斜二测画法画出它的直观图A'B'C'D'(如图所示),其中A'D'=2,B'C'=4,A'B'=1,则DC 的长度是( ).A .√5B .2√2C .2√5D .√3答案 B解析 如图,在直角梯形ABCD 中,由斜二测画法,知AB=2,AD=2,BC=4, 所以DC=√AB 2+(BC -AD)2=√22+(4-2)2=2√2.故选B .对应学生用书第137页几何体表面上点到点的最短距离求几何体表面上点到点的最短距离,先将空间图形问题转化为平面图形问题,再求平面图形上两点之间的最短距离,通过把立体图形转化为平面图形,利用轴对称、平移或旋转几何图形的变换,运用“两点之间线段最短”来解决.一只蚂蚁从正方体ABCD-A 1B 1C 1D 1的顶点A 出发,经正方体的表面,按最短路线爬行到顶点C 1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正(主)视图的是( ).A .①②B .①③C .③④D .②④ 答案 D解析 由点A 经正方体的表面,按最短路线爬行到达顶点C 1的位置,共有6种路线(对应6种不同的展开方式),若把平面ABB 1A 1和平面BCC 1B 1展开到同一个平面内,连接AC 1,则AC 1是最短路线,且AC 1会经过BB 1的中点,此时对应的正(主)视图为②;若把平面ABCD 和平面CDD 1C 1展开到同一个平面内,连接AC 1,则AC 1是最短路线,且AC 1会经过CD 的中点,此时对应的正(主)视图为④.而其他几种展开方式对应的正(主)视图在题中没有出现.故选D .求几何体表面上点到点的最短距离的步骤如下:(1)将几何体剪开后展开,画出其侧面展开图; (2)将所求曲线问题转化为平面上的线段问题; (3)结合已知条件求结果.【突破训练】如图,一立在水平地面上的圆锥形物体的母线长为4 m,一只小虫从圆锥的底面圆上的点P 出发,绕圆锥表面爬行一周后回到点P 处.若该小虫爬行的最短路程为4√3 m,则圆锥底面圆的半径等于 m .答案43解析 把圆锥侧面沿过点P 的母线展开成如图所示的扇形, 由题意得OP=4,PP'=4√3, 则cos ∠POP'=42+42-(4√3)22×4×4=-12,所以∠POP'=2π3.设底面圆的半径为r ,则2πr=2π3×4,所以r=43.对应《精练案》第59页1.(2021南昌二中模拟)给出以下命题:①以直角梯形的一腰所在的直线为轴旋转一周所得的旋转体是圆台; ②圆柱、圆锥、圆台的底面都是圆面;③用一个平面去截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数为( ).A .0B .1C .2D .3答案 B解析 易知②正确,①③错误.2.(2021浙江嘉兴一中模拟)如图所示,一个水平放置的平面图形,其斜二测直观图是△OAB ,其中OB=AB=4,则该直观图所表示的平面图形的面积为( ).A .16√2B .8√2C .16D .8答案 A解析根据斜二测画法可知,该图的直观图为Rt△A'OB,且A'O=2AO=2×√42+42=8√2.×4×8√2=16√2.故选A.故直观图所表示的平面图形的面积为123.若某几何体的三视图如图所示,则这个几何体的直观图可以是().答案 B解析所给选项中,A,C两项的正(主)视图、俯视图不符合,D项的侧(左)视图不符合,只有B项符合题意.4.(2021山东济宁模拟)下面关于四棱柱的命题中,真命题的是().A.若有两个侧面垂直于底面,则该四棱柱为直四棱柱B.若两个过相对侧棱的截面都垂直于底面,则该四棱柱为正四棱柱C.若四个侧面两两全等,则该四棱柱为直四棱柱D.若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱答案 D解析A项错误,必须是两个相邻的侧面;B项错误,两个过相对侧棱的截面都垂直于底面可得到侧棱垂直于底面,则该四棱柱为直四棱柱;C项错误,反例,可以是斜四棱柱;D项正确,对角线两两相等,则两对角线所在的平行四边形为矩形,可得侧棱与底面垂直,则该棱柱为直四棱柱.故选D.5.如图,下面的几何体由一个正方体和两个圆柱体组成,则它的侧(左)视图是().答案 D解析从左边看,底层是一个正方形,正方形里面是一个内切圆,上层是一个正方形.故选D.6.(2021福建厦门模拟)如图所示的是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是().A.3B.2C.1D.0答案 A解析图①,②,③的正(主)视图和俯视图都与题图相同,故选A.7.(2021山东潍坊高三检测)等腰直角三角形的直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积为().A.√2πB.(1+√2)πC.√2π或2√2πD.√2π或(1+√2)π答案 D解析如果是绕直角边旋转,形成圆锥,那么圆锥底面半径为1,高为1,母线长为√2,所以所形成的几何体的表面积S=πrl+πr2=π×1×√2+π×12=(√2+1)π;,两个圆锥的母线长是1, 如果是绕斜边旋转,形成的是上、下两个圆锥,那么圆锥的半径是√22×1=√2π.所以形成的几何体的表面积S=2×πrl=2×π×√22综上可知,所形成几何体的表面积是(√2+1)π或√2π.故选D.8.已知三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧(左)视图是有一条直角边长为2的直角三角形,则该三棱锥的正(主)视图可能为().答案 C解析当正(主)视图为等腰三角形时,则高应为2,且应为虚线,排除A,D两项;当正(主)视图是直角三角形,由条件得一个直观图如图所示,中间的线是看不见的线PA形成的投影,应为虚线,故选C.9.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为.答案2√3解析由三视图还原得如图所示的四棱锥A-BCC1B1,易知,最长的棱为AC1,且AC1=√AC2+CC12=√(22+22)+22=2√3.10.在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2 cm,则在平面直角坐标系xOy中,四边形ABCO 为,面积为cm2.答案矩形8解析由斜二测画法的特点,知该平面图形的直观图的原图,即在平面直角坐标系xOy中,四边形ABCO 是一个长为4 cm,宽为2 cm的矩形,所以四边形ABCO的面积为8 cm2.11.(2021浙江宁波四中检测)如图所示的是水平放置的△ABC的直观图,D'是△A'B'C'中B'C'边上的一点,且D'C'<D'B',又A'D'∥y'轴,那么原△ABC的AB,AD,AC三条线段中().A.最长的是AB,最短的是ACB.最长的是AC,最短的是ABC.最长的是AB,最短的是ADD.最长的是AD,最短的是AC答案 C解析由题意得到原△ABC的平面图如图所示,其中,AD⊥BC,BD>DC,所以AB>AC>AD,所以△ABC的AB,AD,AC三条线段中最长的是AB,最短的是AD.故选C.12.(2021东北四市高三检测)如图,在正方体ABCD-A1B1C1D1中,P是线段CD的中点,则三棱锥P-A1B1A的侧(左)视图为().答案 D解析画出原正方体的侧(左)视图,显然对于三棱锥P-A1B1A,B(C)点均消失了,其余各点均在,从而其侧(左)视图为D.故选D.13.某多面体的三视图如图所示,其中正(主)视图和侧(左)视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为.答案12解析由三视图可知该多面体是一个组合体,下面为一个底面是等腰直角三角形的直三棱柱,上面为一个底面是等腰直角三角形的三棱锥,等腰直角三角形的腰长为2,直三棱柱的高为2,三棱锥的高为2,易知该×2=12.多面体有2个面是梯形,这些梯形的面积之和为(2+4)×2214.某几何体的一条棱长为√7,在该几何体的正视图中,这条棱的投影是长为a 的线段,在该几何体的侧(左)视图与俯视图中,这条棱的投影分别是长为√6和b 的线段,则a 2+b 2的值为 .答案 8解析 不妨设该几何体为底面是长方形,且一条侧棱垂直于底面的四棱锥,把它补全为一个长方体如图所示,设长方体的长、宽、高分别为m ,n ,k ,体对角线长为√7,体对角线在三个相邻面上的正投影长分别为a ,√6,b.则由题意,得√m 2+n 2+k 2=√7,√n 2+k 2=√6, 解得m=1或m=-1(舍去),所以{√k 2+1=a,√n 2+1=b,所以(a 2-1)+(b 2-1)=6,即a 2+b 2=8.15.(2021湖北襄阳高三模拟)如图,往透明塑料制成的长方体容器ABCD-A 1B 1C 1D 1内灌进一些水,固定容器一边BC 于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的命题是( ).A .水面EFGH 所在四边形的面积为定值B .随着容器倾斜度的不同,A 1C 1始终与水面所在平面平行 C .没有水的部分有时呈棱柱形有时呈棱锥形D .当容器倾斜至如图③所示时,BE ·BF 为定值答案 D解析 在图①中,水面EFGH 所在四边形的面积为棱柱底面的面积,在图②中,水面EFGH 所在四边形的面积大于原棱柱底面的面积,故A 项错误.在图①中,A 1C 1与水面所在平面平行,在图②,图③中,A 1C 1与水面所在平面均不平行,故B 项错误. 棱柱在绕BC 旋转的过程中,没有水的部分始终呈棱柱形,故C 项错误.在图③中,有水的部分形成一个直三棱柱,该三棱柱的底面为三角形,高为BC ,根据水的体积为定值可得底面三角形的面积为定值,故BE ·BF 为定值,故D 项正确.16.如图所示的是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是 .答案 3√3解析 作出直观图如图所示,通过计算可知AF ,DC 最长,且DC=AF=√BF 2+AB 2=3√3.17.如图所示的是△ABC 水平放置的直观图Rt △A'B'C',其中A'C'⊥B'C',B'O'=O'C'=1,则△ABC 的面积为( ). A .2√2 B .38C .4√23D .34答案 A解析 由直观图画法规则将△A'B'C'还原为△ABC ,如图所示,△ABC 是一个等腰三角形,则有BO=OC=B'O'=O'C'=1,AO=2A'O'=2√2. 所以S △ABC =12BC ·AO=12×2×2√2=2√2.18.(2021安徽合肥一中最后一卷)一个四棱锥的三视图如图所示,一只蚂蚁从该四棱锥底面上的一个顶点出发,经过四棱锥的侧面爬到与其不相邻的另一个顶点(同一条棱上的两个端点称为相邻顶点),则这只蚂蚁经过的最短路程为( ).A.1+√2B.√3C.√2+√3D.√3+√6答案 B解析四棱锥P-ABCD如图所示,PD⊥平面ABCD,BD⊥DC,底面为平行四边形,且PD=DC=1,AD=√2,PC=√2,PA=√3,①沿着侧面从A到C,若沿着侧面PAD与侧面PDC展成平面图形,则最短的路程为1+√2;若沿着侧面PAB与侧面PBC展成平面图形,则由余弦定理得最短路程为√3+√6.②沿着侧面从B到D,若沿着侧面PAB与侧面PAD展成平面图形,得最短路程为√3;若沿着侧面PBC与侧面PCD展成平面图形,则最短路程为√6+√2,2综上,最短路程为√3.故选B.。

《物流配送中心规划与设计》练习题第一章概述一、简答题1．配送中心与物流中心有什么不同？物流中心是综合性、地域性、少品种、大批量的物资位移集中地，它集商流、物流、信息流和资金流为一体，功能健全，具有一定的存储和调节能力，是产销企业间的物流桥梁和纽带。

配送中心是以组织配送型销售或供应，执行物流配送为主要职能的流通型结点，它既有集货中心（集零为整）的职能，又有分货中心(化整为零）的职能.为了优质、高效的配送，他还有较强的流通加工能力。

也可以说配送中心实际上是集货中心、分货中心和加工中心功能的高度综合。

与物流中心相比,配送中心具有规模小，多品种、小批量，专业性强，以配送功能为主、存储功能为辅等特点。

(1）从功能上看：物流中心可单可全，而配送中心较为全面；(2）从辐射范围来说：物流中心辐射范围大，而配送中心辐射范围小; （3）从在供应链的位置看:物流中心在配送中心的上游，而配送中心在物流中心的下游； (4) 从物流的特点看：物流中心是少品种、大批量、少供应商，而配送中心多品种、小批量、多供应商；(5）从服务的对象看：物流中心通常提供第三方物流服务,而配送中心一般为公司内部服务。

2．什么是第三方物流?第三方物流是指生产经营企业为集中精力搞好主业，把原来属于自己处理的物流活动，以合同方式委托给专业物流服务企业，同时通过信息系统与物流企业保持密切联系，以达到对物流全程管理控制的一种物流运作与管理方式。

3．现代物流中心的特征是什么？以对需求订单做出快速反应为首要条件，以提高物流服务水平为宗旨，以减少对各种需求订单的错误处理和缺货为控制要素，在此基础上，尽可能的优化物流管理，减少物流成本.物流反应快速化、物流功能集成化、物流服务系列化、物流作业规范化、物流目标系统化、物流手段现代化、物流组织网络化、物流经营市场化、物流信息电子化以及自动化、省力化的物流设备与技术、系统化的物流管理系统。

4．传统仓库的功能是什么？传统仓库是以提高商品的保管效率为中心,在仓库系统的内部,企业一般依赖于一个非自动化的、以纸张文件为基础的系统来记录、追踪进出的货物，以人为记忆实施仓库内部的管理。

专题10空间中的位置关系与夹角问题知识点一 直线与直线的位置关系⎩⎨⎧共面直线⎩⎪⎨⎪⎧平行直线相交直线异面直线：不同在任何一个平面内，没有公共点异面直线的公垂线定义:同时和两条异面直线垂直相交的直线，叫做异面直线的公垂线. 知识点二 平行与垂直的判定及性质 1．平行的判定文字语言图形语言符号语言判定定理 平面外一条直线与此平面内的一条直线平行，则直线与此平面平行．性质定理如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行．文字语言图形语言 符号语言判定定理 一个平面内有两条相交直线与另一个平面平行，则这两个平面平行性质定理如果两个平行平面同时与第三个平面相交，那么它们的交线平行2．垂直的判定（一）直线和平面垂直的定义直线l 与平面α内的任意一条直线都垂直，就说直线l 与平面α互相垂直文字语言图形语言符号语言判 定 定 理 一条直线与平面内的两条相交直线都垂直，则该直线与此平面垂直推论如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直这个平面性质定理垂直于同一个平面的两条直线平行文字语言图形语言符号语言判定定理 一个平面过另一个平面的一条垂线，则这两个平面互相垂直性质定理两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面【例 1】已知a ，b 为异面直线.对空间中任意一点P ,存在过点P 的直线 （ ）. A. 与a ，b 都相交 B. 与a ，b 都垂直 C. 与a 平行, 与b 垂直 D. 与a ，b 都平行【例 2】(青羊区校级模拟)在正四棱柱1111ABCD A B C D -中，14AA =，2AB =，点E ，F 分别为棱1BB ，1CC 上两点，且114BE BB =，112CF CC =，则（ ） A ．1D E AF ≠，且直线1D E ，AF 异面 B ．1D E AF ≠，且直线1D E ，AF 相交 C ．1D E AF =，且直线1D E ，AF 异面D ．1DE AF =，且直线1D E ，AF 相交【例3】(翠屏区校级月考)已知α，β是两个不重合的平面，直线a α⊂，:p a β∥，:q αβ∥，则p 是q 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【例4】(2018•浙江卷)已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m ∥n ”是“m ∥α”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【例5】(2021•浙江卷)如图，已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则（ ） A ．直线1A D 与直线1D B 垂直，直线MN ∥平面ABCDB ．直线【解析】由αβ∥，直线a α⊂，可得a β∥，反之不成立，α与β可能相交．p ∴是q 的必要不充分条件．故选：B ．1A D 与直线1D B 平行，直线MN ⊥平面11BDD B C ．直线1A D 与直线1D B 相交，直线MN ∥平面ABCD D ．直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B【例6】(2021•新高考Ⅱ卷)如图，下列正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点，则满足MN OP ⊥的是（ ）A ．B ．C ．D ．【例7】(青岛二模)已知正方体1111ABCD A B C D -，动点P 在线段BD 上，则下述正确的是（ ） A ．11PC AD ∥ B ．11PC AC ⊥ C ．1PC ⊥平面1A BDD ．1PC ∥平面11AB D【解题总结】几个常用的结论：（1）过空间任一点有且只有一条直线与已知平面垂直；（2）过空间任一点有且只有一个平面与已知直线垂直；（3）垂直于同一平面的两条直线互相平行；（4）垂直于同一直线的两个平面互相平行．（5）此类判断题要警惕“线在面内”的特殊情况．【例8】(金东区校级期中)如图，在三棱柱111ABC A B C -中，1AA ⊥面ABC ，122AB BC BB ===，90ABC ∠=︒，D 为BC 的中点．求证：1A B ∥平面1ADC ；【例9】(沙坪坝区校级模拟)如图，在三棱柱111ABC A B C -中，ABC △是边长为4的等边三角形，D 是BC 的中点，123C D =．（1）求证：1A B ∥平面1AC D ；【例10】在正方体1111ABCD A B C D -中, E 是AB 的中点,点F 在1CC 上, 且12CF FC =. 若点P 是侧面11AA D D 上一动点,且1PB ∥平面DEF , 则tan ABP ∠的取值范围是 ．【例11】(日照一模)如图所示，在四棱锥P ABCD -中，AD BC ∥，AD DC ⊥，PA AB ⊥，12BC CD AD ==，E 是边AD 的中点，异面直线PA 与CD 所成角为2π． （1）在平面PAB 内找一点M ，使得直线CM ∥平面PBE ，并说明理由；【例12】(鹤壁模拟)如图，在多面体ABCDEF 中，底面ABC 是边长为2的等边三角形．AD ⊥底面ABC ，AD BE CF ∥∥，4AD =，3CF =，45DAE ∠=︒． （1）证明：AE DF ⊥；【例13】(2022•全国甲卷)在四棱锥P ABCD -中，PD ⊥底面ABCD ，//CD AB ，1AD DC CB ===，2AB =，3DP（1）证明：BD PA ⊥； 【解题总结】线面与面面垂直的题型最终都归结在线线垂直的证明，而显现垂直的思路可总结为： 证明12l l ⊥，先看两直线的位置关系，如果：⎧⎪⇒⎨⎪⎩三线合一（有等腰三角形就必用）共面勾股定理（题目中线段数据多）其他（初中平面几何学习的其他垂直证明方法）⇒⇒⇒异面考虑用线面垂直推导异面垂直找重垂线在重垂线对应平面内找垂直知识点三 投影与三垂线定理 1.投影的概念光是直线传播的，由于光的照射，在不透明物体后面的屏幕上会留下这个物体的影子，这种现象叫 做投影.其中的光线叫做投影线，留下物体影子的屏幕叫做投影面.2.投影的分类:(1)中心投影:把光由一点向外散射形成的投影叫做中心投影.(2)平行投影:把在一束平行光线照射下形成的投影叫做平行投影.在平行投影中，投影线正对着(即垂直)投影面时叫做正投影，否则叫做斜投影. 高中阶段我们只考虑正投影. 3.正投影的性质:(1)直线或线段的平行投影仍然是直线或线段. (2)平行直线的平行投影是平行或是重合的.(3)平行于投射面的线段，它的投影与这条线段平行且等长. (4)与投射面平行的图形，它的投影与这个图形全等.(5)在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比.注：在立体几何中，通常会运用到直线或线段的投影，只需找直线或线段中两个不重合的点，分别向平面做垂线，垂足间的连线即为投影直线.4.三垂线定理:在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直.三垂线定理的逆定理:在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直.（射影即投影）证明:①三垂线定理:已知直线1l x A =，过直线上任意点P 作PO x ⊥连接OA ，则OA 为直线1l 的投影为2l x ⊂，所以2PO l ⊥，若2OA l ⊥，OA PO O =，故2l ⊥平面OAP ， 又因为1l ⊂平面OAP ，所以12l l ⊥. 记为投影垂直于平面上的线，则斜线垂直平面上的线. ②三垂线定理的逆定理:已知直线1l x A =,过直线上任意点P 作PO x ⊥，连接OA ，则OA 为直线1l 的投影，因为2l x ⊂，所以2PO l ⊥，若2PA l ⊥，POPA P =，故2l ⊥平面OAP ，又因为OA ⊂平面OAP ，所以2OA l ⊥. 记为斜率垂直于平面上的直线，则斜线在平面的投影垂直该直线.注：此定理用在大题中，需要注明.由于三垂线定理的本质就是异面直线垂直与线面垂直，所以我们可以运用逆向思维，利用三垂线定理解决线线垂直与线面垂直问题.【例14】(2017•新课标Ⅲ)在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则（ ） A ．11A E DC ⊥ B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥【例15】(2022秋•甘井子区校级月考)如图，在正方体1111ABCD A B C D -中，点E 是线段1CD （含端点）上的动点，则下列结论错误的是（ ）A ．存在点E ，使1B E AC ⊥B ．异面直线1B E 与AD 所成的角最小值为4π C ．无论点E 在线段1CD 的什么位置，都有11AC B E ⊥D ．无论点E 在线段1CD 的什么位置，都有1B E ∥平面1A BD【例16】(浦东新区校级开学)如图，在直三棱柱111ABC A B C -中，2BAC π∠=，11AB AC AA ===，已知G与E 分别为11A B 和1CC 的中点，D 和F 分别为线段AC 和AB 上的动点(不包括端点)，若GD EF ⊥，则线段DF 的长度的平方取值范围为（ ）A ．(12)，B ．11[)52，C ．12(5，D ．1[1)5，知识点四夹角问题1.几何法求线面角与二面角：对于线面角，一般指斜线与斜线在平面的投影所成的夹角；只需在斜线上找一点向平面做垂线，构造直角三角形求夹角，或构造垂直平面且过直线的平面，利用余弦定理求夹角. 对于二面角，一般指两个相交半平面形成的夹角，常用在平面上且垂直两平面交线的两条射线的夹角来表示二面角的平面角；只需在两个平面上分别找到垂直交线的直线，构造三角形，利用余弦定理求夹角.2.空间向量求夹角：空间向量是求夹角最常用的方式，此类问题将在本书专题14详细叙述.3.投影面积法求二面角:二面角:cos S Sθθ'=，其中S 为斜面面积，S '为投影面积在四棱锥P ABCD -中，ABCD 为正方形，PA ⊥平面ABCD ，PA AB a ==，求平面PBA 与平面PDC 所成二面角的大小(投影面积法)如图，AD PA AD AB AD PA AB A ⎫⎪⇒⎬⎪=⎭⊥⊥⊥平面PBA 于A ，同时，BC ⊥平面BPA 于B ，故PBA △是PCD △在平面PBA 上的射影，设平面PBA 与平面PDC 所成二面角大小为θ，则2cos 45PAB PCD S S θθ==⇒=△△. 4.已知异面直线段AB a =，CD b =，异面直线夹角θ，且异面直线距离为d 则四面体ABCD 体积为:1sin 6ABCD V abd θ=.5.空间余弦定理:空间四边形ABCD 的两条异面直线AC 与BD 夹角为θ，则满足:2222||||||||cos 2|||||AB CD AD BC AC BD θ+--=⋅【证明】如图所示，四边形ABCD 中，2222|()()()|||||||AD BC AB CD AD AB AD AB BC CD +--+⋅-+=+.()()()()2BC CD AD AB BD BD BC CD AD AB BC CD BD AC BD -=+⋅+⋅-=++-⋅=⋅，则有2222||||||||2||co ||||s A B C BD AB CD AD BC AC D ++-=⋅⋅，于是2222|||||||cos 2|||||AB CD AD BC AC BD θ--=+⋅.特别地当AC BD ⊥时，有2222||||||||AB CD AD BC +=+.6.设二面角C OB A --大小为α，1COB θ∠=，2AOB θ∠=，AOC θ∠=，如图所示，此时三余弦定理可推广为:1212cos cos cos sin sin cos θθθθθα=+，特别地，当2πα=时，有12cos cos cos θθθ=.【证明】设1OB =，则有11||cos CO θ=，21||cos AO θ=，1||tan CB θ=，2||tan AB θ=，于是2211||()cos AC θ=+2221212212111()2cos (tan (tan 2tan tan cos cos cos cos ))θθθθθαθθθ-⋅⋅=+-，化简得到12cos cos cos θθθ=+12sin sin cos θθα.特别地，当2πα=时，有12cos cos cos θθθ=.7.最小角定理:平面的斜线和它在平面内的射影所成的锐角，是这条斜线和平面内任一直线所成角中的最小者，即线面角是最小的线线角.(由三余弦定理cos cos cos PAB OAB θ∠=⋅∠可得)8.最大角定理:对于一个锐二面角，在其中一个半平面内的任一条直线与另一个半平面所成的线面角的最大值等于二面角的平面角，即二面角是最大的线面角.(由三正弦定理sin sin sin PAB θα=⋅∠可得)【例17】如图所示为一个半圆柱，E 为半圆弧CD 上一点，5CD .（1）若25AD =，求四棱锥E ABCD -的体积的最大值；（2）有三个条件：①4DE DC EC DC ⋅=⋅；②直线AD 与BE 所成角的正弦值为23；③sin 6sin EAB EBA ∠∠.请你从中选择两个作为条件，求直线AD 与平面EAB 所成角的余弦值.【例18】如图，几何体的底面ABCD 是边长为2的菱形，60ABC ∠=︒，PCD △和PAD △均为正三角形，M ，N 分别为CD ，PB 的中点.（1）求证：PA MN ⊥；（2）求二面角P CM N --的余弦值.【例19】如图，已知直三棱柱111ABC A B C -中，120ABC ∠=，2AB =，11BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为（ ） 3 15 10 3【例20】如图，在三棱锥V ABC -中，平面VAC ⊥平面ABC ，ABC △和VAC △均是等腰直角三角形，AB =BC ，2AC CV ==，M ，N 分别为VA ，VB 的中点.(1)求证:AB ∥平面CMN ; (2)求证:AB VC ⊥;(3)求直线VB 与平面CMN 所成角的正弦值.【例21】如图，在三棱柱111ABC A B C -中，侧棱1AA ⊥平面ABC ，ABC △为等腰直角三角形，90BAC ∠=，且12AB AA ==，E ，F 分别是1CC ，BC 的中点. (1)求证:EF ⊥平面1AB F ;(2)求锐二面角1B AE F --的平面角的余弦值.【例22】(2022·浙江卷)如图，已知正三棱柱111ABC A B C -，1AC AA =，E ，F 分别是棱BC ，11A C 上的点.记EF 与1AA 所成的角为α，EF 与平面ABC 所成的角为β，二面角F BC A --的平面角为γ，则（ ）A.αβγ≤≤B.βαγ≤≤C.βγα≤≤D.αγβ≤≤同步训练1.(2016•新课标Ⅱ)α，β是两个平面，m ，n 是两条直线，有下列四个命题: ①如果m n ⊥，m α⊥，n β∥，那么αβ⊥． ①如果m α⊥，n α∥，那么m n ⊥． ①如果αβ∥，m α⊂，那么m β∥．①如果m n ∥，αβ∥，那么m 与α所成的角和n 与β所成的角相等．其中正确的命题是 ．(填序号)2.(焦作月考)在三棱锥P ABC -中，PB PC =，D ，E ，F 分别为BC ，AC ，AB 的中点，G 为PD 的中点，若EG AC ⊥且EG PD ⊥，则下列结论中不一定正确的是( ) A ．BC ∥平面EFG B ．PA ∥平面EFGC ．AC ⊥平面EFGD ．PD ⊥平面EFG3.(山东模拟)已知正方体1111ABCD A B C D -，棱长为2，E 为线段1B C 上的动点，O 为AC 的中点，P 为棱1CC上的动点，Q 为棱1AA 的中点，则以下选项中正确的有( ) A ．1AE B C ⊥B ．直线1B D ⊥平面11A BCC ．异面直线1AD 与1OC 所成角为3π D ．若直线m 为平面BDP 与平面11B D P 的交线，则m ∥平面11B D Q4.如图， 在正方体 1111ABCD A B C D - 中， O ，E 分别为1B D ，AB 的中点.求证: OE ∥ 平面11BCC B .5.(天河区三模)一几何体的平面展开图如图所示，其中四边形ABCD 为正方形，E 、F 分别为PB 、PC 的中点，在此几何体中，下面结论错误的是（ ）A ．直线AE 与直线BF 异面B ．直线AE 与直线DF 异面C ．直线EF ∥平面PAD D ．直线EF ∥平面ABCD 6.(徐州期中)在三棱锥P ABC -中，D ，E 分别是PB ，BC 中点，若F 在线段AC 上，且满足AD ∥平面PEF ，则AFFC的值为 ． 7.(邢台月考)如图，在四棱锥P ABCD -中，四边形ABCD 是平行四边形，E ，F 分别是线段AC ，PD 的中点，则（ ）A ．EF ∥平面PAB B ．EF ∥平面PBC C ．CF ∥平面PABD ．AF ∥平面PBC8.如图，平面EFGH 分别与空间四边形ABCD 中的BD 、AD 、AC 、BC 交于E 、F 、G 、H ，且AB ∥平面EFGH ，CD ∥平面EFGH ，CD a =，AB b =，CD AB ⊥．(1)求证EFGH 为矩形；(2)点G 在什么位置时，EFGH S 最大？9.(2022•新高考2卷) 如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 是PB 的中点． (1)求证:OE ∥平面PAC ；10.(烟台三模)如图，在平面五边形PABCD 中，PAD △为正三角形，AD BC ∥，90DAB ∠=︒且22AD AB BC ===．将PAD △沿AD 翻折成如图所示的四棱锥P ABCD -，使得7PC ．F ，Q 分别为AB ，CE 的中点．(1)求证:FQ ∥平面PAD ；11.如图， 在正四棱锥 P ABCD - 中， E 是 PC 中点，PB 与底面所成角的正切值为 6， 请在平面 PAB 中找一点 F ，使 得 FE ⊥ 平面 PCD .12.(2018•全国Ⅱ卷)如图，在三棱锥P ABC -中，22AB BC ==4PA PB PC AC ====，O 为AC 的中点．(1)证明:PO ⊥平面ABC ；(2)若点M 在棱BC 上，且2MC MB =，求点C 到平面POM 的距离．13.(2020•全国I 卷)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，ABC △是底面的内接正三角形，P 为DO 上一点，90APC ∠=︒．(1)证明:平面PAB ⊥平面PAC ；14.(江都区校级月考)如图，在四棱锥P ABCD -中，ABCD 是矩形，PA AB =，E 为PB 的中点． (1)若过C ，D ，E 的平面交PA 于点F ，求证:F 为PA 的中点； (2)若平面PAB ⊥平面PBC ，求证:BC PA ⊥．15.(2021•乙卷)如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，M 为BC 的中点，且PB AM ⊥． （1）证明:平面PAM ⊥平面PBD ；16.如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，底面ABCD 为平行四边形，E 为CD 的中点，12AE CD =. (1)证明: PC AD ⊥；17．(北京期末)如图，在正方体1111ABCD A B C D -中，过点A 且与直线1BD 垂直的所有面对角线的条数为（ ）A ．0B ．1C ．2D ．318．(金台区期末)如图，在正方体1111ABCD A B C D -中，PQ 与直线1A D 和AC 都垂直，则直线PQ 与1BD 的关系是（ ）A ．异面B ．平行C ．垂直不相交D ．垂直且相交19．在梯形ABCD 中，//AD BC ，90ABC ∠=︒，点M ，N 分别在边AB ，BC 上，沿直线MD ，DN ，NM 分别将AMD △，CDN △，BMM △折起，点A ，B ，C 重合于一点P .(1)证明:平面PM D ⊥平面PND ； (2)若3cos 5DPN ∠=，5DP =，求直线DP 与平面DNM 所成角的正弦值. 20．如图所示，四边形ABCD 中，AB BC ⊥，AD DC ⊥，1BC CD ==，(1)AB AD t t ==>，将其沿对角线AC 翻折(如图)，使得60BCD ∠=︒.(1)求证:AC BD ⊥；(2)设AC 与平面BCD 所成角为1θ，二面角B AC D --的平面角为2θ，若12θθ=，求t 的值.21.如图，已知正三棱柱111ABC A B C -的各条棱长都相等，M 是侧棱1CC 的中点，则异面直线1AB 和BM 所成的角的大小是?22.在三棱柱ABC A B C '-''中，各棱长相等，侧棱垂直于底面，点D 是侧面BB C C ''的中心，则AD 与平面BB C C ''所成角的大小是（ ）A.30B.45C.60D.9023.(2019·浙江卷)设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则（ ） A.βγ<，αγ< B.βα<，βγ< C.βα<，γα< D.αβ<，γβ<。

第一部分基础理论题第1章概论1.What’s your comprehension of the concepts of GIS?2.What are the difference and the relation between the basic function and the applied function of GIS?3.With the development of the modern information technique, what kind of changes has brought to the survey ing and mapping technique and geographic analysis technique?4.What are the difference and the relation between instrumental GIS and appl ied GIS?5、试将GIS的输入设备按照不同的分类方法进行分类，并说明其特点。

6、现代空间定位技术有哪些主要方法？对GIS技术的发展产生什么影响？7、网络技术的出现与发展对GIS技术产生哪些主要的变化8、说明GIS在几个不同发展阶段的标志性技术是什么，它们的出现如何促进GIS的发展？第2章地理空间数学基础1.What are the relations between the earth surface, the geoid, and the Earth spherop?2.How many coordinate systems are there to describe the geographic spatial data? What are the relations between them?3.What are the advantage and the disadvantage of describing a point on the ground by using geodetic coordinate and geocentric coordinate?4.What are the main characteristics and the applicability of the UTM Projection and the Lambert Projection?5. How to transform the elevation of the different datum?6、高斯投影的变形特征是什么？为什么常常被用作大比例尺普通地图的地图投影？7、在数字地图中，地图比例尺在含义与表现形式上有哪些变化？8、除地形分幅外，谈谈还有何种地理空间框架？他们如何进行编码？9、GPS数据如何与地图数字化数据进行集成？10、选择投影需要考虑哪些因素？如果要制作1：10万的土地利用图，该选何种类型的地图投影？第3章空间数据模型1.What are the main characters of the spatial objects?2.What’s the meaning of spatial relationship? What’s the advantage of spatial relationship in describing the spatialobjects?3、空间数据的概念模型有哪些组成部分？试分析他们之间的关系？4、试分析GIS的几种主要的数据模型各自的优缺点。

幼儿园大班数学教程方案《幼儿园大班数学教案宫》第一章：认识数字1-101.1 教学目标让学生能够认识并掌握数字1-10培养学生对数字的敏感性提高学生的数学思维能力1.2 教学内容数字1-10的认识和书写数字1-10的顺序和大小比较数字1-10的运用和计算1.3 教学方法直观教学法：通过实物、图片等引导学生认识数字游戏教学法：通过数字游戏，让学生在游戏中学习数字情境教学法：创设生活情境，让学生在实际情境中学习数字1.4 教学步骤导入：引导学生复习已学的数字0-9新课：介绍数字1-10，让学生认识和书写练习：进行数字大小比较和运用计算的练习总结：对本节课的内容进行总结和回顾第二章：认识形状2.1 教学目标让学生能够认识并掌握基本的形状，如圆形、正方形、长方形等培养学生对形状的观察和识别能力提高学生的空间思维能力2.2 教学内容基本形状的认识和识别形状的名称和特征形状的运用和创造2.3 教学方法直观教学法：通过实物、图片等引导学生认识形状观察教学法：培养学生观察和识别形状的能力动手操作教学法：让学生动手操作，创造形状2.4 教学步骤导入：引导学生复习已学的数字和基本形状新课：介绍新的形状，让学生认识和识别练习：进行形状的分类和运用的练习总结：对本节课的内容进行总结和回顾第三章：认识颜色3.1 教学目标让学生能够认识并掌握基本的颜色，如红、橙、黄、绿等培养学生对颜色的观察和识别能力提高学生的审美能力3.2 教学内容基本颜色的认识和识别颜色的名称和特征颜色的运用和创作3.3 教学方法直观教学法：通过实物、图片等引导学生认识颜色观察教学法：培养学生观察和识别颜色的能力动手操作教学法：让学生动手操作，创作颜色3.4 教学步骤导入：引导学生复习已学的数字、形状和基本颜色新课：介绍新的颜色，让学生认识和识别练习：进行颜色的分类和运用的练习总结：对本节课的内容进行总结和回顾第四章：认识时间4.1 教学目标让学生能够认识并掌握时间的基本概念，如早上、下午、晚上等培养学生对时间的观察和识别能力提高学生的日常生活能力4.2 教学内容时间的基本概念的认识和识别时间的名称和特征时间的运用和安排4.3 教学方法直观教学法：通过实物、图片等引导学生认识时间观察教学法：培养学生观察和识别时间的能力情境教学法：创设生活情境，让学生在实际情境中学习时间4.4 教学步骤导入：引导学生复习已学的数字、形状、颜色和基本时间概念新课：介绍新的时间概念，让学生认识和识别练习：进行时间的排序和运用的练习总结：对本节课的内容进行总结和回顾第五章：认识空间5.1 教学目标让学生能够认识并掌握空间的基本概念，如上、下、前、后等培养学生对空间的观察和识别能力提高学生的空间思维能力5.2 教学内容空间的基本概念的认识和识别空间的名称和特征空间的运用和创造5.3 教学方法直观教学法：通过实物、图片等引导学生认识空间观察教学法：培养学生观察和识别空间的能力动手操作教学法：让学生动手操作，创造空间5.4 教学步骤导入：引导学生复习已学的数字、形状、颜色、时间基本概念新课：介绍新的空间概念，让学生认识和识别练习：进行空间的分类和运用的练习总结：对本节课的内容进行总结和回顾第六章：简单的加减法6.1 教学目标让学生能够理解并掌握加减法的概念培养学生通过实际操作解决简单问题的能力提高学生的数学思维能力6.2 教学内容加减法的概念和基本运算规则利用实物和图片进行加减法运算解决生活中的简单加减法问题6.3 教学方法直观教学法：通过实物、图片等引导学生理解加减法概念操作教学法：让学生通过实际操作进行加减法运算情境教学法：创设生活情境，让学生在实际情境中应用加减法6.4 教学步骤导入：引导学生复习已学的数字和基本概念新课：介绍加减法的基本概念和运算规则练习：进行实际的加减法运算练习总结：对本节课的内容进行总结和回顾第七章：认识货币让学生能够认识并掌握基本的货币单位，如元、角、分等培养学生对货币的观察和识别能力提高学生的日常生活能力7.2 教学内容货币单位的认识和识别货币的名称和特征货币的运用和计算7.3 教学方法直观教学法：通过实物、图片等引导学生认识货币观察教学法：培养学生观察和识别货币的能力情境教学法：创设生活情境，让学生在实际情境中学习货币7.4 教学步骤导入：引导学生复习已学的数字、简单的加减法和基本概念新课：介绍货币的基本单位和运用练习：进行货币的计算和运用练习总结：对本节课的内容进行总结和回顾第八章：认识日历8.1 教学目标让学生能够认识并掌握日历的基本知识，如年、月、日等培养学生对日历的观察和识别能力提高学生的日常生活能力日历的基本知识的认识和识别日历的名称和特征日历的运用和安排8.3 教学方法直观教学法：通过实物、图片等引导学生认识日历观察教学法：培养学生观察和识别日历的能力情境教学法：创设生活情境，让学生在实际情境中学习日历8.4 教学步骤导入：引导学生复习已学的数字、简单的加减法、货币和基本概念新课：介绍日历的基本知识和运用练习：进行日历的排序和运用的练习总结：对本节课的内容进行总结和回顾第九章：认识几何图形9.1 教学目标让学生能够认识并掌握基本的几何图形，如三角形、正方形、圆形等培养学生对几何图形的观察和识别能力提高学生的空间思维能力9.2 教学内容基本几何图形的认识和识别几何图形的名称和特征几何图形的运用和创造直观教学法：通过实物、图片等引导学生认识几何图形观察教学法：培养学生观察和识别几何图形的能力动手操作教学法：让学生动手操作，创造几何图形9.4 教学步骤导入：引导学生复习已学的数字、简单的加减法、货币、日历和基本概念新课：介绍新的几何图形，让学生认识和识别练习：进行几何图形的分类和运用的练习总结：对本节课的内容进行总结和回顾第十章：数学在日常生活中的应用10.1 教学目标让学生能够理解数学在日常生活中的应用培养学生运用数学解决实际问题的能力提高学生的日常生活能力10.2 教学内容数学在日常生活中的实例和应用实际问题的解决方法和策略生活中的数学知识和技巧10.3 教学方法实例教学法：通过生活实例引导学生理解数学的应用问题解决教学法：培养学生解决实际问题的能力情境教学法：创设生活情境，让学生在实际情境中应用数学导入：引导学生复习已学的数字、简单的加减法、货币、日历、几何图形和基本概念新课：介绍数学在日常生活中的应用实例练习：进行实际问题的解决练习总结：对本节课的内容进行总结第十一章：认识分数11.1 教学目标让学生能够理解分数的概念培养学生掌握分数的读写法和比较大小提高学生运用分数解决实际问题的能力11.2 教学内容分数的定义和基本性质分数的读写法和比较大小分数在实际情境中的应用11.3 教学方法直观教学法：通过实物、图片等引导学生认识分数观察教学法：培养学生观察和识别分数的能力操作教学法：让学生动手操作，理解分数的概念11.4 教学步骤导入：引导学生复习已学的数字、简单的加减法、货币、日历、几何图形和基本概念新课：介绍分数的基本概念和性质练习：进行分数的读写和比较大小的练习总结：对本节课的内容进行总结和回顾第十二章：认识倍数12.1 教学目标让学生能够理解倍数的概念培养学生掌握倍数的运算方法提高学生运用倍数解决实际问题的能力12.2 教学内容倍数的定义和基本性质倍数的运算方法倍数在实际情境中的应用12.3 教学方法直观教学法：通过实物、图片等引导学生认识倍数观察教学法：培养学生观察和识别倍数的能力操作教学法：让学生动手操作，理解倍数的概念12.4 教学步骤导入：引导学生复习已学的数字、简单的加减法、货币、日历、几何图形、分数和基本概念新课：介绍倍数的基本概念和性质练习：进行倍数的运算和应用的练习总结：对本节课的内容进行总结和回顾第十三章：认识计量单位13.1 教学目标让学生能够认识并掌握常见的计量单位，如米、千克、秒等培养学生对计量单位的观察和识别能力提高学生的日常生活能力13.2 教学内容常见计量单位的认识和识别计量单位的名称和特征计量单位的运用和换算13.3 教学方法直观教学法：通过实物、图片等引导学生认识计量单位观察教学法：培养学生观察和识别计量单位的能力情境教学法：创设生活情境，让学生在实际情境中学习计量单位13.4 教学步骤导入：引导学生复习已学的数字、简单的加减法、货币、日历、几何图形、分数、倍数和基本概念新课：介绍常见的计量单位及其运用练习：进行计量单位的换算和运用的练习总结：对本节课的内容进行总结和回顾第十四章：数学思维训练14.1 教学目标让学生能够运用数学思维解决问题培养学生逻辑推理和判断能力提高学生创新思维和综合素质14.2 教学内容数学思维方法和解题策略逻辑推理和判断题的训练创新思维和综合素质的培养14.3 教学方法实例教学法：通过生活实例引导学生运用数学思维问题解决教学法：培养学生解决实际问题的能力情境教学法：创设生活情境，让学生在实际情境中运用数学思维14.4 教学步骤导入：引导学生复习已学的数字、简单的加减法、货币、日历、几何图形、分数、倍数、计量单位和基本概念新课：介绍数学思维方法和解题策略练习：进行逻辑推理和判断题的训练总结：对本节课的内容进行总结和回顾第十五章：课程复习与总结15.1 教学目标让学生对所学知识进行复习和巩固培养学生运用所学知识解决实际问题的能力提高学生的综合运用能力15.2 教学内容复习已学的数字、简单的加减法、货币、日历、几何图形、分数、倍数、计量单位和数学思维等知识总结课程的重点和难点提高学生的综合运用能力15.3 教学方法直观教学法：通过实物、图片等引导学生复习知识观察教学法：培养学生观察和识别知识的能力情境教学法：创设生活情境，让学生在实际情境中运用所学知识15.4 教学步骤导入：重点和难点解析本文主要介绍了幼儿园大班数学教程方案《幼儿园大班数学教案宫》，内容包括数字1-10的认识、形状、颜色、时间、空间、简单加减法、货币、日历、几何图形、分数、倍数、计量单位和数学思维训练等。

第10章 空间直线与平面（基础、典型、新文化、压轴）分类专项训练【基础】一、单选题1．（2021·上海市嘉定区安亭高级中学高二阶段练习）“直线l 与平面α没有公共点”是“直线l 与平面α平行”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】C【分析】从充分性和必要性两方面来分析即可.【详解】若直线l 与平面α没有公共点，那直线l 与平面α只能平行，故充分条件成立；若直线l 与平面α平行，则直线l 与平面α没有公共点，故必要性也成立，所以“直线l 与平面α没有公共点”是“直线l 与平面α平行”的充分必要条件.故选：C2．（2022·上海市建平中学高二阶段练习）空间四个点中，三点共线是这四个点共面的（ ） A ．充分非必要条件； B ．必要非充分条件； C ．充要条件；D ．既非充分又非必要条件．【答案】A【分析】空间四个点中，有三个点共线，根据一条直线与直线外一点可以确定一个平面得到这四个点共面，前者可以推出后者，当四个点共面时，不一定有三点共线，后者不一定推出前者．【详解】解：空间四个点中，有三个点共线，根据一条直线与直线外一点可以确定一个平面得到这四个点共面，前者可以推出后者，当四个点共面时，不一定有三点共线，后者不一定推出前者，∴空间四个点中，有三个点共线是这四个点共面的充分不必要条件， 故选：A ．二、填空题3．（2021·上海市徐汇中学高二阶段练习）在平行六面体1111ABCD A B C D -的所有棱中，既与AB 共面，又与1CC 共面的棱的条数为___________.【答案】5【分析】有两条平行直线确定一个平面，和两条相交直线确定一个平面可得答案，【详解】解：如图，满足条件的有BC ，DC ，1BB ，1AA ，11D C ，故答案为：5.4．（2021·上海·华东师大附属枫泾中学高二期中）不共线的三点确定___________个平面.（填数字）【答案】1【分析】由空间几何的公理求解即可【详解】不在同一条直线上的三个点确定唯一的一个平面故答案为：15．（2022·上海市建平中学高二阶段练习）不同在任何一个平面上的两条直线的位置关系是_________【答案】异面【分析】根据异面直线的定义，直接判断.【详解】不同在任何一个平面上的两条直线的位置关系是异面.故答案为：异面6．（2021·上海·西外高二期中）空间中两条直线的位置关系有___________.【答案】平行、相交、异面【分析】根据空间中两条直线的位置关系即可作答.【详解】空间中两条直线的位置关系有：平行、相交、异面.故答案为：平行、相交、异面.7．（2021·上海市复兴高级中学高二阶段练习）如图，在棱长为1的正方体1111ABCD A B C D 中，异面直线1AB与1BC 所成角的大小为___________.【答案】60︒##3π 【分析】连接1,DC BD ，由正方体的结构特征知：11//DC AB 且△1BDC 为等边三角形，即可知异面直线1AB 与1BC 所成角.【详解】连接1,DC BD ，由正方体的结构特征知：11//DC AB ，∴1DC 与1BC 所成角即为异面直线1AB 与1BC 所成角，又△1BDC 为等边三角形，∴1DC 与1BC 所成角60︒，即异面直线1AB 与1BC 所成角为60︒.故答案为：60︒8．（2022·上海虹口·高二期末）在正四面体ABCD 中，直线BC 与AD 所成角的大小为________．【答案】2π 【分析】根据空间位置关系直接证明判断即可.【详解】如图所示，取BC 中点E ，连接AE ，DE ，由已知ABCD 为正四面体，则ABC ，DBC △均为正三角形，所以AE BC ⊥，DE BC ⊥，所以BC ⊥平面ADE ，故BC AD ⊥，即直线BC 与直线AD 的夹角为2π， 故答案为：2π. 9．（2021·上海市行知中学高二阶段练习）过直线外一点有_________条直线与该直线垂直．【答案】无数【分析】根据点和直线、直线和直线的位置关系即可得出结果.【详解】空间中过直线外一点可以作无数条直线与该直线垂直.故答案为：无数10．（2021·上海市宝山中学高二阶段练习）若平面α∥平面β，,a b αβ⊂⊂，则直线a 和b 的位置关系是_____________.【答案】异面或平行【分析】利用分别在两个平行平面内的两个直线没有公共点即可判断作答.【详解】因平面α∥平面β，则平面α与平面β没有公共点，而a α⊂，b β⊂，于是得直线a 和b 没有公共点，所以直线a 和b 是异面直线或者是平行直线.故答案为：异面或平行11．（2020·上海松江·高二期末）已知正方体1111ABCD A B C D -的棱长为a ，异面直线BD 与11A B 的距离为__________.【答案】a【分析】根据线面垂直性质可得1BB BD ⊥，又111BB A B ⊥，可知所求距离为1BB ，从而得到结果.【详解】1BB ⊥平面ABCD ，BD ⊂平面ABCD 1BB BD ∴⊥又111BB A B ⊥ ∴异面直线BD 与11A B 之间距离为1BB a =故答案为a【点睛】本题考查异面直线间距离的求解，属于基础题.12．（2022·上海·复旦附中高二期中）棱长为1的正方体中，异面直线1A D 与11B C 之间的距离为______．【答案】1【分析】根据题意，证得111A B A D ⊥且1111A B B C ⊥，得到11A B 为异面直线1A D 与11B C 的公垂线，即可求解.【详解】如图所示，在正方体1111ABCD A B C D -中，可得11A B ⊥平面11ADD D ，11A B ⊥平面11BCC B ，因为1A D ⊂平面11ADD D ，11B C ⊂平面11BCC B ，所以111A B A D ⊥且1111A B B C ⊥，所以11A B 为异面直线1A D 与11B C 的公垂线，又由正方体的棱长为1，可得111A B =，所以异面直线1A D 与11B C 的距离为1.故答案为：1.13．（2021·上海奉贤区致远高级中学高二期中）若正方体1111ABCD A B C D -的棱长为1，则异面直线AB 与11D B 之间的距离为___________.【答案】1【分析】作出正方体图像，观察即可得到答案﹒【详解】如图：∵1BB 与AB 、11B D 均垂直，∴1BB 即为两异面直线的距离，故答案为：1三、解答题14．（2021·上海市行知中学高二阶段练习）如图，三棱锥P ABC - 中，已知PA ⊥ 平面,ABC 3,6PA PB PC BC ==== .求二面角P BC A --的正弦值 【答案】33【分析】取BC 的中点D ，连结PD ，AD,根据线面垂直关系可知PDA ∠即为二面角P BC A --的平面角,根据所给边长关系可求得PDA ∠的正弦值.【详解】取BC 的中点D ，连结PD ，AD∵PB PC = ∴PD BC ⊥∵PA ⊥平面ABC ，∴PA BC ⊥,且BC PAD ⊥面即BC AD ⊥∴PDA ∠即为二面角P BC A --的平面角∵6PB PC BC ===∴3PD 633==PA sin PDAPD ∠===P BC A --【点睛】本题考查了二面角的求法,关键是找到二面角的平面角,属于基础题.【典型】一、单选题1．（2021·上海·闵行中学高二阶段练习）在空间内，异面直线所成角的取值范围是（ ）A ．0,2π⎛⎫ ⎪⎝⎭B ．0,2π⎛⎤ ⎥⎝⎦C ．0,2π⎡⎫⎪⎢⎣⎭D ．0,2π⎡⎤⎢⎥⎣⎦【答案】B【分析】由异面直线所成角的定义可得出答案.【详解】由异面直线所成角的定义可知,过空间一点分别作相应直线的平行线,两条相交直线所成的直角或锐角为异面直线所成角,所以两条异面直线所成角的取值范围是(0,]2π, 故选B.【点睛】本题考查立体几何中异面直线所成的角,需要学生熟知异面直线的定义以及性质,考查了转化思想,属于基础题.2．（2021·上海·高二专题练习）若a 、b 是异面直线，则下列命题中的假命题为（ ）A ．过直线a 可以作一个平面并且只可以作一个平面α与直线b 平行B ．过直线a 至多可以作一个平面α与直线b 垂直C ．唯一存在一个平面α与直线a 、b 等距D ．可能存在平面α与直线a 、b 都垂直【答案】D 【分析】在A 中，把直线b 平移与直线a 相交，确定一个平面内平行于b ；在B 中，反设过直线a 能作平面α、β使得b α⊥、b β⊥，推出矛盾；在C 中，过异面直线a 、b 的公垂线段的中点作与该公垂线垂直的平面可满足条件；在D 中，若存在平面α与直线a 、b 都垂直，则//a b .【详解】在A 中，由于a 、b 是异面直线，把直线b 平移与直线a 相交，可确定一个平面，这个平面与直线b 平行，A 选项正确；在B 中，若过直线a 能作平面α、β使得b α⊥、b β⊥，则//αβ，这与a αβ⋂=矛盾，所以，过直线a 最多只能作一个平面α与直线b 垂直，由a α⊂，可得b a ⊥，当直线a 与b 不垂直时，过直线a 不能作平面与直线b 垂直，B 选项正确；在C 中，由于a 、b 是异面直线，则两直线的公垂线段只有一条，过该公垂线段的中点作平面α与该公垂线垂直，这样的平面α有且只有一个，且这个平面α与直线a 、b 等距，C 选项正确；在D 中，若存在平面α与直线a 、b 都垂直，由直线与平面垂直的性质定理可得//a b ，D 错误.故选：D.【点睛】本题考查命题真假的判断，着重考查与异面直线相关的性质，考查推理能力，属于中等题. 3．（2021·上海市宝山中学高二阶段练习）对于两个平面,αβ和两条直线,m n ，下列命题中真命题是 A ．若,m m n α⊥⊥，则//n αB ．若//,m ααβ⊥，则m β⊥C ．若//,//,m n αβαβ⊥，则m n ⊥D ．若,,m n αβαβ⊥⊥⊥，则m n ⊥【答案】D【分析】根据线面平行垂直的位置关系判断．【详解】A 中n 可能在α内，A 错；B 中m 也可能在β内，B 错；m 与n 可能平行，C 错；,ααβ⊥⊥m ，则m β⊂或//m β，若m β⊂，则由n β⊥得n m ⊥，若//m β，则β内有直线//c m ，而易知c n ⊥，从而m n ⊥，D 正确．故选D ．【点睛】本题考查线面平行与垂直的关系，在说明一个命题是错误时可举一反例．说明命题是正确时必须证明．二、填空题4．（2021·上海市亭林中学高二阶段练习）异面直线a 与b 成60°角，若//c a ，则c 与b 所成的角等于__________【答案】60°【分析】由已知可得c 与b 相交或异面.分两种情况，根据异面直线所成的角的概念结合平行公理即可得出结论.【详解】∵,a b 异面，//c a ，∴c 与b 相交或异面.当c 与b 相交时，根据异面直线a 与b 所成角的概念可知c 与b 所成的角为60°角；当c 与b 异面时，自空间不在,,a b c 上的一点分别作,a b 的平行线//,//m a n b ,∵//c a ，∴//m c ,根据异面直线所成角的定义，相交直线,m n 所成的不超过直角的角既是异面直线a 与b 所成的角，又是异面直线c 与b 所成的角，根据异面直线a 与b 成60°角，故异面直线c 与b 所成的角为60°角.故答案为：60°. 5．（2021·上海南汇中学高二阶段练习）二面角l αβ--为60，异面直线a 、b 分别垂直于α、β，则a 与b 所成角的大小是____【答案】60【分析】根据二面角的定义，及线面垂直的性质，我们可得若两条直线a 、b 分别垂直于α、β两个平面，则两条直线的夹角和二面角相等或互补，由于已知的二面角l αβ--为60，故异面直线所成角与二面角相等，即可得到答案.【详解】解：根据二面角的定义和线面垂直的性质设异面直线a 、b 的夹角为θ∵二面角l αβ--为60，异面直线a 、b 分别垂直于α、β则两条直线的夹角和二面角相等或互补，∴60οθ=故答案为60【点睛】本题主要考查二面角的定义、异面直线所成的角和线面垂直的性质.三、解答题6．（2019·上海·华师大二附中高二阶段练习）在正方体A 1B 1C 1D 1﹣ABCD 中，E 、F 分别是BC 、A 1D 1的中点． （1）求证：四边形B 1EDF 是菱形；（2）作出直线A 1C 与平面B 1EFD 的交点（写出作图步骤）．【分析】（1）取AD 中点G ，连接FG ，BG ，可证四边形B 1BGF 为平行四边形，四边形BEDG 为平行四边形，得到四边形B 1EDF 为平行四边形，再由△B 1BE ≌△B 1A 1F ，可得B 1E ＝B 1F ，得到四边形B 1EDF 是菱形；（2）连接A 1C 和AC 1，则A 1C 与AC 1的交点O ，即为直线A 1C 与平面B 1EFD 的交点．【详解】（1）证明：取AD 中点G ，连接FG ，BG ，如图1所示，则B 1B ∥FG ，B 1B ＝FG ，∴四边形B 1BGF 为平行四边形，则BG ∥B 1F ，由ABCD ﹣A 1B 1C 1D 1为正方体，且E ，G 分别为BC ，AD 的中点，可得BEDG 为平行四边形，∴BG ∥DE ，BG ＝DE ，则B 1F ∥DE ，且B 1F ＝DE ，∴四边形B 1EDF 为平行四边形，由△B 1BE ≌△B 1A 1F ，可得B 1E ＝B 1F ，∴四边形B 1EDF 是菱形；（2）连接A 1C 和AC 1，则A 1C 与AC 1的交点O ，即为直线A 1C 与平面B 1EFD 的交点，如图所示．【点睛】本题考查了空间中的平行关系应用问题，也考查了空间想象与逻辑推理能力，是中档题．关键是掌握正方体的性质和熟练使用平行公理.【新文化】一、填空题1．（2021·上海·华东师范大学第三附属中学高二阶段练习）刍甍，中国古代算数中的一种几何形体，《九章算术》中记载：“刍甍者，下有袤有广，而上有袤无广.刍，草也，甍，屋盖也.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”如图为一个刍瓷的五面体，其中四边形ABCD 为矩形，ADE 和BCF △都是等腰三角形，2AE ED BF CF AD ====，//EF AB ，若3AB EF =，且2AD EF =，则异面直线AE 与CF 所成角的大小为______.【答案】3π 【分析】作平行四边形AGFE ，得到//AE GF ，异面直线AE 与CF 所成角为GFC ∠，求出GFC 的边长求角即可.【详解】设1EF =，在AB 上取点G 满足1AG EF ==，如图，故//AG EF 且AG EF =，故四边形AGFE 是平行四边形，故//AE GF异面直线AE 与CF 所成角为GFC ∠或其补角 ，22GF CF ==， 22222222CG GB BC =+=+=故GFC 为等边三角形 故3GFC π∠=故答案为：3π 【压轴】1．（2021·上海·西外高二期中）三棱锥P ABC -满足：AB AC ⊥，AB AP ⊥，2AB =，4AP AC +=，则该三棱锥的体积V 的取值范围是________． 【答案】4(0,]3； 【详解】由于,,,AB AP AB AC AB AP A AB ⊥⊥⋂=∴⊥ 平面APC ，1233APC APC V S AB S ∆∆=⋅= ，在APC ∆ 中，4AP AC +=，要使APC ∆ 面积最大，只需0,90AP AC APC =∠=，APC S ∆的最大值为12222⨯⨯=，V 的最大值为142233⨯⨯=，该三棱锥的体积V 的取值范围是4(0,]3.。