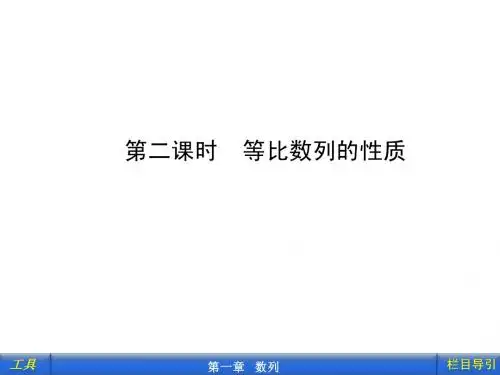
(方法二)设后三个数分别为 a-d,a,a+d(a≠0), 则第一个数为a-a d2.
由题意得a-a d2a-da=27, a-d+a=9,
化简得a2-a-d=d=3,9, 解得ad==63,, ∴这四个数分别为23,3,6,9.
(方法三)设前三个数分别为 a,aq,aq2(a≠0), 则第四个数应为 2aq2-aq.
a·aq·aq2=27, 由题意得aq+aq2=9,
化简得aaqq=1+3,q=9,
解得a=32, q=2,
∴这四个数分别为23,3,6,9.
探究题 4 三个互不相等的实数成等差数列,如果适当安排这三 个数,又可以成等比数列,且这三个数的和为 6,求这三个数. 解:由题意,这三个数成等差数列, 可设这三个数分别为 a-d,a,a+d. ∵a-d+a+a+d=6,∴a=2, 即三个数分别为 2-d,2,2+d. ①若 2-d 为等比中项,则有(2-d)2=2(2+d), 解得 d=6 或 d=0(舍去),此时三个数为-4,2,8.
②若 2+d 是等比中项,则有(2+d)2=2(2-d), 解得 d=-6 或 d=0(舍去),此时三个数为 8,2,-4. ③若 2 为等比中项,则有 22=(2+d)(2-d), 解得 d=0(舍去). 综上可知,这三个数是-4,2,8 或 8,2,-4.
探究题 5 数列{an}的前 n 项和记为 Sn,a1=1,an+1= 2Sn+1(n≥1). (1)求{an}的通项公式; (2)等差数列{bn}的各项为正,其前 n 项和为 Tn,且 T3 =15,又 a1+b1,a2+b2,a3+b3 成等比数列,求 Tn. 解:(1)由 an+1=2Sn+1,可得 an=2Sn-1+1(n≥2), 两式相减,得 an+1-an=2an,an+1=3an(n≥2). 又∵a2=2S1+1=3,∴a2=3a1, 故{an}是首项为 1,公比为 3 的等比数列,∴an=3n-1.