双圆弧齿轮基本齿廓的图形参数化

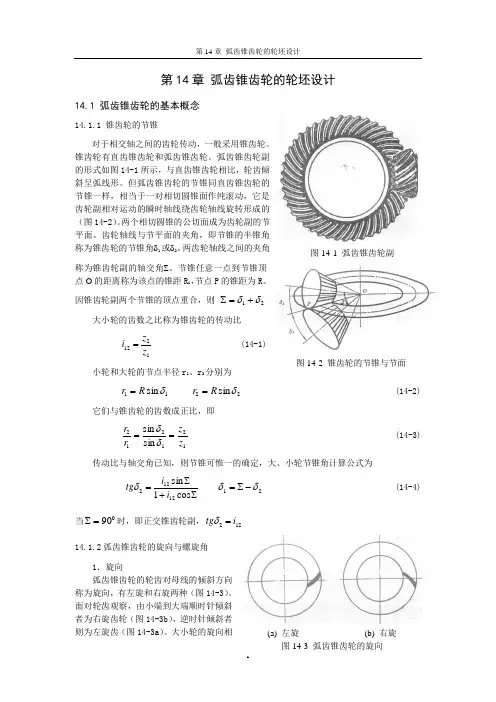
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动，一般采用锥齿轮。

锥齿轮有直齿锥齿轮和弧齿锥齿轮。

弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比，轮齿倾斜呈弧线形。

但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样，相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的（图14-2）。

两个相切圆锥的公切面成为齿轮副的节平面。

齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。

两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。

节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ，节点P 的锥距为R 。

因锥齿轮副两个节锥的顶点重合，则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比，即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时，即正交锥齿轮副，122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向，有左旋和右旋两种（图14-3）。

面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮（图14-3b ），逆时针倾斜者则为左旋齿（图14-3a ）。

大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-3 弧齿锥齿轮的旋向图14-1 弧齿锥齿轮副反时，才能啮合。

一般情况下，工作面为顺时针旋转的（从主动轮背后看，或正对被动轮观察），主动锥齿轮的螺旋方向为左旋，被动轮为右旋（图14-1）；工作面为逆时针旋转的，情况相反。

齿轮机构的齿廓啮合基本规律特点和类型齿轮机构是一种重要的传动机构，用于将转动的运动和转矩传递的机械元件。

齿轮的齿廓啮合是齿轮机构工作的核心部分，其基本规律、特点和类型对于齿轮机构的设计和应用具有重要的参考价值。

一、基本规律1.齿廓规律：齿廓规律描述了齿轮齿廓线的几何形状。

常见的齿廓规律有圆弧齿廓、渐开线齿廓和非渐开线齿廓等。

(1)圆弧齿廓：圆弧齿廓是通过圆弧曲线来描述齿槽的齿轮齿廓。

圆弧齿廓的优点是简单，易于加工，但啮合时存在齿间间隙和传动误差。

(2)渐开线齿廓：渐开线齿廓是常用的齿廓规律，可以在齿轮齿廓上实现圆顶啮合，具有传动平稳、效率高、传动误差小等优点。

常见的渐开线齿廓包括标准渐开线、修形渐开线和端面渐开线等。

(3)非渐开线齿廓：非渐开线齿廓是指不能用一个等角参数来描述的齿廓，例如双曲线齿廓和伞齿轮齿廓等。

非渐开线齿廓的优点是能够实现更大的传动比和更平滑的啮合过程。

2.齿廓规律的选择：选择合适的齿廓规律可以提高齿轮机构的传动效率和运动平稳性。

在选择齿廓规律时，需要考虑以下因素：(1)传动要求：根据齿轮机构的传动要求，选择适合的齿廓规律。

例如，要求传动平稳和效率高的应选用渐开线齿廓，要求传动比大且运动平稳的应选用非渐开线齿廓。

(2)制造和加工因素：考虑齿轮的加工工艺和精度要求，选择适合加工的齿廓规律。

例如，圆弧齿廓适合用铣床加工，而渐开线齿廓适合用滚齿机加工。

二、特点1.几何特点：齿廓啮合过程中，齿轮的齿廓线和花键的啮合点始终保持一定的关系，包括齿廓的曲率半径和齿廓线与法线的夹角等特征。

这些几何特点决定了齿轮的啮合性能和传动特性。

2.运动特点：齿轮机构的齿廓啮合过程中，齿轮的运动特点包括啮合速度、传动比和传动误差等。

齿轮的啮合速度是指齿轮工作时齿廓线移动的速度，而传动比是指输入轴和输出轴的转速之比。

传动误差则是齿轮啮合过程中由于齿廓不完美造成的传动误差，会导致振动和噪声。

三、类型1.直齿轮：直齿轮是最常见的齿轮类型，其齿廓线是直线，适用于输送大扭矩或平稳传动的场合。

机
第 48 卷
第 11 期
电 工 程
技 术
MECHANICAL & ELECTRICAL ENGINEERING TECHNOLOGY
Vol.48 No.11
DOI: 10. 3969 / j. issn. 1009-9492. 2019. 11. 051
胡时林，秦昊，张昱. 基于Solidworks的双圆弧柔轮参数化设计 ［J］ . 2019，48 （11）：153-156.
the flexible gear are chosen as the key parameters， while the other dimensions are constrained according to them. A prototypical double arc flexible
gear is created through the above-mentioned method， proving the feasibility of parametric design by only modules and inner diameter of the flexible
轮设计尺寸重复多次修改，对柔轮的结构尺寸进行综合协
[1]
器人、军事、光学仪器以及通用机械等领域 。谐波齿轮
调、参数优化等，从大量机械系列柔轮产品设计图纸中可
传动中，柔轮作为主要结构件之一，是影响其承载能力的
以发现，柔轮基本结构形式的零部件，其图形结构具有一
薄弱环节，传动的基础是依靠柔轮不断的发生弹性形变来
基于 Solidworks 的双圆弧柔轮参数化设计*
胡时林 1，秦
（1. 昆明理工大学 机电工程学院， 云南昆明
昊 2※，张

Ｊ
—／／／‘、
（１）摆线轮单齿齿廓
ｙ ｙ
（ｂ）两齿差摆线轮完整单支摆线（ｃ）三齿差拯线轮完整单支摆线
图２摆线轮齿廓图
２齿根过渡曲线
通过上述的分析，已经可以按照小齿轮的摆线齿 形方程式，绘出理论摆线等距曲线的齿廓。由图２所 示，小轮理论摆线齿形是一个连续的摆线等距曲线，而 实际的摆线齿轮齿形是由齿根圆、摆线齿廓曲线和齿 顶圆３部分组成的ｌ条连续曲线。小轮完整理论齿形 的绘制除了和圆弧啮合的摆线部分外，还应考虑齿根 的过渡曲线以及齿廓曲线有效部分的范围［２｜。理论上 摆线轮齿根曲线为大轮齿顶圆弧的共轭曲线，但由于 齿根曲线不参与啮合，而且实际上为避免齿根干涉，小 轮的齿根与大轮齿顶之间留有一定的间隙，鉴于此，为 方便小轮齿根曲线的处理，我们编制程序时采用单圆 弧和双圆弧两种方式来构成小轮的齿根曲线。 ２．１齿根单圆弧曲线
线，该垂线与０２Ｐ的夹角为驴。由图１中几何关系易知
ｒ
，ｒ
，
、
｛Ｐ２ ２百一Ｌ妒¨’
（、】。）
【ｃ∞驴：。ｉｎｒ／Ｋｌ
ｒ：ａｘｃｔａｎ芒ｔ！－＝ｔ…２） 在Ａ０２ｐｏ：中，根据正弦定理得
ｒ ２旃ｃ而
式（２）建立了转子转角与齿廓公法线方向角之间的联
系，使摆线齿廓方程的形式和计算变得简单。
弧齿上肘点在Ｘ２０２Ｙ２坐标系中的方程为圆方程
另外需要说明的是，根据优化得到的齿根过渡曲 线在实际中如何加工也是值得讨论的问题。假设齿廓 由标准滚刀加工而成，则滚刀刀顶圆角部分切出过渡 曲线为一外摆线［１０】１１４７。如果已知齿根过渡曲线为“超 椭圆”曲线，如何运用齿廓运动学方法反求滚刀刀顶曲 线将是作者以后研究的方向。
参考 文 献
［１］陈秀宁，丁红钢，卫世俊，等．渐开线齿轮齿根过渡曲线的优化研 究［Ｊ］．中国机械工程，１９９５，（０２）：５９—６０．

双圆弧正弦曲线齿型摘要：一、双圆弧正弦曲线齿型的概念和特点二、双圆弧正弦曲线齿型的设计方法三、双圆弧正弦曲线齿型的应用领域四、双圆弧正弦曲线齿型的发展趋势和前景正文：双圆弧正弦曲线齿型是一种常见的齿轮齿型，具有较高的传动效率和良好的抗磨损性能。

本文将对其概念、设计方法、应用领域以及发展趋势进行详细介绍。

一、双圆弧正弦曲线齿型的概念和特点双圆弧正弦曲线齿型是一种连续变螺旋角曲线齿型，其齿面为两个圆弧正弦曲线组合而成。

相较于传统的直齿和斜齿齿型，双圆弧正弦曲线齿型具有以下特点：1.传动平稳：双圆弧正弦曲线齿型的齿廓曲线较为平滑，使得齿轮传动过程中冲击和噪声减小，提高了传动平稳性。

2.齿面磨损均匀：双圆弧正弦曲线齿型的齿面磨损分布均匀，有利于延长齿轮的使用寿命。

3.良好的润滑性能：双圆弧正弦曲线齿型的齿面连续且螺旋角变化较小，有利于润滑油的分布和保持，降低了齿轮的磨损和故障率。

二、双圆弧正弦曲线齿型的设计方法双圆弧正弦曲线齿型的设计主要涉及齿廓曲线的设计和螺旋角的设计。

其中，齿廓曲线的设计需要考虑齿轮的啮合条件、齿面磨损均匀性等因素；螺旋角的设计则需权衡齿轮的传动性能、抗磨损性能等因素。

目前，双圆弧正弦曲线齿型的设计方法主要有解析法和数值法。

解析法主要包括数学解析法和工程计算法，其优点是计算简便，但适用范围有限。

数值法主要包括有限元法和遗传算法等，其优点是计算精度高，但计算复杂度较高。

三、双圆弧正弦曲线齿型的应用领域双圆弧正弦曲线齿型广泛应用于各种齿轮传动系统中，如汽车、船舶、飞机、工业机器人等。

尤其在高速、重载、高温等恶劣工况下，双圆弧正弦曲线齿型的优越性能更加明显。

四、双圆弧正弦曲线齿型的发展趋势和前景随着工业技术的不断发展，对齿轮传动性能的要求越来越高。

双圆弧正弦曲线齿型作为一种具有优良性能的齿轮齿型，其研究和发展将不断深入。

未来的发展趋势主要包括：1.大规模定制：通过计算机辅助设计和制造技术，实现双圆弧正弦曲线齿型的快速、精确和个性化定制。

2024年第48卷第2期Journal of Mechanical Transmission双圆弧齿廓椭圆齿轮建模与运动学仿真袁新梅杨立昭黄天成唐伟（长江大学机械结构强度与振动研究所，湖北荆州434023）摘要为了满足齿轮变传动比运动、提高轮齿承载能力，结合齿轮啮合理论和双圆弧齿廓曲线结构参数特征，提出了一种新型双圆弧齿廓椭圆齿轮。

阐述了其节曲线的设计方法，利用Solid⁃Works软件建立了双圆弧齿廓椭圆齿轮三维模型；使用Adams软件对双圆弧齿廓椭圆齿轮副模型进行了运动学仿真，分析了不同偏心率对双圆弧椭圆齿轮副传动比变化规律的影响，并对比理论传动比曲线，分析了仿真传动比曲线存在波动误差的影响因素；为了减小齿轮副振动脉冲，给出了偏心率适当的取值范围。

本文的设计方法和分析结果对双圆弧齿廓非圆齿轮的参数化设计有理论参考价值，可为双圆弧齿廓椭圆齿轮副数控加工制造及应用提供依据。

关键词双圆弧齿廓椭圆齿轮运动学仿真变传动比Modeling and Kinematics Simulation of Elliptical Gears with Double CircularArc ProfilesYuan Xinmei Yang Lizhao Huang Tiancheng Tang Wei(Institute of Strength and Vibration of Mechanical Structures, Yangtze University, Jingzhou 434023, China)Abstract In order to meet the requirements of variable transmission ratios and improve the bearing capac⁃ity of gear teeth, a new type of double-circular-arc tooth profile elliptical gear is proposed based on the meshing theory and the structural parameter characteristics of the double-circular-arc tooth circular profile curve. The design method of its pitch curve is described. A three-dimensional model of the double-circular-arc tooth circu⁃lar profile elliptical gear is established using SolidWorks software. Adams software is used to simulate the kine⁃matics of the elliptical gear pair model with double-circular-arc tooth profiles, and the influence of different ec⁃centricities on the variation rule of the double-circular-arc gear pair transmission ratio is analyzed; compared with the theoretical transmission ratio curve, the influencing factors of the fluctuation error of the simulation transmission ratio curve are analyzed. In order to reduce the vibration pulse of the gear pair, the appropriate val⁃ue range of eccentricities is given. The design method and analysis results in this study have theoretical refer⁃ence value for parametric design of non-circular gears with double-circular-arc tooth profiles, and can provide a basis for NC manufacturing and application of elliptic gear pairs with double-circular-arc tooth profiles.Key words Double-circular-arc tooth profile Elliptic gear Kinematics simulation Variable trans⁃mission ratio0 引言非圆齿轮具有结构紧凑、效率高、工作可靠、寿命长的特点，可以传递动力和变传动比运动[1]，在机械系统中常用于实现换向、摆动、周期运转和间歇运动等功能。

齿轮几何要素的名称、代号齿顶圆：通过圆柱齿轮轮齿顶部的圆称为齿顶圆，其直径用 d a 表示。

齿根圆：通过圆柱齿轮齿根部的圆称为齿根圆，直径用 d f 表示。

齿顶高：齿顶圆 d a 与分度圆d 之间的径向距离称为齿顶高，用 h a 来表示。

齿根高：齿根圆 d f 与分度圆 d 之间的径向距离称为齿根高，用 h f 表示。

齿顶高与齿根高之和称为齿高，以h 表示，即齿顶圆与齿根圆之间的径向距离。

以上所述的几何要素均与模数 m 、齿数z 有关。

齿形角：两齿轮圆心连线的节点Ｐ处，齿廓曲线的公法线（齿廓的受力方向）与两节圆的内公切线（节点P 处的瞬时运动方向）所夹的锐角，称为分度圆齿形角，以α表示，我国采用的齿形角一般为20°。

传动比：符号i ，传动比i 为主动齿轮的转速n 1（r/min ）与从动齿轮的转速n 2（r/min ）之比，或从动齿轮的齿数与主动齿轮的齿数之比。

即i= n 1/n 2 = z 2/z 1中心距：符号a ，指两圆柱齿轮轴线之间的最短距离，即：a=(d 1+d 2)/2=m(z 1+z 2)/2齿轮几何参数计算压痕法是在被测齿轮的齿顶涂色后，使其在一张纸上滚动，这张纸上就留下了齿顶滚过的痕迹，根据压痕作出齿顶线的延长线及辅助线，然后用量角器测量出齿向角度，该角即为齿轮齿顶处的螺旋角β，然后再根据齿轮其它几何参数，计算出齿轮分度圆处的螺旋角β。

1) 什么是「模数」？模数表示轮齿的大小。

R模数是分度圆齿距与圆周率（π）之比,单位为毫米(mm)。

除模数外,表示轮齿大小的还有ＣＰ（周节：Circular pitch）与ＤＰ（径节：Diametral pitch）。

【参考】齿距是相邻两齿上相当点间的分度圆弧长。

2) 什么是「分度圆直径」？分度圆直径是齿轮的基准直径。

决定齿轮大小的两大要素是模数和齿数、分度圆直径等于齿数与模数(端面)的乘积。

过去,分度圆直径被称为基准节径。

最近,按ISO标准,统一称为分度圆直径。

双圆弧正弦曲线齿轮摘要：1.双圆弧正弦曲线齿轮的概述2.双圆弧正弦曲线齿轮的特点与应用3.双圆弧正弦曲线齿轮的制造工艺4.双圆弧正弦曲线齿轮的优缺点分析5.双圆弧正弦曲线齿轮在我国的发展前景正文：一、双圆弧正弦曲线齿轮的概述双圆弧正弦曲线齿轮，是一种新型齿轮设计，其齿面为双圆弧形状，齿廓线为正弦曲线。

这种齿轮在传动过程中具有较高的平稳性和传动效率，逐渐在我国齿轮制造业中崭露头角。

二、双圆弧正弦曲线齿轮的特点与应用1.高平稳性：双圆弧正弦曲线齿轮的齿面形状和齿廓线设计使其在传动过程中具有较低的振动和噪音，提高了传动的平稳性。

2.高传动效率：双圆弧正弦曲线齿轮的齿廓线设计使其在啮合过程中齿面接触面积较大，减小了齿面滑动，从而提高了传动效率。

3.抗疲劳性能好：双圆弧正弦曲线齿轮的齿面形状和材料选择使其具有良好的抗疲劳性能，延长了齿轮的使用寿命。

4.应用广泛：双圆弧正弦曲线齿轮广泛应用于各类传动装置，如减速器、变速器等，尤其适用于高精度、高扭矩、低噪音的传动场合。

三、双圆弧正弦曲线齿轮的制造工艺1.锻造：通过锻造工艺生产出齿轮的毛坯，为后续加工提供基础。

2.粗加工：采用车削、铣削等加工方法，初步加工出齿轮的齿形。

3.精加工：采用齿轮磨削、滚齿等精密加工方法，精确加工出齿轮的齿形。

4.热处理：对齿轮进行热处理，提高齿轮的硬度和强度。

5.装配：将齿轮与传动轴等其他部件装配在一起，形成完整的传动系统。

四、双圆弧正弦曲线齿轮的优缺点分析优点：1.平稳性好，噪音低。

2.传动效率高，节省能源。

3.抗疲劳性能好，使用寿命长。

4.适应性强，应用范围广。

缺点：1.制造工艺复杂，成本较高。

2.对材料性能要求较高，材料成本增加。

五、双圆弧正弦曲线齿轮在我国的发展前景随着我国科技实力的不断提升和制造业的快速发展，双圆弧正弦曲线齿轮在我国的应用将越来越广泛。

此外，我国正大力推动绿色制造和智能制造，双圆弧正弦曲线齿轮的高传动效率和低噪音特性使其成为未来传动领域的重要研究方向。

双圆弧正弦曲线齿轮
双圆弧正弦曲线齿轮是一种特殊类型的齿轮，它的齿形由两个相互连接的圆弧形成，而不是传统的直线或曲线齿轮。

这种齿轮的齿形曲线是基于正弦函数生成的。

双圆弧正弦曲线齿轮具有以下特点：
1. 齿形平滑：由于齿形曲线是基于正弦函数生成的，所以齿轮的齿形曲线是连续的圆弧形状，使得齿轮之间的接触更加平滑，减少了噪音和振动。

2. 齿轮传动效率高：正弦曲线齿轮的齿形曲线与传统的齿轮相比更加光滑，减少了齿轮之间的相对滑动，提高了传动效率。

3. 可实现更高速比：由于齿形曲线是连续的圆弧形状，双圆弧正弦曲线齿轮可以实现更高的速比。

4. 制造难度较高：双圆弧正弦曲线齿轮的制造难度较高，需要精确的计算和加工。

双圆弧正弦曲线齿轮在一些需要高精度和低噪音的应用中较为常见，例如高精度仪器、机械传动系统等。

齿厚si rf
rb
齿槽宽ei
ra r ri
分度圆 齿顶圆 基圆 齿根圆
上同，Pb一一其圆个模上齿d数b轮的p/ 在zi大不小同是ms直i不co径同s的的ei圆。周
三轮上•高齿的分是基计模是度决本齿齿齿算数齿圆定参齿顶根全的和轮渐数数高高高基压上开。，hhh准力一a线模f 圆角个形数。为人状，h规标为的压定准地三力h分值约个角a 度。定 圆的hf
2、压力角α：∵COSακ=rb/rk 由渐开线特性可知，齿廓 各点的压力角不等，为了便于设计、制造及互换使用，将齿 轮分度圆上的比值规定为标准值，并使该圆上的压力角规定 为标准值。我国规定标准压力角α=20°。
6
顶隙（也称径向间隙）
顶隙 —— 一对相互啮
合的齿轮中，一个齿轮
的齿根圆与另一个齿轮
的齿顶圆之间在连心线
国标压力o角的标准值为=20°
模数的标准系列见GB1357-87 分度圆上的参数分别用d、r、 m、p、e及表示。
p m ，d mz
当基圆半径趋 向无穷大时，齿轮 变成齿条，齿轮上 的各圆都变成齿条 上相应的线，齿条 上同侧齿廓互相平行，所以齿廓上任意点的齿距都相等， 只有在分度线上的齿厚和齿槽宽才相等
o2
a

r1
r2

r1

r2

m 2
( z1

z2 )
8
3、齿顶高系数ha*：为了使齿形匀称（ha=ha*m），正常齿 ha*=1 4、径向间隙系数C*：径向间隙是指一对齿啮合时，一个齿 轮的齿顶圆到另一个齿轮的齿根圆的距离，C=C*m，正常齿 C*=0.25 5、齿数Z：与传动比有关
公法线长度
标准直齿圆柱齿轮的所有尺寸均可用上述5个参数来表 示，几何尺寸的计算公式见表11.4

齿轮基本参数概念和参数计算----------项子澄6-11于五征前言齿抡中主要数学基础是几何,三角和解析几何,还有一点微积分,所以无需高深的数学.只有研究螺旋伞齿时才需要.但它很繁琐,要对各参数的相互关系有很清晰的几何概念并非易事.有人一直从事齿变速箱设计数十年,他能按公式计算齿轮但他对齿轮的概念很不清晰.一旦遇到计算矛盾就难着手分析.这次讲课重在概念和实用及与概念有关的公式推导.我对所讲到的所有公式都进行过推导如有要深入研究可问我.再有欢迎课堂中提问希望变被动学习为主动一,渐开线形成原理(图一)如图一可看作一条绳子的端点绕圆r b展开,或一根竿子在圆r b上滚动其端点的轨迹.如A⌒K⌒E即为渐开线. r b圆(NO)即为基圆..图中α角为啮合角(压力角),φ为渐开线展开角, θ为渐开线函数角,.KN为K点的曲率半径ρ..以上几个参数非重要.请注意它们角度关系r b----------基圆α-----压力角φ-----渐开线展开角,θ-----渐开线函数角ρ(如图KN)----- K点的曲率半径=N⌒A二, 渐开线性质(图二)1,2,渐开线上任何一点的法线必切于基圆r b3,渐开线形状只取决于基圆r b的大小4,当基圆r b=∞时渐开线为直线∴可用齿条刀具加工齿轮5,ρ=kN-----是K点的曲率半径, ρ=kN-=N⌒A弧长6,一对渐开线齿啮合的充分和必要的条件是它们的基节相等.(见图三,以后节讲)7,所谓变位齿轮就是其齿形在渐开线上选用不同的区段.(见图三,在下一节讲)三, 渐开线方程因极坐标方便直观我们只讲极坐标方程.(如图二)以O为座标原点,由⊿ONK可得r k=OK= r b/Cosαk---------------(1) 式中r b = ON, r k =OKθk=tgαk-αk---------------(2) (从直观可见, 当用弧度表示θk和αk时即得此式(证明:θk=φK-αk∵长度NK= N⌒A弧长∴, N⌒A弧度= (N⌒A弧长/ r b-) = (NK/ r b)= tgαk)θk称为渐开线角θk=invαk= tgαk-αk-.这是个超越函数. inv是involute 的缩写invαk称为渐开线函数亦可得ρ= r b tgαk------------------(1)’三渐开线齿轮基本知识1分类斜齿轮(1)圆柱齿轮直齿轮蜗轮蜗杆直锥齿轮(2,)锥齿轮 格里森螺旋伞齿抡 奥林肯 双曲线齿轮克林根贝尔格2功能:两者都可为改变传动比, 传动力和换向3,左右旋向的确定.伸出双手,手心向上,齿轮的轴心线与手一致.观察旋线和那个大呣指一致,4,齿轮所涉及的内容齿形的设计计算强度计算齿轮精度及公差齿轮测量齿轮加工工艺材料选用和热处理5,为什么渐开线齿轮被广泛地被使用有保证稳定传动所必须的性能即当传入稳定的转速和扭矩时传出的转速和扭矩亦必须稳定的,这就要求作用在齿面上的法向力和变角速度相对于齿整体轮是不变的(见四(8)节).而渐开线齿形能做到这点 中心距变化后啮合仍符合啮合条件(见五节).制造简单可广泛使用变位齿轮大大改善性能(见五节)四,一对标准齿轮相啮合的啮合特性(见图三)1分度圆r 或d(直径)------齿轮在加工时与刀具作纯滚动的圆称为分度圆加工两O 1齿O 2齿标准齿轮时O 1齿O 2齿的r 1和r 2与刀具节线GPS 作纯滚动.此处刀具的齿厚=齿槽宽d=mZ-------------(3) (有了d后可定义m=d/Z称模数是表示齿大小有量刚的比值系数,Z为齿数)2,节点P, 即两齿轮作纯滚动的圆的切点.两齿啮合时,按齿数比例分割中心连线O1O2的点必为节点P.它的圆为节圆.单个齿不存在节点P标准齿轮啮合时,既然r1和r2都与刀具节线GPS作纯滚动∴r1和r2之间亦作纯滚动. ∴两O1齿O2齿标准齿轮的分度圆与节圆重合3,α1,α2-------分度圆压力角.即滚刀刀具压力角,或齿轮加工时与刀具作纯滚动的点上的压力角.或者说齿轮被加工时的节点上的压力角.. 分度圆压力角=刀具压力角一对标准齿啮合啮合时其节圆和分度圆重合α=.α’4,r e1和r e2--------齿顶半径5,r b1和r b2-------基圆半径由⊿PO1N1可得r b =r Cosα------------(4)6,PP’------周节p—在分度圆上相邻两齿廓的圆弧距离. p=mπ-----(5)∵在分度圆上齿轮的齿厚S=齿槽宽, ∴S= p/2= mπ/2--------------(6)(由圆周长L=πd p=L/Z可求得)7,EE’------基节p b----在基圆上相邻两齿廓的圆弧距离.p b= p Cosα------------(7)8,N1N2-----由图三知,两基圆相切的切点连线称为啮合线. 该对齿在啮合时一定在N1N2上接触啮合.∵(1)一对齿啮合时它们的法线方向是一致的,(2)根据渐开线的特性该点的法线必分别切于基圆r b1和r b2-(3)∴唯有此线即N1N2线能满足(1)(2)要求∴将N1N2线称为啮合线. 既然两齿始终沿N1N2线接触方向不变∴这两齿只能同步前进.在啮合啮合线上的啮合角即为节圆压力角.这是相对于成对啮合齿轮而言(而不是相对于某一牙齿的齿廓,一对齿轮的啮合角和此点的压力角的定义是不同的(,见图三’和图十一)9,既然两齿在N1N2线上作方相始终不变能稳定地传递扭矩和运动.在N1N2线走过的路程即为基圆滚过的路程亦就是O1和O2齿轮所滚过的基节是相等的. ∴两齿啮合的最基本的条件是两齿的基节必须相等另由图三’,当两齿啮合点不在节点P上,而是转到γ点接触时,作用力对整个齿轮而言相对于O1O2中心线的啮合角仍为α但对单齿形的压力角为αK10, AB--------啮合线的工作区(图三). A和B分别为O1和O2齿轮的外圆与啮合线的交点A和B(1)假如O1为主动齿轮,则啮合从A点开始到B点脱开. 外径越大啮合线的工作区越长(2).AB长与基节p b之比即为啮合重合系数ε(3)A点在基点N1之上则可正确啮合,否则会产生啮合干涉如这现象发生在加工,则产生根切..五, 变位或移距齿轮啮合时的重要关系式(见图四,图五和图六)(一),基本特征1,移距的加工特徴(见图四)红色的齿形和刀具是标准齿此时AA线既是刀具的分度线又是刀具的加工节线.与齿轮的分度圆r相切于AA线P点.刀具在AA线上的齿厚=齿槽即PG=GS(亦=齿轮的分度圆弧齿厚).绿色为加工正移距的齿形的刀具图.此时刀具的分度线从AA移到A’A’,移距量为ξm, 此时刀具在原AA上的齿槽变宽为P’’G’’而齿厚相应变窄G’’S’’,其变化值由⊿P P’P’’可知为ΔS=2ξm,tgα,----------------(8) (ξ为移距系数(或称变位系数,修正系数)它的标准符号用χ表示,但∵χ与x和乘号X很近∴我用ξ)注意: 此时加工的节线仍为AA,机床的挂轮没有变仅仅是将刀具外移∴齿轮的分度圆亦仍为r但此时刀具在绿线A”A”上的齿厚=齿槽,即P’G’=S’G’而刀具在家工节线上的齿厚P’’G’’增加了ΔS=2ξm,tgα亦就是齿轮在分度圆上的齿厚增加了2ξm,tgα.齿轮的外径亦由r e1变为r’e1就是说正移距齿具有(1) 渐开线齿形外移(2)齿厚变厚(3)齿顶高h a变高(以分度圆为界)2移距齿轮啮合时的特徴(见图五)(1) 如图五当(ξ1+ξ2)＞0时称为正移距角度变位齿轮付时,图红色圆为节圆,其半径=r’,青色圆为分度圆, 其半径=r* 图例为是ξ1和ξ2都为正时的状况图即r’＞r,即为正移距角度变位齿轮付此时α’ >α(**当r’＜r时为负移距角度变位齿轮付, 即(ξ1+ξ2) ＜0, 此时α’<α(略)正移距角度变位齿轮付的直接特徴α’ >αA’ >AS’ >S(2)如图六当(ξ1+ξ2) =0或ξ1 =(-ξ2 )≠0 此时r’＝r为零移距角度变位齿轮付即此时α’=α即节点的啮合角=分度圆压力角现分析(ξ1+ξ2) =0的几何关系:O1齿分析:这是标准齿轮啮合关系O1齿的相应齿条刀槽是Ggcp P槽(图六)如果将刀具向上移动ξm,距离来加工O1,齿,(见图六)就是将原加工标准齿的刀具节线APA向上移到A’A’,而其它加工的运动关系不变,即加工时的刀具节线和齿O1的加工节圆r1不变r1仍为分度圆,而刀具的分度线变为A”A’在其上的bp=pg而在刀具加工节线AA上GP＞PB则此时弧齿厚P⌒u由原bp增到GP.增量ΔS=GP-pg=2ξm,tgα,O2齿分析: O2为负移具,其刀具的分度线同样由AA移到A’A’而加工节线仍为AA线∴O2的分度圆仍为r2∵是反相移距, ∴可将p P eBb看作刀具齿槽来切O2齿,显然O2的分度弧圆齿厚S2=P B,其厚度少了ΔS=pb-PB = 2ξm,tgα,结论:由于O`1和O2移距大小相等方向相反它们分度圆上的齿厚变化亦是大小相等正负相反它们在分度圆上接触条件没有变只是将分度圆上的齿厚相互增减∴分度圆和节圆重合..(二), 移距齿轮啮合时的α’和α的关系式(见图五)由⊿N1O1P得Cosα’=r b/r’---------------(9)得r b=r’Cosα’------------(10)或r’= r b / Cosα’--------------(11)由青色的直角三角形⊿P0O1 N0中可得r b=r Cosα-----------(12)(10)=(12)得,Cosα’= r1 Cosα/ r’1-----(13)∵中心距A,A’与半径r,r’是成比例的∴(13) 式可改为Cosα’= A Cosα/ A’--------(14)即当知道A’便可知节圆压力角α’六,变位对齿形的影响(或称移距,修正)见图七由于使用标准齿齿轮时易造成根切,其齿厚及因渐开线靠近基圆的曲线段使其啮合性能不佳等原因在齿轮设计时多采用变位.1,齿厚变化(见图七)图中r为分度圆也就是加工时的节圆MM为刀具加工节线,此时刀具的刀刃ABCD范成出齿廓为标准齿(见白色线齿廓),齿轮上分度圆弧齿厚如分度圆上的S⌒S,=刀具在节线上的齿槽SS.即SS=S⌒S当刀具向外移动ξm(ξ为移具系数, m为模数),值即刀具原节线MM移倒M’M’.即刀具的位置改为A’B’C’D’请注意(1)此时分度圆和加工节线不变仍分别为r和MM, 只是刀具外移.(2)M’M’此时是刀具的分度线,在齿线上刀具的齿厚=刀具的齿的齿槽.(3)此时刀具在加工节线上的齿槽SS变为S’S’∴刀具移距后所对应的齿轮分度圆弧齿厚为S’⌒S’=S’S’令ΔS=S’S’-SS=2ξm tgα-------------(15)2,齿廓变化(见图七)如图齿廓由白色齿廓变为青色齿廓. 齿廓外移(或内移)则造成齿轮啮合一系列性能变化可供我们选择(以后讨论)3,分离系数的产生.(图八所示是一对都为正移距齿的啮合的关系图)当(ξ1+ξ2)≠0时就会有(ξ1+ξ2)m≠ΔA=A’-A的现象.令(ξ1+ξ2)-ΔA/m=λ叫作分离系数如图D-D线------是齿条刀刀具的刀刃(红线所示)M-M线-----同是O1齿轮和O2齿轮作标准齿加工时的刀具分度线.(但不是加工节线)即为(图八)中的MM在此线上刀具的齿厚=刀具的齿槽宽∵O1和O2两齿轮都作正移距加工M1M1线-----是O1齿轮的加工时的节线,圆r1即O1齿的分度圆M2M2线-----是O2齿轮的加工时的节线,圆r2即O2齿的分度圆法线N1P1∥N2P2是两加工节点的压力角即分度圆压力角线r01,r o2 为基圆半径E1点和E2点----是刀刃在D-D加工位置同时用左右刀刃分别在切削O1和O2的齿廓E1点和E2点标(其中假设E1和P1是重合的.)．由图,其总移距量和为(ξ1+ξ2)m,假定图中的中心距按O1O2= (r1+r2)+ (ξ1+ξ2)m, 令=A’’注意:如此时将刀刃D-D拿走则会发现O1和O2的齿廓并不接触.只有将中心距移近一点才能使O1和O2的齿廓作无齿隙啮合.这移近的距离称为分离值令=ΔA=λm λ称为分离系数∴结论:对于角变位齿轮付,两齿作无齿隙啮合时的中心距A’≠(r1+r2)+ (ξ1+ξ2)m,而是应为A’ =(r1+r2)+ (ξ1+ξ2)m-λm--------------(16)令(ξ1+ξ2)= ξ c 令(r1+r2)=A 代入(11)得A’=A+ξ c m-λm-----------------(17)λ值可推算得λ=((Z1+Z2)/2)((Cosα/ Cosα’)-1)-----------------(18)或可从手册中根据Z1和Z2查得相对分离系数σ0值σ0=λ/(Z1+Z2)-----------------(19)七,齿轮基本要素.(见图九)GB规定压力角为20°标准齿顶高系数为1其实质就是当齿数Z和模数m确定后为你划定了你所使用的渐开线的性质和使用此渐开线的区段.齿形移距是改变使用此渐开线的区段但不改变渐开线的性质.确定齿轮要素应按GB的规定,但测绘引进国外产品则按原机或原图基本要素: .(见图九)Z-----齿数r,或d---分度圆半径或直径,是与加工刀具作纯滚动的圆d=Z m--------------(20)m----是显示齿厚等齿轮尺寸大小的比例参数.它和齿形特征无关只和大小有机联系着m= d/Z------------------------(21)r’-----节圆半径,是一对齿啮合时作纯滚动的圆半径,单个齿不存在r’(见图五)r’= r b / Cosα’-------------------------------见前式(11)r b ---基圆半径- r b=r Cosα-----------------见前式(12)α-----刀具压力角,或称分度圆压力角.我国标准为20°α’----节圆压力角Cosα’=r b/r’--------------(不存单个齿在见图五)-见前式(9)h------齿全高= ha-+ hf- ------(22) GB规定ha-= m h-=2.25 mha----齿顶高(以分度圆为界)标准齿顶高ha-= m--------(23)h f----齿根高标准齿根高h f-=1.25--------------------24r a,- --d a,-----外径标准齿的外径d a,=d+2 ha------------------(25)r f- --d f,------根径标准齿的外径d f,=d+2 hf--------------------(26)p-----周节, 是在分度圆r上相邻齿廓的弧长p=πm-------见前(5)p b---基节是在基圆r b上相邻齿廓的弧长p b-= p Cosα---见前(7)标准齿分度圆弧齿厚S=πm-/2-------------------------------见前(6)移距后分度圆弧齿厚S=(6)式+(15)式=(πm-/2)+ 2ξm tgα---------(27)八, 齿轮齿厚测量计算齿厚测接触量参数有分度圆弦齿厚,S(如图九aq,或vb的弦长),固定弦齿厚,Sc(见图七AB)公法线长度W,量棒距M几种.∵当采用常规的齿轮卡尺来测量分度圆弦齿厚和固定弦齿厚时,其精度不高,在圆柱齿上少采用但近来开始应用光学仪器测量其精度较高但仍少用于生产线上.不过在直锥齿轮的齿厚测量中度圆弦齿厚和固定弦齿厚被广泛应用∴这里不讲了.此处只将公法线长度W,量棒距M的计公式. ∵W和M都是无基准测量(即以齿形本身为基准).很方便当精度亦很高∴被广泛应用1, 公法线长度测厚度(见图九),(1)如卡n个齿就有(n-1)个齿槽如图九卡2个齿有1个齿槽.2个齿,依此类推.(2) 公法线长度W=AB线,切于基圆. r b 切点在齿槽中心线(卡偶数齿)或齿厚中心线(卡奇数齿)(3) 弧齿厚S与公法线长度W的关系:所谓齿厚是指分度圆上的弧齿厚S,如图=a⌒q弧长.公法线长度AD实际上测的是n个基节齿厚+(n-1)个基节齿槽宽,即(n-1)个基节+1个基节齿厚. 公法线长度AD=基圆E⌒F弧长∴公法线长度AD与分度圆上的弧a⌒b弧长的关系即为基圆E⌒F弧长与分度圆上的弧a⌒b弧长的关系. 但它们不是简单地分度圆半径r与基圆半径r b的关系.根据公法线长度AD实际上测的是(n-1)个基节+1个基节齿厚由图九’(a)先看看可基节与周节的关系: 对比基节的夹角与周节的夹角,可见周节夹角在左侧少了个θ角则在右侧多了一个θ角∴它们的夹角都是(2π/Z) ∴基节与周节的关系亦就分度圆半径r与基圆半径r b的关系.再由图九’看看分度圆弧齿厚与基节厚的关系:由图可知基节的夹角比周节大2θ角∴它们不是简单的比例关系.当齿厚增加后,由图九’’可知由于移距后分度圆弧齿厚加厚,但绿色齿廓(移距后)和白色齿廓(移距前)其两厚度虽不同但其θ角是相同的∴新增加的分度圆弧齿厚ΔS与基节上增加的ΔS b之间的关系应是分度圆半径r与基圆半径r b的关系. 即ΔS b=ΔSCosα∵ΔS b=ΔW代入(15)式得ΔS b=ΔW=ΔSCosα=2ξm Sinα------------------------------(15)’这就是弧齿厚增量与公法线增量的关系式(4)W值只反映理论弧齿厚本身的厚度是不能反应当齿轮因变形产生椭圆或另件安装定位误差造成的径向跳动引起对某齿的分度圆直径变化所造成分度圆上的弧齿厚变化(可以九图为例)(5)能反应因加工分度误差造成的齿厚误差和机床主轴的定位误差所造成的齿厚误差(6)它能测量运动精度所要求的公法线长度变动量F W(7)W所测的厚度是所卡齿数的平均值不是某个单齿(8)公法线长度W的计算机公式由图九知公法线长度AD=E⌒H+H⌒F即一个基节t b-加一个基圆弧齿厚Sb,可以类推,如卡3个齿则公法线长度=二个基节t b-加一个基圆弧齿厚S b具体的公式推导省略有愿深入者可随时找我.标准齿的公法线长度W0公式W0=m Cosα(π(n-0.5)+Z invα)---------------------(28)式中n--------为所卡齿数,inv------是渐开线函数变位齿的公法线长度W公式∵由于变位造成的分度圆弧齿厚增量ΔS可由式(15)’ΔW=ΔSCosα=2ξm Sinα----------------------------(29)W= W0 +ΔW= W0 +2ξmSinα= m Cosα(π(n-0.5)+Z invα)+ 2ξmSinα---------------(30)对于斜齿轮只需将invα改为invαt即W= m Cosα(π(n-0.5)+Z invαt)+ 2ξmSinα----------(30)’αt为端面压力角tgαt=tgα/Cosβ式中β为螺旋角(8)所卡齿数n的计算. 当压力角α=20°时n≈0.1111Z+0.5---------------------------------------(31)2跨棒距M测量(见图十)(1)如图十跨棒距M就是量棒中心的尺寸OO’加量棒直经Dp 即M=OO’+dp------------------(32)(2)M的测量精度比公法线长度W高,亦是无基准测量(即以齿形本身为基准)∴检测方便(3)M是能用直接接触测量法测量内齿轮的唯一方法M能测量与基准无关的齿轮自身的椭圆度,不能反映几何偏心,加工偏心造成的齿形变化M所测出的齿厚是两个齿的平均齿厚值当压力角α=20°时,量棒直径大致为dp =1.476m---------------(33)(8) 计算无变位直齿标准齿轮M的步骤及其公式(a)先求出量棒中心点O’(或称量棒接触点)的压力角αM其公式为:invαM=invα±(dp/Zm Cosα) -/+(π/2Z)---------(34)斜齿: invαMt=invαt±(dp/Zm Cosα) -/+(π/2Z)-----(34)’注；在±和-/+中,分子用于外齿轮,分母用于内齿轮(b)求M值M= (Zm Cosα/Cos αM) ±dp (偶数齿)------------------(35)其中(Zm Cosα/ CosαM)即(32)式中的OO’斜齿: M= (Zm t Cosαt/Cos αMt) ±dp (偶数齿)------------------(35)’M= (Zm Cosα/ CosαM)( Cos(90°/Z))±dp (奇数齿)-------(36)斜齿: M=(Zm t Cosαt/CosαMt)( Cos(90°/Z))±dp (奇数齿)-------(36)(9) 计算变位非标准直齿轮M’的步骤及其公式(图十)(a)先求出量棒中心点O’的压力角αMinvαM=invα±(dp/Zm Cosα) -/+(π/2Z)+(2ξtgα/Z)-----(37)斜齿: invαMt=invαt±(dp/Zm Cosα) -/+(π/2Z)+(2ξtgα/Z)-(37)’(b) 求M’值: 同(35) (36)式至此我们可开始个种齿轮计算如何合理选取参数是一个综合性的问题等以后可作专题讲座.在我过去设计时都已编程20多程序. 现将常用几个程序给大家供参考只要将红色的参数输入即可得出结果数值.具体有:(计算程序中所使用的公式的符号是我自已常用得符号)1,成对齿轮验算2,单直齿求L(W)值,3单斜齿求L(W)值4,成对齿求L(W)值5,求M值(外斜齿)6求M值(内斜齿)7求任一点的弧齿厚。

双圆弧正弦曲线齿型
（原创实用版）
目录
1.双圆弧正弦曲线齿型的定义
2.双圆弧正弦曲线齿型的特点
3.双圆弧正弦曲线齿型的应用
4.双圆弧正弦曲线齿型的优缺点
正文
双圆弧正弦曲线齿型是一种齿轮设计方式，其齿廓曲线由两个圆弧和正弦曲线组成，因此被称为双圆弧正弦曲线齿型。

这种设计方式使得齿轮的接触面积更大，传动效率更高，噪音更小，因此在各种机械传动系统中得到了广泛的应用。

双圆弧正弦曲线齿型的最大特点是其齿廓曲线的设计。

由于其曲线由两个圆弧和正弦曲线组成，使得齿轮的齿廓更加平滑，接触面积更大，因此能够承受更大的载荷，具有更高的传动效率和更小的噪音。

双圆弧正弦曲线齿型在各种机械传动系统中都有应用，例如在汽车、机床、电梯等领域的齿轮设计中，都可以看到双圆弧正弦曲线齿型的身影。

双圆弧正弦曲线齿型的优点主要体现在其接触面积大、传动效率高、噪音小等方面。

然而，其设计与制造过程相对复杂，成本较高，这也是其应用范围的主要限制。

第1页共1页。

1，齿数z一个齿轮的轮齿总数。

2，模数m齿距与齿数的乘积等于分度圆的周长，即pz=πd,式中z是自然数，π是无理数。

为使d为有理数的条件是p/π为有理数，称之为模数。

即：m=p/π3，分度圆直径d齿轮的轮齿尺寸均以此圆为基准而加以确定，d=mz4，齿顶圆直径da和齿根圆直径df由齿顶高、齿根高计算公式可以推出齿顶圆直径和齿根圆直径的计算公式：da=d+2ha df=d-2hf=mz+2m=mz-2×1.25m=m(z+2)=m(z-2.5)5，模数z:齿轮的分度圆是设计、计算齿轮各部分尺寸的基准,而齿轮分度圆的周长=πd=z p,于是得分度圆的直径d=z p/π由于在上式中π为一无理数,不便于作为基准的分度圆的定位.为了便于计算,制造和检验,现将比值p/π人为地规定为一些简单的数值,并把这个比值叫做模数(module),以m表示,即令其单位为mm.于是得:模数m是决定齿轮尺寸的一个基本参数.齿数相同的齿轮模数大,则其尺寸也大.为了便于制造,检验和互换使用,齿轮的模数值已经标准化了.6，分度圆直径d：在齿轮计算中必须规定一个圆作为尺寸计算的基准圆，定义：直径为模数乘以齿数的乘积的圆。

实际在齿轮中并不存在，只是一个定义上的圆。

其直径和半径分别用d和r表示，值只和模数和齿数的乘积有关，模数为端面模数。

与变位系数无关。

标准齿轮中为槽宽和齿厚相等的那个圆（不考虑齿侧间隙）就为分度圆。

标准齿轮传动中和节圆重合。

但若是变位齿轮中，分度圆上齿槽和齿厚将不再相等。

若为变位齿轮传动中高变位齿轮传动分度圆仍和节圆重合。

但角变位的齿轮传动将分度圆和节圆分离。

7，压力角α——在两齿轮节圆相切点P处，两齿廓曲线的公法线（即齿廓的受力方向）与两节圆的公切线（即P点处的瞬时运动方向）所夹的锐角称为压力角，也称啮合角。

对单个齿轮即为齿形角。

标准齿轮的压力角一般为20”。

小压力角齿轮的承载能力较小；而大压力角齿轮，虽然承载能力较高，但在传递转矩相同的情况下轴承的负荷增大，因此仅用于特殊情况。

同步带轮（同步带轮（Pulley Pulley Pulley））圆弧齿同步带轮Arc tooth timing tooth梯形齿同步带轮Dimension of linear type pulley1、同步带轮的型式(Pulley Types)2、齿型尺寸、公差及技术参数(Dimension,Tolerances&Technical Parameters)3、各种型号同步带轮齿面宽度尺寸表(Dimension of Pulley Tooth Flank Width)单圆弧齿轮传动小齿轮的凸齿工作齿廓在节圆以外，齿廓圆心在节圆上；大齿轮的凹齿工作齿廓在节圆内﹐齿廓圆心略偏於节圆以外(图2单圆弧齿轮传动的嚙合情况)。

由於大齿轮的齿廓圆弧半径p2略大於小齿轮的齿廓半径p1﹐故当两齿廓转到K 点﹐其公法线通过节点c 时﹐齿便接触﹐旋即分离﹐但与它相邻的另一端面的齿廓随即接触﹐即两轮齿K1﹑K'1﹐K2﹑K'2﹑K3﹑K'3……各点依次沿嚙合线接触。

因此﹐圆弧齿轮任一端面上凹﹑凸齿廓仅作瞬时嚙合。

一对新圆弧齿轮在理论上是瞬时点嚙合﹐故圆弧齿轮传动又常称为圆弧点嚙合齿轮传动。

轮齿经过磨合后﹐实际上齿廓能沿齿高有相当长的一段线接触。

圆弧齿轮传动的特点是﹕(1)综合曲率半径比渐开线齿轮传动大很多﹐其接触强度比渐开线齿轮传动约高0.5～1.5倍﹔(2)两轮齿沿嚙合线方向的滚动速度很大﹐齿面间易於形成油膜﹐传动效率较高﹐一般可达0.99～0.995﹔(3)圆弧齿轮沿齿高方向磨损均匀﹐且容易跑合﹔(4)圆弧齿轮无根切现象﹐故最小齿数可以少。

但圆弧齿轮对中心距﹑切齿深度和螺旋角的误差敏感性很大﹐这三项误差对承载能力影响较大﹐故圆弧齿轮对製造和安装精度要求较高。

此外，单圆弧齿轮轮齿弯曲强度较弱﹔切削同一模数的大、小齿轮，需用两把不同的滚刀切削，并严格控制装配误差.双圆弧齿轮传动工作时，从一个端面看，先是主动轮齿的凹部推动从动轮齿的凸部，离开后，再以它的凸部推动对方的凹部，故双圆弧齿轮传动在理论上同时有两个接触点，经跑合后，这种传动实际上有两条接触线，因此可以实现多对齿和多点嚙合。

逐渐逼近，直至上方出现"ok!" 下方是超越方程结果 (最低也能精确到0.4") 1.10274717600038,不行
名义弦齿深ha
当前时间： 2016/7/14 15:06
2009.11.18 跨齿数Ka 全齿高 齿顶高
结果
ห้องสมุดไป่ตู้
39110274717600038不行端面压力角ta计算结果双圆弧圆柱齿轮主要测量尺寸计算公式输入参数螺旋角只需填写红框内参数模数m端面压力角初次输入0
双圆弧圆柱齿轮主要测量尺寸计算公式 张永 输入参数 计算结果 模 齿数 公法线长度W 螺旋角β 分度圆d 端面压力角 数 Z 度 分 秒 αta 请调整端面压力角 Mn 5 123 25 20 33 0.46164 弦齿厚Sa 测量齿高ha 0.46164536 只需填写红框内参数 端面压力角初次输入0.45, 上方是αta值(效验用) 齿顶圆直径da 齿根圆直径df

齿轮基本参数和概念齿轮基本参数概念和参数计算----------项⼦澄6-11于五征前⾔齿抡中主要数学基础是⼏何,三⾓和解析⼏何,还有⼀点微积分,所以⽆需⾼深的数学.只有研究螺旋伞齿时才需要.但它很繁琐,要对各参数的相互关系有很清晰的⼏何概念并⾮易事.有⼈⼀直从事齿变速箱设计数⼗年,他能按公式计算齿轮但他对齿轮的概念很不清晰.⼀旦遇到计算⽭盾就难着⼿分析.这次讲课重在概念和实⽤及与概念有关的公式推导.我对所讲到的所有公式都进⾏过推导如有要深⼊研究可问我.再有欢迎课堂中提问希望变被动学习为主动⼀,渐开线形成原理(图⼀)如图⼀可看作⼀条绳⼦的端点绕圆r b展开,或⼀根竿⼦在圆r b上滚动其端点的轨迹.如A⌒K⌒E即为渐开线. r b 圆(NO)即为基圆..图中α⾓为啮合⾓(压⼒⾓),φ为渐开线展开⾓, θ为渐开线函数⾓,.KN为K点的曲率半径ρ..以上⼏个参数⾮重要.请注意它们⾓度关系r b----------基圆α-----压⼒⾓φ-----渐开线展开⾓,θ-----渐开线函数⾓ρ(如图KN)----- K点的曲率半径=N⌒A⼆, 渐开线性质(图⼆)1,圆上任⼀点都可向左向右各展开⼀条渐开线,圆内⽆渐开线2,渐开线上任何⼀点的法线必切于基圆r b3,渐开线形状只取决于基圆r b的⼤⼩4,当基圆r b=∞时渐开线为直线∴可⽤齿条⼑具加⼯齿轮5,ρ=kN-----是K点的曲率半径, ρ=kN-=N⌒A弧长6,⼀对渐开线齿啮合的充分和必要的条件是它们的基节相等.(见图三,以后节讲)7,所谓变位齿轮就是其齿形在渐开线上选⽤不同的区段.(见图三,在下⼀节讲)三, 渐开线⽅程因极坐标⽅便直观我们只讲极坐标⽅程.(如图⼆)以O为座标原点,由⊿ONK可得r k=OK= r b/Cosαk---------------(1) 式中r b = ON, r k =OKθk=tgαk-αk---------------(2) (从直观可见, 当⽤弧度表⽰θk和αk时即得此式(证明:θk=φK-αk∵长度NK= N⌒A弧长∴, N⌒A弧度= (N⌒A弧长/ r b-) = (NK/ r b)= tgαk)θk称为渐开线⾓θk=invαk= tgαk-αk-.这是个超越函数. inv是involute 的缩写invαk称为渐开线函数亦可得ρ= r b tgαk------------------(1)’三渐开线齿轮基本知识1分类斜齿轮(1)圆柱齿轮直齿轮蜗轮蜗杆直锥齿轮(2,)锥齿轮格⾥森螺旋伞齿抡奥林肯双曲线齿轮克林根贝尔格2功能:两者都可为改变传动⽐, 传动⼒和换向3,左右旋向的确定.伸出双⼿,⼿⼼向上,齿轮的轴⼼线与⼿⼀致.观察旋线和那个⼤呣指⼀致,4,齿轮所涉及的内容齿形的设计计算强度计算齿轮精度及公差齿轮测量齿轮加⼯⼯艺材料选⽤和热处理5,为什么渐开线齿轮被⼴泛地被使⽤有保证稳定传动所必须的性能即当传⼊稳定的转速和扭矩时传出的转速和扭矩亦必须稳定的,这就要求作⽤在齿⾯上的法向⼒和变⾓速度相对于齿整体轮是不变的(见四(8)节).⽽渐开线齿形能做到这点中⼼距变化后啮合仍符合啮合条件(见五节).制造简单可⼴泛使⽤变位齿轮⼤⼤改善性能(见五节)四,⼀对标准齿轮相啮合的啮合特性(见图三)1分度圆r或d(直径)------齿轮在加⼯时与⼑具作纯滚动的圆称为分度圆加⼯两O1齿O2齿标准齿轮时O1齿O2齿的r1和r2与⼑具节线GPS作纯滚动.此处⼑具的齿厚=齿槽宽d=mZ-------------(3) (有了d后可定义 m=d/Z称模数是表⽰齿⼤⼩有量刚的⽐值系数,Z为齿数)2,节点P, 即两齿轮作纯滚动的圆的切点.两齿啮合时,按齿数⽐例分割中⼼连线O1O2的点必为节点P.它的圆为节圆.单个齿不存在节点P标准齿轮啮合时,既然r1和r2都与⼑具节线GPS作纯滚动∴r1和r2之间亦作纯滚动. ∴两O1齿O2齿标准齿轮的分度圆与节圆重合3,α1,α2-------分度圆压⼒⾓.即滚⼑⼑具压⼒⾓,或齿轮加⼯时与⼑具作纯滚动的点上的压⼒⾓.或者说齿轮被加⼯时的节点上的压⼒⾓.. 分度圆压⼒⾓=⼑具压⼒⾓⼀对标准齿啮合啮合时其节圆和分度圆重合α=.α’4,r e1和r e2--------齿顶半径5,r b1和r b2-------基圆半径由⊿PO1N1可得r b =r Cosα------------(4)6,PP’------周节p—在分度圆上相邻两齿廓的圆弧距离. p=mπ-----(5)∵在分度圆上齿轮的齿厚S=齿槽宽, ∴S= p/2= mπ/2--------------(6)(由圆周长L=πd p=L/Z可求得)7,EE’------基节p b----在基圆上相邻两齿廓的圆弧距离.p b= p Cosα------------(7)8,N1N2-----由图三知,两基圆相切的切点连线称为啮合线. 该对齿在啮合时⼀定在N1N2上接触啮合.∵(1)⼀对齿啮合时它们的法线⽅向是⼀致的,(2)根据渐开线的特性该点的法线必分别切于基圆r b1和r b2-(3)∴唯有此线即N1N2线能满⾜(1)(2)要求∴将N1N2线称为啮合线. 既然两齿始终沿N1N2线接触⽅向不变∴这两齿只能同步前进.在啮合啮合线上的啮合⾓即为节圆压⼒⾓.这是相对于成对啮合齿轮⽽⾔(⽽不是相对于某⼀⽛齿的齿廓,⼀对齿轮的啮合⾓和此点的压⼒⾓的定义是不同的(,见图三’和图⼗⼀)9,既然两齿在N1N2线上作⽅相始终不变能稳定地传递扭矩和运动.在N1N2线⾛过的路程即为基圆滚过的路程亦就是O1和O2齿轮所滚过的基节是相等的. ∴两齿啮合的最基本的条件是两齿的基节必须相等另由图三’,当两齿啮合点不在节点P上,⽽是转到γ点接触时,作⽤⼒对整个齿轮⽽⾔相对于O1O2中⼼线的啮合⾓仍为α但对单齿形的压⼒⾓为αK10, AB--------啮合线的⼯作区(图三). A和B分别为O1和O2齿轮的外圆与啮合线的交点A和B(1)假如O1为主动齿轮,则啮合从A点开始到B点脱开. 外径越⼤啮合线的⼯作区越长(2).AB长与基节p b之⽐即为啮合重合系数ε(3)A点在基点N1之上则可正确啮合,否则会产⽣啮合⼲涉如这现象发⽣在加⼯,则产⽣根切..五, 变位或移距齿轮啮合时的重要关系式(见图四,图五和图六)(⼀),基本特征1,移距的加⼯特徴(见图四)红⾊的齿形和⼑具是标准齿此时AA线既是⼑具的分度线⼜是⼑具的加⼯节线.与齿轮的分度圆r相切于AA线P点.⼑具在AA线上的齿厚=齿槽即PG=GS(亦=齿轮的分度圆弧齿厚).绿⾊为加⼯正移距的齿形的⼑具图.此时⼑具的分度线从AA移到A’A’,移距量为ξm, 此时⼑具在原AA上的齿槽变宽为P’’G’’⽽齿厚相应变窄G’’S’’,其变化值由⊿P P’P’’可知为ΔS=2ξm,tgα,----------------(8) (ξ为移距系数(或称变位系数,修正系数)它的标准符号⽤χ表⽰,但∵χ与x和乘号X很近∴我⽤ξ)注意: 此时加⼯的节线仍为AA,机床的挂轮没有变仅仅是将⼑具外移∴齿轮的分度圆亦仍为r但此时⼑具在绿线A”A”上的齿厚=齿槽,即P’G’=S’G’⽽⼑具在家⼯节线上的齿厚P’’G’’增加了ΔS=2ξm,tgα亦就是齿轮在分度圆上的齿厚增加了2ξm,tgα.齿轮的外径亦由r e1变为r’e1就是说正移距齿具有(1) 渐开线齿形外移(2)齿厚变厚(3)齿顶⾼h a变⾼(以分度圆为界)2移距齿轮啮合时的特徴(见图五)(1) 如图五当(ξ1+ξ2)＞0时称为正移距⾓度变位齿轮付时,图红⾊圆为节圆,其半径=r’,青⾊圆为分度圆, 其半径=r* 图例为是ξ1和ξ2都为正时的状况图即r’＞r,即为正移距⾓度变位齿轮付此时α’ >α(**当r’＜r时为负移距⾓度变位齿轮付, 即(ξ1+ξ2) ＜0, 此时α’<α(略)正移距⾓度变位齿轮付的直接特徴α’ >αA’ >AS’ >S(2)如图六当(ξ1+ξ2) =0或ξ1 =(-ξ2)≠0 此时r’＝r为零移距⾓度变位齿轮付即此时α’=α即节点的啮合⾓=分度圆压⼒⾓现分析(ξ1+ξ2) =0的⼏何关系:O1齿分析:先回顾⼀下图三这是标准齿轮啮合关系加⼯O1齿的相应齿条⼑槽是Ggcp P槽(图六)如果将⼑具向上移动ξm,距离来加⼯O1,齿,(见图六)就是将原加⼯标准齿的⼑具节线APA向上移到A’A’,⽽其它加⼯的运动关系不变,即加⼯时的⼑具节线和齿O1的加⼯节圆r1不变r1仍为分度圆,⽽⼑具的分度线变为A”A’ 在其上的bp=pg⽽在⼑具加⼯节线AA上GP＞PB则此时弧齿厚P⌒u由原bp增到GP.增量ΔS=GP-pg=2ξm,tgα,O2齿分析: O2为负移具,其⼑具的分度线同样由AA移到A’A’⽽加⼯节线仍为AA线∴O2的分度圆仍为r2∵是反相移距, ∴可将p P eBb看作⼑具齿槽来切O2齿,显然O2的分度弧圆齿厚S2=P B,其厚度少了ΔS=pb-PB = 2ξm,tgα,结论:由于O`1和O2移距⼤⼩相等⽅向相反它们分度圆上的齿厚变化亦是⼤⼩相等正负相反它们在分度圆上接触条件没有变只是将分度圆上的齿厚相互增减∴分度圆和节圆重合..(⼆), 移距齿轮啮合时的α’和α的关系式(见图五)由⊿N1O1P得Cosα’=r b/r’---------------(9)得r b=r’Cosα’------------(10)或r’= r b / Cosα’--------------(11)由青⾊的直⾓三⾓形⊿P0O1 N0中可得r b=r Cosα-----------(12)(10)=(12)得,Cosα’= r1 Cosα/ r’1-----(13)∵中⼼距A,A’与半径r,r’是成⽐例的∴ (13) 式可改为Cosα’= A Cosα/ A’--------(14)即当知道A’便可知节圆压⼒⾓α’六,变位对齿形的影响(或称移距,修正)见图七由于使⽤标准齿齿轮时易造成根切,其齿厚及因渐开线靠近基圆的曲线段使其啮合性能不佳等原因在齿轮设计时多采⽤变位.1,齿厚变化(见图七)图中r为分度圆也就是加⼯时的节圆MM为⼑具加⼯节线,此时⼑具的⼑刃ABCD范成出齿廓为标准齿(见⽩⾊线齿廓),齿轮上分度圆弧齿厚如分度圆上的S⌒S,=⼑具在节线上的齿槽SS.即SS=S⌒S当⼑具向外移动ξm(ξ为移具系数, m为模数),值即⼑具原节线MM移倒M’M’.即⼑具的位置改为A’B’C’D’请注意(1)此时分度圆和加⼯节线不变仍分别为r和MM, 只是⼑具外移.(2)M’M’此时是⼑具的分度线,在齿线上⼑具的齿厚=⼑具的齿的齿槽.(3)此时⼑具在加⼯节线上的齿槽SS变为S’S’∴⼑具移距后所对应的齿轮分度圆弧齿厚为S’⌒S’=S’S’令ΔS=S’S’-SS=2ξm tgα-------------(15)2,齿廓变化(见图七)如图齿廓由⽩⾊齿廓变为青⾊齿廓. 齿廓外移(或内移)则造成齿轮啮合⼀系列性能变化可供我们选择(以后讨论)3,分离系数的产⽣.(图⼋所⽰是⼀对都为正移距齿的啮合的关系图)当(ξ1+ξ2)≠0时就会有(ξ1+ξ2)m≠ΔA=A’-A的现象.令(ξ1+ξ2)-ΔA/m=λ叫作分离系数如图D-D线------是齿条⼑⼑具的⼑刃(红线所⽰)M-M线-----同是O1齿轮和O2齿轮作标准齿加⼯时的⼑具分度线.(但不是加⼯节线)即为(图⼋)中的MM在此线上⼑具的齿厚=⼑具的齿槽宽∵O1和O2两齿轮都作正移距加⼯M1M1线-----是O1齿轮的加⼯时的节线,圆r1即O1齿的分度圆M2M2线-----是O2齿轮的加⼯时的节线,圆r2即O2齿的分度圆法线N1P1∥N2P2是两加⼯节点的压⼒⾓即分度圆压⼒⾓线r01,r o2 为基圆半径E1点和E2点----是⼑刃在D-D加⼯位置同时⽤左右⼑刃分别在切削O1和O2的齿廓E1点和E2点标(其中假设E1和P1是重合的.)．由图,其总移距量和为(ξ1+ξ2)m,假定图中的中⼼距按O1O2= (r1+r2)+ (ξ1+ξ2)m, 令=A’’注意:如此时将⼑刃D-D拿⾛则会发现O1和O2的齿廓并不接触.只有将中⼼距移近⼀点才能使O1和O2的齿廓作⽆齿隙啮合.这移近的距离称为分离值令=ΔA=λm λ称为分离系数∴结论:对于⾓变位齿轮付,两齿作⽆齿隙啮合时的中⼼距A’ ≠(r1+r2)+ (ξ1+ξ2)m,⽽是应为A’ =(r1+r2)+ (ξ1+ξ2)m-λm--------------(16)令(ξ1+ξ2)= ξc 令(r1+r2)=A 代⼊(11)得A’=A+ξc m-λm-----------------(17)λ值可推算得λ=((Z1+Z2)/2)((Cosα/ Cosα’)-1)-----------------(18)或可从⼿册中根据Z1和Z2查得相对分离系数σ0值σ0=λ/(Z1+Z2)-----------------(19)七,齿轮基本要素.(见图九)GB规定压⼒⾓为20°标准齿顶⾼系数为1其实质就是当齿数Z和模数m确定后为你划定了你所使⽤的渐开线的性质和使⽤此渐开线的区段.齿形移距是改变使⽤此渐开线的区段但不改变渐开线的性质.确定齿轮要素应按GB的规定,但测绘引进国外产品则按原机或原图基本要素: .(见图九)Z-----齿数r,或d---分度圆半径或直径,是与加⼯⼑具作纯滚动的圆d=Z m--------------(20)m----是显⽰齿厚等齿轮尺⼨⼤⼩的⽐例参数.它和齿形特征⽆关只和⼤⼩有机联系着m= d/Z------------------------(21)r’-----节圆半径,是⼀对齿啮合时作纯滚动的圆半径,单个齿不存在r’(见图五)r’= r b / Cosα’-------------------------------见前式(11)r b ---基圆半径- r b=r Cosα-----------------见前式(12)α-----⼑具压⼒⾓,或称分度圆压⼒⾓.我国标准为20°α’----节圆压⼒⾓Cosα’=r b/r’--------------(不存单个齿在见图五)-见前式(9)h------齿全⾼= ha-+ hf- ------(22) GB规定ha-= m h-=2.25 mha----齿顶⾼(以分度圆为界)标准齿顶⾼ha-= m--------(23)h f----齿根⾼标准齿根⾼h f-=1.25--------------------24r a,- --d a,-----外径标准齿的外径d a,=d+2 ha------------------(25)r f- --d f,------根径标准齿的外径d f,=d+2 hf--------------------(26)p-----周节, 是在分度圆r上相邻齿廓的弧长p=πm-------见前(5)p b---基节是在基圆r b上相邻齿廓的弧长p b-= p Cosα---见前(7)标准齿分度圆弧齿厚S=πm-/2-------------------------------见前(6)移距后分度圆弧齿厚S=(6)式+(15)式=(πm-/2)+ 2ξm tgα---------(27)⼋, 齿轮齿厚测量计算齿厚测接触量参数有分度圆弦齿厚,S(如图九aq,或vb的弦长),固定弦齿厚,Sc(见图七AB)公法线长度W,量棒距M⼏种.∵当采⽤常规的齿轮卡尺来测量分度圆弦齿厚和固定弦齿厚时,其精度不⾼,在圆柱齿上少采⽤但近来开始应⽤光学仪器测量其精度较⾼但仍少⽤于⽣产线上.不过在直锥齿轮的齿厚测量中度圆弦齿厚和固定弦齿厚被⼴泛应⽤∴这⾥不讲了.此处只将公法线长度W,量棒距M的计公式. ∵W和M都是⽆基准测量(即以齿形本⾝为基准).很⽅便当精度亦很⾼∴被⼴泛应⽤1, 公法线长度测厚度(见图九),(1)如卡n个齿就有(n-1)个齿槽如图九卡2个齿有1个齿槽.2个齿,依此类推.(2) 公法线长度W=AB线,切于基圆. r b 切点在齿槽中⼼线(卡偶数齿)或齿厚中⼼线(卡奇数齿)(3) 弧齿厚S与公法线长度W的关系:所谓齿厚是指分度圆上的弧齿厚S,如图=a⌒q弧长.公法线长度AD实际上测的是n个基节齿厚+(n-1)个基节齿槽宽,即(n-1)个基节+1个基节齿厚. 公法线长度AD=基圆E⌒F弧长∴公法线长度AD与分度圆上的弧a⌒b弧长的关系即为基圆E⌒F弧长与分度圆上的弧a⌒b弧长的关系. 但它们不是简单地分度圆半径r与基圆半径r b的关系.根据公法线长度AD实际上测的是(n-1)个基节+1个基节齿厚由图九’ (a)先看看可基节与周节的关系: 对⽐基节的夹⾓与周节的夹⾓,可见周节夹⾓在左侧少了个θ⾓则在右侧多了⼀个θ⾓∴它们的夹⾓都是(2π/Z) ∴基节与周节的关系亦就分度圆半径r与基圆半径r b的关系.再由图九’看看分度圆弧齿厚与基节厚的关系:由图可知基节的夹⾓⽐周节⼤2θ⾓∴它们不是简单的⽐例关系.当齿厚增加后,由图九’’可知由于移距后分度圆弧齿厚加厚,但绿⾊齿廓(移距后)和⽩⾊齿廓(移距前)其两厚度虽不同但其θ⾓是相同的∴新增加的分度圆弧齿厚ΔS与基节上增加的ΔS b之间的关系应是分度圆半径r与基圆半径r b的关系. 即ΔS b=ΔSCosα∵ΔS b=ΔW代⼊(15)式得ΔS b=ΔW=ΔSCosα=2ξm Sinα------------------------------(15)’这就是弧齿厚增量与公法线增量的关系式(4)W值只反映理论弧齿厚本⾝的厚度是不能反应当齿轮因变形产⽣椭圆或另件安装定位误差造成的径向跳动引起对某齿的分度圆直径变化所造成分度圆上的弧齿厚变化(可以九图为例)(5)能反应因加⼯分度误差造成的齿厚误差和机床主轴的定位误差所造成的齿厚误差(6)它能测量运动精度所要求的公法线长度变动量F W(7)W所测的厚度是所卡齿数的平均值不是某个单齿(8)公法线长度W的计算机公式由图九知公法线长度AD=E⌒H+H⌒F即⼀个基节t b-加⼀个基圆弧齿厚Sb,可以类推,如卡3个齿则公法线长度=⼆个基节t b-加⼀个基圆弧齿厚S b具体的公式推导省略有愿深⼊者可随时找我.标准齿的公法线长度W0公式W0=m Cosα(π(n-0.5)+Z invα)---------------------(28)式中n--------为所卡齿数,inv------是渐开线函数变位齿的公法线长度W公式∵由于变位造成的分度圆弧齿厚增量ΔS可由式(15)’ΔW=ΔSCosα=2ξm Sinα----------------------------(29)W= W0 +ΔW= W0 +2ξmSinα= m Cosα(π(n-0.5)+Z invα)+ 2ξmSinα---------------(30)对于斜齿轮只需将invα改为invαt即W= m Cosα(π(n-0.5)+Z invαt)+ 2ξmSinα----------(30)’αt为端⾯压⼒⾓tgαt=tgα/Cosβ式中β为螺旋⾓(8)所卡齿数n的计算. 当压⼒⾓α=20°时n≈0.1111Z+0.5---------------------------------------(31)2跨棒距M测量(见图⼗)(1)如图⼗跨棒距M就是量棒中⼼的尺⼨OO’加量棒直经Dp 即M=OO’+dp------------------(32)(2)M的测量精度⽐公法线长度W⾼,亦是⽆基准测量(即以齿形本⾝为基准)∴检测⽅便(3)M是能⽤直接接触测量法测量内齿轮的唯⼀⽅法M能测量与基准⽆关的齿轮⾃⾝的椭圆度,不能反映⼏何偏⼼,加⼯偏⼼造成的齿形变化M所测出的齿厚是两个齿的平均齿厚值当压⼒⾓α=20°时,量棒直径⼤致为dp =1.476m---------------(33)(8) 计算⽆变位直齿标准齿轮M的步骤及其公式(a)先求出量棒中⼼点O’(或称量棒接触点)的压⼒⾓αM其公式为:invαM=invα±(dp/Zm Cosα) -/+(π/2Z)---------(34)斜齿: invαMt=invαt±(dp/Zm Cosα) -/+(π/2Z)-----(34)’注；在±和-/+中,分⼦⽤于外齿轮,分母⽤于内齿轮(b)求M值M= (Zm Cosα/Cos αM) ±dp (偶数齿)------------------(35)其中(Zm Cosα/ CosαM)即(32)式中的OO’斜齿: M= (Zm t Cosαt/Cos αMt) ±dp (偶数齿)------------------(35)’M= (Zm Cosα/ CosαM)( Cos(90°/Z))±dp (奇数齿)-------(36)斜齿: M=(Zm t Cosαt/CosαMt)( Cos(90°/Z))±dp (奇数齿)-------(36)(9) 计算变位⾮标准直齿轮M’的步骤及其公式(图⼗)(a)先求出量棒中⼼点O’的压⼒⾓αMinvαM=invα±(dp/Zm Cosα) -/+(π/2Z)+(2ξtgα/Z)-----(37)斜齿: invαMt=invαt±(dp/Zm Cosα) -/+(π/2Z)+(2ξtgα/Z)-(37)’(b) 求M’值: 同(35) (36)式⾄此我们可开始个种齿轮计算如何合理选取参数是⼀个综合性的问题等以后可作专题讲座.在我过去设计时都已编程20多程序. 现将常⽤⼏个程序给⼤家供参考只要将红⾊的参数输⼊即可得出结果数值.具体有: (计算程序中所使⽤的公式的符号是我⾃已常⽤得符号)1,成对齿轮验算2,单直齿求L(W)值 ,3单斜齿求L(W)值4,成对齿求L(W)值 5,求M值(外斜齿)6求M值(内斜齿)7求任⼀点的弧齿厚。

基于solidwork圆弧齿轮参数化建模随着生产的发展，齿轮传动得到了广泛的使用，而圆弧齿轮传动又具有渐开线齿轮传动无法比拟的特点，使其在齿轮传动中得到了广泛的应用。

圆弧齿轮的齿轮参数对齿轮传动的动态传动性能产生重要的影响，由于圆弧齿轮的轮齿是一个空间螺旋体，形状非常复杂，因而利用先进的设计计算方法和计算机技术对圆弧齿轮参数进行研究具有特别重要的意义。

本文依据圆弧齿轮啮合原理，建立了圆弧齿轮加工中的坐标系和刀具齿面方程。

通过建立处于啮合状态的圆弧逸轮的齿面方程，对圆弧齿轮的齿面进行了啮合分析，给出了齿轮啮合迹线的方程和齿面接触线的形状。

本文在分析圆弧齿轮齿形约束及尺寸参数的基础上，建立了圆弧齿轮的结构参数化实体模型，实现了实体模型与参数化系统设计变量之间的数据通讯，从而可以用参数化设计系统的输出结果参数来驱动所建的模型，完成机械工程设计与参数化设计系统的连接，为实现系列产品的快速开发设计提供可能。

本文利用现代设计方法，建立了一种寻求齿轮参数化设计的方法。

考虑圆弧齿轮结构的复杂性，本文基于Sold Work实体设计系统中的参数化建模功能，使用VC++．Net 编译环境建立了圆弧齿轮参数化建模系统。

目录一绪论 ................................................... 错误!未定义书签。

1.1 引言 ................................................ 错误!未定义书签。

1.2圆弧齿轮发展史 ...................................... 错误!未定义书签。

1.3 国内外圆弧齿轮的研究状况 (2)1.4圆弧齿轮的形成原理 (4)1.5 课题的主要研究内容 (5)二参数化圆弧齿轮齿面方程研究 (7)2.1 圆弧齿轮共轭原理 (7)2.2圆弧齿轮加工中的坐标系与刀具齿面 (7)2.2.1坐标系的建立 (7)2.2.2刀具齿面方程 (9)2.3 圆弧齿轮的齿面方程 (12)2.3.1刀具齿面与被加工圆弧齿轮接触的相对速度 (12)2.3.2 圆弧齿轮的齿面方程 (12)三圆弧齿轮的参数化建模研究 (14)3.1 计算机辅助几何建模技术简介 (14)3.1.1 图形的生成 (14)3.1.2 几何建模技术 (14)3.1.3 三维实体造型系统的表示方法 (14)3.2 系统参数化建模 (15)3.3 原型系统VISUAI C++ NET开发实现 (16)3.3.1 主框架组织方式 (17)3.3.2 SOLID WORK API对象概述 (17)3.3.3 主框架的执行过程 (23)3.3.4 主框架关键函数说明 (24)3.3.5 几个需要注意的工程配置问题 (24)3.3.6 可以被主框架中调用的动态联接库模块开发方法 (26)3.3.7 参数化设计的实现 (28)总结 (34)第一章绪论1．1引言齿轮传动是现代各类机械中应用最广的一种基本传动形式。