第24讲 圆的有关性质(含答案点拨)

第二十四章 圆的有关性质知识点思维导图能力培养：符号意识、几何直观、推理能力、运算能力 【实战篇】知识点一：圆的有关概念 1. 圆的定义（1）描述性定义：如图，在一个平面内，线段OA 绕它固定的一个端点O 旋转一周，另一个端点A 所形成的图形叫做圆. 其固定的端点O 叫做圆心，线段OA 叫做半径.（2）集合性定义：圆可以看成是所有到定点（圆心）的距离等于定长（半径）的点的集合. 2. 圆的表示方法：以点O 为圆心的圆，记作⊙O ，读作“圆O ”. 3. 圆具有的特性（1）圆上各点到定点（圆心O ）的距离都等于定长（半径r ）； （2）到定点的距离等于定长的点都在同一个圆上.注意：（1）确定一个圆取决于两个因素：圆心和半径. 圆心确定圆的位置，半径确定圆的大小.（2）同一个圆中的所有半径都相等，所以圆上任意两点和圆心（三点不共线）构成的三角A形都是等腰三角形.4. 圆的有关概念【例1】如图，在Rt△ABC中，∠C＝90°，AB＝10，若以点C为圆心、CB长为半径的圆恰好经过AB的中点D，则AC的长为______________.【例1】【解析】同一个圆中的所有半径都相等，所以在圆中“连半径”是常用的辅助线，本题先连接CD，根据直角三角形斜边上的中线的性质得出CD＝5，所以半径BC＝CD＝5，又由已知AB＝10，利用勾股定理得出AC==【答案】 【巩固】1. 如图，AB 是⊙O 的直径，点C 在圆上，∠ABC ＝65°，那么∠OCA 的度数是（ ） A. 25°B. 35°C. 15°D. 20°2. 如图，在⊙O 中，下列说法不正确的是（ ） A. AB 是⊙O 的直径B. 有5条弦C. AD 和BD 都是劣弧，ABD 是优弧D. CO 是圆O 的半径【巩固答案】 1. A 2.B知识点二：垂直于弦的直径CB DAABBA1. 圆的轴对称性圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴. 2. 垂径定理垂直于弦的直径平分弦，并且平分弦所对的两条弧. 符号语言：∵如图，CD 是直径，CD ⊥AB 于点M ，∴AM ＝BM ，AC ＝BC ，AD ＝BD .3. 垂径定理的推论平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧. 符号语言：∵如图，CD 是直径，AM ＝BM （AB 不是直径），∴CD ⊥AB ，AC ＝BC ，AD ＝BD .【例2】如图，AB ，BC 是⊙O 的两条弦，AO ⊥BC ，垂足为D ，若⊙O 的半径为5，BC ＝8，则AB 的长为（ ） A. 8B. 10C.34D. 54【例2】【解析】连接OB ，根据垂径定理求出BD ＝12BC ＝4，已知半径OB ＝5，在Rt △OBD中，由勾股定理求出OD3，所以AD ＝8，在Rt △ABD 中，再由勾股定理求出AB.【答案】D 【巩固】1. 下列说法不正确的是（ ）A. 圆既是轴对称图形又是中心对称图形B. 圆有无数条对称轴C. 圆的每一条直径都是它的对称轴D. 圆的对称中心是它的圆心2. 如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，OC ＝5 cm ，CD ＝8 cm ，则AE 的长为（ ） A. 8 cmB. 5 cmC. 3 cmD. 2 cm【巩固答案】 1. C 2. A知识点三：弧、弦、圆心角 1. 圆的旋转对称性圆具有旋转不变性，把圆绕圆心旋转任意一个角度，所得的图形都与原图形重合. 因此，圆也是中心对称图形，圆心就是它的对称中心. 2. 圆心角的定义顶点在圆心的角叫做圆心角.如图：∠AOB 是AB 所对的圆心角，AB 是∠AOB 所对的弧. 注意：一条弧所对的圆心角只有一个. 3. 弧、弦、圆心角之间的关系A【例3】如图，点A ，B ，C ，D 在⊙O 上，且AB ＝CD . 求证：AC ＝BD .【例3】【解析】根据圆心角、弧、弦的关系，由AB ＝CD 得到AB ＝CD ，进而AB ＋BC ＝CD ＋BC ，即AC ＝BD ，所以AC ＝BD . 【答案】证明：∵AB ＝CD ∴AB ＝CD ，∴AB＋BC ＝CD ＋BC ， 即AC ＝BD ， ∴AC ＝BD . 【巩固】1. 如图，在⊙O 中，∠AOB ＝∠COD ，那么AC 和BD 的大小关系是（ ）A. AC ＞BDB. AC ＜BDC. AC ＝BDD. 无法确定D2. 如图，C 是⊙O 上的点，CD ⊥OA 于点D ，CE ⊥OB 于点E ，且CD ＝CE ，则AC 与BC 的关系是（ ）A. AC ＝BCB. AC ＞BCC. AC ＜BCD. 不能确定【巩固答案】 1. C 2. A知识点四：圆周角 1. 圆周角的定义顶点在圆上，并且两边都与圆相交的角叫做圆周角.注意：（1）圆周角必须具备两个条件：①顶点在圆上；②两边都与圆相交. （2）同一条弧所对的圆周角有无数个. 2. 圆周角和圆心角的区别和联系3. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.如图，∠ACB ＝21∠AOB .4. 圆周角定理的推论推论1 同弧或等弧所对的圆周角相等.推论2 （1）半圆（或直径）所对的圆周角是直角； （2）90°的圆周角所对的弦是直径. 5. “五量关系”定理在同圆或等圆中，如果两个圆心角、两条弧、两条弧所对的圆周角、两条弦、两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等.【例4】如图，AB 为⊙O 的直径，C 、D 为⊙O 上两点，∠BCD ＝40°，则∠ABD 的大小为（ ） A. 60°B. 50°C. 40°D. 20°【例4】【解析】本题考查的是圆周角定理的两个推论，根据题意先连接AD ，根据圆周角定理的推论可知，∠A ＝∠BCD ＝40°，又由AB 为⊙O 的直径知∠ADB ＝90°，所以∠ABD ＝90°－∠A ＝50°. 故选B.【答案】B 【巩固】1. 如图，点A ，B ，C 在⊙O 上，若∠OAB ＝54°，则∠C 的度数为（ ） A. 54°B. 46°C. 36°D. 27°BAAB2. 如图，点A，B，C，D在⊙O上，BC＝CD，∠CAD＝30°，∠ACD＝50°，则∠ADB ＝___________.【巩固答案】1.C2.70°知识点五：圆内接多边形1.圆内接多边形的定义如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.2.圆内接四边形的性质圆内接四边形的对角互补.注意：每一个圆都有无数个内接四边形，但并不是所有的四边形都有外接圆，只有对角互补的四边形才有外接圆.拓展：圆内接四边形的每一个外角都等于它的内对角.【例5】如图，四边形ABCD为⊙O的内接四边形，E是BC延长线上的一点，已知∠BOD ＝130°，则∠DCE的度数为（）A. 45°B. 50°C. 65°D. 75°【例5】【解析】根据圆周角定理求出∠A ＝12∠BOD ＝65°，再根据圆内接四边形的性质得出∠BCD ＝180°－∠A ＝115°，则∠DCE ＝180°－∠BCD ＝65°. 故选C. 【答案】C 【巩固】1. 如图，在⊙O 中，∠AOB ＝120°，P 为劣弧AB 上的一点，则∠APB 的度数是_____________.2. 如图，四边形ABCD 为⊙O 的内接四边形，已知∠C ＝∠D. 问AB 与CD 有怎样的位置关系，请说明理由.【巩固答案】 1. 120° 2. 解：AB ∥CDB理由如下：∵四边形ABCD为⊙O的内接四边形，∴∠A＋∠C＝180°，∵∠C＝∠D，∴∠A＋∠D＝180°，∴AB∥CD.。

第二十四章圆章节知识点思维导图：一、圆的有关性质（一）与圆有关的概念1、定义：在一个平面内线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

2、弦：连接圆上任意两点的线段叫做弦，经过圆心的弦，叫做直径。

3、弧：圆上任意两点间的部分（曲线）叫做圆弧，简称弧。

能够互相重合的弧叫等弧。

圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆，大于半圆的弧叫优弧；小于半圆的弧叫劣弧，由弦及其所对的弧组成的圆形叫弓形。

4、圆心角：我们把顶点在圆心的角叫做圆心角。

5、圆周角：顶点在圆上，并且两边都与圆相交的角叫做圆周角。

注意：在圆中，同一条弦所对的圆周角有无数个。

6、弦心距：从圆心到弦的距离叫弦心距。

7、同心圆、等圆：圆心相同，半径不相等的两个圆叫同心圆；能够重合的两个圆叫等圆。

8、点的轨迹：1）圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；2）垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）； 3）角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4）到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5）到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

（二）圆的性质1、对称性：圆是轴对称图形，任何一条直径所在直线都是它的对称轴；圆也是以圆点为对称中心的中心对称图形。

2、性质：①垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧；推论1 ：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个，就可推出另外三个：①过圆心；②垂直于弦；③平分弦（不是直径）；④平分弦所对的优弧；⑤平分弦所对的劣弧。

推论2：圆两条平行弦所夹的弧相等。

②圆心角定理（圆心角、弧、弦、弦心距之间的关系）：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所对的弦心距相等；圆心角的度数与它所对的度数相等。

第四章图形的性质第24节圆的有关概念与性质■知识点一：圆的有关概念(1)圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆，其中定点为圆心，定长为半径．(2)弧：圆上任意两点间的部分叫做圆弧，简称弧，大于半圆的弧称为优弧，小于半圆的弧称为劣弧．(3)弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径．(4)相关概念：同心圆、弓形、等圆、等弧．(5)圆心角：顶点在圆心的角叫做圆心角．(6)圆周角：顶点在圆上，并且两边和圆相交的角是圆周角．(7)确定圆的条件：过已知一点可作无数个圆，过已知两点可作无数个圆，过不在同一条直线上的三点可作一个圆．(8)圆的对称性：圆是轴对称图形，其对称轴是直径所在的直线；圆是中对称图形，对称中心为圆心，并且圆具有旋转不变性．■知识点二：垂径定理及推论：①垂直于弦的直径平分弦，并且平分弦所对的两条弧．②平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧，③弦的垂直平分线经过圆心，并且平分弦所对的两条弧．④平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．⑤圆的两条平行弦所夹的弧相等．■知识点三：圆心角、弧、弦的关系（1）定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．（2）推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧．（3）正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为：在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等．这源于圆的旋转不变性，即：圆绕其圆心旋转任意角度，所得图形与原图形完全重合．（4）在具体应用上述定理解决问题时，可根据需要，选择其有关部分．■知识点四：圆周角定理及推论①圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半．推论１：在同圆或等圆中，同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧也相等．推论2：直径所对的网周角是直角；90°的圆周角所对的弦是直径．推论3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．②圆内接四边形的任意一组对角互补．■考点1.圆的有关概念◇典例：（2017年黑龙江大庆）如图，点M，N在半圆的直径AB上，点P，Q在上，四边形MNPQ 为正方形．若半圆的半径为，则正方形的边长为．【考点】正方形的性质；勾股定理；圆的认识．【分析】连接OP，设正方形的边长为a，则ON=，PN=a，再由勾股定理求出a的值即可．解：连接OP，设正方形的边长为a，则ON=，PN=a，在Rt△OPN中，ON2+PN2=OP2，即（）2+a2=（）2，解得a=2．故答案为：2．【点评】本题考查的是正方形的性质，勾股定理；圆的认识，根据题意作出辅助线，构造出直角三角形是解答此题的关键．◆变式训练（2017•宁夏）如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为 __________■考点2.垂径定理及其推论◇典例：（2018年黑龙江省龙东、七台河、佳木斯、鸡西、伊春、鹤岗、双鸭山）如图，AB为⊙O 的直径，弦CD⊥AB于点E，已知CD=6，EB=1，则⊙O的半径为．【考点】垂径定理，勾股定理【分析】连接OC，由垂径定理知，点E是CD的中点，AE=CD，在直角△OCE中，利用勾股定理即可得到关于半径的方程，求得圆半径即可．解：连接OC，∵AB为⊙O的直径，AB⊥CD，∴CE=DE=CD=×6=3，设⊙O的半径为xcm，则OC=xcm，OE=OB﹣BE=x﹣1，在Rt△OCE中，OC2=OE2+CE2，∴x2=32+（x﹣1）2，解得：x=5，∴⊙O的半径为5，故答案为：5．【点评】本题利用了垂径定理和勾股定理求解，熟练掌握并应用定理是解题的关键．◆变式训练1.（2018年山东省烟台）如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C 三点的圆的圆心坐标为．2.（2018年浙江省绍兴市）如图，公园内有一个半径为20米的圆形草坪，A，B是圆上的点，O为圆心，∠AOB=120°，从A到B只有路，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB．通过计算可知，这些市民其实仅仅少走了步（假设1步为0.5米，结果保留整数）．（参考数据：≈1.732，π取3.142）■考点3. 圆心角、弧、弦的关系◇典例（2017•牡丹江）如图，在⊙O中，=，CD⊥OA于D，CE⊥OB于E，求证：AD=BE．【考点】圆心角、弧、弦的关系；垂径定理．【分析】连接OC，先根据=得出∠AOC=∠BOC，再由已知条件根据AAS定理得出△COD ≌△COE，由此可得出结论．证明：连接OC，∵=，∴∠AOC=∠BOC．∵CD⊥OA于D，CE⊥OB于E，∴∠CDO=∠CEO=90°在△COD与△COE中，∵，∴△COD≌△COE（AAS），∴OD=OE，∵AO=BO，∴AD=BE．【点评】本题考查的是圆心角、弧、弦的关系，熟知在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等是解答此题的关键．◆变式训练（2017•宜昌）如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（）A．AB=AD B．BC=CD C． D．∠BCA=∠DCA■考点4. 圆周角定理及其推论◇典例：1.（2018 年广西梧州市）如图，已知在⊙O 中，半径 OA=2，弦 AB=2，∠BAD=18°，OD 与AB 交于点 C，则∠ACO=__________度．【考点】圆周角定理，勾股定理的逆定理，等腰三角形的性质【分析】根据勾股定理的逆定理可以判断△AOB 的形状，由圆周角定理可以求得∠BOD 的度数，再根据三角形的外角和不相邻的内角的关系，即可求得∠AOC的度数．解：∵OA=2，OB=2，AB=2，∴OA 2+OB2=AB2，OA=OB，∴△AOB 是等腰直角三角形，∠AOB=90°，∴∠OBA=45°，∵∠BAD=18°，∴∠BOD=36°，∴∠ACO=∠OBA+∠BOD=45°+36°=81°，故答案为：81．【点评】本题考查圆周角定理、勾股定理的逆定理、等腰三角形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．◆变式训练1.（2018年四川省南充）如图，BC是⊙O的直径，A是⊙O上的一点，∠OAC=32°，则∠B 的度数是（）A．58° B．60° C．64° D．68°2.（2017•锦州）如图，四边形ABCD是⊙O的内接四边形，AD与BC的延长线交于点E，BA与CD的延长线交于点F，∠DCE=80°，∠F=25°，则∠E的度数为（）A．55°B．50°C．45°D．40°一、选择题1.（2018年广西柳州市）如图，A，B，C，D是⊙O上的四个点，∠A=60°，∠B=24°，则∠C的度数为（）A．84°B．60°C．36°D．24°2.（2018年内蒙古赤峰市）如图，AB是⊙O的直线，C是⊙O上一点（A．B除外），∠AOD=130°，则∠C的度数是（）A．50°B．60°C．25°D．30°3.（2018年浙江省衢州市）如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（）A．75°B．70°C．65°D．35°4.（2018年湖北省襄阳）如图，点A，B，C，D都在半径为2的⊙O上，若OA⊥BC，∠CDA=30°，则弦BC的长为（）A．4 B．2C． D．25.（2018年四川省甘孜州）如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是（）A．AC=AB B．∠C=∠BOD C．∠C=∠B D．∠A=∠BOD二、填空题6.（2018年广东省）同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是．7.（2018年青海省）如图，A．B、C是错误!未找到引用源。

人教版九年级数学上册第二十四章圆24.1 圆的有关性质一：考点归纳考点一、圆在一个平面内，一条线段O A绕它的一个端点O旋转一周，另一个端点A所形成的图形叫作圆. 圆心：固定的端点叫作圆心.半径：线段OA的长度叫作这个圆的半径.（1）圆的表示方法：以点O为圆心的圆，记作“ ⊙O ”，读作“圆O”. 同圆的第二定义：所有到定点的距离等于定长的点组成的图形叫作圆.考点二、垂直于弦的直径（1）圆是轴对称图形，任何一条直径所在的直线都是它的对称轴，圆有无数条对称轴.（2）垂直于弦的直径平分弦，并且平分弦所对的弧；平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧.考点三、弧、弦、圆心角（1）顶点在圆心的角叫做圆心角 .（2）在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等.（3）在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等. 在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等.考点四、圆周角（1）圆周角定义：顶点在圆上，并且两边都和圆相交的角叫圆周角. 特征：①角的顶点在圆上；②角的两边都与圆相交.（2）同弧所对的圆周角的度数没有变化，并且它的度数恰好等于这条弧所对的圆心角的度数的一半.（3）在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.（4）半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径.（5）如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.圆内接四边形的对角互补.二：【题型归纳】【题型一】圆1．下列说法正确的是（）①弦是圆上两点间的部分；②直径是弦；③经过圆心的每一条直线都是圆的对称轴；A．0个B．1个C．2个D．3个2．下列说法：①直径是弦；②长度相等的两条弧是等弧；③半圆是弧，但弧不一定是半圆；④圆的对称轴是直径；⑤外心在三角形的一条边上的三角形是直角三角形，正确的命题有（）A．1个B．2个C．3个D．4个【题型二】垂直于弦的直径3．如图，DC是⊙O的直径，弦AB⊥CD于点F，连接BC，BD，则错误结论为（）A．OF=CF B．AF=BF C．AD BDD．∠DBC=90°4．如图，在⊙O中，半径OC垂直弦AB于D，点E在⊙O上，∠E＝22.5º，AB＝2，则半径OB等（）A ．1B ．22C ．2D ．2【题型三】弧、弦、圆心角5．给出下列命题：①弦是直径；②圆上两点间的距离叫弧；③长度相等的两段弧是等弧；④圆心角的度数与它所对的弧的度数相等；⑤圆是轴对称图形，不是中心对称图形；⑥直径是弦．其中正确的个数为（ ）A ．1B ．2C ．3D ．46．如图，AB 为O 的直径，点D 是弧AC 的中点，过点D 作DE AB ⊥于点E ，延长DE 交O 于点F ，若12AC =，3AE =，则O 的直径长为（ ）A ．10B ．13C ．15D ．16．7．O 是四边形ABCD 的外接圆，AC 平分BAD ∠，则正确结论是（ ）A ．AB AD = B ．BC CD = C ．AB BD = D ．ACB ACD ∠=∠【题型四】圆周角8．如图，O 是ABC 的外接圆，CD 是O 的直径，35B ∠=︒，则ACD ∠的度数是（ ）A ．45︒B ．50︒C ．55︒D ．60︒9．如图，AB 为⊙O 的直径，CD 为⊙O 的弦，∠ACD=40°，则∠BAD 的大小为（）A ．60ºB ．30ºC ．45ºD ．50º三：基础巩固和培优一、单选题1．如图，点A 、B 、C 在⊙O 上，CO 的延长线交AB 于点D ，∠A ＝50°，∠B ＝30°，∠ACD 的度数为（ ）A ．10°B ．15°C ．20°D ．30°2．如图，在5×5的正方形网格中，一条圆弧经过A ，B ，C 三点，那么这条弧所在圆的半径是（ ）A ．2B ．5C ．22D ．33．如图是我市环北路改造后一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB 宽为4m ，水面最深地方的高度为1m ，则该输水管的半径为（ ）A ．2mB ．2.5mC ．4mD ．5m4．如图，在⊙O 中，半径OC 垂直弦AB 于D ，点E 在⊙O 上，∠E ＝22.5º，AB ＝2，则半径OB 等（ ）A ．1B ．22C ．2D ．25．下列说法中，正确的是（ ）A ．直径所对的弧是半圆B ．相等的圆周角所对的弦相等C ．两个半圆是等弧D ．一条弧所对的圆心角等于它对的圆周角的一半6．如图，已知抛物线()()31916y x x =---与x 轴交于,A B 两点，对称轴与抛物线交于点C ，与x 轴交于点D ，C 的半径为2，G 为C 上一动点，P 为AG 的中点，则DP 的最大值为（ ）A ．412B ．23C ．72D ．57．如图，AB 是O 的直径，弦CD 交AB 于点P ，4AP =，8BP =，45APC ∠=︒，则CD 的长为（ ）A ．34B ．62C ．234D ．128．已知，AB 为圆O 的一条弦，∠AOB=80°，则弦AB 所对的圆周角的度数为（ ）A ．40︒B ．140︒C ．70︒D ．40︒或140︒9．下列说法：①直径是弦；②长度相等的两条弧是等弧；③半圆是弧，但弧不一定是半圆；④圆的对称轴是直径；⑤外心在三角形的一条边上的三角形是直角三角形，正确的命题有 （ ）A ．1个B ．2个C ．3个D ．4个10．如图，已知100BOC ∠=︒，则A ∠的度数为（ ）A ．50︒B ．80︒C ．100︒D ．130︒二、填空题 11．圆弧形蔬菜大棚的剖面如图，已知AB =16m ，半径OA =10m ，OC ⊥AB ，则中柱CD 的高度为_________m ．12．若圆的半径为6cm ，圆中一条弦长为3cm ，则此弦中点到此弦所对弧的中点的距离为_______cm.13．如图，在⊙O中，CA DB，∠1=30°，则∠2=_________°．14．如图，⊙O的半径为10，弦AB的长为12，OD⊥AB，交AB于点D，交⊙O于点C，则CD=______．15．如图，△ABC的三个顶点都在⊙O上，∠ACB=40°，则∠OAB=______．三、解答题16．如图，⊙O的半径OD⊥弦AB于点C，联结AO并延长交⊙O于点E，联结EC．已知AB＝8，CD＝2．（1）求OA的长度；（2）求CE的长度．17．如图，已知，AB是O的直径，弦CD⊥AB于点E，∠ACD=30°，AE=3cm，求BD的长度．18．如图，D 是O 弦BC 的中点，A 是BC 上一点，OA 与BC 交于点E ，已知8AO =，12BC =． （1）求线段OD 的长．（2）当2EO BE =时，求ED ，EO 的长．19．已知P 是O 上一点，过点P 作不过圆心的弦PQ ，在劣弧PQ 和优弧PQ 上分别有动点A B 、 (不与P ，Q 重合)，连接AP 、BP 若=APQ BPQ ∠∠．（1）如图1，当=45APQ ∠︒，=1AP ，=22BP O 的半径；（2）如图2，选接AB ，交PQ 于点M ，点N 在线段PM 上(不与P M 、重合)，连接ON OP 、，若+2=90NOP OPN ∠∠︒，探究直线AB 与ON 的位置关系，并证明．20．如图，90BCD ∠=︒，BC DC =，直线PQ 经过点D ．设PDC α∠=（45135α︒<<︒），BA PQ ⊥于点A ，将射线CA 绕点C 按逆时针方向旋转90︒，与直线PQ 交于点E ．（1）判断：ABC ∠________PDC ∠（填“>”或“=”或“<”）；（2）猜想ACE △的形状，并说明理由；（3）若ABC的外心在其内部（不含边界），直接写出 的取值范围．参考答案题型归纳【解析】：1【详解】①弦是连接圆上两点间线段，故不正确；②直径是最长的弦，故正确；③经过圆心的每一条直线都是圆的对称轴，故正确；故选C．2．【详解】解：①直径是弦，是真命题；②在同圆与等圆中，长度相等的两条弧是等弧，原命题是假命题；③半圆是弧，但弧不一定是半圆，是真命题；④圆的对称轴是直径所在的直线，原命题是假命题；⑤外心在三角形的一条边上的三角形是直角三角形，是真命题；故选：C．【解析】3．【详解】解：∵DC是⊙O直径，弦AB⊥CD于点F，∴AF=BF，AD BD，∠DBC=90°，∴B、C、D正确；∵点F不一定是OC的中点，∴A错误．故选：A．4．【详解】解：∵半径OC⊥弦AB于点D，∴=AC BC，∴∠E=12∠BOC=22.5°，∴∠BOD=45°，∴△ODB是等腰直角三角形，∵AB=2，10∴DB=OD=1，则半径OB．故选：D．【解析】：5【详解】解：①弦不一定是直径，原命题是假命题；②圆上任意两点间的部分叫弧，原命题是假命题；③在同圆或等圆中，长度相等的两段弧是等弧，原命题是假命题；④圆心角的度数与它所对的弧的度数相等，是真命题；⑤圆是轴对称图形，也是中心对称图形，原命题是假命题；⑥直径是弦，是真命题．故选：B．6【详解】解：连接OD交AC于点G，∵AB⊥DF，∴AD AF=，DE=EF．又点D是弧AC的中点，∴AD CD AF==，OD⊥AC，∴AC DF=，∴AC=DF=12，∴DE=6．设O的半径为r，∴OE=AO-AE=r-3，在Rt△ODE中，根据勾股定理得，OE2+DE2=OD2，∴(r-3)2+62=r2，解得r=152．∴O的直径为15．故选：C．7．【详解】解：ACB ∠与ACD ∠的大小关系不确定，AB ∴与AD 不一定相等，故选项A 错误； AC 平分BAD ∠，BAC DAC ∴∠=∠，BC CD ∴=，故选项B 正确；ACB ∠与ACD ∠的大小关系不确定，∴AB 与AD 不一定相等，选项C 错误；∵BCA ∠与DCA ∠的大小关系不确定，选项D 错误；故选B ．8．【详解】解：连接AD ，∵CD 是圆的直径，∴∠DAC=90°，∵∠B=∠D=35°，∴∠ACD=90°-∠D=90°-35°=55°，故选C ．9．【详解】连结BD ，∵同弧所对的圆周角相等，∴∠B=∠C=40º，∵AB 为直径，∴∠ADB=90º，∴∠DAB+∠B=90º，∴∠DAB=90º-40º=50º．故选择：Ｄ．二：基础巩固和培优1．C【详解】解：∵∠A=50°，∴∠BOC=2∠A=100°，∵∠B=30°，∠BOC=∠B+∠BDC，∴∠BDC=∠BOC-∠B=100°-30°=70°，∴∠ACD=70°-50°=20°；故选：C．2．B【详解】解：如图线段AB的垂直平分线和线段BC的垂直平分线的交点M，即点M为圆心，22+125故选：B．3．B【详解】过点O作OD⊥AB于点D，连接OA，设OA=x，则OD=x-1，在Rt△AOD中， x2=（x-1）2+22，解得x=2.5m．故选B．4．D【详解】解：∵半径OC⊥弦AB于点D，∴=AC BC，∴∠E=12∠BOC=22.5°，∴∠BOD=45°，∴△ODB是等腰直角三角形，∵AB=2，∴DB=OD=1，则半径OB2211=2．故选：D．5．A【详解】解：A、直径所对的弧是半圆，正确，符合题意；B、同圆或等圆中，相等的圆周角所对的弦相等，故原命题错误，不符合题意；C、半径相等的两个半圆是等弧，故原命题错误，不符合题意；D、同圆或等圆中，一条弧所对的圆心角等于它对的圆周角的一半，故原命题错误，不符合题意，故选：A．6．C【详解】如图，连接BG，由题意可得：A(1,0)，B(9,0)，D是AB的中点，∴AB=8，∴BD=4， 3y=(1)(9)16x x ---=23(5)316x --+， ∴C(5,3)，∴CD=3，由D 、P 分别是AB 、AG 的中点可得：DP 是ABG 的中位线， ∴DP=12BG ，要求DP 的最大值，即要求BG 的最大值，当G 、C 、B 三点共线时，BG 最大，BC=22345+=，BG=5+2=7，DP=12BG=72．故选：C ．7．C【详解】解：∵4AP =，8BP =，∴AB=12，AO=6，∴PO=2，作OM ⊥CD ，连接OC ，∵45DPB APC ∠=∠=︒，∴∠AOM=45°，△MOP 为等腰直角三角形，∴222MO OP ，在Rt △OCM 中根据勾股定理22226(2)34CMCO OM ， ∴2234CD CM ．故选：C ．8．D【详解】解：如图，弦AB 所对的圆周角为C D ∠∠，，80AOB ∠=︒，40D ∴∠=︒，四边形ADBC 为O 的内接四边形，180C D ∴∠+∠=︒，=140C ∴∠︒．故选D ．9．C【详解】解：①直径是弦，是真命题；②在同圆与等圆中，长度相等的两条弧是等弧，原命题是假命题； ③半圆是弧，但弧不一定是半圆，是真命题；④圆的对称轴是直径所在的直线，原命题是假命题；⑤外心在三角形的一条边上的三角形是直角三角形，是真命题； 故选：C ．10．A【详解】解：∵100BOC ∠=︒，∴A ∠=1250BOC ∠=︒，故选A ．11．4【详解】解：∵CD 垂直平分AB ，∴AD ＝8．∴OD ＝22108-＝6m ，∴CD ＝OC−OD ＝10−6＝4（m ）．故答案是：412．3或9【详解】在⊙O 中，弦AB=63cm ，半径6R =；过圆心O 作直径MN ，且MN ⊥AB 于点C ，连接OB ；则AC=BC=12AB=33，OB=6， 由勾股定理得：()22226333OB BC -=-=，∴CM=6+3=9，CN=6-3=3；∵MN ⊥AB ，且MN 为⊙O 的直径，∴点M 、N 分别为AMB 、ANB 的中点， ∴AB 弦中点到弦所对应的弧的中点的距离分别为3或9． 故答案为：3或9．13．30【详解】解：CA DB =，BC BC =，∴AB CD =，∴∠1=∠2，∠1=30°，∴∠2=30°；故答案为30．14．2【详解】∵OD ⊥AB ，OD 过圆心O ， ∴162AD BD AB ===，由勾股定理可得：8OD ===， ∴1082CD CO OD =-=-=； 故答案是2．15．50°【详解】解：根据圆周角定理得：∠AOB=2∠ACB ，∵∠ACB=40°，∴∠AOB=2×40°=80°，∵OA=OB ，∴∠OAB=∠OBA ，∴∠OAB+∠OBA+∠AOB=180°， ∴∠OAB=50°．故答案为： 50°．16．（1）5；（2）【详解】解：（1）∵在⊙O 中，OD ⊥弦AB ， ∴AC ＝BC ＝12AB ＝4，设OA 为x ，则OD ＝OA ＝x ，∵CD ＝2，∴OC＝x﹣2在Rt△ACO中，AC2+OC2＝AO2∴42+（x﹣2）2＝x2，解得x＝5，∴OA＝5；（2）连接BE，∵OA＝OE，AC＝BC，∴OC∥BE且OC＝12 BE，∴∠EBA＝∠OCA＝90°，∵OC＝OD﹣CD＝5﹣2＝3，∴BE＝6，在Rt△ECB中，BC2+EB2＝EC2∴42+62＝EC2，∴CE＝213．17．63BD cm=【详解】连接OC、OD，AB是⊙O的直径，弦CD⊥AB，∴CE=DE，∠AEC=∠DEB=90°，AC AD=，∴30ACD ∠=︒，∴260COA DOA ACD ∠=∠=∠=︒， OC =OA ，∴AOC △是等边三角形，∴AE =EO =3cm ，∴AO =DO =OB =6cm ，∴BE =9cm ，DE =22226333OD OE -=-=cm ， ∴BD =22229(33)63BE DE +=+=cm ． ∴DB 的长为63cm ．18．（1）线段OD 的长为27；（2）ED 2=，EO=42【详解】解：（1）连接OB ．∵OD 过圆心，且D 是弦BC 中点， ∴OD ⊥BC ，BD=12BC ， 在Rt △BOD 中，OD 2+BD 2=BO 2． ∵BO=AO=8，BD=6．∴22228627BO BD --= （2）在Rt △EOD 中，OD 2+ED 2=EO 2． 设BE=x ，则2x ，DE=6x -， (())222762x x +-＝， 整理得：212640x x +-=，解得：12416x x ==-，(舍去)．∴BE=4，ED=642-=，EO=42．19．（1） ☉O 的半径是32；（2）A B ∥ON ，证明见解析 【详解】解：（1）连接AB ，在☉o 中，o APQ BPQ 45∠=∠=，o APB APQ BPQ 90∴∠=∠+∠=AB ∴是☉0的直径．Rt APB ∴∆在中，22AB AP BP =+AB=3∴∴☉0的半径是32（2）AB//ON证明：连接OA ， OB ， OQ ，在☉0中， AQ AQ =， BQ BQ =，Q 2APQ,B0Q 2BPO AO ∴∠=∠∠=∠．又APQ BPQ ∠=∠，AOQ BOQ ∴∠=∠．在AOB ∆中，OA OB =， AOQ BOQ ∠=∠，OC AB ∴⊥，即o OCA 90∠=连接OQ ，交AB 于点C在☉0中，OP OQ =OPN OQP.∴∠=∠延长PO 交☉0于点R ，则有2OPN QOR ∠=∠o NOP 2OPN 90∴∠+∠=，又:o NOP NOQ QOR 180∠+∠+∠=，NOQ 90O ∴∠=NOQ OCA 180O ∴∠+∠= ．AB//ON ∴20．（1）=；（2）ACE △是等腰直角三角形；理由见解析；（3）4590α︒<<︒．【详解】解：（1） 90AB AD DCB ⊥∠=︒，，3609090180CDA ABC ∴∠+∠=︒-︒-︒=︒，180CDA CDE ∠+∠=︒，.EDC ABC ∴∠=∠故答案为：=．（2）ACE △是等腰直角三角形．理由如下：由旋转可得：90ACE BCD ∠=∠=︒，90ECD DCA DCA BCA ∴∠+∠=︒=∠+∠，ECD BCA ∴∠=∠，在ECD 与ACB △中，ECD BCA CD CBEDC ABC ∠=∠⎧⎪=⎨⎪∠=∠⎩()ECD ACB ASA ∴≌EC AC ∴=，又90ACE ∠=︒ACE ∴是等腰直角三角形．（3）当∠ABC=α=90°时， ABC 的外心在其斜边上，∠ABC=α＞90°时，ABC 的外心在其外部，由PDC ∠＞45EAC ∠=︒，PDC DCA EAC ∠=∠+∠＜135︒， ∴ 45°＜α＜135°，故：4590α︒<<︒．。

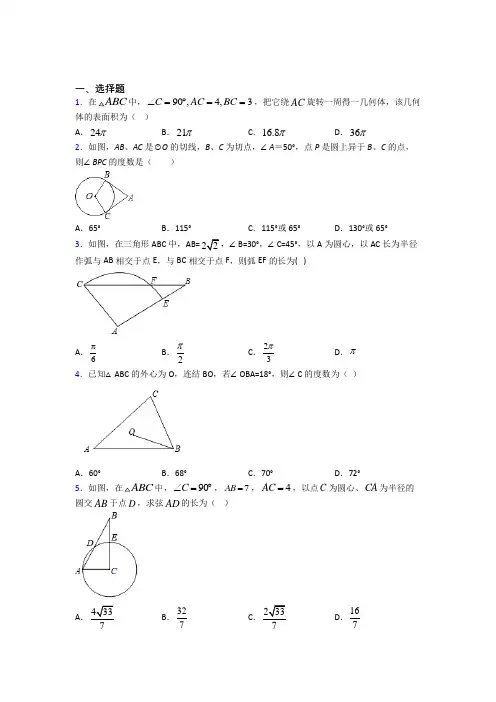
一、选择题1．在ABC 中，90,4,3C AC BC ∠=︒==，把它绕AC 旋转一周得一几何体，该几何体的表面积为（ ）A ．24πB ．21πC ．16.8πD ．36π 2．如图，AB 、AC 是⊙O 的切线，B 、C 为切点，∠A ＝50°，点P 是圆上异于B 、C 的点，则∠BPC 的度数是（ ）A ．65°B ．115°C ．115°或65°D ．130°或65° 3．如图，在三角形ABC 中，AB=22，∠B=30°，∠C=45°，以A 为圆心，以AC 长为半径作弧与AB 相交于点E ，与BC 相交于点F ，则弧EF 的长为( )A ．6πB ．2πC ．23πD ．π4．已知△ABC 的外心为O ，连结BO ，若∠OBA=18°，则∠C 的度数为（ ）A ．60°B ．68°C ．70°D ．72°5．如图，在ABC 中，90C ∠=︒，7AB =，4AC =，以点C 为圆心、CA 为半径的圆交AB 于点D ，求弦AD 的长为（ ）A 433B ．327C ．337D ．1676．如图，正方形ABCD 内接于O ，直径//MN AD ，则阴影部分的面积占圆面积的（ ）A ．12B ．16C ．13D ．147．若圆锥的底面半径为5cm ，侧面积为265cm π，则该圆锥的高是（ ） A ．13cm B ．12cm C ．11cm D ．10cm 8．如图，ABC 的三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将ABC 绕点B 顺时针旋转到A B C '''的位置，且点A '、C '仍落在格点上，则线段AB 扫过的图形的面积是（ ）平方单位（结果保留）A ．254πB ．134πC ．132πD ．136π 9．如图，在⊙O 中，AB 是直径，弦AC=5，∠BAC=∠D ．则AB 的长为（ ）A ．5B ．10C ．52D ．10210．如图，AB 是⊙O 的直径，C ，D 是⊙O 上的点，28CDB ∠=︒，过点C 作⊙O 的切线交AB 的延长线于点E ，则E ∠等于（ ）A ．28︒B ．34︒C ．44︒D ．56︒ 11．如图，⊙O 的半径为1，点 O 到直线 a 的距离为2，点 P 是直线a 上的一个动点，PA 切⊙O 于点 A ，则 PA 的最小值是（ ）A ．1B ．3C ．2D ．5 12．如图，ABC 的顶点A 是O 上的一个动点，90ACB ∠=︒，30BAC ∠=︒，边AC ，AB 分别交O 于点E ，D ，分别过点E ，D 作O 的切线交于点F ，且点F 恰好在边BC 上，连接OC ，若O 的半径为6，则OC 的最大值为（ ）A ．393+B ．2103+C ．353+D ．53 13．如图，点M 是矩形ABCD 的边BC 、CD 上的点，过点B 作BN ⊥AM 于点P ，交矩形ABCD 的边于点N ，连接DP ，若AB=6，AD=4，则DP 的长的最小值为（ ）A ．2B ．121313C ．4D ．514．如图，在平行四边形ABCO 中，45C ∠=︒，点A ，B 在O 上，点D 在ADB 上，DA DB =，则AOD ∠的度数为（ ）A．112.5°B．120°C．135°D．150°15．在△ABC中，∠ACB为锐角，分别以AB，AC为直径作半圆，过点B，A，C作弧BAC，如图所示．若AB=4，AC=2，图中两个新月形面积分别为S1，S2，两个弓形面积分别为S3，S4，S1-S2=14π，则S3-S4的值是( )A．294πB．234πC．114πD．54π二、填空题16．如图，⊙O是△ABC的内切圆，若∠A＝70°，则∠BOC＝________°．17．如图，四边形ABCD是O的内接四边形，对角线AC，BD交于点E，且AC BD AB==，若70AEB∠=︒，则AOB∠等于______︒．18．已知半径为5的圆O中，弦AB=8，则以AB为底边的等腰三角形腰长为___________．19．如图，PA，PB分别与O相切于A、B两点，点C为劣弧AB上任意一点，过点C的切线分别交AP，BP于D，E两点．若8AP=，则PDE△的周长为______．20．如图，O 的半径为6，AB 、CD 是互相垂直的两条直径，点P 是O 上任意一点，过点P 作PM AB ⊥于M ，PN CD ⊥于N ，点Q 是MN 的中点，当点P 沿着圆周从点D 逆时针方向运动到点C 的过程中，当∠QCN 度数取最大值时，线段CQ 的长为______．21．如图，已知正方形ABCD 的边长为2，点M 和N 分别从B 、C 同时出发，以相同的速度沿BC 、CD 方向向终点C 和D 运动．连接AM ，BN 交于点P ，则PC 长的最小值为____________．22．如图，直线AB 、CD 相交于点,30O AOC ∠=︒，半径为1cm 的⊙P 的圆心在直线AB 上，且与点O 的距离为8cm ，如果⊙P 以2cm/s 的速度，由A 向B 的方向运动，那么_________秒后⊙P 与直线CD 相切.23．在矩形ABCD 中，43AB =6BC =，若点P 是矩形ABCD 上一动点，要使得60APB ∠=︒，则AP 的长为__________．24．小明用一张扇形纸片做一个圆锥的侧面，已知该扇形的半径是10cm ，弧长是12πcm 2，那么这个圆锥的高是________cm ．参考答案25．如图，在⊙O 中，弦AC 、BD 相交于点E ，且AB BC CD ==，若∠BEC=130°，则∠ACD 的度数为_____26．如图，已知空间站A 与星球B 距离为a ，信号飞船C 在星球B 附近沿圆形轨道行驶，B ，C 之间的距离为b ．数据S 表示飞船C 与空间站A 的实时距离，那么S 的最小值________．三、解答题27．如图，AB 是O 的弦，CD 是O 的直径，CD AB ⊥，垂足为E ．1CE =，3ED =．（1）求O 的半径．（2）求AB 的长．28．如图，在Rt △ABC 中，∠C =90°，以BC 为直径的圆O 交AB 于点D ，切线DE 交AC 于点E ．（1）求证：∠A =∠ADE ；（2）若AD =8，DE =5，求BC 的长．29．如图，一条公路的转弯处是一段圆弧CD ，点O 是CD 的圆心，E 为 CD 上一点，OE ⊥CD ，垂足为F ．已知CD=300m ，EF=50m ，求这段弯路的半径．30．如图，半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N，求劣弧MN 的长度．。

合作探究探究点1 圆的定义情景激疑在准备好的一张纸上以点〇为圆心、3 cm为半径画一个圆，观察画图过程.由此你会得出什么结论？知识讲解定义1:在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的圆形叫做圆.其固定的端点O叫做圆心，线段OA叫倣半径.以O点为圆心的圆，记作O,读作“圆O〞.定义2：圆心为O、半径为r的圆可以看成是所有到定点O的间隔等于定长r的点的集合.注意〔1)圆心确定圆的位置，半径确定圆的大小.(2) 确定一个圆首先确定圆心，再确定半径，二者缺一不可.(3) 定点是圆心，定长是半径.(4) “圆〞指的是“圆周〞，而不是“圆平面〞.典例剖析例1 以下说法错误的有 ( )(1) 经过P点的圆有无数个；(2) 以P点为圆心的圆有无数个；(3) 半径为3cm且经过P点的圆有无数个。

(4) 以P点为圆心、3cm为半径的圆有无数个.A. 1个B. 2个C. 3个D. 4个解析确定一个圆必须满足两个条件，即圆心和半径，只满足一个条件或不满足任何一个条件的圆都有无数个，故(1)(2)正确，(3)虽然半径,但P点不是圆心，实际上也只是一个条件，能作无数个圆，故(3)正确;(4)满足两个条件，只能作一个圆，所以(4)错误.综上所述，错误的说法有1个，应选A答案 A错因分析导致此题错误的主要原因是对于确定一个圆的两个要素(圆心和半径)理解不够准确。

类题打破1 以O点为圆心画圆，可以画______ 个圆;以4 cm为半径画圆.可以面_____个圆.答案无数无数点拨确定圆的条件:一是圆心，二是半径.探究点2 与圆有关的概念知识讲解连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径。

圆上任意两点间的局部AB.读作“圆弧AB〞或“弧AB〞，圆的任意一条直径的两个端点把图分成两条弧，每一条弧都叫做半圆。

注意 (1)弦和弧是有区别的，弦是线段，而弧是曲线。

(2)直径是圆中最长的弦，而弦不都是直径。

第24讲圆的基本性质1. (16，河北)如图所示的为4×4的网格图，A，B，C，D，O均在格点上，点O是( )第1题图第2题图第3题图例1题图A. △ACD的外心B. △ABC的外心C. △ACD的内心D. △ABC的内心2. (15，河北)如图，AC，BE是⊙O的直径，弦AD与BE相交于点F.下列三角形中，外心不是点O的是( )A. △ABEB. △ACFC. △ABDD. △ADE3. (12，河北)如图，CD是⊙O的直径，AB是弦(不是直径)，AB⊥CD于点E，则下列结论正确的是( )A. AE>BEB. »AD＝»BCC. ∠D＝12∠AEC D. △ADE∽△CBE圆的有关概念例1 (2019，扬州邗江区一模)如图，⊙O的直径BA的延长线与弦DC的延长线相交于点E，且CE＝OB.已知∠DOB ＝72°，则∠E的度数为( )A. 36° B. 30° C. 18° D. 24°训练1题图训练2题图训练3题图例3题图针对训练1如图所示的圆规，点A是铁尖的端点，点B是铅笔芯尖的端点，已知点A与点B的距离是2 cm.若铁尖的端点A固定，铅笔芯尖的端点B绕点A旋转一周，则作出的圆的直径是( )A. 1 cmB. 2 cmC. 4 cmD. πcm针对训练2 (2019，海口模拟)如图，AB是⊙O的直径，点C，D在⊙O上，且点C，D在AB的异侧，连接AD，OD，OC.若∠AOC＝70°，且AD∥OC，则∠AOD的度数为( )A. 70° B. 60° C. 50° D. 40°确定圆的条件例2 (2019，北京)在平面内，给定不在同一条直线上的点A，B，C，如图所示，点O到点A，B，C的距离均等于a(a为常数)，到点O的距离等于a的所有点组成图形G，∠ABC的平分线交图形G于点D，连接AD，CD.(1)求证：AD＝CD；(2)过点D作DE⊥BA，垂足为E，作DF⊥BC，垂足为F，延长DF交图形G于点M，连接CM.若AD＝CM，求直线DE与图形G的公共点个数．例2题图针对训练3 (10，河北)如图，在5×5的正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是( )A. 点P B. 点Q C. 点R D. 点M针对训练4 (2019，绥化)半径为5的⊙O是锐角三角形ABC的外接圆，AB＝AC，连接OB，OC，延长CO交弦AB 于点D.若△OBD是直角三角形，则弦BC的长为（）.圆的基本性质例3 (19，沈阳)如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连接AC，AD，BD，CD.若⊙O的半径是13，BD＝24，则sin∠ACD的值是( )A. 1213 B.125 C.512 D.513针对训练5 (2019，绵阳)如图，AB 是⊙O 的直径，C 为»BD的中点，CF 为⊙O 的弦，且CF ⊥AB ，垂足为E ，连接BD 交CF 于点G ，连接CD ，AD ，BF .(1)求证：△BFG ≌△CDG ；(2)若AD ＝BE ＝2，求BF 的长．训练5题图垂径定理及其应用 例4 (2019，梧州)如图，在半径为13的⊙O 中，弦AB 与CD 相交于点E ，∠DEB＝75°，AB ＝6，AE ＝1，则CD 的长是( )A. 2 6 B. 210 C. 211 D. 4 3例4题图训练6题图针对训练6 (19，黄冈)如图，一条公路的转弯处是一段圆弧(»AB )，点O 是这段弧所在圆的圆心，AB ＝40 m ，C 是»AB 的中点，D 是AB 的中点，且CD ＝10 m ，则这段弯路所在圆的半径为( )A. 25 m B. 24 m C. 30 m D. 60 m1. (2019，广元)如图，AB ，AC 分别是⊙O 的直径和弦，OD ⊥AC于点D ，连接BD ，BC ，且AB ＝10，AC ＝8，则BD 的长为( )A. 2 5 B. 4 C. 213 D. 4.81题图2题图3题图4题图5题图2. (2019，吉林)如图，在⊙O 中，»AB 所对的圆周角∠ACB ＝50°.若P 为»AB 上一点，∠AOP ＝55°，则∠POB 的度数为( )A. 30° B. 45° C. 55° D. 60°3. (2019，白银)如图，点A ，B ，S 在圆上，若弦AB 的长度等于圆半径的2倍，则∠ASB 的度数是( )A. 22.5°B. 30°C. 45°D. 60°4. (19镇江如图，四边形ABCD 是半圆的内接四边形，AB 是直径，»»DC CB ＝.若∠C ＝110°，则∠ABC 的度数为( )A. 55°B. 60°C. 65°D. 70°5. (2019，贵港)如图，AD 是⊙O 的直径，»»AB CD ＝.若∠AOB ＝40°，则圆周角∠BPC 的度数是( ) A. 40° B. 50° C. 60° D. 70°6. (2019，聊城)如图，BC 是半圆O 的直径，D ，E 是»BC上两点，连接BD ，CE 并延长相交于点A ，连接OD ，OE .如果∠A ＝70°，那么∠DOE 的度数为( )A. 35° B. 38° C. 40° D. 42°7. (2019，安顺)如图，半径为3的⊙A 经过原点O 和点C (0，2)，B 是y 轴左侧⊙A 优弧上一点，则tan ∠OBC 的值为( )A. 13 B. 2 2 C. 223 D. 248. (2019，天水)如图，四边形ABCD 是菱形，⊙O 经过点A ，C ，D ，与BC 相交于点E ，连接AC ，AE .若∠D ＝80°，则∠EAC的度数为( )A. 20° B. 25° C. 30° D. 35°第6题图第7题图第8题图第9题图9. (2019，通辽)如图，等边三角形ABC内接于⊙O.若⊙O的半径为2，则图中阴影部分的面积等于( )A. π3 B.2π3 C.4π3 D. 2π10. (19，菏泽)如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD分别与BC，OC相交于点E，F，则下列结论不一定成立的是( ) A. OC∥BD B. AD⊥OC C. △CEF≌△BED D. AF＝FD11. (2019，陕西)如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB相交于点C，连接OF.若∠AOF＝40°，则∠F的度数是( )A. 20° B. 35° C. 40° D. 55°第10题图第11题图第12题图第13题图12. (2019，赤峰)如图，AB是⊙O的弦，OC⊥AB交⊙O于点C，D是⊙O上一点，∠ADC＝30°，则∠BOC的度数为( )A. 30° B. 40° C. 50° D. 60°.13. (2019，宁夏)如图，AB是⊙O的弦，OC⊥AB，垂足为C，将劣弧»AB沿弦AB折叠交于OC的中点D.若AB＝210，则⊙O的半径为（）.14. (2019，盐城)如图，点A，B，C，D，E在⊙O上，且»AB所对的圆心角为50°，则∠E＋∠C＝°.第14题图第15题图第16题图第17题图15. (2019，安徽)如图，△ABC内接于⊙O，∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D.若⊙O的半径为2，则CD的长为（）.16. (2019，广元)如图，△ABC是⊙O的内接三角形，且AB是⊙O的直径，P为⊙O上的动点，且∠BPC＝60°，⊙O的半径为6，则点P到AC距离的最大值是（）.17. (2019，嘉兴)如图，在⊙O中，弦AB＝1，点C在AB上移动，连接OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为（）.18. (2019，包头)如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝23，弦BM平分∠ABC交AC于点D，连接MA，MC.(1)求⊙O的半径；(2)求证：AB＋BC＝BM.(1)解：如答图①，连接OA，OC，过点O作OH⊥AC于点H.第18题图19. (2019，荆门)如图，已知锐角三角形ABC的外接圆圆心为O，半径为R. (1)求证：ACsin B＝2R；(2)若在△ABC 中，∠A ＝45°，∠B ＝60°，AC ＝3，求BC 的长及sin C 的值．第19题图1. (2019，湘潭)《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积＝12(弦×矢＋矢2)．弧田是由圆弧和其所对的弦围成(如图中的阴影部分)，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理(当半径OC ⊥弦AB 时，OC 平分AB )可以求解．现已知弦AB ＝8 m ，半径等于5 m 的弧田，按照上述公式计算出弧田面积为 m 2.第1题图第2题图2. (2019，潍坊)如图，在平面直角坐标系xOy 中，一组同心圆的圆心为坐标原点O ，它们的半径分别为1，2，3，…，按照“加1”依次递增；一组平行线l 0，l 1，l 2，l 3，…都与x 轴垂直，相邻两直线的间距为1，其中l 0与y 轴重合．若半径为2的圆与l 1在第一象限内交于点P 1，半径为3的圆与l 2在第一象限内交于点P 2……半径为n ＋1的圆与l n 在第一象限内交于点P n ，则点P n 的坐标为 ．(n 为正整数)3. (2019，福建)如图，四边形ABCD 内接于⊙O ，AB ＝AC ，BD ⊥AC ，垂足为E ，点F 在BD 的延长线上，且DF ＝DC ，连接AF ，CF .(1)求证：∠BAC ＝2∠DAC ；(2)若AF ＝10，BC ＝45，求tan ∠BAD 的值．第3题图4. (2019，温州)如图，在△ABC 中，∠BAC ＝90°，点E 在BC 边上，且CA ＝CE ，过A ，C ，E 三点的⊙O 交AB 于另一点F ，作直径AD ，连接DE 并延长交AB 于点G ，连接CD ，CF .(1)求证：四边形DCFG 是平行四边形； (2)当BE ＝4，CD ＝38AB 时，求⊙O 的直径． 第4题图第24讲圆的基本性质1. (16，河北)如图所示的为4×4的网格图，A，B，C，D，O均在格点上，点O是(B)第1题图第2题图第3题图A. △ACD的外心B. △ABC的外心C. △ACD的内心D. △ABC的内心【解析】由网格图，知点O是边AC，BC的垂直平分线的交点．根据三角形外心的定义，知点O是△ABC的外心．2. (15，河北)如图，AC，BE是⊙O的直径，弦AD与BE相交于点F.下列三角形中，外心不是点O的是(B)A. △ABEB. △ACFC. △ABDD. △ADE【解析】只有△ACF的三个顶点不都在⊙O上，故外心不是点O的是△ACF.3. (12，河北)如图，CD是⊙O的直径，AB是弦(不是直径)，AB⊥CD于点E，则下列结论正确的是(D)A. AE>BEB. »AD＝»BCC. ∠D＝12∠AEC D. △ADE∽△CBE 【解析】∵CD是⊙O的直径，AB是弦(不是直径)，AB⊥CD于点E，∴AE＝BE，»».AC BC＝∴选项A，B错误．∵∠AEC不是圆心角，∴∠D≠12∠AEC. ∴选项C错误．∵∠AED＝∠CEB＝90°，∠DAE＝∠BCE，∴△ADE∽△CBE.∴选项D正确．圆的有关概念例1 (2019，扬州邗江区一模)如图，⊙O的直径BA的延长线与弦DC的延长线相交于点E，且CE＝OB.已知∠DOB ＝72°，则∠E的度数为(D)A. 36° B. 30° C. 18° D. 24°【解析】如答图，连接CO.可知CE＝OB＝CO，得∠E ＝∠1.由∠2是△EOC的外角，得∠2＝∠E＋∠1＝2∠E.由OC＝OD，得∠D＝∠2＝2∠E.由∠3是△ODE的外角，得∠3＝∠E＋∠D＝∠E＋2∠E＝3∠E.由∠3＝72°，得3∠E＝72°.解得∠E＝24°.1题图1答图训练1题图训练2题图针对训练1如图所示的圆规，点A是铁尖的端点，点B是铅笔芯尖的端点，已知点A与点B的距离是2 cm.若铁尖的端点A固定，铅笔芯尖的端点B绕点A旋转一周，则作出的圆的直径是(C)A. 1 cmB. 2 cmC. 4 cmD. πcm 【解析】∵AB＝2 cm，∴圆的直径是4 cm.针对训练2 (2019，海口模拟)如图，AB是⊙O的直径，点C，D在⊙O上，且点C，D在AB的异侧，连接AD，OD，OC.若∠AOC＝70°，且AD∥OC，则∠AOD的度数为(D)A. 70° B. 60° C. 50° D. 40°【解析】∵AD∥OC，∴∠AOC＝∠DAO＝70°.又∵OD＝OA，∴∠ADO＝∠DAO＝70°.∴∠AOD＝180－70°－70°＝40°.确定圆的条件例2 (2019，北京)在平面内，给定不在同一条直线上的点A，B，C，如图所示，点O到点A，B，C的距离均等于a(a为常数)，到点O的距离等于a的所有点组成图形G，∠ABC的平分线交图形G于点D，连接AD，CD.(1)求证：AD＝CD；(2)过点D作DE⊥BA，垂足为E，作DF⊥BC，垂足为F，延长DF交图形G于点M，连接CM.若AD＝CM，求直线DE与图形G的公共点个数．(1)证明：如答图．∵到点O的距离等于a的所有点组成图形G，∴图形G为△ABC的外接圆⊙O.∵BD平分∠ABC，∴∠ABD＝∠CBD.∴»»AD CD＝.∴AD＝CD. (2)解：如答图，连接OD.∵AD＝CM，AD＝CD，∴CD＝CM.∵DF⊥BC，∴BC垂直平分DM.易得BC为直径．∵OB＝OD，∴∠OBD＝∠ODB＝∠ABD.∴OD∥AB.∵DE ⊥AB ，∴OD ⊥DE .∴DE 为⊙O 的切线．∴直线DE 与图形G 的公共点个数为1.2题图 例2答图训练3题图 训练3答图针对训练3 (10，河北)如图，在5×5的正方形网格中，一条圆弧经过A ，B ，C 三点，那么这条圆弧所在圆的圆心是(B )A. 点P B. 点Q C. 点R D. 点M【解析】 如答图，连接BC ，作AB 和BC 的垂直平分线，它们相交于点Q ，则点Q 即为圆心．针对训练4 (2019，绥化)半径为5的⊙O 是锐角三角形ABC 的外接圆，AB ＝AC ，连接OB ，OC ，延长CO 交弦AB 于点D .若△OBD 是直角三角形，则弦BC 的长为（ 53或5 2 ）. 【解析】 如答图①，当∠ODB ＝90°时，CD ⊥AB ，∴AD ＝BD.∴AC ＝BC.∵AB ＝AC ，∴△ABC 是等边三角形．∴∠DBO ＝30°.∵OB ＝5，∴BD ＝32OB ＝532.∴BC ＝AB ＝2BD ＝5 3.如答图②，当∠DOB ＝90°时，∠BOC ＝90°.∴△BOC 是等腰直角三角形．∴BC ＝2OB ＝5 2.综上所述，若△OBD 是直角三角形，则弦BC 的长为53或5 2.训练4答图例3图训练5图训练5答图圆的基本性质 例3 (19，沈阳)如图，AB 是⊙O 的直径，点C 和点D 是⊙O 上位于直径AB 两侧的点，连接AC ，AD ，BD ，CD .若⊙O 的半径是13，BD ＝24，则sin ∠ACD 的值是(D )A. 1213 B. 125 C. 512 D. 513【解析】 ∵AB 是直径，∴∠ADB ＝90°.∵⊙O 的半径是13，∴AB ＝2×13＝26.在Rt △ABD 中，由勾股定理得AD ＝10，∴sin B ＝AD AB ＝1026＝513.∵∠ACD ＝∠B ，∴sin ∠ACD ＝sin B ＝513. 针对训练5 (2019，绵阳)如图，AB 是⊙O 的直径，C 为»BD的中点，CF 为⊙O 的弦，且CF ⊥AB ，垂足为E ，连接BD 交CF 于点G ，连接CD ，AD ，BF .(1)求证：△BFG ≌△CDG ；(2)若AD ＝BE ＝2，求BF 的长．(1)证明：∵C 是»BD的中点，∴»»CD BC ＝.∵AB 是⊙O 的直径，且CF ⊥AB ，∴»»BC BF ＝.∴»»CD BF ＝.∴CD ＝BF . 在△BFG 和△CDG 中，⎩⎪⎨⎪⎧∠F ＝∠CDG ，∠FGB ＝∠DGC ，BF ＝CD ，∴△BFG ≌△CDG (AAS)．(2)解：如答图，连接OC ，交BD 于点H ，连接OD ，BC .∵C 是»BD的中点，∴DC ＝BC .∵OD ＝OB ，∴OC 垂直平分BD .∴OC ⊥BD .∴DH ＝BH .∵OA ＝OB ，∴OH ＝12AD ＝1.∵OC ＝OB ，∠COE ＝∠BOH ，∠OEC ＝∠OHB ＝90°，∴△COE ≌△BOH (AAS)．∴OE ＝OH ＝1.∴OB ＝OE ＋BE ＝1＋2＝3.∴OC ＝3.∵CF ⊥AB ，∴CE ＝EF .在Rt △OEC 中，CE ＝OC 2－OE 2＝32－12＝22，∴EF ＝2 2.在Rt △BEF 中，BF ＝BE 2＋EF 2＝22＋()222＝2 3.垂径定理及其应用 例4 (19梧州)如图，在半径为13的⊙O 中，弦AB 与CD 相交于点E ，∠DEB ＝75°，AB ＝6，AE ＝1，则CD 的长是(C )A. 2 6 B. 210 C. 211 D. 43 【解析】 如答图，过点O 作OF ⊥CD于点F ，OG ⊥AB 于点G ，连接OB ，OD ，OE ，则DF ＝CF ，AG ＝BG ＝12AB ＝3.∴EG ＝AG －AE ＝2.在Rt △BOG 中，OG ＝OB 2－BG 2＝13－9＝2，∴EG ＝OG .∴△EOG 是等腰直角三角形．∴∠OEG ＝45°，OE ＝2OG ＝2 2.∵∠DEB ＝75°，∴∠OEF ＝30°.∴OF ＝12OE ＝ 2.在Rt △ODF 中，DF ＝OD 2－OF 2＝13－2＝11，∴CD ＝2DF ＝211. 例4题图例4答图训练6题图训练6答图针对训练6 (19黄冈)如图，一条公路的转弯处是一段圆弧(»AB )，点O 是这段弧所在圆的圆心，AB ＝40 m ，C 是»AB 的中点，D 是AB 的中点，且CD ＝10 m ，则这段弯路所在圆的半径为(A ) A. 25 m B. 24 m C. 30 m D. 60 m【解析】 如答图，连接OD.由题意可知点O ，D ，C 共线，且OC ⊥AB ，AD ＝DB ＝12AB ＝20 m ．在Rt △AOD 中，OA 2＝OD 2＋AD 2.设这段弯路所在圆的半径为r ，得r 2＝(r －10)2＋202.解得r ＝25(m )．∴这段弯路所在圆的半径为25 m .1. (2019，广元)如图，AB ，AC 分别是⊙O 的直径和弦，OD ⊥AC 于点D ，连接BD ，BC ，且AB ＝10，AC ＝8，则BD 的长为(C )A. 2 5 B. 4 C. 213 D. 4.8【解析】 ∵AB 为直径，∴∠ACB ＝90°.∴BC ＝AB 2－AC 2＝102－82＝6.∵OD ⊥AC ，∴CD ＝AD ＝12AC ＝4.在Rt △CBD 中，BD ＝42＋62＝213. 第1题图第2题图第3题图第3题答图2. (2019，吉林)如图，在⊙O 中，»AB 所对的圆周角∠ACB ＝50°.若P 为»AB 上一点，∠AOP ＝55°，则∠POB 的度数为(B )A. 30° B. 45° C. 55° D. 60°【解析】 ∵∠ACB ＝50°，∴∠AOB ＝2∠ACB ＝100°.∵∠AOP ＝55°，∴∠POB ＝45°.3. (19白银)如图，点A ，B ，S 在圆上，若弦AB 的长度等于圆半径的2倍，则∠ASB 的度数是(C )A. 22.5°B. 30°C. 45°D. 60° 【解析】 如答图设圆心为O ，连接OA ，OB.∵弦AB 的长度等于圆半径的2倍，即AB ＝2OA ，∴OA 2＋OB 2＝AB 2.∴△OAB 为等腰直角三角形，即∠AOB ＝90°.∴∠ASB ＝12∠AOB ＝45°. 4. (19镇江如图，四边形ABCD 是半圆的内接四边形，AB 是直径，»»DCCB ＝.若∠C ＝110°，则∠ABC 的度数为(A )第4题图第4题答图第5题图A. 55°B. 60°C. 65°D. 70° 【解析】 如答图，连接AC.∵四边形ABCD 是半圆的内接四边形，∴∠DAB ＝180°－∠BCD ＝70°.∵»»DCCB ＝，∴∠CAB ＝12∠DAB ＝35°.∵AB 是直径，∴∠ACB ＝90°.∴∠ABC ＝90°－∠CAB ＝55°. 5. (2019，贵港)如图，AD 是⊙O 的直径，»»AB CD ＝.若∠AOB ＝40°，则圆周角∠BPC 的度数是(B )A. 40°B. 50°C. 60°D. 70° 【解析】 ∵»»AB CD ＝，∠AOB ＝40°，∴∠COD ＝∠AOB ＝40°.∵∠AOB ＋∠BOC ＋∠COD ＝180°，∴∠BOC ＝100°.∴∠BPC ＝12∠BOC ＝50°. 6. (2019，聊城)如图，BC 是半圆O 的直径，D ，E 是»BC上两点，连接BD ，CE 并延长相交于点A ，连接OD ，OE .如果∠A ＝70°，那么∠DOE 的度数为(C )A. 35° B. 38° C. 40° D. 42°【解析】 如答图，连接CD.∵BC 是半圆O 的直径，∴∠BDC ＝90°.∴∠ACD ＝90°－∠A ＝20°.∴∠DOE ＝2∠ACD ＝40°第6题图第6题答图第7题图第7题答图7. (2019，安顺)如图，半径为3的⊙A 经过原点O 和点C (0，2)，B 是y 轴左侧⊙A 优弧上一点，则tan ∠OBC 的值为(D )A. 13 B. 2 2 C. 223 D. 24【解析】 如答图，设⊙A 与x 轴负半轴相交于点D ，连接CD.∵∠COD ＝90°，∴CD 是直径．在Rt △OCD 中，CD ＝6，OC ＝2，∴OD ＝CD 2－OC 2＝4 2.∴tan ∠CDO ＝OC OD ＝24.由圆周角定理得∠OBC ＝∠CDO ，则tan ∠OBC ＝24. 8. (2019，天水)如图，四边形ABCD 是菱形，⊙O 经过点A ，C ，D ，与BC 相交于点E ，连接AC ，AE .若∠D ＝80°，则∠EAC 的度数为(C )A. 20° B. 25° C. 30° D. 35°第8题图第9题图第9题答图第10题图【解析】 ∵四边形ABCD 是菱形，∠D ＝80°，∴∠ACB ＝12∠DCB ＝12(180°－∠D)＝50°.∵四边形AECD 是圆内接四边形，∴∠AEC ＝180°－∠D ＝100°.∴∠EAC ＝180°－∠AEC －∠ACB ＝180°－100°－50°＝30°.9. (2019，通辽)如图，等边三角形ABC 内接于⊙O .若⊙O 的半径为2，则图中阴影部分的面积等于(C )A. π3B. 2π3C. 4π3D. 2π 【解析】 如答图，连接OC.∵△ABC 为等边三角形，∴∠AOC ＝120°，S △AOB ＝S △AOC .∴阴影部分的面积＝S 扇形AOC ＝120·π×22360＝4π3. 10. (2019，菏泽)如图，AB 是⊙O 的直径，C ，D 是⊙O 上的两点，且BC 平分∠ABD ，AD 分别与BC ，OC 相交于点E ，F ，则下列结论不一定成立的是(C )A. OC ∥BDB. AD ⊥OCC. △CEF ≌△BEDD. AF ＝FD【解析】 ∵AB 是⊙O 的直径，BC 平分∠ABD ，∴∠ADB ＝90°，∠OBC ＝∠DBC.∴AD ⊥BD.∵OB ＝OC ，∴∠OCB ＝∠OBC.∴∠DBC ＝∠OCB.∴OC ∥BD ，选项A 成立．∴AD ⊥OC ，选项B 成立．∵OA ＝OB ，OC ∥BD ，∴AF ＝FD ，选项D 成立．∵△CEF 和△BED 中，没有相等的边，∴△CEF 与△BED 不全等，选项C 不成立．11. (2019，陕西)如图，AB 是⊙O 的直径，EF ，EB 是⊙O 的弦，且EF ＝EB ，EF 与AB 相交于点C ，连接OF .若∠AOF ＝40°，则∠F 的度数是(B )A. 20° B. 35° C. 40° D. 55°第11题图第11题答图第12题图【解析】 如答图，连接FB.∵∠AOF ＝40°，∴∠FOB ＝180°－40°＝140°.∴∠FEB ＝12∠FOB ＝70°.∵EF ＝EB ，∴∠EFB ＝∠EBF ＝55°.∵FO ＝BO ，∴∠OFB ＝∠OBF ＝20°.∴∠EFO ＝∠EFB －∠OFB ＝35°.12. (2019，赤峰)如图，AB 是⊙O 的弦，OC ⊥AB 交⊙O 于点C ，D 是⊙O 上一点，∠ADC ＝30°，则∠BOC 的度数为(D )A. 30° B. 40° C. 50° D. 60° 【解析】 ∵∠ADC ＝30°，∴∠AOC ＝2∠ADC ＝60°.∵AB 是⊙O 的弦，OC ⊥AB 交⊙O 于点C ，∴»»AC BC ＝.∴∠AOC ＝∠BOC ＝60°. 13. (2019，宁夏)如图，AB 是⊙O 的弦，OC ⊥AB ，垂足为C ，将劣弧»AB 沿弦AB 折叠交于OC 的中点D .若AB ＝210，则⊙O 的半径为（ 3 2 ）.第13题图第13题答图第14题图第14题答图【解析】 如答图，连接OA.设⊙O 的半径为x.∵将劣弧»AB 沿弦AB 折叠交于OC 的中点D ，∴OC ＝23x.∵OC ⊥AB ，∴AC ＝12AB ＝10.∵OA 2－OC 2＝AC 2，∴x 2－⎝⎛⎭⎫23x 2＝10.解得x ＝3 2.∴⊙O 的半径为3 2. 14. (2019，盐城)如图，点A ，B ，C ，D ，E 在⊙O 上，且»AB 所对的圆心角为50°，则∠E ＋∠C ＝ 155 °. 【解析】 如答图，连接EA.∵»AB 所对的圆心角为50°，∴∠BEA ＝25°.∵四边形DCAE 为⊙O 的内接四边形，∴∠DEA ＋∠C ＝180°.∴∠DEB ＋∠C ＝180°－25°＝155°.15. (2019，安徽)如图，△ABC 内接于⊙O ，∠CAB ＝30°，∠CBA ＝45°，CD ⊥AB 于点D .若⊙O 的半径为2，则CD 的长为（ 2 ）.【解析】 如答图，连接CO 并延长交⊙O 于点E ，连接BE ，则∠E ＝∠A ＝30°，∠EBC ＝90°.∵⊙O 的半径为2，∴CE ＝4.∴BC ＝12CE ＝2.∵CD ⊥AB ，∠CBA ＝45°，∴CD ＝22BC ＝ 2. 第15题图第15题答图第16题图第16题答图16. (2019，广元)如图，△ABC 是⊙O 的内接三角形，且AB 是⊙O 的直径，P 为⊙O 上的动点，且∠BPC ＝60°，⊙O 的半径为6，则点P 到AC 距离的最大值是（ 6＋3 3 ）.解析】 如答图，过点O 作OM ⊥AC 于点M ，延长MO 交⊙O 于点P ，则此时点P 到AC 的距离最大，且点P 到AC 距离的最大值＝PM.∵OM ⊥AC ，∠A ＝∠BPC ＝60°，⊙O 的半径为6，∴OP ＝OA ＝6.∴OM ＝32OA ＝32×6＝3 3.∴PM ＝OP ＋OM ＝6＋3 3.∴点P 到AC 距离的最大值是6＋3 3.17. (2019，嘉兴)如图，在⊙O 中，弦AB ＝1，点C 在AB 上移动，连接OC ，过点C 作CD ⊥OC 交⊙O 于点D ，则CD 的最大值为（ 12）.【解析】 如答图，连接OD.设⊙O 的半径为r.∵CD ⊥OC ，∴∠DCO ＝90°.∴CD ＝OD 2－OC 2＝r 2－OC 2.∴当OC 的值最小时，CD 的值最大．∴当OC ⊥AB 时，OC 最小，此时OC ＝r 2－⎝⎛⎭⎫12AB 2.∴CD 的最大值为r 2－⎝⎛⎭⎫r 2－14AB 2＝12AB ＝12×1＝12.第17题图第17题答图三、 解答题 18. (2019，包头)如图，在⊙O 中，B 是⊙O 上的一点，∠ABC ＝120°，弦AC ＝23，弦BM 平分∠ABC 交AC 于点D ，连接MA ，MC .(1)求⊙O 的半径；(2)求证：AB ＋BC ＝BM . (1)解：如答图①，连接OA ，OC ，过点O 作OH ⊥AC 于点H .第18题图第18题答图∴AH ＝HC ＝12AC .∵OA ＝OC ，∴∠AOH ＝∠COH ＝12∠AOC .∵∠ABC ＝120°∴∠AMC ＝180°－∠ABC ＝60°.∴∠AOC ＝2∠AMC ＝120°.∴∠AOH ＝12∠AOC ＝60°.∵AC ＝23，∴AH ＝12AC ＝ 3. 在Rt △AOH 中，sin ∠AOH ＝AH OA ，∴OA ＝AH sin 60°＝2.∴⊙O 的半径为2. (2)证明：如答图②，在BM 上截取BE ＝BC ，连接CE .∵∠ABC ＝120°，BM 平分∠ABC ，∴∠ABM ＝∠CBM ＝12∠ABC ＝60°.∵BE ＝BC ，∴△EBC 是等边三角形．∴∠BEC ＝60°，BC ＝EC .∴∠MEC ＝120°.∴∠ABC ＝∠MEC .∵∠BAC ＝∠BMC ，∴△ACB ≌△MCE (AAS)．∴AB ＝ME .∵ME ＋EB ＝BM ，∴AB ＋BC ＝BM .19. (2019，荆门)如图，已知锐角三角形ABC 的外接圆圆心为O ，半径为R . (1)求证：AC sin B＝2R ； (2)若在△ABC 中，∠A ＝45°，∠B ＝60°，AC ＝3，求BC 的长及sin C 的值．第19题图第19题答图第1题图(1)证明：如答图①，连接AO 并延长交⊙O 于点D ，连接CD ，则∠DCA ＝90°，∠B ＝∠ADC .在Rt △ACD 中，sin ∠ADC ＝AC AD ＝AC 2R ， ∴sin B ＝AC 2R .∴AC sin B＝2R . (2)解：由(1)同理可得AC sin B ＝AB sin C ＝BC sin A ＝2R . ∵AC ＝3，∠B ＝60°，∴2R ＝3sin 60°＝2.∴BC ＝2R ·sin A ＝2sin 45°＝ 2.如答图②，过点C 作CE ⊥AB 于点E .在Rt △BCE 中，BE ＝BC ·cos B ＝2cos 60°＝22.在Rt △ACE 中，AE ＝AC ·cos A ＝3cos 45°＝62.∴AB ＝AE ＋BE ＝6＋22.∵AB sin ∠ACB＝2R ，∴sin ∠ACB ＝AB 2R ＝6＋24.1. (2019，湘潭)《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积＝12(弦×矢＋矢2)．弧田是由圆弧和其所对的弦围成(如图中的阴影部分)，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理(当半径OC ⊥弦AB 时，OC 平分AB )可以求解．现已知弦AB＝8 m ，半径等于5 m 的弧田，按照上述公式计算出弧田面积为 10 m 2. 【解析】 ∵AB ＝8，OC ⊥AB ，∴AD ＝4.∴OD ＝OA 2－AD 2＝3.∴OC －OD ＝2.∴弧田面积＝12×(8×2＋22)＝10(m 2)． 2. (2019，潍坊)如图，在平面直角坐标系xOy 中，一组同心圆的圆心为坐标原点O ，它们的半径分别为1，2，3，…，按照“加1”依次递增；一组平行线l 0，l 1，l 2，l 3，…都与x 轴垂直，相邻两直线的间距为1，其中l 0与y 轴重合．若半径为2的圆与l 1在第一象限内交于点P 1，半径为3的圆与l 2在第一象限内交于点P 2……半径为n ＋1的圆与l n 在第一象限内交于点P n ，则点P n 的坐标为 (n ，2n ＋1) ．(n 为正整数)【解析】 如答图，连接OP 1，OP 2，OP 3，l 1，l 2，l 3与x 轴分别交于点A 1，A 2，A 3.在Rt △OA 1P 1中，OA 1＝1，OP 1＝2，∴A 1P 1＝OP 21－OA 21＝22－12＝ 3.同理A 2P 2＝32－22＝5，A 3P 3＝42－32＝7.∴点P 1的坐标为(1，3)，点P 2的坐标为(2，5)，点P 3的坐标为(3，7)．按照此规律可得点P n 的坐标是(n ，()n ＋12－n 2)，即(n ，2n ＋1)．3. (2019，福建)如图，四边形ABCD 内接于⊙O ，AB ＝AC ，BD ⊥AC ，垂足为E ，点F 在BD 的延长线上，且DF ＝DC ，连接AF ，CF .(1)求证：∠BAC ＝2∠DAC ；(2)若AF ＝10，BC ＝45，求tan ∠BAD 的值．2题图2题答图3题图3题答图(1)证明：∵AB ＝AC ，∴»»AB AC ＝，∠ABC ＝∠ACB .∴∠ABC ＝∠ADB ，∠ABC ＝12(180°－∠BAC )＝90°－12∠BAC .∵BD ⊥AC ，∴∠ADB ＝90°－∠DAC .∴12∠BAC ＝∠DAC .∴∠BAC ＝2∠DAC . (2)解：∵DF ＝DC ，∴∠DFC ＝∠DCF .∴∠BDC ＝2∠DFC .∴∠BFC ＝12∠BDC ＝12∠BAC ＝∠DAC ＝∠FBC . ∴CB ＝CF ＝4 5.又∵BD ⊥AC ，∴AC 是线段BF 的垂直平分线．∴AB ＝AF ＝10.∴AC ＝10. 设AE ＝x ，则CE ＝10－x .由AB 2－AE 2＝BC 2－CE 2，得100－x 2＝80－(10－x )2.解得x ＝6.∴AE ＝6，CE ＝4.∴BE ＝EF ＝8.设DE ＝y ，则CD ＝DF ＝8－y .在Rt △CDE 中，CD 2＝DE 2＋CE 2，即(8－y )2＝y 2＋42.解得y ＝3，即DE ＝3.∴BD ＝BE ＋DE ＝8＋3＝11.如答图，过点D 作DH ⊥AB ，垂足为H .∵12AB ·DH ＝12BD ·AE ，∴DH ＝BD ·AE AB ＝11×610＝335.在Rt △BDH 中，BH ＝BD 2－DH 2＝445.∴AH ＝AB －BH ＝10－445＝65.∴tan ∠BAD ＝DH AH ＝33565＝112. 4. (2019，温州)如图，在△ABC 中，∠BAC ＝90°，点E 在BC 边上，且CA ＝CE ，过A ，C ，E 三点的⊙O 交AB 于另一点F ，作直径AD ，连接DE 并延长交AB 于点G ，连接CD ，CF .(1)求证：四边形DCFG 是平行四边形； (2)当BE ＝4，CD ＝38AB 时，求⊙O 的直径． 第4题图第4题答图(1)证明：如答图，连接AE .∵∠BAC ＝90°，∴CF 是⊙O 的直径．∵AC ＝EC ，∴CF ⊥AE .∵AD 是⊙O 的直径，∴∠AED ＝90°.∴GD ⊥AE .∴CF ∥DG .∵AD 是⊙O 的直径，∴∠ACD ＝90°.∴∠ACD ＋∠BAC ＝180°.∴AB ∥CD .∴四边形DCFG 是平行四边形． (2)解：由CD ＝38AB ，设CD ＝3x ，则AB ＝8x .由(1)知四边形DCFG 是平行四边形，∴CD ＝FG ＝3x .∵∠AOF ＝∠COD ，∴AF ＝CD ＝3x .∴BG ＝8x －3x －3x ＝2x .∵GE ∥CF ，∴BE EC ＝BG GF ＝23.∵BE ＝4，∴CE＝6.∴AC＝CE＝6，BC＝6＋4＝10.在Rt△ABC中，AB＝102－62＝8＝8x.∴x＝1.在Rt△ACF中，AF＝3，AC＝6，∴CF＝32＋62＝3 5.∴⊙O的直径为3 5.。

九年级数学上册《第二十四章 圆的有关性质》同步练习题附答案(人教版)一、选择题：1．如图，AB 为⊙O 的弦，OA=4，∠AOB=120°，则AB 的长为（ ）A ．4B ．C ．2D ．2．如图，∠C 是⊙O 的圆周角，∠C=38°，则∠OAB= ( ) 度A ．52B ．38C ．60D ．763．如图，A 、D 是O 上的两个点，BC 是直径，若∠D=35°，则∠OAC 等于( )A ．65°B ．35°C ．70°D ．55°4．一个圆形人工湖如图所示，弦AB 是湖上的一座桥，已知桥AB 长100m ，测得圆周角45ACB ∠=︒，则这个人工湖的直径AD 为（ ）A ．502mB ．1002mC ．1502mD ．2002m5．如图，AB 是⊙O 的直径，点C 、D 在⊙O 上，且在AB 异侧，连接OC 、CD 、DA ．若130BOC ∠=︒，则D ∠的大小是（ ）A ．15°B ．25°C ．35°D ．50°6．如图，⊙O 的直径AB=8，P 为⊙O 上任一点（不同于A 、B 两点），∠APB 的平分线交⊙O 于点C ，弦EF 经过AC 、BC 的中点M 、N ，则弦EF 的长为（ ）A ．B ．23C ．33D ．437．如图，AB 为⊙O 的弦，点C 在AB 上，AC ＝4，BC ＝2，CD ⊥OC 交⊙O 于点D ，则CD 的长为（ ）A B ．3 C ．D ．8．如图，AB 是O 的直径，点C ，点D 是半圆上两点，连结AC ，BD 相交于点P ，连结AD ，.OC 已知OC BD ⊥于点E ， 2.AB =下列结论：90CAD OBC ∠+∠=︒①；②若点P 为AC 的中点，则2CE OE =.③若AC BD =，则CE OE =；224BC BD +=④；其中正确的是（ ）A ．①②③B ．②③④C ．①③④D ．①②④二、填空题：9．在半径为1 度．10．圆O的半径OA=6，OA的垂直平分线交圆O于B、C，那么弦BC的长等于.11．如图，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD于点E，AE＝CD，若⊙O的半径为5，则弦CD的长为．12．如图，已知AB是⊙O的弦，半径OC垂直AB，点D是⊙O上一点，且点D与点C位于弦AB两侧，连接AD、CD、OB，若∠BOC=70°，则∠ADC= 度．13．如图，MN是⊙O的直径，MN＝2，点A在⊙O上，∠AMN＝40°，B为弧AN的中点，P是直径MN上一动点，则PA＋PB的最小值为.三、解答题：14．如图，AB为⊙O的弦，AB=8，OC⊥AB于点D，交⊙O于点C，且CD=1 ，求⊙O的半径．15．如图，在⊙O中AC∧=CB∧，点D、E分别在半径OA和OB上，AD=BE求证：CD=CE．16．如图，两个圆的圆心为O，大圆半径OC，OD交小圆于点A，B，判断AB与CD的位置关系，并说明原因．17．如图，已知AB 是⊙O 的一条弦，OD ⊥AB ，垂足为C ，交⊙O 于点D ，点E 在⊙O 上，连接OA 、DE 、BE ．（1）若∠AOD ＝60°，求∠DEB 的度数；（2）若CD ＝2，弦AB ＝8，求⊙O 的半径长．18．如图，四边形ABCD 内接于⊙O ，AC 是⊙O 的直径，E 是AB 上一点30AEO DAC ∠=∠=︒，连接BD . （1）求证：OAE CDB ≌；（2）连接 DE ，若 DE AB ⊥ ， OA=2 ，求 BC 的长.参考答案：1．D 2．A 3．D 4．B 5．B 6．D 7．C 8．A 9．9010．6311．812．3513314．解：172 r=15．证明：连接OC．在⊙O中，∵AC∧=CB∧∴∠AOC=∠BOC∵OA=OB，AD=BE∴OD=OE．在△COD与△COE中∴△COD≌△COE（SAS）∴CD=CE．16．解：AB∥CD．∵OA=OB，OC=OD，∴∠OAB=∠OBA，∠OCD=∠ODC，∴∠OAB= 12（180°﹣∠O），∠OCD=12（180°﹣∠O），∴∠OAB=∠OCD，∴AB∥CD．17．（1）解：∵OD⊥AB∴AD＝BD∴∠BOD＝∠AOD＝60°∴∠DEB＝12∠BOD＝12×60°＝30°；（2）解：设⊙O的半径为r，则OC＝r﹣2 ∵OD⊥AB∴AC ＝BC ＝12AB ＝12×8＝4在Rt △OAC 中，由勾股定理得：（r ﹣2）2+42＝r 2解得：r ＝5即⊙O 的半径长为5．18．（1）证明：∵AC 是 O 的直径 ∴90ADC ∠=︒ .∵30CAD ∠=︒∴2AC CD = .∵2AC OA =∴OA CD = .∵BC BC = CD CD =∴EAO CDB ∠=∠ CAD CBD ∠=∠ . ∵AEO DAC ∠=∠∴AEO CBD ∠=∠ .∴OAE CDB ≌ ；（2）解：连接DE ，过 O 作 OH AB ⊥ 于 H∴AH HB = .∵AO OC =∴2BC OH = .设 OH x =∵30OEA CAD ∠=∠=︒ ∴3HE x = .由（1）知 OAE CDB ≌∴AE DB = .∵AD AD =∴60ABD ACD ∠=∠=︒ .∵DE AB ⊥∴30BDE ∠=︒ .∴2DB BE = AE DB = . ∴2AE BE = .设 AH HB y ==则 3AE y x =+ 3BE y x = . ∴()323y x y x += . ∴33y x = .在 Rt OAH 中 2OA = 33AH x = OH x = 222OH AH OA +=()222332x x += .解得 17x = 27x = （舍去）. ∴7OH =∴272BC OH ==。

2021年中考数学真题分类汇编：专题24圆的有关性质一、单选题1．（2021·甘肃武威市·中考真题）如图，点,,,,A B C D E 在O 上，,42AB CD AOB =∠=︒，则CED ∠=（ ）A ．48︒B ．24︒C ．22︒D ．21︒ 【答案】D【分析】先证明,AB CD =再利用等弧的性质及圆周角定理可得答案．【详解】 解： 点,,,,A B C D E 在O 上，,42AB CD AOB =∠=︒，,AB CD ∴=114221,22CED AOB ∴∠=∠=⨯︒=︒ 故选：.D【点睛】本题考查的两条弧，两个圆心角，两条弦之间的关系，圆周角定理，等弧的概念与性质，掌握同弧或等弧的概念与性质是解题的关键．2．（2021·广西玉林市·中考真题）学习圆的性质后，小铭与小熹就讨论起来，小铭说：“被直径平分的弦也与直径垂直”，小熹说：“用反例就能说明这是假命题” ．下列判断正确的是（ ）A ．两人说的都对B ．小铭说的对，小燕说的反例不存在C ．两人说的都不对D ．小铭说的不对，小熹说的反例存在【答案】D【分析】根据垂径定理可直接进行排除选项．【详解】解：由垂径定理的推论“平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧”可知：小铭忽略了垂径定理中的“弦不能是直径”这一条件，因为一个圆中的任意两条直径都互相平分，但不垂直，所以小铭说法错误，小熹所说的反例即为两条直径的情况下；故选D．【点睛】本题主要考查垂径定理，熟练掌握垂径定理是解题的关键．3．（2021·青海中考真题）如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交AB 厘米．若从目前太阳所处位置到太阳完全跳出于A，B两点，他测得“图上”圆的半径为10厘米，16海平面的时间为16分钟，则“图上”太阳升起的速度为（）．A．1.0厘米/分B．0.8厘米分C．12厘米/分D．1.4厘米/分【答案】A【分析】首先过⊙O的圆心O作CD⊙AB于C，交⊙O于D，连接OA，由垂径定理，即可求得OC的长，继而求得CD的长，又由从目前太阳所处位置到太阳完全跳出海面的时间为10分钟，即可求得“图上”太阳升起的速度．【详解】解：过⊙O的圆心O作CD⊙AB于C，交⊙O于D，连接OA，⊙AC=12AB=12×16=8（厘米），在Rt⊙AOC中，6OC===（厘米），⊙CD=OC+OD=16（厘米），⊙从目前太阳所处位置到太阳完全跳出海面的时间为16分钟，⊙16÷16=1（厘米/分）．⊙“图上”太阳升起的速度为1.0厘米/分．故选：A．【点睛】此题考查了垂径定理的应用．解题的关键是结合图形构造直角三角形，利用勾股定理求解．4．（2021·山东聊城市·中考真题）如图，A，B，C是半径为1的⊙O上的三个点，若AB⊙CAB＝30°，则⊙ABC的度数为（）A．95°B．100°C．105°D．110°【答案】C【分析】连接OB，OC，根据勾股定理逆定理可得⊙AOB＝90°，⊙ABO＝⊙BAO＝45°，根据圆周角定理可得⊙COB＝2⊙CAB＝60°，⊙OBC＝⊙OCB＝60°，由此可求得答案．【详解】解：如图，连接OB，OC，⊙OA ＝OB ＝1，AB⊙OA 2＋OB 2＝AB 2，⊙⊙AOB ＝90°，又⊙OA ＝OB ，⊙⊙ABO ＝⊙BAO ＝45°，⊙⊙CAB ＝30°，⊙⊙COB ＝2⊙CAB ＝60°，又⊙OC ＝OB ，⊙⊙OBC ＝⊙OCB ＝60°，⊙⊙ABC ＝⊙ABO ＋⊙OBC ＝105°，故选：C ．【点睛】本题考查了勾股定理的逆定理，等腰三角形的性质，圆周角定理，熟练掌握圆周角定理是解决本题的关键． 5．（2021·湖北鄂州市·中考真题）已知锐角40AOB ∠=︒，如图，按下列步骤作图：⊙在OA 边取一点D ，以O 为圆心，OD 长为半径画MN ，交OB 于点C ，连接CD ．⊙以D 为圆心，DO 长为半径画GH ，交OB 于点E ，连接DE ．则CDE ∠的度数为（ ）A ．20︒B ．30C ．40︒D ．50︒【答案】B【分析】 根据画图过程，得到OD =OC ，由等边对等角与三角形内角和定理得到⊙ODC =⊙OCD =70︒，同理得到⊙DOE =⊙DEO =40⊙，由⊙OCD 为⊙DCE 的外角，得到结果．【详解】解：⊙以O 为圆心，OD 长为半径画MN ，交OB 于点C ，⊙OD =OC ，⊙⊙ODC =⊙OCD ，⊙⊙AOB =40⊙，⊙⊙ODC =⊙OCD =118040702⨯︒-︒=︒， ⊙以D 为圆心，DO 长为半径画GH ，交OB 于点E ，⊙DO =DE ，⊙⊙DOE =⊙DEO =40⊙，⊙⊙OCD 为⊙DCE 的外角，⊙⊙OCD =⊙DEC +⊙CDE ，⊙70⊙=40⊙+⊙CDE ，⊙⊙CDE =30⊙，故选：B ．【点睛】本题考查了等腰三角形的判定与性质、以及三角形外角的性质，关键在于等边对等角与三角形的外角等于与它不相邻的两个内角之和两个知识点的熟练运用．6．（2021·海南中考真题）如图，四边形ABCD 是O 的内接四边形，BE 是O 的直径，连接AE ．若2BCD BAD ∠=∠，则DAE ∠的度数是（ ）A ．30B ．35︒C ．45︒D ．60︒【答案】A【分析】 先根据圆内接四边形的性质可得60BAD ∠=︒，再根据圆周角定理可得90BAE ∠=︒，然后根据角的和差即可得．【详解】 解：四边形ABCD 是O 的内接四边形，180BCD BAD ∴∠+∠=︒，2BCD BAD ∠=∠，1180603BAD =⨯︒∴∠=︒， BE 是O 的直径，90BAE ∴∠=︒，906030DAE BAE BAD ∴∠=∠-∠=︒-︒=︒，故选：A ．【点睛】本题考查了圆内接四边形的性质、圆周角定理，熟练掌握圆内接四边形的性质是解题关键．7．（2021·四川眉山市·中考真题）如图，在以AB 为直径的O 中，点C 为圆上的一点，3BC AC =，弦CD AB ⊥于点E ，弦AF 交CE 于点H ，交BC 于点G ．若点H 是AG 的中点，则CBF ∠的度数为（ ）A ．18°B ．21°C ．22.5°D ．30°【答案】C【分析】根据直径所对的圆周角是90︒，可知90ACB AFB ∠=∠=︒，根据3BC AC =，可知ABC ∠、BAC ∠的度数，根据直角三角形斜边上的中线等于斜边的一半可知，AHC 为等腰三角形，再根据CAE BFG BCA ∽∽可求得CBF ∠的度数．【详解】解：⊙AB 为O 的直径，⊙90ACB AFB ∠=∠=︒，⊙3BC AC =，⊙=22.5ABC ∠︒，=67.5BAC ∠︒，⊙点H 是AG 的中点，⊙CE AH =，⊙CAH ACH ∠=∠，⊙CD AB ⊥，⊙AEC GCA ∽，又⊙,CAF CBF CGA FGB ∠=∠∠=∠，⊙AEC GCA GFB ∽∽，⊙90ACE ECB ABC ECB ∠+∠=∠+∠=︒，⊙ABE ABC ∠=∠，⊙AEC GCA GFB ACB ∽∽∽，⊙22.5ABC ACE GAC GBF ∠=∠=∠=∠=︒，⊙=22.5CBF ∠︒，故选：C ．【点睛】本题主要考查圆周角定理，垂径定理，相似三角形，直角三角形斜边上中线等知识点，找出图形中几个相似三角形是解题关键．8．（2021·四川南充市·中考真题）如图，AB 是O 的直径，弦CD AB ⊥于点E ，2CD OE =，则BCD ∠的度数为（ ）A ．15︒B ．22.5︒C ．30D ．45︒【答案】B【分析】连接OD ，根据垂径定理得CD =2DE ，从而得ODE 是等腰直角三角形，根据圆周角定理即可求解．【详解】解：连接OD ，⊙AB 是O 的直径，弦CD AB ⊥于点E ，⊙CD =2DE ，⊙2CD OE =，⊙DE =OE ，⊙ODE 是等腰直角三角形，即⊙BOD =45°，⊙BCD ∠=12⊙BOD =22.5°， 故选B ．【点睛】本题主要考查圆的基本性质，熟练掌握垂径定理和圆周角定理，是解题的关键．9．（2021·四川广安市·中考真题）如图，公园内有一个半径为18米的圆形草坪，从A 地走到B 地有观赏路（劣弧AB ）和便民路（线段AB ）.已知A 、B 是圆上的点，O 为圆心，120AOB ∠=︒，小强从A 走到B ，走便民路比走观赏路少走（ ）米.A ．6π-B ．6π-C ．12π-D ．12π-【答案】D【分析】 作OC ⊙AB 于C ，如图，根据垂径定理得到AC =BC ，再利用等腰三角形的性质和三角形内角和计算出⊙A ，从而得到OC 和AC ，可得AB ，然后利用弧长公式计算出AB 的长，最后求它们的差即可．【详解】解：作OC ⊙AB 于C ，如图，则AC =BC ，⊙OA =OB ，⊙⊙A =⊙B =12（180°-⊙AOB ）=30°， 在Rt ⊙AOC 中，OC =12OA =9，AC =⊙AB =2AC =又⊙12018180AB π⨯⨯==12π，⊙走便民路比走观赏路少走12π-故选D ．【点睛】本题考查了垂径定理：垂径定理和勾股定理相结合，构造直角三角形，可解决计算弦长、半径、弦心距等问题．10．（2021·重庆中考真题）如图，AB 是⊙O 的直径，AC ，BC 是⊙O 的弦，若20A ∠=︒，则B 的度数为（ ）A ．70°B ．90°C ．40°D ．60°【答案】A【分析】直接根据直径所对的圆周角为直角进行求解即可．【详解】⊙AB 是⊙O 的直径，⊙⊙ACB =90°，⊙在Rt ⊙ABC 中，⊙B =90°-⊙A =70°，故选：A ．【点睛】本题考查直径所对的圆周角为直角，理解基本定理是解题关键．11．（2021·浙江丽水市·中考真题）如图，AB 是O 的直径，弦CD OA ⊥于点E ，连结,OC OD ．若O 的半径为,m AOD α∠=∠，则下列结论一定成立的是（ ）A ．tan OE m α=⋅B ．2sin CD m α=⋅C ．cos AE m α=⋅D ．2sin COD S m α=⋅【答案】B【分析】 根据垂径定理、锐角三角函数的定义进行判断即可解答．【详解】解：⊙AB 是O 的直径，弦CD OA ⊥于点E ， ⊙12DE CD = 在Rt EDO ∆中，OD m =，AOD α∠=∠ ⊙tan =DE OEα ⊙=tan 2tan DE CD OE αα=，故选项A 错误，不符合题意；又sin DE ODα= ⊙sin DE OD α=⊙22sin CD DE m α==，故选项B 正确，符合题意； 又cos OE ODα= ⊙cos cos OE OD m αα==⊙AO DO m ==⊙cos AE AO OE m m α=-=-，故选项C 错误，不符合题意；⊙2sin CD m α=，cos OE m α= ⊙2112sin cos sin cos 22COD S CD OE m m m αααα∆=⨯=⨯⨯=，故选项D 错误，不符合题意； 故选B ．【点睛】本题考查了垂径定理，锐角三角函数的定义以及三角形面积公式的应用，解本题的关键是熟记垂径定理和锐角三角函数的定义．12．（2021·山东泰安市·中考真题）如图，在ABC 中，6AB =，以点A 为圆心，3为半径的圆与边BC 相切于点D ，与AC ，AB 分别交于点E 和点G ，点F 是优弧GE 上一点，18CDE ∠=︒，则GFE ∠的度数是（ ）A ．50°B ．48°C ．45°D ．36°【答案】B【分析】 连接AD ，由切线性质可得⊙ADB =⊙ADC =90°，根据AB=2AD 及锐角的三角函数可求得⊙BAD =60°，易求得⊙ADE =72°，由AD=AE 可求得⊙DAE =36°，则⊙GAC =96°，根据圆周角定理即可求得⊙GFE 的度数．【详解】解：连接AD ，则AD =AG =3，⊙BC与圆A相切于点D，⊙⊙ADB=⊙ADC=90°，在Rt⊙ADB中，AB=6，则cos⊙BAD=ADAB=12，⊙⊙BAD=60°，⊙⊙CDE=18°，⊙⊙ADE=90°﹣18°=72°，⊙AD=AE，⊙⊙ADE=⊙AED=72°，⊙⊙DAE=180°﹣2×72°=36°，⊙⊙GAC=36°+60°=96°，⊙⊙GFE=12⊙GAC=48°，故选：B．【点睛】本题考查切线性质、锐角的三角函数、等腰三角形的性质、三角形的内角和定理、圆周角定理，熟练掌握切线性质和圆周角定理，利用特殊角的三角函数值求得⊙BAD=60°是解答的关键．13．（2021·浙江绍兴市·中考真题）如图，正方形ABCD内接于O，点P在AB上，则P∠的度数为（）A．30B．45︒C．60︒D．90︒【答案】B【分析】连接OB ，OC ，由正方形ABCD 的性质得90BOC ∠=°，再根据圆周角与圆心角的关系即可得出结论．【详解】解：连接OB ，OC ，如图，⊙正方形ABCD 内接于O ，⊙90BOC ∠=° ⊙11904522BPC BOC ∠=∠=⨯︒=︒ 故选：B ．【点睛】此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．14．（2021·四川凉山彝族自治州·中考真题）点P 是O 内一点，过点P 的最长弦的长为10cm ，最短弦的长为6cm ，则OP 的长为（ ）A ．3cmB ．4cmC ．5cmD ．6cm 【答案】B【分析】根据直径是圆中最长的弦，知该圆的直径是10cm ；最短弦即是过点P 且垂直于过点P 的直径的弦；根据垂径定理即可求得CP 的长，再进一步根据勾股定理，可以求得OP 的长．【详解】解：如图所示，CD ⊙AB 于点P ．根据题意，得AB =10cm ，CD =6cm ．⊙OC =5，CP =3⊙CD ⊙AB ，⊙CP =12CD =3cm ．根据勾股定理，得OP ．故选B ．【点睛】此题综合运用了垂径定理和勾股定理．正确理解圆中，过一点的最长的弦和最短的弦．15．（2021·四川自贡市·中考真题）如图，AB 为⊙O 的直径，弦CD AB ⊥于点F ，OE AC ⊥于点E ，若3OE =，5OB =，则CD 的长度是（ ）A ．9.6B ．C ．D ．19【答案】A【分析】 先利用垂径定理得出AE =EC ，CF =FD ，再利用勾股定理列方程即可【详解】解：连接OC⊙AB ⊙CD , OE ⊙AC⊙ AE =EC ，CF =FD⊙OE =3，OB =5⊙OB =OC =OA =5⊙在Rt ⊙OAE 中4AE =⊙AE =EC =4设OF =x ，则有2222AC AF OC OF -=-22228(5)5x x -+=-x =1.4在Rt ⊙OFC 中， 4.8FC ==⊙29.6CD FC ==故选：A【点睛】本题考查垂径定理、勾股定理、方程思想是解题关键16．（2021·山东临沂市·中考真题）如图，PA 、PB 分别与O 相切于A 、B ，70P ∠=︒，C 为O 上一点，则ACB ∠的度数为（ ）A ．110︒B ．120︒C ．125︒D ．130︒ 【答案】C【分析】由切线的性质得出⊙OAP =⊙OBP =90°，利用四边形内角和可求⊙AOB =110°，再利用圆周角定理可求⊙ADB =55°，再根据圆内接四边形对角互补可求⊙ACB ．【详解】解：如图所示，连接OA ，OB ，在优弧AB 上取点D ，连接AD ，BD ，⊙AP 、BP 是切线，⊙⊙OAP =⊙OBP =90°，⊙⊙AOB =360°-90°-90°-70°=110°，⊙⊙ADB =55°，又⊙圆内接四边形的对角互补，⊙⊙ACB =180°-⊙ADB =180°-55°=125°．故选：C ．【点睛】本题考查了切线的性质、圆周角定理、圆内接四边形的性质．解题的关键是连接OA 、OB ，求出⊙AOB ．17．（2021·湖北鄂州市·中考真题）如图，Rt ABC 中，90ACB ∠=︒，AC =3BC =．点P 为ABC ∆内一点，且满足22PA PC +2AC =．当PB 的长度最小时，ACP ∆的面积是（ ）A ．3B ．CD 【答案】D【分析】由题意知90APC ∠=︒，又AC 长度一定，则点P 的运动轨迹是以AC 中点O 为圆心，12AC 长为半径的圆弧，所以当B 、P 、O 三点共线时，BP 最短；在Rt BCO ∆中，利用勾股定理可求BO 的长，并得到点P 是BO 的中点，由线段长度即可得到PCO ∆是等边三角形，利用特殊Rt APC ∆三边关系即可求解．【详解】解：222PA PC AC +=∴90APC ∠=︒取AC 中点O ，并以O 为圆心，12AC 长为半径画圆 由题意知：当B 、P 、O 三点共线时，BP 最短AO PO CO ∴== 11322CO AC BC ==⨯==BO ∴=BP BO PO ∴=-=∴点P 是BO 的中点∴在Rt BCO ∆中，12CP BO PO === ∴PCO ∆是等边三角形∴60ACP ∠=︒ ∴在Rt APC ∆中，tan 603AP CP =⨯︒=12APC S AP CP ∆∴=⨯==【点睛】本题主要考察动点的线段最值问题、点与圆的位置关系和隐形圆问题，属于动态几何综合题型，中档难度．解题的关键是找到动点P 的运动轨迹，即隐形圆．18．（2021·浙江嘉兴市·中考真题）如图，在ABC ∆中，90BAC ∠=︒，AB =AC =5，点D 在AC 上，且2AD =，点E 是AB 上的动点，连结DE ，点F ，G 分别是BC ，DE 的中点，连接AG ，FG ，当AG =FG 时，线段DE 长为（ ）A B ．2C D ．4 【答案】A【分析】连接DF ，EF ，过点F 作FN ⊙AC ，FM ⊙AB ，结合直角三角形斜边中线等于斜边的一半求得点A ，D ，F ，E 四点共圆，⊙DFE =90°，然后根据勾股定理及正方形的判定和性质求得AE 的长度，从而求解．【详解】解：连接DF ，EF ，过点F 作FN ⊙AC ，FM ⊙AB⊙在ABC ∆中，90BAC ∠=︒，点G 是DE 的中点，⊙AG =DG =EG又⊙AG =FG⊙点A ，D ，F ，E 四点共圆，且DE 是圆的直径⊙⊙DFE =90°⊙在Rt ⊙ABC 中，AB =AC =5，点F 是BC 的中点，⊙CF =BF =122BC =，FN =FM =52 又⊙FN ⊙AC ，FM ⊙AB ，90BAC ∠=︒⊙四边形NAMF 是正方形⊙AN =AM =FN =52又⊙90NFD DFM ∠+∠=︒，90DFM MFE ∠+∠=︒⊙NFD MFE ∠=∠⊙⊙NFD ⊙⊙MFE⊙ME =DN =AN -AD =12 ⊙AE =AM +ME =3⊙在Rt ⊙DAE 中，DE故选：A ．【点睛】本题考查直径所对的圆周角是90°，四点共圆及正方形的判定和性质和用勾股定理解直角三角形，掌握相关性质定理正确推理计算是解题关键．19．（2021·四川自贡市·中考真题）如图，()8,0A，()2,0C -，以点A 为圆心，AC 长为半径画弧，交y 轴正半轴于点B ，则点B 的坐标为（ ）A ．()0,5B ．()5,0C ．()6,0D ．()0,6 【答案】D【分析】先根据题意得出OA =8，OC =2，再根据勾股定理计算即可【详解】解：由题意可知：AC =AB⊙()8,0A ，()2,0C -⊙OA =8，OC =2⊙AC =AB =10在Rt ⊙OAB 中，6OB ==⊙B (0，6)故选：D【点睛】本题考查勾股定理、正确写出点的坐标，圆的半径相等、熟练进行勾股定理的计算是关键 20．（2021·广西来宾市·中考真题）如图，O 的半径OB 为4，OC AB ⊥于点D ，30BAC ∠=︒，则OD 的长是（ ）A B C ．2 D ．3【答案】C【分析】 根据圆周角定理求出⊙COB 的度数，再求出⊙OBD 的度数，根据“30°的锐角所对的直角边等于斜边的一半”求出OD 的长度．【详解】⊙ ⊙BAC =30°，⊙⊙COB =60°，⊙⊙ODB =90°，⊙⊙OBD =30°，⊙OB =4，⊙OD =12OB =142⨯=2． 故选：C ．【点睛】本题考查了圆周角定理，直角三角形的性质，掌握相关定理和性质是解题的关键．21．（2021·湖北荆州市·中考真题）如图，矩形OABC 的边OA ，OC 分别在x 轴、y 轴的正半轴上，点D 在OA 的延长线上．若()2,0A ，()4,0D ，以О为圆心、OD 长为半径的弧经过点B ，交y 轴正半轴于点E ，连接DE ，BE 、则BED ∠的度数是（ ）A ．15︒B ．22.5︒C ．30D ．45︒【答案】C【分析】连接OB ，由题意易得⊙BOD =60°，然后根据圆周角定理可进行求解．【详解】解：连接OB ，如图所示：⊙()2,0A ，()4,0D ，⊙2,4OA OB OE OD ====， ⊙12OA OB =， ⊙四边形OABC 是矩形，⊙90OAB ∠=︒，⊙30OBA ∠=︒，⊙9060BOD OBA ∠=︒-∠=︒， ⊙1302BED BOD ∠=∠=︒； 故选C ．【点睛】本题主要考查圆周角定理、矩形的性质及含30°的直角三角形的性质，熟练掌握圆周角定理、矩形的性质及含30°的直角三角形的性质是解题的关键．22．（2021·湖北宜昌市·中考真题）如图，C ，D 是O 上直径AB 两侧的两点．设25ABC ∠=︒，则BDC ∠=（ ）A ．85︒B ．75︒C ．70︒D ．65︒【答案】D【分析】 先利用直径所对的圆周角是直角得到⊙ACB =90°，从而求出⊙BAC ，再利用同弧所对的圆周角相等即可求出⊙BDC ．【详解】解：⊙C ，D 是⊙O 上直径AB 两侧的两点，⊙⊙ACB =90°，⊙⊙ABC =25°，⊙⊙BAC =90°-25°=65°，⊙⊙BDC =⊙BAC =65°，故选：D ．【点睛】本题考查了圆周角定理的推论，即直径所对的圆周角是90°和同弧或等弧所对的圆周角相等，解决本题的关键是牢记相关概念与推论，本题蕴含了属性结合的思想方法．23．（2021·河北中考真题）如图，等腰AOB 中，顶角40AOB ∠=︒，用尺规按⊙到⊙的步骤操作： ⊙以O 为圆心，OA 为半径画圆；⊙在O 上任取一点P （不与点A ，B 重合），连接AP ；⊙作AB 的垂直平分线与O 交于M ，N ；⊙作AP 的垂直平分线与O 交于E ，F ．结论⊙：顺次连接M ，E ，N ，F 四点必能得到矩形；结论⊙：O 上只有唯一的点P ，使得OFM OAB S S =扇形扇形．对于结论⊙和⊙，下列判断正确的是（ ）A ．⊙和⊙都对B ．⊙和⊙都不对C ．⊙不对⊙对D ．⊙对⊙不对【答案】D【分析】 ⊙、根据“弦的垂直平分线经过圆心”，可证四边形MENF 的形状；⊙、在确定点P 的过程中，看⊙MOF =40°是否唯一即可．【详解】解：⊙、如图所示．⊙MN 是AB 的垂直平分线，EF 是AP 的垂直平分线，⊙MN 和EF 都经过圆心O ，线段MN 和EF 是⊙O 的直径．⊙OM =ON ，OE =OF ．⊙四边形MENF 是平行四边形．⊙线段MN 是⊙O 的直径，⊙⊙MEN =90°．⊙平行四边形MENF 是矩形．⊙结论⊙正确；⊙、如图2，当点P 在直线MN 左侧且AP =AB 时，⊙AP =AB ，⊙AB AP =．⊙MN ⊙AB ，EF ⊙AP ， ⊙1122AE AP AN AB ==，． ⊙AE AN =． ⊙1===202AOE AON AOB ∠∠∠．⊙40EON =∠．⊙=40MOF EON =∠∠．⊙扇形OFM 与扇形OAB 的半径、圆心角度数都分别相等，⊙OFM OAB S S =扇形扇形．如图3，当点P 在直线MN 右侧且BP =AB 时，同理可证：FOM AOB S S =扇形扇形．⊙结论⊙错误．故选：D【点睛】本题考查了圆的有关性质、矩形的判定、扇形面积等知识点，熟知圆的有关性质、矩形的判定方法及扇形面积公式是解题的关键．24．（2021·湖北黄冈市·中考真题）如图，O 是Rt ABC △的外接圆，OE AB ⊥交O 于点E ，垂足为点D ，AE ，CB 的延长线交于点F ．若3OD =，8AB =，则FC 的长是（ ）A ．10B ．8C ．6D ．4【答案】A【分析】 先根据垂径定理可得4=AD ，再利用勾股定理可得5OE OA ==，然后根据三角形中位线定理即可得．【详解】解：,8OE AB AB ⊥=，142AD AB ∴==， 3OD =，5OA ∴=，5OE ∴=，OE AB ⊥，90A ADO BC =︒∠∴∠=，//OE FC ∴，又OA OC =，OE ∴是ACF 的中位线，210FC OE ∴==，故选：A ．【点睛】本题考查了垂径定理、三角形中位线定理等知识点，熟练掌握垂径定理是解题关键．25．（2021·湖南邵阳市·中考真题）如图，点A ，B ，C 是O 上的三点．若90AOC ∠=︒，30BAC ∠=︒，则AOB ∠的大小为（ ）A ．25︒B ．30C ．35︒D ．40︒【答案】B【分析】首先根据圆周角定理求得BOC ∠的度数，根据AOC ∠的度数求AOB AOC BOC ∠=∠-∠即可．【详解】解：⊙30BAC ∠=︒⊙⊙BOC=223060BAC ∠=⨯︒=︒，⊙90AOC ∠=︒，906030AOB AOC BOC ，故选：B ．【点睛】考查了圆周角定理及两锐角互余性质，求得BOC ∠的度数是解题的关键．26．（2021·湖南长沙市·中考真题）如图，点A ，B ，C 在⊙O 上，54BAC ∠=︒，则BOC ∠的度数为（）A ．27︒B ．108︒C ．116︒D ．128︒【答案】B【分析】直接利用圆周角定理即可得．【详解】解：54BAC ∠=︒，∴由圆周角定理得：2108BOC BAC ∠=∠=︒，故选：B ．【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题关键．27．（2021·湖北武汉市·中考真题）如图，AB 是O 的直径，BC 是O 的弦，先将BC 沿BC 翻折交AB 于点D ．再将BD 沿AB 翻折交BC 于点E ．若BE DE =，设ABC α∠=，则α所在的范围是（ ）A ．21.922.3α︒<<︒B ．22.322.7α︒<<︒C ．22.723.1α︒<<︒D ．23.123.5α︒<<︒【答案】B【分析】 将⊙O 沿BC 翻折得到⊙O ′，将⊙O ′沿BD 翻折得到⊙O ″，则⊙O 、⊙O ′、⊙O ″为等圆．依据在同圆或等圆中相等的圆周角所对的弧相等可证明AC DC DE EB ===，从而可得到弧AC 的度数，由弧AC 的度数可求得⊙B 的度数．【详解】解：将⊙O 沿BC 翻折得到⊙O ′，将⊙O ′沿BD 翻折得到⊙O ″，则⊙O 、⊙O ′、⊙O ″为等圆．⊙⊙O 与⊙O ′为等圆，劣弧AC 与劣弧CD 所对的角均为⊙ABC ，⊙AC CD =．同理：DE CD =．又⊙F 是劣弧BD 的中点，⊙DE BE =．⊙AC DC DE EB ===．⊙弧AC 的度数=180°÷4=45°．⊙⊙B =12×45°=22.5°． ⊙α所在的范围是22.322.7α︒<<︒；故选：B ．【点睛】本题主要考查的是圆的综合应用，解答本题主要应用了翻折的性质、弧、弦、圆周角之间的关系、圆内接四边形的性质，等腰三角形的判定，找出图形中的等弧是解题的关键．二、填空题28．（2021·黑龙江中考真题）如图，在O 中，AB 是直径，弦AC 的长为5cm ，点D 在圆上，且30ADC ∠=︒，则O 的半径为_____．【答案】5cm【分析】连接BC ，由题意易得30ABC ADC ∠=∠=︒，进而问题可求解．【详解】解：连接BC ，如图所示：⊙30ADC ∠=︒，⊙30ABC ADC ∠=∠=︒，⊙AB 是直径，⊙90ACB ∠=︒，⊙5cm AC =，⊙210cm AB AC ==，⊙O 的半径为5cm ；故答案为5cm ．【点睛】本题主要考查圆周角定理及含30°直角三角形的性质，熟练掌握圆周角定理及含30°直角三角形的性质是解29．（2021·安徽中考真题）如图，圆O 的半径为1，ABC 内接于圆O ．若60A ∠=︒，75B ∠=︒，则AB =______．【分析】先根据圆的半径相等及圆周角定理得出⊙ABO =45°，再根据垂径定理构造直角三角形，利用锐角三角函数解直角三角形即可【详解】解：连接OB 、OC 、作OD ⊙AB⊙60A ∠=︒⊙⊙BOC =2⊙A =120°⊙OB =OC⊙⊙OBC =30°又75B ∠=︒⊙⊙ABO =45°在Rt ⊙OBD 中，OB =1⊙BD⊙BD =AD =⊙AB【点睛】本题考查垂径定理、圆周角定理，正确使用圆的性质及定理是解题关键30．（2021·湖南张家界市·中考真题）如图，ABC 内接于O ，50A ∠=︒，点D 是BC 的中点，连接OD ，OB ，OC ，则BOD ∠=_________．【答案】50︒【分析】圆上弧长对应的圆周角等于圆心角的一半，再利用等腰三角形三线合一的性质，即可得出答案．【详解】解:根据圆上弦长对应的圆周角等于圆心角的一半，12A BOC ∠=∠， 100BOC ∴∠=︒，OB OC =， BOC ∴为等腰三角形， 又点D 是BC 的中点，根据等腰三角形三线合一，OD ∴为BOC ∠的角平分线，50BO D ∴∠=︒，故答案是：50︒．【点睛】本题考查了弦长所对应的圆周角等于圆心角的一半和等腰三角形三线合一的性质，解题的关键是：根据性质求出BOC ∠，再利用角平分线或三角形全等都能求出解．31．（2021·广东中考真题）在ABC 中，90,2,3ABC AB BC ∠=︒==．点D 为平面上一个动点，45ADB ∠=︒，则线段CD 长度的最小值为_____．-【分析】由已知45ADB ∠=︒，2AB =，根据定角定弦，可作出辅助圆，由同弧所对的圆周角等于圆心角的一半可知，点D 在以O 为圆心OB 为半径的圆上，线段CD 长度的最小值为CO OD -．【详解】如图： 以12AB 为半径作圆，过圆心O 作,ON AB OM BC ⊥⊥， 以O 为圆心OB 为半径作圆，则点D 在圆O 上，45ADB ∠=︒90AOB ∠=︒∴2AB =1AN BN ==AO ∴==112ON OM AB ===,3BC =OC ∴==CO OD ∴-线段CD 长度的最小值为-．-【点睛】 本题考查了圆周角与圆心角的关系，圆外一点到圆上的线段最短距离，勾股定理，正确的作出图形是解题的关键．32．（2021·江苏宿迁市·中考真题）如图，在Rt⊙ABC 中，⊙ABC =90°，⊙A =32°，点B 、C 在O 上，边AB 、AC 分别交O 于D 、E 两点﹐点B 是CD 的中点，则⊙ABE =__________．【答案】13︒【分析】如图，连接,DC 先证明,BDC BCD ∠=∠再证明,ABE ACD ∠=∠利用三角形的外角可得：,BDC A ACD A ABE ∠=∠+∠=∠+∠再利用直角三角形中两锐角互余可得：()2902,BDC A ABE ∠=︒-∠+∠再解方程可得答案．【详解】解：如图，连接,DC B 是CD 的中点，,,BD BC BDC BCD ∴=∠=∠,DE DE =,ABE ACD ∴∠=∠,BDC A ACD A ABE ∴∠=∠+∠=∠+∠90,32,ABC A ∠=︒∠=︒()2902,BDC A ABE ∴∠=︒-∠+∠45453213.ABE A ∴∠=︒-∠=︒-︒=︒故答案为：13.︒【点睛】本题考查的是圆周角定理，三角形的外角的性质，直角三角形的两锐角互余，掌握圆周角定理的含义是解题的关键．33．（2021·江苏南京市·中考真题）如图，AB 是O 的弦，C 是AB 的中点，OC 交AB 于点D ．若8cm,2cm AB CD ==，则O 的半径为________cm ．【答案】5【分析】连接OA ，由垂径定理得AD =4cm ，设圆的半径为R ，根据勾股定理得到方程2224(2)R R =+-，求解即可【详解】解：连接OA ，⊙C 是AB 的中点，⊙OC AB ⊥ ⊙14cm 2AD AB == 设O 的半径为R ，⊙2cm CD =⊙(2)cm OD OC CD R =-=-在Rt OAD ∆中，222OA AD OD =+，即2224(2)R R =+-，解得，5R =即O 的半径为5cm故答案为：5【点睛】本题考查的是垂径定理及勾股定理，根据垂径定理判断出OC 是AB 的垂直平分线是解答此题的关键． 34．（2021·湖北随州市·中考真题）如图，O 是ABC 的外接圆，连接AO 并延长交O 于点D ，若50C ∠=︒，则BAD ∠的度数为______．【答案】40︒【分析】连接BD ，则C D ∠=∠，再根据AD 为直径，求得BAD ∠的度数【详解】如图，连接BD ，则50D C ∠=∠=︒AD 为直径90ABD ∴∠=︒90905040BAD D ∴∠=︒-∠=︒-︒=︒故答案为40︒【点睛】此题主要考查了圆周角定理，圆周角定理是中考中考查重点，熟练掌握圆周角定理是解决问题的关键． 35．（2021·江苏连云港市·中考真题）如图，OA 、OB 是O 的半径，点C 在O 上，30AOB ∠=︒，40OBC ∠=︒，则OAC ∠=______︒．【答案】25【分析】连接OC ，根据等腰三角形的性质和三角形内角和定理得到⊙BOC =100°，求出⊙AOC ，根据等腰三角形的性质计算．【详解】解：连接OC ，⊙OC =OB ，⊙⊙OCB =⊙OBC =40°，⊙⊙BOC =180°-40°×2=100°，⊙⊙AOC =100°+30°=130°，⊙OC =OA ，⊙⊙OAC =⊙OCA =25°，故答案为：25．【点睛】本题考查的是圆的基本性质、等腰三角形的性质，三角形内角和定理，掌握三角形内角和等于180°是解题的关键．36．（2021·四川成都市·中考真题）如图，在平面直角坐标系xOy 中，直线33y x =+与O 相交于A ，B 两点，且点A 在x 轴上，则弦AB 的长为_________．【答案】【分析】过O 作OE ⊙AB 于C ，根据垂径定理可得AC =BC =12AB ，可求OA =2，OD Rt ⊙AOD 中，由勾股定理AD =，可证⊙OAC ⊙⊙DAO ，由相似三角形性质可求AC 即可． 【详解】 解：过O 作OE ⊙AB 于C ，⊙AB 为弦，⊙AC =BC =12AB ，⊙直线33y x =+与O 相交于A ，B 两点，⊙当y =00x +=，解得x =-2， ⊙OA =2，⊙当x =0时，y =⊙OD=3， 在Rt ⊙AOD中，由勾股定理3AD ===， ⊙⊙ACO =⊙AOD =90°，⊙CAO =⊙OAD ，⊙⊙OAC ⊙⊙DAO ，AC AO AO AD =即2AO AC AD === ⊙AB =2AC故答案为【点睛】本题考查直线与圆的位置关系，垂径定理，直线与两轴交点，勾股定理，三角形相似判定与性质，掌握以上知识、正确添加辅助线是解题关键．37．（2021·江苏扬州市·中考真题）在一次数学探究活动中，李老师设计了一份活动单：“追梦”学习小组通过操作、观察、讨论后汇报：点A 的位置不唯一，它在以BC 为弦的圆弧上（点B 、C 除外），……．小华同学画出了符合要求的一条圆弧（如图1）．（1）小华同学提出了下列问题，请你帮助解决．⊙该弧所在圆的半径长为___________；⊙ABC 面积的最大值为_________；（2）经过比对发现，小明同学所画的角的顶点不在小华所画的圆弧上，而在如图1所示的弓形内部，我们记为A '，请你利用图1证明30BA C '∠>︒；（3）请你运用所学知识，结合以上活动经验，解决问题：如图2，已知矩形ABCD 的边长2AB =，3BC =，点P 在直线CD 的左侧，且4tan 3DPC ∠=． ⊙线段PB 长的最小值为_______；⊙若23PCD PAD S S =，则线段PD 长为________．【答案】（1）⊙2；2；（2）见解析；（3）；⊙4 【分析】（1）⊙设O 为圆心，连接BO ，CO ，根据圆周角定理得到⊙BOC =60°，证明⊙OBC 是等边三角形，可得半径；⊙过点O 作BC 的垂线，垂足为E ，延长EO ，交圆于D ，以BC 为底，则当A 与D 重合时，⊙ABC 的面积最大，求出OE ，根据三角形面积公式计算即可；（2）延长BA ′，交圆于点D ，连接CD ，利用三角形外角的性质和圆周角定理证明即可；（3）⊙根据4tan 3DPC ∠=，连接PD ，设点Q 为PD 中点，以点Q 为圆心，12PD 为半径画圆，可得点P 在优弧CPD 上，连接BQ ，与圆Q 交于P ′，可得BP ′即为BP 的最小值，再计算出BQ 和圆Q 的半径，相减即可得到BP ′；⊙根据AD ，CD 和23PCD PAD S S =推出点P 在⊙ADC 的平分线上，从而找到点P 的位置，过点C 作CF ⊙PD ，垂足为F ，解直角三角形即可求出DP ．【详解】解：（1）⊙设O 为圆心，连接BO ，CO ，⊙⊙BAC =30°，⊙⊙BOC =60°，又OB =OC ，⊙⊙OBC 是等边三角形，⊙OB =OC =BC =2，即半径为2；⊙⊙⊙ABC 以BC 为底边，BC =2，⊙当点A 到BC 的距离最大时，⊙ABC 的面积最大，如图，过点O 作BC 的垂线，垂足为E ，延长EO ，交圆于D ，⊙BE =CE =1，DO =BO =2，⊙OE⊙DE 2，⊙⊙ABC 的最大面积为)1222⨯⨯2；（2）如图，延长BA ′，交圆于点D ，连接CD ，⊙点D 在圆上，⊙⊙BDC =⊙BAC ，⊙⊙BA ′C =⊙BDC +⊙A ′CD ，⊙⊙BA ′C ＞⊙BDC ，⊙⊙BA ′C ＞⊙BAC ，即⊙BA ′C ＞30°；（3）⊙如图，当点P在BC上，且PC=32时，⊙⊙PCD=90°，AB=CD=2，AD=BC=3，⊙tan⊙DPC=CDPC=43，为定值，连接PD，设点Q为PD中点，以点Q为圆心，12PD为半径画圆，⊙当点P在优弧CPD上时，tan⊙DPC=43，连接BQ，与圆Q交于P′，此时BP′即为BP的最小值，过点Q作QE⊙BE，垂足为E，⊙点Q是PD中点，⊙点E为PC中点，即QE=12CD=1，PE=CE=12PC=34，⊙BE=BC-CE=3-34=94，⊙BQ4，⊙PD 52，⊙圆Q的半径为155 224⨯=，⊙BP′=BQ-P′Q，即BP；⊙⊙AD =3，CD =2，23PCD PAD S S =， 则23CD AD =， ⊙⊙P AD 中AD 边上的高=⊙PCD 中CD 边上的高，即点P 到AD 的距离和点P 到CD 的距离相等，则点P 到AD 和CD 的距离相等，即点P 在⊙ADC 的平分线上，如图，过点C 作CF ⊙PD ，垂足为F ，⊙PD 平分⊙ADC ，⊙⊙ADP =⊙CDP =45°，⊙⊙CDF 为等腰直角三角形，又CD =2，⊙CF =DF⊙tan⊙DPC =CF PF =43，⊙PF =4，⊙PD =DF +PF【点睛】本题是圆的综合题，考查了圆周角定理，三角形的面积，等边三角形的判定和性质，最值问题，解直角三角形，三角形外角的性质，勾股定理，知识点较多，难度较大，解题时要根据已知条件找到点P 的轨迹． 38．（2021·辽宁本溪市·中考真题）如图，由边长为1的小正方形组成的网格中，点A ，B ，C 都在格点上，以AB 为直径的圆经过点C 和点D ，则tan =ADC ∠________．。

人教版 九年级数学 第24章24.1 ---24.4复习题（含答案） 24.1 圆的有关性质一、选择题（本大题共10道小题）1. 如图，已知直径MN ⊥弦AB ，垂足为C ，有下列结论：①AC ＝BC ；②AN ︵＝BN ︵；③AM ︵＝BM ︵；④AM ＝BM .其中正确的个数为( )A ．1B ．2C ．3D ．42. 小红不小心把家里的一块圆形玻璃镜打碎了，需要配制一块同样大小的玻璃镜，工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A ，B ，C ，给出三角形ABC ，则这块玻璃镜的圆心是 ( )A .AB ，AC 边上的中线的交点 B .AB ，AC 边上的垂直平分线的交点 C .AB ，AC 边上的高所在直线的交点D .∠BAC 与∠ABC 的角平分线的交点3.如图，点B ，C ，D 在⊙O 上，若∠BCD ＝130°，则∠BOD 的度数是( )A ．50°B ．60°C ．80°D ．100°4. 如图，AB ，AC分别是⊙O 的直径和弦，OD AC ⊥于点D ，连接BD ，BC ，且10AB =，8AC =，则BD 的长为A．5B．4C．13D．4.85.如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF.若∠AOF＝40°，则∠F的度数是( )A．20°B．35°C．40°D．55°6. 如图，在半径为5的⊙O中，弦AB＝6，OP⊥AB，垂足为P，则OP的长为() A．3 B．2.5 C．4 D．3.57. 如图，AB为⊙O的直径，C，D为⊙O上两点．若∠BCD＝40°，则∠ABD的大小为()A．60°B．50°C．40°D．20°8. 如图，四边形ABCD是菱形，⊙O经过点A，C，D，与BC相交于点E，连接AC ，AE .若∠D ＝80°，则∠EAC 的度数为( )A ．20°B ．25°C ．30°D ．35°9. 如图，在半径为5的⊙O 中，AB ，CD 是互相垂直的两条弦，垂足为P ，且AB ＝CD ＝8，则OP 的长为( )A ．3B ．4C ．3 2D ．4 210. 如图，⊙P与x 轴交于点A(—5，0)，B(1，0)，与y 轴的正半轴交于点C.若∠ACB ＝60°，则点C 的纵坐标为( )A.13＋ 3B ．2 2＋ 3C ．4 2D ．2 2＋2二、填空题（本大题共8道小题）11. 如图所示，AB 为☉O 的直径，点C 在☉O 上，且OC ⊥AB ，过点C 的弦CD 与线段OB 相交于点E ，满足∠AEC=65°，连接AD ，则∠BAD= 度.12. (2019•娄底)如图，C 、D 两点在以AB 为直径的圆上，2AB =，30ACD ∠=︒，则AD __________．13. 如图，以△ABC的边BC为直径的⊙O分别交AB，AC于点D，E，连接OD，OE.若∠A＝65°，则∠DOE＝________°.14. 如图，在⊙O中，BD为⊙O的直径，弦AD的长为3，AB的长为4，AC平分∠DAB，则弦CD的长为________．15. 如图，在⊙O中，半径OA垂直于弦BC，点D在圆上，且∠ADC＝30°，则∠AOB的度数为________．16. 如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E 在边BC上，连接AE.若∠ABC＝64°，则∠BAE的度数为________．17. 当宽为3 cm 的刻度尺的一边与⊙O 相切于点A 时，另一边与⊙O 的两个交点B ，C 处的读数如图所示(单位： cm)，那么该圆的半径为________cm.18. 如图，△ABC 内接于⊙O ，若∠OAB ＝32°，则∠C ＝________°.三、解答题（本大题共4道小题）19. 如图，在⊙O 中，M ，N 分别是半径OA ，OB 的中点，且CM ⊥OA 交⊙O 于点C ，DN ⊥OB 交⊙O 于点D .求证：AC ︵＝BD ︵.20. 如图，AB 为O 的直径，点C 在O 上．(1)尺规作图：作BAC 的平分线，与O 交于点D ；连接OD ，交BC 于点E (不写作法，只保留作图痕迹，且用黑色墨水笔将作图痕迹加黑)； (2)探究OE 与AC 的位置及数量关系，并证明你的结论．21. 如图，直线AB经过⊙O的圆心，与⊙O相交于点A，B，点C在⊙O上，且∠AOC＝30°，P是直线AB上的一个动点(与点O不重合)，直线PC与⊙O相交于点Q.在直线AB上使QP＝QO成立的点P共有几个？请相应地求出∠OCP的度数．22. 如图，点E是△ABC的内心，线段AE的延长线交BC于点F(∠AFC≠90°)，交△ABC的外接圆于点D.(1)求点F与△ABC的内切圆⊙E的位置关系；(2)求证：ED＝BD；(3)若∠BAC＝90°，△ABC的外接圆的直径是6，求BD的长；(4)B，C，E三点可以确定一个圆吗？若可以，则它们确定的圆的圆心和半径分别是什么？若不可以，请说明理由．人教版 九年级数学 24.1 圆的有关性质 课后训练-答案一、选择题（本大题共10道小题） 1. 【答案】D2. 【答案】B[解析]本题实质上是要确定三角形外接圆的圆心，三角形外接圆的圆心是三边垂直平分线的交点，故选B .3. 【答案】D[解析] 由同弧所对的圆周角等于圆心角的一半， 可知∠α＝2∠BCD ＝260°. 而∠α＋∠BOD ＝360°， 所以∠BOD ＝100°.4. 【答案】C【解析】∵AB 为直径，∴90ACB ∠=︒，∴6BC ===， ∵OD AC ⊥，∴142CD AD AC ===，在Rt CBD △中，BD ==C ．5. 【答案】B6. 【答案】C7. 【答案】B[解析] 如图，连接AD.∵AB 为⊙O 的直径，∴∠ADB ＝90°.∵∠A 和∠BCD 都是BD ︵所对的圆周角，∴∠A ＝∠BCD ＝40°，∴∠ABD ＝90°－40°＝50°.故选B.8. 【答案】C9. 【答案】C[解析] 如图，过点O 作OE ⊥AB ，OF ⊥CD ，垂足分别为E ，F ，连接AO.∵OE ⊥AB ，∴AE ＝12AB ＝4.在Rt △OAE 中，OA ＝5，由勾股定理可得OE ＝3，同理得OF ＝3.又∵AB ⊥CD ，∴四边形OEPF 是正方形，∴PE ＝OE ＝ 3.在Rt △OPE 中，由勾股定理可得OP ＝3 2.10. 【答案】B[解析] 如图，连接PA ，PB ，PC ，过点P 作PD ⊥AB 于点D ，PE⊥OC 于点E.∵∠ACB ＝60°，∴∠APB ＝120°. ∵PA ＝PB ，∴∠PAB ＝∠PBA ＝30°. ∵A(－5，0)，B(1，0)， ∴AB ＝6， ∴AD ＝BD ＝3，∴PD ＝3，PA ＝PB ＝PC ＝2 3. ∵PD ⊥AB ，PE ⊥OC ，∠AOC ＝90°，∴四边形PEOD 是矩形，∴OE ＝PD ＝3，PE ＝OD ＝3－1＝2， ∴CE ＝PC2－PE2＝12－4＝2 2， ∴OC ＝CE ＋OE ＝2 2＋3， ∴点C 的纵坐标为2 2＋ 3. 故选B.二、填空题（本大题共8道小题）11. 【答案】20 [解析]如图，连接DO ，∵CO ⊥AB ， ∴∠COB=90°，∵∠AEC=65°，∴∠C=25°，∵OD=OC ，∴∠ODC=∠C=25°，∴∠DOC=130°，∴∠DOB=40°，∵2∠BAD=∠DOB ， ∴∠BAD=20°.12. 【答案】1【解析】∵AB 为直径，∴90ADB ∠=︒，∵30B ACD ∠=∠=︒，∴112122AD AB ==⨯=． 故答案为：1．13. 【答案】50[解析] 由三角形的内角和定理，得∠B ＋∠C ＝180°－∠A .再由OB ＝OD ＝OC ＝OE ，得到∠BDO ＝∠B ，∠CEO ＝∠C .在等腰三角形BOD 和等腰三角形COE 中，∠DOB ＋∠EOC ＝180°－2∠B ＋180°－2∠C ＝360°－2(∠B ＋∠C )＝360°－2(180°－∠A )＝2∠A ，所以∠DOE ＝180°－2∠A ＝50°.14. 【答案】52 2 [解析] ∵BD 为⊙O 的直径，∴∠DAB ＝∠DCB ＝90°. ∵AD ＝3，AB ＝4，∴BD ＝5.又∵AC 平分∠DAB ，∴∠DAC ＝∠BAC ＝45°， ∴∠DBC ＝∠DAC ＝45°，∠CDB ＝∠BAC ＝45°， 从而CD ＝CB ，∴CD ＝52 2.15. 【答案】60°[解析] ∵OA ⊥BC ，∴AB ︵＝AC ︵，∴∠AOB ＝2∠ADC.∵∠ADC＝30°，∴∠AOB ＝60°.16. 【答案】52°[解析] ∵四边形ABCD 是圆内接四边形，∴∠B ＋∠D ＝180°.∵∠B ＝64°，∴∠D ＝116°.又∵点D 关于AC 的对称点是点E ， ∴∠AEC ＝∠D ＝116°.又∵∠AEC ＝∠B ＋∠BAE ，∴∠BAE ＝52°.17. 【答案】25618. 【答案】58[解析] 方法一：如图①，连接OB.∵在△OAB 中，OA ＝OB ，∴∠OAB ＝∠OBA.又∵∠OAB ＝32°，∴∠OBA ＝32°，∴∠AOB ＝180°－2×32°＝116°.又∵∠C ＝12∠AOB(一条弧所对的圆周角是它所对的圆心角的一半)， ∴∠C ＝58°.方法二：如图②，过点A 作直径AD ，连接BD ，则∠ABD ＝90°，∴∠C ＝∠D ＝90°－32°＝58°(同弧所对的圆周角相等)．三、解答题（本大题共4道小题）19. 【答案】证明：如图，连接OC ，OD ，则OC ＝OD .∵M ，N 分别是半径OA ，OB 的中点， ∴OM ＝ON .∵CM ⊥OA ，DN ⊥OB ，∴∠OMC ＝∠OND ＝90°. 在Rt △OMC 和Rt △OND 中，⎩⎨⎧OC ＝OD ，OM ＝ON ，∴Rt △OMC ≌Rt △OND (HL)， ∴∠MOC ＝∠NOD ，∴AC ︵＝BD ︵.20. 【答案】(1)如图所示：(2)OE AC ∥，12OE AC =． 理由如下：∵AD 平分BAC ∠， ∴12BAD BAC ∠=∠， ∵12BAD BOD ∠=∠，∴BOD BAC ∠=∠， ∴OE AC ∥，∵OA OB =，∴OE 为ABC △的中位线， ∴OE AC ∥，12OE AC =．21. 【答案】解：在直线AB 上使QP ＝QO 成立的点P 共有3个． (1)如图①.在△QOC 中，OC ＝OQ ，∴∠OQC ＝∠OCQ . 在△OPQ 中，QP ＝QO ，∴∠QOP ＝∠QPO .又∵∠QPO ＝∠OCQ ＋∠AOC ，且∠AOC ＝30°，∠QOP ＋∠QPO ＋∠OQC ＝180°，∴3∠OCQ ＝120°， ∴∠OCQ ＝40°. 即∠OCP ＝40°.(2)如图②. ∵QO ＝QP ， ∴∠QPO ＝∠QOP .设∠QPO ＝x ，则∠OQC ＝∠QPO ＋∠QOP ＝2x .又∵OC ＝OQ ， ∴∠OCQ ＝∠OQC ＝2x ，∴∠AOC ＝∠OPC ＋∠OCP ＝x ＋2x ＝3x . ∵∠AOC ＝30°，∴3x ＝30°，解得x ＝10°， ∴∠OCP ＝2x ＝20°. (3)如图③.∵QO ＝QP ，∴∠QOP ＝∠QPO . ∵OC ＝OQ ，∴∠OQC ＝∠OCQ .设∠QPO ＝y ，则∠OQC ＝∠OCQ ＝∠QPO ＋∠AOC ＝y ＋30°，∴在△OPQ中，有y＋y＋y＋30°＝180°，解得y＝50°，∴∠OCP＝180°－50°－30°＝100°.综上所述，在直线AB上使QP＝QO成立的点P共有3个，∠OCP的度数分别为40°，20°，100°.22. 【答案】解：(1)设⊙E切BC于点M，连接EM，则EM⊥BC.又线段AE的延长线交BC 于点F，∠AFC≠90°，∴EF>EM，∴点F在△ABC的内切圆⊙E外．(2)证明：∵点E是△ABC的内心，∴∠BAD＝∠CAD，∠ABE＝∠CBE.∵∠CBD＝∠CAD，∴∠BAD＝∠CBD.∵∠BED＝∠ABE＋∠BAD，∠EBD＝∠CBE＋∠CBD，∴∠BED＝∠EBD，∴ED＝BD.(3)如图①，连接CD.设△ABC的外接圆为⊙O.∵∠BAC＝90°，∴BC是⊙O的直径，∴∠BDC＝90°.∵⊙O的直径是6，∴BC＝6.∵E为△ABC的内切圆的圆心，∴∠BAD＝∠CAD，∴BD＝CD.又∵BD2＋CD2＝BC2，∴BD＝CD＝3 2.(4)B，C，E三点可以确定一个圆．如图②，连接CD.∵点E是△ABC的内心，∴∠BAD＝∠CAD，∴BD＝CD.又由(2)可知ED＝BD，∴BD＝CD＝ED，∴B，C，E三点确定的圆的圆心为点D，半径为BD(或ED，CD)的长度．24.2 点和圆、直线和圆的位置关系一、选择题（本大题共8道小题）1. 已知⊙O的半径为5 cm，圆心O到直线l的距离为5 cm，则直线l与⊙O的位置关系为()A．相交B．相切C．相离D．无法确定2. 2019·武汉江岸区期中点P到直线l的距离为3，以点P为圆心，以下列长度为半径画圆，能使直线l与⊙P相交的是()A．1 B．2 C．3 D．43. 2020·武汉模拟在Rt△ABC中，∠BAC＝90°，AB＝8，AC＝6，以点A为圆心，4.8为半径的圆与直线BC的公共点的个数为()A．0 B．1 C．2 D．不能确定4. 如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与图中7×4方格中的格点相连，连线能够与该圆弧相切的格点有()A．1个B．2个C．3个D．4个5.如图，AP为⊙O的切线，P为切点，若∠A＝20°，C、D为圆周上两点，且∠PD C＝60°，则∠OBC等于( )A. 55°B. 65°C. 70°D. 75°6. 如图，在△MBC中，∠MBC＝90°，∠C＝60°，MB＝2 3，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为()A. 2B. 3 C．2 D．37. 如图，在△ABC中，AB＝10，AC＝8，BC＝6，经过点C且与边AB相切的动圆与CA，CB分别相交于点P，Q，则线段PQ的最小值为()A．5 B．4 2 C．4.75 D．4.88. 一把直尺、含60°角的三角尺和光盘如图所示摆放，A为60°角与直尺的交点，AB＝3，则光盘的直径是()A．3 B．3 3 C．6 D．6 3二、填空题（本大题共8道小题）9. 直角三角形的两条直角边分别是5和12，则它的内切圆半径为.10. 如图，P A，PB是☉O的切线，A，B为切点，点C，D在☉O上.若∠P=102°，则∠A+∠C=.11. 设⊙O 的半径为3，点O 到直线l 的距离为d ，若直线l 与⊙O 至少有一个公共点，则d 的取值范围是________．12. 如图，AB是⊙O 的直径，⊙O 交BC 于点D ，DE ⊥AC ，垂足为E ，要使DE是⊙O 的切线，则图中的线段应满足的条件是____________．13. 如图，在△ABC 中，∠A ＝60°，BC ＝5 cm.能够将△ABC 完全覆盖的最小圆形纸片的直径是________cm.14. 已知l 1∥l 2，l 1，l 2之间的距离是3 cm ，圆心O 到直线l 1的距离是1 cm ，如果圆O 与直线l 1，l 2有三个公共点，那么圆O 的半径为________cm.15. 如图，AB 是⊙O的直径，OA ＝1，AC 是⊙O 的弦，过点C 的切线交AB 的延长线于点D.若BD ＝2－1，则∠ACD ＝________°.16. 如图所示，在半圆O 中，AB 是直径，D是半圆O 上一点，C 是AD ︵的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE，CB于点P，Q，连接AC，有下列结论：①∠BAD＝∠ABC；②GP＝GD；③点P是△ACQ的外心．其中正确的结论是________(只需填写序号)．三、解答题（本大题共4道小题）17. 在△ABC中，AB＝AC＝10，BC＝16，⊙A的半径为7，判断⊙A与直线BC 的位置关系，并说明理由．18. 如图，AC是⊙O的直径，PA切⊙O于点A，PB切⊙O于点B，且∠APB＝60°.(1)求∠BAC的度数；(2)若PA＝1，求点O到弦AB的距离．19. 已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D.(1)如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；(2)如图②，当直线l与⊙O相交于点E，F时，求证：∠BAF＝∠DAE.20. 如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O交于点F，连接DF，DC.已知OA＝OB，CA＝CB.(1)求证：直线AB是⊙O的切线；(2)求证：∠CDF＝∠EDC；(3)若DE＝10，DF＝8，求CD的长．人教版九年级数学24.2 点和圆、直线和圆的位置关系培优训练-答案一、选择题（本大题共8道小题）1. 【答案】B2. 【答案】D3. 【答案】B4. 【答案】C[解析] 如图，连接AB，BC，作AB，BC的垂直平分线，可得点A，B，C所在的圆的圆心为O′(2，0)．只有当∠O′BF＝∠O′BD＋∠DBF＝90°时，BF与圆相切，此时△BO′D≌△FBE，EF＝DB＝2，此时点F的坐标为(5，1)．作过点B，F的直线，直线BF经过格点(1，3)，(7，0)，此两点亦符合要求．即与点B的连线，能够与该圆弧相切的格点是(5，1)或(1，3)或(7，0)，共3个．5. 【答案】B【解析】连接OP ，如解图，则OP ⊥AP .∵∠D ＝60°，∴∠COP ＝120°，∵∠A ＝20°，∠APO ＝90°，∴∠AOP ＝70°，∴∠AOC ＝50°，∵OB ＝OC ，∴∠OBC ＝180°－50°2＝65°.解图6. 【答案】C[解析] 在Rt △BCM 中，∠MBC ＝90°，∠C ＝60°，∴∠BMC ＝30°，∴BC ＝12MC ，即MC ＝2BC.由勾股定理，得MC2＝BC2＋MB2.∵MB ＝2 3， ∴(2BC)2＝BC2＋12，∴BC ＝2.∵AB 为⊙O 的直径，且AB ⊥BC ，∴BC 为⊙O 的切线．又∵CD 也为⊙O 的切线，∴CD ＝BC ＝2.7. 【答案】D[解析] 如图，设PQ 的中点为F ，⊙F 与AB 的切点为D ，连接FD ，FC ，CD .∵AB ＝10，AC ＝8，BC ＝6， ∴∠ACB ＝90°， ∴PQ 为⊙F 的直径．∵⊙F 与AB 相切，∴FD ⊥AB ，FC ＋FD ＝PQ ，而FC ＋FD ≥CD ，∴当CD 为Rt △ABC 的斜边AB 上的高且点F 在CD 上时，PQ 有最小值，为CD 的长，即CD 为⊙F 的直径．∵S △ABC ＝12BC ·AC ＝12CD ·AB ，∴CD ＝4.8.故PQ 的最小值为4.8.8. 【答案】D[解析] 设光盘的圆心为O ，连接OA ，OB ，则OB⊥AB ，∠OAB ＝12×(180°－60°)＝60°. ∵AB ＝3，∴OA ＝6，OB ＝3 3， ∴光盘的直径是6 3.故选 D.二、填空题（本大题共8道小题）9. 【答案】2 [解析]直角三角形的斜边==13，所以它的内切圆半径==2.10. 【答案】219°[解析]连接AB ，∵P A ，PB 是☉O 的切线， ∴P A=PB. ∵∠P=102°，∴∠P AB=∠PBA=(180°-102°)=39°. ∵∠DAB +∠C=180°，∴∠P AD +∠C=∠P AB +∠DAB +∠C=180°+39°=219°.11. 【答案】0≤d≤312. 【答案】BD ＝CD或AB ＝AC (答案不唯一)[解析] (1)连接OD .要使DE 是⊙O 的切线，结合DE ⊥AC ，只需OD ∥AC ，根据O 是AB 的中点，只需BD ＝CD 即可；(2)根据(1)中探求的条件，要使BD ＝CD ，则连接AD ，由于∠ADB ＝90°，只需AB ＝AC ，根据等腰三角形的三线合一即可．13. 【答案】10 33 如图，能够将△ABC 完全覆盖的最小圆形纸片是△ABC 的外接圆⊙O.连接OB ，OC ，则∠BOC ＝2∠A ＝120°.过点O 作OD ⊥BC 于点D ，则∠BOD ＝12∠BOC ＝60°.∴∠OBD ＝30°，∴OB ＝2OD.由垂径定理，得BD ＝12BC ＝52 cm ，在Rt △BOD 中，由勾股定理，得OB2＝OD2＋BD2，即(2OD)2＝OD2＋(52)2，解得OD ＝56 3 cm.∴OB ＝5 33cm ，∴能够将△ABC 完全覆盖的最小圆形纸片的直径是10 33 cm.14. 【答案】2或4 [解析] 设圆O 的半径为r cm 如图①所示，r －1＝3，得r ＝4；如图②所示，r ＋1＝3，得r ＝2.15. 【答案】112.5 [解析] 如图，连接OC.∵CD 是⊙O 的切线，∴OC ⊥CD.∵BD ＝2－1，OA ＝OB ＝OC ＝1，∴OD ＝2，∴CD ＝OD2－OC2＝（2）2－12＝1，∴OC ＝CD ，∴∠DOC ＝45°.∵OA ＝OC ，∴∠OAC ＝∠OCA ，∴∠OCA ＝12∠DOC ＝22.5°，∴∠ACD ＝∠OCA ＋∠OCD ＝22.5°＋90°＝112.5°.16. 【答案】②③ [解析] ∵在半圆O 中，AB 是直径，D 是半圆O 上一点，C 是AD ︵的中点，∴AC ︵＝DC ︵，但不一定等于DB ︵，∴∠BAD 与∠ABC 不一定相等，故①错误．如图，连接OD ，则OD ⊥GD ，∠OAD ＝∠ODA .∵∠ODA ＋∠GDP ＝90°，∠OAD ＋∠GPD ＝∠OAD ＋∠APE ＝90°， ∴∠GPD ＝∠GDP ，∴GP ＝GD ，故②正确．补全⊙O ，延长CE 交⊙O 于点F .∵CE ⊥AB ，∴A 为FC ︵的中点，即AF ︵＝AC ︵.又∵C 为AD ︵的中点，∴CD ︵＝AC ︵，∴AF ︵＝CD ︵，∴∠CAP ＝∠ACP ，∴AP ＝CP .∵AB 为⊙O 的直径，∴∠ACQ ＝90°，∴∠ACP ＋∠PCQ ＝90°，∠CAP ＋∠PQC ＝90°，∴∠PCQ ＝∠PQC ，∴PC ＝PQ ，∴AP ＝PQ ，即P 为Rt △ACQ 的斜边AQ 的中点，∴点P 为Rt △ACQ 的外心，故③正确．三、解答题（本大题共4道小题）17. 【答案】解：⊙A 与直线BC 相交．理由：过点A 作AD ⊥BC 于点D ，则BD ＝CD ＝8.∵AB ＝AC ＝10，∴AD ＝6.∵6＜7，∴⊙A 与直线BC 相交．18. 【答案】解：(1)∵PA 切⊙O 于点A ，PB 切⊙O 于点B ，∴PA ＝PB ，∠PAC ＝90°.∵∠APB ＝60°，∴△APB 是等边三角形，∴∠BAP ＝60°，∴∠BAC ＝90°－∠BAP ＝30°.(2)过点O 作OD ⊥AB 于点D ，如图所示，则AD ＝BD ＝12AB.由(1)得△APB是等边三角形，∴AB＝PA＝1，∴AD＝1 2.在Rt△AOD中，∵∠BAC＝30°，∴OD＝12OA.由勾股定理，得OA2＝OD2＋AD2，即(2OD)2＝OD2＋(1 2)2，∴OD＝36，即点O到弦AB的距离为36.19. 【答案】证明：(1)如图①，连接OC.∵直线l与⊙O相切于点C，∴OC⊥l.又∵AD⊥l，∴AD∥OC，∴∠DAC＝∠ACO.∵OA＝OC，∴∠ACO＝∠CAO，∴∠DAC＝∠CAO，即AC平分∠DAB.(2)如图②，连接BF.∵AB是⊙O的直径，∴∠AFB＝90°，∴∠BAF＝90°－∠B.∵∠AEF＝∠ADE＋∠DAE＝90°＋∠DAE，又由圆内接四边形的性质，得∠AEF＋∠B＝180°，∴90°＋∠DAE＋∠B＝180°，∴∠DAE＝90°－∠B，∴∠BAF＝∠DAE.20. 【答案】解：(1)证明：如图，连接OC.∵OA＝OB，AC＝CB，∴OC⊥AB.又∵点C在⊙O上，∴直线AB是⊙O的切线．(2)证明：∵OA＝OB，AC＝CB，∴∠AOC＝∠BOC.∵OD＝OF，∴∠ODF＝∠OFD.∵∠AOB＝∠ODF＋∠OFD＝∠AOC＋∠BOC，∴∠BOC＝∠OFD，∴OC∥DF，∴∠CDF＝∠OCD.∵OD＝OC，∴∠ODC＝∠OCD，∴∠CDF＝∠EDC.(3)如图，过点O作ON⊥DF于点N，延长DF交AB于点M. ∵ON⊥DF，∴DN＝NF＝4.在Rt△ODN中，∵∠OND＝90°，OD＝5，DN＝4，∴ON＝OD2－DN2＝3.由(2)知OC∥DF，∴∠OCM＋∠CMN＝180°.由(1)知∠OCM＝90°，∴∠CMN＝90°＝∠OCM＝∠MNO，∴四边形OCMN是矩形，∴CM＝ON＝3，MN＝OC＝5.在Rt△CDM中，∵∠DMC＝90°，CM＝3，DM＝DN＋MN＝9，∴CD＝DM2＋CM2＝92＋32＝310.24.3正多边形和圆一、选择题1．如图，四边形ABCD是⊙O的内接四边形，AB为⊙0直径，点C为劣弧BD 的中点，若∠DAB=40°，则∠ABC=（）．A．140°B．40°C．70°D．50°2．如图，圆O是△ABC的外接圆，连接OA、OC，∠OAC＝20°，则∠ABC的度数为（）A．140°B．110°C．70°D．40°3．如图，已知△ABC为⊙O的内接三角形，AB＞AC．E为BAC的中点，过E 作EF⊥AB于F．若AF＝1，AC＝4，∠C＝60°，则⊙O的面积是（）A．8πB．10πC．12πD．18π4．如图，四边形ABCD 内接于O ，9AB =，15AD =，120BCD ∠=︒，弦AC 平分BAD ∠，则AC 的长是（ ）A ．73B ．83C ．12D ．135．如图，AB 为⊙O 的直径，点C 为圆上一点，∠BAC ＝20°，将劣弧AC 沿弦AC 所在的直线翻折，交AB 于点D ，则弧AD 的度数等于（ ）A ．40°B ．50C ．80°D ．1006．如图，等边△ABD 与等边△ACE ，连接BE 、CD ，BE 的延长线与CD 交于点F ，下列结论：（1）BE=CD ；（2）AF 平分∠EAC ； （3）∠BFD=60°；（4）AF+FD=BF 其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个7．正方形ABCD 中，对角线AC 、BD 交于O ，Q 为CD 上任意一点，AQ 交BD 于M ，过M作MN ⊥AM 交BC 于N ，连AN 、QN ．下列结论：①MA=MN ；②∠AQD=∠AQN ； ③S △AQN =12S 五边形ABNQD ；④QN 是以A 为圆心，以AB 为半径的圆的切线．其中正确的结论有（ ）A ．①②③④B ．只有①③④C ．只有②③④D ．只有①② 8．如图，在菱形ABCD 中，点P 是BC 边上一动点，连结AP ，AP 的垂直平分线交BD 于点G ，交 AP 于点E ，在P 点由B 点到C 点的运动过程中，∠APG 的大小变化情况是( )A ．变大B ．先变大后变小C ．先变小后变大D ．不变9．如图，矩形ABCD 为⊙O 的内接四边形，AB ＝2，BC ＝3，点E 为BC 上一点，且BE ＝1，延长AE 交⊙O 于点F ，则线段AF 的长为（ ）A ．755B ．5C ．5+1D ．35210．在四边形ABCD 中，M 、N 分别是CD 、BC 的中点， 且AM ⊥CD ，AN ⊥BC ，已知∠MAN=74°，∠DBC=41°，则∠ADB 度数为（ ）．A ．15°B ．17°C ．16°D ．32°二、填空题11．如图，C 为半圆O 上一点，AB 为直径，且AB 2a =，COA 60∠=．延长AB 到P ，使1BP AB 2=，连CP 交半圆于D ，过P 作AP 的垂线交AD 的延长线于H ，则PH 的长度为________．12．如图，边长为4的正方形ABCD内接于⊙O，点E是弧AB上的一动点（不与点A、B重合），点F是弧BC上的一点，连接OE，OF，分别与交AB，BC于点G，H，且∠EOF=90°，连接GH，有下列结论：①弧AE=弧BF；②△OGH是等腰直角三角形；③四边形OGBH的面积随着点E位置的变化而变化；④△GBH周长的最小值为4+22．其中正确的是_____．（把你认为正确结论的序号都填上）13．如图，在Rt△ABC中，∠BAC＝90°，BC＝5，AB＝3，点D是线段BC上一动点，连接AD，以AD为边作△ADE∽△ABC，点N是AC的中点，连接NE，当线段NE最短时，线段CD的长为_____．14．如图，四边形ABCD内接于⊙O，∠1+∠2=64°，∠3+∠4=__________°.15．如图，边长一定的正方形ABCD，Q为CD上一个动点，AQ交BD于点M，过M作MN⊥AQ交BC于点N，作NP⊥BD于点P，连接NQ，下列结论：①AM＝MN；②MP＝12BD；③BN＋DQ＝NQ；④AB BNBM2是_____．三、解答题16．如图，四边形ABCD 是O 的内接四边形，42BC =，45BAC ∠=，75ABC ∠=，求AB 的长．17．如图，已知∠MON=120°，点A ，B 分别在OM ，ON 上，且OA =OB =a ，将射线OM 绕点O 逆时针旋转得到OM′，旋转角为α（0120α≤<︒︒且60α≠︒），作点A 关于直线OM′的对称点C ，画直线BC 交于OM′与点D ，连接AC ，AD ．有下列结论：有下列结论：①∠BDO + ∠ACD = 90°；②∠ACB 的大小不会随着a 的变化而变化；③当 30︒=α时，四边形OADC 为正方形；④ACD ∆23a ．其中正确的是________________．(把你认为正确结论的序号都填上） 18．我们定义：有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形 （1）概念理解①根据上述定义举一个等补四边形的例子：②如图1，四边形ABCD 中，对角线BD 平分∠ABC ，∠A +∠C ＝180°，求证：四边形ABCD是等补四边形（2）性质探究：③小明在探究时发现，由于等补四边形有一组对角互补，可得等补四边形的四个顶点共圆，如图2，等补四边形ABCD内接于⊙O，AB＝AD，则∠ACD∠ACB（填“＞”“＜”或“＝“）；④若将两条相等的邻边叫做等补四边形的“等边”，等边所夹的角叫做“等边角”，它所对的角叫做“等边补角”连接它们顶点的对角线叫做“等补对角线”，请用语言表述③中结论：（3）问题解决在等补四边形ABCD中，AB＝BC＝2，等边角∠ABC＝120°，等补对角线BD 与等边垂直，求CD的长．19．定义：在凸四边形中，我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”（1）在正方形、矩形、菱形中，一定是“完美四边形”的是______．（2）如图1，在△ABC中，AB=2，BC=52，AC=3，D为平面内一点，以A、B、C、D四点为顶点构成的四边形为“完美四边形”，若DA，DC的长是关于x的一元二次方程x2-(m+3)x+14(5m2-2m+13)=0(其中m为常数)的两个根，求线段BD的长度．（3）如图2，在“完美四边形”EFGH中，∠F=90°，EF=6，FG=8，求“完美四边形”EFGH面积的最大值．20．如图，O 是ABC 的外接圆，ABC 的外角DAC ∠的平分线交O 于点E ，连接CE 、BE .（1）求证：BE CE =；（2）若60CAB ∠=︒，23BC =，求劣弧BC 的长度.21．（1）已知：如图1，AB 是O 的直径，点P 为O 上一点（且点P 不与A 、B 重合）连接PA ，PB ，APB ∠的角平分线PC 交O 于点C ． ①若86PA PB ==，，求AB 的长 ②求证：2PA PB PC +=（2）如图2，在正方形ABCD 中，52AB 2=，若点P 满足3PC =，且90APC ∠=︒，请直接写出点B 到AP 的距离.22．如图(1) ，折叠平行四边形ABCD ，使得,B D 分别落在,BC CD 边上的,B D ''点，,AE AF 为折痕(1)若AE AF =，证明:平行四边形ABCD 是菱形; (2)若110BCD ︒∠= ，求B AD ''∠的大小;(3)如图(2) ，以,AE AF 为邻边作平行四边形AEGF ，若AE EC =，求CGE ∠的大小23．在平面直角坐标系xOy 中，已知(0,2)A ，动点P 在3y x =的图像上运动（不与O 重合），连接AP ，过点P 作PQ AP ⊥，交x 轴于点Q ，连接AQ ．（1）求线段AP 长度的取值范围；（2）试问：点P 运动过程中，QAP ∠是否问定值？如果是，求出该值；如果不是，请说明理由．（3）当OPQ ∆为等腰三角形时，求点Q 的坐标．【参考答案】1．C 2．B 3．C 4．B 5．D 6．C 7．A 8．D 9．A 10．C 113 12．①②④ 13．411014．64 15．①②③④ 16．317．①②④18．（1）①正方形；②略；（2）③＝；④等补四边形的“等补对角线”平分“等边补角”；（3）CD 的值为2或4． 19．（1）正方形、矩形；（2）3；（3）49． 20．（1）略；（2）43π21．（1）①10AB =，②略；（2）72或12 22．（1）略；（2）30°；（3）45°.23．（1）3AP ≥；（2）QAP ∠为定值，QAP ∠=30°；（3）1(234,0)Q +，2(234,0)Q -，3(23,0)Q -，423(,0)3Q24.4 弧长和扇形面积一、 选择题 （本题共计 10 小题 ，每题 3 分 ，共计30分 ， ） 1. 如图是一圆锥的侧面展开图，其弧长为，则该圆锥的全面积为A.B.C.D.2. 一扇形面积是，半径为，则该扇形圆心角度数是（ ） A.B.C.D.3. 圆锥的底面半径为，母线长为，则该圆锥的侧面积为（ ） A.B.C.D.4. 如图，在边长为的正方形内部，以各边为直径画四个半圆，则图中阴影部分的面积是（ ）A. B. C. D.5. 如果圆柱的底面直径为，母线长为，那么圆柱的侧面展开图的面积等于（）A. B. C. D.6. 一个扇形占其所在圆的面积的，则该扇形圆心角是（）A. B. C. D.无法计算7. 如图，圆锥的底面半径，高，则这个圆锥的侧面展开图的圆心角是（）A. B. C. D.8. 一个圆锥的底面圆的周长是，母线长是，它的侧面展开图的圆心角的度数是（）A. B. C. D.9. 已知一个圆锥的侧面积是，它的侧面展开图圆心角为，则这个圆锥的底面半径为A. B. C. D.10. 如图，边长为米的正方形池塘的周围是草地，池塘边、、、处各有一棵树，且米．现用长米的绳子将一头羊拴在其中的一棵树上．为了使羊在草地上活动区域的面积最大，应将绳子拴在（）A.处B.处C.处D.处二、填空题（本题共计10 小题，每题3 分，共计30分，）11. 如果圆柱的母线长为，底面半径为，那么这个圆柱的侧面积是________．12. 一个圆锥的侧面展开图是一个圆心角为，面积为的扇形，则这个圆锥的高是________．13. 一个圆柱体底面积直径是高的倍，如果底面积半径是分米，则它的表面积是________平方分米．14. 一个扇形的圆心角是，面积为，那么这个扇形的弧长为________．15. 用一个圆心角为的扇形作一个圆锥的侧面，若这个圆锥的底面半径恰好等于，则这个圆锥的母线长为________．16. 已知圆锥的底面周长为，母线长为，那么这个圆锥的侧面积是________（结果保留）．17. 如图，已知的半径，弦，且，点在上，则图中的阴影部分的面积是________．18. 如图，为的弦，点为的中点，，当点、在上运动一周时，点所走过的路径与围成的图形面积是________．19. 如图所示，已知的半径，，则所对的弧的长为________．20. 现有圆周的一个扇形彩纸片，该扇形的半径为，小红同学为了在“六一”儿童节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为的圆锥形纸帽（接缝处不重叠），那么剪去的扇形纸片的圆心角为________．三、解答题（本题共计6 小题，共计60分，）21. 如图，扇形的圆心角，半径，若将此扇形围成一个圆锥的侧面，求圆锥的底面面积的半径．22. 如图，圆锥的底面半径为，高为，求这个圆锥的侧面积和表面积．23. 如图，圆锥的底面半径，高．求这个圆锥的表面积．取24. 如图，在中，，，以腰为直径作半圆，分别交，于点，．求，的长．25. 有一直径为圆形纸片，从中剪出一个圆心角是的最大扇形（如图所示）．（1）求阴影部分的面积（2）用所剪的扇形纸片围城一个圆锥，该圆锥的底面圆的半径是多少？26. 如图，一个圆锥的高为，侧面展开图是半圆．求圆锥的母线长与底面半径之比；求的度数；求圆锥的侧面积（结果保留）．参考答案与试题解析一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】B【解答】解：设圆锥的底面圆的半径为，扇形的半径为，根据题意得，解得，，解得，所以该圆锥的全面积．故选．2.【答案】A【解答】解：设扇形圆心角的度数为，∴，∴．即扇形圆心角度数为．故选．3.【答案】C【解答】圆锥的侧面展开图为扇形，由扇形面积公式可以得出此圆锥侧面积为：＝．4.【答案】D【解答】解：如图所示，．故选．5.【答案】A【解答】解：圆柱的侧面积，故选．6.【答案】B【解答】解：∵一个扇形占其所在圆的面积的，∴该扇形的圆心角占它所在圆的圆心角的，即．故选．7.【答案】C【解答】解：圆锥的母线长，设这个圆锥的侧面展开图的圆心角为，根据题意得，解得，即这个圆锥的侧面展开图的圆心角为．故选．8.【答案】C【解答】解：圆锥侧面展开图的扇形面积半径为，弧长为，代入扇形弧长公式，即，解得，即扇形圆心角为度．故选．9.【答案】【解答】此题暂无解答10.【答案】B【解答】解：①；②；③；④，故选二、填空题（本题共计10 小题，每题 3 分，共计30分）11.【答案】【解答】解：这个圆柱的侧面积．故答案为：．12.【答案】【解答】解：设母线长为，底面圆的半径为，，解得：，底面圆的周长为：，解得：，∴这个圆锥的高是：．故答案为：．13.【答案】【解答】解：∵一个圆柱体底面直径是高的倍，如果底面半径是分米，∴高为分米，底面周长为：（分米），则其侧面积为：（平方分米），上下两底面积为：（平方分米）．故它的表面积是：平方分米．14.【答案】【解答】解：设这个扇形的半径是．根据扇形面积公式，得，解得（负值舍去）．故半径为．弧长是：．故答案为．15.【答案】【解答】解：设圆锥的母线长为，根据题意得：，解得：.故答案为：.16.【答案】【解答】解：圆锥的侧面积．17.【答案】【解答】解：连接，，∵，∴，∵，∴是等边三角形，∴，，∴，故答案为：．18.【答案】【解答】解：如图，连接、，点所走过的路径为小圆，∵点为的中点，，∴，且，∴点所走过的路径与围成的图形面积是，故答案为：．19.【答案】【解答】解：所对的弧的长，故答案为：．20.【答案】【解答】解：解得：，∵扇形彩纸片是圆周，因而圆心角是∴剪去的扇形纸片的圆心角为．剪去的扇形纸片的圆心角为．故答案为．三、解答题（本题共计 6 小题，每题10 分，共计60分）21.【答案】圆锥的底面圆的半径为．【解答】解：设圆锥的底面圆的半径为，根据题意得，解得．22.【答案】解：∵圆锥的底面半径为，高为，∴圆锥的母线长为，∴.∵圆锥的底面积，∴．【解答】解：∵圆锥的底面半径为，高为，∴圆锥的母线长为，∴.∵圆锥的底面积，∴．23.【答案】解：在中，，，由勾股定理知，侧面积，底面积，∴圆锥的表面积．【解答】解：在中，，，由勾股定理知，侧面积，底面积，∴圆锥的表面积．24.【答案】解：连接，∵，，∴，∴的长，连接、，∵为圆的直径，∴，又，∴，∴，∴的长．【解答】解：连接，∵，，∴，∴的长，连接、，∵为圆的直径，∴，又，∴，∴，∴的长．25.【答案】解：（1）连接，，∵，，∴是圆的直径，，∵圆的直径为，则，故．∴阴影；（2）的长，则，解得：．故该圆锥的底面圆的半径是．【解答】解：（1）连接，，∵，，∴是圆的直径，，∵圆的直径为，则，故．∴阴影；（2）的长，则，解得：．故该圆锥的底面圆的半径是．26.【答案】解：设此圆锥的高为，底面半径为，母线长，∵，∴；由中图所示，∵，，∴，，∴，同理,则；由中图可知，，∴，即，解得，∴，∴圆锥的侧面积为．【解答】解：设此圆锥的高为，底面半径为，母线长，∵，∴；由中图所示，∵，，∴，，∴，同理,则；由中图可知，，∴，即，解得，∴，∴圆锥的侧面积为．。

中考数学专题复习第二十四讲与圆有关的位置关系【基础知识回顾】一、点与圆的位置关系：1、点与圆的位置关系有种，若圆的半径为r点P到圆心的距离为d则：点P在圆内<＝> 点P在圆上<＝>点P在圆外<＝>2、过三点的圆：⑴过同一直线上三点作用，过三点，有且只有一个圆⑵三角形的外接圆：经过三角形各顶点的圆叫做三角形的外接圆的圆心叫做三角形的这个三角形叫做这个圆的⑶三角形外心的形成：三角形的交点，外心的性质：到相等【赵老师提醒：1、锐角三角形外心在三角形直角三角形的外心是锐角三角形的外心在三角形】一、直线与圆的位置关系：1、直线与圆的位置关系有种：当直线和圆有两个公共点时，叫做直线和圆直线叫圆的线，这的直线叫做圆的直线和圆没有公共点时，叫做直线和圆2、设Qo的半径为r，圆心o到直线l的距离为d，则：直线l与Qo相交<＝>d r,直线l与Qo相切<＝>d r直线l与Qo相离<＝>d r3、切线的性质和判定：⑴性质定理：圆的切线垂直于经过切点的【赵老师提醒：根据这一定理，在圆中遇到切线时，常用连接圆心和切点，即可的垂直关系】⑵判定定理：经过半径的且这条半径的直线式圆的切线【赵老师提醒：在切线的判定中，当直线和圆的公共点标出时，用判定定理证明。

当公共点未标出时，一般可证圆心到直线的距离d=r来判定相切】4、切线长定理：⑴切线长定义：在经过圆外一点的圆的切线上，这点和切点之间的长叫做这点到圆的切线长。

⑵切线长定理：从圆外一点到圆的两条切线，它们的相等，并且圆心和这一点的连线平分的夹角5、三角形的内切圆：⑴与三角形各边都的圆，叫做三角形的内切圆，内切圆的圆心叫做三角形的⑵三角形内心的形成：是三角形的交点内心的性质：到三角形各的距离相等，内心与每一个顶点的连接线平分【赵老师提醒：三类三角形内心都在三角形若△ABC三边为a、b、c面积为s，内切圆半径为r，则s= ，若△ABC为直角三角形，则r= 】二、圆和圆的位置关系：圆和圆的位置关系有种，若Qo1半径为R，Qo2半径为r，圆心距外，则Qo1 与Qo2 外距<＝> Qo1 与Qo2 外切<＝>两圆相交<＝> 两圆内切<＝>两圆内含<＝>【赵老师提醒：两圆相离无公共点包含和两种情况，两圆相切有唯一公共点包含和两种情况，注意题目中两种情况的考虑圆心同是两圆此时d= 】三、反证法：假设命题的结论，由此经过推理得出由矛盾判定所作的假设从而得到原命题成立，这种证明命题的方法叫反证法【赵老师提醒：反证法正题的关键是提出即假设所证结论的反面成立，择推理论证得出的矛盾可以与相矛盾，也可以与相矛盾，从而肯定原命题成立】【典型例题解析】考点一：切线的性质线，证明：AB=4PD．考点：切线的性质；等边三角形的判定与性质；含30度角的直角三角形；圆心角、弧、弦的关系；圆周角定理．专题：几何综合题．分析：（1）PO与BC的位置关系是平行；（2）（1）中的结论成立，理由为：由折叠可知三角形APO与三角形CPO全等，根据全等三角形的对应角相等可得出∠APO=∠CPO，再由OA=OP，利用等边对等角得到∠A=∠APO，等量代换可得出∠A=∠CPO，又根据同弧所对的圆周角相等得到∠A=∠PCB，再等量代换可得出∠COP=∠ACB，利用内错角相等两直线平行，可得出PO与BC平行；（3）由CD为圆O的切线，利用切线的性质得到OC垂直于CD，又AD垂直于CD，利用平面内垂直于同一条直线的两直线平行得到OC与AD平行，根据两直线平行内错角相等得到∠APO=∠COP，再利用折叠的性质得到∠AOP=∠COP，等量代换可得出∠APO=∠AOP，再由OA=OP，利用等边对等角可得出一对角相等，等量代换可得出三角形AOP三内角相等，确定出三角形AOP为等边三角形，根据等边三角形的内角为60°得到∠AOP为60°，由OP 平行于BC，利用两直线平行同位角相等可得出∠OBC=∠AOP=60°，再由OB=OC，得到三角形OBC为等边三角形，可得出∠COB为60°，利用平角的定义得到∠POC也为60°，再加上OP=OC，可得出三角形POC为等边三角形，得到内角∠OCP为60°，可求出∠PCD为30°，在直角三角形PCD中，利用30°所对的直角边等于斜边的一半可得出PD为PC的一半，而PC等于圆的半径OP等于直径AB的一半，可得出PD为AB的四分之一，即AB=4PD，得证．解答：解：（1）PO与BC的位置关系是PO∥BC；（2）（1）中的结论PO∥BC成立，理由为：由折叠可知：△APO≌△CPO，∴∠APO=∠CPO，又∵OA=OP，∴∠A=∠APO，∴∠A=∠CPO，又∵∠A与∠PCB都为PB所对的圆周角，∴∠A=∠PCB，∴∠CPO=∠PCB，对应训练1．（2012•玉林）如图，已知点O为Rt△ABC斜边AC上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E，与AC相交于点D，连接AE．（1）求证：AE平分∠CAB；（2）探求图中∠1与∠C的数量关系，并求当AE=EC时，tanC的值．考点：切线的性质；特殊角的三角函数值．专题：探究型．分析：（1）连接OE，则OE⊥BC，由于AB⊥BC，故可得出AB∥OE，进而可得出∠2=∠AEO，由于OA=OE，故∠1=∠AEO，进而可得出∠1=∠2；（2）由三角形外角的性质可知∠1+∠AEO=∠EOC，，因为∠1=∠AEO，∠OEC=90°，所以2∠1+∠C=90°；当AE=CE时，∠1=∠C，再根据2∠1+∠C=90°即可得出∠C的度数，由特殊角的三角函数值得出tanC即可．解答：（1）证明：连接OE，∵⊙O与BC相切于点E，∴OE⊥BC，∴∠OBP+∠ABP=90°，∠ACP+∠APC=90°，∵OP=OB，∴∠OBP=∠OPB，∵∠OPB=∠APC，∴∠ACP=∠ABC，∴AB=AC；（2）延长AP交⊙O于D，连接BD，∵设圆半径为r，则OP=OB=r，PA=5-r，∴AB2=OA2-OB2=52-r2，AC2=PC2-PA2=(25)2-（5-r）2，∴52-r2=(25)2-（5-r）2，解得：r=3，∴AB=AC=4，∵PD是直径，∴∠PBD=90°=∠PAC，∵∠DPB=∠CPA，∴△DPB∽△CPA，∴CP AP PD BP=，∴2553 33BP-=+，解得：PB=655．考点二：切线的判定（2）解：作BG⊥CD，垂足是G，在Rt△ABD中∵AB=10，sin∠DAB=35，又∵sin∠DAB=BD AB，∴BD=6∵C是弧AB的中点，∴∠ADC=∠CDB=45°，∴BG=DG=BDsin45°=6×22=32，∵∠DAB=∠DCB∴tan∠DCB=BGCG=34，∴CG=42，∴CD=CG+DG=42+32=72，∴S△CBD=12CD•BG=7232212⨯=．点评：本题考查的是切线的判定定理，涉及到圆周角定理、解直角三角形及三角形的面积公式，根据题意作出辅助线，构造出直角三角形是解答此题的关键．对应训练考点三：三角形的外接圆和内切圆例4 （2012•阜新）如图，在△ABC中，BC=3cm，∠BAC=60°，那么△ABC能被半径至少为cm的圆形纸片所覆盖．考点：三角形的外接圆与外心；圆周角定理；锐角三角函数的定义．专题：计算题．分析：作圆O的直径CD，连接BD，根据圆周角定理求出∠D=60°，根据锐角三角函数的定义得出sin∠D= BCCD，代入求出CD即可．解答：解：作圆O的直径CD，连接BD，∵弧BC对的圆周角有∠A、∠D，∴∠D=∠A=60°，∵直径CD，A．r B．2r C．2r D．2r考点：三角形的内切圆与内心；矩形的判定；正方形的判定；切线长定理．专题：计算题．分析：连接OD、OE，求出∠ODB=∠DBE=∠OEB=90°，推出四边形ODBE是正方形，得出BD=BE=OD=OE=r，根据切线长定理得出MP=DM，NP=NE，代入MB+NB+MN得出BD+BE，求出即可．解答：解：连接OD、OE，∵⊙O是Rt△ABC的内切圆，∴OD⊥AB，OE⊥BC，∵∠ABC=90°，∴∠ODB=∠DBE=∠OEB=90°，∴四边形ODBE是矩形，∵OD=OE，∴矩形ODBE是正方形，∴BD=BE=OD=OE=r，∵⊙O切AB于D，切BC于E，切MN于P，∴MP=DM，NP=NE，∴Rt△MBN的周长为：MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r，故选C．点评：本题考查的知识点是矩形的判定、正方形的判定、三角形的内切圆和内心、切线长定理等，主要考查运用这些性质进行推理和计算的能力，题目比较好，难度也适中．对应训练4．（2012•台州）已知，如图1，△ABC中，BA=BC，D是平面内不与A、B、C重合的任意一点，∠ABC=∠DBE，BD=BE．（1）求证：△ABD≌△CBE；∴sin∠D=BCCD=45，∴CD=25 4，答：三角形ABC外接圆的直径是254．（2）解：连接IC、BI，且延长BI交AC于F，过I作IE⊥AB于E，∵AB=BC=5，I为△ABC内心，∴BF⊥AC，AF=CF，∵sin∠A=45=BFAB，∴BF=4，在Rt△ABF中，由勾股定理得：AF=CF=3，AC=2AF=6，∵I是△ABC内心，IE⊥AB，IF⊥AC，IG⊥BC，∴IE=IF=IG，设IE=IF=IG=R，∵△ABI、△ACI、△BCI的面积之和等于△ABC的面积，∴12AB×R+12BC×R+12AC×R=12AC×BF，即5×R+5×R+6×R=6×4，∴R=32，在△AIF中，AF=3，IF=32，由勾股定理得：AI=352．答：AI的长是352．点评：本题考查了三角形的面积公式，三角形的内切圆和内心，勾股定理，等腰三角形的性质，圆周角定理等知识点的应用，主要考查学生运用性质进行推理和计算的能力，题目综合性比较强，有一定的难度．考点三：圆与圆的位置关系例6（2012•毕节地区）第三十奥运会将于2012年7月27日在英国伦敦开幕，奥运会旗图案有五个圆环组成，如图也是一幅五环图案，在这个五个圆中，不存在的位置关系是（）A．外离B．内切C．外切D．相交考点：圆与圆的位置关系．分析：根据两圆的位置关系易得到它们的位置关系有外切、外离、相交．解答：解：观察图形，五个等圆不可能内切，也不可能内含，并且有的两个圆只有一个公共点，即外切；有的两个圆没有公共点，即外离；有的两个圆有两个公共点，即相交．故选B．点评：本题考查了圆与圆的位置关系：若两圆的半径分别为R，r，圆心距为d，若d＞R+r，两圆外离；若d=R+r，两圆外切；若R-r＜d＜R+r（R≥r），两圆相交；若d=R-r（R＞r），两圆内切；若0≤d＜R-r（R＞r），两圆内含．对应训练6．（2012•德阳）在平面直角坐标系xOy中，已知点A（0，2），⊙A的半径是2，⊙P的半径是1，满足与⊙A及x轴都相切的⊙P有个．6．4考点：圆与圆的位置关系；坐标与图形性质；直线与圆的位置关系．分析：分两圆内切和两圆外切两种情况讨论即可得到⊙P的个数．解答：解：如图，满足条件的⊙P有4个，故答案为4．点评：本题考查了圆与圆的位置关系、坐标与图形的性质及直线与圆的知识，能充分考虑到分内切和外切是解决本题的关键．【聚焦山东中考】1．（2012•济南）已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根，若圆心距O1O2=5，则⊙O1和⊙O2的位置关系是（）A．外离B．外切C．相交D．内切考点：圆与圆的位置关系．分析：先根据一元二次方程根与系数的关系，可知圆心距=两圆半径之和，再根据圆与圆的位置关系即可判断．解答：解：∵⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根，∴两根之和=5=两圆半径之和，又∵圆心距O1O2=5，∴两圆外切．故选B．点评：此题综合考查一元二次方程根与系数的关系及两圆的位置关系的判断．圆和圆的位置与两圆的圆心距、半径的数量之间的关系：①两圆外离⇔d＞R+r；②两圆外切⇔d=R+r；③两圆相交⇔R-r＜d＜R+r（R≥r）；④两圆内切⇔d=R-r（R＞r）；⑤两圆内含⇔d＜R-r（R＞r）．2．（2012•青岛）已知，⊙O1与⊙O2的半径分别是4和6，O1O2=2，则⊙O1与⊙O2的位置关系是（）A．内切B．相交C．外切D．外离考点：圆与圆的位置关系．分析：由⊙O1与⊙O2的半径分别是4和6，O1O2=2，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．解答：解：∵⊙O1与⊙O2的半径分别是4和6，O1O2=2，∴O1O2=6-4=2，∴⊙O1与⊙O2的位置关系是内切．故选A．点评：此题考查了圆与圆的位置关系．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．3．（2012•泰安）如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠ABC=120°，OC=3，则BC的长为（）A．π B．2πC．3π D．5π考点：切线的性质；弧长的计算．分析：连接OB，由于AB是切线，那么∠ABO=90°，而∠ABC=120°，易求∠OBC，而OB=OC，那么∠OBC=∠OCB，进而求出∠BOC的度数，在利用弧长公式即可求出BC的长．解答：解：连接OB，∵AB与⊙O相切于点B，∴∠ABO=90°，∵∠ABC=120°，∴∠OBC=30°，∵OB=OC，∴∠OCB=30°，∴∠BOC=120°，∴ BC 的长为nπr 180 =120×π×3 180 =2π，故选B．点评：本题考查了切线的性质、弧长公式，解题的关键是连接OB，构造直角三角形．4．（2012•潍坊）已知两圆半径r1、r2分别是方程x2-7x+10=0的两根，两圆的圆心距为7，则两圆的位置关系是（）A．相交B．内切C．外切D．外离考点：圆与圆的位置关系；解一元二次方程-因式分解法．分析：首先解方程x2-7x+10=0，求得两圆半径r1、r2的值，又由两圆的圆心距为7，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．解答：解：∵x2-7x+10=0，∴（x-2）（x-5）=0，∴x1=2，x2=5，即两圆半径r1、r2分别是2，5，∵2+5=7，两圆的圆心距为7，∴两圆的位置关系是外切．故选C．点评：此题考查了圆与圆的位置关系与一元二次方程的解法．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．5．（2012•济南）如图，在Rt△ABC中，∠B=90°，AB=6，BC=8，以其三边为直径向三角形外作三个半圆，矩形EFGH的各边分别与半圆相切且平行于AB或BC，则矩形EFGH的周长是．5．4848考点：切线的性质；勾股定理；矩形的性质．分析：首先取AC的中点O，过点O作MN∥EF，PQ∥EH，由题意可得PQ⊥EF，PQ⊥GH，MN⊥EH，MN⊥FG，PL，KN，OM，OQ分别是各半圆的半径，OL，OK是△ABC的中位线，又由在Rt△ABC中，∠B=90°，AB=6，BC=8，即可求得个线段长，继而求得答案．解答：解：取AC的中点O，过点O作MN∥EF，PQ∥EH，∵四边形EFGH是矩形，∴EH∥PQ∥FG，EF∥MN∥GH，∠E=∠H=90°，∴PQ⊥EF，PQ⊥GH，MN⊥EH，MN⊥FG，∵AB∥EF，BC∥FG，∴AB∥MN∥GH，BC∥PQ∥FG，∴AL=BL，BK=CK，∴OL=12BC=12×8=4，OK=12AB=12×6=3，∵矩形EFGH的各边分别与半圆相切，∴PL=12AB=12×6=3，KN=12BC=12×8=4，在Rt△ABC中，AC= ，∴OM=OQ=12AC=5，∴EH=FG=PQ=PL+OL+OQ=3+4+5=12，EF=GH=MN=OM+OK+NK=5+3+4=12，∴矩形EFGH的周长是：EF+FG+GH+EH=12+12+12+12=48．故答案为：48．点评：此题考查了切线的性质、矩形的性质，三角形中位线的性质以及勾股定理等知识．此题难度较大，解题的关键是掌握辅助线的作法，注意数形结合思想的应用．6．（2012•菏泽）如图，PA，PB是⊙O是切线，A，B为切点，AC是⊙O的直径，若∠P=46°，则∠BAC= 度．6．23考点：切线的性质．专题：计算题．分析：由PA、PB是圆O的切线，根据切线长定理得到PA=PB，即三角形APB为等腰三角形，由顶角的度数，利用三角形的内角和定理求出底角的度数，再由AP为圆O的切线，得到OA与AP垂直，根据垂直的定义得到∠OAP为直角，再由∠OAP-∠PAB即可求出∠BAC 的度数．解答：解：∵PA，PB是⊙O是切线，∴PA=PB，又∠P=46°，∴∠PAB=∠PBA=180-462=67°，又PA是⊙O是切线，AO为半径，∴OA⊥AP，∴∠OAP=90°，∴∠BAC=∠OAP-∠PAB=90°-67°=23°．故答案为：23。

专题24.1 圆的有关性质目录圆的认识 (1)圆的相关概念 (3)求相关角度 (4)求相关长度 (6)有关证明 (8)垂径定理的计算 (10)垂径定理的应用 (13)圆周角圆心角相关概念 (18)圆周角与圆心角求角度 (20)圆周角与圆心角求长度 (22)垂径定理的推论 (26)内接四边形 (28)证明综合....................................................................................................................................................31圆的认识【例1】下列结论正确的是（ ）A ．半径相等的两条弧是等弧B ．半圆是弧C ．半径是弦D ．弧是半圆【解答】解：A 、在等圆或同圆中，半径相等的两条弧是等弧，原结论不正确；B 、半圆是弧，原结论正确；C 、半径只有一个端点位于圆上，不是弦，原结论不正确；D、根据半圆的定义可知，半圆是弧，但弧不一定是半圆，原结论不正确；【变式训练1】数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是（ ）A．学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”B．车轮做成圆形，应用了“圆是中心对称图形”C．射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”D．地板砖可以做成矩形，应用了“矩形对边相等”【解答】解：A．学校门口的伸缩门由菱形而不是其他四边形组成，应用了“四边形的不稳定性”，故本选项错误，不合题意；B．车轮做成圆形，应用了“圆上各点到圆心的距离相等”，故本选项错误，不合题意；C．射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”，故本选项正确，符合题意D．地板砖可以做成矩形，应用了“矩形四个内角都是直角”的性质，故本选项错误，不合题意．故选：C．【变式训练2】下列说法错误的是（ ）A．直径是圆中最长的弦B．半径相等的两个半圆是等弧C．面积相等的两个圆是等圆D．半圆是圆中最长的弧【解答】解：A、直径是圆中最长的弦，说法正确，不符合题意；B、半径相等的两个半圆是等弧，说法正确，不符合题意；C、面积相等的两个圆是等圆，说法正确，不符合题意；D、由于半圆小于优弧，所以半圆是圆中最长的弧说法错误，符合题意．【变式训练3】在平面内与点P的距离为1cm的点的个数为（ ）A．无数个B．3个C．2个D．1个【解答】解：在平面内与点P的距离为1cm的点的个数为为：所有到定点P的距离等于1cm的点的集合，故选：A．圆的相关概念【例2】已知⊙O的半径是3cm，则⊙O中最长的弦长是（ ）A．3cm B．6cm C．1.5cm D【解答】解：∵圆的直径为圆中最长的弦，∴⊙O中最长的弦长为2×3＝6（cm）．故选：B．【变式训练1】已知⊙O中最长的弦为12厘米，则此圆半径为　6　厘米．【解答】解：∵直径是圆中最长的弦，⊙O中最长的弦为12厘米，∴⊙O的直径是12厘米．∴⊙O的半径是6厘米．故答案为：【例3】下列说法：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，但弧不一定是半圆．正确的说法有（ ）A．1个B．2个C．3个D．4个【解答】解：①直径是弦，正确，符合题意；②弦不一定是直径，错误，不符合题意；③半径相等的两个半圆是等弧，正确，符合题意；④能够完全重合的两条弧是等弧，故原命题错误，不符合题意；⑤根据半圆的定义可知，半圆是弧，但弧不一定是半圆，正确，符合题意，正确的有3个，故选：C．【变式训练1】下列说法：（1）长度相等的弧是等弧，（2）相等的圆心角所对的弧相等，（3）劣弧一定比优弧短，（4）直径是圆中最长的弦．其中正确的有（ ）A．1个B．2个C．3个D．4个【解答】解：（1）长度相等的弧不一定是等弧，弧的度数必须相同，故错误；（2）同圆或等圆中相等的圆心角所对的弧相等，故错误；（3）同圆或等圆中劣弧一定比优弧短，故错误；（4）直径是圆中最长的弦，正确，正确的只有1个，故选：A．求相关角度【例4】如图所示，MN为⊙O的弦，∠N＝52°，则∠MON的度数为（ ）A．38°B．52°C．76°D．104°【解答】解：∵OM＝ON，∴∠M＝∠N＝52°，∴∠MON＝180°﹣2×52°＝76°．故选：C．【变式训练1】如图，将一个含有60°角的三角板，按图所示的方式摆放在半圆形纸片上，O为圆心，则∠ACO的度数为（ ）A．150°B．120°C．100°D．60°【解答】解：∵OC＝OB，∴∠OCB＝∠B＝60°，∴∠ACO＝180°﹣60°＝120°．故选：B．【例5】如图，在△ABC中，∠C＝90°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E．若∠A＝25°，求∠DCE的度数．【解答】解：∵∠C＝90°，∠A＝25°，∴∠B＝90°﹣∠A＝65°，∵CB＝CD，∴∠CDB＝∠B＝65°，∵∠CDB＝∠DCE+∠A，∴∠DCE＝65°﹣25°＝40°．【变式训练1】如图，CD是⊙O的直径，点A在DC的延长线上，∠A＝20°，AE交⊙O 于点B，且AB＝OC．（1）求∠AOB的度数．（2）求∠EOD的度数．【解答】解：（1）连OB，如图，∵AB＝OC，OB＝OC，∴AB＝BO，∴∠AOB＝∠1＝∠A＝20°；（2）∵∠2＝∠A+∠1，∴∠2＝2∠A，∵OB＝OE，∴∠2＝∠E ，∴∠E ＝2∠A ，∴∠DOE ＝∠A +∠E ＝3∠A ＝60°．求相关长度【例6】如图，在△ABC 中，∠C ＝90°，AB ＝若以点C 为圆心，CA 长为半径的圆恰好经过AB 的中点D ，则⊙C 的半径为（ ）A ．B ．8C ．6D ．5【解答】解：如图，连结CD ，∵CD 是直角三角形斜边上的中线，∴CD =12AB =12×10＝5故选：D ．【变式训练1】如图，AB 是⊙O 的弦，点C 是优弧AB 上的动点（C 不与A 、B 重合），CH ⊥AB ，垂足为H ，点M 是BC 的中点．若⊙O 的半径是3，则MH 长的最大值是（ ）A．3B．4C．5D．6【解答】解：∵CH⊥AB，垂足为H，∴∠CHB＝90°，∵点M是BC的中点．∴MH=12 BC，∵BC的最大值是直径的长，⊙O的半径是3，∴MH的最大值为3，故选：A．【变式训练2】如图，OA是⊙O的半径，B为OA上一点（且不与点O、A重合），过点B作OA的垂线交⊙O于点C．以OB、BC为边作矩形OBCD，连结BD．若CD＝6，BC＝8，则AB的长为（ ）A．6B．5C．4D．2【解答】解：如图，连接OC．∵四边形OBCD是矩形，∴∠OBC＝90°，OB＝CD＝6，∴OC＝OA10，∴AB＝OA﹣OB＝4，故选：C ．【变式训练3】如图，在矩形ABCD 中，已知AB ＝3，BC ＝4，点P 是BC 边上一动点（点P 不与B ，C 重合），连接AP ，作点B 关于直线AP 的对称点M ，则线段MC 的最小值为（ ）A ．2B ．52C ．3D 【解答】解：连接AM ，∵点B 和M 关于AP 对称，∴AB ＝AM ＝3，∴M 在以A 圆心，3为半径的圆上，∴当A ，M ，C 三点共线时，CM 最短，∵AC =5，AM ＝AB ＝3，∴CM ＝5﹣3＝2，故选：A ．有关证明【例7】已知，如图，在⊙O 中，C 、D 分别是半径OA 、BO 的中点，求证：AD ＝BC ．【解答】解：∵OA 、OB 是⊙O 的两条半径，∴AO ＝BO ，∵C、D分别是半径OA、BO的中点，∴OC＝OD，在△OCB和△ODA中，AO=BO∠O=∠O，OD=OC∴△OCB≌△ODA（SAS），∴AD＝BC．【变式训练1】已知：如图，AB是⊙O的直径，点C、D在⊙O上，CE⊥AB于E，DF⊥AB 于F，且AE＝BF，AC与BD相等吗？为什么？【解答】解：AC与BD相等．理由如下：连接OC、OD，如图，∵OA＝OB，AE＝BF，∴OE＝OF，∵CE⊥AB，DF⊥AB，∴∠OEC＝∠OFD＝90°，在Rt△OEC和Rt△OFD中，OE=OFOC=OD，∴Rt△OEC≌Rt△OFD（HL），∴∠COE＝∠DOF，∴AC=BD，∴AC＝BD．垂径定理的计算【例8】如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为P ．若CD ＝AP ＝8，则⊙O 的半径为（ ）A ．10B ．8C ．5D ．3【解答】解：连接OC ，∵AB ⊥CD ，AB 过圆心O ，CD ＝8，∴CP ＝DP ＝4，设⊙O 的半径为R ，∵AP ＝8，∴OP ＝8﹣R ，在Rt △COP 中，由勾股定理得：CP 2+OP 2＝OC 2，即（8﹣R ）2+42＝R 2，解得：R ＝5，∴⊙O 的半径为5，故选：C．【变式训练1】如图，CD 是圆O 的弦，直径AB ⊥CD ，垂足为E ，若AB ＝12，BE ＝3，则四边形ACBD 的面积为（ ）A ．B ．C ．D ．【解答】解：如图，连接OC ，∵AB ＝12，BE ＝3，∴OB ＝OC ＝6，OE ＝3，∵AB ⊥CD ，在Rt △COE 中，EC =∴CD ＝2CE ＝∴四边形ACBD 的面积=12AB ⋅CD =12×12×=故选：A ．【变式训练2】如图，正方形ABCD 和正方形BEFG 的顶点分别在半圆O 的直径和圆周上，若BG ＝4，则半圆O 的半径是（ ）A．4+B．9C．D．【解答】解：连接OC，OF，设OB＝x，∵四边形ABCD是正方形且顶点D和C在圆上，∴AB＝BC＝2x，∠OBC＝90°，∵BG＝4，四边形BEFG是正方形，∴OE＝x+4，EF＝BE＝BG＝4，∠FEB＝90°，在Rt△BCO中，OC=，在Rt△FEO中，OF=∵OF＝OC，∴5x2＝x2+8x+32，解得x＝4或x＝﹣2（舍去）当x＝4时，OC＝则半圆O的半径是故选：C．【变式训练3】已知⊙O的直径CD＝10，CD与⊙O的弦AB垂直，垂足为M，且AM＝4.8，则直径CD上的点（包含端点）与A点的距离为整数的点有（ ）A ．1个B ．3个C ．6个D ．7个【解答】解：∵CD 是直径，∴OC ＝OD =12CD =12×10＝5，∵AB ⊥CD ，∴∠AMC ＝∠AMD ＝90°，∵AM ＝4.8，∴OM ==1.4，∴CM ＝5+1.4＝6.4，MD ＝5﹣1.4＝3.6，∴AC =8，AD ==6，∵AM ＝4.8，∴A 点到线段MD 的最小距离为4.8，最大距离为6，则A 点到线段MD 的整数距离有5，6，A 点到线段MC 的最小距离为4.8，最大距离为8，则A 点到线段MC 的整数距离有5，6，7，8，直径CD 上的点（包含端点）与A 点的距离为整数的点有6个，故选：C ．垂径定理的应用【例9】往圆柱形容器内装入一些水以后，截面如图所示，若水面宽AB ＝48cm ，水的最大深度为16cm ，则圆柱形容器的截面直径为（ ）cm ．A ．10B ．14C ．26D ．52【解答】解：如图所示：由题意得，OC⊥AB于D，DC＝16cm，∵AB＝48cm，∴BD=12AB=12×48＝24（cm），设半径为rcm，则OD＝（r﹣16）cm，在Rt△OBD中，r2＝242+（r﹣16）2，解得r＝26，所以2r＝52，故选：D．【变式训练1】一装有某种液体的圆柱形容器，半径为6cm，高为18cm．小强不小心碰倒，容器水平静置时其截面如图所示，其中圆心O到液面AB的距离为3cm，若把该容器扶正竖直，则容器中液体的高度为（ ）A．12πcm B．2πcm C．πcm D．2cm【解答】解：连接OA，OB，如图，根据题意得：OA＝6cm，弦心距OC＝3cm，∴cos∠AOC=OCOA=36=12，∴∠AOC ＝60°，则∠AOB ＝120°，∴AC ＝，AB ＝2AC ＝，∴S 阴影＝S 扇形OAB ﹣S △OAB =120π×62360−12××3=cm 2）．设把该容器扶正竖直后容器中液体的高度为h （cm ），依题意得：62πℎ=，∴ℎ故选：B ．【变式训练2】往直径为78cm 的圆柱形容器内装入一些水以后，截面如图所示，若水面宽AB ＝72cm ，则水的最大深度为（ ）A ．36cmB ．27cmC ．24cmD ．15cm【解答】解：连接OA ，过点O 作OD ⊥AB 交AB 于点C 交⊙O 于D ．∵OC ⊥AB ，∴AC ＝CB ＝36（cm ），∵OA ＝OB ＝39cm ，∴OC ==15（cm ），∴CD ＝39﹣15＝24（cm ），故选：C ．【变式训练3】如图，某同学测试一个球体在水中的下落速度，他测得截面圆的半径为5cm ，假设球的横截面与水面交于A ，B 两点，AB ＝8cm ．若从目前所处位置到完全落入水中的时间为4s ，则球体下落的平均速度为（ ）A．0.5cm/s B．0.75cm/s C．1cm/s D．2cm/s 【解答】解：设圆心为O，连接OB，则OB＝5，过点O作OC⊥AB，交⊙O于点C，交AB于点D，则BD=12AB=4cm，在Rt△BOD中，OD=3cm，∴CD＝OC﹣OD＝5﹣3＝2cm，∴从目前所处位置到究全落入水中，球体下落的平均速度为2÷4＝0.5cm/s．故选：A．【例10】如图所示，某地有一座圆弧形的拱桥，桥下的水面宽度AB为7.2m，拱顶高出水面（CD）2.4m，现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里，则货船能顺利通过这座拱桥吗？请作出判断并说明理由．【解答】解：货船能顺利通过这座拱桥，理由如下：如图，连接ON、OA．∵OC⊥AB，AB＝7.2m，∴AD=12AB＝3.6（m），设OB＝OC＝ON＝rm，则OD＝（r﹣2.4）m，在Rt△AOD中，根据勾股定理得：r2＝（r﹣2.4）2+3.62，解得：r＝3.∵CD＝2.4m，船舱顶部为正方形并高出水面1.5m，∴CH＝2.4﹣1.5＝0.9（m），∴OH＝3.9﹣0.9＝3（m），在Rt△OHN中，HN2＝ON2﹣OH2＝3.92﹣32＝6.21（m2），∴HN=m），∴MN＝2HN＝m）＞3m，∴货船能顺利通过这座拱桥．【变式训练1】诗句“君到姑苏见，人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州．小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥，现测得桥下水面AB宽度16m时，拱顶高出水平面4m，货船宽12m，船舱顶部为矩形并高出水面3m．（1）请你帮助小勇求此圆弧形拱桥的半径；（2）小勇在解决这个问题时遇到困难，请你判断一下，此货船能顺利通过这座拱桥吗？说说你的理由．【解答】解：（1）如图，连接OB．∵OC⊥AB，∴D为AB中点，∵AB＝16m，∴BD=12AB＝8（m），又∵CD＝4m，设OB＝OC＝r，则OD＝（r﹣4）m．在Rt△BOD中，根据勾股定理得：r2＝（r﹣4）2+82，解得r＝答：此圆弧形拱桥的半径为10m．（2）此货船不能顺利通过这座拱桥，理由如下：连接ON，∵CD＝4m，船舱顶部为长方形并高出水面3m，∴CE＝4﹣3＝1（m），∴OE＝r﹣CE＝10﹣1＝9（m），在Rt△OEN中，由勾股定理得：EN=∴MN＝2EN＝＜12m．∴此货船B不能顺利通过这座拱桥．圆周角圆心角相关概念【例11】下列说法中，正确的个数为（ ）（1）在同圆或等圆中，弦相等则所对的弧相等；（2）优弧一定比劣弧长；（3）弧相等则所对的圆心角相等；（4）在同圆或等圆中，圆心角相等则所对的弦相等．A．1个B．2个C．3个D．4个【解答】解：（1）在同圆或等圆中，弦相等则所对的弧相等，错误，弦所对的弧有优弧或劣弧，不一定相等．（2）优弧一定比劣弧长，错误，条件是同圆或等圆中；（3）弧相等则所对的圆心角相等．正确；（4）在同圆或等圆中，圆心角相等则所对的弦相等．正确；故选：B．【变式训练1】下列说法正确的是（ ）A．同弧或等弧所对的圆心角相等B．所对圆心角相等的弧是等弧C．弧长相等的弧一定是等弧D．平分弦的直径必垂直于弦【解答】解：A、同弧或等弧所对的圆心角相等，正确，本选项符合题意；B、所对圆心角相等的弧是等弧，错误，条件是同圆或等圆中，本选项不符合题意；C、弧长相等的弧一定是等弧，错误，条件是同圆或等圆中，本选项不符合题意；D、平分弦的直径必垂直于弦，错误此弦不能是直径，本选项不符合题意．故选：A．【变式训练2】下列说法中，正确的是（ ）A．同心圆的周长相等B．面积相等的圆是等圆C．相等的圆心角所对的弧相等D．平分弧的弦一定经过圆心【解答】解：A、错误，同心圆的周长不相等，本选项不符合题意．B、正确，本选项符合题意．C、错误，条件是同圆或等圆中，本选项不符合题意．D、错误，平分弧的弦不一定经过圆心，本选项不符合题意．故选：B．【变式训练3】下列说法中，正确的有（ ）①相等的圆心角所对的弧相等；②平分弦的直径也平分弦所对的弧；③长度相等的两条弧是等弧；④经过圆心的每一条直线将圆分成两条等弧A．1个B．2个C．3个D．4个【解答】解：①在同圆或等圆中，相等的圆心角所对的弧相等，本小题说法错误；②平分弦（不是直径）的直径也平分弦所对的弧，本小题说法错误；③能够重合的两条弧是等弧，本小题说法错误；④经过圆心的每一条直线将圆分成两条等弧，本小题说法正确；故选：A．圆周角与圆心角求角度【例12】如图，AB是⊙O的直径，∠D＝32°，则∠AOC等于（ ）A．158°B．58°C．64°D．116°【解答】解：∵∠D＝32°，∴∠BOC＝2∠D＝64°，∴∠AOC＝180°﹣64°＝116°．故选：D．【变式训练1】如图，在⊙O中，AB是弦，C是弧AB上一点．若∠OAB＝25°，∠OCA＝40°，则∠BOC的度数为（ ）A．30°B．40°C．50°D．60°【解答】解：∵OA＝OB，∠OAB＝25°，∴∠OBA＝∠OAB＝25°，∴∠AOB＝180°﹣∠OAB﹣∠OBA＝130°，∵OA＝OC，∠OCA＝40°，∴∠OAC＝∠OCA＝40°，∴∠AOC＝180°﹣∠OAC﹣∠OCA＝100°，∴∠BOC＝∠AOB﹣∠AOC＝130°﹣100°＝30°，故选：A．【变式训练2】如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC＝75°，则∠OAC的大小是（ ）A．25°B．50°C．65°D．75°【解答】解：∵根据圆周角定理得：∠AOC＝2∠ABC，∵∠ABC+∠AOC＝75°，∴∠AOC=23×75°＝50°，∵OA＝OC，∴∠OAC＝∠OCA=12（180°﹣∠AOC）＝65°，故选：C．【变式训练3】如图，⊙O在△ABC三边上截得的弦长相等，即DE＝FG＝MN，∠A＝50°，则∠BOC＝（ ）A．100°B．110°C．115°D．120°【解答】解：如图，过点O作OP⊥AB于点P，OQ⊥AC于点Q，OK⊥BC于点K，∴∠APO＝∠AQO＝90°，∵∠A＝50°，∴∠POQ＝360°﹣90°﹣90°﹣50°＝130°，∵DE＝FG＝MN，∴OP＝OK＝OQ，∴OB、OC平分∠ABC和∠ACB，∴∠BOC=12×(360°−130°)=115°．故选：C．圆周角与圆心角求长度【例13】如图，AB是⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AE＝2，⊙O的直径为10，则AC长为（ ）A．5B．6C．7D．8【解答】解：连接OF，如图：∵DE⊥AB，AB过圆心O，∴DE＝EF，AD=AF，∵D为弧AC的中点，∴AD=DC，∴ADC=DAF，∴AC＝DF，∵⊙O的直径为10，∴OF＝OA＝5，∵AE＝2，∴OE＝OA﹣AE＝5﹣2＝3，在Rt△OEF中，由勾股定理得：EF==4，∴DE＝EF＝4，∴AC＝DF＝DE+EF＝4+4＝8，故选：D．【变式训练1】如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AE＝3，⊙O的直径为15，则AC长为（ ）A．10B．13C．12D．11【解答】解：连接OF，∵DE⊥AB，AB过圆心O，∴DE＝EF，AD=AF，∵D为弧AC的中点，∴AD=DC，∴ADC=DAF，∴AC＝DF，∵⊙O的直径为15，∴OF＝OA=15 2，∵AE＝3，∴OE＝OA﹣AE=9 2，在Rt△OEF中，由勾股定理得：EF==6，∴DE＝EF＝6，∴AC＝DF＝DE+EF＝6+6＝12，故选：C．【变式训练2】如图，在半径为⊙O中，弦AB，CD互相垂直，垂足为点P．若AB＝CD＝8，则OP的长为（ ）A．B．C．4D．2【解答】解：连接OA、OC，过O作OE⊥CD于E，OF⊥AB于F，则∠OFP＝∠OEP＝∠CEO＝∠AFO＝90°，∵AB⊥CD，∴∠EPF＝90°，∴四边形OFPE是矩形，∴OE＝FP，EP＝OF，∵OF⊥AB，OF过O，AB＝8，∴AF＝BF＝4，由勾股定理得：OF==2，同理OE＝2，即FP＝OE＝2，在Rt△OFP中，由勾股定理得：OP==故选：B．【变式训练3】如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AC＝12，AE＝3，则⊙O的直径长为（ ）A．10B．13C．15D．16【解答】解：如图，连接OF．∵DE ⊥AB ，∴DE ＝EF ，AD =AF ，∵点D 是弧AC 的中点，∴AD =CD ，∴AC =DF ，∴AC ＝DF ＝12，∴EF =12DF ＝6，设OA ＝OF ＝x ，在Rt △OEF 中，则有x 2＝62+（x ﹣3）2，解得x =152，∴AB ＝2x ＝15，故选：C ．垂径定理的推论【例14】如图，DC 是⊙O 的直径，弦AB ⊥CD 于M ，则下列结论不一定成立的是（ ）A ．AM ＝BMB ．CM ＝DMC ．AC =BCD ．AD =BD【解答】解：∵弦AB ⊥CD ，CD 过圆心O ，∴AM ＝BM ，AC =BC ，AD =BD，即选项A、C、D都正确，当根据已知条件不能推出CM和DM一定相等，故选：B．【变式训练1】如图，CD是⊙O的直径，弦AB⊥CD于点E，则下列结论不一定成立的是（ ）A．AE＝BE B．OE＝DE C．AC=BC D．AD=BD【解答】解：∵AB⊥CD，CD过圆心O，∴AE＝BE，AC=BC，AD=BD，不能推出OE＝DE，所以选项A、选项C、选项D都不符合题意，只有选项B符合题意；故选：B．【变式训练2】如图，AB是⊙O的直径，弦CD与AB相交于点E．不能推出CE＝DE的条件是（ ）A．AB⊥CD B．AC=AD C．BC=BD D．OE＝ED【解答】解：当AB⊥CD时，CE＝DE．故A正确；当BC=BD或AC=AD时，CE＝DE，故BC都正确；故选：D．【变式训练3】如图，CD是⊙O的弦，AB是⊙O的直径，AB⊥CD于点E，下列结论：①AC=AD；②BC=BD；③EO＝EB；④EC＝ED．其中一定成立的是（ ）A ．①③B ．①④C ．①②④D ．①②③④【解答】解：∵AB 是直径，AB ⊥CD ，∴AC =AD ，BC =BD ，EC ＝DE ，故①②④正确．故选：C ．内接四边形【例15】如图，四边形ABCD 是⊙O 的内接四边形，连接OA ，OC ．若∠ABC ＝108°，则∠AOC 的度数为（ ）A ．72°B ．108°C ．144°D ．150°【解答】解：∵四边形ABCD 是⊙O 的内接四边形，∴∠D +∠ABC ＝180°，∵∠ABC ＝108°，∴∠D ＝72°，∴∠BOC ＝2∠D ＝144°，故选：C ．【变式训练1】如图，四边形ABCD 内接于⊙O ，对角线BD 垂直平分半径OC ，若∠ABD ＝50°，则∠ADC的大小为（ ）A．130°B．120°C．110°D．100°【解答】解：设BD交OC于E，连接OD，OA，∵BD垂直平分OC，∴OE=12OC=12OD，∠OED＝90°，∴∠ODE＝30°，∴∠DOC＝90°﹣30°＝60°，∵OC＝OD，∴△OCD是等边三角形，∴∠ODC＝60°，∵∠ABD＝50°，∴∠AOD＝2∠ABD＝100°，∵OA＝OD，∴∠ADO＝∠OAD=12（180°﹣∠AOD）＝40°，∴∠ADC＝∠ADO+∠ODC＝40°+60°＝100°，故选：D．【变式训练2】如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝15°，则∠BDC＝（ ）A．85°B．75°C．70°D．65°【解答】解：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠ABC＝15°，∴∠CAB＝75°，∴∠BDC＝∠CAB＝75°，故选：B．【变式训练3】如图，AB是⊙O的直径，弦CD垂直平分OB，P是AD上一点，则∠APD等于（ ）A．120°B．125°C．135°D．150°【解答】解：连接OC，AC．∵弦CD垂直平分OB，∴OE=12OB=12OC，∴∠OCD＝30°，∴∠COB＝60°，∵OA＝OC，∴∠BAC＝30°，∴∠ACD＝60°．∴∠APD＝180°﹣60°＝120°，故选：A．证明综合【例16】如图，AB为⊙O的直径，CD为弦，CD⊥AB于点E，连接DO并延长交⊙O于点F，连接AF交CD于点G，连接AC，且AC∥DF．（1）求证：CG＝AG；（2）若AB＝12，求∠CAO和GD的长．【解答】（1）证明：∵AC∥DF，∴∠CDF＝∠ACD，∵CF=CF，∴∠CAF＝∠CDF，∴∠ACD＝∠CAF，∴AG＝CG；（2）解：如图，连接CO，∵AB⊥CD，∴AC=AD，CE＝DE，∵∠DCA＝∠CAF，∴AD=CF，∴AC=AD=CF，∴∠AOD＝∠AOC＝∠COF，∵DF是直径，∴∠AOD＝∠AOC＝∠COF＝60°，∵OA＝OC，∴△AOC是等边三角形，∴AC＝AO＝6，∠CAO＝60°，∵CE⊥AO，∴AE＝EO＝3，∠ACD＝30°，∴CE＝DE，∵AG2＝GE2+AE2，∴AG2＝（AG）2+9，∴AG＝∴GE=∴DG＝【变式训练1】如图，AB是⊙O的直径，点C在⊙O上，AC=BC，点D是BC的中点，连结OC，AD，交于点E，连结BE，BD．（1）求∠EBA的度数．（2）求证：AE=．（3）若DE＝1，求⊙O的面积．【解答】解：（1）连接AC，∵AC=BC，∴∠AOC＝∠BOC＝90°∴∠CAB＝45°，∵点D是BC的中点，∴CD=BD，∴∠CAD＝∠EAB＝22.5°；（2）由（1）知，OC垂直平分AB，∴AE＝BE，∴∠DEB＝2∠EAB＝45°，∵AB是直径，∴∠D＝90°，∴BD＝sin45°BE，∴BE=，∴AE=；（3）∵DE＝1∴BD＝DE＝1，∴AE＝BE=∴AD=+1，在Rt△ABD中，AD2+BD2＝（2OA）2，）2+1＝4OA2，∴OA2∴圆的面积为πOA2=一．选择题（共8小题）1．下列说法正确的是( )A ．直径是圆中最长的弦，有4条B ．长度相等的弧是等弧C ．如果A e 的周长是B e 周长的4倍，那么A e 的面积是B e 面积的8倍D ．已知O e 的半径为8，A 为平面内的一点，且8OA =，那么点A 在O e 上【解答】解：A 、直径是圆中最长的弦，有无数条，故该选项不符合题意；B 、在同圆或等圆中长度相等的弧是等弧，故该选项不符合题意；C 、如果A e 的周长是B e 周长的4倍，那么A e 的面积是B e 面积的16倍，故该选项不符合题意；D 、已知O e 的半径为8，A 为平面内的一点，且8OA =，那么点A 在O e 上，故该选项符合题意．故选：D ．2．小明在半径为5的圆中测量弦AB 的长度，下列测量结果中一定是错误的是( )A ．4B ．5C ．10D ．11【解答】解：Q 半径为5的圆，直径为10，\在半径为5的圆中测量弦AB 的长度，AB 的取值范围是：010AB <…，\弦AB 的长度可以是4，5，10，不可能为11．故选：D ．3．如图，O e 的直径BA 的延长线与弦DC 的延长线交于点E ，且CE OB =，已知72DOB Ð=°，则E Ð等于( )A ．36°B ．30°C ．18°D ．24°【解答】解：如图：CE OB CO ==，得1E Ð=Ð．由2Ð是EOC D 的外角，得212E E Ð=Ð+Ð=Ð．由OC OD =，得22D E Ð=Ð=Ð．由3Ð是三角形ODE D 的外角，得323E D E E E Ð=+Ð=Ð+Ð=Ð．由372Ð=°，得372E Ð=°．解得24E Ð=°．故选：D ．4．如图，O e 的直径12AB =，弦CD 垂直AB 于点P ．若2BP =，则CD 的长为()A ．B ．C ．D ．【解答】解：如图，连接OC ，12AB =Q ，6OC OB \==，2PB =Q ，4OP \=，在Rt OPC D 中，CP ==，CD AB ^Q ，CP DP \=，2CD PC\==．故选：C．5．已知Oe的半径为5，点O到弦AB的距离为3，则Oe上到弦AB所在直线的距离为2的点有( )A．4个B．3个C．2个D．1个【解答】解：过O点作OC AB^，交Oe于P，如图，3OC\=，而5OA=，2PC\=，即点P到直线AB的距离为2；在直线的另一边，圆上的点到直线的最远距离为8，而圆为对称图形，\在直线AB的这边，还有两个点M，N到直线AB的距离为2．故选：B．6．如图所示的是一圆弧形拱门，其中路面2AB m=，拱高3CD m=，则该拱门的半径为( )A．53m B．2m C．83m D．3m【解答】解：如图，取圆心为O ，连接OA ，设O e 的半径为r m ，则OC OA r ==m ，Q 拱高3CD m =，(3)OD r m \=-，OD AB ^，2AB m =Q ，112AD BD AB m \===，222OA AD OD =+Q ，2221(3)r r \=+-，解得：53r =，\该拱门的半径为53m ，故选：A ．7．如图，在Rt ACB D 中60ACB Ð=°，以直角边AB 为直径的O e 交线段AC 于点E ，点M 是弧AE 的中点，OM 交AC 于点D ，O e 的半径是6，则MD 的长度为( )A B ．32C ．3D ．【解答】解：90ABC Ð=°Q ，60ACB Ð=°，30A \Ð=°，M Q 为弧AE 的中点，OM 过圆心O ，OM AD \^，90ADO \Ð=°，116322OD OA \==´=，633MD OM OD \=-=-=，故选：C ．8．如图，在O e 中，¶¶¶AB BCCD ==，连接AC ，CD ，则AC 与CD 的关系是( )A ．2AC CD =B ．2AC CD <C ．2AC CD >D ．无法比较【解答】解：如图，连接AB 、BC ，在O e 中，¶¶¶AB BCCD ==，AB BC CD \==，在ABC D 中，AB BC AC +>．2AC CD \<．故选：B ．二．填空题（共4小题）9．运动场上的环形跑道的跑道宽都是相同的，若一条跑道的两个边缘所在的环形周长的差等于125p 米，则跑道的宽度为 65　米．【解答】解：设运动场上的小环半径为r 米，大环半径半径为R 米，根据题意得：122()5R r p p -=，解得：65R r -=，即跑道的宽度为65米．故答案为：65．10．大圆的半径是R ，小圆的半径是大圆半径的一半，则大圆面积比小圆面积大 234R p ．【解答】解：由题意得，大圆面积为2R p ，小圆面积为21()24R R p p ×=，1344R R R p p p -=，\大圆面积比小圆面积大234R p ，故答案为：234R p ．11．我们规定：将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等分线”，“等分线”被这个平面图形截得的线段叫做该图形的“等分线段”（例如圆的直径就是圆的“等分线段” )．已知等边三角形的边长为4，则它的“等分线段”长度x 的取值范围是 x …【解答】解：如图，①等边三角形的高AD 是最长的“等分线段”，4AD ==；②当//EF BC 时，EF 为最短“等分线段”，此时，21()2EF BC =，即4EF =，解得EF =．所以，它的“等分线段”长x …故答案为：x …．12．如图，在平面直角坐标系中，放置半径为1的圆，圆心到两坐标轴的距离都等于半径，若该圆向x 轴正方向滚动2022圈（滚动时在x 轴上不滑动），此时该圆圆心的坐标为 (40441,1)p +　．【解答】解：如图，点(1,1)P ，点(1,0)A ，该圆向x 轴正方向滚动2022圈，点A 移动过的距离为2120224044p p ´´=，这点到原点O 的距离为40441p +，因此点P 的对应点的坐标为(40441,1)p +，故答案为：(40441,1)p +．三．解答题（共3小题）13．在平面内，给定不在同一直线上的点A ，B ，C ，如图所示．点O 到点A ，B ，C 的距离均等于(r r 为常数），到点O 的距离等于r 的所有点组成图形G ，ABC Ð的平分线交图形G 于点D ，连接AD ，CD ．求证：AD CD =．【解答】证明：根据题意作图如下：BD Q 是圆周角ABC 的角平分线，ABD CBD \Ð=Ð，\¶¶AD CD =，AD CD \=．14．如图，O e 的半径OC AB ^，D 为¶BC上一点，DE OC ^，DF AB ^，垂足分别为E 、F ，3EF =，求直径AB 的长．【解答】解：OC AB ^Q ，DE OC ^，DF AB ^，\四边形OFDE 是矩形，3OD EF \==，6AB \=．15．已知：如图，BD 、CE 是ABC D 的高，M 为BC 的中点．试说明点B 、C 、D 、E 在以点M 为圆心的同一个圆上．【解答】证明：连接ME 、MD ，BD Q 、CE 分别是ABC D 的高，M 为BC 的中点，12ME MD MC MB BC \====，\点B 、C 、D 、E 在以点M 为圆心的同一圆上．。

初中数学章节解析汇编---第24章 圆的有关性质一、选择题1、如图1，AB 是⊙O 的直径，∠AOC =130°，则∠D 的度数是（ B ）.A 、65°B 、25°C 、15°D 、35°图1 图2 图3 图42、如图2，点A 、B 、C 是⊙O 上三点，∠AOC=120°，则∠ABC 等于（ B ）.A 、50°B 、60°C 、65°D 、70°3、如图3，△ABC 内接于⊙O ，∠ABC=71º，∠CAB=53°，点D 在AC 弧上，则∠ADB 的大小为（ C ）.A 、46°B 、53°C 、56°D 、71°4、如图4，⊙O 的半径是3，点P 是弦AB 延长线上一点，连接OP ，OP=4，∠APO=30°，则弦AB 的长为（ A ）.A 、2√5B 、√5C 、2√13D 、√135、如图5，在⊙O 中，∠AOB=45°，则∠C 为（ A ）.A ．22.5°B ．45°C ．60°D ．90°图5 图6 图7 图8 6、如图6，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB=30°，⊙O 的半径为3cm ，则弦CD 的长为（ B ）.A 、1.5cmB 、3cmC 、2√3cmD 、9cm7、如图7，点A 、B 、C 、D 在⊙O 上，且四边形OABC 是平行四边形，则∠D 的度数为（ B ）.A 、45°B 、60°C 、75°D 、不能确定8、如图8，在平面直角坐标系中，⊙M 与y 轴相切于原点O ，平行于x 轴的直线交⊙M 于P ，Q 两点，点P 在点Q 的右方，若点P 的坐标是(－1，2)，则点Q 的坐标是（ A ）.A 、(－4，2)B 、(－4.5，2)C 、(－5，2)D 、(－5.5，2)9、如图9，矩形ABCD 为⊙O 的内接四边形，AB=2，BC=3，点E 为BC 上一点，且BE=1，延长 AE 交⊙O 于点F ，则线段AF 的长为（ A ）.A 、75 5B 、5C 、5＋1D 、325图9 图1010、如图10，在等边△ABC 中，AB 、AC 都是圆O 的弦，OM ⊥AB ，ON ⊥AC ，垂足分别为M 、N ，如果MN ＝1，那么△ABC 的面积（ B ）.A 、3B 、√3C 、4D 、√33⁄二、填空题11、如图11，AB 是⊙O 的直径，CD 是⊙O 的弦，若∠BAC=23°，则∠ADC 的度数为 67° .图11 图12 图13 图14 图1512、如图12，⊙O 的直径CD 垂直于弦AB ，∠AOC=40°，则∠CDB 的度数为 20° .13、如图13，⊙O 是△ABD 的外接圆，AB 是⊙O 的直径，CD 是⊙O 的弦，∠ABD=58°，则∠BCD= 32° .14、如图14，⊙O 的半径OD ⊥弦AB 于点C ，连结AO 并延长交⊙O 于点E ，连结EC ．若AB ＝8，CD ＝2，则EC 的长为 2√3 . 15、如图15，△ABC 是⊙O 的内接三角形，∠C ＝50°，则∠OAB ＝40°.三、解答题16、如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝5，CB ＝12，AD 是△ABC 的角平分线，过A 、C 、D 三点的圆与斜边AB 交于点E ，连接DE 。

24.1圆的有关性质（讲练）一、知识点（1）圆：平面上到定点的距离等于定长的所有点组成的图形．如图所示的圆记做⊙O.（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦.（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧.（4）圆心角：顶点在圆心的角叫做圆心角.（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角.（6）弦心距：圆心到弦的距离.知识点二：垂径定理及其推论定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论(1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧；(2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧.延伸根据圆的对称性，如图所示，在以下五条结论中：①弧AC=弧BC;②弧AD=弧BD；③AE=BE;④AB⊥CD;⑤CD是直径.只要满足其中两个，另外三个结论一定成立，即推二知三.关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形.3.圆心角、弧、弦的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．（1）定理：一条弧所对的圆周角等于它所对的圆心角的一半.( 2 )推论：① 在同圆或等圆中，同弧或等弧所对的圆周角相等.如图b ，∠A=∠C.② 直径所对的圆周角是直角.如图c,∠C=90°.③ 圆内接四边形的对角互补.如图a ，∠A+∠C=180°，∠ABC+∠ADC=180°.二、标准例题：例1：如图，⊙O 的半径为3，点P 是弦AB 延长线上的一点，连接OP ，若4OP =，30P ∠=︒，则弦AB 的长为（ ）．A B ．C ．D ．2【答案】C【解析】 解：如图：过点O 作OH ⊥AB 于点H ，连接OA ，∵在Rt △OHP 中，∠P=30°，OP=4，∴122OH OP==∵在Rt△OAH中，OA=3，∴AH==2AB AH∴==故选C．总结：本题考查了垂径定理以及勾股定理.此题难度不大，但掌握辅助线的作法和数形结合思想的应用是解答本题的关键.例2：如图，CD是⊙O的直径，弦AB⊥CD，连接OA，OB，BD，若∠AOB＝100°，则∠ABD ＝________度。

24.1 圆的有关性质知识要点：1．弦与直径：（1）弦是连接圆上任意两点的线段，直径是经过圆心的弦.（2）直径是弦，是圆中最长的弦，但弦不一定是直径.2．弧与半圆：（1）圆上任意两点分圆成两段弧，圆上任意一条直径的两个端点把圆分成两条孤，每一条弧叫作半圆.（2）半圆是弧，但弧不一定是半圆3.垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．4.在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．5.一条弧所对的圆周角等于它所对的圆心角的一半．一、单选题1．如图，⊙O是△ABC的外接圆，∠ACO=45°，则∠B的度数为（）A．30°B．35°C．40°D．45°2．如图，⊙O是△ABC的外接圆，连结OB、OC，若OB=BC，则∠BAC等于（）A．60°B．45°C．30°D．20°3．下列四个命题：①直径所对的圆周角是直角；②圆既是轴对称图形，又是中心对称图形；③在同圆中，相等的圆周角所对的弦相等；④三点确定一个圆．其中正确命题的个数为（）A．1 B．2 C．3 D．44．如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于12EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD 5．如图，直线AB、CD相交于点O，OD平分∠BOF，OE⊥CD于O，若∠EOF＝α，下列说法①∠AOC＝α﹣90°；②∠EOB＝180°﹣α；③∠AOF＝360°﹣2α，其中正确的是（）A．①②B．①③C．②③D．①②③6．如图所示，AD 、AE 分别是△ABC 的高和角平分线，且∠B=76°，∠C=36°，则∠DAE 等于（ ）A ．20°B ．18°C ．45°D ．30°7．如图，AB CD ∥，CE 平分ACD ∠，交A 于点E ，20AEC ∠=o ，点F 在CA 延长线上，则BAF ∠的度数为（ ）A ．20B ．30C ．40D ．508．已知⊙O 的半径为10cm ，弦MN ∥EF,且MN=12cm,EF=16cm,则弦MN 和EF 之间的距离为 ( )cm.A ．14或2B ．14C ．2D ．69．如图，一块直角三角板ABC 的斜边AB 与量角器的直径恰好重合，点D 对应的刻度是60°，则∠ACD 的度数为( )A ．60°B ．30°C ．120°D ．45°10．如图，石拱桥的桥顶到水面的距离CD 为8m ，桥拱半径OC 为5m ，则水面AB 宽为（ ）A.4mB.5mC.6mD.8m二、填空题11．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，则BE=______．12．如图，AB 是⊙O 的直径，点C 在⊙O 上，∠BAC＝46°，点P 在线段OB 上运动．设∠ACP＝x°，则x 的最小值为_________，最大值为________．13．如图，AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=______14．Rt△ABC中，∠C=90°，AC=6cm,BC=8cm,则其外接圆的半径为____________ .15．如图，AB 是圆O 的弦，OC AB ⊥，垂足为点C ，将劣弧AB 沿弦AB 折叠交于OC的中点D ，若AB =，则圆O 的半径为_____．三、解答题16．如图，⊙O 的直径AB 为8cm,∠B=300, ∠ACB 的平分线交⊙O 于D ，连接AD ．（1）求BC 的长；（2）求∠CAD 的度数．17．已知⊙O 中，弦AB ⊥弦CD 于E ，求证：180AOD BOC ∠+∠=︒．18．如图，⊙O 是△ABC 的外接圆，AD 是△ABC 的高，AE 是⊙O 的直径，求证：BAE CAD ∠=∠．19．如图，在⊙O 中，AB ．AC 是弦，ABO ACO BOC αβθ∠=∠=∠=，，，求αβθ，，的关系．答案1．D2．C3．C4．B5．D6．A7．C8．A9．B10．D11．4-12．46︒90︒13．50°14．5cm15．16．解：（1）∵AB是⊙O的直径，∴∠ACB=90°，∵AB=8cm，∠B=30°，∴AC=12AB=4cm，BC∴==（2）连接OD，∵CD是∠ACB的角平分线，AD BD∴=∴∠BOD=12∠AOB=90°，∴∠BAD=12∠BOD=45°，∵∠BAC=90°-∠B=60°，∴∠CAD=∠BAC+∠BAD=105°．17．连接AC，BD，由圆周角定理得：∠AOD=2∠ABD ，∠BOC=2∠CDB ，∠CAB=∠CDB ， ∵弦AB ⊥弦CD ，∴∠BED=90°，∴∠ABD+∠BDC=90°，∴∠AOD+∠BOC=2∠ABD+2∠BDC=2（∠ABD+∠CDB ）=2×90°=180°. 18．连接BE ，∵AE 是⊙O 的直径，∴∠ABE ＝90°，∴90BAE E ∠+∠=︒，∵AD 是ABC △边上的高，∴90ADC ∠=︒，∴90CAD ACB ∠+∠=︒，∵∠E ＝∠ACB ，∴∠BAE ＝∠CAD ．19．过A 作⊙O 的直径，交⊙O 于D ；OAB 中，OA OB =，则2BOD OBA OAB α∠=∠+∠=， 同理可得：2COD OCA OAC β∠=∠+∠=，∵BOC BOD COD ∠=∠+∠，∴22θαβ=+。