1.1.2弧度制

弧 度 制基础归纳：1、弧度与角度的换算：360°＝2π弧度；180°＝π弧度．2、弧长公式：l ＝|α|r ，扇形面积公式：S 扇形＝12lr ＝12|α|r 2. 其中R 是扇形的半径，l 是弧长，α(0<α<2π)为圆心角，S 是扇形面积．知识点一 弧度制的概念1、 定义：把长度等于半径长的圆弧所对的圆心角叫做1弧度的角，记作1rad ，读作1弧度.2、 如果半径为r 的圆的圆心角α所对的弧长为l ，那么，角α的弧度数的绝对值|α|＝lr3、 约定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为0.4、用“弧度”做单位来度量角的制度叫做弧度制．比值lr与所取的r 的大小无关，仅与角的大小有关．例1、在半径不等的两个圆内，1弧度的圆心角（ C ） A ．所对弧长相等 B ．所对的弦长相等C ．所对弧长等于各自半径D ．所对弧长等于各自半径知识点二 角度制与弧度制互换1、将角度化为弧度2、将弧度化为角度例1A. 6π radB.－6π rad C. 12πrad D.－12πrad例2、将下列弧度转化为角度： （1）12π= °；（2）－87π= ° ′；（3）613π= °； 例3、将下列角度转化为弧度：（1）36°= rad ；（2）－105°= rad ；（3）37°30′= rad ； 答案： 15 -157 30； 390 5π；127π-；245π．知识点三 弧长及扇形面积公式1、弧长公式2、扇形面积公式 例1、半径为πcm ，中心角为120o 的弧长为（ D ）rad π2360=︒rad π=︒18001745.01801≈=︒rad πrad n 0=︒=3602π︒=180π(0=n rl •=α22121r r l S •=•=αA ．cm 3πB ．cm 32π C ．cm 32πD ．cm 322π 例2、(1)已知扇形周长为10，面积是4，求扇形的圆心角．(2)已知扇形周长为40，当它的半径和圆心角取何值时，才使扇形面积最大？(1)设圆心角是θ，半径是r ，则⎩⎪⎨⎪⎧ 2r ＋rθ＝1012θ·r 2＝4⇒⎩⎪⎨⎪⎧ r ＝1，θ＝8(舍)，⎩⎪⎨⎪⎧r ＝4，θ＝12，故扇形圆心角为12. (2)设圆心角是θ，半径是r ，则2r ＋rθ＝40.S ＝12θ·r 2＝12r (40－2r )＝r (20－r )＝－(r －10)2＋100≤100， 当且仅当r ＝10时，S max ＝100.所以当r ＝10，θ＝2时，扇形面积最大．若本例(1)中条件变为：圆弧长度等于该圆内接正方形的边长，则其圆心角的弧度数是________．解析：设圆半径为R ，则圆内接正方形的对角线长为2R ， ∴正方形边长为2R ，∴圆心角的弧度数是2RR＝ 2. 答案： 2巩固练习：1、圆的半径变为原来的2倍，而弧长也增加到原来的2倍，则( )A ．扇形的面积不变B ．扇形的圆心角不变C ．扇形的面积增大到原来的2倍D ．扇形的圆心角增大到原来的2倍 2、如图，用弧度制表示下列终边落在阴影部分的角的集合（不包括边界）．3、某种蒸汽机上的飞轮直径为1.2m ，每分钟按逆时针方向转300周，求: （1）飞轮每秒钟转过的弧度数。

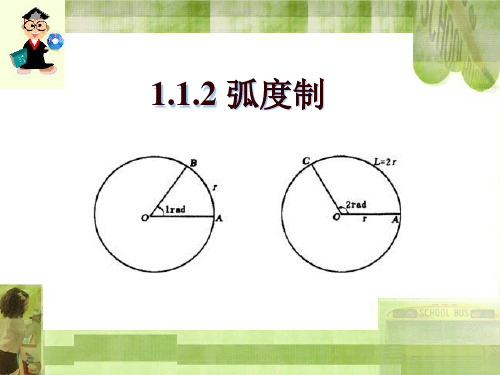
1.1.2 弧度制学习目标：1.了解弧度制的表示方法，并能进行弧度与角度的换算。

2.知道弧长公式和扇形面积公式. 重难点重点：理解并掌握弧度制定义；熟练地进行角度制与弧度制地互化换算；弧度制的运用. 难点：理解弧度制定义，弧度制的运用. 知识连接角度制规定：将一个圆周分成360份，每一份叫做1度，故一周等于360度，平角等于180度，直角等于90度等等. 自主研讨：（预习教材P6-P9）探究1：（1）弧度制定义：长度等于半径长的圆弧所对的圆心角叫做1弧度角，记作1rad ，这种度量角的单位制称为 。

(2) 如图,半径为r 的圆的圆心与原点重合,角α的终边与x 轴的正半轴重合,交圆于点A ,终边与圆交于点B .请完成表格.弧AB 的长OB 旋转的方向 AOB ∠的弧度数 AOB ∠的度数r π逆时针方向 2r π逆时针方向r12r2-π-180︒360︒一般地， 正角的弧度数是 数，负角的弧度数是 数，零角的弧度数是 。

(3) 如果一个半径为r 的圆的圆心角α所对的弧长是l ,那么角α的弧度数的绝对值是：___________，其中，α的正负由角α的终边的旋转方向来决定.yxAαOB探究2：弧度与角度的换算 360︒=_____ rad, 180︒=_____ rad,1︒=rad rad 01745.0_____≈, '1857__________1 =≈=rad 归纳：把角从弧度化为度的方法是：把角从度化为弧度的方法是：特殊角的角度数与弧度数的对应值表：弧度数表示弧长与半径的比,是一个实数,这样在角集合与实数集之间就建立了一个一一对应关系.课中案例1.把'6730︒化成弧度:变式练习：把下列各角从度化为弧度：(1)22 º30′ （2）—210º (3)1200º角度 0° 30°90° 120° 135° 150° 180° 360° 弧度4π 3π正角 零角 负角 正实数 零 负实数例2.将85π换算成角度变式练习：把下列各角从弧度化为度：（1）12π （2）—34π （3）103π例3.利用弧度制证明下列关于扇形的公式:(1)l R α=; (2)212S R α=; (3)12S lR =.其中R 是半径,l 是弧长,(02)ααπ<<为圆心角,S 是扇形的面积. 分析: 利用角度制表示的弧长公式、扇形面积公式．（2）扇形的圆心角为2，半径等于5，求扇形的面积变式练习 一个扇形的周长为4，面积为1，求圆心角的弧度数当堂检测1、把125π-化成角度制；把270°化成弧度制。

1.1.2弧度制教学重点弧度的概念．弧长公式及扇形的面积公式的推导与证明．教学难点“角度制”与“弧度制”的区别与联系．规定把周角的{ EMBED Equation.3 |3601作为1度的角,用度做单位来度量角的制度叫做角度制我们规定,长度等于半径的弧所对的圆心角叫做1弧度的角；用弧度来度量角的单位制叫做弧度制．在弧度制下, 1弧度记做1rad ．在实际运算中，常常将rad单位省略3．思考：（1）一定大小的圆心角所对应的弧长与半径的比值是否是确定的？与圆的半径大小有关吗？弧度制的性质：①半圆所对的圆心角为 ②整圆所对的圆心角为③正角的弧度数是一个正数． ④负角的弧度数是一个负数．⑤零角的弧度数是零． ⑥角α的弧度数的绝对值|α|=4．角度与弧度之间的转换：①将角度化为弧度：②将弧度化为角度； ；；．5．常规写法：① 用弧度数表示角时,常常把弧度数写成多少π 的形式, 不必写成小数． ② 弧度与角度不能混用． 6．特殊角的弧度角度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°弧度0 7．弧长公式|α|=弧长等于弧所对应的圆心角(的弧度数)的绝对值与半径的积例1．把67°30＇化成弧度．例2．把化成度．例3．计算：； (2)sin例4．将下列各角化成0到2π的角加上2kπ（k∈Z）的形式：；．例5．将下列各角化成2kπ + α(k∈Z,0≤α＜2π)的形式,并确定其所在的象限．；．R lO证法一:∵圆的面积为,∴圆心角为1rad的扇形面积为,又扇形弧长为l,半径为R,∴扇形的圆心角大小为rad, ∴扇形面积．证法二:设圆心角的度数为n，则在角度制下的扇形面积公式为，又此时弧长，∴．可看出弧度制与角度制下的扇形面积公式可以互化，而弧度制下的扇形面积公式显然要简洁得多．随堂练习一、选择题1．的值是（）．A．B．C．D．2．一条弦长等于半径的，则此弦所对圆心角（）．A．等于弧度B．等于弧度C．等于弧度D．以上都不对3．把化为的形式是（）．A．B．C．D．4．扇形的周长是16，圆心角是2弧度，则扇形面积是（）．A．B．C．16 D．32二、填空题1．度；弧度．2．半径为2的圆中，长为2的弧所对的圆周角的弧度数为__________，度数为____________．3．3弧度的角的终边在第_____________象限，7弧度的角的终边在第_____________象限．4．扇形的圆心角为，半径为，则弧长为____________．5．若的圆心角所对的弧长为，则此圆的半径为______________．三、解答题1．在半径为的圆中，扇形的周长等于半圆的弧长，那么扇形的圆心角是多少度？扇形的面积是多少？2．在直径为的滑轮上有一条弦，其长为，且为弦的中点，滑轮以每秒5弧度的角速度旋转，则经过后，点转过的弧长是多少？3．扇形的面积为，它的周长为，求扇形圆心角的弧度数4．一扇形周长是，扇形的圆心角为多少弧度时，这个扇形的面积最大？最大面积是多少？参考答案：一、选择题1．B 2．D 3．D 4．C二、填空题1．36，2．，3．二、一4．5．三、解答题1．，2．3．，4．圆心角为2弧度时，最大值为．。