1.1.2 弧度制--讲义

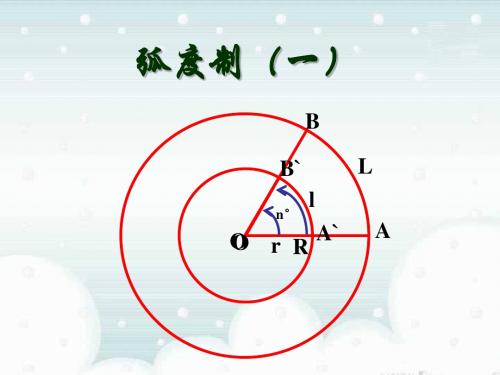
1．1.2 弧度制1.了解弧度制的意义．2.能正确的将弧度与角度互化．3.掌握弧长公式和扇形面积公式．1．角度制规定周角的1360为1度的角，记作1°.用度作为单位来度量角的单位制叫做角度制．2．弧度制(1)长度等于半径的圆弧所对的圆心角叫做1弧度的角，记作1 rad ．用弧度作为角的单位来度量角的单位制称为弧度制．(2)弧度数①正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是0．②角α的弧度数的绝对值|α|＝lr (其中l 是以角α作为圆心角时所对圆弧的弧长，r 为圆半径)．3．角度与弧度之间的互化及关系(1)度化弧度：360°＝2π rad ，180°＝π rad ，1°＝π180 rad ≈0.017 45 rad.(2)弧度化度：2π rad ＝360°，π rad ＝180°，1 rad ＝180°π≈57.30°.4．扇形的弧长及面积公式(1)弧长公式：l ＝|α|·r ，(r 为圆半径，|α|为圆心角的弧度数)，两个变形：|α|＝l r ，r ＝l|α|.(2)面积公式：S 扇形＝12l ·r (r 为扇形半径，l 为扇形的弧长)，两个变形：S 扇形＝12|α|·r 2，S 扇形＝12l 2|α|(α为扇形圆心角的弧度数)．1．判断(正确的打“√”，错误的打“×”) (1)1弧度指的是1度的角．( )(2)弧长为π，半径为2的扇形的圆心角是直角．( )解析：(1)错误.1弧度指的是长度等于半径长的弧所对的圆心角． (2)正确．若弧长为π，半径为2，则|α|＝π2，故其圆心角是直角．★答案★：(1)× (2)√ 2.8π5弧度化为角度是( ) A ．278° B ．280° C ．288° D ．318°★答案★：C3．半径为2，圆心角为π3的扇形的面积是( )A ．4π3B ．πC ．2π3D ．π3★答案★：C4．(1)18°＝________rad ；(2)310π＝________．★答案★：(1)π10(2)54°角度与弧度的互化(1)将下列各角度化成弧度： ①1 080°，②－750°； (2)将下列各弧度化成角度： ①－7π9，②512.【解】 (1)①1 080°＝1 080×π180 rad ＝6π rad ，②－750°＝－750×π180 rad ＝－25π6 rad.(2)①－7π9 rad ＝－7π9×180°π＝－140°，②512 rad ＝512×180°π＝75°π.角度制与弧度制的互化原则(1)角度与弧度的换算关系式是角度与弧度互化的重要依据，其中应记住关系式：π＝180°，它能够帮助我们更快、更准确地进行运算．(2)如果角度以度、分、秒的形式给出时，应先将它化为度，再转化为弧度；如果弧度给出的是实数，如2弧度，化为度应是2×180°π＝360°π.1.将下列角度与弧度进行互化．①20°＝________； ②－15°＝________； ③－115π＝________．解析：①20°＝20×π180＝π9.②－15°＝－15×π180＝－π12.③－115π＝－115π×180°π＝－396°.★答案★：π9 －π12－396°终边相同的角和区域角的弧度制表示(1)设角α1＝－570°，α2＝750°，将α1，α2用弧度制表示出来 ，并指出它们各自所在的象限；(2)用弧度制表示第二象限角的集合，并判断－10π3 是不是第二象限角．【解】 (1)因为－570°＝－19π6＝－4π＋5π6， 750°＝25π6＝4π＋π6.所以α1在第二象限，α2在第一象限． (2)在[0，2π)范围内，第二象限角α∈⎝⎛⎭⎫π2，π. 所以终边落在第二象限的所有角可表示为 ⎩⎨⎧⎭⎬⎫α⎪⎪2k π＋π2<α<2k π＋π，k ∈Z ，而－10π3＝－4π＋2π3∈⎝⎛⎭⎫－4π＋π2，－4π＋π， 所以－10π3是第二象限角．熟练掌握角度与弧度的互化，准确判断角所在的象限是学习三角函数知识的必备基本功．若需要在某一指定范围内求具有某种特性的角时，通常转化为解不等式去求对应的k 值．[注意] 用弧度制表示角时，不能与角度制混用，如β＝2k π－60°(k ∈Z )这种写法是不正确的．2.(1)在区间(0，2π)内，与－34π5终边相同的角是( )A ．π5B ．2π5C ．4π5D ．6π5(2)①把－1 480°写成α＋2k π(k ∈Z )的形式，其中0≤α＜2π；②在[0，4π]中找出与2π5角终边相同的角．解：(1)选D ．因为－34π5＝－8π＋6π5，则－34π5与6π5终边相同，选D ．(2)①因为－1 480°＝－1 480×π180 rad＝－749π rad ，又－749π＝－10π＋169π，其中α＝169π，所以－1 480°＝169π－10π.②终边与2π5角相同的角为θ＝2π5＋2k π(k ∈Z )，当k ＝0时，θ＝2π5；当k ＝1时，θ＝12π5，所以在[0，4π]中与2π5角终边相同的角为2π5，12π5.弧长与扇形面积公式的应用已知一扇形的圆心角是α，半径是r .(1)若α＝60°，r ＝10 cm ，求扇形的弧所在的弓形面积；(2)若扇形的周长是一定值c (c >0)，则当α为多少弧度时，该扇形的面积最大？ 【解】 (1)设弧长为l ，弓形的面积为S 弓． 因为α＝60°＝π3，r ＝10 cm ，所以l ＝αr ＝103π(cm)，所以S 弓＝S 扇－S △＝12×103π×10－34×102＝50⎝⎛⎭⎫π3－32(cm2)．(2)由已知2r＋l＝c，所以r＝c－l2(l<c)，所以S＝12rl＝12·c－l2·l＝14(cl－l2)＝－14⎝⎛⎭⎫l－c22＋c216，所以当l＝c2时，S max＝c216，此时α＝lr＝c2c－c22＝2，所以当扇形圆心角为2弧度时，扇形的面积有最大值c216.(1)求扇形的弧长和面积①记公式：弧度制下扇形的面积公式是S＝12lr＝12αr2(其中l是扇形的弧长，α是扇形圆心角的弧度数，0＜α＜2π)．②找关键：涉及扇形的半径、周长、弧长、圆心角、面积等的计算问题，关键是分析题目中已知哪些量、求哪些量，然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解．(2)扇形周长及面积的最值问题①当扇形周长一定时，扇形的面积有最大值．其求法是把面积S转化为关于r的二次函数，但要注意r的取值范围．特别注意一个扇形的弧长必须满足0＜l＜2πr.②当扇形面积一定时，扇形的周长有最小值，其求法是把周长C转化为关于r的函数，用基本不等式可求得扇形周长的最小值．特别注意一个扇形的弧长必须满足0＜l＜2πr.3.(1)在半径为12 cm的圆上，有一条弧的长是18 cm，求该弧所对的圆心角的弧度数和该扇形的面积．(2)已知一扇形的周长为40 cm，当它的半径和圆心角取什么值时，才能使扇形的面积最大？最大面积是多少？解：(1)设该弧所对的圆心角为α，则α＝lr＝1812＝32(rad)，该扇形面积为S＝12lr＝12×18×12＝108(cm2)．(2)设扇形的圆心角为θ，半径为r，弧长为l，面积为S，则l＋2r＝40，所以l ＝40－2r ，所以S＝12lr ＝12×(40－2r )r ＝－(r －10)2＋100.所以当半径r ＝10 cm 时，扇形的面积最大，这个最大值为100 cm 2，这时θ＝l r ＝40－2×1010＝2 rad.“度”与“弧度”的区别与联系 区别(1)定义不同 (2)单位不同．弧度制是以“弧度”为单位，单位可以省略，而角度制是以“度”为单位，单位不能省略(3)弧度制是十进制，而角度制是六十进制 联系(1)不管以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径大小无关的值，仅和半径与所含的弧这两者的比值有关 (2)“弧度”与“角度”之间可以相互转化已知扇形的周长为10 cm ，面积为4 cm 2，求扇形圆心角的弧度数． 【解】 设扇形圆心角的弧度数为θ(0<θ<2π)，弧长为l ，半径为r ， 依题意有⎩⎪⎨⎪⎧l ＋2r ＝10，①12lr ＝4，②①代入②得r 2－5r ＋4＝0， 解得r 1＝1，r 2＝4. 当r ＝1 cm 时，l ＝8 cm ， 此时θ＝8 rad>2π rad(舍去)； 当r ＝4 cm 时，l ＝2 cm ， 此时θ＝24＝12(rad)．有关扇形的弧长l ，圆心角α，面积S 的题目，一般是知二求一的题目，解此类题目的关键在于灵活运用l ＝|α|r ，S ＝12lr ＝12|α|r 2两组公式，采用消元思想或二次函数思想加以解决．1．1 920°转化为弧度数为( )A ．163B ．323C ．163πD ．323π解析：选D ．因为1°＝π180，所以1 920°＝1 920·π180＝32π3.2．在半径为8 cm 的圆中，5π3的圆心角所对的弧长为( ) A ．403π cmB ．203π cmC ．2003π cmD ．4003π cm解析：选A ．根据弧长公式，得l ＝5π3×8＝40π3(cm)．3．一钟表的分针长为5 cm ，经过40分钟后，分针外端点转过的弧长是________cm. 解析：经过40分钟，分针转过的角是α＝－4×π3＝－43π，则l ＝|α|r ＝5×43π＝203π(cm)．★答案★：203π[学生用书P79(单独成册)])[A 基础达标]1.3π4对应的角度为( ) A ．75° B ．125° C ．135°D ．155°解析：选C ．由于1 rad ＝⎝⎛⎭⎫180π°， 所以3π4＝34π×⎝⎛⎭⎫180π°＝135°，故选C ．2．用弧度制表示与150°角的终边相同的角的集合为( ) A ．⎩⎨⎧⎭⎬⎫β⎪⎪β＝－5π6＋2k π，k ∈Z B ．⎩⎨⎧⎭⎬⎫β⎪⎪β＝5π6＋k ·360°，k ∈Z C ．⎩⎨⎧⎭⎬⎫β⎪⎪β＝2π3＋2k π，k ∈ZD ．⎩⎨⎧⎭⎬⎫β⎪⎪β＝5π6＋2k π，k ∈Z 解析：选D ．150°＝150×π180＝5π6，故与150°角终边相同的角的集合为 ⎩⎨⎧⎭⎬⎫β⎪⎪β＝5π6＋2k π，k ∈Z .3．一段圆弧的长度等于其所在圆的圆内接正方形的边长，则这段圆弧所对的圆心角为( )A ．π2B ．π3C ． 2D ． 3解析：选C ．设圆内接正方形的边长为a ，则该圆的直径为2a ，所以弧长等于a 的圆弧所对的圆心角α＝l r ＝a22a ＝2，故选C ．4．钟的分针在1点到3点20分这段时间里转过的弧度为( ) A ．143 πB ．－143πC ．718πD ．－718π解析：选B ．显然分针在1点到3点20分这段时间里，顺时针转过了73周，转过的弧度为－73×2π＝－143π.5．扇形的半径变为原来的2倍，而弧长也增加到原来的2倍，则( ) A ．扇形的圆心角大小不变 B ．扇形的圆心角增大到原来的2倍 C ．扇形的圆心角增大到原来的4倍 D ．扇形的圆心角减小到原来的一半解析：选A ．设扇形原来的半径为r ，弧长为l ，圆心角为α，则变化后半径为2r ，弧长为2l ，圆心角为β，所以α＝l r ，β＝2l 2r ＝lr＝α，即扇形的圆心角大小不变．6．在△ABC 中，若A ∶B ∶C ＝3∶5∶7，则角A ，B ，C 的弧度数分别为________． 解析：A ＋B ＋C ＝π，又A ∶B ∶C ＝3∶5∶7， 所以A ＝3π3＋5＋7＝π5，B ＝5π3＋5＋7＝π3，C ＝7π15.★答案★：π5，π3，7π157．火车站钟楼上有座大钟，这座大钟的分针20 min 所走的圆弧长是π3 m ，则这座大钟分针的长度为________ m.解析：因为分针20 min 转过的角为－2π3，所以由l ＝|α|r ，得r ＝l|α|＝π32π3＝0.5(m)，即这座大钟分针的长度为0.5 m.★答案★：0.58．一条铁路在转弯处成圆弧形，圆弧的半径为2 km ，一列火车用30 km/h 的速度通过，10 s 内转过的弧度为________．解析：10 s 内列车转过的圆形弧长为103 600×30＝112(km)．转过的角α＝1122＝124(弧度)．★答案★：1249．一个半径为r 的扇形，若它的周长等于弧所在的半圆的弧长，那么扇形的圆心角是多少弧度？扇形面积是多少？解：设弧长为l ，所对圆心角为α，则l ＋2r ＝πr ， 即l ＝(π－2)r . 因为|α|＝lr ＝π－2，所以α的弧度数是π－2， 从而S 扇形＝12lr ＝12(π－2)r 2.10．设集合A ＝⎩⎨⎧x ⎪⎪⎭⎬⎫k π－π4≤x ≤k π＋π4，k ∈Z ， B ＝{x |x 2≤36}，试求集合A ∩B ． 解：由集合A ＝⎩⎨⎧x ⎪⎪⎭⎬⎫k π－π4≤x ≤k π＋π4，k ∈Z ，可知A ＝…∪⎣⎡⎦⎤－9π4，－7π4∪⎣⎡⎦⎤－5π4，－3π4 ∪⎣⎡⎦⎤－π4，π4∪ ⎣⎡⎦⎤3π4，5π4∪⎣⎡⎦⎤7π4，9π4∪….由B ＝{x |x 2≤36}，可得B ＝{x |－6≤x ≤6}，在数轴上将两个集合分别作出，如图．可得集合A ∩B ＝⎣⎡⎦⎤－6，－7π4∪ ⎣⎡⎦⎤－5π4，－3π4∪⎣⎡⎦⎤－π4，π4∪⎣⎡⎦⎤3π4，5π4∪⎣⎡⎦⎤7π4，6.[B 能力提升]1．设角α的终边为射线OP ，射线OP 1与OP 关于y 轴对称，射线OP 2与OP 1关于直线y ＝－x 对称，则以OP 2为终边的角的集合是( )A ．{β|β＝k ·2π＋α，k ∈Z }B ．{β|β＝(2k ＋1)·π＋α，k ∈Z }C ．{β|β＝k ·2π＋π2＋α，k ∈Z }D ．{β|β＝k ·2π＋32π＋α，k ∈Z }解析：选C ．依题意，射线OP 1所对应的角γ满足α＋γ＝k 1·2π＋π，k 1∈Z ，① 射线OP 2所对应的角β满足γ＋β＝k 2·2π－π2，k 2∈Z ，②②－①得β－α＝(k 2－k 1)·2π－32π，即β＝k ·2π＋π2＋α，k ∈Z .2．如图，动点P ，Q 从点A (4，0)出发，沿圆周运动，点P 按逆时针方向每秒钟转π3弧度，点Q 按顺时针方向每秒钟转π6弧度，则(1)P ，Q 第一次相遇时所用的时间为________． (2)P ，Q 点各自走过的弧长为________，________． 解析：设P ，Q 第一次相遇时所用的时间是t 秒， 则t ·π3＋t ·⎪⎪⎪⎪－π6＝2π， 解得t ＝4.所以第一次相遇时所用的时间是4秒，第一次相遇时点P 已经运动到角π3·4＝43π的终边与圆的交点位置，点Q 已经运动到角－2π3的终边与圆的交点位置，所以点P 走过的弧长为43π×4＝163π， 点Q 走过的弧长为⎪⎪⎪⎪－2π3×4＝23π×4＝83π. ★答案★：(1)4秒 (2)163π 83πRuize 3．已知扇形AOB 的圆心角为120°，半径长为6，求：(1)AB ︵的长；(2)扇形所含弓形的面积．解：(1)因为120°＝120180π＝23π， 所以l ＝|α|·r ＝6×23π＝4π， 所以AB ︵的长为4π.(2)因为S 扇形OAB ＝12lr ＝12×4π×6＝12π， 如图所示有S △OAB ＝12×AB ×OD ＝12×2×6cos 30°×3＝9 3.(D 为AB 中点) 所以弓形的面积为S 扇形OAB －S △OAB ＝12π－9 3.4．(选做题)将一条绳索绕在半径为40 cm 的轮圈上，绳索的下端处悬挂着物体B ，如果轮子按逆时针方向每分钟旋转6圈，现将物体B 的位置向上提升100 cm ，那么需要多长时间才能完成？解：如图，设将物体向上提升100 cm ，需要的时间为t s.当BB ′＝100 cm 时，AA ′︵的长是100 cm ，AA ′︵所对的圆心角∠AOA ′＝10040＝52(rad)． 因为轮子每分钟匀速旋转6圈，所以每秒匀速转过6×2π60＝π5(rad)． 于是t s 转过π5t rad ， 所以π5t ＝52， 得t ＝252π≈4(s)．。

1.1.2 弧度制和弧度制与角度制的换算1．角度制与弧度制的定义(1)角度制：用度作单位来度量角的制度叫做角度制．角度制规定60分等于1度，60秒等于1分．(2)弧度制：长度等于半径长的圆弧所对的圆心角叫做1弧度的角，记作1 rad.以弧度为单位来度量角的制度叫做弧度制．2．角的弧度数的计算在半径为r 的圆中，弧长为l 的弧所对圆心角为α rad ，则α＝lr . 3．角度与弧度的互化4．一些特殊角与弧度数的对应关系思考1：某同学表示与30°角终边相同的角的集合时写成S ＝{α|α＝2k π＋30°，k ∈Z }，这种表示正确吗？为什么？[提示] 这种表示不正确，同一个式子中，角度、弧度不能混用，否则产生混乱，正确的表示方法应为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α＝2k π＋π6，k ∈Z或{α|α＝k ·360°＋30°，k ∈Z }． 5．扇形的弧长与面积公式设扇形的半径为r ，弧长为l ，α为其圆心角，则思考2：在弧度制下的扇形面积公式S ＝12lr 可类比哪种图形的面积公式加以记忆？[提示] 此公式可类比三角形的面积公式来记忆．1．1 080°等于( ) A ．1 080 B ．π10 C ．3π10D ．6πD [1 080°＝180°×6，所以1 080°化为弧度是6π.] 2．与角23π终边相同的角是( ) A ．113πB ．2k π－23π(k ∈Z ) C ．2k π－103π(k ∈Z )D ．(2k ＋1)π＋23π(k ∈Z )C[选项A中11π3＝2π＋53π，与角53π终边相同，故A项错；2kπ－23π，k∈Z，当k＝1时，得[0,2π)之间的角为43π，故与43π有相同的终边，B项错；2kπ－103π，k∈Z，当k＝2时，得[0,2π)之间的角为23π，与23π有相同的终边，故C项对；(2k＋1)π＋23π，k∈Z，当k＝0时，得[0,2π)之间的角为53π，故D项错．]3．圆心角为π3弧度，半径为6的扇形的面积为________．6π[扇形的面积为12×62×π3＝6π.]A．“度”与“弧度”是度量角的两种不同的度量单位B．1°的角是周角的1360，1 rad的角是周角的12πC．1 rad的角比1°的角要大D．用角度制和弧度制度量角，都与圆的半径有关[思路探究]由题目可获取以下主要信息：各选项中均涉及到角度与弧度，解答本题可从角度和弧度的定义着手．D[根据角度和弧度的定义，可知无论是角度制还是弧度制，角的大小与圆的半径长短无关，而是与弧长与半径的比值有关，所以D项是假命题，A、B、C 项均为真命题．]弧度制与角度制的区别与联系1．下列各说法中，错误的说法是( ) A ．半圆所对的圆心角是π rad B ．周角的大小等于2πC ．1弧度的圆心角所对的弧长等于该圆的半径D ．长度等于半径的弦所对的圆心角的大小是1弧度 [答案] D【例2】 设角α1＝－570°，α2＝750°，β1＝35π，β2＝－73π. (1)将α1，α2用弧度制表示出来，并指出它们各自所在的象限；(2)将β1，β2用角度制表示出来，并在－720°～0°之间找出与它们终边相同的所有角．[思路探究] 由题目可获取以下主要信息：(1)用角度制给出的两个角－570°，750°，用弧度制给出的两个角35π，－73π； (2)终边相同的角的表示．解答本题(1)可先将－570°，750°化为弧度角再将其写成2k π＋α(k ∈Z,0≤α<2π)的形式，解答(2)可先将β1、β2用角度制表示，再将其写成β＋k ·360°(k ∈Z )的形式．[解] (1)要确定角α所在的象限，只要把α表示为α＝2k π＋α0(k ∈Z,0≤α0<2π)的形式，由α0所在象限即可判定出α所在的象限．α1＝－570°＝－196π＝－4π＋56π， α2＝750°＝256π＝4π＋π6.∴α1在第二象限，α2在第一象限． (2)β1＝3π5＝108°，设θ＝β1＋k ·360°(k ∈Z )， 由－720°≤θ<0°，得－720°≤108°＋k ·360°<0°， ∴k ＝－2或k ＝－1，∴在－720°～0°间与β1有相同终边的角是－612°和－252°. 同理β2＝－420°且在－720°～0°间与β2有相同终边的角是－60°.角度制与弧度制的转换中的注意点(1)在进行角度与弧度的换算时，抓住关系式π rad ＝180°是关键.由它可以得：度数×π180＝弧度数，弧度数×⎝ ⎛⎭⎪⎫180π°＝度数. (2)特殊角的弧度数与度数对应值今后常用，应该熟记.(3)在同一个式子中，角度与弧度不能混合用，必须保持单位统一，如α＝2k π＋30°，k ∈Z 是不正确的写法.(4)判断角α终边所在的象限时，若α[－2π，2π]，应首先把α表示成α＝2k π＋β，β∈[－2π，2π]的形式，然后利用角β终边所在的象限来确定角α终边所在的象限.2．用弧度表示终边落在如图所示阴影部分内(不包括边界)的角θ的集合．[解] 因为30°＝π6 rad,210°＝7π6 rad ，这两个角的终边所在的直线相同，因为终边在直线AB 上的角为α＝k π＋π6，k ∈Z ，而终边在y 轴上的角为β＝k π＋π2，k ∈Z ，从而终边落在阴影部分内的角的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫θ⎪⎪⎪k π＋π6<θ<k π＋π2，k ∈Z.1.用公式|α|＝lr 求圆心角时，应注意什么问题？[提示] 应注意结果是圆心角的绝对值，具体应用时既要注意其大小，又要注意其正负．2．在使用弧度制下的弧长公式及面积公式时，若已知的角是以“度”为单位，需注意什么问题？[提示] 若已知的角是以“度”为单位，则必须先把它化成弧度后再计算，否则结果出错．【例3】 (1)设扇形的周长为8 cm ，面积为4 cm 2，则扇形的圆心角的弧度数是( )A ．1 radB ．2 radC ．3 radD ．4 rad(2)已知扇形的周长为20 cm ，当它的半径和圆心角各取什么值时，才能使扇形的面积最大？最大面积是多少？[思路探究] (1)可由扇形周长和面积建立方程组，通过解方程组求得；(2)可通过建立扇形面积的目标函数来求解．(1)B [设扇形半径为r ，弧长为l ，由题意得⎩⎨⎧2r ＋l ＝8，12l ·r ＝4，解得⎩⎪⎨⎪⎧l ＝4，r ＝2，则圆心角α＝lr ＝2 rad.](2)解：设扇形的半径为r ，弧长为l ，面积为S .则l ＝20－2r ，∴S ＝12lr ＝12(20－2r )·r ＝－r 2＋10r ＝－(r －5)2＋25(0＜r ＜10)． ∴当半径r ＝5 cm 时，扇形的面积最大，为25 cm 2. 此时α＝l r ＝20－2×55＝2 rad.∴当它的半径为5 cm ，圆心角为2 rad 时，扇形面积最大，最大值为25 cm 2.(变条件)弧度制下解决扇形相关问题的步骤：(1)明确弧长公式和扇形的面积公式：l ＝|α|r ，S ＝12αr 2和S ＝12lr ；(这里α必须是弧度制下的角)(2)分析题目的已知量和待求量，灵活选择公式； (3)根据条件列方程(组)或建立目标函数求解.(教师用书独具)1．释疑弧长公式及扇形的面积公式(1)公式中共四个量分别为α，l ，r ，S ，由其中的两个量可以求出另外的两个量，即知二求二．(2)运用弧度制下的弧长公式及扇形的面积公式明显比角度制下的公式简单得多，但要注意它的前提是α为弧度制．(3)在运用公式时，还应熟练地掌握这两个公式的变形运用： ①l ＝α·r ，α＝l r ，r ＝l α；②S ＝12αr 2，α＝2Sr 2. 2．角度制与弧度制的比较1．把56°15′化为弧度是( ) A.5π8 B.5π4 C.5π6D.5π16D[56°15′＝56.25°＝2254×π180＝5π16.]2．在半径为10的圆中，240°的圆心角所对弧长为()A.403π B.203πC.2003π D.4003πA[240°＝240×π180rad＝43π rad，∴弧长l＝α·r＝43π×10＝403π，选A.]3．将－1 485°化成2kπ＋α(0≤α<2π，k∈Z)的形式为________．－10π＋74π[由－1 485°＝－5×360°＋315°，所以－1 485°可以表示为－10π＋74π.]4．一个扇形的面积为1，周长为4，求该扇形圆心角的弧度数．[解]设扇形的半径为r，弧长为l，圆心角为α，则2r＋l＝4. ①由扇形的面积公式S＝12lr，得12lr＝1. ②由①②得r＝1，l＝2，∴α＝lr＝2 rad.∴扇形的圆心角为2 rad.。