112弧度制xg精品PPT课件
- 格式：pptx
- 大小：1.89 MB
- 文档页数：23
下载文档原格式
合集下载
第5_1_2弧度制优质教学课件PPT
扇形的弧长 扇形的面积
l= nπR
180
S= nπR2
360
l=⑨ αR
1
S= 1lR=⑩ 2αR2
2
第1讲 描述运动的第基本五概章念 三角函数
判断正误，正确的画“√” ，错误的画“ ✕” .
1.1 rad的角和1°的角相等. ( ✕ )
π
2.405°可以转化为360°+ 4 . ( ✕ )
提示:角度与弧度不可同时使用,405°可化为2π+
度 0° 1° 30° 45° 60° 90°
120° 135° 150° 180° 270° 360°
弧度 0
π
π
⑦
π
180 6
3
π
4
π
⑧
3π
5π π
2
4
6
2π
3
3π 2π
2
第1讲 描述运动的第基本五概章念 三角函数
扇形的弧长及面积公式
设扇形的半径为R,弧长为l,圆心角为n°(α为其圆心角的弧度数),则
第1讲 描述运动的基本概念
高中数学 必修第一册 人教A版
第1讲 描述运动的第基本五概章念 三角函数
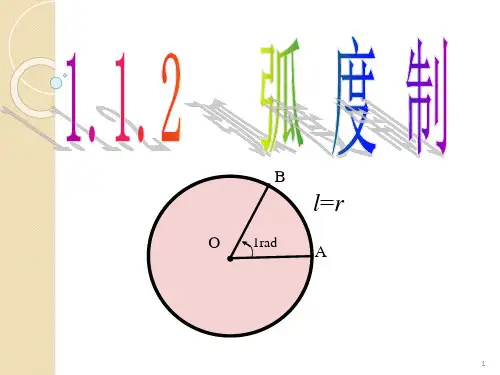
5.1.2 弧度制
通过教材中的探究,明确角度制与弧度制的关系,掌握角度与弧度的互化公式 及弧度制下的弧长公式及扇形面积公式,体会数学抽象的过程,加强问题探究与数 学运算素养的培养.学习本节要注意以下问题: 1.了解弧度制的概念,能进行弧度与角度的互化. 2.掌握并能运用弧长公式和扇形面积公式.
第1讲 描述运动的第基本五概章念 三角函数
近年来,
随着我市经济的快速发展,政府对民生越来越关注.市区现有一块近似正三角形的 土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶
高中数学 112弧制和弧制与角制的换算课件 新人教B版必修4
扇形的面积为 S＝12lr＝12(20－2r)r＝－r2＋10r＝－(r－ 5)2＋25 π1＋01<r<10，
当 r＝5 时，S 最大，此时 l＝10，α＝rl＝2.
[点评] 当扇形周长一定时，扇形的面积有最大 值．其求法是把面积S转化为关于r的二次函数，但要注意r 的取值范围．特别注意一个扇形的弧长必须满足0<l<2πr.
[例 1] (1)将 92°30′化成弧度；(2)将－178π 化成度． [分析] 利用 n°＝n·1π80rad 和 α＝18π0α°进行角度和 弧度的互化． [解析] (1)92°30′＝1825°＝1825×1π80＝3772π；
(2)－71π8＝－178π×18π0°＝－70°.
把α＝1690°写成β＋2kπ(k∈Z，β∈[0,2π))的形式． [解析] 1690°＝18π0×1690＝8π＋2158π.
[例 2] 将下列各角化成 2kπ＋α(0<α<2π，k∈Z)的形 式，并指出角的终边所在的象限．
(1)274π；(2)396π.
[解析] (1)∵247π＝6π＋34π， ∴274π与34π终边相同． 又∵34π是第二象限角，∴247π是第二象限角． (2)396π＝6π＋36π＝6π＋π2，∴369π与π2的终边相同． 又∵π2是象限界角，∴369π也是象限界角，它不属于任 何象限．
1．1.2弧度制和弧度制与角度制的 换算
1．弧度制的概念
我们把弧长等于半径长的弧所对的圆心角叫做1弧度的
角，用符号rad表示，读作弧度．
用 弧度 作为单位来度量角的制度叫做弧度制．
用度作为单位来度量角的制度叫做角度制．
2．角度与弧度的互化
360°＝ 2π rad,180°＝ π rad，
当 r＝5 时，S 最大，此时 l＝10，α＝rl＝2.
[点评] 当扇形周长一定时，扇形的面积有最大 值．其求法是把面积S转化为关于r的二次函数，但要注意r 的取值范围．特别注意一个扇形的弧长必须满足0<l<2πr.
[例 1] (1)将 92°30′化成弧度；(2)将－178π 化成度． [分析] 利用 n°＝n·1π80rad 和 α＝18π0α°进行角度和 弧度的互化． [解析] (1)92°30′＝1825°＝1825×1π80＝3772π；
(2)－71π8＝－178π×18π0°＝－70°.
把α＝1690°写成β＋2kπ(k∈Z，β∈[0,2π))的形式． [解析] 1690°＝18π0×1690＝8π＋2158π.
[例 2] 将下列各角化成 2kπ＋α(0<α<2π，k∈Z)的形 式，并指出角的终边所在的象限．
(1)274π；(2)396π.
[解析] (1)∵247π＝6π＋34π， ∴274π与34π终边相同． 又∵34π是第二象限角，∴247π是第二象限角． (2)396π＝6π＋36π＝6π＋π2，∴369π与π2的终边相同． 又∵π2是象限界角，∴369π也是象限界角，它不属于任 何象限．
1．1.2弧度制和弧度制与角度制的 换算
1．弧度制的概念
我们把弧长等于半径长的弧所对的圆心角叫做1弧度的
角，用符号rad表示，读作弧度．
用 弧度 作为单位来度量角的制度叫做弧度制．
用度作为单位来度量角的制度叫做角度制．
2．角度与弧度的互化
360°＝ 2π rad,180°＝ π rad，
112(2)弧度制精品PPT课件
时α/6的终边图.
【课本难题解答】
课本第12页练习第10题，答案： 弧度数为1.2 第13页习题4.2第12题，答案 64°；13题：答案约57.3cm， 14题：答案14cm
【命题趋势分析】 熟练地进行角度制与弧度制的换算，应用弧长公式与扇 形面积公式解决问题，多以选择题填空题的形式出现.
例1 (1)把-1480°写成α+2kπ(k∈Z)的形式，其中0≤α＜2π. (2)若β∈ 4π，0)，且β与(1)中α终边相同，求β.
分析：利用互化公式将-1480°化为弧度制即可.根据β的范围及β=α+2kπ，即可求出β.
解：(1)因为-1480=- 74 =-8π-=-10π+π.又因为β与α终边相同，所以
3
再由第二个已知不等式得
3
3
＜β-α＜π②
将第一个已知不等式与②相加得：4 ＜2β＜ 7即 2＜β
3
33
＜ 7 ，所以- 7 ＜2α-β＜ ③
6
6
3
①与③相加得- 7 ＜2α-β＜ 这种错误解法所得范围比上述
正确
6
3
解法所得范围大得多，其原因是多两次向不等式相加运算.
例2 设α是第一象限的角，试确定 所在的角限.
2
(2)若已知角α所在的象限，如何确定 n(n＞1,n∈Z)的 终边所在象限呢?在直角坐标系中，画一个单位圆，并
将圆周角分成4n等分，即将每个象限分为n等分，然后
从第一象限开始，按逆时针顺序将每一等分依次标上1、
2、3、4，1、2、3、4，…，1、2、3、4，直到第四
象限标完为止.这样就得到α/n的终边图.如上图是n=6
3
2
分析：交换集合的形式，找出两个集合中元素的异、同.
必修4第一章112 弧度制教学(共24张)PPT课件
18
把弧度换成角度：
例2、把 —53 rad 化成度。
2rad360
rad180
1rad 180
5.3 7 0 5 1 7 8
解： 3 rad =
5
3
5
×
180
3 180
108
5
[总结] 换算中带 的形式 常 可 用 180º来代 换 ； 换算中不带 的形式 可用 其 弧 度 数 乘 以 180 ,Bl来自rO 1radA
1
1．1.2 弧 度 制
预习课本P6～9，思考并完成以下问题
(1)1 弧度的角是如何定义的？ (2)如何求角 α 的弧度数？ (3)如何进行弧度与角度的换算？ (4)以弧度为单位的扇形弧长、面积公式是什么？
2
42寸
电视机的尺寸问题
1英寸 ≈ 2.54厘米 1厘米≈ 0.3937英寸
O r A（B)
若l = 2π r，则∠AOB=
l r
=
2π弧度
360°= 2 π 弧度
14
弧度数公式
正角的弧度数是一个正数，
负角的弧度数是一个负数，
零角的弧度数是0； 角α的弧度数的绝对值
l
r
➢ l 是圆心角α所对的弧长 ➢ r是圆的半径
15
用弧度来度量角，实际上角的集合 与实数集R之间建立一一对应的关系：
正角
正实数
对应角的 弧度数
零角
零
负角
负实数
角的集合
实数集R
16
弧度制与角度制的换算
换算公式 360º= 2 rad
180º= rad
．
1 rad 0.017r4a5d
180
1
ra
把弧度换成角度：
例2、把 —53 rad 化成度。
2rad360
rad180
1rad 180
5.3 7 0 5 1 7 8
解： 3 rad =
5
3
5
×
180
3 180
108
5
[总结] 换算中带 的形式 常 可 用 180º来代 换 ； 换算中不带 的形式 可用 其 弧 度 数 乘 以 180 ,Bl来自rO 1radA
1
1．1.2 弧 度 制
预习课本P6～9，思考并完成以下问题
(1)1 弧度的角是如何定义的？ (2)如何求角 α 的弧度数？ (3)如何进行弧度与角度的换算？ (4)以弧度为单位的扇形弧长、面积公式是什么？
2
42寸
电视机的尺寸问题
1英寸 ≈ 2.54厘米 1厘米≈ 0.3937英寸
O r A（B)
若l = 2π r，则∠AOB=
l r
=
2π弧度
360°= 2 π 弧度
14
弧度数公式
正角的弧度数是一个正数，
负角的弧度数是一个负数，
零角的弧度数是0； 角α的弧度数的绝对值
l
r
➢ l 是圆心角α所对的弧长 ➢ r是圆的半径
15
用弧度来度量角，实际上角的集合 与实数集R之间建立一一对应的关系：
正角
正实数
对应角的 弧度数
零角
零
负角
负实数
角的集合
实数集R
16
弧度制与角度制的换算
换算公式 360º= 2 rad
180º= rad
．
1 rad 0.017r4a5d
180
1
ra
112弧度制课件
1 rad, rad, 2π rad可分别写成：
1 , 2, 2π
类似地有：
①若圆的半径为r，圆心角∠AOB（正角）所
对的圆弧长为2r，那么 ∠AOB的弧度数就是
2r r
2
②若圆的半径为r，圆
心角∠AOB（正角）
所对的圆弧长为2πr，
则 ∠AOB的弧度数就是
2r
r
2
所以我们有：
360o=2πrad
故扇形的面积为
l
r r
S 1 rl 4 (cm2) 2
跟踪练习：
已知半径为10cm的圆上,有一段弧的长
度是
10 3
cm，求此弧所对的圆心角的弧
度数和该扇形的面积。
小结
（1）弧度制的概念
（2） 180 rad；
（3）“角化弧” : 即把角从度化为弧度，如果是no
就可将
n乘以
180
的角化成弧度，
请回忆：什么是角度制？
我们已学习过角的度量，规定周角
的
1 360
为1度的角，这种用度作为单位来
度量角的单位制叫做角度制。
周角等于360o 平角等于180o 直角等于90o
弧度制定义
我们把长度等于半径长的圆弧所对的圆心 角叫做1弧度的角．
记作1 rad
用弧度作为角的单位来度量角的单位制称为 弧度制 用弧度表示角的大小时，只要不引起误解， 可以省略单位，例如：
在数学里有很多以欧拉命名的公式和定理。在我们的数学课 本上常见的：sin,cos（三角函数符号）,f(x)（函数符号），以及 高二要用到的∑（求和符号），i(即－1的平方根）等都是他创立 并推广的。
今天我们要学习的弧度制雏形起源于印度，然而严格的弧度 概念却是由欧拉于1748年引入的。
1 , 2, 2π
类似地有：
①若圆的半径为r，圆心角∠AOB（正角）所
对的圆弧长为2r，那么 ∠AOB的弧度数就是
2r r
2
②若圆的半径为r，圆
心角∠AOB（正角）
所对的圆弧长为2πr，
则 ∠AOB的弧度数就是
2r
r
2
所以我们有：
360o=2πrad
故扇形的面积为
l
r r
S 1 rl 4 (cm2) 2
跟踪练习：
已知半径为10cm的圆上,有一段弧的长
度是
10 3
cm，求此弧所对的圆心角的弧
度数和该扇形的面积。
小结
（1）弧度制的概念
（2） 180 rad；
（3）“角化弧” : 即把角从度化为弧度，如果是no
就可将
n乘以
180
的角化成弧度，
请回忆：什么是角度制？
我们已学习过角的度量，规定周角
的
1 360
为1度的角，这种用度作为单位来
度量角的单位制叫做角度制。
周角等于360o 平角等于180o 直角等于90o
弧度制定义
我们把长度等于半径长的圆弧所对的圆心 角叫做1弧度的角．
记作1 rad
用弧度作为角的单位来度量角的单位制称为 弧度制 用弧度表示角的大小时，只要不引起误解， 可以省略单位，例如：
在数学里有很多以欧拉命名的公式和定理。在我们的数学课 本上常见的：sin,cos（三角函数符号）,f(x)（函数符号），以及 高二要用到的∑（求和符号），i(即－1的平方根）等都是他创立 并推广的。
今天我们要学习的弧度制雏形起源于印度，然而严格的弧度 概念却是由欧拉于1748年引入的。
《弧度制》【公开课教学PPT课件】
解析：|α|＝rl＝42＝2.
练__习_π3_2_．__若_，扇面形积的S圆＝心_角__π为6__6_0_°_．，半径为1，则扇形的弧长l＝ 解析：因为 α＝60°＝π3 ，r＝1，所以 l＝|α|·r＝π3 ， S＝12r·l＝12×1×π3 ＝π6 .
练习3.已知扇形的周长为8 cm，面积为4 cm2，求该扇形 的圆心角的弧度数.
1. 把角度换成弧度
2. 把弧度换成角度
3 6 0 0 2 ra d 180 rad
2 ra d 3 6 0
ra d 1 8 0
10 rad 0.01745rad
180
1rad 1800 57.300 57018'
例 1 把下列各角的度数化为弧度.
弧 度
0π
6
4
π 3
2
2π 3π 5 346
3π
2 2
1 rad
180
1rad (180)
1 rad
180
1rad (180)
1.把下列各角化成弧度. (1)120°(2)75°(3)300°(4)-210°（5）
. . . . 解：(1)2π 3
弧度的角．
B
AB的长=r 1 rad
O
r
A
弧度制：这种以弧度作为单位来度量角的单位 制叫做弧度制，它的单位是弧度，单位符号是
rad.
注：用弧度为单位表示角的大小时，“弧度”二字通常省略不写， 但用“度”（ °）为单位不能省。
理解概念
当弧AB的长度为2r、3r时， 正角∠AOB为多少弧度？ 一个圆弧所对的圆心角的弧度数是多少？半个圆弧 所对的圆心角的弧度数是多少？
练__习_π3_2_．__若_，扇面形积的S圆＝心_角__π为6__6_0_°_．，半径为1，则扇形的弧长l＝ 解析：因为 α＝60°＝π3 ，r＝1，所以 l＝|α|·r＝π3 ， S＝12r·l＝12×1×π3 ＝π6 .
练习3.已知扇形的周长为8 cm，面积为4 cm2，求该扇形 的圆心角的弧度数.
1. 把角度换成弧度
2. 把弧度换成角度
3 6 0 0 2 ra d 180 rad
2 ra d 3 6 0
ra d 1 8 0
10 rad 0.01745rad
180
1rad 1800 57.300 57018'
例 1 把下列各角的度数化为弧度.
弧 度
0π
6
4
π 3
2
2π 3π 5 346
3π
2 2
1 rad
180
1rad (180)
1 rad
180
1rad (180)
1.把下列各角化成弧度. (1)120°(2)75°(3)300°(4)-210°（5）
. . . . 解：(1)2π 3
弧度的角．
B
AB的长=r 1 rad
O
r
A
弧度制：这种以弧度作为单位来度量角的单位 制叫做弧度制，它的单位是弧度，单位符号是
rad.
注：用弧度为单位表示角的大小时，“弧度”二字通常省略不写， 但用“度”（ °）为单位不能省。
理解概念
当弧AB的长度为2r、3r时， 正角∠AOB为多少弧度？ 一个圆弧所对的圆心角的弧度数是多少？半个圆弧 所对的圆心角的弧度数是多少？
必修四112弧度制PPT课件
角的弧度数
实数集R
2、弧度与角度的换算
若l=2 π r，
则∠AOB=
l r
= 2π弧度
此角为周角 即为360°
360°= 2π 弧度
180°= π 弧度
l=2 π r O r A(B)
例题： （1）把 67 30化为弧度；
（2）把 3 化为角度；
5
(3)把下列特殊角化为弧度 数
度 00 3 0 0 4 5 0 6 0 0 9 0 0 1 2 0 0 1 3 5 0 1 5 0 0 1 8 0 0 2700 360 0
弧 度
0 6
43
2
2 3 5 3 2
346
2
四、例题讲解
例1（1）把67°30′化成弧度制。
（2）把 9 化成角度制。
4
解（1）∵67°30′=67.5°=
(135 )，
2
又∵1°= 180
∴67°30′=67.5
180
=
3 8
（2） 9 = 9 180°=405°
4
4
例2 用弧度制表示 （1）终边落在x轴上的角的集合 （2）终边落在y轴上的角的集合
{α| α=k·1800+900, k∈Z}
4.终边在第一象限上的角的集合为 {α| k·3600<α<k·3600+900, k∈Z}
5.已知α是第三象限的角，判断α/2是第几 象限的角
写出满足下列条件的角的集合. （1） 锐 角 （2） 0 到 90 的 角 （3） 第 一 象 限 的 角 （4） 小 于 90 的 角
②1弧度是等于半径长的圆弧所对的圆心角（或该弧）
的大小，而 1
是圆的 1
1.1.2 弧度制 课件(共29张PPT)
【名师点评】
表示角的集合，既可以用角度，也
可以用弧度，但必须要统一单位，不能既含有角度 又含有弧度，如在“α＋2kπ(k∈Z)”中，α必须是用 弧度制表示的角，在“α ＋ k· 360°， (k ∈ Z)”中， α
必须是用角度制表示的角．
跟踪训练 2．用弧度表示终边落在如图所示的阴影部分内 (不包括边界)的角的集合．
(2)特殊角的弧度数与度数对应值今后常用，应该熟记．
跟踪训练
1．将下列角转化为另一种度量形式表示． 3 (1)－ 18° ； (2) π； (3)－2 rad. 10
π π 解：(1)－18° ＝ ×(－ 18) rad＝－ rad. 180 10 3 3 180 (2) π＝ π·( )° ＝54° . 10 10 π 180 (3)－ 2 rad＝－2× ( )° ≈－57.30° × 2＝－114.60° . π
π 180 1° ＝ __________rad ≈ 0.017
2π
45 rad；
1
180 rad＝ (________)° ≈ 57.30° ＝ 57° 18′ . π
做一做 2.填表：
度
0° 30° 45° 60° 90° 120° 135° 150°
弧度
0
____ ____ ____ ____ ____ ____ ____
π 4 π 3 π 2 2π 3 3π 4 5π 6
π 答案： 6
3．扇形的弧长及面积公式
公式 度量制 角度制 弧度制 弧长公式 nπr l＝ 180 l＝ |α|· r 扇形面积公式 nπr2 S＝ 360 1 1 2 S＝ lr＝ |α|r 2 2
做一做
5π 3.半径为 2，圆心角为 的圆弧的长度为________， 3 扇形面积为________．
弧度制ppt完美版PPT
R210R(R5)225.1 01R10 当 R5时 ， 即 L10R5
2时 ， Sm ax25
练习1．化下列各角为度数或弧度：
1）－225°
2）
12
2．已知扇形OAB的圆心角为120°，
半径为6，求扇形弧长及所含弓形的面积。
思考：钟表分针和时针在3点到5点40分 这段时间里 分针转过_______弧度的角， 时针转过___弧度的角。
例2：设集A={x｜2kπ≤x≤2kπ+π,k∈Ζ},
B={x| X2 -36<0},求A∩B
解∵A={x|2kπ≤x≤2kπ+π,k∈Ζ}=┄∪{x｜
-2π≤x≤-π}∪ {x｜0≤x≤π} ∪{x｜
2π≤x≤2π+π}∪┄，
B={x｜-6≤x≤6}, ∴A∩B={x｜圆图的的中半阴径影弧为部1分所个角单的对位集长合应度。时的，圆圆心角心角称为1弧度的角，记为1rad
7下(节3)课(4直). 线与圆的(即位置在关系单中将位会重圆点表中达！,弧长为1的弧所对应的圆心角称为
1弧度的角) 方向可用“-”、“+”表示。
﹟ 1°周角的弧度数为2π； 2°正角的弧度数为正,负角的弧度数为负； 零角的弧度数为零。
假设时针转过3cm,那么时针转过的弧长 是
作业:_P_习__题_1_._(_1)_ 2.(1),(3) 4. 6. 7 (3) (4). 8.
小结：
角的度量形式(角度制,弧度制),弧度的单 位.弧度的意义,角度制与弧度制间的互 换.会用弧度研究有关问题(弧长,扇形面 积等)
小宝结：剑锋从磨砺出 本节课重点学习了圆的标准方程和一
思考：弧度数
与实数是一一 对应的
例3 1)扇形所在圆半径为5，圆心角 为135°，求扇形面积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
例4 利用计算器比较sin1.5和sin85的大小．
解：由计算器可得 sin1.5 0.9974
sin85 0.9961． sin1.5＞sin85．
1.设集合 M={α|α= kπ - π ，k∈Z}，N={α|－π＜α＜π} ，
25
则 M∩N=（ Ｃ ）
A．{－ π , 3π }
5 10
（1）l R;
(2)S= 1 R2;
证明:由公式 l 可得，l R.
r
(3)S= 1 lR. 2
由于半径为R,圆心角为n的扇形的弧长公式和面积公式分别是：
l n R , S n R2
180
360
将n转换为弧度，得 = n ,
180
于是，S= 1 R2.
2
将l R代入上式，即得S= 1 lR.
-2rad.
弧长l的所对的圆心角的大小 如果半径为r的圆的圆心角α所对的弧长为l，
那么，角α的弧度数的绝对值如何计算？
l
r
角度与弧度的换算
思考1：一个圆周角以度为单位度量是多少度？ 以弧度为单位度量是多少弧度？由此可
得
角度与18弧0度=有怎r样ad的换算关系？
180 = rad
思考2：根据上述关系，1°等于多少弧度？ 1rad等于多少度？
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
22
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
讲师：XXXXXX XX年XX月XX日
让学生测量在不同的圆中, 等于半径长的圆弧所对圆心
角，并观察所得到的结果有什么规律？
１．弧度的概念
我们把长度等于半径长的圆弧所对的圆心角 叫做1弧度的角，记作1rad，读作1弧度. 约定： 正角的弧度数为正数，
负角的弧度数为负数， 零角的弧度数为0.
如果将半径为r圆的一条半径OA，绕圆心 顺时针旋转到OB，若弧AB长为2r，那么∠AOB的 大小为多少弧度？
6 43 2 3 4 6
2
注意：用弧度制表示角时，“弧度”二字或“rad”通常
略去不写，而只写该角所对应的弧度数.如α=2表
示α是2rad的角.
弧度制下角的集合与实数集的一一对应：
正角
正实数
零角
零
负角
负实数
弧度制的应用
思考：已知一个扇形所在圆的半径为R，弧长为l，
圆心角为α，那么扇形的面积如何0计算？ 2 注意:弧长公式l r
（1） = 15°；（2）－ 7 = -157°
12
8
30′；
（3） 13 = 390°；
6
4.将下列角度转化为弧度：
．
（1）36°=
（rad）；（2）－105°=
5 5
7
12
（rad）；
（3）37°30′= 24 （rad）；
5.将分针拨快 10 分钟，则分针转过的弧度数是 3 ．
1．什么叫1弧度角? 2.“角度制”与“弧度制”的联系与区别； 3．弧长公式与扇形面积公式．
1.1.2 弧度制
1．了解弧度制的概念; 2．能进行弧度与角度的互化； 3．会推导弧度制下的弧长公式及扇形的面积公式.
演示： 分别以“米”和“尺”为单位,测量一根无
刻度的“尺子”. 结论：
(1)同一个量可用不同的度量制度来度量; (2)不同的结果之间存在换算关系.
弧度制 每个小组发一个硬纸做成的圆形图片，一段细铁丝，
1° rad 0.01745rad 180
1rad （180 ）° 57.30° 57° 18
练习：根据度与弧度的换算关系，下表中各特殊角对应的 弧度数分别是多少？
度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧
度0
2 3
5
3 2
B．{－ 7p , 4p }
10 5
C．{－ π , 3π ,- 7π , 4π }
5 10 10 5
D．{ 3π ,- 7π }
10 10
2.半径为 cm，中心角为 120o 的弧长为 （ Ｄ ）.
A． π cm
3
B． π2 cm
3
C． 2π cm
3
D． 2π2 cm
3
3.将下列弧度转化为角度：
2
67° 30= π rad 135 = 3 π rad
180
28
（2）利用计算器有
MODE MODE 2
67 。，,, 30 。，,, SHIFT DRG 1 =
1.178097245.因此，67°30′≈1.178 rad.
例2 将3.14rad换算成角度（用度数表示，精确到0.001).
例３．利用弧度制证明下列关于扇形的公式：
S 1 lR 1 R2 22
思考：在弧度制下，与角α终边相同的角如何表示？ 终边在坐标轴上的角如何表示？
2k，k Z
终边x轴上： =k，k Z
终边y轴上：
=
2
k，k
Z
例1 按照下列要求，把67°30′化成弧度： （1）精确值； （2）精确到0.001的近似值.
解 : (1)因为67° 30=( 135 )°，所以