河海大学2010级大禹材材料力学期末试卷.doc

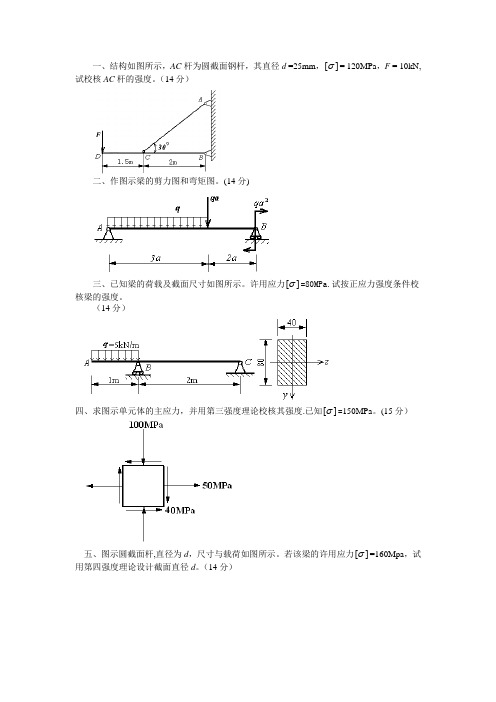
[σ= 120MPa，F = 10kN,一、结构如图所示，AC杆为圆截面钢杆，其直径d =25mm，]试校核AC杆的强度。

（14分）二、作图示梁的剪力图和弯矩图。

(14分)[σ=80MPa.试按正应力强度条件校三、已知梁的荷载及截面尺寸如图所示。

许用应力]核梁的强度。

（14分）[σ=150MPa。

(15分）四、求图示单元体的主应力，并用第三强度理论校核其强度.已知][σ=160Mpa，试五、图示圆截面杆,直径为d，尺寸与载荷如图所示。

若该梁的许用应力]用第四强度理论设计截面直径d。

（14分）六、外伸梁如图所示。

若q 、a 、EI 为已知，求B 截面挠度。

（15分）七、两端固定的实心圆截面杆承受轴向压力。

直径d =30mm ，杆长l =950mm,求该压杆的临界载荷cr F 。

弹性模量E =210Gpa ，材料的s λ=41。

6,P λ =123。

（a =310MPa,b =1。

2MPa ）(14分)一、已知实心圆轴直径d =40mm,轴所传递的功率为30kW ，轴的转速n ＝1400r ／min,材料的许用切应力][τ=40MPa ，切变模量G=80GPa ，许用扭转角]'[ϕ=2m /︒.试校核该轴的强度和刚度。

（14分）二、作图示梁的剪力图和弯矩图。

（14分)三、单元体如图所示。

试求⑴主应力数值;⑵最大切应力.（14分）四、结构如图所示.F = 20kN ，横梁AC 采用No 。

22a 工字钢,其截面面积2cm 128.42=A ，对中性轴的抗弯截面系数3cm 309=W ，材料的许用应力][σ=160Mpa,试校核该横梁强度。

(14分)五、图示刚架各杆的EI 皆相等,求C 截面的竖直位移.（15分）六、图示超静定刚架各杆的EI 皆相等，求C 处的约束反力。

（15分）七、一段固定、一端铰支的空心圆截面杆承受轴向压力。

外径D =52mm ，内径d =44mm ，杆长l =950mm ，求该压杆的临界载荷cr F .弹性模量E =210Gpa,材料的s λ=41.6，P λ =123。

一、一、填空题（每小题5分，共10分）1、如图，若弹簧在Q作用下的静位移st20=∆冲击时的最大动位移mmd60=∆为：3Q。

2、在其它条件相同的情况下，用内直径为d实心轴，若要使轴的刚度不变的外径D。

二、二、选择题（每小题5分，共10分）1、置有四种答案：(A)截面形心；（B）竖边中点A（C）横边中点B；（D）横截面的角点正确答案是：C2、足的条件有四种答案：（A）;zyII=（A）;zyII>（A）;zyII<（A）yzλλ=。

正确答案是： D 三、1、（15P=20KN,[]σ解：ABMn=ABmaxM=危险点在A2、图示矩形截面钢梁，A 端是固定铰支座，B 端为弹簧支承。

在该梁的中点C 处受到的重解：（1）求st δ、max st σ。

将重力P 按静载方式沿铅垂方向加在梁中心C 处，点C 的挠度为st δ、静应力为max st σ，惯性矩 )(12016.004.012433m bh I ⨯==由挠度公式)2(21483K PEI Pl st +=δ得， 83339310365.112)10(104010210488.040---⨯⨯⨯⨯⨯⨯⨯=st δmm m 1001.01032.25240213==⨯⨯⨯+mm m 1001.0==根据弯曲应力公式z st W M =maxσ得，其中4Pl M =， 62bh W z =代入max st σ得，MPa bhPlst 12401.004.068.0406422max =⨯⨯⨯⨯==σ（2）动荷因数K d12160211211=⨯++=++=K std hδ（3）梁内最大冲击应力M P a st d d 1441212max =⨯=K =σσ3、（10分）图中的1、2杆材料相同，均为园截面压杆，若使两杆在大柔度时的临界应力相等，试求两杆的直径之比d 1/d 2,以及临界力之比21)/()(cr cr P P 。

并指出哪根杆的稳定性较好。

大 连 理 工 大 学课 程 名 称：材料力学 试 卷： A一．选择题：（每小题3分，共15分） 1. 图示简支梁挠曲线大致形状为 A 。

2. 某梁横截面形状有四种，如图所示。

若外力作用线与图中虚线重合，则发生斜弯曲变形的梁为 D 。

3. 下列说法正确的是 C 。

A. 拉压杆内不存在切应力。

B. 拉压杆内各点的应力应变关系满足胡克定律。

姓名： 学号： 院系： 级 班题一、1图(B)(C)(A)(D)C. 杆件受压后体积会变小。

D. 滑移线是由切应力造成的。

4. 混凝土立柱所受压力的作用线与轴线平行但不重合，若力的作用点在截面核心区域内，则横截面上 B 。

A. 只存在拉应力。

B. 只存在压应力。

C. 既存在拉应力，又存在压应力。

D. 既存在正应力，又存在切应力。

5. 图示平面刚架分别受到集中力（图a ）和集中力偶（图b ）的作用，若F 与e M 数值上相等，则 D 。

A. b a B C θθ=b a B C w w =b a B C w 和θ数值相等 D. b a B C w θ和数值相等二、（15分）图示结构中杆AB 、CD 材料相同，横截面也相同，均为矩形截面，截面的高08=h mm ，宽03=b mm 。

材料的100P =λ，600=λ，206=E GPa ，304=a MPa ，12.1=b MPa ，若规定稳定安全因数3=w n ，试根据稳定条件求结构的许可荷载[q ]。

CD 杆为压杆 8.8003.0289.017.0=⨯⨯==ilμλ题一、5图F(a)(b)p 0λλλ<<为中长杆kN 7.51303.008.010)8.8012.1304()(6cr =⨯⨯⨯⨯-=-=A b a F λ171.2kN 37.513][cr cr ===w n F F取AB 杆为对象，列平衡方程∑=0A M ，075.0][5.11][cr =⨯-⨯q F ，kN/m 152][=q三、（15分）作图示外伸梁的剪力图和弯矩图，方法不限。

2010—2011材料力学试题及答案 A一、单选题（每小题2分，共10小题，20分）1、 工程构件要正常安全的工作，必须满足一定的条件。

下列除（ ）项，其他各项是必须满足的条件。

A 、强度条件B 、刚度条件C 、稳定性条件D 、硬度条件 2、内力和应力的关系是（ ）A 、内力大于应力B 、内力等于应力的代数和C 、内力是矢量，应力是标量D 、应力是分布内力的集度 3、根据圆轴扭转时的平面假设，可以认为圆轴扭转时横截面（ ）。

A 、形状尺寸不变，直径线仍为直线。

B 、形状尺寸改变，直径线仍为直线。

C 、形状尺寸不变，直径线不保持直线。

D 、形状尺寸改变，直径线不保持直线。

4、建立平面弯曲正应力公式zI My =σ,需要考虑的关系有（ ）。

A 、平衡关系,物理关系，变形几何关系；B 、变形几何关系，物理关系，静力关系；C 、变形几何关系，平衡关系，静力关系；D 、平衡关系, 物理关系，静力关系； 5、利用积分法求梁的变形，不需要用到下面那类条件（ ）来确定积分常数。

A 、平衡条件。

B 、边界条件。

C 、连续性条件。

D 、光滑性条件。

6、图示交变应力的循环特征r 、平均应力m σ、应力幅度a σ分别为（ ）。

A -10、20、10；B 30、10、20；C 31-、20、10； D 31-、10、20 。

7、一点的应力状态如下图所示，则其主应力1σ、2σ、3σ分别为（）。

A 30MPa、100 MPa、50 MPaB 50 MPa、30MPa、-50MPaC 50 MPa、0、-50Mpa、D -50 MPa、30MPa、50MPa8、对于突加载的情形，系统的动荷系数为（）。

A、2B、3C、4D、59、压杆临界力的大小，（）。

A 与压杆所承受的轴向压力大小有关；B 与压杆的柔度大小有关；C 与压杆材料无关；D 与压杆的柔度大小无关。

10、利用图乘法计算弹性梁或者刚架的位移，要求结构满足三个条件。

2011--2012学年第二学期材料力学期中试卷（文天学院土木、水工、港航和机械专业）班级_________姓名___________学号______________得分________一、基本题1、试在图中标出低碳钢的比例极限σp 、弹性极限σe 、屈服极限σs 、破坏极限σb 、延伸率δ和弹性模量E 。

(6分)2、试画出以下不同截面圆轴受扭矩M x 作用时的切应力分布图。

（6分）σp实心圆截面 空心圆截面 薄壁圆截面3、图示悬臂梁，图（a ）和（b ）是正方形截面的两种不同放置形式。

试比较两种情况的容许荷载F 的大小(材料的容许应力为[σ] )。

(6分)解：由[]z Fl W ≤σ， 得[][]3()/6za W a F llσσ≤=，[][]3()/zb W a F ll σσ≤=所以[][]()()a b F F =4、作图示梁的弯矩图，并根据梁的弯矩和支撑条件，画出挠曲线大致形状。

（7分）解：作弯矩图如图所示 由0,0,Mw ''==挠曲线为直线，由A 端的边界条件，AB 为水平线；<0,>0M w ''，挠曲线为上凸的曲线，C处的挠度为零：B 处挠度连续，C 处挠度和转角连续。

画出挠曲线如图所示M(a)z（b ）二、计算题1、图示结构，AB 杆为刚性杆，A 端铰接于墙壁上，B 端受力F 的作用，C 、D 处分别由同材料、同面积的1、2两杆支撑，设1、2两杆的弹性模量为E ，横截面面积为A 。

求1、2两杆的内力。

（15分）解：平衡位置如图所示，变形协调几何条件：2△1=△2 伸长——拉力，缩短——压力 力与变形之间的物理条件：1212,F l F l E AE A∆=∆=代入几何条件，得补充方程：2F 1=F 2最后由平衡条件：120,23A M F l F l F l ∑=⨯+⨯=⨯ 解得：1236,55F F F F ==2、图示圆轴,直径d =100mm 。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载河海大学材料力学习题册答案解析地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容学号姓名2-1 求下列结构中指定杆内的应力。

已知(a)图中杆的横截面面积A1=A2=1150mm2。

AECDB2-2 求下列各杆内的最大正应力。

（3）图(c)为变截面拉杆，上段AB的横截面积为40mm2，下段BC的横截面积为30mm2，杆材料的ρg=78kN/m3。

2-4 一直径为15mm，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm，直径缩小了0.022mm，确定材料的弹性模量E、泊松比ν。

2-6图示短柱，上段为钢制，长200mm，截面尺寸为100×100mm2；下段为铝制，长300mm，截面尺寸为200×200mm2。

当柱顶受F力作用时，柱子总长度减少了0.4mm，试求F值。

已知E钢=200GPa，E铝=70GPa。

2-7 图示等直杆AC，材料的容重为ρg，弹性模量为E，横截面积为A。

求直杆B截面的位移ΔB。

学号姓名2-8 图示结构中，AB可视为刚性杆，AD为钢杆，面积A1=500mm2，弹性模量E1=200GPa；CG为铜杆，面积A2=1500mm2，弹性模量E2=100GPa；BE为木杆，面积A3=3000mm2，弹性模量E3=10GPa。

当G点处作用有F=60kN时，求该点的竖直位移ΔG。

2-11 图示一挡水墙示意图，其中AB杆支承着挡水墙，各部分尺寸均已示于图中。

若AB杆为圆截面，材料为松木，其容许应力［σ］=11MPa，试求AB 杆所需的直径。

2-12 图示结构中的CD杆为刚性杆，AB杆为钢杆，直径d=30mm，容许应力［σ］=160MPa，弹性模量E=2.0×105MPa。

材料力学期末考试复习题及答案配高等教育出版社第五版一、填空题：1.受力后几何形状和尺寸均保持不变的物体称为。

2.构件抵抗的能力称为强度。

3.圆轴扭转时，横截面上各点的切应力与其到圆心的距离成比。

4.梁上作用着均布载荷，该段梁上的弯矩图为。

5.偏心压缩为的组合变形。

6.柔索的约束反力沿离开物体。

7.构件保持的能力称为稳定性。

8.力对轴之矩在情况下为零。

9.梁的中性层与横截面的交线称为。

10.图所示点的应力状态，其最大切应力是。

11.物体在外力作用下产生两种效应分别是。

12.外力解除后可消失的变形，称为。

13.力偶对任意点之矩都。

14.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则杆中最大正应力为。

15.梁上作用集中力处，其剪力图在该位置有。

16.光滑接触面约束的约束力沿指向物体。

17.外力解除后不能消失的变形，称为。

18.平面任意力系平衡方程的三矩式，只有满足三个矩心的条件时，才能成为力系平衡的充要条件。

19.图所示，梁最大拉应力的位置在点处。

20.图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是。

21.物体相对于地球处于静止或匀速直线运动状态，称为。

22.在截面突变的位置存在集中现象。

23.梁上作用集中力偶位置处，其弯矩图在该位置有。

24.图所示点的应力状态，已知材料的许用正应力[σ]，其第三强度理论的强度条件是。

25.临界应力的欧拉公式只适用于杆。

26.只受两个力作用而处于平衡状态的构件，称为。

27.作用力与反作用力的关系是。

28.平面任意力系向一点简化的结果的三种情形是。

29.阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则截面C的位移为。

30.若一段梁上作用着均布载荷，则这段梁上的剪力图为。

二、计算题：1.梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m，M=10kN·m，求A、B、C处的约束力。

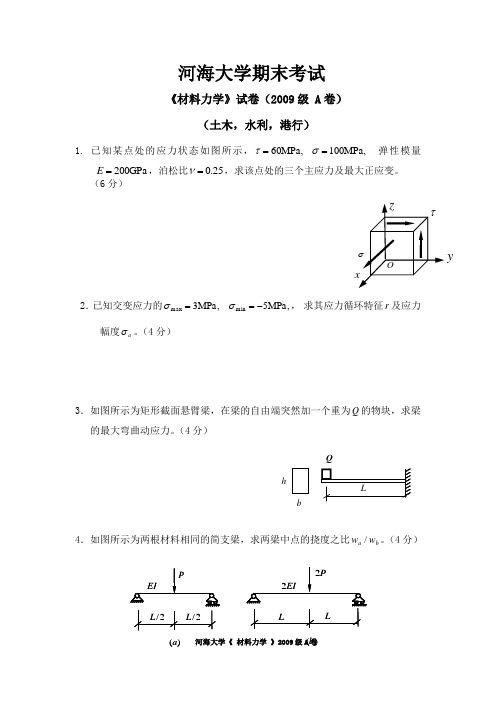
河海大学期末考试《材料力学》试卷（2009级 A 卷）（土木，水利，港行）1. 已知某点处的应力状态如图所示，,MPa 100,MPa 60==στ弹性模量GPa 200=E ，泊松比25.0=ν，求该点处的三个主应力及最大正应变。

（6分）2．已知交变应力的,MPa 5,MPa 3min max -==σσ， 求其应力循环特征r 及应力幅度a σ。

（4分）3．如图所示为矩形截面悬臂梁，在梁的自由端突然加一个重为Q 的物块，求梁的最大弯曲动应力。

（4分）4．如图所示为两根材料相同的简支梁，求两梁中点的挠度之比b a w w /。

（4分）yQhbL L2/L 2/L5．两块相同的钢板用5个铆钉连接如图所示，已知铆钉直径d，钢板厚度t，宽度b，求铆钉所受的最大切应力，并画出上钢板的轴力图。

（6分）6．超静定结构如图所示，所有杆件不计自重，AB为刚性杆，试写出变形协调方程。

（4分）7、铸铁梁的载荷及截面尺寸如图所示，其中4cm5.6012,mm5.157==ZCIy。

已知许用拉应力MPa40][=tσ，许用压应力MPa160][=Cσ。

试按正应力条件校核梁的强度。

若载荷不变，但将截面倒置，问是否合理？为什么？（14分）P200Pa a a2/AF8、圆截面直角弯杆ABC 放置于图示的水平位置，已知cm 50=L ，水平力kN 40=F ，铅垂均布载荷m /kN 28=q ，材料的许用应力MPa 160][=σ，试用第三强度理论设计杆的直径d 。

（14分）C9、 如图所示的结构中，各杆的重量不计，杆AB 可视为刚性杆。

已知cm 50,cm 100==b a ，杆CD 长m 2=L ，横截面为边长cm 5=h 的正方形，材料的弹性模量,GPa 200=E 比例极限MPa 200=P σ，稳定安全系数3=st n 。

求结构的许可外力][P 。

（12分）BP已知某点处的应力状态如图所示，,MPa 100,MPa 60==στ弹性模量GPa 200=E ，泊松比25.0=ν，求该点处的三个主应力及最大正应变。

***学院期末考试试卷一、填空题（总分20分，每题2分）1、杆件在外力作用下，其内部各部分间产生的 ，称为内力。

2、杆件在轴向拉压时强度条件的表达式是 。

3、低碳钢拉伸时，其应力与应变曲线的四个特征阶段为 阶段， 阶段， 阶段， 阶段。

4、线应变指的是 的改变，而切应变指的是 的改变。

5.梁截面上弯矩正负号规定，当截面上的弯矩使其所在的微段梁凹向下时为 。

6.梁必须满足强度和刚度条件。

在建筑中，起控制做用的一般是 条件。

7、第一和第二强度理论适用于 材料，第三和第四强度理论适用于 材料。

8、求解组合变形的基本方法是 。

9、力作用于杆端方式的不同，只会使与杆端距离在较小的范围内受到影响，该原理被称为 。

10、欧拉公式是用来计算拉（压）杆的 ，它只适用于 杆。

二、 单项选择(总分20分，每题2分)1、用截面法可求出图示轴向拉压杆a-a 截面的内力12N P P =-，下面说法正确的是（ ） A. N 其实是应力 B. N 是拉力C. N 是压力D. N 的作用线与杆件轴线重合2、构件的强度是指( )A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持原有平衡态的能力C. 在外力作用下构件抵抗破坏的能力D. 在外力作用下构件保持原有平稳态的能力 3、现有钢、铸铁两种杆材，其直径相同。

从承载能力与经济效益两个方面考虑，图示结构中两种合理选择方案是( )A. 1杆为钢，2杆为铸铁B. 1杆为铸铁，2杆为钢C. 2杆均为钢D. 2杆均为铸铁4、从拉压杆轴向伸长（缩短）量的计算公式EANll =∆可以看出，E 和A 值越大，l ∆越小，故（ ）。

A. E 为杆的抗拉（压）刚度。

B. 乘积EA 表示材料抵抗拉伸（压缩）变形的能力。

C. 乘积EA 为杆的抗拉（压）刚度D. 以上说法都不正确。

5、空心圆轴的外径为D ，内径为d ，α=d /D 。

其抗扭截面系数为（ ）。

A )1(163απ-=D W P B )1(1623απ-=D W PC )1(1633απ-=D W P D )1(1643απ-=D W P6、在没有荷载作用的一段梁上，（ ）A. 剪力图为一水平直线B.剪力图为一斜直线 C ．没有内力 D.内力不确定7、在平行移轴公式21Z Z I I a A =+中，其中Z 轴和轴1Z 轴互相平行，则（ ）。

三明学院《材料力学》期末考试卷10（考试时间：120分钟）使用班级： 学生数： 任课教师： 考试类型 闭卷一．填空题（每题3，共30分）1. 构件所受的外力可以是各式各样的，有时是很复杂的。

材料力学根据构件的典型受力情况及截面上的内力分量可分为 拉伸或压缩 、 剪切 、 扭转 、 弯曲 四种基本变形。

2. 现代工程中常用的固体材料种类繁多，物理力学性能各异。

所以，在研究受力后物体（构件）内部的力学响应时，除非有特别提示，一般将材料看成由 连续性 、 均匀性 、 各向同性 的介质组成。

3. 为保证工程结构或机械的正常工作，构件应满足三个要求，即 强度 、 刚度 、 稳定性 。

4. 为了求解静不定问题，必须研究构件的 变形 ，从而寻找出 变形协调方程 。

5. 矩形截面梁的弯曲剪力为FS ，横截面积为A ，则梁上的最大切应力为A F s=σ 。

6. 用主应力表示的广义胡克定律是()[]32111σσμσε+-=E ；()[]331211σσμσε+-=E ； ()[]21331σσμσε+-=E 。

7. 压杆稳定问题中，欧拉公式成立的条件是：）E（Pσπλλλ211:=≥其中 。

8. 轴向拉压变形中，横向应变与轴向应变的关系是 μεε=' 。

9. 图示外伸梁受均布载荷作用，欲使C B A M M M -==，则要求a l /的比值为22/=a l ；欲使0=C M ，则要求比值为2/=a l 。

10. 图示矩形截面纯弯梁受弯矩M 作用，梁发生弹性变形，横截面上图示阴影面积上承担的弯矩为 7M/8 。

二．选择题（每题3分，共15分）1．平面弯曲梁的横截面上，最大正应力出现在（ D ） A ．中性轴；B ．左边缘；C ．右边缘；D ．离中性轴最远处 。

2．第一强度理论适用于（ A ）A ．脆性材料；B ．塑性材料；C ．变形固体；D ．刚体。

3．在计算螺栓的挤压应力时，在公式bsbsbs A F =σ中，bsA 是（B ）A ．半圆柱面的面积；B ．过直径的纵截面的面积；C ．圆柱面的面积；D ．横截面积。

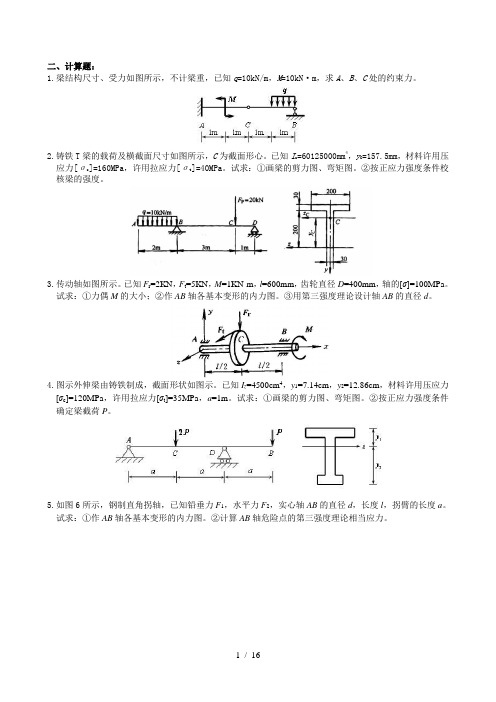
二、计算题：1.梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m，M=10kN·m，求A、B、C处的约束力。

2.铸铁T梁的载荷及横截面尺寸如图所示，C为截面形心。

已知I z=60125000mm4，y C=157.5mm，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa。

试求：①画梁的剪力图、弯矩图。

②按正应力强度条件校核梁的强度。

3.传动轴如图所示。

已知F r=2KN，F t=5KN，M=1KN·m，l=600mm，齿轮直径D=400mm，轴的[σ]=100MPa。

试求：①力偶M的大小；②作AB轴各基本变形的内力图。

③用第三强度理论设计轴AB的直径d。

4.图示外伸梁由铸铁制成，截面形状如图示。

已知I z=4500cm4，y1=7.14cm，y2=12.86cm，材料许用压应力[σc]=120MPa，许用拉应力[σt]=35MPa，a=1m。

试求：①画梁的剪力图、弯矩图。

②按正应力强度条件确定梁截荷P。

5.如图6所示，钢制直角拐轴，已知铅垂力F1，水平力F2，实心轴AB的直径d，长度l，拐臂的长度a。

试求：①作AB轴各基本变形的内力图。

②计算AB轴危险点的第三强度理论相当应力。

6.图所示结构，载荷P=50KkN，AB杆的直径d=40mm，长度l=1000mm，两端铰支。

已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数n st=2.0，[σ]=140MPa。

试校核AB杆是否安全。

7.铸铁梁如图5，单位为mm，已知I z=10180cm4，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa，试求：①画梁的剪力图、弯矩图。

②按正应力强度条件确定梁截荷P。

8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。

已知M=200GPa，μ=0.3，[σ]=140MPa。

材料力学一、填空题（每空4分，共40分）1．一长,横截面面积为A 的等截面直杆，其密度为ρ，弹性模量为E ，则杆自由悬挂时由自重引起的最大应力=m ax σ;杆的总伸长＝。

2．对图中铆钉进行强度计算时，,=bs σ。

3．矩形截面梁的F smax 、M max 及截面宽度不变，若将截面高度增加一倍，则最大弯曲正应力为原来的倍,最大弯曲切应力为原来的倍.4．图示两梁的材料相同,最小截面面积相同,在相同的冲击载荷作用下，图所示梁的最大正应力较大。

5．图示等截面梁AC 段的挠曲线方程为)2/(20EI x M w -=,则该段的转角方程为;截面B 的转角和挠度分别为和.二、选择题(每题4分共20分）1．矩形截面细长压杆,b/h = 1/2。

如果将b 改为 h 后仍为细长压杆，临界压力是原来的多少倍？（ ）（A)2倍；（B) 4倍；（C ） 8倍；（D ）16倍。

2． 图示应力状态，用第三强度理论校核时，其相当应力为：（ )（A ）τσ=3r ； （B ）τσ=3r ；（C ）τσ33=r ；（D ）τσ23=r 。

第2题图第3题图3．一空间折杆受力如图,则AB 杆的变形：（ ）(A) 纵横弯曲；（B ） 弯扭组合；（C ） 偏心拉伸； (D) 拉、弯、扭组合。

4．一内外直径之比D d /=α的空心圆轴，当两端受力偶矩作用产生扭转变形时，横截面的最大切应力为，则横截面的最小切应力：( ） （A) ； （B) ατ； （C) ()τα31-； （D) ()τα41-。

5．对于图示交变应力,它是：(A ）对称循环交变应力；（B)脉动循环交变应力；（C ）静循环交变应力。

( ）三、图示杆系结构中AB 杆为刚性杆，①、②杆刚度为 EA ，外加载荷为 P,求①、②杆的轴力。

（40分）σmtσminσmaxσo材料力学参考答案一、填空题1．g l ρσ=max ，El g 22ρ2．22d P π,dtP3．0．25，0．54．（a ）5．EI x M 0-,EI a M 0-，)tan()(2020EI aM a l EI a M ---二、选择题1．(B) 2．（D ） 3．(C ） 4．(B ） 5.(B)三、解:（1)静力平衡方程如图b 所示，F N1，F N2为①，②杆的内力；Fx 、F Y 为A 处的约束力,未知力个数为4，静力平衡方程个数为3(平面力系），故为一次超静定问题. 由0=∑A M 得Pa aF a F N N 3221=+即 P F F N N 3221=+ (a) （2分）（2）变形协调方程,或 (b)（2分）（3）物理方程 EA l F l N 11=∆, EA lF l N 22=∆ （c ）（2分）由（c)(d)得补充方程122N N F F = （d ） (2分）（4）由（a)和（d)式得P F N 531=，(拉力） （2。

考研专业课复习是考研备考中至关重要的一环，真题是必不可少的备考资料。

中公考研为大家整理了2010年河海大学813材料力学考研专业课真题及答案，供大家下载使用，并且提供东南大学考研专业课辅导，更多真题敬请关注中公考研网！《材料力学》2010年硕士研究生入学考试试题科目代码：____813______ 科目名称：___材料力学_____ 满分：__________ 注意：1，认真阅读答题纸上的注意事项；2，所以答案必须写在答题纸上，写在本试题纸或草稿纸上均无效；3，本试题纸须随答题纸一起装入试题袋中交回！1、作图示组合梁的剪力图和弯矩图，（图中F=q0a）（15分）2、T形外伸梁如图放置，受图示荷载，已知F=10kN，q=10kN/m，M e=10kN m ，容许拉应力[σt]=40MPa，容许压应力[σc]=90MPa，容许切应力[τ]=70MPa，校核梁的强度（h=170mm，t=30mm，b=200mm）（25分）。

3、超静定梁柱结构如图，已知材料均为钢材，弹性模量E=200GPa，AB梁为矩形截面，（h×b=120×60mm2），受均布荷载，q=12 kN/m；CD柱为圆截面，长为2米，不考虑稳定问题。

当A、B、C三处约束力相等时，求CD柱的直径d（25分）。

4、直径为D的实心圆截面杆，两端受外扭矩T和弯矩M作用，在杆表面A、B两点处沿图示方向测得εA=500×10-6，εB=450×10-6，已知W z=6000mm3，E=200GPa，泊松比ν=0.25，[σ]=100MPa，试求T和M，并按第四强度理论校核强度（25分）。

5、图示两杆均为d=40mm的圆截面杆，AC长为2米，BC长为1.5米，σp =160MPa，σs =240MPa，E=200GPa，求该结构失稳时的临界力F（25分）。

6、圆截面立柱，直径d=0.1m，高L=5m，E=200GPa，σp =200MPa，[σ]=80MPa，重物P=1.4 kN，从离柱顶H=0.2m处落下，求其动荷系数K d1；若开始时，重物具有初速度υ=2m/s，校核柱的安全（20分）。