13-8 热力学第二定律的统计解释 - 湖北大学
- 格式:ppt
- 大小:454.50 KB
- 文档页数:12


热力学第二定律的统计推导热力学第二定律是热力学中的重要定律,它告诉我们关于能量转化的方向性。
热力学第二定律的统计推导是通过统计力学的分子观点,从微观角度解释热力学定律的推论。
要理解热力学第二定律的统计推导,需要首先了解分子的运动行为。
根据统计力学的基本假设,分子是以一定的速度和方向运动的。
当一个物体被加热时,分子的热运动速度增加,它们会散布到更广泛的区域。
在一个封闭系统中,如果两个物体处于温度不同的状态,根据统计力学,分子会通过热传导从高温物体转移到低温物体。
这是因为高温物体的分子运动速度较快,碰撞频率较高,而低温物体的分子运动速度较慢,碰撞频率较低。
分子的碰撞会导致能量传递,从而实现热传导。
然而,根据热力学第二定律,自然界中热量不会自发地从低温物体传递到高温物体。
这样的过程是不可逆的。
为什么会出现这种不可逆性呢?统计推导告诉我们,不可逆性可以通过熵的概念进行解释。
熵是一个描述系统无序程度的物理量。
根据统计力学的分子观点,系统的熵与分子的排列方式有关。
更多的排列方式对应着更高的熵值。
假设有一个系统由高温物体和低温物体构成,初始状态下高温物体的熵较低,低温物体的熵较高。
如果可以实现热量自发地从低温物体传递到高温物体,系统的总熵会减小。
这会导致高温物体的熵增加,低温物体的熵减小。
由于熵的增加对应着无序程度的增加,这个过程是不可逆的。
根据热力学第二定律,自然界中热量传导的方向是从高温物体到低温物体,目的是实现整个系统的熵增加。
这样,高温物体的熵减小,低温物体的熵增加,系统的总熵增加。
除了热传导,热力学第二定律还有另外一个重要的推论:热量不可完全转化为功。
这是因为能量转化的过程中总会存在一定的损耗,导致无用能量的产生。
统计推导告诉我们,能量转化的损耗与分子碰撞的非弹性特性有关。
在能量转化的过程中,分子发生碰撞时会出现能量的损失,例如摩擦力引起的热量散失等。
这些非弹性碰撞会导致系统熵的增加,从而导致能量转化的不可逆性。

热力学第二定律热力学第二定律是热力学中一条重要的基本定律,它描述了能量在自然界中传递和转化的方向性。
本文将围绕热力学第二定律展开讨论,从基本原理、熵增定律和热机效率等方面进行深入解析。
一、热力学第二定律的基本原理热力学第二定律的基本原理可以通过几种不同的形式来表达,其中最常见的是开尔文计划和克劳修斯表述。
无论采用何种表述形式,热力学第二定律的核心思想都是能量在自然界中的传递必然是向着熵增的方向进行的。
二、熵增定律熵是热力学中的一个重要概念,可以用来描述系统的无序程度。
熵增定律可以概括为,在一个孤立系统中,熵总是趋于增加的。
这意味着在自然界中,所有的自发过程都是无法恢复的,而系统的状态会趋向于更加混乱。
三、热机效率热机效率是衡量热机性能的重要指标,它可以用来评估热量转化为有用功的能力。
根据卡诺定理,所有工作于同一温度源的热机中,效率最高的是卡诺热机,其效率与工作温度有关。
四、热力学第二定律的应用热力学第二定律在工程实践中有着广泛的应用。
例如,在能源领域,热力学第二定律可以告诉我们如何提高能源利用率,降低能源损耗。
此外,热力学第二定律也与生态系统的可持续发展密切相关,能够引导我们在资源利用和环境保护方面做出更加科学的决策。
五、热力学第二定律的发展与挑战虽然热力学第二定律已经在科学界得到广泛认可,并在实践中得到了应用,但仍然存在一些概念和理论上的挑战。
例如,热力学第二定律的微观基础仍不十分明确,人们仍在探索更加深入的机制解释。
此外,与量子力学和相对论等领域的结合也是一个重要的研究方向。
结语热力学第二定律是热力学的基石,对于能量传递和转化过程的理解具有重要意义。
通过对热力学第二定律的研究和应用,我们可以更好地理解自然界中的各种现象,并为能源利用和环境保护等问题提供科学的解决方案。
尽管热力学第二定律仍然存在一些挑战,但随着科学技术的进步,我们相信对于这一定律的认识将会不断深化和完善。


热力学第二定律热力学第二定律是热力学领域中的核心概念之一,它揭示了热能转化的方向性和不可逆性。
本文将详细介绍热力学第二定律的基本原理和重要性,并讨论它在自然界和工程应用中的实际应用。
热力学第二定律的基本原理建立在热力学第一定律的基础之上。
热力学第一定律表明能量守恒,即能量不会自发地消失或产生。
然而,热力学第一定律没有告诉我们在能量转化过程中是否存在某种特定的方向性。
热力学第二定律填补了这一缺漏,它规定了热能传递的方向性和不可逆性。
热力学第二定律有几种不同的表述方式,最常见的是“热量不能自发地从低温物体传递到高温物体”。
这是因为自然界中,热量会自发流向温度较低的物体,而不会自发流向温度更高的物体。
这个过程被称为热能的自发转移,它是不可逆的。
热力学第二定律还可以用熵的增加来表述。
熵是描述系统无序程度的物理量,也可以理解为系统的混乱程度。
根据热力学第二定律,一个孤立系统的熵不会自发减少,而只会增加或保持不变。
这意味着熵增加是一个不可逆的过程,也可以理解为系统朝着更加混乱的状态演化。
热力学第二定律的重要性在于揭示了热能转化的限制性质。
它告诉我们在自然界中存在着一种不可逆的趋势,使得热能总是从高温物体传递到低温物体,而不会反向发生。
这个不可逆性限制了人类在能源利用和热工过程中的效率。
在自然界中,热力学第二定律产生了很多重要的现象和现象,如热传导、热辐射和热机的工作原理。
这些现象都是基于热力学第二定律的限制性质进行解释的。
在工程应用中,热力学第二定律也具有广泛的应用价值。
例如,在能源利用和能源转换中,我们必须充分考虑热力学第二定律的限制性质,以提高能源利用效率。
在热力学循环和热能转换装置的设计中,热力学第二定律也是一个重要的指导原则。
此外,热力学第二定律对环境保护也具有重要意义。
根据热力学第二定律,所有放热的过程都会产生废热,这会对环境造成负面影响。
因此,在工业生产和能源利用过程中,我们需要采取措施来最大限度地减少废热排放,以保护环境和提高能源利用效率。


热力学第二定律的统计意义
热力学第二定律是热力学中的一个基本定律,它描述了热能的转化过程中存在的不可逆性。
热力学第二定律的统计意义是将宏观不可逆过程与微观粒子运动的随机性联系起来,从而解释热力学第二定律的基本原理。
在热力学中,熵是一个重要的概念,它描述了系统中的混乱程度。
热力学第二定律可以被表述为熵在任何一个孤立系统中总是增加的原则。
这个原则可以通过微观粒子的随机热运动来解释。
在一个系统中,随着时间的推移,分子的位置和速度会随机变化,使得系统的状态逐渐变得更为混乱。
因此,熵增加代表着系统的混乱程度增加,也就是更接近于平均状态。
此外,热力学第二定律还可以通过热力学概率来解释。
热力学概率是指一个系统处于某个状态的概率。
根据热力学第二定律,处于高熵(即更为混乱)状态的概率更大,因为这样的状态更接近于平均状态。
这也反映了分子热运动的随机性,即处于高熵状态的概率更大,因为更多的状态都是高熵状态。
总之,热力学第二定律的统计意义是将宏观的不可逆过程与微观粒子的随机性联系起来,从而解释热力学第二定律的基本原理。
这个原理可以通过系统中的熵增加、分子热运动的随机性以及热力学概率等方面来进行解释。



高二物理必修一知识点:热力学第二定律的统计意义高中最重要的阶段,大家一定要掌握好高中,多做题,多练习,为高考奋战,小编为大家整理了14高二物理必修一知识点,希望对大家有协助。
热现象是与少量分子无规那么热运动相联络的。
我们以上述不可逆进程(如例1中理想气体的真空自在收缩)为例,来复杂说明热力学第二定律的统计意义。
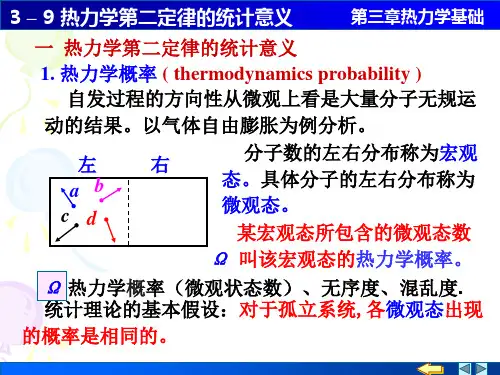
如图1所示,拉开隔板后,A局部的理想气体将进入B(原为真空)中,从而充溢A、B整个空间。
这个进程是不可逆的,我们从没有见过这种现象:气体自动地由整个容器收缩到A 局部,而使B局部红为真空。
这是为什么呢?
设容器中有1个分子,它退回到A局部的几率为1/2;设容器中有2个分子,它们全部退回到A局部的几率为1/22=1/4;设容器中有3个分子,它们全部退回A局部的几率为
1/23=1/8;设容器中有1mol某种理想气体(约6.021023个分子)。
打一个有
趣的比喻:假假定从植物园中逃出一只黑猩猩,溜进了计算机室,用爪子在键盘上乱按。
而将打印出的纸张按顺序装订,恰巧是一部数百万字的巨著大英百科全书。
上述几率比这个笑话的几率还要小得不可比拟。
经过对上述复杂例子的剖析,理想上是有普通意义的,即热力学第二定律的统计意义是:一个不受外界影响的孤立系
统,其外部发作的进程,总是由几率小的形状向几率大的形状停止,由包括微观形状数目少的微观形状向包括微观形状数目多的微观形状停止。
查字典物理网小编为大家整理了14高二物理必修一知识点,希望对大家有所协助。
热力学第二定律的推导与应用热力学第二定律是热力学中的一个重要定律,它描述了热量在能量传递过程中的方向性和不可逆性。
本文将对热力学第二定律进行推导,并探讨其在实际应用中的意义和重要性。
一、热力学第二定律的基本概念热力学第二定律在19世纪中叶由卡诺和开尔文等科学家总结出来,其核心概念是热量自然向高温流动的趋势。
该定律可以通过以下几个方面来描述:1.热量不会自动从低温物体传递到高温物体;2.热量会自然地从高温物体传递到低温物体;3.不论热量如何传递,总有一部分能量转化为不可利用的形式,即熵增。
二、热力学第二定律的数学推导热力学第二定律可以通过熵的概念和热力学过程来进行数学推导。
在此我们以卡诺循环为例来阐述。
卡诺循环是一个理想的热机循环,在这个循环过程中,系统从高温热源吸热,向低温热源放热,然后通过准静态过程将其恢复为初始状态。
在卡诺循环中,热机的效率可以表示为:η = (Q_h - Q_l) / Q_h,其中,η表示热机的效率,Q_h表示吸收的热量,Q_l表示放出的热量。
根据热力学第一定律,系统内的能量守恒,即Q_h = Q_l + W,其中W表示对外做功。
将等式代入热机效率的表达式中,可得:η = (Q_h - Q_l) / Q_h = (Q_h - (Q_h - W)) / Q_h,整理可得:η = W / Q_h.由于卡诺循环是一个理想循环,热机的效率是最高的,因此可以得到以下结论:η_卡诺≥ η_任意。
这个结论即为卡诺定理,它是热力学第二定律的数学表达。
三、热力学第二定律的应用热力学第二定律在能源利用和环境保护等方面具有重要的应用价值。
以下是几个应用领域的例子:1.能源利用:根据热力学第二定律,热机的效率受到温度差的限制,即将热量转化为有用的功的效率存在上限。
在实际应用中,我们需要设计和改进热机系统,以提高能源的利用效率,降低能源的浪费。
2.热力学循环:热力学第二定律可以指导热力学循环的设计和优化,包括汽车发动机、蒸汽涡轮和核能发电等系统。
热力学第二定律热力学第二定律是热力学的基本原理之一,它描述了单一热源和工作物体之间能量转换的方向以及转换过程中不可逆性的规律。
本文将深入探讨热力学第二定律的概念、表述方式以及其在实际应用中的作用。
1. 热力学第二定律概述热力学第二定律是热力学中关于热能转换方向的基本原则。
它可以用不同的表述方式来描述,包括:- 克劳修斯表述:不可能将热量从低温物体传递给高温物体而不产生其他变化。
- 开尔文表述:不可能通过循环过程将热量从单一热源完全转化为有用的功,并不产生其他影响。
- 朗缪尔表述:熵在任何一个孤立系统中总是增加的。
2. 热力学第二定律的理解与应用热力学第二定律揭示了自然界中不可逆过程的普遍性,例如热量从高温物体传递到低温物体。
我们可以通过以下几个方面来理解和应用热力学第二定律:2.1 卡诺循环卡诺循环是一种理想热机循环过程,在此过程中,工作物体从两个热源之间吸收热量,产生功,并将剩余的热量传递给低温热源。
热力学第二定律揭示了卡诺循环的最高效率,即卡诺效率,该效率仅取决于两个热源之间的温度差异。
2.2 熵的概念熵是描述系统无序程度的物理量,也是热力学第二定律的核心概念之一。
根据熵增定律,任何一个孤立系统的熵都趋向于增加,而热力学第二定律将这种趋势与不可逆过程联系起来。
2.3 热力学第二定律应用举例热力学第二定律的应用不仅限于理论研究,还具有广泛的实际应用价值。
例如:- 制冷与空调技术:制冷循环原理是基于热力学第二定律的,通过热泵将热量从低温环境吸收然后排放到高温环境以实现制冷效果。
- 热电耦合发电:热电耦合发电技术将热能转化为电能,其中热力学第二定律约束了热电转换的效率。
- 生物热力学:热力学第二定律帮助解释了生物体内部的能量传递与代谢过程,揭示了生物体内能量转化的方向性。
3. 热力学第二定律的发展与争议热力学第二定律的发展经历了长期的探索与争议。
早期科学家对于热力学第二定律的理解存在分歧,例如理论热力学与统计热力学的出现为热力学第二定律提供了不同的解释。
热力学第二定律(英文:seco nd law of thermody namics )是热力学的四条基本定律之一,表述热力学过程的不可逆性一一孤立系统自发地朝着热力学平衡方向最大熵状态演化,同样地,第二类永动机永不可能实现。
这一定律的历史可追溯至尼古拉•卡诺对于热机效率的研究,及其于1824年提出的卡诺定理。
定律有许多种表述,其中最具代表性的是克劳修斯表述(1850 年)和开尔文表述(1851年),这些表述都可被证明是等价的。
定律的数学表述主要借助鲁道夫•克劳修斯所引入的熵的概念,具体表述为克劳修斯定理。
虽然这一定律在热力学范畴内是一条经验定律,无法得到解释,但随着统计力学的发展,这一定律得到了解释。
这一定律本身及所引入的熵的概念对于物理学及其他科学领域有深远意义。
定律本身可作为过程不可逆性旦:P.262及时间流向的判据。
而路德维希•玻尔兹曼对于熵的微观解释一一系统微观粒子无序程度的量度,更使这概念被引用到物理学之外诸多领域,如信息论及生态学等克劳修斯表述克劳修斯克劳修斯表述是以热量传递的不可逆性(即热量总是自发地从高温热源流向低温热源)作为出发点。
虽然可以借助制冷机使热量从低温热源流向高温热源,但这过程是借助外界对制冷机做功实现的,即这过程除了有热量的传递,还有功转化为热的其他影响。
1850年克劳修斯将这一规律总结为: 不可能把热量从低温物体传递到高温物体而不产生其他影响开尔文表述参见:永动机#第二类永动机开尔文勋爵开尔文表述是以第二类永动机不可能实现这一规律作为出发点。
第二类永动机是指可以将从单一热源吸热全部转化为功,但大量事实证明这个过程是不可能实现的。
功能够自发地、无条件地全部转化为热;但热转化为功是有条件的,而且转化效率有所限制。
也就是说功自发转化为热这一过程只能单向进行而不可逆。
1851年开尔文勋爵把这一普遍规律总结为:不可能从单一热源吸收能量,使之完全变为有用功而不产生其他影响两种表述的等价性上述两种表述可以论证是等价的:1.如果开尔文表述不真,那么克劳修斯表述不真:假设存在违反开尔文表述的热机A,可以从低温热源匚吸收热量’”并将其全部转化为有用功:…。