热力学第二定律的经典表述

第三章热力学第二定律热力学第一定律过程的能量守恒热力学第二定律过程的方向和限度§3.1 热力学第二定律（1）过程的方向和限度自发过程：体系在没有外力作用下自动发生的变化过程，其有方向和限度。

例如：水位差、温度差、压力差等引起的变化过程。

自发过程，有做功能力方向：始态终态反自发过程，需消耗外力平衡状态限度：始态终态无做功能力自发过程的共同特征：不可逆性（2）热力学第二定律的表达式经典表述：人们不能制造一种机器（第二类永动机），这种机器能循环不断地工作，它仅仅从单一热源吸取热量均变为功，而没有任何其它变化。

一般表述：第二类永动机不能实现。

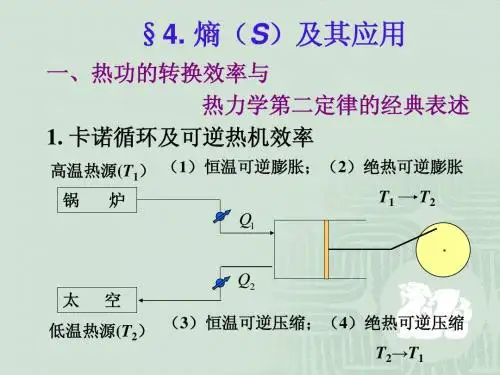
§3.2 卡诺循环1824年，法国工程师卡诺（Carnot）使一个理想热机在两个热源之间，通过一个特殊的可逆循环完成了热→功转换，给出了热机效率表达式。

这个循环称卡诺循环。

（1）卡诺循环过程设热源温度T1 > T2，工作物质为理想气体。

卡诺循环1. 恒温可逆膨胀（A → B ）：0U 1=∆ 12111V V lnnRT W Q == 2. 绝热可逆膨胀（B → C ）：0q =， )T T (nC U W 21V 22-=∆-=3. 恒温可逆压缩（C → D ）：0U 3=∆， 342322V V lnnRT W q Q ==-= 4. 绝热可逆压缩（D → A ）：0q =， )T T (nC U W 12V 44-=∆-=整个循环过程的总功为：34212112V 34221V 1214321V Vln nRT V V lnnRT )T T (nC V Vln nRT )T T (nC V V ln nRT W W W W W +=-++-+=+++= 热机循环一周有：0U =∆， W q Q Q Q Q 2121=-=+=热机效率：1213421211V V ln nRT V Vln nRT V V lnnRT Q W+==η对于绝热可逆膨胀：k12312V V T T -⎪⎪⎭⎫ ⎝⎛=对于绝热可逆压缩： k14121V V T T-⎪⎪⎭⎫ ⎝⎛=比较得：1423V V V V =或 4312V V V V = 则： 121121Q Q Q T T T +=-=η η— 卡诺热机效率（2） 卡诺定理卡诺定理：一切工作于高温热源T 1与低温热源T 2之间的热机效率，以可逆热机的效率为最大。

1.热力学第二定律的克劳修斯表述：不可能把热量由低温物体传到高温物体而不引起其他变化。

开尔文表述：不可能从单一热源吸收热量使之完全变成有用功而不引起其它变化。

2.准静态过程：热力学过程中任何一个中间过程都在无限接近平衡状态的过程。

3.可逆过程：某一系统在某一过程由状态1变为状态2后如果能使系统和环境都完全复原，同时消除原过程对环境产生的一切影响。

4.特性函数：如果选择适当的变量。

只要知道单个热力学函数就可以通过求偏导数而求得均匀系统的全部热力学函数从而把系统的平衡性质完全确定。

5.熵增加原理：系统经可逆绝热过程熵不变，经不可逆绝热过程熵增加。

在绝热过程中，熵减小是不可能实现的、6.等概率原理：对于处在平衡态的孤立系统，系统可能的微观状态数出现的概率相等。

7.粒子全同性原理：全同粒子是不可分辨的，在含有许多全同粒子的系统中，将任何两个相同粒子加以对换，不改变整个系统圆微观状态。

8.能量均分定理：对于处在温度为T的平衡态的经典系统，粒子能量中每个平方相的平均值等于kT/29.玻色-爱因斯坦凝聚：无相互作用的玻色子在足够低的温度下，将发生相变，即全部玻色子会分布在相同的最低能级上。

当玻色系统的温度低于某特定温度T时，粒子向零能级e0聚集的现象，称为玻色爱因斯坦凝聚，T称为凝聚温度。

10.热力学第零定律：如果两个热力学系统中的每一个都与第三个热力学系统处于平衡状态，则他们彼此也必定处于热平衡。

对：无摩擦的准静态过程有一个重要的性质，即在准静态过程中对系统对的作用力，可以用描写系统平衡状态的参量表达出来。

在p-v图上，绝热线比等温线陡些，因为r=Cp/Cv >1绝热过程方程对准静态过程和非准静态过程都适用。

在等温等容过程中，若系统只有体积变化功，则系统的自由能永不增加。

当孤立系统达到平衡态时，其熵必定达到极大值。

固相，液相，气相之间发生一级相变时，有相变潜热产生，有比容突变。

粒子和波动二相性的一个重要结果是微观粒子不可能同时具有确定的动量和坐标。

解读“热力学第二定律”江苏省如东高级中学（226400）刘永华热力学第二定律是热力学的主要理论基础之一，许多学生在对热力学第二定律的理解上存在着一些似是而非的认识。

在课堂教学中，教师可从如下三个层面来帮助学生准确理解热力学第二定律。

一两种经典表述1 按照热传导的方向性来表述(克劳修斯表述)克劳修斯在对许多自然界中的现象观察时发现，热量的传递有一种规律性，这就是：热量不能自发地从低温物体传向高温物体。

于是在1850年将热力学第二定律表述为：不可能使热量从低温物体传向高温物体，而不引起其他变化。

理解时特别注意，这里所谓“自发地”或“不引起其他变化”，指的是没有任何外界的帮助或影响。

可见，在表述中特别强调了不需要任何外界的帮助，如果引起了其他变化，热量是可以从低温物体传向高温物体的。

例如，电冰箱在外界对其做功的情况下(耗电)，显然能够不断地把热量由低温物体(电冰箱内部)传向高温物体(电冰箱外部)的；而一旦切断电源，电冰箱就不能把其内部的热量传给外界的空气，相反外界的热量却会自发地传给冰箱，使其内部温度逐渐升高。

2 按照机械能与内能转化过程的方向性来表述(开尔文表述)课本中是以内燃机为例，来阐述热机必须有热源和冷凝器，没有冷凝器的热机，即“理想热机——第二类永动机”是不可能制成的。

对这段内容可这样理解：设气缸中气体得到燃料燃烧时产生的热量为Q1，推动活塞做的功为W，然后排出废气，同时将Q2的热量散发到大气中。

由能量守恒可得Q1=W+Q2，热机的效率η=W/Q1，要想使η=100%，就必须使Q2=0，即要求工作物质在一个循环过程中，把从高温热源吸收的热量Q1，全部变为有用的机械功W，而工作物质本身又回到初始状态，并不放出任何能量到低温热源中去。

这种“理想热机”并没有违背热力学第一定律。

然而尝试提高热机效率的大量实践表明，在任何情况下，热机都不可能只有一个热源，热机要不断地把吸收到的热量变为有用功，就不可避免地要把热量传给外界的低温热源，所以热机必须有热源和冷凝器，没有冷凝器的热机是不存在的，热机的效率也必然小于100%。

热力学第二定律（英文：second law of thermodynamics）是热力学的四条基本定律之一，表述热力学过程的不可逆性——孤立系统自发地朝着热力学平衡方向──最大熵状态──演化，同样地，第二类永动机永不可能实现。

这一定律的历史可追溯至尼古拉·卡诺对于热机效率的研究，及其于1824年提出的卡诺定理。

定律有许多种表述，其中最具代表性的是克劳修斯表述（1850年）和开尔文表述（1851年），这些表述都可被证明是等价的。

定律的数学表述主要借助鲁道夫·克劳修斯所引入的熵的概念，具体表述为克劳修斯定理。

虽然这一定律在热力学范畴内是一条经验定律，无法得到解释，但随着统计力学的发展，这一定律得到了解释。

这一定律本身及所引入的熵的概念对于物理学及其他科学领域有深远意义。

定律本身可作为过程不可逆性[2]:p.262及时间流向的判据。

而路德维希·玻尔兹曼对于熵的微观解释——系统微观粒子无序程度的量度，更使这概念被引用到物理学之外诸多领域，如信息论及生态学等克劳修斯表述克劳修斯克劳修斯表述是以热量传递的不可逆性（即热量总是自发地从高温热源流向低温热源）作为出发点。

虽然可以借助制冷机使热量从低温热源流向高温热源，但这过程是借助外界对制冷机做功实现的，即这过程除了有热量的传递，还有功转化为热的其他影响。

1850年克劳修斯将这一规律总结为：不可能把热量从低温物体传递到高温物体而不产生其他影响。

开尔文表述参见：永动机#第二类永动机开尔文勋爵开尔文表述是以第二类永动机不可能实现这一规律作为出发点。

第二类永动机是指可以将从单一热源吸热全部转化为功，但大量事实证明这个过程是不可能实现的。

功能够自发地、无条件地全部转化为热；但热转化为功是有条件的，而且转化效率有所限制。

也就是说功自发转化为热这一过程只能单向进行而不可逆。

1851年开尔文勋爵把这一普遍规律总结为：不可能从单一热源吸收能量，使之完全变为有用功而不产生其他影响。

热力学第二定律1 概论1.1 热力学第二定律的经典表述热力学第一定律是关于能量在传递和转换过程中的守恒定律，确定了体系有一个状态函数内能的存在。

热力学第二定律是关于热功转换的效率和方向性问题的定律，确定了状态函数熵的存在，进而用于解决过程方向性问题。

19世纪初，蒸汽机的使用对工业革命起着十分重要的影响。

但还缺乏相应的理论。

人们需要解决一些与蒸汽机技术密切相关的理论问题，如热机效率的极限是否存在？功热转换效率问题？能否从单一热源取热将其全部转化为功？1824年，Carnot对热机的理论研究提出了著名的Carnot定律。

“所有工作于两个不同温度的热源之间的热机，以可逆热机的效率为最大”。

Carnot定律的结论是正确的，但要证明这条定律，需要引入一个新的原理。

1850年Clausius和1851年Kelvin依据当时刚刚建立的能量守恒原理分别重新考察了Carnot定律，提出了热力学第二定律的经典表述。

Clausius的表述为：不可能以热的形式将低温物体的能量传递到高温而不引起其它变化。

Kelvin 的表述为：不可能以热的形式将单一热源的能量转变为功，而不发生其它变化。

Kelvin的说法断定了热与功的转换不是完全等价的，功可以无条件的100%转化为热，但热不能无条件的100%转化为功。

Kelvin的说法后来被Ostward表述为：第二种永动机是不可能造成的。

所谓第二种永动机是一种从单一热源吸热，并将所吸热完全变为功，而不产生其它变化的机器。

热功交换问题的讨论最初仅局限于热机效率。

但客观世界是彼此联系，相互渗透的。

人们思考这样一个问题：功热交换和热量传递的方向性，仅仅是自然界的一个具体事例。

自然界存在许许多多的具有方向性变化的事例。

这些方向性变化是否存在一种联系？或者说它们的共性是否隐含一条基本的自然规律？这是对功热交换方向性的更深层次的思考。

1.2 自然过程方向性及限度的事例过程的方向性是指：过程进行终了后，若使体系和环境再回至原状，那么体系和环境所产生的后果不能自动消除。