第六讲立体的投影
- 格式:doc
- 大小:319.00 KB
- 文档页数:6

初中数学知识归纳立体形的投影和表面积初中数学知识归纳:立体形的投影和表面积在初中数学中,我们学习了许多有关几何形状的知识,其中包括立体形的投影和表面积计算。
掌握这些知识对于解决与空间有关的问题至关重要。
本文将对立体形的投影和表面积进行归纳总结,方便大家理解和记忆。
一、投影1. 平行投影平行投影是指在平行于某一方向的平面上,将一个立体形所出现的投影。
平行投影的结果是立体形在该平面上的一个简化形状。
当我们面对一个立方体或长方体时,我们可以明显地看到其平行投影是一个相同形状的图形。
2. 正交投影正交投影是指在垂直于某一方向的平面上,将一个立体形所出现的投影。
正交投影的结果是立体形在该平面上的一个简化形状。
常见的正交投影有正视图、俯视图和侧视图。
通过这三个视图,我们可以全面地了解立体形的形状和尺寸。
二、表面积1. 立方体的表面积立方体是指六个面都是正方形的立体形状。
计算立方体的表面积可以通过以下公式得出:表面积 = 6 × a²,其中a代表正方形的边长。
2. 长方体的表面积长方体是指六个面中,有两个面是正方形,其余四个面是矩形的立体形状。
计算长方体的表面积可以通过以下公式得出:表面积 = 2 ×(lw + lh + wh),其中l、w、h分别代表长方体的长、宽和高。
3. 圆柱体的表面积圆柱体是指由一个圆和与其平行的两个相交圆周上两个点之间的曲线围成的面积与两个相交圆周所夹部分的面积共同构成的立体形状。
计算圆柱体的表面积可以通过以下公式得出:表面积= 2πr² + 2πrh,其中r代表圆柱体的底面半径,h代表圆柱体的高。
4. 圆锥体的表面积圆锥体是指由一个圆和通过圆上各点并交于一点的一系列射线围成的面积与这些射线所围空间共同构成的立体形状。
计算圆锥体的表面积可以通过以下公式得出:表面积= πr² + πrl,其中r代表圆锥体的底面半径,l代表圆锥体的斜高。





数学知识点归纳立体形的投影与视数学知识点归纳——立体形的投影与视在空间几何中,立体形是三维物体的统称,它可以通过投影与视的方式来呈现在二维平面上。
本文将对立体形的投影与视这一数学知识点进行归纳与探讨。
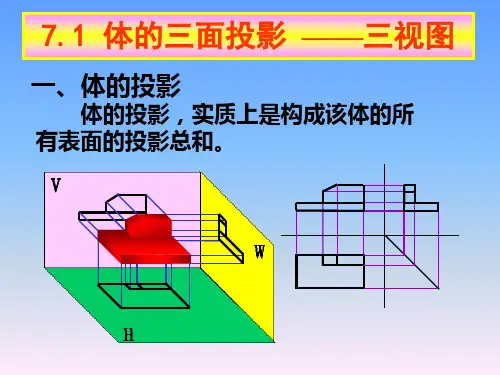
1、立体形的投影立体形的投影是指将三维物体在某个方向上的投射到二维平面上形成的图像。
投影的方式有平行投影和透视投影两种。
1.1 平行投影平行投影是指沿着平行于某个方向的光线,将立体形的各个顶点投影到一个平行于该方向的平面上。
它主要包括正交投影和斜投影两种形式。
1.1.1 正交投影正交投影是指光线与投影面成直角,投影的结果是各个边在投影面上的长度等于在立体形上的长度。
常见的正交投影有平行线投影和垂直投影。
1.1.2 斜投影斜投影是指光线与投影面不成直角,投影的结果会造成边在投影面上的长度与在立体形上的长度不一致的情况。
斜投影可以通过旋转、倾斜等方式来实现。
1.2 透视投影透视投影是指从视点出发,通过透视原理将立体形的各个顶点投影到视平面上形成的图像。
透视投影呈现出的图像更符合我们在现实世界中的视觉感受,在绘画、建筑等领域中得到广泛应用。
2、立体形的视立体形的视是指我们观察三维物体时,从不同的方位和角度所产生的视觉效果。
在数学中,常用的视包括俯视和仰视。
2.1 俯视俯视是指我们从物体上方往下看的视角。
在俯视下,上部分的面积变小,下部分的面积变大,物体的高度相对较小。
这种视角常用于描述建筑物的平面布局、地图等。
2.2 仰视仰视是指我们从物体下方往上看的视角。
在仰视下,上部分的面积变大,下部分的面积变小,物体的高度相对较大。
这种视角常用于描述建筑物的立面图、人物的立绘等。
3、应用举例立体形的投影与视在现实生活中应用广泛,以下举几个例子来说明:3.1 建筑设计在建筑设计中,通过对建筑物的投影与视进行分析与规划,可以帮助设计师更好地把握建筑物的形态、比例和空间布局,提高设计质量和效果。
3.2 工程制图在工程制图中,通过对工件的各个侧面进行投影与视的呈现,可以清晰地展示工件的结构、尺寸和特征,有助于制造工艺的分析与评估。


识图立体的投影教案教案标题:识图立体的投影教案目标:1. 学生能够理解和应用识图立体的投影概念。
2. 学生能够通过练习和实践,熟练地绘制和解读识图立体的投影。
教案步骤:引入:1. 通过展示一些日常生活中的立体物体的图片,引起学生对于立体物体的注意和兴趣。
2. 引导学生思考和讨论,立体物体在平面上的投影是什么样的形状。
讲解:1. 介绍识图立体的投影的概念和意义,解释立体物体在平面上的投影是其在平行于平面的投影面上的映射。
2. 解释不同角度和位置观察立体物体所得到的投影形状会有所不同。
3. 通过示例和图示,讲解正交投影和斜投影两种常见的投影方法。
练习:1. 分发练习题,要求学生根据给定的立体物体图形,绘制其在平面上的投影。
2. 引导学生观察和分析不同角度和位置观察立体物体所得到的投影形状的变化规律。
3. 组织学生进行小组讨论,分享彼此的投影绘制方法和经验。
拓展:1. 引导学生思考和讨论,立体物体的投影在实际生活中的应用,如建筑设计、工程制图等领域。
2. 鼓励学生自主探索和研究其他投影方法,如透视投影等。
总结:1. 总结识图立体的投影的概念和方法。
2. 强调练习和实践的重要性,通过不断绘制和解读投影图形,提高学生的技能和理解能力。
教学资源:1. 立体物体的图片和模型。
2. 投影练习题。
3. 投影绘制工具,如铅笔、直尺、量角器等。
评估方式:1. 观察学生在课堂上的参与和表现。
2. 检查学生完成的练习题,评估其对于识图立体的投影的理解和应用能力。
教案扩展:1. 将识图立体的投影与其他几何概念结合,如平行投影、相似性等。
2. 引导学生应用识图立体的投影概念,解决实际问题,如计算建筑物的投影面积、体积等。
单元课时计划
唐山工业职业技术学院
第四章立体的投影
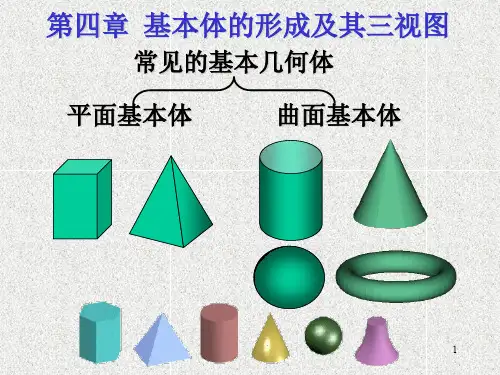
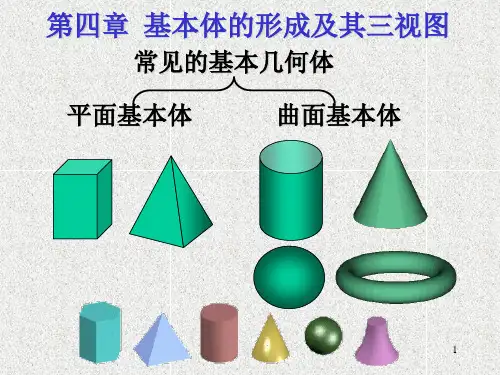
引入:立体表面由若干面围成,表面均为平面的立体称为平面立体,表面为曲面或平面与曲面的立体称为曲面立体。
工程制图中,通常把棱柱、棱锥、圆柱、圆锥、球、圆环等简单立体称为基本几何体,简称基本体。
本章主要讨论这两类立体的三视图画法及在立体表面上取点、线的作图问题。
图4-1 基本立体
正课:§4.1 基本体的投影及其表面取点
一、平面立体的投影及其表面取点
1.棱柱
(1)棱柱的投影如图4-2所示,作图时先画水平投影正六边形,再根据投影规律和棱柱高度作出其他两个投影。
图4-2 棱柱的投影及表面取点
(2)棱柱表面取点先确定点所在的平面,根据该平面的投影特性来确定点的投影。
若该平面垂直于某一投影面,则点在该投影面上的投影必定落在此
平面的积聚性投影上。
(举例说明)
例4-1已知棱柱表面上点M的正面投影m′,求作点M的其他两投影m、m″。
因为m′可见,因此点M必定在棱面ABCD上。
此棱面是铅垂面,其水平投影积聚成直线,点M的水平投影m必在该直线上,由m′和m即可求得侧面投影m″。
又知点N的水平投影,求其他两个投影。
因为n可见,因此点N必定在六棱柱顶面,n′,n″分别在顶面的积聚直线上。
2.棱锥
(1)棱锥的投影
图4—3为正三棱锥的投影,作图时先画出底面三角形的各个投影,再作出锥顶S的各个投影,然后连接各棱线即得正三棱锥的三面投影。
图4-3 棱锥的投影及表面取点
(2)棱锥表面取点
首先确定点所在的平面,根据该平面的投影特性来确定点的投影,该平面为一般位置平面时,可采用辅助直线法求出点的投影。
例4-2 如图4—3所示,已知正三棱锥表面上点M的正面投影m’.求作点M其他两投影m、m”。
因为m’可见,因此点M必定在棱面△SAB上。
△SAB 是一般位置平面,过点M及锥顶点S作—条辅助直线SK,与底边AB交于点K,作出直线SK的三面投影。
根据点的从属关系,求出点M的其它两个投影。
又知点N的水平投影n,求其他两个投影。
因为n可见,因此点N必定在棱面△SAC上,n”必定在直线s”a”(c”)上,由n、n”即可求出n’。
二、回转体的投影及其表面取点
1.圆柱
首先介绍圆柱面的形成。
(1)圆柱的投影如图4-4所示,圆柱表面由圆柱面和上、下底面圆组成。
作图时先画出水平投影的圆,再画出其他两个投影。
图4-4圆柱的投影及表面取点
(2)圆柱表面取点根据圆柱面水平投影具有积聚性的特征,圆柱面上的点必定落在水平投影圆上。
由此确定点的投影。
例4-3如图4—4所示,已知圆柱表面上点M的正面投影m’,求作点M其他两投影m、m''。
因为m’可见,所以点M必在前半个圆柱面上,根据该圆柱面水平投影具有积聚性的特征,m必定落在前半水平投影圆上,由m、m’即可求出m''。
2.圆锥
(1)圆锥的投影如图4-5所示,圆锥面是一直母线绕与它相交的轴线回转而成。
作图时,先画出底面圆的各个投影,再画出锥顶的投影,然后分别画出其外形轮廓素线,即完成圆锥的各个投影。
(2) 棱锥表面取点: 可采用下列两种方法:辅助素线法和辅助圆法。
(重点介绍)
图4-5 圆锥的投影及表面取点
例4-4如图4—5所示,已知圆锥表面上点M的正面投影m’,求作点M 其他两投影m、m''。
因为m’可见,所以点M必在前半个圆锥面上,
方法一:辅助素线法:
过锥顶S和点M作一辅助线SⅠ,由已知条件可确定正面投影s'1'求出它的水平投影s1和侧面投影s''1'',再根据点在直线上的投影性质,由m’求出m和m”。
方法二:辅助圆法:
过点M作一垂直于回转轴线的水平辅助圆,该圆的正面投影过m’,且平行于底面圆的正面投影,它的水平投影为一直径等于2'3’的圆,m必在此圆周上,由m'和m可求出m''。
3.球
(1)球的投影:如图4-6所示,球面是由一个圆母线绕其通过圆心且在同一平面上的轴线回转而成。
作图时,可先确定球心的三个投影,再画出三个与球等直径的圆。
(2) 球表面取点: 球面的投影没有积聚性,且球面上也不存在直线,所以必须采用辅助圆法求作其表面上点的投影。
例4-5如图4—6所示,己知球面上点M的水平投影m,求作点M的其他两投影m'm''。
(分析并画图)
图
4-6 球的投影及表面取点
小结:1.平面立体的投影及其表面取点。
2.画出基本体的三面投影,并在投影图上把组成基本体的平面、曲
面、棱线表示出来,并判别其可见性。
作业:习题集15页1、2、3、4、5、6。