弹塑性本构关系简介
- 格式:ppt
- 大小:2.00 MB
- 文档页数:40









金属材料弹性塑性本构关系解析金属材料是工程领域中常用的材料之一,具有优良的强度和韧性。
材料的力学行为对设计和制造过程中的性能和可靠性有着重要影响。
因此,对金属材料的力学行为进行解析是非常重要的。
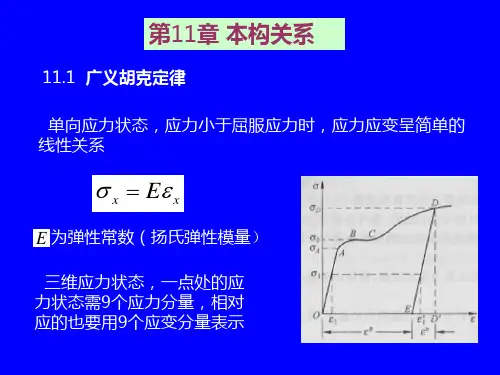
弹性塑性理论是描述金属材料力学行为的基础。
材料的弹性是指在外力作用下,金属可以发生一定的形变,但在去除外力后能够完全恢复原状的性质。
而塑性则是指金属在外力作用下可以发生形变,并保持一定程度的留存。
弹性塑性本构关系是描述金属材料力学行为的数学模型。
本构关系描述了材料的应力-应变关系,即在给定应力下,材料的应变响应。
常见的本构关系有线弹性模型、柯西模型、带硬化的本构模型等。
线弹性模型是最简单的本构模型之一。
它假设应力与应变之间的关系为线性,即材料的应力随应变的变化呈线性关系。
然而,在实际应用中,金属材料的线弹性行为较为有限,只能描述较小的应力应变范围。
相比之下,柯西模型是一种更为复杂的本构模型。
它采用了非线性的弹性本构关系,能更准确地描述金属材料的力学行为。
柯西模型可以考虑材料的应变硬化效应,即当金属材料受到塑性变形时,其硬度会增加,使得应力-应变关系不再是线性的。
带硬化的本构模型是在柯西模型的基础上引入了塑性硬化理论。
塑性硬化理论认为,金属材料在应力作用下会出现晶格滑移和位错运动,导致塑性变形。
这些变形会引起材料内部的晶粒发生变化,使得材料的硬度增加。
带硬化的本构模型可以更好地描述金属材料的变形行为。
解析金属材料的弹性塑性本构关系主要有两种方法:实验法和数值模拟法。
实验法通过对金属材料进行力学试验,如拉伸试验、压缩试验等,测量应力-应变曲线,从而得到材料的弹性塑性本构关系。
数值模拟法则借助计算机软件,通过建立数学模型和力学方程,模拟金属材料的力学行为,从而得到材料的应力-应变关系。
在工程领域中,正确解析金属材料的弹性塑性本构关系对设计和制造过程至关重要。
它不仅可以预测材料在外力作用下的变形行为,还可以指导工程师选择适当的金属材料,并优化材料的成形和加工过程。
第二部分弹塑性问题的有限元法第四章弹塑性体的本构理论第五章弹塑性体的有限元法第四章弹塑性体的本构理论4-1塑性力学的基本内容和地位塑性力学是有三大部分组成的:1) 塑性本构理论,研究弹塑性体的应力和应变之间的关系;2) 极限分析,研究刚塑性体的应力变形场,包括滑移线理论和上下限法;3) 安定分析,研究弹塑性体在低周交变载荷作用下结构的安定性问题。
塑性力学虽然是建立在实验和假设基础之上的,但其理论本身是优美的,甚至能够以公理化的方法来建立整个塑性力学体系。
塑性力学是最简单的材料非线性学科,有很多其它更复杂的学科,如损伤力学、粘塑性力学等,都是借用塑性本构理论体系而发展起来的。
4-2关于材料性质和变形特性的假定材料性质的假定1)材料是连续介质,即材料内部无细观缺陷;2)非粘性的,即在本构关系中,没有时间效应;3)材料具有无限韧性,即具有无限变形的可能,不会出现断裂。
常常根据材料在单向应力状态下的σ-ε曲线,将弹塑性材料作以下分类:硬化弹塑性材料理想弹塑性材料弹塑性本构理论研究的是前三种类型的材料,但要注意对于应变软化材料,经典弹塑性理论尚存在不少问题。
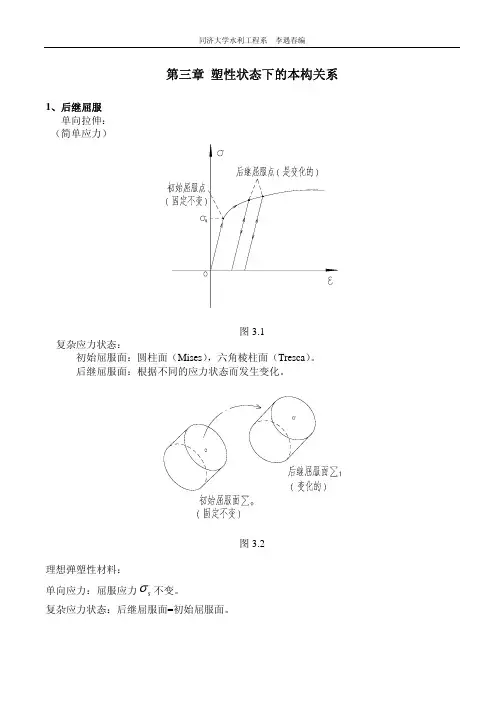
变形行为假定 1)应力空间中存在一初始屈服面,当应力点位于屈服面以内时,应力和应变增量的是线性的;只有当应力点达到屈服面时,材料才可能开始出现屈服,即开始产生塑性变形。
因此初始屈服面界定了首次屈服的应力组合,可表示为()00=σf(1)2) 随着塑性变形的产生和积累,屈服面可能在应力空间中发生变化而产生后继屈服面,也称作加载面。
对于硬化材料加载面随着塑性变形的积累将不断扩张,对于理想弹塑性材料加载面就是初始屈服面,它始终保持不变,对于软化材料随着塑性变形的积累加载面将不断收缩。
因此加载面实际上界定了曾经发生过屈服的物质点的弹性范围,当该点的应力位于加载面之内变化时,不会产生新的塑性变形,应力增量与应变增量的关系是线性的。
只有当应力点再次达到该加载面时,才可能产生新的塑性变形。