第四节固定床吸附过程的计算固定床吸附器结构简单，但由于气体吸附过程是气—固传质，对任一时间或任一颗粒来说都是不稳定过程，因此固定床吸附器的吸附操作是非稳态的，计算过程非常复杂，一般要涉及到物料衡算方程、吸附等温线方程和传热速率方程及热量衡算。
而在气态污染物的吸附净化设计中，由于所涉及到的物系是低浓度的气态混合物，且气量一般比较大，吸附热相对较小，因此可近似地按等温过程处理，可不考虑传热速率方程和热量方程（升温脱附除外）。
这样在设计过程中可采用简化了的方法进行近似计算，计算时往往提出如下假设：（1）气相中吸附质浓度低；（2）吸附操作在等温下进行；（3）传质区通过整个床层时长度保持不变；（4）床层长度比传质区长度大得多。
这些简化限制条件对目前工业上应用的吸附器来说，一般是符合的。
设计中较常采用的是希洛夫近似计算法和透过曲线计算法。
计算过程一般是在吸附剂的选择、吸附设备的选择和吸附效率确定之后进行的。
设计计算的任务是求出吸附器的床层直径和高度，吸附剂的用量，吸附器的一次循环工作时间，床层压降等。
下面首先介绍固定床吸附器的吸附过程。
一、固定床吸附器的吸附过程在固定床吸附器的吸附操作中，一般是混合气体从床层的一端进入，净化了的气体从床层的另一端排出。
因此，首先吸附饱和的应是靠近进气口一端的吸附剂床层。
随着吸附的进行，整个床层会逐渐被吸附质饱和，床层末端流出污染物，此时吸附应该停止，完成了一个吸附过程。
为了描述吸附过程，提出了以下概念。
（一）吸附负荷曲线与透过曲线1. 吸附负荷曲线在实际操作中，对于一个固定床吸附器，气体以等速进入床层，气体中的吸附质就会按某种规律被吸附剂所吸附。
吸附一定时间后，吸附质在吸附剂上就会有一定的浓度，我们把这一定的浓度称为该时刻的吸附负荷。
如果把这一瞬间床层内不同截面上的吸附负荷对床层的长度（高度）作一条曲线，即得吸附负荷曲线。
也就是说，吸附负荷曲线是吸附床层内吸附质浓度x随床层长度z变化的曲线。
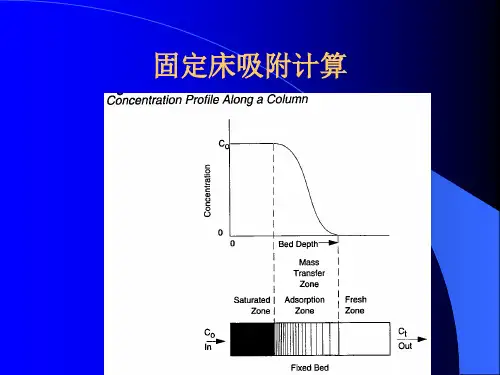
在理想状态下，若床层完全没有阻力，吸附会在瞬间达到平衡，即吸附速率无穷大，则在床层内所有断面上的吸附负荷均为一个相同的值，吸附负荷曲线将是一个直角形的折线，如图3-12所示。
但实际上是不可能的，在实际操作中由于床层中存在着阻力，在某一瞬间床层内各个截面上的吸附负荷会有差异，我们这时所绘制的曲线将是图3-13所示的吸附负荷曲线。
图中把曲线分成了三个区域：饱和区（所有吸附剂已经达到了饱和）、传质区（有一部分吸附剂还正在吸附）和未用区（所有吸附剂上均未有吸附质）。
如果经过一段时间的吸附，绘制另一时刻的吸附负荷曲线时，会发现曲线前进到了II线的位置，所以我们又形象地把吸附负荷曲线称为吸附波或吸附前沿。
当吸附波的下端到达床层未端时，说明已有吸附质漏出，这时床层被穿透，当床层被穿透的这个时刻，称为破点。
此时流出气体中吸附质的浓度称为破点浓度。
在实际工作中，由于吸附剂中吸附质的浓度（即吸附负荷）不易测定，故目前许多场合，曲线的纵坐标都以床层中混合气体的浓度c来表示。
因此，吸附负荷曲线又可定义为在稳定吸附状态下，床层中气相中吸附质的浓度随床层高度（长度）变化的曲线。
由于床层的阻力不同，吸附负荷曲线会有不同的形状。
床层阻力愈大，某一时刻床层内各截面上浓度差别越大，吸附负荷曲线也就变得越平缓，这当然是我们不希望出现的情况。
2. 透过曲线吸附负荷曲线表达了床层中浓度分布的情况，可直观地了解床层内操作的状况。
但要从床层中各部位采出吸附剂样品进行分析是相当困难的，这样易破坏床层的稳定。
因此通常改用在一定的时间间隔内。
分析床层流出物中吸附质浓度的变化，以流出物中吸附质浓度y为纵坐标。
时间τ为横坐标，则随时间的推移可画出一条τ-y曲线。
如图3-14所示，开始时流出物中吸附质浓度为y B ，它是与吸附剂中的xB浓度相平衡的（xB为破点时床层出口端的吸附负荷）。
流出物中吸附质浓度开始上升，到τE 时升到yE,即接近床层进口浓度，这时床层已完全没有吸附能力，吸附波的末端也离开床层了。
于是在τ-y图上，从τB 到τE呈现一个S型曲线，这条曲线称“透过曲线”。
它的形状与吸附负荷曲线是完全相似的，只是方向相反。
由于它与吸附负荷曲线成镜面对称相似，所以也称吸附负荷曲线为“吸附波”或“传质前沿”。
由于透过曲线易于测定和标绘出来，因此也用它来反映床层内吸附负荷曲线的形状，而且也能准确地求出破点。
如果透过曲线比较陡，说明吸附过程比较快，反之则速度较慢。
如果透过曲线是一条竖直的直线，则说明吸附过程是飞快的，是理想的吸附波。
（二）保护作用时间保护作用时间是固定床吸附器的有效工作时间。
它定义为从吸附操作开始到床层被穿透所经历的时间称为保护作用时间，如图3-14所示的由τ0到τB所经历的时间，到达τB 时，床层内吸附剂还没有完全饱和。
图中的yB>0，是根据排放标准规定出的一个值。
图3-14还出现一个点，即τE ，时间到达τE时，吸附波整个移出床层，说明床层内的吸附剂已完全饱和，完全失去了吸附能力，这一点称为耗竭点或称干点，到达干点时，床层内流出的气体中，吸附质浓度基本回复到进口浓度。
在实际操作中，一旦达到了破点，就应停止操作，切换到另一吸附床，穿透了的吸附床转入脱附再生。
（三）传质区高度把一个吸附波所占据的床层高度称为传质区高度，用Za表示。
从理论上讲，传质区高度应是流出气体中溶质浓度从0变到y这个区间内吸附波在Z 轴上占据的长度，但实际上再生后的吸附剂中还残留一定量的吸附质（一般为初始浓度y的5%～10%），而吸附剂完全达到饱和的时间又太长，所以一般把由破点时间τB 对应的气体浓度yB到干点时间τE对应的气体浓度yE这段时间内吸附波在Z轴上所占据的长度称为传质区高度。
为了使吸附操作比较可靠，就必须使床层有足够的长度，起码要包含一个稳定的传质区。
而形成一个稳定的传质区需要一定时间。
如果吸附器床层长度比传质区长度还短，那就不能出现一个稳定的传质区，操作不稳定，出现破点的时间会比计算的来得快，为避免此点，吸附器床层长度一定要比传质区长度长。
例如实验室内所用吸附柱高度就规定应至少是传质区长度的两倍，而吸附柱直径最少应是最大吸附剂颗粒直径的10倍。
（四）传质区吸附饱和率（度）和剩余饱和能力分率 这两个概念可用下式表示：这也是量度固定吸附床操作性能的两个指标，吸附饱和率越大，剩余饱和吸附能力分率越小，说明吸附床的操作性能越好。
二、希洛夫近似计算法 （一）希洛夫公式在理想状态下，在理想保护作用时间τˊB 内通过吸附床的吸附质将全部被吸附，即通过床层的吸附质的量一定等于床层内所吸附的量，即： (3-19)式中 G S ——气体通过床层的速率，kg/(m 2·s)；A ——吸附床层截面积，m 2；x T ——吸附剂的静活性（平衡吸附量），kg/kg ； τˊB ——理想保护作用时间，min ；c 0——气体中污染物初始浓度，kg/m 3； ρB ——吸附剂堆积密度，kg/m 3； Z ——床层长度，m 。
由上式可得：(3-20)对于一定的吸附系统和操作条件，ρB 、x T 、G s 、co 均已确定，因此可令(3-21) 则（3-21）式可变成：τ ˊB =KZ (3-22)但对一个实际的操作过程，由于床层存在阻力，因此实际上的保护作用时间τB 要比理想保护作用时间τˊB 短，我们把被缩短的这段时间称为保护作用时间损失，用τo 来表示。
阻力越大，τo 越大。
三个时间的关系可表示如下：吸附能力内吸附剂达到饱和时的力内吸附剂仍具有吸附能剩余饱和吸附能力分率附量内吸附剂达饱和时的吸内吸附剂实际的吸附量度吸附饱和率Za Za Za Za ==〉〈TB o B S x ZA Ac G ρτ=/Z c G x S T B B 0/ρτ=K c G x S TB =0ρτB =τˊB —τo (3-23) 将(3-22)式代入上式，即得：(3-24)（3-24）式即为具有实用价值的希洛夫公式，Z o 可以称为床层长度损失。
τo 和Z o 均可由实验求得。
（二）利用希洛夫公式的简化计算在吸附净化的设计中，常利用希洛夫公式进行简化计算。
简化计算还是以实验作基础，利用希洛夫公式求出K 与τo ，再根据生产要求的操作周期求出吸附床层长度，并根据气速，求出所需床层半径或截面积。
具体步骤简述如下：1. 选择吸附剂，确定操作条件，包括温度、压力和流速。
固定吸附床的气体流速一般掌握在0.2～0.6m/s 之间；2. 规定出合适的破点浓度；3. 在一定气速u 下，测不同床层长度Z 的保护作用时间τB ，作出τB -Z 直线，求出K 和τ0；4. 定出操作周期τB ，化为min ；5. 将K 、τ0、τB 代入希洛夫公式，求出Z ，若Z 过长可以分层。
6. 用下式计算床层直径：(3-25) 7、求吸附剂用量W ：(3-26)式中 ρB ——吸附剂堆积密度，kg/m 3。
为避免装填损失，可多取10%装填量。
[例3-1] 用活性炭固定床吸附器吸附净化废气。
常温常压下废气流量为1000m 3/h ，废气中四氯化碳初始浓度为2000mg/m 3，选定空床气速为20m/min 。
活性炭平均粒径为3mm ，堆积密度为450kg/m 3，操作周期为40小时。
在上述条件下，进行动态吸附实验取得如下数据：床层高度Z/m 0.1 0.15 0.2 0.25 0.3 0.35 透过时间τB /min 109 231 310 462 550 650 请计算固定床吸附器的直径、高度和吸附剂用量。
解：以Z 为横坐标，τB 为纵坐标将上述实验数据描绘在坐标图上得一直线（例3-1附图）。
依据图，求出直线的斜率即为K ，截距即为-τ0，得K=2143（min/m ）τ0=95(min)将K 、τ0、τB 代入希洛夫公式得：)(00Z Z K KZ B -=-=ττuVD π4=BAZ W ρ=)(164.121439560400m K Z B =+⨯=+=ττ取Z=1.20m 。
采用立式园柱床进行吸附，计算出吸附床直径：可取D=1m 。
所需吸附剂量考虑装填损失，所需吸附剂量W 为： 423.9×1.1=466kg 三、透过曲线计算法透过曲线计算方法与希洛夫近似计算法相比要复杂一些，但还是要假定吸附体系是一个很简单的恒温体系，混合气体中只有一种可被吸附的吸附质，该体系得到的仅有一个吸附波或传质区。
此时固定床吸附器计算的主要内容为传质区高度Za,保护作用时间τB 和全床饱和度S 。
（一）传质区高度的确定图3-15为一理想透过曲线。
气体的初始浓度为y 0（kg 溶质/kg 无溶质气体），气体流过床层的质量流速为G s (kg/m 2 ·h)，经过一段时间后流出物总量为W （kg 无溶质气体/m 3）。
