高阶偏导数(教案)

《高阶导数数分教案》课件一、教学目标1. 理解高阶导数的定义和性质。

2. 学会计算常见函数的高阶导数。

3. 掌握高阶导数在实际问题中的应用。

二、教学内容1. 高阶导数的定义：二阶导数、三阶导数等。

2. 高阶导数的计算法则：和的导数、乘积的导数、商的导数等。

3. 高阶导数的性质：单调性、极值、拐点等。

三、教学重点与难点1. 重点：高阶导数的定义和计算法则。

2. 难点：高阶导数的性质的理解和应用。

四、教学方法1. 采用讲解法，引导学生理解高阶导数的定义和性质。

2. 采用案例教学法，让学生通过计算具体函数的高阶导数，加深对高阶导数计算法则的理解。

3. 采用问题驱动法，引导学生运用高阶导数解决实际问题。

五、教学过程1. 导入：回顾一阶导数的定义和计算法则，引导学生思考高阶导数的概念。

2. 新课：讲解高阶导数的定义，引导学生理解二阶导数、三阶导数等概念。

3. 案例分析：计算常见函数的二阶导数、三阶导数，让学生掌握高阶导数的计算法则。

4. 性质讲解：讲解高阶导数的单调性、极值、拐点等性质，引导学生理解高阶导数在实际问题中的应用。

5. 问题解决：布置练习题，让学生运用高阶导数解决实际问题。

7. 作业布置：布置课后作业，巩固所学内容。

六、教学活动设计1. 互动提问：在讲解高阶导数之前，先回顾一阶导数的概念和计算方法，通过提问方式检查学生对一阶导数的掌握情况。

2. 小组讨论：让学生分组讨论高阶导数的定义，每组提出自己的理解和观点，促进学生之间的交流和思考。

3. 实例分析：选取几个具体函数，让学生计算其二阶导数和三阶导数，通过实际操作加深对高阶导数概念的理解。

七、教学评价1. 课堂参与度：观察学生在课堂上的发言和提问情况，评估学生对高阶导数的理解和掌握程度。

2. 练习题完成情况：检查学生完成课后练习题的情况，评估学生对高阶导数计算法则和性质的应用能力。

3. 小组讨论报告：评估学生在小组讨论中的表现，包括观点提出、交流和合作能力。

高阶偏导数说课稿韩桂玲本节内容主要讲解了二元函数的二阶偏导数及高阶偏导数的定义及求法和二阶连续混合偏导数相等的定理证明，以为后面学习复合二元函数的高阶偏导数的求法、二元函数的泰勒公式及极值问题作铺垫。

本节主要以老师讲授为主，由老师带领学生复习回顾二元函数的一阶偏导数的定义引入到对二阶偏导数的讲解，还是以极限定义出发，（它是以一阶偏导函数的函数改变量与自变量改变量的比值的极限）此时并提醒学生对二阶偏导数符号的多种表示及求导顺序的注意。

由此类似得出n 阶偏导数及高阶偏导数的定义及求法下面举一个简单的例子：例1求函数3233y y x x z +-=的二阶偏导数，引导学生共同完成，使得学生知道公式法求二阶偏导数的具体方法与过程。

但在这个例子中发现=∂∂∂y x z 2xy z ∂∂∂2即两个混合偏导数相等对学生说明并不是所有函数的高阶混合偏导数都与求导顺序无关。

紧接着举出相关例子即例2：⎪⎩⎪⎨⎧=+≠++-=0,00,),(22222222y x y x y x y x xy y x f 在原点处)0,0(xy f '')0,0(yx f ''≠ 在讲解这个例子时，提醒学生022=+y x 时对),(y x f 的一阶偏导数只能用定义法，022≠+y x 时对),(y x f 的一阶偏导数用可用定义法也可用公式法，公式法更为简单。

当然由一阶偏导数求两个混合偏导数)0,0(xyf ''与)0,0(yx f ''必须用定义法。

但例1又不是偶然，事实上，它满足定理1：若函数),(y x f 在点)(0,0y x P 的邻域G 存在二阶混合偏导数),(y x f xy''与),(y x f yx ''，并且它们在点)(0,0y x P 连续，则=''),(00y x f xy),(00y x f yx ''。

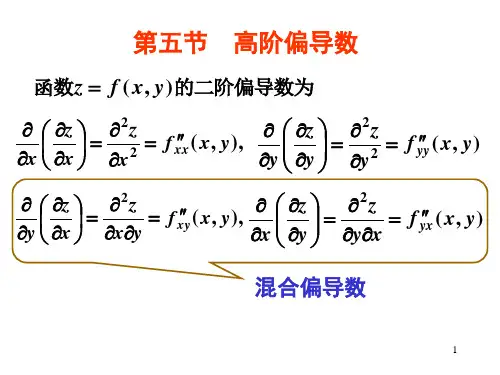
高阶偏导数韩桂玲教学目标： 1.掌握二元函数的二阶偏导数及高阶偏导数的定义2.会求二元函数的二阶偏导数3..理解二阶连续混合偏导数相等的定理证明教学重点： 1.掌握二元函数的二阶偏导数及高阶偏导数的定义2.会恰当的用定义法和公式法求二元函数的二阶及高阶偏导数教学难点： 二阶连续混合偏导数相等的定理证明教学方法： 讲授法教学过程：引入：若二元函数),(y x f z =在区域D 存在x 与y 的一阶偏导数，对D y x ∈∀),(xy x f y x x f y x f x z x x ∆-∆+='=∂∂→∆),(),(lim ),(0 (把y 看作常数) yy x f y y x f y x f y z y y ∆-∆+='=∂∂→∆),(),(lim ),(0 (把x 看作常数) 1.二阶偏导数定义若二元函数),(y x f z =在区域D 存在x 与y 的（一阶）偏导数),(y x f xz x '=∂∂与),(y x f y z y '=∂∂则在D 内它们都是x 与y 的二元函数。

若它们关于x 与y 的偏导数存在，即),()(22y x f xz x z x xx ''=∂∂=∂∂∂∂x y x f y x x f x x x ∆'-∆+'=→∆),(),(lim 0 (把y 看作常数) 定义法表出 ),()(2y x f y x z x z y xy ''=∂∂∂=∂∂∂∂yy x f y y x f x x y ∆'-∆+'=→∆),(),(lim 0 (把x 看作常数) 定义法表出 ),()(2y x f x y z y z x yx ''=∂∂∂=∂∂∂∂xy x f y x x f y y x ∆'-∆+'=→∆),(),(lim 0(把y 看作常数) 定义法表出 ),()(22y x f yz y z y yy ''=∂∂=∂∂∂∂y y x f y y x f y y y ∆'-∆+'=→∆),(),(lim 0(把x 看作常数) 定义法表出 则称它们是二元函数),(y x f z =的二阶偏导数，其中第二、三个二阶偏导数称为混合偏导数。

第30课偏导数复习（10 min）【教师】提前设计好复习题目，并针对学生存在的问题及时讲解【学生】做复习题目复习所学内容，为讲授新课打好基础讲授新课（20 min）【教师】讲解偏导数的概念，并通过例题介绍其求法定义1 设函数()z f x y=，在点00()x y，的某一邻域内有定义，当y固定在y，而x在x处有改变量x∆时，相应地函数有改变量0000()()f x x y f x y+∆-，，，称其为函数z对x的偏增量，记为xz∆．若极限000000()()lim limxx xz f x x y f x yx x∆→∆→∆+∆-=∆∆，，存在，则称此极限值为函数()z f x y=，在点00()x y，处对x的偏导数，记为x xy yzx==∂∂，x xy yfx==∂∂，x xxy yz=='，00()xf x y'，．类似地，当x固定在x，而y在y处有改变量y∆时，若极限000000()()lim limyy yz f x y y f x yy y∆→∆→∆+∆-=∆∆，，存在，则称此极限为函数()z f x y=，在点00()x y，处对y的偏导数，记为x xy yzy==∂∂，x xy yfy==∂∂，x xyy yz=='，00()yf x y'，．若函数()z f x y=，在区域D内每一点()x y，处对x的偏导数都存在，且这个偏导数仍是x y，的函数，则称这个偏导数为函数()z f x y=，对自变量x的偏导函数，简称偏导数，记为zx∂∂，fx∂∂，xz'，()xf x y'，．类似地，可以定义函数()z f x y=，对自变量y的偏导函数，简称偏导数，记为zy∂∂，fy∂∂，yz'，()yf x y'，．从偏导数的定义可以看出，偏导数的实质就是把一个学习偏导数的概念及求法。

边做边讲，及时巩固练习，实现教学做一体化。

《高阶导数数分教案》课件教案章节一：高阶导数的概念与计算1.1 引入高阶导数的概念解释高阶导数的定义举例说明高阶导数的含义1.2 高阶导数的计算方法演示如何计算基本函数的高阶导数介绍高阶导数的运算法则教案章节二：链式法则与高阶导数2.1 链式法则的介绍解释链式法则的定义和应用演示如何使用链式法则求解高阶导数2.2 链式法则在高阶导数中的应用举例说明链式法则在高阶导数计算中的重要性练习题：使用链式法则计算复杂函数的高阶导数教案章节三：隐函数与高阶导数3.1 隐函数的介绍解释隐函数的定义和特点举例说明隐函数在实际问题中的应用3.2 隐函数的高阶导数介绍如何求解隐函数的高阶导数练习题：求解隐函数的高阶导数教案章节四：参数方程与高阶导数4.1 参数方程的介绍解释参数方程的定义和应用举例说明参数方程在实际问题中的应用4.2 参数方程的高阶导数介绍如何求解参数方程的高阶导数练习题：求解参数方程的高阶导数教案章节五：高阶导数在实际问题中的应用5.1 高阶导数在物理问题中的应用举例说明高阶导数在物理学中的重要性练习题：使用高阶导数解决物理问题5.2 高阶导数在经济学问题中的应用举例说明高阶导数在经济学中的重要性练习题：使用高阶导数解决经济学问题教案章节六：高阶导数与曲线的凹凸性6.1 凹凸性的定义与判定解释凹凸性的概念演示如何利用高阶导数判断曲线的凹凸性6.2 应用：拐点的寻找介绍拐点的定义和性质练习题：找出给定函数的拐点教案章节七：高阶导数与函数的渐近线7.1 渐近线的概念与求法解释渐近线的定义和类型演示如何利用高阶导数求解函数的渐近线7.2 应用：函数图像的描绘介绍如何利用渐近线和凹凸性分析函数图像练习题：分析给定函数的图像特征教案章节八：高阶导数与最大值、最小值问题8.1 最大值、最小值问题的提出解释最大值和最小值问题的实际意义举例说明如何应用高阶导数解决最大值、最小值问题8.2 应用：实际问题的求解介绍高阶导数在实际问题中的应用方法练习题：使用高阶导数解决实际问题教案章节九：高阶导数与函数的稳定性9.1 函数稳定性的概念与判定解释函数稳定性的概念演示如何利用高阶导数判断函数的稳定性9.2 应用：实际问题的分析介绍高阶导数在分析实际问题中的应用练习题：分析给定函数的稳定性回顾本节课的主要内容和知识点强调高阶导数在实际问题中的应用价值10.2 拓展与思考提出与高阶导数相关的拓展问题鼓励学生思考高阶导数在其他领域的应用前景教案章节六：高阶导数与曲线的凹凸性6.1 凹凸性的定义与判定重点：凹凸性是函数图像的重要特征，它描述了函数图像在某一区间内的凹凸状态。

一、教学目标1. 知识与技能目标：（1）理解偏导数的概念，掌握偏导数的计算方法。

（2）学会运用偏导数求解多元函数的一阶偏导数和二阶偏导数。

（3）了解偏导数在实际问题中的应用。

2. 过程与方法目标：（1）通过实例分析，培养学生对偏导数的直观理解。

（2）通过实际问题，引导学生运用偏导数解决问题。

（3）培养学生分析问题、解决问题的能力。

3. 情感态度与价值观目标：（1）激发学生对数学的兴趣，提高学生的数学素养。

（2）培养学生严谨、求实的科学态度。

（3）培养学生团结协作、勇于探索的精神。

二、教学内容1. 偏导数的概念及计算方法2. 偏导数的几何意义3. 偏导数的应用三、教学过程1. 导入新课通过实际问题引入偏导数的概念，如：求平面曲线在某点的切线斜率，激发学生的学习兴趣。

2. 偏导数的概念及计算方法（1）引导学生回顾导数的概念，类比一元函数的导数，引入偏导数的概念。

（2）通过实例讲解偏导数的计算方法，包括直接求导法和复合函数求导法。

（3）进行课堂练习，巩固所学知识。

3. 偏导数的几何意义（1）通过图形展示，让学生直观理解偏导数的几何意义。

（2）讲解偏导数与曲线切线斜率的关系，引导学生将偏导数应用于实际问题。

（3）进行课堂练习，巩固所学知识。

4. 偏导数的应用（1）通过实例讲解偏导数在求解多元函数极值、拐点等方面的应用。

（2）引导学生运用偏导数解决实际问题，如：求多元函数的最值、最优化问题等。

（3）进行课堂练习，巩固所学知识。

5. 总结与反思（1）回顾本节课所学内容，总结偏导数的概念、计算方法及应用。

（2）引导学生反思自己在学习过程中的收获与不足，提出改进措施。

6. 布置作业（1）完成课后练习题，巩固所学知识。

（2）思考偏导数在实际问题中的应用，撰写一篇小论文。

四、教学评价1. 课堂表现：观察学生在课堂上的学习态度、参与程度等。

2. 作业完成情况：检查学生完成课后练习题的情况，了解学生对知识的掌握程度。

3. 小论文：评价学生运用偏导数解决实际问题的能力。

高中数学高阶导数定理教案教案标题：高中数学高阶导数定理教案教案目标：1. 理解高阶导数的概念和意义；2. 掌握高阶导数的计算方法；3. 理解高阶导数定理的应用。

教案步骤：步骤一：导入与概念解释（5分钟）1. 引导学生回顾导数的概念和计算方法；2. 引入高阶导数的概念，解释高阶导数表示导数的导数；3. 引导学生思考高阶导数的意义和应用。

步骤二：高阶导数的计算方法（15分钟）1. 提供一些简单的函数表达式，引导学生计算一阶和二阶导数；2. 解释高阶导数的计算方法，引导学生逐步计算三阶、四阶导数；3. 给出一些练习题，让学生巩固高阶导数的计算方法。

步骤三：高阶导数定理的讲解（10分钟）1. 介绍高阶导数定理的概念和表述；2. 解释高阶导数定理的应用场景，如曲线的拐点、极值点等；3. 提供一些实际问题，引导学生运用高阶导数定理解决问题。

步骤四：综合应用与拓展（15分钟）1. 给出一些综合应用题，让学生运用所学知识解决复杂问题；2. 引导学生思考高阶导数定理在实际问题中的应用；3. 鼓励学生自主拓展，探索高阶导数的更多应用领域。

步骤五：课堂总结与反思（5分钟）1. 总结高阶导数的概念、计算方法和定理；2. 鼓励学生提出问题、分享经验和疑惑；3. 对学生的学习情况进行评价和反馈。

教学资源：1. 教材：高中数学教材；2. 计算工具：计算器、数学软件等；3. 练习题和实际问题。

教学评估：1. 课堂参与度：观察学生的积极参与程度；2. 练习题表现：检查学生对高阶导数计算方法的掌握情况；3. 应用问题解决能力：评估学生运用高阶导数定理解决实际问题的能力。

教学延伸：1. 鼓励学生自主学习，深入了解高阶导数的更多应用；2. 引导学生进行相关研究，探索高阶导数在其他学科领域的应用；3. 提供更多拓展练习和挑战题，满足学生的不同需求。

教学反思：1. 教学过程中是否引导学生主动思考和解决问题；2. 学生对高阶导数概念的理解和掌握程度；3. 学生对高阶导数定理的应用能力和创新思维。

第8讲 高阶导数与二元函数极值讲授内容一、高阶偏导数由于),(y x f z =的偏导函数),(),,(y x f y x f y x 仍然是自变量x 与y 的函数，如果它们关于x 与y 的偏导数也存在，则说函数f 具有二阶偏导数，二元函数的二阶偏导数有如下四种情形：),(22y x f x z x xz xx =⎪⎭⎫⎝⎛∂∂∂∂=∂∂， ).,(22y x f y z y y z yy =⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂ ),,(2y x f x z y y x zxy =⎪⎭⎫⎝⎛∂∂∂∂=∂∂∂ ),(2y x f y z x x y z yx=⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂∂例1 求函数xy z arctan=的所有二阶偏导数. 解：()22222222y x xyyx yx xz +=⎪⎪⎭⎫ ⎝⎛+-∂∂=∂∂， ().22222222y x xyy x x y yz +-=⎪⎪⎭⎫ ⎝⎛+∂∂=∂∂(),22222222y x y x yx yy y x z+--=⎪⎪⎭⎫ ⎝⎛+-∂∂=∂∂∂ (),22222222y x y x y x x x x y z +--=⎪⎪⎭⎫ ⎝⎛+∂∂=∂∂∂注意：从上面例子看到， 关于x 和y 的不同顺序的两个二阶偏导数都相等（称为混合偏导数），但这个结论并不对任何函数都成立（见例2）.例2 设函数()⎪⎩⎪⎨⎧=+≠++-=.0 ,0,0 ,,22222222y x y x y x y x xy y x f解： 它的一阶偏导数为()()()()()⎪⎩⎪⎨⎧=+≠++++-=,0 ,0,0 ,4,2222222222222y x y x yx y x y y x y x y y x f x ()()()()()⎪⎩⎪⎨⎧=+≠++-+-=,0 ,0,0 ,4,2222222222222y x y x yx y x x y x y x x y x f y 进而求f 在（0，0）处的混合偏导数，得 ()()(),1lim0,0,0lim0,00-=∆∆-=∆-∆=→∆→∆yy yf y f f y x x y xy ()()()1lim0,00,lim0,00=∆∆=∆-∆=→∆→∆xx xf x f f x y y x yx ．由此看到，这里的()y x f ,在原点处的两个二阶混合偏导数与求导顺序有关，那么，在什么条件下混合偏导数与求导顺序无关呢？定理17.7 若),(),(y x f y x f yx xy 和都在点),(00y x 连续，则()()0000,,y x f y x f yx xy = .这个定理的结论对n 元函数的混合偏导数也成立。