相贯线的画法
- 格式:pptx
- 大小:1.71 MB
- 文档页数:49



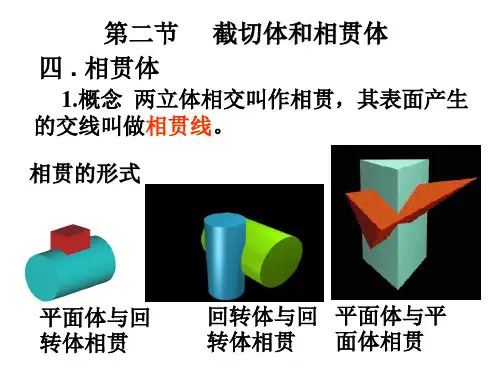





相贯线的画法及应用条件相贯线是指两个或多个线段之间的交线或交点形成的线段。
它是由两个或多个线段或直线相互交叉而形成的新线段。
在几何学中,相贯线常常用于构造三角形、四边形或多边形的边界。
在绘制相贯线时,需要满足以下的应用条件:1.线段相交:相贯线的基本条件是有两个或更多的线段交叉或相交。
这就意味着至少有两个线段有一个交点或共享一个共同点。
如果只有一个共同点,那么它们的交线就数学上不能称为线段,而是点。
2.交点位置:相贯线的位置取决于线段的相对位置。
如果两个线段相交于一个共同的端点,那么交线将包含这个共同的端点。
如果两个线段相交于一个内部点,那么交线将穿过这个内部点。
3.线段延长:相贯线通常会延长线段。
当两个线段相交时,相贯线可能会延伸到任何一个相交的线段的外部或无限远处。
然而,不同的情况下,相贯线并不一定要延长,它可能只是在线段之间形成一个短暂的交点。
4.线段平行:当两个线段平行时,它们不会有交点,因此不会形成相贯线。
相贯线在几何学和一些实际应用中具有重要的作用。
以下是一些相贯线的实际应用:1.三角形的相贯线:在三角形中,三条边的中线、角平分线和高线都是相贯线。
这些相贯线在三角形的重心、内心、外心和垂心等重要点上相交,可以用于求解三角形的各个性质。
2.四边形的相贯线:在四边形中,对角线是相贯线。
对角线相交于一个共同点,将四边形分成两个三角形。
对角线还具有一些特殊性质,比如平行四边形的对角线相等、矩形的对角线相等等。
3.多边形的相贯线:多边形的边界线可以通过边的延长或相交来形成相贯线。
相贯线可以用于判断多边形的凸凹性、边界内外点的位置关系等。
4.交通规划:相贯线在交通规划中经常用于设计道路交叉口。
交叉口中的道路的延长线交叉形成的交点可以用于确定交叉口的布局和设计。
5.建筑设计:相贯线在建筑设计中可以用于绘制建筑物的轮廓线、墙壁交接处等。
相贯线的位置和延伸可以用于确定建筑物的外形和内部布局。
总结起来,相贯线是由两个或多个线段相交或交叉形成的新线段。