信号处理中基于小波变换的信号降噪技术研究
- 格式:docx
- 大小:37.69 KB
- 文档页数:3

小波阈值降噪技术在振动信号处理中的应用 9 文章编号:1006—1355(2008)06-0009-04 小波阈值降噪技术在振动信号处理中的应用 王秉仁 , 杨艳霞 , 蔡伟 , 杨士青 (1.华北电力大学机械工程系,河北保定071003;2.山东陵县供电公司,山东陵县253500) 摘要:通过对转子不对中故障信号的模拟仿真,用小波阈值降噪法消噪,分析比较几种不同小波函数降噪 的效果,对比默认阈值方法与自适应阈值消噪方法的降噪效果,结果表明,自适应阈值比默认阈值更具有可信度。 关键词:振动与波;小波;阈值降噪;振动信号 中图分类号:TH117 文献标识码:A Application of Wavelet Threshold De-noising Technique in Vibration Signals Processing WANG Bing—ren ,YANG Yah—xia ,CAI Wei,YANG Shi—qing (1.School of Mechanical Engineering,North China Electric Power University,Baoding Hebei 071003,China; 2.Electricity Supply Co.,Lingxian Shangdong 253500,China) Abstract:Employing the signal simulation with the fault of eccentricity of the rotor and the wavelet threshold de—noising technique,the de—noising effects of several wavelet functions were analyzed.The de- noising effects of the default threshold method and the self-adaptive threshold method were compared.The result shows that the serf-adaptive threshold method is more reliable than the default threshold method. Key words:vibration and wave;wavelet;threshold denoising;vibration signal 利用振动信号对设备进行监测诊断,是设备故 障诊断中最有效、最常用的方法之一。机械设备和 结构在运行过程中的振动及其本质特征是反映系 统整体及其变化规律的主要信息。由于设备所处 的环境复杂,噪声干扰比较多,经常使有用信号淹 没在较强的噪声中,难以进行准确的故障诊断。目 前,用于振动信号降噪的方法很多,通常采用降噪 效果较好的小波分析方法。由于故障信息通常隐 含在低频信号或一些比较平稳的信号中,而噪声一 般是高频信号,所以采用小波变换可以根据信号特 性将其分解到不同尺度(对应不同的频段)下,对小 波分解系数进行处理后再重构,即可达到原信号的 降噪目的。在基于小波技术的消噪过程中,小波基 函数的选择以及阈值的选取是两个关键的问题。 不同性质的信号应该选择不同的小波基函数以及 收稿日期:2008—02一l0;修改日期:2008—03—18 作者简介:王秉仁(1948一),男,保定市人,教授级高工,现从事教学 和科研工作,主要研究方向为机电设备状态监测与故障 诊断、机械系统动特性分析、信号分析与处理。 阈值规则,才能取得更好的降噪效果。本文对转子 不对中信号进行仿真,利用图象和计算数据说明不 同小波函数和不同的阈值规则的降噪效果。 1小波阈值降噪 1.1小波阈值降噪原理 设一非平稳的、含噪声、一维信号的模型为如 下表示形式 5(i0=.厂( )+ ・e( ), =0,…,n一1 (1) 其中 i)为真实信号;e(i)为噪声,噪声性质未知; (i)为含噪声信号系列。在这里要对该含噪信号进 行去噪处理,,以提高信号的信噪比,从而进行有效 的信号分析和故障诊断。 以最简单的噪声模型为例,即认为e(i)为高斯 白噪声Ⅳ(0,1)。在实际采集的振动信号中,有用 信号通常表现为低频部分或是一些比较平稳的信 号,而噪声信号通常表现为高频信号,降噪过程可 按如下方法进行处理:

第25卷第3期 2013年6月 军械工程学院学报 Journal of Ordnance Engineering College V01.25 NO.3 Jun.2O13
doi:10.3969/j.issn.1008—2956.2013.03.009
基于EMD的改进小波阈值降噪法
在超声信号处理中的应用
王峰林,王长龙,朱红运
(军械工程学院无人机工程系,河北石家庄050003)
摘要:针对超声检测回波信号中的大量噪声,分析了超声检测回波信号的特性,考虑经验模式分解(EMD)和小波 哗噪的优点,在改进阈值函数基础上提出一种基于EMD的小波阈值降噪方法.该方法利用EMD对超声信号进行 分解,对高频分量用改进小波阈值函数方法进行处理,再结合低频分量重构得到降噪信号.仿真实验结果表明,该 方法降噪效果优于小波软、硬阂值降噪,进一步提高了重建信号的信噪比,降低了其均方根误差,是一种可行的超 声信号降噪方法. 关键词:超声检测;经验模式分解;降噪;小波变换 中图分类号:TB553 文献标识码:A 文章编号:1008—2956(2013)03—0035~05
Application of Improved Wavelet Threshold De-noising Based on
Empirical Mode Decomposition on Ultrasonic Signal Processing
WANG Feng—lin,WANG Chang—long,ZHU Hong~yun (Unmanned Aerial Systems Engineering Department,Ordnance Engineering College,Shijiazhuang 050003,China)
Abstract:With regard to the noise contained in the ultrasonic testing echo signal,the characteris—

1512011年第05期,第44卷 通 信 技 术 Vol.44,No.05,2011 总第233期 Communications Technology No.233,Totally 基于小波变换实现脉搏信号降噪处理 王 智, 殷奎喜, 赵 华, 张倩茹 (南京师范大学 物理科学与技术学院,江苏 南京 210046) 【摘 要】脉搏波形复杂而且测量过程中易受各种噪声影响,因此降噪处理是提取清晰、有效的脉搏信息的关键步骤。在去噪过程中,由于脉搏信号具有非平稳特性且污染噪声分布范围大,限制了传统线性滤波器的使用。这里利用小波变换的多层分解将脉搏信号分成具有不同尺度的小波系数,然后根据小波分解的底层低频系数和各层高频系数进行一维小波重构,在重构的过程中可以剔除与噪声相关的系数,保留信号中的有用成分。 【关键词】小波分解;小波重构;脉搏;降噪 【中图分类号】TP274.2 【文献标识码】A 【文章编号】1002-0802(2011)05-0151-03 Pulse Signal Noise Reduction based on Wavelet Transform WANG Zhi, YIN Kui-xi, ZHAO Hua, ZHANG Qian-ru (School of Physical Science and Technology, Nanjing Normal University, Nanjing Jiangsu 210046, China) 【Abstract】Pulse wave is complex, and its measurement is easily impacted by noise, so the reduction of pulse wave noise is a very important process. Pulse wave is not a smooth process and spreads a big noise pollution, and traditional filter is limited in reducing pulse wave noise. With wavelet decomposition, pulse wave can be decomposed into various dimensions of the coefficients and recomposed according to the low-frequency coefficient of the bottom and the high-frequency coefficients of various layers. In the process of pulse wave recomposition, the coefficients related to noise could be rejected while the valuable information in the signal maintained. 【Key words】wavelet decomposition; wavelet recomposition; pulse; noise reduction 0 引言 脉搏是由于心脏射血活动引起的一种血液和血管壁振荡。这种振荡在主动脉的根部形成,沿着动脉树迅速向外周血管传播,从而形成各部分脉搏的表现波[1-3]。所以脉搏波的波形和幅度包含了心脏和血管情况的重要生理信息。大量的研究发现高血压和动脉粥硬化的初期,血压、血流、血管阻力、血管弹性等一系列心血管血流参数发生变化并表现在脉搏波的幅值和波形的变化中[4]。通过Matlab拟合健康人体的脉搏波形如下:脉搏波形主要由主波A、反射波B、重搏波C和波谷D组成,如图1所示。 在病理状态下,动脉血管壁的弹性变差或者外界阻力增加,心脏射血形成的前向波会被顺应性较差的外周动脉反射,形成的反射波B的强度和幅度大大增强,这时会出现主波A的幅度低于反射波B的幅度。并且随着反射波的幅度增加,重搏波C的波形幅度减小,会与波谷D逐渐混为一体[5]。 图1 健康人体的脉搏波形 因此脉搏波形可用于心血管疾病的早期追踪以及治疗过程中的疗效观察。通过定期定时的检测人体的脉搏,可以了解血管结构和功能的改变。随着脉搏分析技术的日益成熟,脉搏波形将在临床中得到更广泛的应用。 1 脉搏信号噪声的来源及模拟仿真 1.1 脉搏信号噪声的来源 脉搏信号采集与传输过程如图2所示,脉搏信号在采集、数模转换和无线发送接收过程中,不可避免的受到各种类型的噪声干扰,这些干扰使得得到的脉搏信号的信噪比较低,甚至淹没了脉搏信号。通常脉搏信号中主要包括工频干扰、00.20.4 0.6 0.80204060
第26卷第5期 振动与冲击 JOURNAL OF VIBRATION AND SHOCK
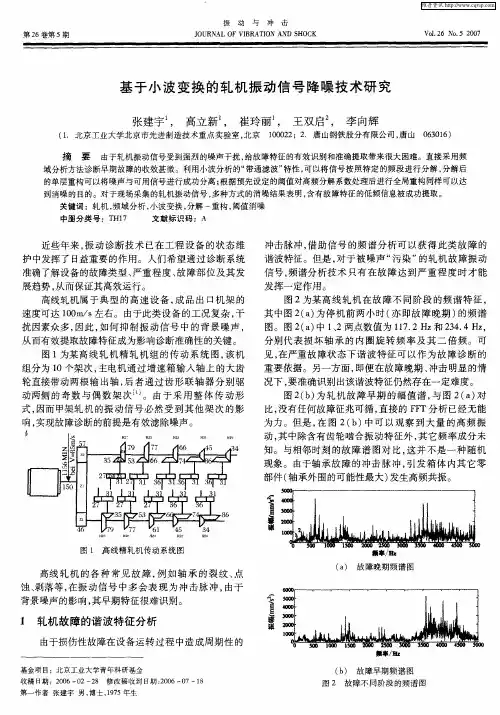
基于小波变换的轧机振动信号降噪技术研究
张建宇 , 高立新 , 崔玲丽 , 王双启 , 李向辉 (1.北京工业大学北京市先进制造技术重点实验室,北京100022;2.唐山钢铁股分有限公司,唐山063016) 摘 要 由于轧机振动信号受到强烈的噪声干扰,给故障特征的有效识别和准确提取带来很大困难。直接采用频 域分析方法诊断早期故障的收效甚微。利用小波分析的“带通滤波”特性,可以将信号按照特定的频段进行分解,分解后 的单层重构可以将噪声与可用信号进行成功分离;根据预先设定的阈值对高频分解系数处理后进行全局重构同样可以达 到消噪的目的。对于现场采集的轧机振动信号,多种方式的消噪结果表明,含有故障特征的低频信息被成功提取。 关键词:轧机,频域分析,小波变换,分解一重构,阈值消噪 中图分类号 TH17 文献标识码:A 近些年来,振动诊断技术已在工程设备的状态维 护中发挥了日益重要的作用。人们希望通过诊断系统 准确了解设备的故障类型、严重程度、故障部位及其发 展趋势,从而保证其高效运行。 高线轧机属于典型的高速设备,成品出口机架的 速度可达100m/s左右。由于此类设备的工况复杂,干 扰因素众多,因此,如何抑制振动信号中的背景噪声, 从而有效提取故障特征成为影响诊断准确性的关键。 图1为某高线轧机精轧机组的传动系统图,该机 组分为10个架次,主电机通过增速箱输入轴上的大齿 轮直接带动两根输出轴,后者通过齿形联轴器分别驱 动两侧的奇数与偶数架次¨J。由于采用整体传动形 式,因而甲架轧机的振动信号必然受到其他架次的影 响,实现故障诊断的前提是有效滤除噪声。
图1高线精轧机传动系统图 高线轧机的各种常见故障,例如轴承的裂纹、点 蚀、剥落等,在振动信号中多会表现为冲击脉冲,由于 背景噪声的影响,其早期特征很难识别。 1 轧机故障的谐波特征分析 由于损伤性故障在设备运转过程中造成周期性的

Computer Engineering and Applications计算机工程与应用
基于小波变换的激光多普勒血流信号处理研究
王萑1,史仪凯1,姚钦 ,耶亚林
WANG Huan 。SHI Yi—kai ,YAO Qin ,YE Ya-lin ,
1.西北工业大学机电学院,西安710072
2.西安通信学院,西安710106 1.Northwestern Polytechnical University,Xi’an 710072,China
2.Xi’an Communication College,Xi’an 710106,China
E—mail:denny_3@163.con
WANG Huan。SHI Yi—kai,YAO Qin,et a1.Research on laser Doppler blood flow signal’S treatment method based on
wavelet transform.Computer Engineering and Applications,2008,44(24):246—248.
Abstract:The Dhotoelectric signal picked—up by laser Doppler blood flow detecting system contains large white Gaussian noise.
To rem0ve this disturbance and pick—up laser Doppler signal,this paper has put forward a processing method based on wavelet
transform.which contained five layer discrete wavelet decomposition,threshold transform,signal de-noising and signal reconstruc-

第26卷第3期 2007年8月 VoI.26 No 3 Aug 2007 78 Journal of Shandong University of Science and Technology 《 证 《 啪《
基于小波变换的心电信号处理研究
公茂法,张晓丽
(山东科技大学信息与电气工程学院,山东青岛266510)
Study on ECG Signals Processing Based on Wavelet Transformation
GONG Mao—fa,ZHANG Xiao一“
(College of Info and Electrical Eng,,SUST,Qingdao,Shandong 266510,China)
Abstract:In this paper,the fundamental theory of wavelet transformation is studied,the characteristics of ECG sig-
nals and its study contents are briefly introduced,and the current research situation of ECG signals processing based
on wavelet transformation at home and abroad are summarized from the following tWO aspects:firstly,noise abate—
ment,the research results of wavelet threshold of noise abatement are highlighted,and the current research situa—
tions are also outlined in terms of extracting fetal ECG from the composite abdominal signals,myopotential noise

Q: Science and TechnOlogy lnnovation Herald 基于小波变换的信号降噪处理 徐斌 (湖北工业大学理学院 湖北武汉 61 0031) 工程技术
摘要:在介绍小波变换的消噪原理和方法的基础上,研究了影响小波变辏降噪效果的两个主要因素:小波基函数和分解尺度。通过模拟 的方法对同一信号分别采用db小波和sym小波进行降噪处理;以及用相同的小波基函数,采用不同的分解层数,对其降噪处理。 关键词.JJ、波变挟 信号降噪 处理 中图分类号:TK4 21+.6 文献标识码:A 文章编号:16 74—098X(201 2)O5(c)一0118-02 1引言 现代科技中的实验观测数据不可避免 的混杂有大量噪声,对实验观测时域信号 进行降噪处理、提取出有用原始信号是非 常必要的。传统傅里叶变换是信号降噪处 理的常用方法,它是把信号波形分解成不 同频率的正弦信号的线性叠加,表现了频 域的局部信息…。但从傅立叶变换的表现 形式来看,它却要求提供信号的全部信 息,时域信号的局部变化会影响频域的全 局改变,反之依然。这样在信号分析中就 面临着时域和频域局部化矛盾_21。小波分 析是近年来发展起来的一门新的数学理 论和方法,它克服了Fourier变换的一些不 足,以其卓越优良的性能在信号分析、特 征提取、数据压缩等很多领域得到了成功 的应用。与傅立叶变换相比,小波变换可 以同时在时域和频域充分突出信号局部 特征 。在实际应用中,信号分析结果的好 坏很大程度上依赖小波基函数、分解层数 和闽值的选择。与傅立叶变换不同,小波 基函数不具有惟一性,不同的小波基函数 波形差别很大。因此,对同一个信号选用 不同的小波基波进行处理所得的结果往 往差别很大,这势必影响到最终的处理结 果。同时,小波变换又是一种在基波不变 的情形下实现分解尺度可变的信号分析 方法,它可在不同尺度下对信号进行分析 处理。基于以上两点,本文通过模拟数据 重点研究了小波基函数与分解尺度的选 择对信号降噪效果的影响。

微电机
基于小波变换的电机信号消噪技术的研究
贺昌权,包广清
(兰州理工大学电气工程与信息工程学院,兰州730050)
摘要:在分析小波变换消噪原理和方法的基础上,针对信噪比较高的信号,进行小波消噪和傅里叶
消噪仿真分析。结果表明,采用小波消噪能达到比较理想的效果。但对于信噪比较低的信号,必须采 取多种方法相结合,才能取得满意的消噪效果。文章提出了将时域平均法和小波软阀值消噪法相结合
和基于相关性分析与小波变换相结合两种方案消噪。通过对这两种方案进行仿真实验,结果表明,这
两种方案可以有效地去除信号中的干扰噪声,提高信号的信噪比,取得良好的降噪效果。
关键词:小波变换;时域平均;软阀值;分析;消噪 中图分类号:TP202+2:TM306 文献标志码:A 文章编号:1001—6848(2010)O3—0028—04
Research on Motor Signal Denoising Technology Based
On Wavelet Transform
HE Chang—quan,BAO Guang—qing
(College of Electrical and Information Engineering,Lanzhou University of Technology,Lanzhou 730050,China) Abstract:Based on the analysis of the de—noising principles and methods of the wavelet transform, when the signal・to-noise ratio(SNR)of a signal is high,wavelet transform is proved to be an effective method by the simulation analysis after comparing with the wavelet transform and fourier transform in re— gard signal denoising.But when the SNR is low,it’S must be adopted a combined method with an excel- lent result.Two combined methods were suggested to reduce the noise in this paper.The combination of time domain average and wavelet soft—thresholding,the correlation analysis and wavelet transform as wel1.The results show that the noise can be reduced effectively by bh simulation and experiments. Key Words:Wavelet transform;Time domain average;Soft—thresholding;Analysis;De—noising

小波包变换在金属磁记忆信号处理中的应用研究 123
文章编号:1006—1355(2010)03-0123-03
小波包变换在金属磁记忆信号处理中的应用研究
张西勇,张永祥,明廷涛
(海军工程大学,武汉430033)
摘要:金属磁记忆技术是对金属部件进行早期损伤检测行之有效的方法.针对磁记忆信号中存在干扰磁 场,不利于应力集中区特征信号的识别的问题,运用小波包分解重构的滤波方法。小波包将信号分解到各个不同 的频段,截取感兴趣的频段,再重构信号,达到降低干扰信号的目的。仿真分析验证了该方法的可行性。通过对实 测磁记忆信号进行小波包分解重构,使得应力集中区的特征更易识别,取得了较好的效果,降低了误判的几率。 关键词:振动与波;金属磁记忆;小波包;滤波 中图分类号:TG 115.28文献标识码:A D0I编码:10.3969/j.issn.1006—1355.2010.03.032
Application of Wavelet Packet Transform in
Metal Magnetic Memory Signal Processing
ZHANG Xi一 ,ZHANG 一xiang,MING 一tao
(Naval University of Engineering,Wuhan 430033,China)
Abstract:The metal magnetic memory technique is very effective in early damage detection for met—
al pans.However,information of disturbing magnetic fields also exists in the magnetic memory signals SO
that the characteristic signals in the stress concentration area can not be recognized easily.This paper puts forward a new filtering method based on wavelet packet decomposition and reconstruction.Wavelet

2013年第17期 0高校讲:L20 科技信息
小波变换在信号降噪处理中的应用
别亦男许文慧余兵杰吴高伟徐斌 (湖北工业大学理学院,湖北武汉430068)
【摘要】本文在介绍小波变换的消噪原理和方法的基础上,研究了影响小波变换降噪效果的两个主要因素:小波基函数和阁值。通过模拟 的方法对同一信号分别采用db小波和sym小波进行降噪处理;以及用相同的小波基函数,采用不同的阈值,对其降噪处理。 【关键词】IJ、波变换;信号降噪;信号处理
0引言 傅里叶(Fourier1变换是传统的信号分析方法。在信号降噪方面。傅 里叶变换是将时域混合信号转换成不同频率的频域信号.去除掉高频 噪声成分.保留低频成分有用信号.然后再对低频信号做逆变换恢复 原始信号 这样虽然能去掉高频噪声.但同时也丢失了有用信号中的 高频信息。产生了高频失真。傅里叶变换使用的是一种全局的变换,不 能很好的表述信号的局部信息 小波变换是在傅里叶变换的基础上的 发展起来的.它避免了信号中时域的瞬间变化不能反映到频域的缺 陷.在去除掉高频噪声的同时可以很好的保留了信号的高频成分 小 波分析具有多分辨率分析的特点.在时域和频域都有描述信号局部信 息。由于小波变换的良好性质.使得小波变换广泛地应用在信号处理 和故障诊断等领域。另外小波变换在形式和取法上的多样性增加了人 们处理问题的灵活性.使之在信号降噪方面具有傅立叶变换所不可比 拟的优点.小波变换把时域与频域联系起来.通过频域信息来研究时 域特征 将信号分解成一个个相互正交小波函数的线性组合.可以表示信 号的重要特征,但这并不是小波分析的全部,小波分析的另一个重要 的方面就是在分析,比较,处理小波系数后,根据新得到的系数取重构 信号。 2分析与结果讨论 对同一染噪信号选用不同的小波基函数和不同的阈值进行处理 一般会得到差别很大的结果。对于这个问题,下面模拟出一加噪信号, 分别采用不同小波基函数和不同阈值进行降噪后的结果。

第33卷第31期 ・6・ 2 0 0 7年1 1月 山 西 建 筑 SHANXI ARCHITECrURE V01.33No.31 Nov.2007
文章编号:1009.6825(2007)31.0006.02
小波变换用于磁记忆信号降噪技术研究*
张起欣张世富
摘要:介绍了利用小波变换对获取的磁记忆检测信号进行去噪处理的三种方法,指出基于小波变换的非线性方法能够
获得较理想的处理效果,详细介绍了基于该方法的信号处理原理,并重点探讨了影响去噪效果的三项因素,以推广该法
的广泛使用。
关键词:小波变换,信号处理,去噪方法
中图分类号:TP391 文献标识码:A
由于检测仪器本身和外界环境的干扰,获取的金属磁记忆信
号通常有一些附加的噪声叠加在信号上,使信号本身产生畸变,
给信号识别和分析工作带来困难,因此,利用适当的信号处理技
术,将有用信号有效地分离出来是极为关键的。传统的基于傅立
叶变换的消噪方法,只能用于信号和噪声频带重叠部分非常小或
者两者完全分开的情况下,然后通过滤波的方法将信号和噪声分
开,而实际获取的磁记忆信号谱和噪声是任意重叠的,显然使用
傅立叶方法不能达到有效的去噪效果。相比之下,小波变换具有
良好的自动对焦功能,能有效地区分有用信号和噪声,而且小波
变换是线性变换,变换后的信号特征不会发生畸变,同时可以将
突变的信号通过小波变换明显地反映出来,能够达到有效的信号
分离和识别效果。
1 基于小波变换的信号去噪方法
1.1基于模极大值的去噪方法
许多信号都很难只根据原始观察数据来做出解释,总是要提
取信号的某些特征来描述它。提取什么样的特征要根据信号的
分析目的而定。信号的过零点、极值点以及信号的急剧变化等常
常是分析的关键之处。由于小波的能量聚焦属性适合于对信号
瞬态信息的局部分析,因此找出信号的小波变换的过零点、极值 点与信号本身的过零点、极值点的对应关系,就能实现瞬态信息
的位置和相对幅度的判定。由于过零点易受噪声干扰,所以通常
科技资讯
科技资讯SIN&TNOLOGYINFORMTION2008NO.27SCIENCE&TECHNOLOGYINFORMATION学术论坛在过去,我们曾用短时傅立叶变换(SFFT)在频域内对语音信号进行分析去噪,但它有一定的局限性。小波变换是传统傅立叶变换的继承和发展。由于小波的多分辨率分析具有良好的空间域和频率域局部化特性,对高频采用逐渐精细的时域或空域步长,可以聚焦分析对象的任意细节,因此特别适合于非平稳信源的处理,已经成为应用于语音信号处理的一种新手段。1语音信号去噪问题描述由于语音信号可以被分为浊音段和清音段两部分,而这两部分又有很大区别;浊音呈现出准周期性,其周期为该段的基因周期,且含有较多的低频成分。清音的信号波形类似于白噪声,与浊音相比,频率较高且无周期性。若语音中参入了含高频成分的噪声,对浊音和清音段应采用不同的阈值方案,才能获得最佳的去噪效果。因此,在阈值处理之前,必须把清音段识别分割处理,然后对浊音和清音段应采用不同的阈值处理方法。阈值去噪的原理就是将小波变换后的小波系数低于阈值的部分置零,从而去除噪声,从原则上讲,阈值去噪时希望尽可能地将噪声对应的小波系数都置零,同时尽量保留信号对应的小波系数,其中最关键的问题就是如何有效的选定合适的阈值。下来我们就来研究一下几种阈值选取规则。2阈值的选取规则①通用阈值(sqtwolog规则)设含噪信号f(t)在尺度1—j(1
2008年6月 噪声与振动控制 第3期 文章编号:1006—1355(2008)03—0074—04
小波降噪在信号基于EMD的Hilbert 变换中的应用
徐仁林,安伟 (江南大学机械工程学院,江苏无锡214122)
摘要:提出用小波降噪后再用经验模态分解(EMD)对信号进行分析,利用小波包对信号分解重构,去除噪声 干扰信号,然后再对信号进行EMD分解。该方法减少噪声对EMD分解的干扰,从而减少由于分解无用的噪声信 号引入的边界效应误差和分解层数,提高EMD分解的准确性和时效性,使EMD算法在信号的分析中更具实用性。 关键词:振动与波;EMD;小波变换;边缘效应 中图分类号:TP206 文献标识码:A Wavelet Denoise Application in the Signal Hilbert Transform Based on EMD XU Ren—lin,AN Wei (School of Mechanical Engineering,Jiangnan University,Wuxi Jiangsu 214122,China) Abstract:To analyse signal based on empirical mode decomposition(EMD)after wavelet denoise is proposed.This method can decrease unnecessary noise influence upon EMD,reduce the edge effects of EMD and decomposition layers of signals,improve the accuracy and time effect of EMD.It makes this al— gorithm more practica1. Key words:vibration and wave;EMD;wavelet transfer;edge effect 对非平稳信号运用传统的傅立叶变换分析的结 果是用谐波线性相加来模拟非平稳信号的瞬时特 性,不能从根本上获得非平稳信号的瞬时特性。 Hilbert变换是提取信号瞬时参数的有效手段,但该 方法要求被分析信号是一单频率成分或窄带信号, 这就限制了Hilbert变换的应用范围。1998年美国 国家宇航局的Norden.E.Huang首先提出了希尔伯 特黄变换(HHT)¨J。该方法是对一列时间序列数 据进行经验模态分解(EMD),分解成若干个IMF信 号(Intrinsic mode function),然后对各个IMF分别做 希尔伯特变换的信号处理方法。该方法的分析的好 坏很大程度上取决于EMD分解的质量,但是EMD 分解中是采用三次样条插值来获取信号的瞬时平 均,在分解过程中引入了边缘效应 J,有的情况下, 这种边缘效应会严重影响整个信号的分析。目前人 们不断在探索研究减少边缘效应的方法,本文提出 先对信号进行小波去噪处理,减少EMD分解的次 数,以减少多次分解带来的端点效应累积误差。
第3期 2013年3月 机械设计与制造
Machinery Design&Manufacture 81
基于小波变换的齿轮箱振动信号降噪处理
李浩,董辛曼,陈宏,张继兴
(郑州大学振动工程研究所,河南郑州450001)
摘要:应用了小波变换理论和小波降噪的原理,对齿轮箱的振动信号进行了小波降噪处理,有效的从含有噪声的齿轮
箱振动信号中提取出该信号更加准确和真实的故障特征,从而为提高齿轮箱故障诊断的准确性以及检测齿轮箱的早期
微弱故障信号提供了重要的参考价值。通过对仿真信号的降噪处理,然后进行F丌变换,并且和没经过信号降噪处理就
进行FFT变换的对比,显示了小波降噪的优越性。最后通过对齿轮箱的实际振动信号的降噪处理,进一步表明了小波降
噪在消除噪声干扰方面有效性。
关键词:小波分析;小波降噪;傅里叶变换;故障诊断
中图分类号:TH16;TP29 文献标识码:A 文章编号:1001—3997(2013)03—0081—03
De-Noising Study of Gearbox Vibration Signal Based on Wavelet Analysis
LI Hao,DONG Xin—min,CHEN Hong,ZHANG Ji-xing
(Research Institute of Vibration Engineering,Zhengzhou University,He’nan Zhengzhou 450001,China)
Abstract:The theory ofwavelet transform and the principle ofwavelet de—noising ave used to carry out the wavelet de-noising
r the vibration signals ofgearbox and extractfeaturefrom noise signals,which is to improve the accuracy offault diagnosis
基于小波变换的信号降噪研究
摘要:本文分析了通信系统信号处理中噪声的小波分析特性,用一维小波对含有噪声的信号进行了分析和研究,提出了基于小波分析理论对于高频信号和高频噪声干扰相混叠的信号中小波变换用于对含有噪声信号进行的小波分解仿真实验。利用小波变换对含噪信号进行小波分解,实现了信号的降噪处理。
关键词:小波分析 降噪 MATLAB
1 引言
在这个科技飞速发展,信息传递日益方便快捷的时代。信息资源中的信号应用日益广泛,信号的结构越来越复杂,为了更加清楚的分析和研究实际工程中信号的有用信息,对信号进行消噪处理是至关重要的,而且在现实生活和工作中,噪声无处不在,在许多领域中,如天文、医学图像和计算机视觉方面收集到的数据常常是含有噪声的。噪声可能来自获取数据的过程,也可能来自环境影响。在工程实际测试得到的信号中,由于种种原因,总会存在噪声,噪声的存在往往会掩盖信号本身所要表现的信息,所以在根据测试信号对设备进行故障诊断时,一般首先要对信号进行消噪处理,消噪的主要基础就是噪声和信号的频率特征不同。
小波分析是近年来发展起来的一种新的信号处理工具,这种方法源于傅立叶分析,小波(wavelet),即小区域的波,仅仅在非常有限的一段区间有非零值,而不是像正弦波和余弦波那样无始无终[4]。小波可以沿时间轴前后平移,也可按比例伸展和压缩以获取低频和高频小波,构造好的小波函数可以用于滤波或压缩信号,从而可以提取出已含噪声信号中的有用信号。
2 小波分析基本理论
设Ψ(t)∈L 2( R) ( L 2( R) 表示平方可积的实数空间,即能量有限的信号空间) , 其傅立叶变换为Ψ(t)。当Ψ(t)满足条件[4,7]:
2()RtdwwC (1)
时,我们称Ψ(t)为一个基本小波或母小波,将母小波函数Ψ(t)经伸缩和平移后,就可以得到一个小波序列:
,1()()abtbtaa ,,0abRa (2)
第35卷第6期
、『01.35 NO.6 河北工业大学学报
JOURNAL OF HEBEI UNIVERSITY OF TECHNOLOGY 2006年l2月
December 2006
文章编号:1007.2373(2006)06—0030.04
基于小波变换的脑电信号降噪方法的研究
高振斌,贾 希,贾志成
(河北工业大学信息工程学院,天津300130)
摘要通过小波变换方法对左右手运动想象脑电信号进行降噪.在对各种小波闽值降噪方法(固定阈值形式
Sqtwolog及硬闽值法;使用Birge-Massart惩罚函数的阈值形式及软阈值法;使用分层阈值及改进的阈值法)的
讨论比较之后,给出一种改进方案.然后对不同降噪方法处理后的脑电信号用概率神经网络进行分类.最后对分
类效果进行比较,证明了此改进方案具有可行性.
关键词 小波变换;脑电信号;降噪;概率神经网络;闽值
中图分类号TN911.4 文献标识码A
EEG Signal Denoising Based on Wavelet Transform
GAO Zhen.bin,JIA Xi,JIA Zhi.cheng
【School ofInformation Engineering,Hebei University ofTechnology,Tianjin 300130。China)
Abstract In this paper the use ofwavelet transformation as a preprocessing tool for EEG signal de-noising is examined
and a novel threshold iS proposed for wavelet threshold de.noising method.First,hard threshold.soft threshold and the
信号处理中基于小波变换的信号降噪技术研究
随着科技的不断进步,数字化社会的到来,人们越来越依赖于数字信号处理,其中信号降噪技术则是数字信号处理中一个比较重要的技术领域。信号降噪技术的目的是消除对信号进行采集和传输过程中所引入的噪音,提高信息传输的质量和可靠性,从而实现对信号的精确定量分析和处理。在信号降噪技术的研究中,基于小波变换的信号降噪技术被广泛应用于各个领域。本文将对小波变换原理以及其在信号降噪中的应用进行探讨。
一、小波变换原理
小波变换(Wavelet Transform,WT)是信号处理领域中一种基于时间尺度的信号分析方法,其基本原理是将原始信号分解成多个不同比例和位置的小波函数,并得到每个小波函数的系数。小波函数具有良好的时频局部性质,能够在时域和频域上对信号进行局部描述,因此小波变换在信号分析以及信号降噪处理中得到广泛应用。
小波变换的基本公式为:
$$\tilde{f}(a,b)=\frac{1}{\sqrt{|a|}}\int_{-\infty}^{+\infty}f(t)\psi(\frac{t-b}{a})dt$$
其中,$\psi$为小波基函数,$a$和$ b$分别为比例因子和平移因子。对于原始信号 $f(t)$,可以通过不同尺度和位置的小波函数来描述,将信号变形表示为基于小波基函数的控制系数和基函数的线性组合,即:
$$f(t)=\sum_{j=0}^{J-1}\sum_{k}\tilde{f_{j,k}}\psi_{j,k}(t)+\Delta_j (t)$$ 其中,$J$为分解层数,$\psi_{j,k}$为小波基函数,$k$为平移量,$\tilde{f_{j,k}}$为小波系数,$\Delta_j$为分解残差。基于小波分解后的信号,可以对其进行多尺度分析和处理。
二、小波变换在信号降噪中的应用
小波变换作为一种非线性的信号分析方法,能够在时域和频域上进行综合性的信号分析,具有较强的抗噪能力。因此,小波变换在信号降噪处理中得到广泛应用。
(一)小波阈值降噪法
小波阈值降噪法(Wavelet-Thresholding)是目前最常用的信号降噪方法之一。其基本原理是对基于小波分解的信号进行滤波,去除小于预设阈值的小波系数,从而达到信噪比的提高和信号还原的目的。
小波阈值降噪算法流程如下:
(1)对输入信号进行小波变换,并得到小波系数。
(2)对小波系数进行阈值处理,使小于阈值的小波系数清零。
(3)进行逆小波变换,得到处理后的信号。
其中阈值的选取是信号降噪效果的关键,常用的阈值选取方法有设定固定阈值、固定阈值与带宽无关(Universal threshold)和基于小波系数分布的自适应阈值选取方法等。
(二)小波包变换法
小波包变换(Wavelet Packet Transform,WPT)相较于小波变换来说,则是对信号进行更细致的分解和信息提取。小波包变换将小波基函数的分解进一步扩展,得到更多尺度和位置的基函数,从而提高了信号的分辨率和特征提取效率,可以更好的实现对信号的精细化分析和降噪处理。 小波包变换与小波变换的区别在于小波包变换在每层分解时,是将当前的基函数分解成两个子基函数,得到更多的分解分支,从而进行更细致的信号分解和处理,使得小波包变换的精度和处理效率均得到提高。
三、总结
小波变换作为数字信号处理领域中一种基于时间尺度的分析方法,在信号降噪处理中发挥着重要的作用。小波变换能够在时域和频域上对信号进行综合性分析,具有较强的抗噪能力,成为数字信号处理中信号降噪处理的主要手段。随着数字信号处理技术的不断发展,小波变换在信号处理中的应用也将更加广泛和深入,对于信息处理和自动化控制领域的发展具有重大意义。