电磁场的边界条件

电磁场的边界条件姓名：学号：专业：班级：提交日期：桑薇薇0990*******通信工程电工 1401 2016.5.28成绩：电磁场的边界条件1.引言2.边界条件分类3.边界条件的作用4.结束语5.参考文献1. 引言在两种不同媒质的分界面上，场矢量E,D,B,H 各自满足的关系，称为电磁场的边界条件。

在实际的电磁场问题中， 总会遇到两种不同媒质的分界面 （例如： 空气与玻璃的分界面、导体与空气的分界面等） ，边界条件在处理电磁场问题中占据十分重要的地位。

2. 边界条件分类1、电场法向分量的边界条件如图 3.9 所示的两种媒质的分界面， 第一种媒质的介电常数、磁导率和电导率分别为1，1和1，第二种媒质的介电常数、磁导率和电导率分别为2，2和 2 。

在这两种媒质分界面上取一个小的柱形闭合面，图 3.9 电场法向分量的边界条件如图 3.9 所示，其高h 为无限小量，上下底面与分界面平行，并分别在分界面两侧， 且底面积 S 非常小，可以认为在 S 上的电位vv v移矢量 D和面电荷密度S是均匀的。

n 1 n 2分别为上下底面的外法线单位矢量， ， 在柱形闭合面上应用电场的高斯定律? v vv v S v vSSD gdS n 1 gD 1 n 2 gD 2 SS故v v v vn 1gD 1 n 2 gD 2S(3.48a)vv vvv若规定 n 为从媒质Ⅱ指向媒质Ⅰ为正方向，则 n 1 n ，n2n，式 (3.48a) 可写为v vvng(D 1D 2 )S(3.48b)或D1nD2nS(3.48c)式 (3.48 ) 称为电场法向分量的边界条件。

vvv 因为 DE ，所以式 (3.48) 可以用 E 的法向分量表示v v v v1n 1gE 12 n 2 gE 2S(3.49a)或1E 1n2 E 2nS(3.49b)若两种媒质均为理想介质时， 除非特意放置， 一般在分界面上不存在自由面电荷，即S，所以电场法向分量的边界条件变为D1nD2n(3.50a)或1E1n 2E2 n(3.50b)若媒质Ⅰ为理想介质，媒质Ⅱ为理想导体时， 导体内部电场为零，即E2，D2，在导体表面存在自由面电荷密度，则式(3.48) 变为v vn 1 gD 1 D 1nS(3.51a)或1E1ns(3.51b)2 、电场切向分量的边界条件在两种媒质分界面上取一小的矩形闭合回路 abcd ，如图 3.10 所示，该回路短边 h 为无限小量，其两个长边为l ，且平行于分界面，并分别在分界面两侧。

电磁场理论中的边界条件与边值问题解析研究引言：电磁场理论是物理学中的重要分支，广泛应用于电磁波传播、电路分析等领域。

其中，边界条件和边值问题是电磁场理论中的核心概念，对于解析研究电磁场的性质和行为具有重要意义。

本文将就电磁场理论中的边界条件与边值问题进行探讨。

一、边界条件的概念与分类边界条件是指电磁场在两个不同介质的交界面上需要满足的条件。

根据边界条件的不同形式，可以将其分为电场边界条件和磁场边界条件。

1. 电场边界条件电场边界条件是指电场在介质交界面上满足的条件。

其中，最基本的电场边界条件是法向分量的连续性条件，即电场的法向分量在两个介质交界面上的值相等。

此外，还有切向分量的连续性条件和切向分量的不连续性条件等。

2. 磁场边界条件磁场边界条件是指磁场在介质交界面上满足的条件。

与电场边界条件类似，磁场的法向分量在两个介质交界面上的值相等，即磁场的法向分量是连续的。

此外，磁场的切向分量也需要满足一定的条件，如切向分量的连续性条件和切向分量的不连续性条件等。

二、边值问题的解析研究边值问题是指在给定边界条件的情况下，求解电磁场的数学模型。

在电磁场理论中，边值问题的解析研究是十分重要的，可以帮助我们深入理解电磁场的行为和性质。

1. 边值问题的数学模型边值问题的数学模型是由麦克斯韦方程组和边界条件共同构成的。

通过求解这个数学模型，我们可以得到电磁场的解析解，从而揭示电磁场的基本特性。

2. 边值问题的解析方法边值问题的解析方法主要有分离变量法、格林函数法和辐射条件法等。

其中，分离变量法是应用最广泛的一种方法，它将电磁场分解为多个独立的分量，并通过求解每个分量的方程来得到整个电磁场的解析解。

格林函数法则是通过引入格林函数，将边值问题转化为积分方程的形式，从而求解电磁场的解析解。

辐射条件法则是在边界条件已知的情况下，通过辐射条件来求解电磁场的解析解。

三、边界条件与边值问题的应用边界条件与边值问题在电磁场理论的应用中起着重要的作用，可以帮助我们研究电磁波的传播、电路的分析等问题。

1)麦克斯韦方程组可以应用于任何连续的介质内部。

2)在两种介质界面上，介质性质有突变，电磁场也会突变。

3)分界面两边按照某种规律突变，称这种突变关系为电磁场的边值关系或边界条件。

4)推导边界条件的依据是麦克斯韦方程组的积分形式。

一、边界条件的一般形式 1、B 的边界条件:2、D 的边界条件结论：电位移矢量 在不同媒质分界面两侧的法向分量不连续，其差值等于分界面上自由电荷面密度。

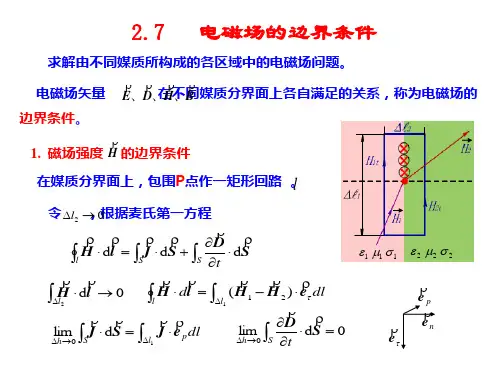
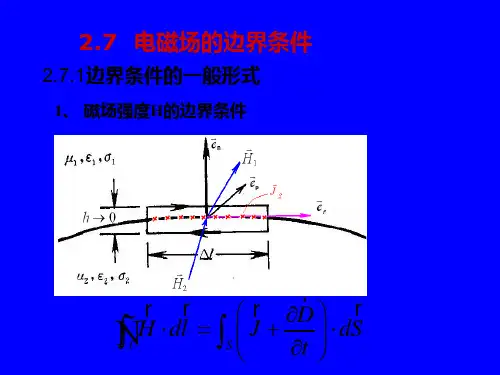
3. H 的边界条件h∆→n-2B11220B dS B dS ⇒⋅+⋅=120B n B n ⇒⋅-⋅=210lim S h D H l H l J sl t→∂⇒⋅-⋅=⋅-⋅∂2t t SH H J⇒-=12()S n H H J⇒⨯-=21,S H l H l J s l n s⇒⋅-⋅=⋅=⨯()C sD H dl J dSt∂=+∂⎰⎰μ1μ2Hn1Hh →ls12()S n H H J⨯-=12()D D n σ-⋅=⇒2εε2D 1D n S∆n-n12n n D D σ⇔-=0S B dS ⋅=⎰12()0n B B ⋅-=21n nB B⇒=SD dS q =⋅⎰⇒⇒式中： S J 为介质分界面上的自由电流面密度。

结论：磁场强度 D 在不同媒质分界面两侧的切向分量不连续，其差值等于分界面上的电流面密度S J4.E 的边界条件结论：电场强度E 在不同每只分界面两侧的切向分量连续。

二、理想介质是指电导率为零的媒质，0=γ2)在理想介质内部和表面上，不存在自由电荷和自由电流。

结论：在理想介质分界面上，E 、H 矢量切向连续； 在理想介质分界面上，B 、D 矢量法向连续。

三、理想导体表面上的边界条件1)理想介质是指电导率为无穷大的导体，12t t E E⇒=12()0n E E ⇒⨯-= 2ε1ε2En1E2θl sl S BE dl d St∂⋅=-⋅∂⎰⎰12()0n E E ⨯-=⇒12t t EE=0s J =0ρ=12t t H H =⇒12n n D D=12()0n D D ⋅-=⇒12()0n B B ⋅-=12n n B B=⇒12()0n H H ⨯-=2)电场强度和磁感应强度均为零。

电磁场三类边界条件电磁场三类边界条件电磁场的边界条件是指在介质边界处，电场和磁场的变化情况。

根据边界条件的不同，可以将其分为三类：第一类边界条件、第二类边界条件和第三类边界条件。

下面将详细介绍这三类边界条件。

一、第一类边界条件第一类边界条件也称为零法向电场和零切向磁场边界条件。

它是指在介质表面上，法向于表面的电场强度和切向于表面的磁感应强度均为零。

1. 零法向电场在介质表面上，由于介质内部和外部存在不同的电荷分布情况，因此会产生一个法向于表面方向的电场。

而当这个电场穿过介质表面时，就会发生反射和折射现象。

为了描述这种现象，我们需要引入一个重要的物理量——法向于表面方向上的电通量密度。

根据高斯定理可知，在任意一个闭合曲面内部，通过该曲面的总电通量等于该曲面所包围空间内部所有自由电荷之代数和。

因此，在介质表面附近，我们可以将其看作一个微小的闭合曲面。

则在该曲面上的电通量密度可以表示为：$$\vec{D_1}\cdot\vec{n}=\rho_s$$其中，$\vec{D_1}$表示介质1内部的电位移矢量，$\vec{n}$表示介质表面法向矢量，$\rho_s$表示表面自由电荷密度。

当我们将这个式子应用于介质表面时，可以得到：$$D_{1n}=\rho_s$$其中，$D_{1n}$表示介质1内部法向于表面方向上的电场强度。

由于介质表面上不存在自由电荷，因此$\rho_s=0$。

因此，在第一类边界条件下，法向于介质表面方向上的电场强度为零。

2. 零切向磁场在介质表面上，由于介质内部和外部存在不同的磁场分布情况，因此会产生一个切向于表面方向的磁感应强度。

而当这个磁场穿过介质表面时，就会发生反射和折射现象。

为了描述这种现象，我们需要引入一个重要的物理量——切向于表面方向上的磁通量密度。

根据安培环路定理可知，在任意一个闭合回路上，通过该回路的总磁通量等于该回路所包围空间内部所有电流之代数和。

因此，在介质表面附近，我们可以将其看作一个微小的闭合回路。

电磁场边界条件的推导
电磁场边界条件的推导
1、电荷边界条件
电荷边界条件指的是在一个给定时刻，电场空间分布的边界处，电荷的分布应符合一定的规律，常表示为
E（r,t）=ρ（r,t）/ε
其中，E（r,t）为电场在位置r处和时刻t时的电场强度，ρ（r,t）为该位置处以及时刻t时的电荷密度，ε为真空介质的介电常数。

2、磁荷边界条件
磁荷边界条件指的是在一个给定时刻，磁场空间分布的边界处，磁荷的分布应符合一定的规律，常表示为
B（r,t）=μ㎡（r,t）
其中，B（r,t）为磁场在位置r处和时刻t时的磁场强度，μ㎡（r,t）为该位置处以及时刻t时的磁荷密度，μ为真空介质的磁导率。

3、电流边界条件
电流边界条件指的是在一个给定时刻，电流空间分布的边界处，电流密度的分布应符合一定的规律，常表示为
j（r,t）=σ（r,t）/ε
其中，j（r,t）为电流密度在位置r处和时刻t时的电流密度，σ（r,t）为该位置处以及时刻t时的电荷密度，ε为真空介质的介电常数。

4、磁流边界条件
磁流边界条件指的是在一个给定时刻，磁流空间分布的边界处，磁流密度的分布应符合一定的规律，常表示为
m（r,t）=μφ（r,t）
其中，m（r,t）为磁流密度在位置r处和时刻t时的磁流密度，φ（r,t）为该位置处以及时刻t时的磁荷密度，μ为真空介质的磁导率。

2.9 电磁场的边界条件自强●弘毅●求是●拓新实际电磁场问题都是在一定的空间和时间范围内发 生的，它有起始状态（静态电磁场例外）和边界状 态。

即使是无界空间中的电磁场问题，该无界空间也可 能是由多种不同介质组成的，不同介质的交界面和 无穷远界面上电磁场构成了边界条件。

边界条件： 即电磁场在不同介质的边界面上服从的条件，也可 以理解为界面两侧相邻点在无限趋近时所要满足的 约束条件。

边界条件是完整的表示需要导出界面两 侧相邻点电磁场矢量所满足的约束关系。

由于在分界面两侧介质的特性参数发生突变，场在界 面两侧也发生突变。

所以Maxwell方程组的微分形式 在分界面两侧失去意义（因为微分方程要求场量连续 可微）。

而积分方程则不要求电磁场量连续，从积分 形式的麦克斯韦方程组出发，导出电磁场的边界条件把积分Maxwell方程组应用到图所表示的两媒质交界 面的扁平圆盘。

根据Gauss定理，让h→0，场在扁平 圆盘壁上的通量为零，得到：    n ˆ ˆ D  ds  D  (  n )  S  D  ( n  S ) D 1 2 S 2 ( D2 n  D1n )S   s Sˆ  s (D2  D1 )  n ˆ 0 (B 2  B1 )  nhr2D1  r1在介质分界面两侧，选取如图所示的积环路，应用安培环路积 分公式：        D H  dl  H   l  H  (   l )  ( H  H )  t  l   ( J  )  ds 1 2 1 2 l S t   t  N n   ( H 2  H1 )  t  ( H 2  H1 )  ( N  n )  ˆ  J N ˆ ˆ  (H  H )  N n2 1 sˆ  ( H 2  H1 )  J s nˆ  ( E 2  E1 )  0 nD   0 E  P, B   0 H  Mn  ( P 2  P1 )    f  n  (M 2  M 1 )  J mˆ  s (D 2  D1 )  nn  ( H 2  H1 )  J s  n  (B 2 B1 )  0 ( J f  J m )n  ( E2  E1 )  ( f   p ) /  0①任何分界面上E的切向分量是连续的 ②在分界面上有面电荷(在理想导体表面上)时，D的法向分量不 连续，其差等于面电荷密度；否则，D的法向分量是连续的 ③在分界面上若存在面电流(仅在理想导体表面上存在)，H的切 向分量 不连续 ，其差等于面电流密度；否则，H的切向分量是 连续的 ④任何分界面上B的法向分量是连续的理想介质理想介质是指  0，即无欧姆损耗的简单媒质。